Generalized Alternating Direction Method of Multipliers: New Theoretical Insights and Applications

Abstract

Recently, the alternating direction method of multipliers (ADMM) has received intensive attention from a broad spectrum of areas. The generalized ADMM (GADMM) proposed by Eckstein and Bertsekas is an efficient and simple acceleration scheme of ADMM. In this paper, we take a deeper look at the linearized version of GADMM where one of its subproblems is approximated by a linearization strategy. This linearized version is particularly efficient for a number of applications arising from different areas. Theoretically, we show the worst-case 𝒪(1/k) convergence rate measured by the iteration complexity (k represents the iteration counter) in both the ergodic and a nonergodic senses for the linearized version of GADMM. Numerically, we demonstrate the efficiency of this linearized version of GADMM by some rather new and core applications in statistical learning. Code packages in Matlab for these applications are also developed.

1 Introduction

A canonical convex optimization model with a separable objective function and linear constraints is:

$$min\{f_1(\mathbf{x})+f_2(\mathbf{y})\mid \mathbf{Ax}+\mathbf{By}=\mathbf{b},\mathbf{x}\in \mathcal{X},\mathbf{y}\in \mathcal{Y}\},$$ (1)

where A ∈ ℝ^n×n₁, B ∈ ℝ^n×n₂, b ∈ ℝⁿ, and 𝒳 ⊂ ℝ^n₁ and 𝒴 ⊂ ℝ^n₂ are closed convex nonempty sets, f₁ : ℝ^n₁ → ℝ and f₂ : ℝ^n₂ → ℝ are convex but not necessarily smooth functions. Throughout our discussion, the solution set of (1) is assumed to be nonempty, and the matrix B is assumed to have full column rank.

The motivation of discussing the particular model (1) with separable structures is that each function f_i might have its own properties, and we need to explore these properties effectively in algorithmic design in order to develop efficient numerical algorithms. A typical scenario is where one of the functions represents some data-fidelity term, and the other is a certain regularization term —- we can easily find such an application in many areas such as inverse problem, statistical learning and image processing. For example, the famous least absolute shrinkage and selection operator (LASSO) model introduced in [44] is a special case of (1) where f₁ is the ℓ₁-norm term for promoting sparsity, f₂ is a least-squares term multiplied by a trade-off parameter, A = I_n×n, B = −I_n×n, b = 0, 𝒳 = 𝒴 = ℝⁿ.

To solve (1), a benchmark is the alternating direction method of multipliers (ADMM) proposed originally in [24] which is essentially a splitting version of the augmented Lagrangian method in [34,42]. The iterative scheme of ADMM for solving (1) reads as

$$\begin{array}{l}{\mathbf{x}}^{t+1}=\underset{\mathbf{x}\in \mathcal{X}}{\text{argmin}}\left\{f_1(\mathbf{x})-{\mathbf{x}}^T{\mathbf{A}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert \mathbf{Ax}+{\mathbf{By}}^t-\mathbf{b}\Vert }^2\right\},\\ {\mathbf{y}}^{t+1}=\underset{\mathbf{y}\in \mathcal{Y}}{\text{argmin}}\left\{f_2(\mathbf{y})-{\mathbf{y}}^T{\mathbf{B}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert {\mathbf{Ax}}^{t+1}+\mathbf{By}-\mathbf{b}\Vert }^2\right\},\\ {\mathit{\gamma }}^{t+1}={\mathit{\gamma }}^t-\rho ({\mathbf{Ax}}^{t+1}+{\mathbf{By}}^{t+1}-\mathbf{b}),\end{array}$$ (2)

where γ ∈ ℝⁿ is the Lagrangian multiplier; ρ > 0 is a penalty parameter, and ||·|| is the Euclidean 2-norm. An important feature of ADMM is that the functions f₁ and f₂ are treated individually; thus the decomposed subproblems in (2) might be significantly easier than the original problem (1). Recently, the ADMM has received wide attention from a broad spectrum of areas because of its easy implementation and impressive efficiency. We refer to [6,13,23] for excellent review papers for the history and applications of ADMM.

In [21], the ADMM was explained as an application of the well-known Douglas-Rachford splitting method (DRSM) in [36] to the dual of (1); and in [14], the DRSM was further explained as an application of the proximal point algorithm (PPA) in [37]. Therefore, it was suggested in [14] to apply the acceleration scheme in [25] for the PPA to accelerate the original ADMM (2). A generalized ADMM (GADMM for short) was thus proposed:

$$\begin{array}{l}{\mathbf{x}}^{t+1}=\underset{\mathbf{x}\in \mathcal{X}}{\text{argmin}}\left\{f_1(\mathbf{x})-{\mathbf{x}}^T{\mathbf{A}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert \mathbf{Ax}+{\mathbf{By}}^t-\mathbf{b}\Vert }^2\right\},\\ {\mathbf{y}}^{t+1}=\underset{\mathbf{y}\in \mathcal{Y}}{\text{argmin}}\left\{f_2(\mathbf{y})-{\mathbf{y}}^T{\mathbf{B}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert \alpha {\mathbf{Ax}}^{t+1}+(1-\alpha )(\mathbf{b}-{\mathbf{By}}^t)+\mathbf{By}-\mathbf{b}\Vert }^2\right\},\\ {\mathit{\gamma }}^{t+1}={\mathit{\gamma }}^t-\rho (\alpha {\mathbf{Ax}}^{t+1}+(1-\alpha )(\mathbf{b}-{\mathbf{By}}^t)+{\mathbf{By}}^{t+1}-\mathbf{b}),\end{array}$$ (3)

where the parameter α ∈ (0, 2) is a relaxation factor. Obviously, the generalized scheme (3) reduces to the original ADMM scheme (2) when α = 1. Preserving the main advantage of the original ADMM in treating the objective functions f₁ and f₂ individually, the GADMM (3) enjoys the same easiness in implementation while can numerically accelerate (2) with some values of α, e.g., α ∈ (1, 2). We refer to [2,8,12] for empirical studies of the acceleration performance of the GADMM.

It is necessary to discuss how to solve the decomposed subproblems in (2) and (3). We refer to [41] for the ADMM’s generic case where no special property is assumed for the functions f₁ and f₂, and thus the subproblems in (2) must be solved approximately subject to certain inexactness criteria in order to ensure the convergence for inexact versions of the ADMM. For some concrete applications such as those arising in sparse or low-rank optimization models, one function (say, f₁) is nonsmooth but well-structured (More mathematically, the resolvent of ∂f₁ has a closed-form representation), and the other function f₂ is smooth and simple enough so that the y-subproblem is easy (e.g., when f₂ is the least-squares term). For such a case, instead of discussing a generic strategy to solve the x-subproblem in (2) or (3) approximately, we prefer to seek some particular strategies that can take advantage of the speciality of f₁ effectively. More accurately, when f₁ is a special function such as the ℓ₁-norm or nuclear-norm function arising often in applications, we prefer linearizing the quadratic term of the x-subproblem in (2) or (3) so that the linearized x-subproblem has a closed-form solution (amounting to estimating the resolvent of ∂f₁) and thus no inner iteration is required. The efficiency of this linearization strategy for the ADMM has been well illustrated in different literatures, see. e.g. [52] for image reconstruction problems, [48] for the Dantzig Selector model, and [50] for some low-rank optimization models. Inspired by these applications, we thus consider the linearized version of the GADMM (“L-GADMM” for short) where the x-subproblem in (3) is linearized:

$$\begin{array}{l}{\mathbf{x}}^{t+1}=\underset{\mathbf{x}\in \mathcal{X}}{\text{argmin}}\left\{f_1(\mathbf{x})-{\mathbf{x}}^T{\mathbf{A}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert \mathbf{Ax}+{\mathbf{By}}^t-\mathbf{b}\Vert }^2+\frac{1}{2}{\Vert \mathbf{x}-{\mathbf{x}}^t\Vert }_{\mathbf{G}}^2\right\},\\ {\mathbf{y}}^{t+1}=\underset{\mathbf{y}\in \mathcal{Y}}{\text{argmin}}\left\{f_2(\mathbf{y})-{\mathbf{y}}^T{\mathbf{B}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert \alpha {\mathbf{Ax}}^{t+1}+(1-\alpha )(\mathbf{b}-{\mathbf{By}}^t)+\mathbf{By}-\mathbf{b}\Vert }^2\right\},\\ {\mathit{\gamma }}^{t+1}={\mathit{\gamma }}^t-\rho (\alpha {\mathbf{Ax}}^{t+1}+(1-\alpha )(\mathbf{b}-{\mathbf{By}}^t)+{\mathbf{By}}^{t+1}-\mathbf{b}),\end{array}$$ (4)

where G ∈ ℝ^n₁×n₁ is a symmetric positive definite matrix. Note that we use the notation ||x||_G to denote the quantity $\sqrt{{\mathbf{x}}^T\mathbf{Gx}}$. Clearly, if 𝒳 = ℝ^n₁ and we choose G = τI_n1 − ρA^TA with the requirement τ > ρ||A^TA||₂, where ||·||₂ denotes the spectral norm of a matrix, the x-subproblem in (4) reduces to estimating the resolvent of ∂f₁:

$${\mathbf{x}}^{t+1}=\underset{\mathbf{x}\in {ℝ}^{n_1}}{\text{argmin}}\left\{f_1(\mathbf{x})+\frac{\tau }{2}{\Vert \mathbf{x}-\frac{1}{\tau }((\tau {\mathbf{I}}_{n_1}-\rho {\mathbf{A}}^T\mathbf{A}){\mathbf{x}}^t-\rho {\mathbf{A}}^T{\mathbf{By}}^t+{\mathbf{A}}^T{\mathit{\gamma }}^t+\rho {\mathbf{A}}^T\mathbf{b}))\Vert }^2\right\},$$

which has a closed-form solution for some cases such as f₁ = ||x||₁. The scheme (4) thus includes the linearized version of ADMM (see. e.g. [48,50,52]) as a special case with G = τI_n1 − ρA^TA and α = 1.

The convergence analysis of ADMM has appeared in earlier literatures, see. e.g. [22,20,29,30]. Recently, it also becomes popular to estimate ADMM’s worst-case convergence rate measured by the iteration complexity (see e.g. [39,40] for the rationale of measuring the convergence rate of an algorithm by means of its iteration complexity). In [31], a worst-case 𝒪(1/k) convergence rate in the ergodic sense was established for both the original ADMM scheme (2) and its linearized version (i.e., the special case of (4) with α = 1), and then a stronger result in a nonergodic sense was proved in [32]. We also refer to [33] for an extension of the result in [32] to the DRSM for the general problem of finding a zero point of the sum of two maximal monotone operators, [11] for the linear convergence of the ADMM under additional stronger assumptions, and [5,27] for the linear convergence of ADMM for the special case of (1) where both f₁ and f₂ are quadratic functions.

This paper aims at further studying the L-GADMM (4) both theoretically and numerically. Theoretically, we shall establish the worst-case 𝒪 (1/k) convergence rate in both the ergodic and a nonergodic senses for L-GADMM. This is the first worst-case convergence rate for L-GADMM, and it includes the results in [8,32] as special cases. Numerically, we apply the L-GADMM (4) to solve some rather new and core applications arising in statistical learning. The acceleration effectiveness of embedding the linearization technique with the GADMM is thus verified.

The rest of this paper is organized as follows. We summarize some preliminaries which are useful for further analysis in Section 2. Then, we derive the worst-case convergence rate for the L-GADMM (4) in the ergodic and a nonergodic senses in Sections 3 and 4, respectively. In Section 5, we apply the L-GADMM (4) to solve some statistical learning applications and verify its numerical efficiency. Finally, we make some conclusions in Section 6.

2 Preliminaries

First, as well known in the literature (see, e.g. [30,31]), solving (1) is equivalent to solving the following variational inequality (VI) problem: Finding w^* = (x^*, y^*, γ^*) ∈ Ω := 𝒳 × 𝒴 × ℝⁿ such that

$$f(\mathbf{u})-f({\mathbf{u}}^{\ast })+{(\mathbf{w}-{\mathbf{w}}^{\ast })}^{T}F({\mathbf{w}}^{\ast })\ge 0,\forall \mathbf{w}\in \mathit{\Omega },$$ (5)

where f(u) = f₁(x) + f₂(y) and

$$\mathbf{u}=\left(\begin{array}{c}\mathbf{x}\\ \mathbf{y}\end{array}\right),\mathbf{w}=\left(\begin{array}{c}\mathbf{x}\\ \mathbf{y}\\ \mathit{\gamma }\end{array}\right),F(\mathbf{w})=\left(\begin{array}{c}-{\mathbf{A}}^T\mathit{\gamma }\\ -{\mathbf{B}}^T\mathit{\gamma }\\ \mathbf{Ax}+\mathbf{By}-\mathbf{b}\end{array}\right).$$ (6)

We denote by VI(Ω, F, f) the problem (5)–(6). It is easy to see that the mapping F(w) defined in (6) is affine with a skew-symmetric matrix; it is thus monotone:

$${({\mathbf{w}}_1-{\mathbf{w}}_2)}^T(F({\mathbf{w}}_1)-F({\mathbf{w}}_2))\ge 0,\forall {\mathbf{w}}_1,{\mathbf{w}}_2\in \mathcal{X}\times \mathcal{Y}\times {ℝ}^n.$$

This VI reformulation will provide significant convenience for theoretical analysis later. The solution set of (5), denoted by Ω^*, is guaranteed to be nonempty under our nonempty assumption on the solution set of (1).

Then, we define two auxiliary sequences for the convenience of analysis. More specifically, for the sequence {w^t} generated by the L-GADMM (4), let

$${\stackrel{\sim }{\mathbf{w}}}^t=\left(\begin{array}{c}{\stackrel{\sim }{\mathbf{x}}}^t\\ {\stackrel{\sim }{\mathbf{y}}}^t\\ {\stackrel{\sim }{\mathit{\gamma }}}^t\end{array}\right)=\left(\begin{array}{c}{\mathbf{x}}^{t+1}\\ {\mathbf{y}}^{t+1}\\ {\mathit{\gamma }}^t-\rho ({\mathbf{Ax}}^{t+1}+{\mathbf{By}}^t-\mathbf{b})\end{array}\right)\text{and}{\stackrel{\sim }{\mathbf{u}}}^t=\left(\begin{array}{c}{\stackrel{\sim }{\mathbf{x}}}^t\\ {\stackrel{\sim }{\mathbf{y}}}^t\end{array}\right).$$ (7)

Note that, by the definition of γ^t+1 in (4), we get

$${\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}=-\rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})+\rho \alpha ({\mathbf{Ax}}^{t+1}+{\mathbf{By}}^t-\mathbf{b}).$$

Plugging the identities ρ(Ax^t+1 + By^t − b) = γ^t − γ̃^t and y^t+1 = ỹ^t (see (7)) into the above equation, it holds that

$${\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}=-\rho \mathbf{B}({\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t)+\alpha ({\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t).$$ (8)

Then we have

$${\mathbf{w}}^t-{\mathbf{w}}^{t+1}=\mathbf{M}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t),$$ (9)

where M is defined as

$$\mathbf{M}=\left(\begin{array}{ccc}{\mathbf{I}}_{n_1}& 0& 0\\ 0& {\mathbf{I}}_{n_2}& 0\\ 0& -\rho \mathbf{B}& \alpha {\mathbf{I}}_n\end{array}\right).$$ (10)

For notational simplicity, we define two matrices that will be used later in the proofs:

$$\mathbf{H}=\left(\begin{array}{ccc}\mathbf{G}& 0& 0\\ 0& \frac{\rho }{\alpha }{\mathbf{B}}^T\mathbf{B}& \frac{1-\alpha }{\alpha }{\mathbf{B}}^T\\ 0& \frac{1-\alpha }{\alpha }\mathbf{B}& \frac{1}{\alpha \rho }{\mathbf{I}}_n\end{array}\right)\text{and}\mathbf{Q}=\left(\begin{array}{ccc}\mathbf{G}& 0& 0\\ 0& \rho {\mathbf{B}}^T\mathbf{B}& (1-\alpha ){\mathbf{B}}^T\\ 0& -\mathbf{B}& \frac{1}{\rho }{\mathbf{I}}_n\end{array}\right).$$ (11)

It is easy to verify that

$$\mathbf{Q}=\mathbf{HM}.$$ (12)

3 A worst-case 𝒪(1/k) convergence rate in the ergodic sense

In this section, we establish a worst-case 𝒪(1/k) convergence rate in the ergodic sense for the L-GADMM (4). This is a more general result than that in [8] which focuses on the original GADMM (3) without linearization.

We first prove some lemmas. The first lemma is to characterize the accuracy of the vector w̃^t to a solution point of VI(Ω, F, f).

Lemma 1

Let the sequence {w^t} be generated by the L-GADMM (4) and the associated sequence {w̃^t} be defined in (7). Then we have

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\stackrel{\sim }{\mathbf{w}}}^t)\ge {(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{Q}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t),\forall \mathbf{w}\in \mathit{\Omega },$$ (13)

where Q is defined in (11).

Proof

This lemma is proved by deriving the optimality conditions for the minimization subproblems in (4) and performing some algebraic manipulation. By deriving the optimality condition of the x-subproblem of (4), as shown in [31], we have

$$f_1(\mathbf{x})-f_1({\mathbf{x}}^{t+1})+{(\mathbf{x}-{\mathbf{x}}^{t+1})}^T\left(-{\mathbf{A}}^T[{\mathit{\gamma }}^t-\rho ({\mathbf{Ax}}^{t+1}+{\mathbf{By}}^t-\mathbf{b})]+\mathbf{G}({\mathbf{x}}^{t+1}-{\mathbf{x}}^t)\right)\ge 0,\forall \mathbf{x}\in \mathcal{X}.$$ (14)

Using x̃^t and γ̃^t defined in (7), (14) can be rewritten as

$$f_1(\mathbf{x})-f_1({\stackrel{\sim }{\mathbf{x}}}^t)+{(\mathbf{x}-{\stackrel{\sim }{\mathbf{x}}}^t)}^T[-{\mathbf{A}}^T{\stackrel{\sim }{\mathit{\gamma }}}^t+\mathbf{G}({\stackrel{\sim }{\mathbf{x}}}^t-{\mathbf{x}}^t)]\ge 0,\forall \mathbf{x}\in \mathcal{X}.$$ (15)

Similarly, deriving the optimality condition for the y-subproblem in (4), we have

$$f_2(\mathbf{y})-f_2({\mathbf{y}}^{t+1})+{(\mathbf{y}-{\mathbf{y}}^{t+1})}^T(-{\mathbf{B}}^T{\mathit{\gamma }}^{t+1})\ge 0,\forall \mathbf{y}\in \mathcal{Y}.$$ (16)

From (8), we get

$${\mathit{\gamma }}^{t+1}={\stackrel{\sim }{\mathit{\gamma }}}^t-\rho \mathbf{B}({\stackrel{\sim }{\mathbf{y}}}^t-{\mathbf{y}}^t)-(1-\alpha )({\stackrel{\sim }{\mathit{\gamma }}}^t-{\mathit{\gamma }}^t).$$ (17)

Substituting (17) into (16) and using the identity y^t+1 = ỹ^t, we obtain that

$$f_2(\mathbf{y})-f_2({\stackrel{\sim }{\mathbf{y}}}^t)+{(\mathbf{y}-{\stackrel{\sim }{\mathbf{y}}}^t)}^T[-{\mathbf{B}}^T{\stackrel{\sim }{\mathit{\gamma }}}^t+\rho {\mathbf{B}}^T\mathbf{B}({\stackrel{\sim }{\mathbf{y}}}^t-{\mathbf{y}}^t)+(1-\alpha ){\mathbf{B}}^T({\stackrel{\sim }{\mathit{\gamma }}}^t-{\mathit{\gamma }}^t)]\ge 0,\forall \mathbf{y}\in \mathcal{Y}.$$ (18)

Meanwhile, the third row of (7) implies that

$$(\mathbf{A}{\stackrel{\sim }{\mathbf{x}}}^t+\mathbf{B}{\stackrel{\sim }{\mathbf{y}}}^t-\mathbf{b})-\mathbf{B}({\stackrel{\sim }{\mathbf{y}}}^t-{\mathbf{y}}^t)+\frac{1}{\rho }({\stackrel{\sim }{\mathit{\gamma }}}^t-{\mathit{\gamma }}^t)=0.$$ (19)

Combining (15), (18) and (19), we get

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{\left(\begin{array}{c}\mathbf{x}-{\stackrel{\sim }{\mathbf{x}}}^t\\ \mathbf{y}-{\stackrel{\sim }{\mathbf{y}}}^t\\ \mathit{\gamma }-{\stackrel{\sim }{\mathit{\gamma }}}^t\end{array}\right)}^T\left\{\left(\begin{array}{c}-{\mathbf{A}}^T{\stackrel{\sim }{\mathit{\gamma }}}^t\\ -{\mathbf{B}}^T{\stackrel{\sim }{\mathit{\gamma }}}^t\\ \mathbf{A}{\stackrel{\sim }{\mathbf{x}}}^t+\mathbf{B}{\stackrel{\sim }{\mathbf{y}}}^t-\mathbf{b}\end{array}\right)+\left(\begin{array}{c}\mathbf{G}({\stackrel{\sim }{\mathbf{x}}}^t-{\mathbf{x}}^t)\\ \rho {\mathbf{B}}^T\mathbf{B}({\stackrel{\sim }{\mathbf{y}}}^t-{\mathbf{y}}^t)+(1-\alpha ){\mathbf{B}}^T({\stackrel{\sim }{\mathit{\gamma }}}^t-{\mathit{\gamma }}^t)\\ -\mathbf{B}({\stackrel{\sim }{\mathbf{y}}}^t-{\mathbf{y}}^t)+\frac{1}{\rho }({\stackrel{\sim }{\mathit{\gamma }}}^t-{\mathit{\gamma }}^t)\end{array}\right)\right\}\ge 0,\forall \mathbf{w}\in \mathit{\Omega }.$$ (20)

By the definition of F in (6) and Q in (11), (20) can be written as

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T[F({\stackrel{\sim }{\mathbf{w}}}^t)+\mathbf{Q}({\stackrel{\sim }{\mathbf{w}}}^t-{\mathbf{w}}^t)]\ge 0,\forall \mathbf{w}\in \mathit{\Omega }.$$

The assertion (13) is proved.

Recall the VI characterization (5)–(6) of the model (1). Thus, according to (13), the accuracy of w̃^t to a solution of VI(Ω, F, f) is measured by the quantity (w − w̃^t)^T Q(w^t − w̃^t). In the next lemma, we further explore this term and express it in terms of some quadratic terms, with which it becomes more convenient to estimate the accuracy of w̃^t and thus to estimate the convergence rate for the scheme (4). Note that the matrix B is of full column rank and the matrix G is positive definite. Thus, the matrix H defined in (11) is positive definite for α ∈ (0, 2) and ρ > 0; and recall that we use the notation

$${\Vert \mathbf{w}-\mathbf{v}\Vert }_{\mathbf{H}}=\sqrt{{(\mathbf{w}-\mathbf{v})}^T\mathbf{H}(\mathbf{w}-\mathbf{v})}$$

for further analysis.

Lemma 2

Let the sequence {w^t} be generated by the L-GADMM (4) and the associated sequence {w̃^t} be defined in (7). Then for any w ∈ Ω, we have

$${(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{Q}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)=\frac{1}{2}({\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2)+\frac{1}{2}{\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{2\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2.$$ (21)

Proof

Using Q = HM and M(w^t − w̃^t) = (w^t − w^t+1) (see (9)), it follows that

$${(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{Q}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)={(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{HM}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)={(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{H}({\mathbf{w}}^t-{\mathbf{w}}^{t+1}).$$ (22)

For the vectors a, b, c, d in the same space and a matrix H with appropriate dimensionality, we have the identity

$${(\mathbf{a}-\mathbf{b})}^T\mathbf{H}(\mathbf{c}-\mathbf{d})=\frac{1}{2}({\Vert \mathbf{a}-\mathbf{d}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{a}-\mathbf{c}\Vert }_{\mathbf{H}}^2)+\frac{1}{2}({\Vert \mathbf{c}-\mathbf{b}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{d}-\mathbf{b}\Vert }_{\mathbf{H}}^2).$$

In this identity, we take

$$\mathbf{a}=\mathbf{w},\mathbf{b}={\stackrel{\sim }{\mathbf{w}}}^t,\mathbf{c}={\mathbf{w}}^t\text{and}\mathbf{d}={\mathbf{w}}^{t+1},$$

and plug them into the right-hand side of (22). The resulting equation is

$${(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{H}({\mathbf{w}}^t-{\mathbf{w}}^{t+1})=\frac{1}{2}({\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2)+\frac{1}{2}({\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{\mathbf{H}}^2-{\Vert {\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{\mathbf{H}}^2).$$

The remaining task is to prove

$${\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{\mathbf{H}}^2-{\Vert {\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{\mathbf{H}}^2={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2.$$ (23)

By the definition of H given in (11), we have

$$\begin{array}{l}{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{\mathbf{H}}^2={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{1}{\alpha \rho }({\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t)\Vert }^2+{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2+2\rho (1-\alpha ){({\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t)}^T{\mathbf{B}}^T({\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t))\\ ={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{1}{\alpha \rho }{\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t)+(1-\alpha )({\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t)\Vert }^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2.\end{array}$$ (24)

On the other hand, we have by (17) and the definition that ũ^t = u^t+1,

$$\begin{array}{l}{\Vert {\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{\mathbf{H}}^2=\frac{1}{\alpha \rho }{\Vert {\mathit{\gamma }}^{t+1}-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2\\ =\frac{1}{\alpha \rho }{\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t)+(1-\alpha )({\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t)\Vert }^2.\end{array}$$ (25)

Subtracting (25) from (24), performing some algebra yields (23), and the proof is completed.

Lemmas 1 and 2 actually reassemble a simple proof for the convergence of the L-GADMM (4) from the perspectives of contraction type methods.

Theorem 1

The sequence {w^t} generated by the L-GADMM (4) satisfies that for all w^* ∈ Ω^*

$${\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2\le {\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2-({\Vert {\mathbf{x}}^t-{\mathbf{x}}^{t+1}\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{{\alpha }^2}{\Vert {\mathbf{v}}^t-{\mathbf{v}}^{t+1}\Vert }_{{\mathbf{H}}_0}^2),$$ (26)

where

$$\mathbf{v}=\left(\begin{array}{c}\mathbf{y}\\ \mathit{\gamma }\end{array}\right)\mathit{and}{\mathbf{H}}_0=\left(\begin{array}{cc}\rho {\mathbf{B}}^T\mathbf{B}& 0\\ 0& \frac{1}{\rho }{\mathbf{I}}_n\end{array}\right).$$ (27)

Proof

Set w = w^* in the assertion of Lemma 2, we get

$${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2-{\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2+2{({\stackrel{\sim }{\mathbf{w}}}^t-{\mathbf{w}}^{\ast })}^T\mathbf{HM}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t).$$

On the other hand, by using (13) and the monotonicity of F, we have

$${({\stackrel{\sim }{\mathbf{w}}}^t-{\mathbf{w}}^{\ast })}^T\mathbf{HM}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)\ge f({\stackrel{\sim }{\mathbf{u}}}^t)-f({\mathbf{u}}^{\ast })+{({\stackrel{\sim }{\mathbf{w}}}^t-{\mathbf{w}}^{\ast })}^{T}F({\stackrel{\sim }{\mathbf{w}}}^t)\ge 0.$$

Consequently, we obtain

$${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_H^2-{\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2\ge {\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2.$$ (28)

Since ỹ^t = y^t+1, it follows from (9) that

$${\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t=\frac{1}{\alpha }(\rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})+({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})).$$

Substituting it into (28), we obtain

$${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2-{\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2\ge {\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{(2-\alpha )}{{\alpha }^2\rho }{\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})+({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})\Vert }^2.$$ (29)

Note that (16) is true for any integer t ≥ 0. Thus we have

$$f_2(\mathbf{y})-f_2({\mathbf{y}}^t)+{(\mathbf{y}-{\mathbf{y}}^t)}^T(-{\mathbf{B}}^T{\mathit{\gamma }}^t)\ge \mathbf{0},\forall \mathbf{y}\in \mathcal{Y}.$$ (30)

Setting y = y^t and y = y^t+1 in (16) and (30), respectively, we get

$$f_2({\mathbf{y}}^t)-f_2({\mathbf{y}}^{t+1})+{({\mathbf{y}}^t-{\mathbf{y}}^{t+1})}^T(-{\mathbf{B}}^T{\mathit{\gamma }}^{t+1})\ge 0$$

and

$$f_2({\mathbf{y}}^{t+1})-f_2({\mathbf{y}}^t)+{({\mathbf{y}}^{t+1}-{\mathbf{y}}^t)}^T(-{\mathbf{B}}^T{\mathit{\gamma }}^t)\ge 0.$$

Adding the above two inequalities yields

$${({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})}^T\mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})\ge 0.$$ (31)

Substituting it in (29) and using x̃^t = x^t+1, we obtain

$${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2-{\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2\ge {\Vert {\mathbf{x}}^t-{\mathbf{x}}^{t+1}\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{{\alpha }^2}(\rho {\Vert \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})\Vert }^2+\frac{1}{\rho }{\Vert {\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}\Vert }^2),$$

and the assertion of this theorem follows directly.

Remark 1

Since the matrix H defined in (11) is positive definite, the assertion (26) implies that the sequence {w^t} generated by the L-GADMM (4) is contractive with respect to Ω^* (according to the definition in [4]). Thus, the convergence of {w^t} can be trivially derived by applying the standard technique of contraction methods.

Remark 2

For the special case where α = 1, i.e., the L-GADMM (4) reduces to the split inexact Uzawa method in [52,53], due to the structure of the matrix H (see (11)), the inequality (26) is simplified to

$${\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2\le {\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2-{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2,\forall {\mathbf{w}}^{\ast }\in {\mathit{\Omega }}^{\ast }.$$

Moreover, when α = 1 and G = 0, i.e., the L-GADMM (4) reduces to the ADMM (2), the inequality (26) becomes

$${\Vert {\mathbf{v}}^{t+1}-{\mathbf{v}}^{\ast }\Vert }_{{\mathbf{H}}_0}^2\le {\Vert {\mathbf{v}}^t-{\mathbf{v}}^{\ast }\Vert }_{{\mathbf{H}}_0}^2-{\Vert {\mathbf{v}}^t-{\mathbf{v}}^{t+1}\Vert }_{{\mathbf{H}}_0}^2,\forall {\mathbf{v}}^{\ast }\in {\mathcal{V}}^{\ast },$$

where v and H₀ are defined in (27). This is exactly the contraction property of the ADMM (2) analyzed in the appendix of [6].

Now, we are ready to establish a worst-case 𝒪(1/k) convergence rate in the ergodic sense for the L-GADMM (4). Lemma 2 plays an important role in the proof.

Theorem 2

Let H be given by (11) and {w^t} be the sequence generated by the L-GADMM (4). For any integer k > 0, let ŵ_k be defined by

$${\widehat{\mathbf{w}}}_k=\frac{1}{k+1}\sum _{t=0}^k{\stackrel{\sim }{\mathbf{w}}}^t,$$ (32)

where w̃^t is defined in (7). Then, we have ŵ_k ∈ Ω and

$$f({\widehat{\mathbf{u}}}_k)-f(\mathbf{u})+{({\widehat{\mathbf{w}}}_k-\mathbf{w})}^{T}F(\mathbf{w})\le \frac{1}{2(k+1)}{\Vert \mathbf{w}-{\mathbf{w}}^0\Vert }_{\mathbf{H}}^2,\forall \mathbf{w}\in \mathit{\Omega }.$$

Proof

First, because of (7) and w^t ∈ Ω, it holds that w̃^t ∈ Ω for all t ≥ 0. Thus, together with the convexity of 𝒳 and 𝒴, (84) implies that ŵ_k ∈ Ω. Second, due to the monotonicity, we have

$${(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F(\mathbf{w})\ge {(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\stackrel{\sim }{\mathbf{w}}}^t),$$ (33)

thus Lemma 1 and Lemma 2 imply that for all w ∈ Ω,

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F(\mathbf{w})+\frac{1}{2}{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2\ge \frac{1}{2}{\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2.$$ (34)

Summing the inequality (34) over t = 0, 1, …, k, we obtain that for all w ∈ Ω

$$(k+1)f(\mathbf{u})-\sum _{t=0}^{k}f({\stackrel{\sim }{\mathbf{u}}}^t)+{\left((k+1)\mathbf{w}-\sum _{t=0}^k{\stackrel{\sim }{\mathbf{w}}}^t\right)}^{T}F(\mathbf{w})+\frac{1}{2}{\Vert \mathbf{w}-{\mathbf{w}}^0\Vert }_{\mathbf{H}}^2\ge 0.$$

Using the notation of ŵ_t, it can be written as for all w ∈ Ω

$$\frac{1}{k+1}\sum _{t=0}^{k}f({\stackrel{\sim }{\mathbf{u}}}^t)-f(\mathbf{u})+{({\widehat{\mathbf{w}}}_k-\mathbf{w})}^{T}F(\mathbf{w})\le \frac{1}{2(k+1)}{\Vert \mathbf{w}-{\mathbf{w}}^0\Vert }_{\mathbf{H}}^2.$$ (35)

Since f(u) is convex and

$${\widehat{\mathbf{u}}}_k=\frac{1}{k+1}\sum _{t=0}^k{\stackrel{\sim }{\mathbf{u}}}^t,$$

we have that

$$f({\widehat{\mathbf{u}}}_k)\le \frac{1}{k+1}\sum _{t=0}^{k}f({\stackrel{\sim }{\mathbf{u}}}^t).$$

Substituting it into (35), the assertion of this theorem follows directly.

For an arbitrary substantial compact set 𝒟 ⊂ Ω, we define

$$D=sup\{{\Vert \mathbf{w}-{\mathbf{w}}^0\Vert }_{\mathbf{H}}\mid \mathbf{w}\in \mathcal{D}\},$$

where w⁰ = (x⁰, y⁰, γ⁰) is the initial point. After k iterations of the L-GADMM (4), we can find a ŵ_k ∈ Ω such that

$$\underset{\mathbf{w}\in \mathcal{D}}{sup}\{f({\widehat{\mathbf{u}}}_k)-f(\mathbf{u})+{({\widehat{\mathbf{w}}}_k-\mathbf{w})}^{T}F(\mathbf{w})\}\le \frac{D^2}{2k}.$$

A worse-case 𝒪(1/k) convergence rate in the ergodic sense is thus proved for the L-GADMM (4).

4 A worst-case 𝒪(1/k) convergence rate in a nonergodic sense

In this section, we prove a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the L-GADMM (4). The result includes the assertions in [32] for the ADMM and its linearized version as special cases.

For the right-hand-side of the inequality (21) in Lemma 2, the first term $\frac{1}{2}({\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2)$ is already in the form of the difference to w of two consecutive iterates, which is ideal for performing recursively algebraic reasoning in the proof of convergence rate (see theorems later). Now we have to deal with the last two terms in the right-hand side of (21) for the same purpose. In the following lemma, we find a bound in the term of ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2$ for the sum of these two terms.

Lemma 3

Let the sequence {w^t} be generated by the L-GADMM (4) and the associated sequence {w̃^t} be defined in (7). Then we have

$${\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2\ge c_{\alpha }{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2,$$ (36)

where

$$c_{\alpha }=min\left\{\frac{2-\alpha }{\alpha },1\right\}>0.$$ (37)

Proof

Similar to (24), it follows from x̃^t = x^t+1 and the definition of H that

$${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{1}{\alpha \rho }({\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})\Vert }^2+{\Vert {\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}\Vert }^2+2(1-\alpha )\rho {({\mathbf{y}}^t-{\mathbf{y}}^{t+1})}^T{\mathbf{B}}^T({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})).$$ (38)

From (31), (8) and the assumption α ∈ (0, 2), we have

$$\begin{array}{l}{\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})\Vert }^2+{\Vert {\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}\Vert }^2+2(1-\alpha )\rho {({\mathbf{y}}^t-{\mathbf{y}}^{t+1})}^T{\mathbf{B}}^T({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})\le {\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})\Vert }^2+{\Vert {\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}\Vert }^2+2\rho {({\mathbf{y}}^t-{\mathbf{y}}^{t+1})}^T{\mathbf{B}}^T({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})\\ ={\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})+({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})\Vert }^2\\ ={\alpha }^2{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2.\end{array}$$ (39)

Using (38) and (39), we have

$${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2\le {\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2.$$

Since α ∈ (0, 2), we get (2 − α)/α > 0, 1 ≥ c_α > 0 and

$$\begin{array}{l}{\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2\ge min\left\{\frac{2-\alpha }{\alpha },1\right\}\left({\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2\right)\\ \ge c_{\alpha }{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2.\end{array}$$

The proof is completed.

With Lemmas 1, 2 and 3, we can find a bound of the accuracy of w̃^t to a solution point of VI(Ω, F, f) in term of some quadratic terms. We show it in the next theorem.

Theorem 3

Let the sequence {w^t} be generated by the L-GADMM (4) and the associated sequence {w̃^t} be defined in (7). Then for any w ∈ Ω, we have

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F(\mathbf{w})\ge \frac{1}{2}\left({\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2\right)+\frac{c_{\alpha }}{2}{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2,$$ (40)

where H and c_α > 0 are defined in (11) and (37), respectively.

Proof

Using the monotonicity of F(w) (see (33)) and replacing the right-hand side term in (13) with the equality (21), we obtain that

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F(\mathbf{w})\ge \frac{1}{2}\left({\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2\right)+\frac{1}{2}\left({\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{\mathbf{G}}^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2\right).$$

The assertion (40) follows by plugging (36) into the above inequality immediately.

Now we show an important inequality for the scheme (4) by using Lemmas 1, 2 and 3. This inequality immediately shows the contraction of the sequence generated by (4), and based on this inequality we can establish its worst-case 𝒪(1/k) convergence rate in a nonergodic sense.

Theorem 4

The sequence {w^t} generated by the L-GADMM (4) satisfies

$${\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2\le {\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2-c_{\alpha }{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2,\forall {\mathbf{w}}^{\ast }\in {\mathit{\Omega }}^{\ast },$$ (41)

where H and c_α > 0 are defined in (11) and (37), respectively.

Proof

Setting w = w^* in (40), we get

$$f({\mathbf{u}}^{\ast })-f({\stackrel{\sim }{\mathbf{u}}}^t)+{({\mathbf{w}}^{\ast }-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\mathbf{w}}^{\ast })\ge \frac{1}{2}\left({\Vert {\mathbf{w}}^{\ast }-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2-{\Vert {\mathbf{w}}^{\ast }-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2\right)+\frac{c_{\alpha }}{2}{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2.$$

On the other hand, since w̃^t ∈ Ω, and w^* ∈ Ω^*, we have

$$0\ge f({\mathbf{u}}^{\ast })-f({\stackrel{\sim }{\mathbf{u}}}^t)+{({\mathbf{w}}^{\ast }-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\mathbf{w}}^{\ast }).$$

From the above two inequalities, the assertion (41) is proved.

Remark 3

Theorem 4 also explains why the relaxation parameter α is restricted into the interval (0, 2) for the L-GADMM (4). In fact, if α ≤ 0 or α ≥ 2, then the constant c_α defined in (37) is only non-positive and the in-equality (41) does not suffice to ensure the strict contraction of the sequence generated by (4); it is thus difficult to establish its convergence. We will empirically verify the failure of convergence for the case of (4) with α = 2 in Section 5.

To establish a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the scheme (4), we first have to mention that the term ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2$ can be used to measure the accuracy of an iterate. This result has been proved in some literatures such as [32] for the original ADMM.

Lemma 4

For a given w^t, let w^t+1 be generated by the L-GADMM (4). When ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2=0$, w̃^t defined in (7) is a solution to (5).

Proof

By Lemma 1 and (22), it implies that for all w ∈ Ω,

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\stackrel{\sim }{\mathbf{w}}}^t)\ge {(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{H}({\mathbf{w}}^t-{\mathbf{w}}^{t+1}).$$ (42)

As H is positive definite, the right-hand side of (42) vanishes if ${\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2=0$, since we have H(w^t+1−w^t) = 0 whenever ${\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^t\Vert }_{\mathbf{H}}^2=0$. The assertion is proved.

Now, we are ready to establish a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the scheme (4). First, we prove some lemmas.

Lemma 5

Let the sequence {w^t} be generated by the L-GADMM (4) and the associated {w̃^t} be defined in (7); the matrix Q be defined in (11). Then, we have

$${({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})}^T\mathbf{Q}[({\mathbf{w}}^t-{\mathbf{w}}^{t+1})-({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\ge 0.$$ (43)

Proof

Setting w = w̃^t+1 in (13), we have

$$f({\stackrel{\sim }{\mathbf{u}}}^{t+1})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{({\stackrel{\sim }{\mathbf{w}}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\stackrel{\sim }{\mathbf{w}}}^t)\ge {({\stackrel{\sim }{\mathbf{w}}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T\mathbf{Q}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t).$$ (44)

Note that (13) is also true for t := t + 1 and thus for all w ∈ Ω,

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^{t+1})+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})}^{T}F({\stackrel{\sim }{\mathbf{w}}}^{t+1})\ge {(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})}^T\mathbf{Q}({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1}).$$

Setting w = w̃^t in the above inequality, we obtain

$$f({\stackrel{\sim }{\mathbf{u}}}^t)-f({\stackrel{\sim }{\mathbf{u}}}^{t+1})+{({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})}^{T}F({\stackrel{\sim }{\mathbf{w}}}^{t+1})\ge {({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})}^T\mathbf{Q}({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1}).$$ (45)

Adding (44) and (45) and using the monotonicity of F, we get (43) immediately. The proof is completed.

Lemma 6

Let the sequence {w^t} be generated by the L-GADMM (4) and the associated {w̃^t} be defined in (7); the matrices M, H and Q be defined in (10) and (11). Then, we have

$${({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)}^T{\mathbf{M}}^T\mathbf{HM}[({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\ge \frac{1}{2}{\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{({\mathbf{Q}}^T+\mathbf{Q})}^2.$$ (46)

Proof

Adding the equation

$${[({\mathbf{w}}^t-{\mathbf{w}}^{t+1})-({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]}^T\mathbf{Q}[({\mathbf{w}}^t-{\mathbf{w}}^{t+1})-({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]=\frac{1}{2}{\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{({\mathbf{Q}}^T+\mathbf{Q})}^2$$

to both sides of (43), we get

$${({\mathbf{w}}^t-{\mathbf{w}}^{t+1})}^T\mathbf{Q}[({\mathbf{w}}^t-{\mathbf{w}}^{t+1})-({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\ge \frac{1}{2}{\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{({\mathbf{Q}}^T+\mathbf{Q})}^2.$$ (47)

Using (see (9))

$${\mathbf{w}}^t-{\mathbf{w}}^{t+1}=\mathbf{M}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)\text{and}\mathbf{Q}=\mathbf{HM},$$

to the term w^t − w^t+1 in the left-hand side of (47), we obtain

$${({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)}^T{\mathbf{M}}^T\mathbf{HM}[({\mathbf{w}}^t-{\mathbf{w}}^{t+1})-({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\ge \frac{1}{2}{\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{({\mathbf{Q}}^T+\mathbf{Q})}^2,$$

and the lemma is proved.

We then prove that the sequence {||w^t − w^t+1||_H} is monotonically non-increasing.

Theorem 5

Let the sequence {w^t} be generated by the L-GADMM (4) and the matrix H be defined in (11). Then, we have

$${\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{t+2}\Vert }_{\mathbf{H}}^2\le {\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2.$$ (48)

Proof

Setting a = M(w^t − w̃^t) and b = M(w^t+1 − w̃^t+1) in the identity

$${\Vert \mathbf{a}\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{b}\Vert }_{\mathbf{H}}^2=2{\mathbf{a}}^T\mathbf{H}(\mathbf{a}-\mathbf{b})-{\Vert \mathbf{a}-\mathbf{b}\Vert }_{\mathbf{H}}^2,$$

we obtain that

$${\Vert \mathbf{M}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{M}({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{\mathbf{H}}^2=2({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t){\mathbf{M}}^T\mathbf{HM}[({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]-{\Vert \mathbf{M}[({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\Vert }_{\mathbf{H}}^2.$$ (49)

Inserting (46) into the first term of the right-hand side of (49), we obtain that

$$\begin{array}{l}{\Vert \mathbf{M}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)\Vert }_{\mathbf{H}}^2-{\Vert \mathbf{M}({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{\mathbf{H}}^2\ge {\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{({\mathbf{Q}}^T+\mathbf{Q})}^2-{\Vert \mathbf{M}[({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\Vert }_{\mathbf{H}}^2\\ ={\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{({\mathbf{Q}}^T+\mathbf{Q})-{\mathbf{M}}^T\mathbf{HM}}^2\\ \ge 0,\end{array}$$ (50)

where the last inequality is by the fact that (Q^T + Q) − M^THM is positive definite. This is derived from the following calculation:

$$\begin{array}{l}({\mathbf{Q}}^T+\mathbf{Q})-{\mathbf{M}}^T\mathbf{HM}=({\mathbf{Q}}^T+\mathbf{Q})-{\mathbf{M}}^T\mathbf{Q}\\ =\left(\begin{array}{ccc}2\mathbf{G}& 0& 0\\ 0& 2\rho {\mathbf{B}}^T\mathbf{B}& -\alpha {\mathbf{B}}^T\\ 0& -\alpha \mathbf{B}& \frac{2}{\rho }{\mathbf{I}}_n\end{array}\right)-\left(\begin{array}{ccc}{\mathbf{I}}_{n_1}& 0& 0\\ 0& {\mathbf{I}}_{n_2}& -\rho {\mathbf{B}}^T\\ 0& 0& \alpha {\mathbf{I}}_n\end{array}\right)\left(\begin{array}{ccc}\mathbf{G}& 0& 0\\ 0& \rho {\mathbf{B}}^T\mathbf{B}& (1-\alpha ){\mathbf{B}}^T\\ 0& -\mathbf{B}& \frac{1}{\rho }{\mathbf{I}}_n\end{array}\right)\\ =\left(\begin{array}{ccc}2\mathbf{G}& 0& 0\\ 0& 2\rho {\mathbf{B}}^T\mathbf{B}& -\alpha {\mathbf{B}}^T\\ 0& -\alpha \mathbf{B}& \frac{2}{\rho }{\mathbf{I}}_n\end{array}\right)-\left(\begin{array}{ccc}\mathbf{G}& 0& 0\\ 0& 2\rho {\mathbf{B}}^T\mathbf{B}& -\alpha {\mathbf{B}}^T\\ 0& -\alpha \mathbf{B}& \frac{\alpha }{\rho }{\mathbf{I}}_n\end{array}\right)\\ =\left(\begin{array}{ccc}\mathbf{G}& 0& 0\\ 0& 0& 0\\ 0& 0& \frac{2-\alpha }{\rho }{\mathbf{I}}_n\end{array}\right).\end{array}$$

As we have assumed that G is positive definite. It is clear that (Q^T + Q) − M^THM is positive definite. By (50), we have shown that

$${\Vert \mathbf{M}({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{\mathbf{H}}^2\le {\Vert \mathbf{M}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)\Vert }_{\mathbf{H}}^2.$$

Recall the fact that w^t − w^t+1 = M(w^t − w̃^t). The assertion (48) follows immediately.

We now prove the worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the L-GADMM (4).

Theorem 6

Let {w^t} be the sequence generated by the L-GADMM (4) with α ∈ (0, 2). Then we have

$${\Vert {\mathbf{w}}^k-{\mathbf{w}}^{k+1}\Vert }_{\mathbf{H}}^2\le \frac{1}{(k+1)c_{\alpha }}{\Vert {\mathbf{w}}^0-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2,\forall k\ge 0,{\mathbf{w}}^{\ast }\in {\mathit{\Omega }}^{\ast },$$ (51)

where H and c_α > 0 are defined in (11) and (37), respectively.

Proof

It follows from (41) that

$$c_{\alpha }\sum _{t=0}^k{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2\le {\Vert {\mathbf{w}}^0-{\mathbf{w}}^{\ast }\Vert }_{\mathbf{H}}^2,\forall {\mathbf{w}}^{\ast }\in {\mathit{\Omega }}^{\ast }.$$ (52)

As shown in Theorem 5, { ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2$} is non-increasing. Therefore, we have

$$(k+1){\Vert {\mathbf{w}}^k-{\mathbf{w}}^{k+1}\Vert }_{\mathbf{H}}^2\le \sum _{t=0}^k{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{\mathbf{H}}^2.$$ (53)

The assertion (51) follows from (52) and (53) immediately.

Notice that Ω^* is convex and closed. Let w⁰ be the initial iterate and d := inf{||w⁰ − w^*||_H | w^* ∈ Ω^*}. Then, for any given ε > 0, Theorem 6 shows that the L-GADMM (4) needs at most ⌈d²/(c_αε) − 1⌉ iterations to ensure that ${\Vert {\mathbf{w}}^k-{\mathbf{w}}^{k+1}\Vert }_{\mathbf{H}}^2\le \epsilon$. It follows from Lemma 4 that w̃^k is a solution of VI(Ω, F, f) if ${\Vert {\mathbf{w}}^k-{\mathbf{w}}^{k+1}\Vert }_{\mathbf{H}}^2=0$. A worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the L-GADMM (4) is thus established in Theorem 6.

5 Numerical Experiments

In the literature, the efficiency of both the original ADMM (2) and its linearized version has been very well illustrated. The emphasis of this section is to further verify the acceleration performance of the L-GADMM (4) over the linearized version of the original ADMM. That is, we want to further show that for the scheme (4), the general case with α ∈ (1, 2) could lead to better numerical result than the special case with α = 1. The examples we will test include some rather new and core applications in statistical learning area. All codes were written in Matlab 2012a, and all experiments were run on a Macbook Pro with an Intel 2.9GHz i7 Processor and 16GB Memory.

5.1 Sparse Linear Discriminant Analysis

In this and the upcoming subsection, we apply the scheme (4) to solve two rather new and challenging statistical learning models, i.e. the linear programming discriminant rule in [7] and the constrained LASSO model in [35]. The efficiency of the scheme (4) will be verified. In particular, the acceleration performance of (4) with α ∈ (1, 2) will be demonstrated.

We consider the problem of binary classification. Let {(x_i, y_i), i = 1, …, n} be n samples drawn from a joint distribution of (X, Y) ∈ ℝ^d × {0, 1}. Given a new data x ∈ ℝ^d, the goal of the problem is to determine the associated value of Y. A common way to solve this problem is the linear discriminant analysis (LDA), see e.g. [1]. Assuming Gaussian conditional distributions with a common covariance matrix, i.e., (X|Y = 0) ~ N(μ₀, Σ) and (X|Y = 1) ~ N(μ₁, Σ), let the prior probabilities π₀ = ℙ(Y = 0) and π₁ = ℙ(Y = 1). Denote Ω = Σ⁻¹ to be the precision matrix; μ_a = (μ₀ + μ₁)/2 and μ_d = μ₁ − μ₀. Under the normality assumption and when π₀ = π₁ = 0.5, by Bayes’ rule, we have a linear classifier

$$\ell (\mathbf{x};{\mathit{\mu }}_0,{\mathit{\mu }}_1,\mathbf{\sum }):=\{\begin{array}{ll}1\hfill & \text{if}{(\mathbf{x}-{\mathit{\mu }}_a)}^T\mathbf{\Omega }{\mathit{\mu }}_d>0,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (54)

As the covariance matrix Σ and the means μ₀, μ₁ are unknown, given n₀ samples of (X|Y = 0) and n₁ samples of (X|Y = 1) respectively, a natural way to build a linear classifier is plugging sample means μ̂₀, μ̂₁ and sample inverse covariance matrix Σ̂⁻¹ into (54) to have ℓ(x; μ̂₀, μ̂₁, Σ̂). However, in high-dimensional case, where d > n, plug-in rule does not work as Σ̂ is not of full rank.

To resolve this problem, we consider the linear programming discriminant (LPD) rule proposed in [7] which assumes the sparsity directly on the discriminant direction β = Ωμ_d instead of μ_d or Ω, which is formulated as following: We first estimate sample mean and sample covariance matrix μ̂₀, Σ̂₀ of (X|Y = 0) and μ̂₁, Σ̂₁ of (X|Y = 1) respectively. Let $\widehat{\mathbf{\sum }}=\frac{n_0}{n}{\widehat{\mathbf{\sum }}}_0+\frac{n_1}{n}{\widehat{\mathbf{\sum }}}_1$ where n₀, n₁ are the sample sizes of (X|Y = 0) and (X|Y = 1) respectively and n = n₀ + n₁. The LPD model proposed in [7] is

$$\begin{array}{l}min{\Vert \mathit{\beta }\Vert }_1\\ \text{s.t.}{\Vert \widehat{\mathbf{\sum }}\mathit{\beta }-{\widehat{\mathit{\mu }}}_d\Vert }_{\infty }\le \lambda ,\end{array}$$ (55)

where λ is a tuning parameter; μ̂_d = μ̂₁ − μ̂₀, and || · ||₁ and || · ||_∞ are the ℓ₁ and ℓ_∞ norms in Euclidean space, respectively.

Clearly, the model (55) is essentially a linear programming problem, thus interior point methods are applicable. See e.g. [7] for a primal-dual interior point method. However, it is well known that interior point methods are not efficient for large-scale problems because the involved systems of equations which are solved by Newton type methods are too computationally demanding for large-scale cases.

Here, we apply the L-GADMM (4) to solve (55). To use (4), we first reformulate (55) as

$$\begin{array}{l}min{\Vert \mathit{\beta }\Vert }_1\\ \text{s.t.}\widehat{\mathbf{\sum }}\mathit{\beta }-{\widehat{\mathit{\mu }}}_d=\mathbf{y},\\ \mathbf{y}\in \mathcal{Y}:=\{\mathbf{y}:{\Vert \mathbf{y}\Vert }_{\infty }\le \lambda \},\end{array}$$ (56)

which is a special case of the model (1), and thus the scheme (4) is applicable.

We then elaborate on the resulting subproblems when (4) is applied to (56). First, let us see the application of the original GADMM scheme (3) without linearization to (56):

$${\mathit{\beta }}^{t+1}=\underset{\mathit{\beta }\in {ℝ}^d}{\text{argmin}}\left\{{\Vert \mathit{\beta }\Vert }_1+\frac{\rho }{2}{\Vert \widehat{\mathbf{\sum }}\mathit{\beta }-{\widehat{\mathit{\mu }}}_d-{\mathbf{y}}^t-\frac{{\mathit{\gamma }}^t}{\rho }\Vert }^2\right\},$$ (57)

$${\mathbf{y}}^{t+1}=\underset{\mathbf{y}\in \mathcal{Y}}{\text{argmin}}\left\{\frac{\rho }{2}{\Vert \mathbf{y}-(\alpha \widehat{\mathbf{\sum }}{\mathit{\beta }}^{t+1}+(1-\alpha )({\widehat{\mathit{\mu }}}_d+{\mathbf{y}}^t)-{\widehat{\mathit{\mu }}}_d)+\frac{{\mathit{\gamma }}^t}{\rho }\Vert }^2\right\},$$ (58)

$${\mathit{\gamma }}^{t+1}={\mathit{\gamma }}^t-\rho \left(\alpha \widehat{\mathbf{\sum }}{\widehat{\mathit{\beta }}}^{t+1}+(1-\alpha )({\mathbf{y}}^t+{\widehat{\mathit{\mu }}}_d)-{\widehat{\mathit{\mu }}}_d-{\mathbf{y}}^{t+1}\right).$$ (59)

For the β-subproblem (57), since Σ̂ is not a full rank matrix in the model (55) (in high-dimensional setting, the rank of Σ̂ is much smaller than d), it has no closed-form solution. As described in (4), we choose G = τI_d − ρΣ̂^TΣ̂ and consider the following linearized version of the β-subproblem (57):

$${\mathit{\beta }}^{t+1}=\underset{\mathit{\beta }\in {ℝ}^d}{\text{argmin}}\left\{{\Vert \mathit{\beta }\Vert }_1+\rho {(\mathit{\beta }-{\mathit{\beta }}^t)}^T{\mathbf{v}}^t+\frac{\tau }{2}{\Vert \mathit{\beta }-{\mathit{\beta }}^t\Vert }^2)\right\},$$ (60)

where ${\mathbf{v}}^t:={\widehat{\mathbf{\sum }}}^T(\widehat{\mathbf{\sum }}{\mathit{\beta }}^t-{\widehat{\mathit{\mu }}}_d-{\mathbf{y}}^t-\frac{{\mathit{\gamma }}^t}{\rho })$ is the gradient of the quadratic term $\frac{1}{2}{\Vert \widehat{\mathbf{\sum }}\mathit{\beta }-{\widehat{\mathit{\mu }}}_d-{\mathbf{y}}^t-\frac{{\mathit{\gamma }}^t}{\rho }\Vert }^2$ at β = β^t. It is seen that (60) is equivalent to

$${\mathit{\beta }}^{t+1}=\underset{\mathit{\beta }\in {ℝ}^d}{\text{argmin}}\left\{{\Vert \mathit{\beta }\Vert }_1+\frac{\rho \tau }{4}{\Vert \mathit{\beta }-({\mathit{\beta }}^t-\frac{2}{\tau }{\mathbf{v}}^t)\Vert }^2\right\}.$$ (61)

Let shrinkage(u, η) := sign(u) · max (0, |u| − η) be the soft shrinkage operater, where sign(·) is the sign function. The closed-form solution of (61) is given by

$${\mathit{\beta }}^{t+1}=\text{shrinkage}\left({\mathit{\beta }}^t-\frac{2}{\tau }{\mathbf{v}}^t,\frac{2}{\rho \tau }\right).$$ (62)

For the y-subproblem (58), by simple calculation, we get its solution is

$${\mathbf{y}}^{t+1}=min\left(max\left(\alpha \widehat{\mathbf{\sum }}{\mathit{\beta }}^{t+1}+(1-\alpha )({\mathbf{y}}^t+{\widehat{\mathit{\mu }}}_d)-{\widehat{\mathit{\mu }}}_d-\frac{{\mathit{\gamma }}^t}{\rho },-\lambda \right),\lambda \right).$$ (63)

Overall, the application of the L-GADMM (4) to the model (55) is summarized in Algorithm 1.

Algorithm 1.

Solving sparse LPD (55) by the L-GADMM (4)

Initialize β0, y0, γ0, τ, ρ.

while Stopping criterion is not satisfied. do

Compute βt+1 by (62).

Compute yt+1 by (63).

Update γt+1 by (59)

end while

To implement Algorithm 1, we use the stopping criterion described in [6]: Let the primal residual at the t-th iteration be r^t = ||Σ̂β^t − μ̂_d − y^t|| and the dual residual be s^t = ||ρ Σ̂ (y^k−y^k−1)||; let the tolerance of the primal and dual residual at the t-th iteration be ${\epsilon }^{\mathit{pri}}=\sqrt{d}\epsilon +\epsilon max(\Vert \widehat{\mathbf{\sum }}{\mathit{\beta }}^t\Vert ,\Vert {\mathbf{y}}^t\Vert ,\Vert {\widehat{\mathit{\mu }}}_d\Vert )$ and ${\epsilon }^{\mathit{dua}}=\sqrt{d}\epsilon +\epsilon \Vert \widehat{\mathbf{\sum }}{\mathit{\gamma }}^t\Vert$, respectively, where ε is chosen differently for different applications; then the iteration is stopped when r^t < ε^pri and s^t < ε^dua.

5.1.1 Simulated Data

We first test some synthetic dataset. Following the settings in [7], we consider three schemes and for each scheme, we take n₀ = n₁ = 150, d = 400 and set μ₀ = 0, μ₁ = (1, …, 1, 0, …, 0)^T, λ = 0.15 for Scheme 1, and λ = 0.1 for Schemes 2 and 3, where the number of 1’s in μ₁ is s = 10. The details of the schemes to be tested is listed below:

• [Scheme 1]: Ω = Σ⁻¹ where Σ_jj = 1 for 1 ≤ j ≤ d and Σ_jk = 0.5 for j ≠ k.

• [Scheme 2]: Ω = Σ⁻¹, where Σ_jk = 0.6^|j−k| for 1 ≤ j, k ≤ d.

• [Scheme 3]: Ω = (B + δI)/(1 + δ), where B = (b_jk)_d×d with independent b_jk = b_kj = 0.5 × Ber(0.2) for 1 ≤ j, k ≤ s, i ≠ j; b_jk = b_kj = 0.5 for s + 1 ≤ j < k ≤ d; b_jj = 1 for 1 ≤ j ≤ d, where Ber(0.2) is a Bernoulli random variable whose value is taken as 1 with the probability 0.2 and 0 with the probability 0.8, and δ = max(−Λ_min(B), 0)+0.05, where Λ_min(W) is the smallest eigenvalue of the matrix W, to ensure the positive definiteness of Ω.

For Algorithm 1, we set the parameters ρ = 0.05 and τ = 2.1||Σ̂^T Σ̂||₂. These values are tuned via experiments. The starting points are that β⁰ = 0, y⁰ = 0 and γ⁰ = 1. We set ε = 5 × 10⁻⁴ for the stopping criterion. Note that, as described by [7], we add δI_d to the sample covariance matrix to avoid the ill conditionness, where δ = 10⁻¹².

Since synthetic dataset is considered, we repeat each scheme ten times and report the averaged numerical performance. In particular, we plot the evolutions of the number of iterations and computing time in seconds with respect to different values of α in the interval [1.0, 1.9] with an equal distance of 0.1, and we further choose finer grids in the interval [1.91, 1.98] with an equal distance of 0.01 in Figure 1¹. To see the performance of Algorithm 1 with α ∈ [1, 2) clearly, for the last simulation case of Scheme 2, we plot the evolutions of objective function value, primal residual and dual residual with respect to iterations for different values of α in Figure 2. The acceleration performance of the relaxation factor α ∈ [1, 2), especially when α is close to 2, over the case where α = 1 is clearly demonstrated. Also, we see that when α is close to 2 (e.g. α = 1.9), the objective value and the primal residual decrease faster than the cases where α is close to 1.

Fig. 1.

Algorithm 1: Evolution of number of iterations and computing time in seconds w.r.t. different values of α′ for synthetic dataset.

Fig. 2.

Algorithm 1: Evolution of objective value, primal residual and dual residual w.r.t. some values of α for Scheme 2

As we have mentioned, the β-subproblem (57) has no closed-form solution; and Algorithm 1 solves it by linearizing its quadratic term and thus only solves the β-subproblem by one iteration because the linearized β-subproblem has a closed-form solution. This is actually very important to ensure the efficiency of ADMM-like method for some particular cases of (1), as emphasized in [48]. One may be curious in comparing with the case where the β-subproblem (57) is solved iteratively by a generic, rather than the special linearization strategy. Note that the β-subproblem (57) is a standard ℓ₁−ℓ₂ model and we can simply apply the ADMM scheme (2) to solve it iteratively by introducing an auxiliary variable v = β and thus reformulating it as a special case of (1). This case is denoted by “ADMM²” when we report numerical results because the ADMM is used both externally and internally. As analyzed in [14,41], to ensure the convergence of ADMM², the accuracy of solving the β-subproblem (57) should keep increasing. Thus, in the implementation of ADMM for the subproblem (57), we gradually decrease the tolerance for the inner problem from ε= 5 × 10⁻² to ε= 5 × 10⁻⁴. Specifically, we take ε= 5 × 10⁻² when min(r^t/ε^pri, s^t/ε^dua) > 50; ε = 5×10⁻³ when 10 < max(r^t/ε^pri, s^t/ε^dua) < 50; and ε = 5×10⁻⁴ when max(r^t/ε^pri, s^t/ε^dua) < 10. We further set the maximal iteration numbers as 1, 000 and 40, 000 for the inner and outer loops executed by the ADMM², respectively.

Table 1.

Numerical comparison between the averaged performance of Algorithm 1 and ADMM²

		Alg. 1 (α = 1)	Alg. 1 (α = 1.9)	ADMM2
Scheme 1	CPU time(s)	100.54	72.25	141.86
	Objective Value	2.1826	2.1998	2.2018
	Violations	0.0081	0.0073	0.0182
Scheme 2	CPU time(s)	54.70	28.33	481.44
	Objective Value	14.3276	14.3345	14.2787
	Violations	0.0099	0.0098	0.0183
Scheme 3	CPU time(s)	49.67	27.94	223.15
	Objective Value	2.4569	2.4537	2.4912
	Violations	0.0078	0.0080	0.0176

We compare Algorithm 1 and ADMM² for their averaged performances. In Table 1, we list the averaged computing time in seconds and the objective function values for Algorithm 1 with α = 1 and 1.9, and ADMM². Recall Algorithm 1 with α = 1 is the linearized version of the original ADMM (2) and ADMM² is the case where the β-subproblem (57) is solved iteratively by the original ADMM scheme. The data in this table shows that achieving the same level of objective function values, Algorithm 1 with α = 1.9 is faster than Algorithm 1 with α = 1 (thus, the acceleration performance of the GADMM with α ∈ (1, 2) is illustrated); and Algorithm 1 with either α = 1 or α = 1.9 is much faster than ADMM² (thus the necessity of linearization for the β-subproblem (57) is clearly demonstrated). We also list the averaged primal feasibility violations of the solutions generated by the algorithms in the table. The violation is defined as ||Σ̂β̂ − μ̂_d, − w||, where β̂ is the output solution and w = min (max(Σ̂β̂ − μ̂_d, − λ), λ) ∈ ℝ^d. It is clearly seen in the table that Algorithm 1 achieves better feasibility than ADMM².

5.1.2 Real Dataset

In this section, we compare Algorithm 1 with ADMM² on a real dataset of microarray dataset in [38]. The dataset contains 13,182 microarray samples from Affymetrixs HGU133a platform. The raw data contains 2,711 tissue types (e.g., lung cancers, brain tumors, Ewing tumor etc.). In particular, we select 60 healthy samples and 60 samples from those with breast cancer. We use the first 1,000 genes to conduct the experiments.

It is believed that different tissues are associated with different sets of genes and microarray data have been heavily adopted to classify tissues, see e.g. [28, 47]. Our aim is to classify those tissues of breast cancer from those healthy tissues. We randomly select 60 samples from each group to be our training set and use another 60 samples from each group as testing set. The tuning parameter λ is chosen by five-fold cross validation as described in [7].

We set ρ = 1 and τ = 2||Σ̂^T Σ̂||₂ for Algorithm 1; and take the tolerance ε = 10⁻³ in the stopping criterion of Algorithm 1. The starting points are β⁰ = 0, z⁰ = 0 and γ⁰ = 0. The comparison among Algorithm 1 with α = 1 and α = 1.9 and ADMM² is shown in Table 2; where the pair “a/b” means there are “a” errors out of “b” samples when iteration is terminated. It is seen that Algorithm 1 outperforms ADMM² in both accuracy and efficiency; also the case where α= 1.9 accelerates Algorithm 1 with α = 1.

Table 2.

Numerical comparison between Algorithm 1 and ADMM² for microarray dataset

	Alg. 1 (α = 1)	Alg. 1 (α = 1.9)	ADMM2
Training Error	1/60	1/60	1/60
Testing Error	3/60	3/60	3/60
CPU time(s)	201.17	167.61	501.95
Objective Value	24.67	24.85	24.81
Violation	0.0121	0.0121	0.0241

5.2 Constrained Lasso

In this subsection, we apply the L-GADMM (4) to the constrained LASSO model proposed recently in [35].

Consider the standard linear regression model

$$\mathbf{y}=\mathbf{X}\mathit{\beta }+\epsilon ,$$

where X ∈ ℝ^n×d is a design matrix; β ∈ ℝ^d is a vector of regression coefficients; y ∈ ℝⁿ is a vector of observations, and ε ∈ ℝⁿ is a vector of random noises. In high-dimensional setting where the number of observations is much smaller than the number of regression coefficients, n ≪ d, the traditional least-squares method does not perform well. To overcome this difficulty, just like the sparse LDA model (55), certain sparsity conditions are assumed for the linear regression model. With the sparsity assumption on the vector of regression coefficients β, we have the following model

$$\underset{\mathit{\beta }}{min}\frac{1}{2}{\Vert \mathbf{y}-\mathbf{X}\mathit{\beta }\Vert }^2+p_{\lambda }(\mathit{\beta }),$$

where p_λ(·) is a penalization function. Different penalization functions have been proposed in the literature, such as the LASSO in [44] where p_λ(β) = λ||β||₁, the SCAD [16], the adaptive LASSO [54], and the MCP [51]. Inspired by significant applications such as portfolio selection [18] and monotone regression [35], the constrained LASSO (CLASSO) model was proposed recently in [35]:

$$\begin{array}{l}{min}_{\mathit{\beta }}\frac{1}{2}{\Vert \mathbf{y}-\mathbf{X}\mathit{\beta }\Vert }^2+\lambda {\Vert \mathit{\beta }\Vert }_1\\ s.t.\mathbf{A}\mathit{\beta }\le \mathbf{b},\end{array}$$ (64)

where A ∈ ℝ^m×d and b ∈ ℝ^m with m < d in some applications like portfolio selection [18]. It is worth noting that many statistical problems such as the fused LASSO [45] and the generalized LASSO [46] can be formulated as the form of (64). Thus it is important to find efficient algorithms for solving (64). Although (64) is a quadratic programming problem that can be solved by interior point methods theoretically, again for high-dimensional cases the application of interior point methods is numerically inefficient because of its extremely expensive computation. Note that existing algorithms for LASSO can not be extended to solve (64) trivially.

In fact, introducing a slack variable to the inequality constraints in (64), we reformulate (64) as

$$\underset{\mathit{\beta },\mathbf{z}\in {ℝ}^d}{min}\frac{1}{2}{\Vert \mathbf{y}-\mathbf{X}\mathit{\beta }\Vert }^2+\lambda {\Vert \mathit{\beta }\Vert }_1\text{s.t.}\mathbf{A}\mathit{\beta }-\mathbf{z}=\mathbf{0},\mathbf{z}\le \mathbf{b},$$ (65)

which is a special case of the model (1) and thus the L-GADMM (4) is applicable. More specifically, the iterative scheme of (4) with G = τI_d − ρ(A^T A) for solving (65) reads as

$${\mathit{\beta }}^{t+1}=\underset{\mathit{\beta }}{\text{argmin}}\left\{\frac{1}{2}{\Vert \mathbf{y}-\mathbf{X}\mathit{\beta }\Vert }^2+\lambda {\Vert \mathit{\beta }\Vert }_1+\rho {(\mathit{\beta }-{\mathit{\beta }}^t)}^T{\mathbf{u}}^t+\frac{\tau }{2}{\Vert \mathit{\beta }-{\mathit{\beta }}^t\Vert }^2\right\},$$ (66)

$${\mathbf{z}}^{t+1}=\underset{\mathbf{z}\le \mathbf{b}}{\text{argmin}}\left\{\frac{\rho }{2}{\Vert \alpha \mathbf{A}{\mathit{\beta }}^{t+1}+(1-\alpha ){\mathbf{z}}^t-\mathbf{z}-\frac{{\mathit{\gamma }}^t}{\rho }\Vert }^2\right\},$$ (67)

$${\mathit{\gamma }}^{t+1}={\mathit{\gamma }}^t-\rho \left(\alpha \mathbf{A}{\mathit{\beta }}^{t+1}+(1-\alpha )(\mathbf{b}-{\mathbf{z}}^t)+{\mathbf{z}}^{t+1}-\mathbf{b}\right),$$ (68)

where ${\mathbf{u}}^t={\mathbf{A}}^T(\mathbf{A}{\mathit{\beta }}^t-{\mathbf{z}}^t-\frac{{\mathit{\gamma }}^t}{\rho })$.

Now, we delineate the subproblems (66)–(68). First, the β-subproblem (66) is equivalent to

$${\mathit{\beta }}^{t+1}=\underset{\mathit{\beta }}{\text{argmin}}\left\{\frac{1}{2}{\mathit{\beta }}^T({\mathbf{X}}^T\mathbf{X}+\tau {\mathbf{I}}_d)\mathit{\beta }-{\mathit{\beta }}^T{\mathbf{w}}^t+\lambda {\Vert \mathit{\beta }\Vert }_1\right\},$$ (69)

where w^t = X^T y + β^t − ρu^t, and I_d ∈ ℝ^d×d is the identity matrix. Deriving the optimality condition of (69), the solution of (69), β^t+1 has to satisfy the following equation:

$$\mathbf{C}{\mathit{\beta }}^{t+1}=\text{shrinkage}({\mathbf{w}}^t,\lambda ),$$

where C = (X^T X + τI_d). As X^T X is positive semidefinite and I_d is of full rank with all positive eigenvalues, we have that C is invertible. We have a closed-form solution for (66) that

$${\mathit{\beta }}^{t+1}={\mathbf{C}}^{-1}\times \text{shrinkage}({\mathbf{w}}^t,\lambda ).$$ (70)

Then, for the z-subproblem (67), its closed-form solution is given by

$${\mathbf{z}}^{t+1}=min\left(\mathbf{b},\alpha \mathbf{A}{\mathit{\beta }}^{t+1}+(1-\alpha ){\mathbf{z}}^t-\frac{{\mathit{\gamma }}^t}{\rho }\right).$$ (71)

Overall, the application of the L-GADMM (4) to the constrained CLASSO model (64) is summarized in Algorithm 2.

We consider two schemes to test the efficiency of Algorithm 2.

• [Scheme 1]: We first generate an n×d matrix X with independent standard Gaussian entries where n = 100 and d = 400, and we standardize the columns of X to have unit norms. After that, we set the coefficient vector β = (1, …, 1, 0, …0)^T with the first s = 5 entries to be 1 and the rest to be 0. Next, we generate a m × d matrix A with independent standard Gaussian entries where m = 100, and we generate b = Aβ + ε̂ where the entries of ε̂ are independent random variables uniformly distributed in [0, σ], and the vector of observations y is generated by y = Xβ + ε with ε ~ N(0, σ²I_d) where σ = 0.1. We set λ = 1 in the model (64).

• [Scheme 2]: We follow the same procedures of Scheme 1, but we change σ to be 0.3

Algorithm 2.

Solving Constrained LASSO (64) by the L-GADMM (4)

Initialize β0, z0, γ0, τ, ρ.

while Stopping criterion is not satisfied. do

Compute βt+1 by (70).

Compute zt+1 by (71).

Update γ+1 by (68).

end while

To implement Algorithm 2, we use the stopping criterion proposed by [48]: Let the primal and dual residual at the t-th iteration be p^t = ||Aβ^t − z^t || and d^t = ||γ^t − γ^t+1||, respectively; the tolerance of primal and dual residuals are set by the criterion described in [6] where ${\epsilon }^{\mathit{pri}}=\sqrt{d}\epsilon +\epsilon max\left(\Vert \mathbf{A}{\mathit{\beta }}^t\Vert ,\Vert {\mathbf{z}}^t\Vert ,\Vert \mathbf{b}\Vert \right)$ and ${\epsilon }^{\mathit{dua}}=\sqrt{m}\epsilon +\epsilon \Vert {\mathbf{A}}^T\mathit{\gamma }\Vert$; then the iteration is stopped when p^t < ε^pri and d^t < ε^dua. We choose ε = 10⁻⁴ for our experiments. We set ρ = 10⁻³ and τ = 20||A^T A||₂ and the starting iterate as β⁰ = 0, z⁰ = 0 and γ⁰ = 0.

Since synthetic dataset is considered, we repeat the simulation ten times and report the averaged numerical performance of Algorithm 2. In Figure 3, we plot the evolutions of number of iterations and computing time in seconds with different values of α ∈ [1, 2] for Algorithm 2 with α chosen the same way as we did in the previous subsection. The acceleration performance when α ∈ (1, 2) over the case where α = 1 is clearly shown by the curves in this figure. For example, the case where α = 1.9 is about 30% faster than the case where α = 1. We also see that when α = 2, Algorithm 2 does not converge after 100,000 iterations. This coincides with the failure of strict contraction of the sequence generated by Algorithm 2, as we have mentioned in Remark 3.

Fig. 3.

Algorithm 2: Evolution of number of iterations and computing time in seconds w.r.t. different values of α for synthetic dataset

Like Section 5.1.1, we also compare the averaged performance of Algorithm 2 with the application of the original ADMM (2) where the resulting β-subproblem is solved iteratively by the ADMM. The penalty parameter is set as 1 and the ADMM is implemented to solve the β-subproblem, whose tolerance ε is gradually decreased from 10⁻² to 10⁻⁴ obeying the same rule as that mentioned in Section 5.1.1. We further set the maximal iteration numbers to be 1, 000 and 10, 000 for inner and outer loops executed by ADMM². Again, this case is denoted by “ADMM²”. In Table 3, we list the computing time in seconds to achieve the same level of objective function values for three cases: Algorithm 2 with α = 1, Algorithm 2 with α = 1.9, and ADMM². We see that Algorithm 2 with either α = 1 or α = 1.9 is much faster than ADMM²; thus the necessity of linearization when ADMM-like methods are applied to solve the constrained LASSO model (64) is illustrated. Also, the acceleration performance of the GADMM with α ∈ (1, 2) is demonstrated as Algorithm 2 with α = 1.9 is faster than Algorithm 2 with α = 1. We also report the averaged primal feasibility violations of the solutions generated by each algorithm. The violation is defined as ||Aβ̂ − w||, where β̂ is the output solution and w = min (b, Aβ̂) ∈ ℝ^m, respectively. It is seen in the table that Algorithm 2 achieves better feasibility than ADMM².

Table 3.

Numerical comparison of the averaged performance between Algorithm 2 and ADMM²

		Alg. 2 (α = 1)	Alg. 2 (α = 1.9)	ADMM2
Scheme 1	CPU time(s)	88.03	71.01	166.17
	Objective Value	5.4679	5.4678	5.4823
	Violations	0.0033	0.0031	0.2850
Scheme 2	CPU time(s)	97.19	82.49	165.90
	Objective Value	5.3861	5.3864	5.6364
	Violations	0.0032	0.0032	0.1158

5.3 Dantzig Selector

Last, we test the Dantzig Selector model proposed in [9]. In [48], this model has been suggested to be solved by the linearized version of ADMM which is a special case of (4) with α = 1. We now test this example again to show the acceleration performance of (4) with α ∈ (1, 2).

The Dantzig selector model in [9] deals with the case where the the number of observations is much smaller than the number of regression coefficients, i.e n ≪ d. In particular, the Dantzig selector model is

$$\begin{array}{l}min{\Vert \mathit{\beta }\Vert }_1\\ s.t.{\Vert {\mathbf{X}}^T(\mathbf{X}\mathit{\beta }-\mathbf{y})\Vert }_{\infty }\le \delta ,\end{array}$$ (72)

where δ > 0 is a tuning parameter, and || · ||_∞ is the infinity norm.

As elaborated in [48], the model (72) can be formulated as

$$\begin{array}{l}min{\Vert \mathit{\beta }\Vert }_1\\ s.t.{\mathbf{X}}^T(\mathbf{X}\mathit{\beta }-\mathbf{y})-\mathbf{x}=0,\\ \mathit{\beta }\in {ℝ}^p,\mathbf{x}\in \mathit{\Omega }:=\{\mathbf{x}:{\Vert \mathbf{x}\Vert }_{\infty }\le \delta \},\end{array}$$ (73)

where x ∈ ℝ^d is an auxiliary variable. Obviously, (73) is a special case of (1) and thus the L-GADMM (4) is applicable. In fact, applying (4) with G = I_d − τ||(X^TX)^T(X^TX)||₂ to (73), we obtain the subproblems as the following:

$${\mathit{\beta }}^{t+1}=\underset{\mathit{\beta }\in {ℝ}^p}{\text{argmin}}\left\{{\Vert \mathit{\beta }\Vert }_1+\frac{\rho }{2}\left(2{({\mathbf{v}}^t)}^T(\mathit{\beta }-{\mathit{\beta }}^t)+\frac{\tau }{2}{\Vert \mathit{\beta }-{\mathit{\beta }}^t\Vert }^2\right)\right\},$$ (74)

$${\mathbf{x}}^{t+1}=\underset{\mathbf{x}\in \mathit{\Omega }}{\text{argmin}}\{\frac{\rho }{2}{\Vert \mathbf{x}-\alpha {\mathbf{X}}^T(\mathbf{X}{\mathit{\beta }}^{t+1}-\mathbf{y})-(1-\alpha ){\mathbf{x}}^t+\frac{{\mathit{\gamma }}^t}{\rho }\Vert }^2\},$$ (75)

$${\mathit{\gamma }}^{t+1}={\mathit{\gamma }}^t-\rho (\alpha {\mathbf{X}}^T(\mathbf{X}{\mathit{\beta }}^{t+1}-\mathbf{y})+(1-\alpha ){\mathbf{x}}^t-{\mathbf{x}}^{t+1}),$$ (76)

where ${\mathbf{v}}^t:={({\mathbf{X}}^T\mathbf{X})}^T[{\mathbf{X}}^T(\mathbf{X}{\mathit{\beta }}^t-\mathbf{y})-{\mathbf{x}}^t-\frac{{\mathit{\gamma }}^t}{\rho }]$. Note that τ ≥ 2||(XX^T)X^TX||₂ is required to ensure the convergence, see [48] for the detailed proof.

The β-subproblem (74) can be rewritten as

$${\mathit{\beta }}^{t+1}=\underset{\mathit{\beta }\in {ℝ}^p}{\text{argmin}}\left\{{\Vert \mathit{\beta }\Vert }_1+\frac{\rho \tau }{4}{\Vert \mathit{\beta }-({\mathit{\beta }}^t-\frac{2}{\tau }{\mathbf{v}}^t)\Vert }^2\right\},$$

whose closed-form solution is given by

$${\mathit{\beta }}^{t+1}=\text{shrinkage}\left({\mathit{\beta }}^t-\frac{2}{\tau }{\mathbf{v}}^t,\frac{2}{\rho \tau }\right).$$ (77)

Moreover, the solution of the x-subproblem (75) is given by

$${\mathbf{x}}^{t+1}=min\{max\{\alpha {\mathbf{X}}^T(\mathbf{X}{\mathit{\beta }}^{t+1}-\mathbf{y})+(1-\alpha ){\mathbf{x}}^t-\frac{{\mathit{\gamma }}^t}{\rho },-\delta \},\delta \}.$$ (78)

Overall, the application of the L-GADMM (4) to the Dantzig Selector model (72) is summarized in Algorithm 3.

Algorithm 3.

Solving Dantzig Selector (72) by the L-GADMM (4)

Given X, y, δ.

Initialize β0, x0, γ0, τ, ρ.

while Stopping criteria is not satisfied. do

Compute βt+1 by (77).

Compute xt+1 by (78).

Update γt+1 by (76).

end while

5.3.1 Synthetic Dataset

We first test some synthetic dataset for the Dantizg Selector model (72). We follow the simulation setup in [9] to generate the design matrix X whose columns all have the unit norm. Then, we randomly choose a set S of cardinality s. β is generated by

$${\mathit{\beta }}_i=\{\begin{array}{ll}{\xi }_i(1+\mid a_i\mid )\hfill & \text{if}i\in S;\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$

where ξ ~ U(−1, 1)(i.e., the uniform distribution on the interval (−1, 1)) and a_i ~ N(0, 1). At last, y is generated by y = Xβ + ε with ε ~ N(0, σ²I).

We consider four schemes as listed below:

• [Scheme 1]: (n, d, s) = (720, 2560, 80), σ = 0.03.

• [Scheme 2]: (n, d, s) = (720, 2560, 80), σ = 0.05.

• [Scheme 3]: (n, d, s) = (1440, 5120, 160), σ = 0.03.

• [Scheme 4]: (n, d, s) = (1440, 5120, 160), σ = 0.05.

We take $\delta =\sigma \sqrt{2logd}$.

To implement Algorithm 3, we set the penalty parameter ρ = 0.1 and τ = 2.5||(XX^T)X^TX||₂ respectively. Again, we use the stopping criterion described in [6]: Let the primal and dual residual at the t-th iteration be r^t = ||X^TXβ^t − x^t − X^Ty|| and s^t = ||ρX^TX(γ^t − γ^t−1)||, respectively; let the tolerance of the primal and dual residual at the t-th iteration be ${\epsilon }^{\mathit{pri}}=\sqrt{d}\epsilon +\epsilon max(\Vert {\mathbf{X}}^T\mathbf{X}{\mathit{\beta }}^t\Vert ,\Vert {\mathbf{x}}^t\Vert ,\Vert {\mathbf{X}}^T\mathbf{y}\Vert )$ and ${\epsilon }^{\mathit{dua}}=\sqrt{n}\epsilon +\epsilon \Vert {\mathbf{X}}^T\mathbf{X}{\mathit{\gamma }}^t\Vert$, respectively; then the iteration is stopped when r^t < ε^pri and s^t < ε^dua simultaneously. We choose ε = 10⁻⁴ for our experiments. We set the starting points as β⁰ = 0, x⁰ = 0 and γ⁰ = 0.

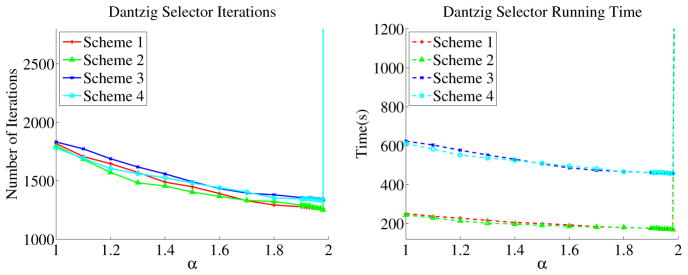
In Figure 4, we plot the evolutions of number of iterations and computing time in seconds with respect to different values of α ∈ [1, 2]. We choose the values of α ∈ [1, 2] for Algorithm 3 with α chosen the same way as we did in the previous subsections. The curves in Figure 4 show the acceleration performance of Algorithm 3 with α ∈ (1, 2) clearly. Also, if α = 2, Algorithm 3 does not converge after 10,000 iterations.

Fig. 4.

Algorithm 3: Evolution of number of iterations and computing time w.r.t. different values of α for synthetic dataset

Like previous sections, we compare the averaged performance of our method with ADMM² which solves the β-subproblem iteratively by ADMM for all of the four schemes. In the implementation of using ADMM to solve the β-subproblem, we use the same stopping criterion as described in the previous sections, and the tolerance ε is gradually decreased from 10⁻² to 10⁻⁴ obeying the same rule as the rule in Section 5.1.1. We further set the maximal iteration numbers to be 1, 000 and 10, 000 for inner and outer loops executed by ADMM², respectively. Also, we set the penalty parameter for inner loop as 1. For the outer loop, we set the tolerance ε = 10⁻⁴ for both Algorithm 3 and ADMM². In Table 4, we present the computing time in seconds to achieve the same level of objective values for three cases: Algorithm 3 with α = 1, Algorithm 3 with α = 1.9, and ADMM². It is seen that Algorithm 3 with either α = 1 or α = 1.9 is much faster than ADMM², and Algorithm 3 with α = 1.9 is faster than Algorithm 3 with α = 1; we have thus demonstrated the necessity of linearization when ADMM-like methods are applied to solve the Dantzig selector model (64) and the acceleration performance of GADMM with α ∈ (1, 2). Also, we list the averaged primal feasibility violation of each algorithm. The violation is defined as ||X^T (Xβ̂ − y) − w||, where β̂ is the output solution and w = min (max (X^T (Xβ̂ − y), −δ), δ) ∈ ℝ^d. Algorithm 3 achieves better feasibility than ADMM² as illustrated in the table.

Table 4.

Numerical comparison of the averaged performance between Algorithm 3 and ADMM²

		Alg. 3 (α = 1)	Alg. 3 (α = 1.9)	ADMM2
Scheme 1	CPU time(s)	215.12	154.7	1045.62
	Objective Value	60.6777	60.6821	60.8028
	Violation	0.0048	0.0050	0.1464
Scheme 2	CPU time(s)	213.80	147.29	1184.98
	Objective Value	54.7704	54.7729	54.7915
	Violation	0.0049	0.0052	0.1773
Scheme 3	CPU time(s)	613.20	462.41	5514.81
	Objective Value	124.0258	124.0208	124.2314
	Violation	0.0072	0.0072	0.2361
Scheme 4	CPU time(s)	607.80	463.58	5357.55
	Objective Value	111.8513	111.8489	112.0675
	Violation	0.0072	0.0071	0.2137

5.3.2 Real Dataset

Then, we test the Dantizg Selector model (72) for a real dataset. In particular, we test the same dataset as in Section 5.1.2. We look at another disease: Ewing’s sarcoma which has drawn much attention in the literature, see e.g. [26]. We have 27 samples diagnosed with Ewing’s sarcoma. Then, we randomly select 55 healthy samples. Next, we select 30 healthy samples and 15 samples diagnosed with Ewing’s sarcoma as training set, and let the remaining 42 samples be the testing set. We use the first 2,000 genes to conduct the analysis. Thus, this dataset corresponds to the model (72) with n = 45 and d = 2, 000. In the implementation, the parameter δ in (72) is chosen by five-fold cross validation, and we set ρ = 0.02 and τ = 9||(X^TX)^TX^TX||₂ for Algorithm 3, and we use the same stopping criterion with ε = 4 × 10⁻⁴. The comparison between Algorithm 3 and ADMM² is listed in Table 5. From this table, we see that Algorithm 3 with either α = 1 or α = 1.9 outperforms ADMM² significantly —- it requires much less computing time to achieve the same level of objective function values with similar primal feasibility and attains the same level of training or testing error. In addition, the acceleration performance of the case where α = 1.9 over the case where α = 1 is again demonstrated for Algorithm 3.

Table 5.

Numerical comparison between Algorithm 3 and ADMM² for microarray dataset

	Alg. 3 (α = 1)	Alg. 3 (α = 1.9)	ADMM2
Training Error	0/45	0/45	0/45
Testing Error	0/37	0/37	0/37
CPU time(s)	1006.68	532.96	2845.27
Objective Value	17.596	17.579	17.771
Violation	0.0131	0.0131	0.0285

6 Conclusion

In this paper, we take a deeper look at the linearized version of the generalized alternating direction method of multiplier (ADMM) and establish its worst-case 𝒪(1/k) convergence rate in both the ergodic and a nonergodic senses. This result subsumes some existing results established for the original ADMM and generalized ADMM schemes; and it provides accountable and novel theoretical support to the numerical efficiency of the generalized ADMM. Further, we apply the linearized version of the generalized ADMM to solve some important statistical learning applications; and enlarge the application range of the generalized ADMM. Finally we would mention that the worst-case 𝒪(1/k) convergence rate established in this paper amounts to a sublinear speed of convergence. If certain conditions are assumed (e.g. some error bound conditions) or the model under consideration has some special properties, it is possible to establish the linear convergence rate for the linearized version of the generalized ADMM by using similar techniques in, e.g.[5,11,27]. We omit the detail of analysis and only focus on the convergence rate analysis from the iteration complexity perspective in this paper.

Appendices

We show that our analysis in Sections 3 and 4 can be extended to the case where both the x- and y-subproblems in (3) are linearized. The resulting scheme, called doubly linearized version of the GADMM (“DL-GADMM” for short), reads as

$$\begin{array}{l}{\mathbf{x}}^{t+1}=\underset{\mathbf{x}\in \mathcal{X}}{\text{argmin}}\left\{f_1(\mathbf{x})-{\mathbf{x}}^T{\mathbf{A}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert \mathbf{Ax}+{\mathbf{By}}^t-\mathbf{b}\Vert }^2+\frac{1}{2}{\Vert \mathbf{x}-{\mathbf{x}}^t\Vert }_{{\mathbf{G}}_1}^2\right\},\\ {\mathbf{y}}^{t+1}=\underset{\mathbf{y}\in \mathcal{Y}}{\text{argmin}}\left\{f_2(\mathbf{y})-{\mathbf{y}}^T{\mathbf{B}}^T{\mathit{\gamma }}^t+\frac{\rho }{2}{\Vert \alpha {\mathbf{Ax}}^{t+1}+(1-\alpha )(\mathbf{b}-{\mathbf{By}}^t)+\mathbf{By}-\mathbf{b}\Vert }^2+\frac{1}{2}{\Vert \mathbf{y}-{\mathbf{y}}^t\Vert }_{{\mathbf{G}}_2}^2\right\},\\ {\mathit{\gamma }}^{t+1}={\mathit{\gamma }}^t-\rho \left(\alpha {\mathbf{Ax}}^{t+1}+(1-\alpha )(\mathbf{b}-{\mathbf{By}}^t)+{\mathbf{By}}^{t+1}-\mathbf{b}\right),\end{array}$$ (79)

where the matrices G₁ ∈ ℝ^n₁×n₁ and G₂ ∈ ℝ^n₂×n₂ are both symmetric and positive definite.

For further analysis, we define two matrices, which are analogous to H and Q in (11), respectively, as

$$\begin{array}{l}{\mathbf{H}}_2=\left(\begin{array}{ccc}{\mathbf{G}}_1& 0& 0\\ 0& \frac{\rho }{\alpha }{\mathbf{B}}^T\mathbf{B}+{\mathbf{G}}_2& \frac{1-\alpha }{\alpha }{\mathbf{B}}^T\\ 0& \frac{1-\alpha }{\alpha }\mathbf{B}& \frac{1}{\alpha \rho }{\mathbf{I}}_n\end{array}\right),\\ {\mathbf{Q}}_2=\left(\begin{array}{ccc}{\mathbf{G}}_1& 0& 0\\ 0& \rho {\mathbf{B}}^T\mathbf{B}+{\mathbf{G}}_2& (1-\alpha ){\mathbf{B}}^T\\ 0& -\mathbf{B}& \frac{1}{\rho }{\mathbf{I}}_n\end{array}\right).\end{array}$$ (80)

Obviously, we have

$${\mathbf{Q}}_2={\mathbf{H}}_2\mathbf{M},$$ (81)

where M is defined in (10). Note that the equalities (8) and (9) still hold.

A A worst-case 𝒪(1/k) convergence rate in the ergodic sense for (79)

We first establish a worst-case 𝒪(1/k) convergence rate in the ergodic sense for the DL-GADMM (79). Indeed, using the relationship (81), the resulting proof is nearly the same as that in Section 3 for the L-GADMM (4). We thus only list two lemmas (analogous to Lemmas 1 and 2) and one theorem (analogous to Theorem 2) to demonstrate a worst-case 𝒪(1/k) convergence rate in the ergodic sense for (79), and omit the details of proofs.

Lemma 7

Let the sequence {w^t} be generated by the DL-GADMM (79) with α ∈ (0, 2) and the associated sequence {w̃^t} be defined in (7). Then we have

$$f(\mathbf{u})-f({\stackrel{\sim }{\mathbf{u}}}^t)+{(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\stackrel{\sim }{\mathbf{w}}}^t)\ge {(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T{\mathbf{Q}}_2({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t),\forall \mathbf{w}\in \mathit{\Omega },$$ (82)

where Q₂ is defined in (80).

Lemma 8

Let the sequence {w^t} be generated by the DL-GADMM (79) with α ∈ (0, 2) and the associated sequence {w̃^t} be defined in (7). Then for any w ∈ Ω, we have

$${(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T{\mathbf{Q}}_2({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)=\frac{1}{2}({\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{{\mathbf{H}}_2}^2)+\frac{1}{2}{\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{{\mathbf{G}}_1}^2+\frac{1}{2}{\Vert {\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t\Vert }_{{\mathbf{G}}_2}^2+\frac{2-\alpha }{2\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2.$$ (83)

Theorem 7

Let H₂ be given by (80) and {w^t} be the sequence generated by the DLGADMM (79) with α ∈ (0, 2). For any integer k > 0, let ŵ_k be defined by

$${\widehat{\mathbf{w}}}_k=\frac{1}{k+1}\sum _{t=0}^k{\stackrel{\sim }{\mathbf{w}}}^t,$$ (84)

where w̃^t is defined in (7). Then, ŵ_k ∈ Ω and

$$f({\widehat{\mathbf{u}}}_k)-f(\mathbf{u})+{({\widehat{\mathbf{w}}}_k-\mathbf{w})}^{T}F(\mathbf{w})\le \frac{1}{2(k+1)}{\Vert \mathbf{w}-{\mathbf{w}}^0\Vert }_{{\mathbf{H}}_2}^0,\forall \mathbf{w}\in \mathit{\Omega }.$$

B A worst-case 𝒪(1/k) convergence rate in a nonergodic sense for (79)

Next, we prove a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the DL-GADMM (79). Note that Lemma 4 still holds by replacing H with H₂. That is, if ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2=0$, w̃^t defined in (7) is an optimal solution point to (5). Thus, for the sequence {w^t} generated by the DL-GADMM (79), it is reasonable to measure the accuracy of an iterate by ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2$.

Proofs of the following two lemmas are analogous to those of Lemmas 5 and 6, respectively. We thus omit them.

Lemma 9

Let the sequence {w^t} be generated by the DL-GADMM (79) with α ∈ (0, 2) and the associated {w̃^t} be defined in (7); the matrix Q₂ be defined in (80). Then, we have

$${({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})}^T{\mathbf{Q}}_2[({\mathbf{w}}^t-{\mathbf{w}}^{t+1})-({\stackrel{\sim }{\mathbf{w}}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\ge 0.$$

Lemma 10

Let the sequence {w^t} be generated by the DL-GADMM (79) with α ∈ (0, 2) and the associated {w̃^t} be defined in (7); the matrices M, H₂, Q₂ be defined in (10) and (80). Then, we have

$${({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)}^T{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}[({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})]\ge \frac{1}{2}{\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^{t+1})\Vert }_{({\mathbf{Q}}_2^T+{\mathbf{Q}}_2)}^2.$$

Based on the above two lemmas, we see that the sequence {||w^t − w^t+1||_H2} is monotonically non-increasing. That is, we have the following theorem.

Theorem 8

Let the sequence {w^t} be generated by the DL-GADMM (79) and the matrix H₂ be defined in (80). Then, we have

$${\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{t+2}\Vert }_{{\mathbf{H}}_2}^2\le {\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2.$$

Note that for the DL-GADMM (79), the y-subproblem is also proximally regularized, and we can not extend the inequality (31) to this new case. This is indeed the main difficulty for proving a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the DL-GADMM (79). A more elaborated analysis is needed. Let us show one lemma first to bound the left-hand side in (31).

Lemma 11

Let {y^t} be the sequence generated by the DL-GADMM (79) with α ∈ (0, 2). Then, we have

$$({\mathbf{y}}^t-{\mathbf{y}}^{t+1}){\mathbf{B}}^T({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})\ge \frac{1}{2}{\Vert {\mathbf{y}}^t-{\mathbf{y}}^{t+1}\Vert }_{{\mathbf{G}}_2}^2-\frac{1}{2}{\Vert {\mathbf{y}}^{t-1}-{\mathbf{y}}^t\Vert }_{{\mathbf{G}}_2}^2.$$ (85)

Proof

It follows from the optimality condition of the y-subproblem in (79) that

$$f_2(\mathbf{y})-f_2({\mathbf{y}}^{t+1})+{(\mathbf{y}-{\mathbf{y}}^{t+1})}^T[-{\mathbf{B}}^T{\mathit{\gamma }}^{t+1}+{\mathbf{G}}_2({\mathbf{y}}^{t+1}-{\mathbf{y}}^t)]\ge 0,\forall \mathbf{y}\in \mathcal{Y}.$$ (86)

Similarly, we also have,

$$f_2(\mathbf{y})-f_2({\mathbf{y}}^t)+{(\mathbf{y}-{\mathbf{y}}^t)}^T[-{\mathbf{B}}^T{\mathit{\gamma }}^t+{\mathbf{G}}_2({\mathbf{y}}^t-{\mathbf{y}}^{t-1})]\ge 0,\forall \mathbf{y}\in \mathcal{Y}.$$ (87)

Setting y = y^t in (86) and y = y^t+1 in (87), and summing them up, we have

$$\begin{array}{l}({\mathbf{y}}^t-{\mathbf{y}}^{t+1}){\mathbf{B}}^T({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1})\ge ({\mathbf{y}}^{t+1}-{\mathbf{y}}^t){\mathbf{G}}_2({\mathbf{y}}^{t+1}-{\mathbf{y}}^t+{\mathbf{y}}^{t-1}-{\mathbf{y}}^t)\\ \ge {\Vert {\mathbf{y}}^t-{\mathbf{y}}^{t+1}\Vert }_{{\mathbf{G}}_2}^2-\frac{1}{2}{\Vert {\mathbf{y}}^t-{\mathbf{y}}^{t+1}\Vert }_{{\mathbf{G}}_2}^2-\frac{1}{2}{\Vert {\mathbf{y}}^{t-1}-{\mathbf{y}}^t\Vert }_{{\mathbf{G}}_2}^2\\ =\frac{1}{2}{\Vert {\mathbf{y}}^t-{\mathbf{y}}^{t+1}\Vert }_{{\mathbf{G}}_2}^2-\frac{1}{2}{\Vert {\mathbf{y}}^{t-1}-{\mathbf{y}}^t\Vert }_{{\mathbf{G}}_2}^2,\end{array}$$

where the second inequality holds by the fact that ${\mathbf{a}}^T\mathbf{b}\ge -\frac{1}{2}({\Vert \mathbf{a}\Vert }^2+{\Vert \mathbf{b}\Vert }^2)$. The assertion (85) is proved.

Two more lemmas should be proved in order to establish a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the DL-GADMM (79).

Lemma 12

The sequence {w^t} generated by the DL-GADMM (79) with α ∈ (0, 2) and the associated {w̃^t} be defined in (7), then we have

$$c_{\alpha }({\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{{\mathbf{G}}_1}^2+{\Vert {\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t\Vert }_{{\mathbf{G}}_2}^2+\frac{\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2)\le {\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2$$ (88)

where c_α is defined in (37).

Proof

By the definition of Q₂, M and H₂, we have

$$\begin{array}{l}{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{{\mathbf{G}}_1}^2+{\Vert {\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t\Vert }_{{\mathbf{G}}_2}^2+\frac{2-\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2\\ \ge min\left\{\frac{2-\alpha }{\alpha },1\right\}({\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{{\mathbf{G}}_1}^2+{\Vert {\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t\Vert }_{{\mathbf{G}}_2}^2+\frac{\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2),\end{array}$$

which implies the assertion (88) immediately.

In the next lemma, we refine the bound of (w − w̃^t)^T Q₂(w^t − w̃^t) in (82). The refined bound consists of the terms ${\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2$ recursively, which is favorable for establishing a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the DL-GADMM (79).

Lemma 13

Let {w^t} be the sequence generated by the DL-GADMM (79) with α ∈ (0, 2). Then, w̃^t ∈ Ω and

$$f(\mathbf{u})-f({\mathbf{u}}^t)+{(\mathbf{w}-\stackrel{\sim }{\mathbf{w}})}^{T}F(\mathbf{w})\ge \frac{1}{2}({\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{{\mathbf{H}}_2}^2)+\frac{1}{2}{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2,\forall \mathbf{w}\in \mathit{\Omega },$$ (89)

where M is defined in (10), and H₂ and Q₂ are defined in (80).

Proof

By the identity Q₂(w^t − w̃^t) = H₂(w^t − w^t+1), it holds that

$${(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T{\mathbf{Q}}_2({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)={(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t)}^T{\mathbf{H}}_2({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^{t+1}),\forall \mathbf{w}\in \mathit{\Omega }.$$

Setting a = w, b = w̃^t, c = w^t and d = w^t+1 in the identity

$${(\mathbf{a}-\mathbf{b})}^T{\mathbf{H}}_2(\mathbf{c}-\mathbf{d})=\frac{1}{2}({\Vert \mathbf{a}-\mathbf{d}\Vert }_{{\mathbf{H}}_2}^2-{\Vert \mathbf{a}-\mathbf{c}\Vert }_{{\mathbf{H}}_2}^2)+\frac{1}{2}({\Vert \mathbf{c}-\mathbf{b}\Vert }_{{\mathbf{H}}_2}^2-{\Vert \mathbf{d}-\mathbf{b}\Vert }_{{\mathbf{H}}_2}^2),$$

we have

$$2(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t){\mathbf{Q}}_2({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)={\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{{\mathbf{H}}_2}^2+{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{H}}_2}^2-{\Vert {\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{H}}_2}^2.$$ (90)

Meanwhile, we have

$$\begin{array}{l}{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{H}}_2}^2-{\Vert {\mathbf{w}}^{t+1}-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{H}}_2}^2={\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{H}}_2}^2-{\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-({\mathbf{w}}^t-{\mathbf{w}}^{t+1})\Vert }_{{\mathbf{H}}_2}^2\\ ={\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{H}}_2}^2-{\Vert ({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)-\mathbf{M}({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)\Vert }_{{\mathbf{H}}_2}^2\\ =({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)(2{\mathbf{H}}_2\mathbf{M}-{\mathbf{M}}^T\mathbf{HM})({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)\\ =({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)({\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T\mathbf{HM})({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t),\end{array}$$

where the last equality comes from the identity Q₂ = H₂M.

Substituting the above identity into (90), we have, for all w ∈ Ω,

$$2(\mathbf{w}-{\stackrel{\sim }{\mathbf{w}}}^t){\mathbf{Q}}_2({\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t)={\Vert \mathbf{w}-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2-{\Vert \mathbf{w}-{\mathbf{w}}^t\Vert }_{{\mathbf{H}}_2}^2+{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2$$

Plugging this identity into (82), our claim follows immediately.

Then, we show the boundedness of the sequence {w^t} generated by the DL-GADMM (79), which essentially implies the convergence of {w^t}.

Theorem 9

Let {w^t} be the sequence generated by the DL-GADMM (79) with α ∈ (0, 2). Then, it holds that

$$\sum _{t=0}^{\infty }{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2\le {\Vert {\mathbf{w}}^0-{\mathbf{w}}^{\ast }\Vert }_{{\mathbf{H}}_2}^2,$$ (91)

where H₂ is defined in (80).

Proof

Setting w = w^* in (89), we have

$$f({\mathbf{u}}^{\ast })-f({\mathbf{u}}^t)+{({\mathbf{w}}^{\ast }-{\stackrel{\sim }{\mathbf{w}}}^t)}^{T}F({\mathbf{w}}^{\ast })\ge \frac{1}{2}({\Vert {\mathbf{w}}^{\ast }-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2-{\Vert {\mathbf{w}}^{\ast }-{\mathbf{w}}^t\Vert }_{{\mathbf{H}}_2}^2)+\frac{1}{2}{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2.$$

Then, recall (5), we have

$${\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2\le {\Vert {\mathbf{w}}^t-{\mathbf{w}}^{\ast }\Vert }_{{\mathbf{H}}_2}^2-{\Vert {\mathbf{w}}^{t+1}-{\mathbf{w}}^{\ast }\Vert }_{{\mathbf{H}}_2}^2.$$

It is easy to see that ${\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}\succcurlyeq \mathbf{0}$. Thus, it holds

$$\sum _{t=0}^{\infty }{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2\le {\Vert {\mathbf{w}}^0-{\mathbf{w}}^{\ast }\Vert }_{{\mathbf{H}}_2}^2,$$

which completes the proof.

Finally, we establish a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the DL-GADMM (79).

Theorem 10

Let the sequence {w^t} be generated by the scheme DL-GADMM (79) with α ∈ (0, 2). It holds that

$${\Vert {\mathbf{w}}^k-{\mathbf{w}}^{k+1}\Vert }_{{\mathbf{H}}_2}^2=\mathcal{O}(1/k).$$ (92)

Proof

By the definition of H₂ in (80), we have

$$\begin{array}{l}{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{{\mathbf{G}}_1}^2+{\Vert {\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t\Vert }_{{\mathbf{G}}_2}^2+\frac{1}{\alpha \rho }({\Vert \rho \mathbf{B}({\mathbf{y}}^t-{\mathbf{y}}^{t+1})\Vert }^2+{\Vert {\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}\Vert }^2+2(1-\alpha )\rho {({\mathbf{y}}^t-{\mathbf{y}}^{t+1})}^T{\mathbf{B}}^T({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}))\\ ={\Vert {\mathbf{x}}^t-{\stackrel{\sim }{\mathbf{x}}}^t\Vert }_{{\mathbf{G}}_1}^2+{\Vert {\mathbf{y}}^t-{\stackrel{\sim }{\mathbf{y}}}^t\Vert }_{{\mathbf{G}}_2}^2+\frac{\alpha }{\rho }{\Vert {\mathit{\gamma }}^t-{\stackrel{\sim }{\mathit{\gamma }}}^t\Vert }^2-2{({\mathbf{y}}^t-{\mathbf{y}}^{t+1})}^T{\mathbf{B}}^T({\mathit{\gamma }}^t-{\mathit{\gamma }}^{t+1}).\end{array}$$ (93)

Using (85), (88), (91) and (93), we obtain

$$\begin{gathered} \sum _{t=1}^k{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2\le \frac{1}{c_{\alpha }}\sum _{t=1}^k{\Vert {\mathbf{w}}^t-{\stackrel{\sim }{\mathbf{w}}}^t\Vert }_{{\mathbf{Q}}_2^T+{\mathbf{Q}}_2-{\mathbf{M}}^T{\mathbf{H}}_2\mathbf{M}}^2 \\ +\sum _{t=1}^k({\Vert {\mathbf{y}}^{t-1}-{\mathbf{y}}^t\Vert }_{{\mathbf{G}}_2}^2-{\Vert {\mathbf{y}}^t-{\mathbf{y}}^{t+1}\Vert }_{{\mathbf{G}}_2}^2)\le \frac{1}{c_{\alpha }}{\Vert {\mathbf{w}}^0-{\mathbf{w}}^{\ast }\Vert }_{{\mathbf{H}}_2}^2+{\Vert {\mathbf{y}}^0-{\mathbf{y}}^1\Vert }_{{\mathbf{G}}_2}^2. \end{gathered}$$

By Theorem 8, the sequence { ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2$} is non-increasing. Thus, we have

$$\begin{array}{l}k{\Vert {\mathbf{w}}^k-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2\le \sum _{t=1}^k{\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2\\ \le \frac{1}{c_{\alpha }}{\Vert {\mathbf{w}}^0-{\mathbf{w}}^{\ast }\Vert }_{{\mathbf{H}}_2}^2+{\Vert {\mathbf{y}}^0-{\mathbf{y}}^1\Vert }_{{\mathbf{G}}_2}^2,\end{array}$$

and the assertion (92) is proved.

Recall that for the sequence {w^t} generated by the DL-GADMM (79), it is reasonable to measure the accuracy of an iterate by ${\Vert {\mathbf{w}}^t-{\mathbf{w}}^{t+1}\Vert }_{{\mathbf{H}}_2}^2$. Thus, Theorem 10 demonstrates a worst-case 𝒪(1/k) convergence rate in a nonergodic sense for the DL-GADMM (79).