A faster escape does not enhance survival in zebrafish larvae

Abstract

An escape response is a rapid manoeuvre used by prey to evade predators. Performing this manoeuvre at greater speed, in a favourable direction, or from a longer distance have been hypothesized to enhance the survival of prey, but these ideas are difficult to test experimentally. We examined how prey survival depends on escape kinematics through a novel combination of experimentation and mathematical modelling. This approach focused on zebrafish (Danio rerio) larvae under predation by adults and juveniles of the same species. High-speed three-dimensional kinematics were used to track the body position of prey and predator and to determine the probability of behavioural actions by both fish. These measurements provided the basis for an agent-based probabilistic model that simulated the trajectories of the animals. Predictions of survivorship by this model were found by Monte Carlo simulations to agree with our observations and we examined how these predictions varied by changing individual model parameters. Contrary to expectation, we found that survival may not be improved by increasing the speed or altering the direction of the escape. Rather, zebrafish larvae operate with sufficiently high locomotor performance due to the relatively slow approach and limited range of suction feeding by fish predators. We did find that survival was enhanced when prey responded from a greater distance. This is an ability that depends on the capacity of the visual and lateral line systems to detect a looming threat. Therefore, performance in sensing, and not locomotion, is decisive for improving the survival of larval fish prey. These results offer a framework for understanding the evolution of predator–prey strategy that may inform prey survival in a broad diversity of animals.

1. Introduction

An escape response allows prey to evade predators with rapid locomotion [1]. Because of its potential to directly affect survivorship, natural selection may favour animals that can execute an escape response with high locomotor performance. Indeed, the physiology and mechanics of locomotion features many traits that appear to be adaptations for a rapid response and fast motion. Escape responses are controlled by large-diameter command neurons (e.g. the giant axon of squid [2]), which often recruit specialized muscles (e.g. the axial musculature of fish [3]), which may animate an appendage that is dedicated to escape behaviour (e.g. the uropods of crayfish [4]). Prey may direct this escape in an optimal direction [5], or may alternatively benefit from moving randomly so as not to be predictable [6,7]. However, it does not necessarily follow that any enhancement in speed or variation in heading will have a positive effect on a prey's survival. Fish predators commonly approach their prey at a relatively slow speed [8,9] and this could permit escape by a prey operating below its maximal capacity. The aim of this study was to test whether improvements in kinematics related to locomotor performance and sensing affect prey survival by examining predator–prey interactions in zebrafish (Danio rerio, Hamilton 1922).

We addressed this aim with a novel approach that combines experimentation with mathematical modelling. Our methodology was developed to meet the challenges to understanding the coupled dynamics of predators and prey. Owing to the sensing of both animals, the actions of the prey may (or may not) be a response to the predator, which may (or may not) be a response to prior motion by the prey. Regression analysis is generally insensitive to such interdependency, yet may succeed in resolving dominant features of successful prey [10] or predators [11]. It has additionally been helpful to study behavioural responses to an artificial predator or prey that is experimentally controlled and therefore not coupled to the actions of the animal [11–15]. An alternative approach has attempted to formulate a behavioural algorithm of one animal by considering their responses to the measured kinematics of the other [16]. Our present approach similarly included measurements of predator–prey kinematics, but these were used as a basis for an agent-based probabilistic model that calculated the trajectories of both animals from a series of behavioural actions. A series of simulations by this model allowed for a predictive consideration of the effects of differences in behaviour on prey survival.

Zebrafish provide an excellent experimental subject for studying the mechanisms of predator–prey interactions. The larval stage of this species serves as a model for the neurophysiological [17–19] and biomechanical [20,21] basis of behaviour. Predator–prey interactions may be experimentally replicated in the lab, where adults and juvenile zebrafish strike at larval zebrafish with suction feeding and the larvae respond with a fast-start escape response [22]. Therefore, the interactions between zebrafish of different life-history stages replicate the principle predator and prey behaviours that characterize a broad diversity of piscivorous interactions [5,10]. When approaching an evasive prey, adult zebrafish move much slower than their maximum speed [22], which is common among suction-feeding fishes [8,9]. A slow approach presumably allows greater control over the direction and timing of the suction feeding, which is limited to a brief duration over a small region in front of the mouth [23,24]. The prey, by contrast, respond with an explosive escape response with speed that generally exceeds that of the predator. As suggested by prior experiments [25] and theory [5], the relative speed and size of predator and prey has the potential to affect the strategy of both animals. Therefore, we performed experiments with juvenile (three- to four-months old, 2.0 ± 0.4 cm, N = 19) and adult (more than or equal to nine-months old, mean ± 1 s.d. = 3.4 ± 0.5 cm, N = 19) predators with a nearly twofold difference in body length to examine the effects of scale.

2. Material and methods

(a). Kinematics

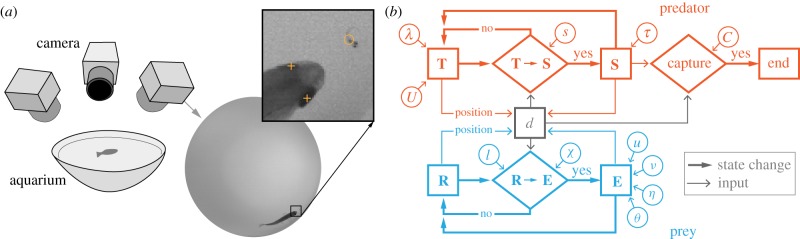
All experiments were conducted using wild-type (AB line) zebrafish larvae (5–7 days post fertilization) as prey (D. rerio). The fish were placed in a hemispherical aquarium (Ø = 8.5 cm) composed of white acrylic, which served as a translucent diffuser of IR illumination (940 nm), provided by three lamps (CM-IR200-940, CMVision, Houston, TX, USA), positioned below (figure 1a). These lamps provided high-intensity illumination that was invisible to the fish [26], while visible illumination at low intensity was provided by overhead fluorescent lights. High-speed video cameras (1000 fps at 1024 × 1024 pixels, FASTCAM Mini UX50, Precision Photron Inc., San Diego, CA, USA) were each fitted with a 55 mm lens (f/2.8 Micro Nikkon AIS, Nikon Inc., Melville, NY, USA) and positioned at a distance that permitted a view of the entire aquarium, where they recorded both predator and prey. Predation experiments were performed by recording the swimming of one predator and one prey fish in the aquarium (figure 1a). This began by placing the fish on opposite sides of a partition. After acclimation (15 min), we lifted the partition and recorded the fish until the predator successfully ingested the prey.

Figure 1.

Kinematic measurements and mathematical modelling for studying predator–prey interactions in zebrafish. (a) Three high-speed video cameras recorded one larval prey and one predator fish (adult or juvenile) that were placed in a hemispherical aquarium. A representative video frame shows an adult in close proximity to the prey. In the inset, orange markers denote the locations of morphological landmarks for the eyes of the predator (+) and the swim bladder in the prey (open circle). (b) A state diagram illustrates the major components of the agent-based probabilistic model used to simulate the interactions between predators and prey (see table 1 for symbol definitions and parameter values). Each fish behaves according to an algorithm specific to a particular behavioural state and the probability of transitioning between states is determined by random-number generators with probability distributions matching our measurements (figure 2). Predators (in red) operate between tracking (T) and striking (S) states and prey are either resting (R) or escaping (E). The outcome of a strike is determined by the capture probability (C, equation (2.2)). Simulations of this model were performed with a Monte Carlo method to generate probability distributions of prey survival (see Material and methods for details).

Our video recordings were used to perform measurements of three-dimensional kinematics. We calibrated the cameras using direct-linear transform (DLT) using ‘Digitizing Tools’ software in MATLAB (2015a, MathWorks, Natick, MA, USA) [27]. We used the position of the predator's two eyes to calculate a mean position that approximated the buccal cavity (figure 1a). The posterior margin of the swim bladder was found on the prey's body, which approximates the centre of mass [28] and the heading was measured by matching an ellipsoid to the body. We acquired these landmarks at five key events in each interaction between predator and prey: (i) the initiation of a predator's approach towards the prey, the (ii) opening and (iii) closing of the predator's mouth during a strike, the (iv) initiation and (v) completion of the prey's escape response.

(b). Descriptive statistics

Descriptive statistics were used to characterize the probability of actions by the predator and prey. We recorded the predator-specific parameters of the strike distance (s), the distance from the prey at which a strike was initiated, and the strike duration (τ), the period between the opening and closing of the mouth during suction feeding. For the prey, we found the reaction distance (l), the distance from the predator at which the escape response was initiated and the escape angle (θ), the change in heading from the resting orientation to the escape path. The escape duration (η) included the C-start and subsequent undulatory swimming, until the larva ceased moving. The frequency distribution for each of these parameters was found to be well approximated by the following log-normal probability density function:

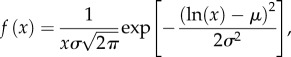2.1

where x is a particular behavioural parameter (s, τ, l, θ or η), μ is the log mean and σ is the log standard deviation. We determined best-fit values for μ and σ for each behavioural parameter by maximum likelihood to binned measured values. The bin size was determined by the Freedman–Diaconis rule, which yielded a number of samples per bin of around 17 measurements. We used the the non-parametric two-sample Kolmogorov–Smirnov test (i.e. KS-test) [29] for statistical comparisons between parameters because they failed to conform to normal distributions.

The probability that the strike of a zebrafish predator is successful depends critically on the distance between the mouth of the predator and the prey [22]. We therefore binned measurements of capture probability (C) and approximated its dependency on distance with the following sigmoidal function:

2.2

where d is the strike distance, d₀ is the decay distance and r is the decay rate. This function additionally approximates the spatial variation in fluid forces that act on prey when subject to suction feeding [30]. The best-fit values for d₀ and r were determined by least squares.

(c). Mathematical model

An agent-based probabilistic model was developed to simulate the conditions of our experiments. This model predicted the two-dimensional motion of a predator and prey [31] according to algorithms that were specific to the behavioural state of each animal (figure 1b). The predator's states were tracking (T) and striking (S) and the prey's were resting (R) and escaping (E), consistent with prior observations [13,22]. The duration of states and probability of transitioning between states were determined by random-number generation that conformed to the log-normal probability distributions (equation (2.1)) and range of measured values. Prey capture was similarly found with a probability that depended on the proximity to the prey distance at mid-gape (equation (2.2)). A simulation was terminated if a strike was successful, otherwise the predator reverted to the tracking state (figure 1b). Single values for speeds and latencies were used for all simulations (table 1), determined by trial and error to replicate measured survivorship and approximate prior measurements [22,32]. The prey escape angle was directed with respect to the right or left side of the body with a probability of moving contralateral to the predator (table 1) as previously measured [13]. Predator and prey kinematics were calculated at a fixed time step (5 ms) and simulations began with random positioning of the prey within one aquarium diameter (Ø = 8.5 cm) of the predator. Simulations were scripted in MATLAB to calculate the motion of both agents and their behavioural states, which consequently determined the number of evasions before prey capture. This model represents a Markov chain that treated the predator and prey's actions as probabilistic, but each outcome also depended on the determinism of their kinematics.

Table 1.

Behavioural parameters and probability distributions.

variable	state	adult predator	juvenile predator
predator
approach speed, U (m s−1)	T	U = 0.13	U = 0.02
predator delay, λ (ms)	T	λ = 10	λ = 100
strike distance, s (m)	T → S	μd =− 4.980, σd = 0.448 (N = 51)	μd =− 5.100, σd = 0.648 (N = 103)
strike duration, τ (s)	S	μτ =− 3.166, στ = 0.331 (N = 53)	μτ =− 3.208, στ = 0.399 (N = 54)
capture probability, C	S	r =− 0.573, d0 = 5.20 (N = 77)	r = 1.99, d0 = 1.60 (N = 91)
prey
reaction distance, l (m)	R → E	μl =− 4.546, σl = 0.587 (N = 73)	μl =− 4.941, σl = 0.582 (N = 91)
escape angle, θ (rad)	E	μθ = 0.144, σθ = 0.449 (N = 206)	μθ = 0.144, σθ = 0.449 (N = 206)
escape duration, η (s)	E	μη =− 1.369, ση = 0.552 (N = 62)	μη =− 1.167, ση = 0.5234 (N = 91)
escape direction, υ	E	υ = 0.696 (N = 206)	υ = 0.696 (N = 206)
escape latency, χ (ms)	E	χ = 8 (N = 15)	χ = 8 (N = 15)
escape speed, u (m s−1)	E	u = 0.4 (N = 12)	u = 0.4 (N = 12)

T, tracking; S, striking; R, resting; E, escaping; μ, log mean; σ, log standard deviation; r, decay rate (mm⁻¹); d₀, decay distance (mm).

Each behavioural state operated by a distinct set of rules. In the tracking state, the predator moved at a fixed approach speed with a direction always headed towards the prey with a time delay (figure 1b). The prey transitioned from rest into the escaping state when the predator moved within the reaction distance with a latency [33]. The prey escaped along a straight path with speed that varied as a single saw-toothed pulse, with the maximum value (the peak of the sawtooth) attained at 20% of the escape duration. This well-characterized prey speed, as determined by a frame-by-frame analysis of escape swimming for 12 larvae.

This model simplified many aspects of the complexity of predator–prey interactions. It assumed two-dimensional kinematics that were not bounded by a barrier. We tested the model's predictions by comparing its predictions of survivorship for 1000 simulations against our measurements (two-sample Kolmogorov–Smirnov). Survivorship was defined as the number of individuals surviving a particular number of strikes, divided by the initial population. We tested whether any single probability distribution was sufficient to predict observed patterns of survivorship by drawing parameter values from a single parameter distribution while leaving all other parameters fixed. These simulations failed to match the measured patterns of survivorship that was achieved by drawing from distributions for all five possible parameters (electronic supplementary material, figure S1), which suggests that variation in all parameters is necessary for a predictive model.

We performed an analysis of the model to evaluate the parameters that had the greatest effect on prey survival. This was achieved by running a Monte Carlo series where individual parameters were varied in increments of 10% between −90% and 100% of their original mean value. For parameters described by a probability distribution, the log-mean parameter, μ, was adjusted to create the desired per cent change in the mean of the distribution with a fixed σ. The range of possible random values for each distribution was also adjusted to retain the same cumulative probability range. The effect of these manipulations was assessed by comparing survivorship against the model's prediction without any parameter variation using a Kruskal–Wallis test.

3. Results

(a). Kinematics

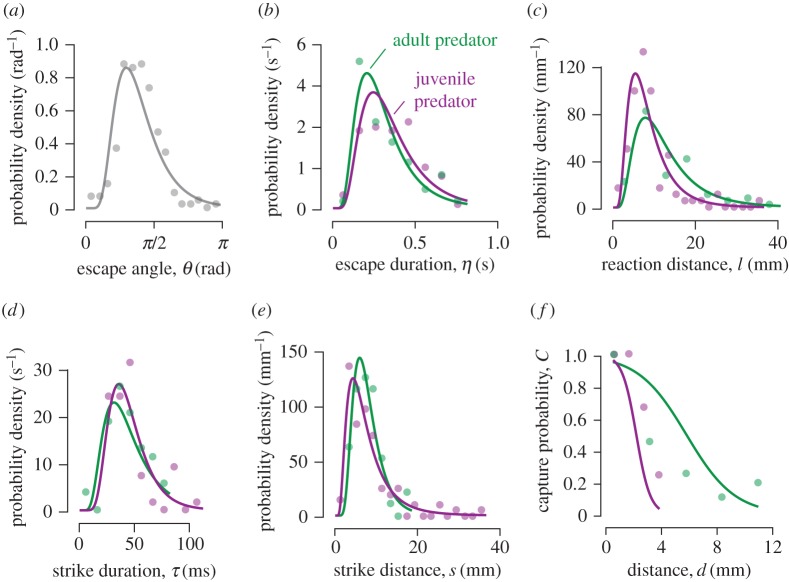
The behaviour of both predator and prey was similar whether the predators were juvenile or adult zebrafish. Prey responded in both cases with indistinguishable differences in escape angle (KS-test: p = 0.86, N = 164). Prey reacted at a mean distance to juvenile predators (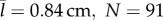) that was about two-thirds the reaction distance to adults (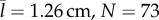), which was a significant difference (KS-test: p < 0.001, N = 164) (figure 2b–c). Escape swimming lasted for about one-third of a second, with a response to juveniles (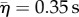, N = 91), that was only 50 ms longer than in response to adults (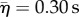, N = 62), but was nonetheless significant (KS-test: p = 0.04, N = 153). Prey also escaped earlier to adult predators by 41 ms, on average, relative to the timing of mid-gape (i.e. mean of times when the predator opened and closed their mouth), a significant difference (KS-test: p = 0.02, N = 89). Juvenile and adult predators were indistinguishable in either strike distance (KS-test: 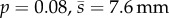, N = 154) or strike duration (KS-test: 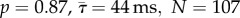) (figure 2d–e). Therefore, much of the behaviour of predator and prey was similar, despite the fact that the adults were nearly twice as large in body length.

Figure 2.

Descriptive statistics of swimming kinematics. (a–e) Measurements of the probability density (circles) for the kinematics of the prey (a–c) and predator (d–e) for experiments that included either a juvenile (purple) or adult (green) predator. Points denote binned measurements for probability density with a sample size determined using the Freedman–Diaconis rule, which yielded N ∼ 17 measurements per point (see table 1 for total sample sizes). Measurements of escape angle (a) were not significantly different between the two types of experiments and these measurements were therefore combined. For each parameter, we performed a nonlinear least-squares fit to the measurements for a log-normal probability density function (equation (2.1)). The log-mean and log-standard deviation values from these fits (table 1) were consequently used to describe the probability of events in our mathematical model (figure 1b). (f) The capture probability was measured as a function of distance between the predator and prey and we similarly performed a curve fit to approximate this relationship (equation (2.2)) for our model.

Although they exhibited similar behaviour, adult predators were more effective than juveniles. Juveniles did not succeed in capturing prey beyond a distance of 3.2 mm (N = 91), whereas adults were successful at a maximum distance that was about three times greater (10.4 mm, N = 77) and showed a decay distance that was greater by about the same factor (table 1, figure 2f). We found that this result was unaltered by excluding the furthest point measured for capture distance among adult predators (figure 2f, KS-test: p = 0.28). We tested whether the superior feeding of adults was due to juveniles approaching the prey with inferior accuracy by measuring the bearing, the prey's radial position relative to the predator's heading. The bearing when prey initiated an escape was not significantly different (KS-test: p = 0.15) between juveniles (N = 91) or adults (N = 77). At mid-gape, however, prey succeeded in evading juvenile predators to the extent that the median bearing (13.1°), was less than half that of adult predators (30.0°), which was a significant difference (KS-test: p < 0.01). Therefore, adult predators were more capable of adjusting their strike towards escaping prey than juvenile predators. This ability was included in our model through the measured probability distributions of capture success (figure 2f).

(b). Mathematical model

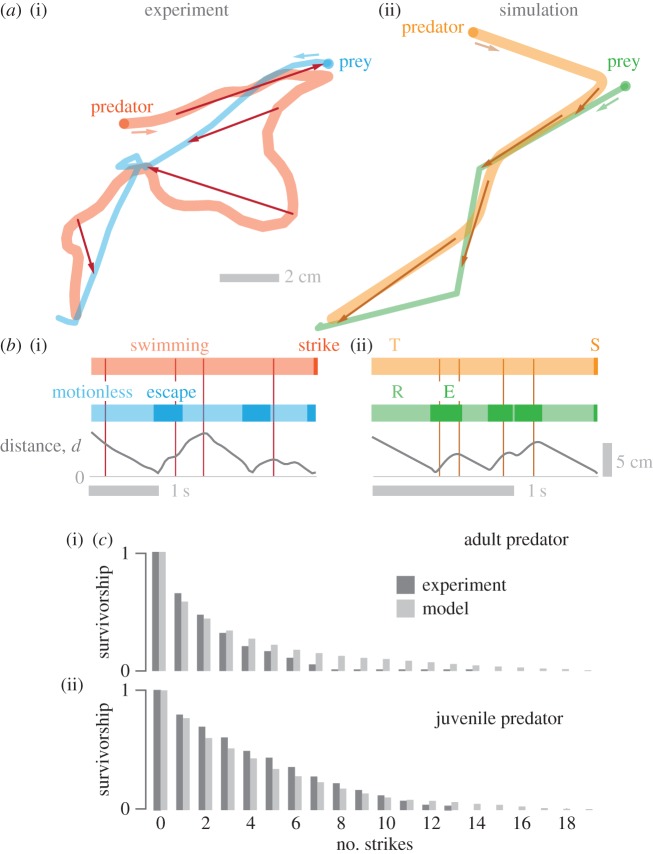
The model predicted kinematics and prey survivorship that were similar to our measurements. The temporal sequence of events in the model offered a reasonable approximation of the kinematics of live predator–prey interactions (figure 3a,b). Measured survivorship decreased monotonically from the first strike and extended to as many as 20 strikes, with a slower decline in survivorship for juvenile predators (figure 3c). The survivorship predicted by the model was statistically indistinguishable for both adult (KS-test: p = 0.93, N = 73) and juvenile (KS-test: p = 0.86, N = 91) predators. Furthermore, all trends from the parameter analysis of the pursuit–evasion model were similar between the adults (figure 4) and juveniles (electronic supplementary material, figure S2).

Figure 3.

Comparison between experimental measurements and modelling. (a) Trajectories of predator and prey from a representative experiment (i) and simulation (ii). The position of predator and prey that correspond to particular time points are shown with connecting arrows. (b) Ethograms for these trajectories illustrate the temporal changes in the predator's swimming and strike (i), which are respectively modelled by the tracking (T) and striking (S) states (ii). The prey's behaviour while motionless and during escape (i) were respectively modelled as resting (R) and escape (E) modes (ii). For both ethograms, the distance (d) between predator and prey are shown. Particular moments in the trajectories are highlighted with vertical lines that correspond with the same-coloured arrows in (a). (c) The probability that a prey survives over a particular number of strikes is shown for adult (i) and juvenile (ii) predators for experiments (dark grey) and simulations (light grey).

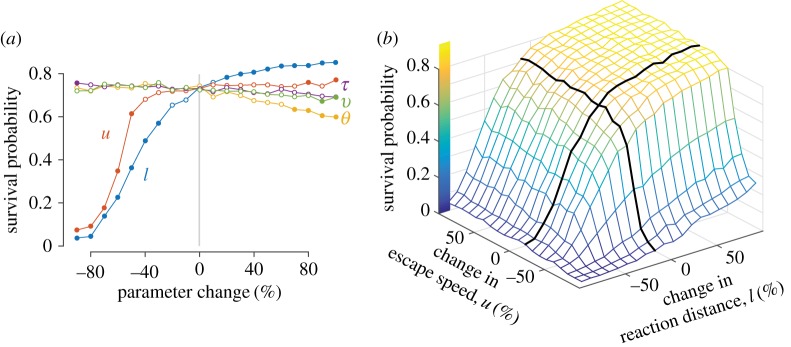
Figure 4.

Parameter analysis of the mathematical model to examine the effects on escape probability. (a) We individually varied the mean of a parameter among simulations by manipulating its probability distribution (figure 2, see table 1 for parameter definitions and values). Each point represents the survival probability of prey among 1000 simulations and filled circles denote a significant difference (KS-test: p < 0.05) from the observed probability. Simulations that varied in escape angle (θ) differed by a interval of 0.127 rad. (b) Variation in escape probability was examined with respect to both escape speed and reaction distance. All simulations shown here used an adult predator, although similar results were obtained with a juvenile predator (electronic supplementary material, figure S2).

Our parameter analysis revealed that escape speed and reaction distance were the only parameters that showed any noteworthy effect on survival. Changes in escape duration, escape direction and escape angle yielded statistically insignificant or otherwise small changes in escape probability (figure 4a). An increase in escape speed similarly had a negligible effect on survival, but survival probability did decline when speed was reduced by 50% or more. By contrast, an increase in reaction distance caused escape probability to elevate by as much as 16% and a decrease of at least 30% had a dramatically adverse effect on survival (figure 4a). A two-dimensional parameter analysis of reaction distance and escape speed (figure 4b) showed little evidence for an interactive effect between these two parameters.

4. Discussion

We found that the survival of larval fish does not increase by escaping at a faster speed or by varying direction, but only by responding from a greater distance. These results were derived from an agent-based probabilistic model (figure 1b) that calculated the trajectories of predator and prey and the outcome of predatory strikes (figure 3a,b). This model successfully replicated prey survivorship (figure 3c) by simulating behavioural actions that matched our measurements (figure 2). Our analysis of its predictions suggests that prey survival in larval fishes may only be enhanced by increasing the sensitivity of predator detection.

(a). Locomotor performance and prey survival

The survival of prey depends largely on the actions of the predator. In contrast with the explosive speed of an escape response [20], adult zebrafish tend to approach their prey substantially slower than their capacity, often by braking [32]. We found that the approach speed amounted to less than one-third the maximum speed of escaping larvae (table 1), which is consistent with previous measurements [22]. This approach relates strategically to the mechanics of feeding. The suction feeding of fishes succeeds in capturing prey in only a small region around the mouth over a duration of merely tens of milliseconds [34–36]. A slow approach is common among suction-feeding fishes and is likely a means of enhancing strike accuracy [8,9]. This style of predation is seen in many species of fish [37]. Furthermore, our data suggest that adult and juvenile zebrafish are more likely to capture when approaching larval zebrafish with a slower approach (electronic supplementary material, figure S4). Therefore, the limited range of suction feeding may constrain some predators to a slow approach while offering prey an opportunity to escape [24]. Despite this strategic advantage for prey, adult zebrafish captured prey on the first strike more than one-quarter of the time and rarely needed more than three strikes to be successful (figure 3c).

The effectiveness of an escape has previously been considered by classic pursuit–evasion models of fish predation. This theory resolves how the direction of an escape affects the distance between predator and prey [5,31], generally by modelling a single encounter with the assumption that both animals move with a fixed heading and speed. A recently developed version of this model suggests that animals like zebrafish operate in a ‘slow-predator’ strategic domain [38], where the predator moves more slowly than the prey. In this domain, no optimal escape angle exists and prey may evade predators with a broad range of effective escape directions. A faster escape speed serves only to modestly expand the range of effective escape angles. Consistent with these predictions, our model found a monotonic decrease in survival as we reduced escape speed below half of the observed value (figure 4a). We additionally found only modest differences in survival between experiments using adult and juvenile predators (figures 2 and 3c), despite a nearly twofold difference in body size and speed.

These predictions would not hold for cases where the predator is faster than the prey. In such a strategic domain, an optimal escape angle arises for the prey and failure to move in that direction is predicted to adversely affect survival [5,38]. Ram-feeding fishes strike at prey while swimming at a relatively high speed and may thereby place prey at a strategic disadvantage. Success in ram feeding may, in-turn, require superior coordination in directing and timing a strike [11]. Ram feeding in this way shows greater similarity in strategy to flying predators such as birds [15], bats [16] and insects [39]. Prey may benefit by escaping in a direction that conforms to an optimal value [5], by being unpredictable [6] or escaping along a trajectory with a small radius of curvature [7,40].

(b). Prey survival depends on reaction distance

The reaction distance has broad strategic significance. Classic pursuit–evasion models support the simple notion that prey are more evasive if they start from further away [5,31,38]. This principle is consistent with evolutionary models that contrast the fitness benefit of responding from a distance against its potential costs [41,42]. For example, escape responses that are initiated unnecessarily may be energetically expensive, prohibit foraging or succeed in revealing cryptic prey [43]. Responding from a great distance may even be inferior on purely strategic grounds. A prey that is slower than a predator, but capable of executing a tight turn, may be more evasive when initiating this manoeuvre at the final moments of a predatory strike, rather than providing the opportunity for the predator to adjust course [7]. Therefore, a greater reaction distance offers a clear strategic benefit in zebrafish (figure 4), but may not be universally advantageous.

The primacy of reaction distance underscores the strategic importance of predator detection. Responding to a predator from afar depends on the sensitivity of receptor organs and the capacity of the nervous system to rapidly recognize a threatening cue and trigger an escape response. As in invertebrate zooplankton [14] and insect prey of spiders [44,45], zebrafish larvae use flow sensing to detect the bow-wave of flow generated by an approaching predator [22]. Flow-sensing may be augmented by olfactory cues [46], though zebrafish do not acquire a sensitivity to the alarm pheromone Schreckstoff until a later stage of growth (more than 48 dpf) [46]. Using the lateral line system, zebrafish larvae may respond to flow up to a distance of 1.3 cm [13] ahead of a gliding zebrafish adult. This range encompasses many of the responses that we recorded (figure 2c), which supports a role of the lateral line in our experiments. This would agree with previous experiments that have shown flow sensing to be necessary for survival in zebrafish larvae [22]. Flow sensing offers the capacity to trigger an escape with a very brief (less than 10 ms) latency [47]. By contrast, a looming visual stimulus succeeds in stimulating an escape response in zebrafish larvae [48], but the demands for visual processing necessitate a latency that is at least 20-fold longer than for flow sensing [49]. Nonetheless, the greatest reaction distances that we observed were outside the range of the lateral line and therefore likely generated by the visual appearance of the predator. The visual system consequently offers prey fish the means to enhance survival by responding to a predatory threat from a distance (figure 4).

(c). Summary

We found that zebrafish larvae operate in a slow-predator strategic domain when preyed upon by adults and juveniles of the same species. As a consequence, increasing the speed or varying the direction of an escape response has a negligible effect on survival (figure 4). Survival may instead be enhanced by initiating the escape from greater distance by rapidly identifying the predator as a threatening visual stimulus. These findings offer valuable insight into the key strategic factors that govern predator–prey interactions in a diversity of similar fishes and other animals that operate with similar strategy.

Data accessibility

Data related to this study may be accessed through the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.mr720 [50].

Author's contributions

The study was designed in collaboration between A.N. and M.J.M.H. A.N. and C.N. performed all experiments and kinematic analysis. The agent-based probabilistic model was created by A.N., with guidance from M.J.M.H. The manuscript was written collaboratively by A.N. and M.J.M.H.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by grants to M.J.M.H. from the National Science Foundation (IOS-1354842) and the Office of Naval Research (N00014-15-1-2249).