Relativistic GW calculations on CH₃NH₃PbI₃ and CH₃NH₃SnI₃ Perovskites for Solar Cell Applications

Abstract

Hybrid AMX₃ perovskites (A = Cs, CH₃NH₃; M = Sn, Pb; X = halide) have revolutionized the scenario of emerging photovoltaic technologies, with very recent results demonstrating 15% efficient solar cells. The CH₃NH₃PbI₃/MAPb(I_1−xCl_x)₃ perovskites have dominated the field, while the similar CH₃NH₃SnI₃ has not been exploited for photovoltaic applications. Replacement of Pb by Sn would facilitate the large uptake of perovskite-based photovoltaics. Despite the extremely fast progress, the materials electronic properties which are key to the photovoltaic performance are relatively little understood. Density Functional Theory electronic structure methods have so far delivered an unbalanced description of Pb- and Sn-based perovskites. Here we develop an effective GW method incorporating spin-orbit coupling which allows us to accurately model the electronic, optical and transport properties of CH₃NH₃SnI₃ and CH₃NH₃PbI₃, opening the way to new materials design. The different CH₃NH₃SnI₃ and CH₃NH₃PbI₃ electronic properties are discussed in light of their exploitation for solar cells, and found to be dominantly due to relativistic effects. These effects stabilize the CH₃NH₃PbI₃ material towards oxidation, by inducing a deeper valence band edge. Relativistic effects, however, also increase the material band-gap compared to CH₃NH₃SnI₃, due to the valence band energy downshift (~0.7 eV) being only partly compensated by the conduction band downshift (~0.2 eV).

Hybrid AMX₃ perovskites (A = Cs, CH₃NH₃, methylammonium, hereafter MA; M = Sn, Pb; X = halide) are attracting considerable attention in the scenario of emerging photovoltaic technologies¹,²,³,⁴,⁵,⁶,⁷. Introduced in 2009 by Kojima et al.¹ as absorbing materials in dye-sensitized solar cells (DSCs) based on a liquid electrolyte, a rapid evolution very recently led to 15% efficient solid-state DSCs based on the MAPbI₃ perovskite and the solid Spiro-MeO-TAD hole transporter². Notably, Lee et al.³ have demonstrated that the MAPb(I_1−xCl_x)₃ perovskite can serve both as light-harvesting and electron conductor in meso-superstructured solar cells³ employing an “inert” Al₂O₃ scaffold and spiro-MeOTAD, reaching a remarkable 12.3% conversion efficiency⁴. Liu et al. very recently demonstrated a 15.4% efficient non-mesostructured planar heterojunction solar cell, obtained by vapor deposition of the MAPbI_3−xCl_x perovskite⁵. The high photovoltaic efficiency of these devices is mainly due to the optimal MAPbI₃/MAPbI_3−xCl_x perovskites band gap (~1.6 eV), which directly influences the solar cell photocurrent density (J_sc) and contributes to the open circuit voltage (V_oc) by setting the main solar cell energetics. Also, a high carrier mobility within the perovskite ensures efficient collection of photo-generated charges.

MAPbI₃ and its Cl-doped MAPb(I_1−xCl_x)₃ analogue have so far dominated the field, while the similar MASnI₃ has been scarcely explored for photovoltaic applications, despite showing a reduced band-gap and interesting electronic properties⁸,⁹. Mixed Sn/Pb MASn_1−xPb_xI₃ perovskites have also been reported⁹. To our knowledge, the only photovoltaic application of Sn-based perovskites is the use of CsSnI₃ as a solid hole transported in DSCs⁶. Replacement of Pb by the more environment-friendly Sn would facilitate the large uptake of perovskite-based photovoltaics. The MAPbI₃ and MASnI₃ perovskites show a similar tetragonal structure⁹ (although in different temperature ranges) but different optical properties, with MASnI₃ (MAPbI₃) having an absorption onset at 1.2 (1.6) eV⁹,¹⁰. Experimental data also indicate that CsSnI₃ and MASnI₃ are excellent hole transporters⁶,⁹, while MAPb(I_1−xCl_x)₃ and MAPbI₃ can sustain high rates of electron and hole transport, respectively³,⁷.

Despite the extremely fast progress, the materials electronic properties which are key to the photovoltaic performance are relatively little understood. Understanding the origin of the different electronic properties of AMX₃ materials, with M = Sn and Pb, and possibly of mixed Sn/Pb materials, could represent a fundamental step towards the large-scale uptake of perovskites-based photovoltaics. In this context, a first principles computational approach capable of reliably calculating the materials band-gap and electronic/optical properties, thus trustfully allowing to design new materials and to interpret their properties, is fundamentally required. While standard Density Functional Theory (DFT) provides reliable structures and stabilities of perovskites¹¹,¹²,¹³, it considerably underestimates the band-gap of these materials and of semiconductors in general. DFT with asymptotically correct functionals partly overcomes this shortcoming¹³. Many body perturbation theory, within the GW approach¹⁴,¹⁵, although more computationally demanding, constitutes a solid framework to improve upon DFT¹²,¹⁶. Contrary to expectations, DFT-calculated band-gaps of MAPbI₃ were in surprisingly good agreement, within ±0.1 eV, with experimental values¹⁷,¹⁸. For the supposedly similar ASnX₃ perovskites, DFT provided a ~1 eV band-gap underestimate⁸,¹¹,¹²,¹⁹. Such an unbalanced description of Sn- and Pb-based materials hampers any predictive materials design/screening or comparative interpretation of their properties.

The large calculated band-gap difference between ASnX₃ and APbX₃ perovskites might be due to relativistic effects¹⁸, particularly strong in Pb²⁰,²¹. Relativistic effects are usually approximated by scalar relativistic (SR) and, to higher order, by spin-orbit coupling (SOC) contributions. A recent DFT investigation has confirmed a relevant SOC in MAPbI₃, leading to a strong, and opposite to the estimated GW correction, band-gap reduction²². A strong band-gap underestimate was however retrieved²², in line with the expected behavior of DFT.

This analysis poses the quest for a reliable and efficient theoretical framework for the electronic structure simulation of ASnX₃ and APbX₃ perovskites and possibly of mixed Sn/Pb compounds. The method of choice is ideally a GW approach incorporating SOC²³. A very effective GW implementation is also required, which was devised by some of us²⁴,²⁵. Here we develop a novel approach to introduce SOC effects into our efficient GW scheme. The resulting SOC-GW method is computationally affordable, allowing us to accurately model the electronic, optical and transport properties of MASnI₃ and MAPbI₃ perovskites, opening the way to new materials design. The different MASnI₃ and MAPbI₃ electronic and optical properties are discussed in light of their exploitation for solar cells applications, and found to be dominantly due to relativistic effects.

Results and discussion

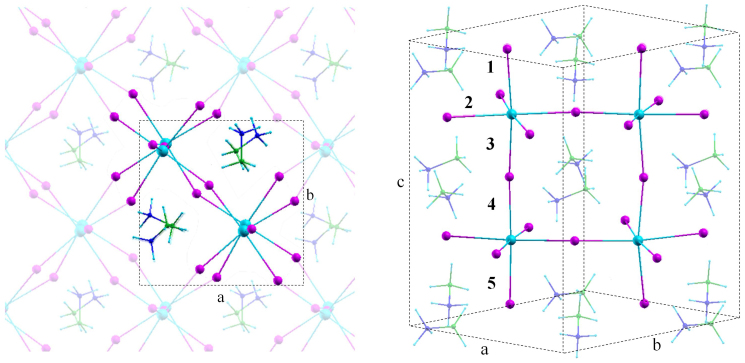
Geometry optimization of the atomic positions (and cell parameters) of MAPbI₃ and MASnI₃ were performed by SOC-DFT (SR-DFT) without any symmetry constraints starting from a tetragonal I4 mcm structure, with a unit cell made of four MAMI₃ units, containing 48 atoms and 200 electrons, see the MAPbI₃ structure in Figure 1. Using the experimental cell parameters, SR-DFT and SOC-DFT provide rather similar geometries, Table 1. Cell relaxation leads to calculated bond lengths and lattice parameters in good agreement (within 1–2%) with experimental data, reproducing the long-short alternation of axial M-I bonds⁹, Figure 1. The expected shortening of M-I bonds upon Pb → Sn substitution is also nicely reproduced by our calculations, Table 1. The calculated band-gap values obtained at various levels of theory are graphically represented in Figure 2. All the investigated systems are characterized by a direct band-gap at the Γ point of the Brilluoin zone¹¹,¹⁸, see below. For MAPbI₃ and MASnI₃ the SR-DFT calculated band-gaps are 1.68 and 0.61 eV, to be compared to experimental values of 1.6 and 1.2 eV, respectively. Thus, while for MAPbI₃ the band-gap is reproduced by SR-DFT, for MASnI₃ a 0.6 eV band-gap underestimate is retrieved. Moving to SOC-DFT, the band-gap values of both materials are strongly underestimated, by as much as 1 eV, although a qualitatively correct Pb → Sn band-gap variation is calculated, with a ~0.3 eV calculated difference against a ~0.4 eV experimental difference. The calculated band-gap underestimate is in line with the expected behavior of DFT and with previous SOC-DFT results for MAPbI₃²². To correct the DFT-calculated band-gaps, we carried out SR- and SOC-GW calculations. SR-GW calculations for MAPbI₃ lead to a ~1 eV overestimate of the band-gap (2.67 vs.1.6 eV), while only ~0.3 eV band-gap overestimate is found for MASnI₃ (1.55 vs. 1.2 eV), again leading to an unbalanced description of the two systems, Figure 2. Rewardingly, SOC-GW delivers calculated band gaps (1.67 and 1.10 eV for MAPbI₃ and MASnI₃, respectively) in excellent agreement, within ±0.1 eV, with experimental values. Notice that ±0.1 eV is the inherent uncertainty of our calculations, as estimated on the basis of the calculations convergence. To check the degree of convergence of our GW-calculated band gaps, we repeated a SR-GW calculation for a supercell containing 2 × 2 × 2 replica of the 48 atoms primitive cell. Addressing this 384 atoms supercell with Gamma point sampling is equivalent to considering the primitive 48 atoms cell and sampling the Brillouin's zone with a regular 2 × 2 × 2 mesh of k-points. We found that the SR-GW band gap of MAPbI₃ decreases by 0.05 eV with the larger cell. An equivalent error is expected for the other GW-calculated band gaps.

Figure 1. SR-DFT optimized structure of MAPbI₃ viewed from two different orientations.

The unit cell is shown on the left. On the right we also show a labeling of the Pb-I bond distances reported in Table 1. Calculated (experimental⁹,²⁶) cell parameters for MAPbI₃: a = 8.78 (8.85–8.86) Å; c = 12.70 (12.64–12.66) Å. Calculated (experimental⁸,⁹) cell parameters for MASnI₃: a = 8.71 (8.76–8.73) Å; c = 12.46 (12.43–12.50) Å. Pb = light blue; I = purple; N = blue; C = green.

Table 1. Calculated average M-I bond distances (Å), see bond definitions in Figure 1, by SR-DFT and SOC-DFT employing the experimental cell parameters (exp. cell) and relaxing both the atomic positions and cell parameters by SR-DFT (relaxed cell).

	MAPbI3
Pb-I bonds	SR-DFT (exp. cell)	SOC-DFT (exp. cell)	SR-DFT (relaxed cell)
1	3.24	3.24	3.21
2	3.20	3.20	3.19
3	3.17	3.16	3.16
4	3.19	3.20	3.21
5	3.19	3.20	3.16

Figure 2.

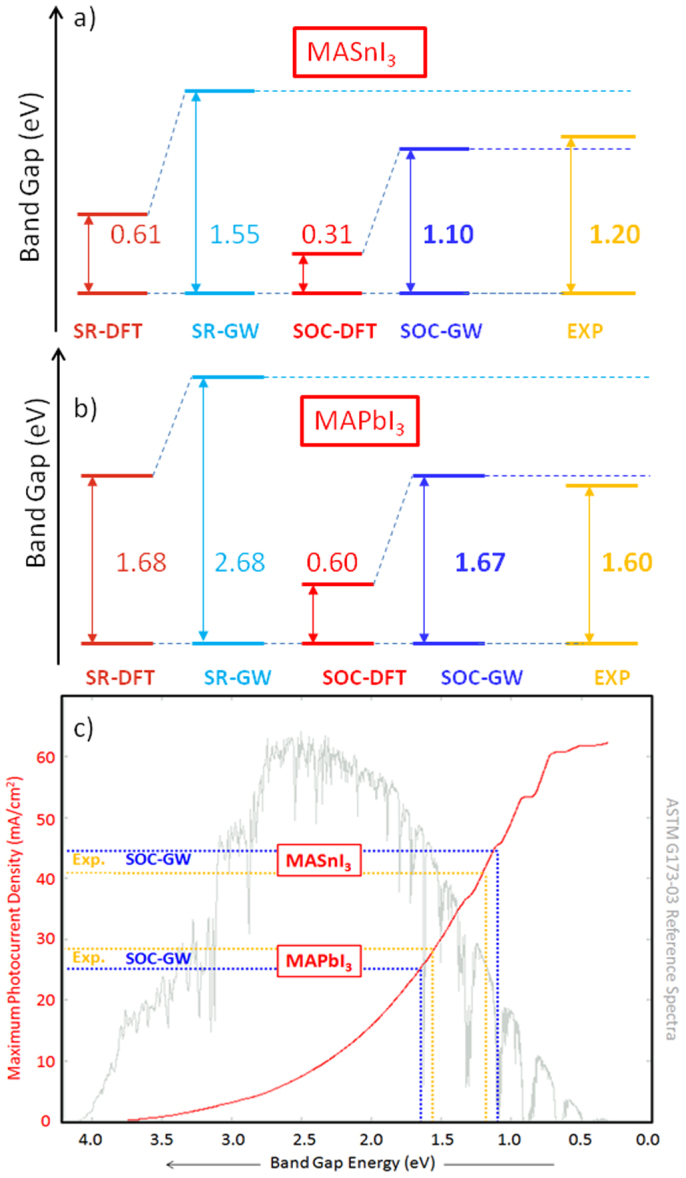
Calculated band-gaps at various levels of theory for MASnI₃ (a) and MAPbI₃ (b) perovskites. (c) Maximum short-circuit photocurrent density which can be extracted from a solar cell employing MASnI₃ and MAPbI₃, as obtained by integration of ASTM G173-03 reference spectrum with the assumption of 100% IPCE above the band-gap. Experimental data from Ref. 1, 30 and 9.

To trace a direct connection between our calculations and the performance of a solar cell employing the investigated perovskites, in Figure 2 we report the maximum J_sc which can be extracted from a solar cell employing a material of varying band gap. The agreement between our SOC-GW calculated band-gaps and the experimental ones allows us to estimate the maximum J_sc within ~10%. As an example, for MAPbI₃ we calculate a maximum J_sc of ~25 mA/cm² against a ~28 mA/cm² value derived from the experimental band-gap. It is also worth noticing the potential of the MASnI₃ perovskite to deliver extremely high J_sc values due to its reduced band gap. This characteristic, along with its good transport properties, make this material potentially promising to replace MAPbI₃, although some sensitivity of the material to the preparation conditions have been reported⁹.

Top J_sc values measured for solar cells based on MAPbI₃ stand at ~21 mA/cm^{2 2},⁵. The reason for the non-optimal photocurrent generation can be traced back to the reduced light harvesting efficiency measured in the 600–800 nm range (~2.0–1.5 eV)², inset of Figure 3. Based on our SOC-GW calculated electronic structure, we thus simulated the optical absorption spectrum of MAPbI₃, albeit neglecting electron-hole interactions, see Method section below. The employed procedure was shown to represent a reasonable approximation to the optical spectra of small band-gap semiconductors²⁷. The results are reported in Figure 3, along with experimental data for MAPbI₃. The calculated data satisfactorily matches the experimental UV-vis spectrum: the band-gap absorption, the rise of the spectrum at higher energy and the spectral feature at ~2.6 eV are nicely reproduced, despite the approximate spectral calculation. Compared to MAPbI₃, the absorption spectrum of MASnI₃ shows a red-shift (in line with the reduced band-gap) and increased intensity, Figure 3. Recently, Even et al.²⁸ reported on the electronic structure of the related CsSnI₃ and CsPbI₃ materials by SOC-DFT and SR-GW calculations, finding a 0.6 eV band-gap for CsSnI₃ by SR-GW. Probably the replacement of MA by Cs and the employed cubic symmetry are at the origin of the considerable band-gap underestimate.

Figure 3. Comparison between the experimental UV-vis spectrum of MAPbI₃ (red line) and the SOC-GW calculated one (blue line).

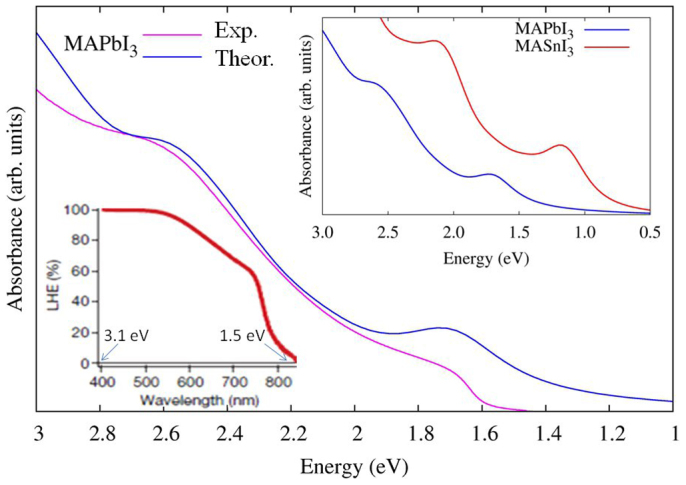
Notice that the experimental spectrum has been scaled to match the intensity of the calculated one in correspondence of the high energy feature. Top right inset: Comparison between the SOC-GW calculated spectra of MASnI₃ (red line) and MAPbI₃ (blue line). Bottom left inset: LHE for the 15% MAPbI₃-based solar cell of Ref. 2. Adapted with permission from Ref. 2. The experimental spectrum was recorded at room temperature for MAPbI₃ casted on a mesoporous TiO₂ film.

To provide a rationale for the observed band-gap and spectral variation, we investigated both structural and electronic factors. A SOC-GW calculation performed for MASnI₃ at the geometry and cell parameters of MAPbI₃ provided a band-gap of 1.48 eV, while rescaling the MAPbI₃ coordinates to the experimental MASnI₃ cell parameters and substituting Pb by Sn, led to a 0.17 eV band-gap increase compared to MASnI₃, as estimated by SOC-DFT. This data suggests that out of the 0.57 eV calculated band-gap difference, ~0.2 eV are due to structural differences between MASnI₃ and MAPbI₃, such as the different degree of tilting of the MI₆ octahedra.

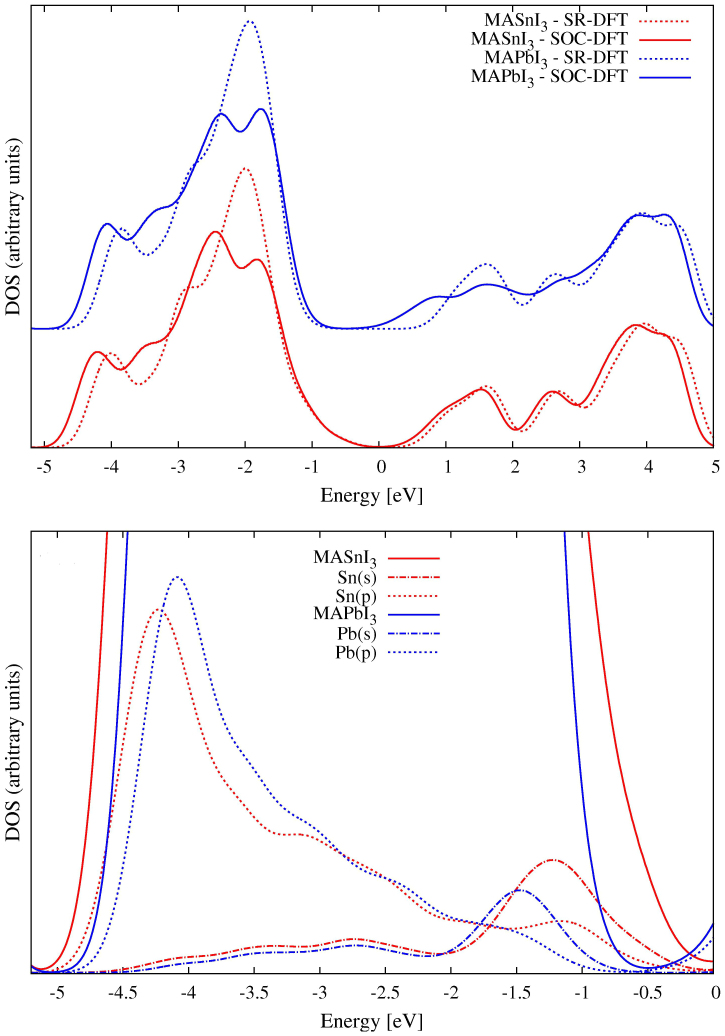
To investigate the electronic factors possibly responsible of the residual band gap variations we analyze the SOC-GW Density of States (DOS) in Figure 4. A comparative picture of the electronic structure of the two systems can be gained by aligning the 2p band of the CH₃NH₃⁺ carbon atoms in the two materials, which appears as a narrow feature at ~8 eV below the valence band (VB) maximum in MAPbI₃, Supplementary Information. This choice is justified by the fact that the organic molecules only weakly interact with the inorganic matrix by possible hydrogen bonding occurring through the ammonium groups. For the investigated systems the VB top is mainly composed by I p orbitals, mixed in variable percentages with Pb or Sn s orbitals, while the conduction band (CB) is mainly contributed by Pb or Sn p orbitals, partly hybridized with I states¹⁷. The VB structure of the investigated systems is relatively similar, although MASnI₃ shows a widening and structuring of the VB compared to MAPbI₃ due to states found within ~1 eV below the VB maximum. The MAPbI₃ CB has a tail at lower energy compared to MASnI_3. Notably, in the absence of SOC the DFT-calculated CB of MAPbI₃ has essentially the same structure as that of MASnI₃, see Figure 5, the latter being only slightly perturbed by SOC compared to the large CB downshift observed for MAPbI₃, Figure 5, as previously noted²². It is also interesting to notice that a ~0.2 eV VB broadening is predicted for both MASnI₃ and MaPbI₃ by SOC-DFT compared to SR-DFT, Figure 5.

Figure 4. Electronic DOS for MASnI₃ (red line) and MAPbI₃ (blue line) calculated by SOC-GW.

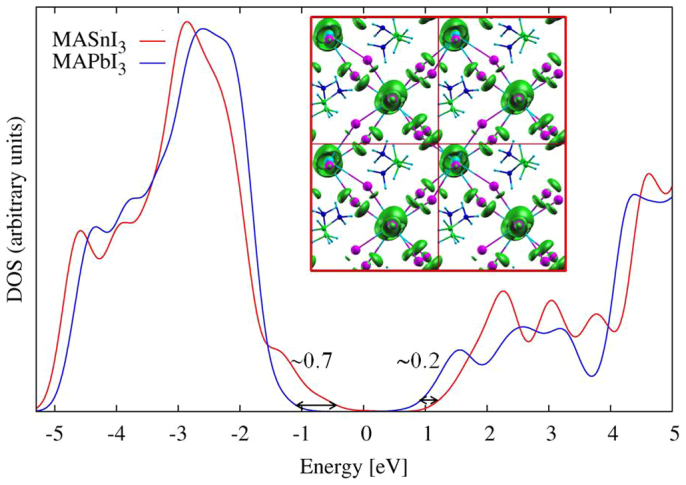
The DOS have been aligned at the carbon 2p peak. Inset: SOC-DFT plot of the electron density associated to the highest occupied state of MASnI₃ at the Γ point of the Brilluoin zone.

Figure 5. Upper panel: Electronic DOS for MASnI₃ (red lines) and MAPbI₃ (blue lines) calculated by SOC-DFT (solid lines) and SR-DFT (dashed lines).

The DOS have been aligned at the carbon 2p peak, setting the zero of the energy of the SOC-DFT HOMO of MaSnI₃. Bottom panel: SOC-DFT DOS for MASnI₃ (red solid lines) and MAPbI₃ (blue solid lines) along with the Sn or Pb s (dash-points) and p (dots) contributions to the total DOS.

The reduced spectral intensity calculated for MAPbI₃ appears thus to be due to the comparatively lower DOS close to the CB bottom, which is due to SOC. We can also compare the relative VB/CB position with available experimental data for MAPbI₃ and the analogous CsSnI₃ which indicate the VB and CB edges at −5.43/−3.93 and −4.92/−3.62 eV, respectively⁶,²⁹. Our calculations are in good agreement with the relative band edges alignment provided by experiments, and provide a ~0.7 (~0.2) eV VB (CB) energy downshift for MAPbI₃ compared to MASnI₃ against a 0.51 (0.31) eV experimental differences (recall we compare VB/CB data for CsSnI₃ to MASnI₃). The analysis of the aligned DOS allows us to understand the origin of the states responsible of the MASnI₃ reduced band gap, i.e. those states protruding out of the main VB peak, which are not found in MAPbI₃. These occupied states, of main I p character, have however a sizable Sn s and p contribution and are the result of the sizable anti-bonding interaction between Sn 5s and I 5p orbitals, Figure 4. The corresponding Pb 6s orbitals are found at lower energy, Figure 5, and have thus a lower tendency to mix with I 5p orbitals, thus the abrupt VB DOS rise found in MAPbI₃ compared to MASnI₃. Notice that the energetics of the 5s/6s shells in Sn/Pb are due to relativistic effects, which substantially stabilize the Pb 6s shell leading to the so-called “inert 6s² lone pair”²⁰,²¹. Thus, if on the one hand, relativistic effects stabilize the CH₃NH₃PbI₃ material towards oxidation, by inducing a deeper valence band edge, on the other hand, they also increase the material band-gap compared to CH₃NH₃SnI₃, due to the valence band energy downshift (~0.7 eV) being only partly compensated by the conduction band downshift (~0.2 eV).

In line with the DOS changes, relativistic effects also deeply modify the band structure of the investigated materials, especially that of the MAPbI₃ perovskite, Supplementary Information. The SOC-GW band structure for MASnI₃ and MAPbI₃ are displayed in Figure 6. Apart from the aforementioned band-gap change, introduction of SOC leads to an increased band dispersion along the investigated high symmetry directions of the Brilluoin zone, see Table 2. This leads to sizable differences for the calculated effective masses of electrons and holes, m_e and m_h, respectively, derived by parabolic band fitting around the Γ point of the Brilluoin zone, which are reported in Table 2. As it can be noticed from the SOC-GW data of Figure 6, the CB dispersion is quite similar for MASnI₃ and MAPbI₃, while for MASnI₃ the VB shows a considerably stronger dispersion, which is directly reflected into the calculated effective masses of Table 2. We can also compare the calculated reduced masses μ = m_e • m_h/(m_e + m_h) with experimental data for MAPbI₃³⁰, for which values of 0.09, 0.12 and 0.15 m₀ (m₀ is the electron mass) have been reported. Our minimum, average and maximum SOC-GW μ values calculated for MAPbI₃ are 0.08, 0.11 and 0.17 m₀, closely matching the experimental range of values. Recent SOC-DFT results for the cubic phases of CsSnI₃ and CsPbI₃ have reported m_h values of 0.12 and 0.04 m₀²⁸, while for pseudo-cubic MAPbI₃ SOC-DFT m_e and m_h values of 0.23 and 0.29 m₀ have been reported³¹. The values obtained for CsSnI₃ and CsPbI₃²⁸ are smaller than our calculated effective masses, in line with the band-gap underestimate discussed above, while the values of Ref. 31 are in slightly larger than our average values³¹. Our results generally agree with previous calculations in predicting a smaller m_h value for MASnI₃ than MAPbI₃; with the predicted reduction of effective masses introduced by SOC-DFT compared to SR-calculations³¹; and with the smaller m_e than m_h value for MAPbI₃³¹.

Figure 6. Calculated band structure (VB and CB highlighted as thick solid lines) for MAPbI₃ (A, blue lines) and MASnI₃ (B, red lines) along the directions Γ (0,0,0) → M (0.5, 0.5,0); Γ → Z (0,0,0.5); Γ → X (0,0.5,0); Γ → A (0.5,0.5,0.5); Γ → R (0,0.5,0.5), as calculated by SOC-GW.

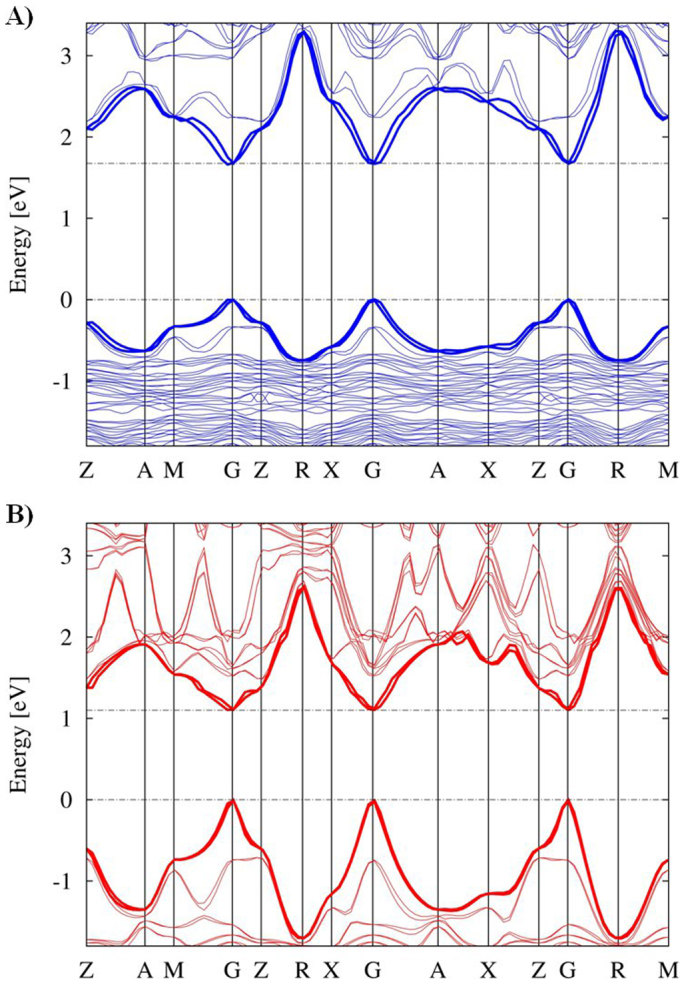
The energy zero is set in both cases at the highest occupied state.

Table 2. SOC-GW, SOC-DFT and SR-DFT effective masses (relative to the electron mass m₀) for holes (m_h) and electrons (m_e) calculated by parabolic fitting of the VB and CB along the directions Γ (0,0,0) → M (0.5, 0.5,0); Γ → Z (0,0,0.5); Γ → X (0,0.5,0); Γ → A (0.5,0.5,0.5); Γ → R (0,0.5,0.5), their average (AVG), and the corresponding reduced masses (μ) for MAPbI₃ and MASnI₃.

	MAPbI3			MASnI3
	mh	me	μ	mh	me	μ
	SOC-GW
Γ → M	0.27	0.17	0.10	0.12	0.31	0.09
Γ → Z	0.40	0.29	0.17	0.20	0.45	0.14
Γ → X	0.20	0.17	0.09	0.10	0.26	0.07
Γ → A	0.22	0.16	0.09	0.11	0.21	0.07
Γ → R	0.18	0.15	0.08	0.09	0.17	0.06
AVG	0.25	0.19	0.11	0.13	0.28	0.09
	SOC-DFT
Γ → M	0.30	0.16	0.10	0.16	0.26	0.10
Γ → Z	0.44	0.26	0.16	0.24	0.38	0.15
Γ → X	0.22	0.16	0.09	0.12	0.22	0.08
Γ → A	0.24	0.14	0.09	0.12	0.18	0.07
Γ → R	0.20	0.14	0.08	0.12	0.14	0.06
AVG	0.28	0.17	0.10	0.15	0.24	0.09
	SR-DFT
Γ → M	0.42	1.30	0.32	0.18	1.08	0.15
Γ → Z	0.48	0.52	0.25	0.26	0.46	0.17
Γ → X	0.30	1.14	0.24	0.22	1.10	0.18
Γ → A	0.36	0.40	0.19	0.14	0.28	0.09
Γ → R	0.26	0.28	0.13	0.12	0.22	0.08
AVG	0.36	0.73	0.23	0.18	0.63	0.13

It is worth noting that when evaluating at the SR level the screened Coulomb interaction W, we can also evaluate the high-frequency dielectric tensor by GW. Averaging over the three Cartesian directions, we find high-frequency dielectric constants of 8.2 and 7.1 for MASnI₃ and MAPbI₃, respectively. We checked, for the case of MAPbI₃, that a similar result (6.6) is obtained by SR-DFT using density functional perturbation theory³² and the same 4 × 4 × 4 k-points grid used for all DFT calculations. It should be noted that such value slightly decreases with denser k-point sampling to a value of 5.5 for a 6 × 6 × 6 grid. We also checked the effects of SOC on the dielectric constant at the DFT level using a finite electric field approach within DFT³⁴,³³ and a 2 × 2 × 2 k-points grid, obtaining a dielectric constant of 5.6. All these results are reasonably in agreement with the experimental dielectric constant of 6.5 for MAPbI₃³⁵ and with previous SR-DFT results by Brivio et al.³⁶, suggesting that SOC-GW should provide a comparable dielectric constant as SR-DFT, in line with the fortuitous agreement on band-gaps previously noted.

Considering average effective mass values, MASnI₃ is predicted to be a better hole transporter than MAPbI₃, while the opposite holds for electron transport. These results, along with the analysis of the DOS width presented above, are in line with the experimental observations, whereby the CsSnI₃ perovskite was used as an efficient hole transporter in DSCs⁶ and the MAPbI₃ and MAPb(I_1−xCl_x)₃ compounds were found to efficiently transport holes and electrons, respectively³,⁷. Our calculations suggest MASnI₃ to be a reasonable electron transporter, in line with recent mobility results⁹, although to our knowledge this material has never been employed in solar cells.

In conclusion, we have devised a computationally efficient GW scheme incorporating SOC which has allowed us to unravel the electronic and optical properties of MAPbI₃ and MASnI₃ perovskites. Notably, SR-DFT predicts MASnI₃ to be a better electron transported than MAPbI₃. The key to the different materials properties, thus to their photovoltaic performance, appears to be due to the different weight of relativistic effects in Sn- and Pb-based perovskites. Our work provides the interpretative basis and the theoretical framework for the optimal exploitation of next generation materials in perovskites-based solar cells, allowing us to trace some conclusions for new materials design rules.

Being able to tune the SOC in organohalide Pb-based materials, by e.g. exploring different crystal structures and or cationic organic molecules, seems to be the key, on the one hand, to achieve moderately lower band-gaps in APbX₃ perovskites. For Sn-based organohalide perovskites, on the other hand, the reduced SOC leads to an almost optimal band-gap for exploitation in solar cells, though stability towards oxidation seems the major issue to be solved.

Methods

We have extended the relativistic DFT scheme of Ref. 37, in which the spin-orbit coupling is included by 2-dimensional spinors and modeled by pseudopotentials. Wave-functions and charge densities are developed on a plane-waves basis sets. The two dimensional spinor exchange operator 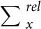is expressed as:

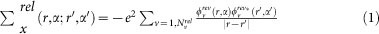where the index α and α′ run over the two spinor components of the 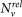occupied relativistic KS states 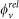. For evaluating the self-energy 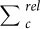we have considered the suggestion of Ref. 23 of approximating the screened relativistic coulomb interaction 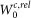with that obtained from a scalar relativistic calculation :

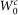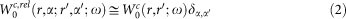For calculating the relativistic correlation part of the self-energy 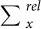we can calculate the DFT relativistic Green's function considering explicitly only the lowest 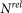relativistic states:

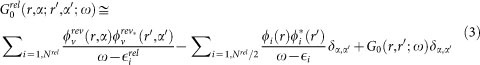where for simplicity in the scalar relativistic calculation we have considered doubly occupied states. In this way we still avoid sums over unoccupied KS states which would be particularly cumbersome when dealing with large model structures. All the presented GW calculations have been performed sampling the Brillouin's zone at the Gamma point only, although the starting DFT calculations and the long range parts of the dielectric matrices are evaluated using a regular 4 × 4 × 4 mesh of k-points. To calculate the band structures and DOS at the GW level we have envisaged a scheme for introducing GW corrections to DFT energy levels calculated at an arbitrary k-point considering only the GW levels calculated at the Γ-point, see Supporting Information for further details. For evaluating the optical properties we have first evaluated the frequency dependent complex dielectric function:

where Ω is the volume of the simulation cell, N_k is the total number of k-points in the BZ, 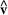is the velocity operator, η is an opportune broadening factor, and the indices v and c run over the occupied and unoccupied states, respectively. The frequency dependent absorption coefficient α(ω) is then given by:

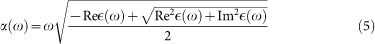It should be noted that in our treatment we omitted any evaluation of the electron-hole coupling. Such effects can be calculated in principle through a scheme based on the Bethe-Salpeter equation for the two-body Green's function³⁹ although such a scheme has only very recently developed for full-relativistic calculations³⁸. However, in the case of small band gap semiconductor neglecting electron-hole coupling still leads to spectra in quite a reasonable agreement with experiment²⁷.

The PBE exchange-correlation functional⁴⁰ and the Quantum Espresso program package⁴¹ was used for all DFT calculations. Scalar relativistic GW calculations were performed using norm-conserving PBE pseudopotentials with an energy cutoff of 70 Ryd defining the plane-waves used for representing the wave-functions. For the full-relativistic GW calculations we used PBE ultrasoft pseudopotentials and energy cut-offs of 45 and 280 for the wave-functions and charge densities, respectively. The scalar relativistic GW calculations were performed developing polarizability operators on a basis sets obtained using an energy cutoff 3 Ry and selecting the 2000 most important basis vectors. The self-energy expectation values are first obtained on imaginary frequency and then analytically continued on the real frequency axis fitting with a two poles expansion. For the GW scalar relativistic case, we have checked that a basis for the polarizability consisting of 1000 vectors would lead to energies of frontier orbitals within 0.05 eV. The full relativistic GW calculations were performed feeding eq. 6 with the first 400 KS states, the first 200 of them are fully occupied. We have checked that if only 240 states are considered (200 valence, 40 conduction), the energy levels of frontier orbitals change of less than 0.06 eV while the energy gap changes of less than 0.03 eV. Geometry optimizations and electronic structure analysis have been carried out using the PWSCF code as implemented in the Quantum-Espresso program package. Electron-ion interactions were described by ultrasoft pseudopotentials with electrons from Pb 5d, 6s, 6p; N and C 2s, 2p; H 1s; I 5s, 5p; Br 4s, 4p; Cl 3s, 3s, shells explicitly included in the calculations. A 4 × 4 × 4 Monkhorst–Pack grid was chosen for sampling the Brillouin zone. Plane-wave basis set cutoffs for the smooth part of the wave functions and the augmented density of 25 and 200 Ry, respectively, were used. Geometry optimizations were performed for all structures employing available lattice parameters, and checking their adequacy by performing atomic and lattice parameters optimizations. Additional computational details for GW and DFT calculations are reported as Supplementary Information.

Supplementary Material

Supplementary Information

Supplementary Information for publication