α-Synuclein’s uniquely long amphipathic helix enhances its membrane binding and remodeling capacity

Abstract

α-Synuclein is the primary protein found in Lewy bodies, the protein and lipid aggregates associated with Parkinson’s disease and Lewy body dementia. The protein folds into a uniquely long amphipathic α-helix (AH) when bound to a membrane, and at high enough concentrations induces large scale remodeling of membranes (tubulation and vesiculation). By engineering a less hydrophobic variant of α-Synuclein, we previously showed that the energy associated with binding of α-Synuclein’s AH correlates with the extent of membrane remodeling¹. Here, we combine fluorescence correlation spectroscopy, electron microscopy and vesicle clearance assays with coarsegrained molecular dynamics simulations to test the impact of decreasing the length of the amphipathic helix on membrane binding energy and tubulation. We show that truncation of α-Synuclein’s AH length by approximately 15% reduces both its membrane binding affinity (by five-fold) and membrane remodeling capacity (by nearly 50% on a per mole of bound protein basis). Results from simulations correlate well with the experiments and lend support to the idea that at high protein density there is a stabilization of individual, protein-induced membrane curvature fields. The extent to which these curvature fields are stabilized, a function of binding energy, dictates the extent of tubulation. Somewhat surprisingly, we find that this stabilization does not correlate directly with the geometric distribution of the proteins on the membrane surface.

Introduction

α-Synuclein (αSyn) is a 140 amino-acid intrinsically disordered neuronal protein, whose N-terminal membrane binding domain (residues 1–93) adopts an amphipathic helix (AH) when bound to a lipid bilayer^2,3. The remainder of the protein remains unstructured in solution. Recent studies of αSyn have suggested that high expression levels associated with disease correlates with gross morphological changes in mitochondrial membranes^4,5. Numerous computational^1,6,7 and in vitro^8–10 studies have offered clues to the biophysical mechanism by which αSyn can cause this kind of membrane remodeling. Particularly, it is known that αSyn can induce membrane curvature in synthetic membrane vesicles and sheets, giving rise to dramatic membrane remodeling (including tubulation and vesiculation). By wedging into the headgroup region of one leaflet of the membrane, the protein splits the headgroups apart, and the energy of binding induces a local, positive curvature field. Collectively, the protein-induced changes in local curvature fields conspire to induce the formation of long tubule protrusions from flat membrane sheets and GUVs^1,8. Exactly what controls this process and how it develops remain open and evolving questions in the field^10,11.

The AH of αSyn is composed of seven imperfect 11-mer repeats¹² imparting two unique characteristics. First, the imperfect nature of the 11-mer repeat introduces heterogeneity in the hydrophobic moment. In particular, the 6th 11-mer of αSyn is almost entirely hydrophobic and comprises the core of the NAC (non-amyloid component) domain, a region of αSyn best known for its role in aggregation¹³. Recent work from our group has shown that the membrane remodeling capacity of αSyn is sensitive to changes in its hydrophobic moment. A NAC-null variant was engineered in which the hydrophobic 6th 11-mer was replaced with a repeat of the amphipathic 5th 11-mer, keeping the overall charge and length of the AH unchanged. The variant displayed a 6-fold loss of binding affinity and a 50% reduction in membrane remodeling capacity¹. MD simulations showed that, at high protein density (400:1 lipid:protein), the NAC-null variant had an increased mobility on the membrane surface that correlated with a reduction in the overall curvature induction. We suggested that a critical relationship between binding energy and protein organization on the membrane dictates tubulation. We were left with a question as to whether a specific geometric organization on the membrane surface is also a pre-requisite for tubulation. We have hypothesized that tight packing (low inter-helix tilt angles) should correlate with high tubulation.

Here, we turned our focus to the 7th 11-mer repeat, to address αSyn’s second unique feature: its length. αSyn contains the longest known AH in the PDB—spanning nearly 15nm^3,7,14—almost 20% longer than any known AH outside the Synuclein family of proteins¹⁵ (β- and γ-Synuclein contain six and seven repeats, respectively)^16–18. Due to its overall positive charge, the extent of αSyn-binding to negative membranes, and therefore the extent to which it induces membrane remodeling, is sensitive to the mole ratio of charged lipids, e.g. those containing PS or PG headgroups. We first asked whether residues 79–100 (this stretch includes the seventh 11-mer from the AH, an additional four, helical residues, as well as seven additional unstructured residues, and carries a +1 charge) contribute to αSyn’s AH binding affinity to a PG bilayer. Focusing on this particular stretch abstracts our questions from αSyn’s biological behavior because it removes the influence of the 40 N-terminal residues. Instead, we are able to focus on basic questions of AH biophysics. Specifically, we asked whether the presence of these 21 residues at the end of the AH influences the binding affinity and remodeling, and in so-doing have further confirmed the correlation between the two. We then asked whether those observed effects can be understood at a molecular scale, specifically in terms of locally induced curvature fields and protein organization of the membrane. To that end, we combined Fluorescence Correlation Spectroscopy (FCS), vesicle clearance assays, Electron Microscopy (EM), and coarse-grained molecular dynamics (MD) simulations. All experiments and simulations were performed in 100% POPG membranes with either αSyn₁₀₀ (residues 1–100) or αSyn₇₈ (residues 1–78). All experiments were performed at equal mass of protein bound, which was established based on the measured binding affinities. This was important in order to ensure that the results were not a trivial consequence of differing amounts of total material on the membrane surface, but instead reflect differences in the length and the chemistry of the two proteins.

Results

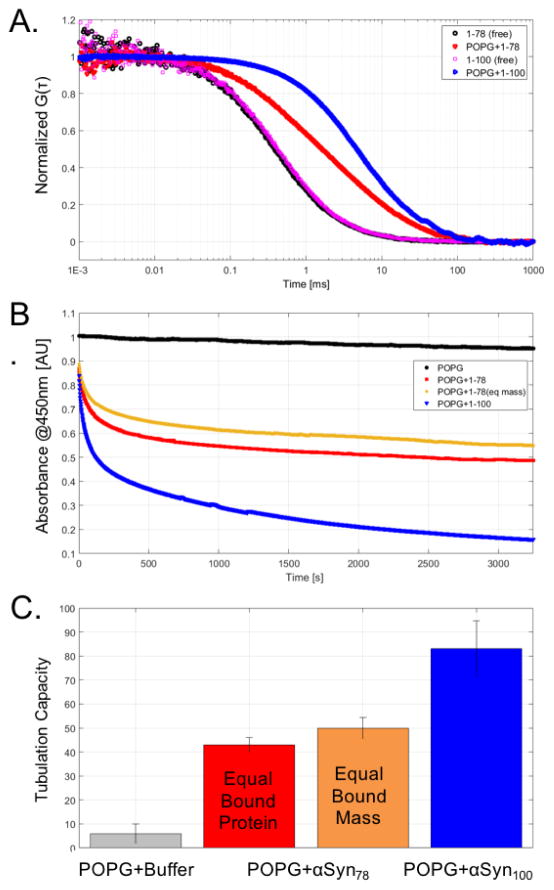
For a direct comparison of the membrane remodeling capacity of αSyn₇₈ and αSyn₁₀₀ it was essential to verify that the binding modality of the protein is unchanged, specifically the transitions from intrinsically disordered in solution to α-helical when bound to a membrane. We preformed circular dichroism (CD) experiments on both constructs and confirmed a consistent α-helical structural transition for both αSyn₇₈ and αSyn₁₀₀ when bound to POPG vesicles (Figure 1). This ensures that we are studying the wedging mechanism, rather than other curvature inducing mechanisms such as steric crowding¹⁰. Using fluorescent correlation spectroscopy (FCS) we then determined the relative binding affinities of αSyn constructs for large unilamellar vesicles composed of POPG. Figure 3A presents the autocorrelation curves for αSyn₇₈ and αSyn₁₀₀ in the absence or presence of 14 μM POPG LUVs. Binding of fluorescently labeled protein to unlabeled vesicles results in longer diffusion times. The greater shift for αSyn₁₀₀ reflects a larger fraction of bound αSyn₁₀₀ relative to αSyn₇₈. The autocorrelation curves were then fit to extract the fraction of bound protein and to determine the apparent binding affinity, K_D. αSyn₇₈ has an ~5-fold reduction in affinity compared to αSyn₁₀₀ (K_D,αSyn78 = 11.5±1.3 μM, K_D,αSyn100 = 2.25±0.2μM).

Figure 1.

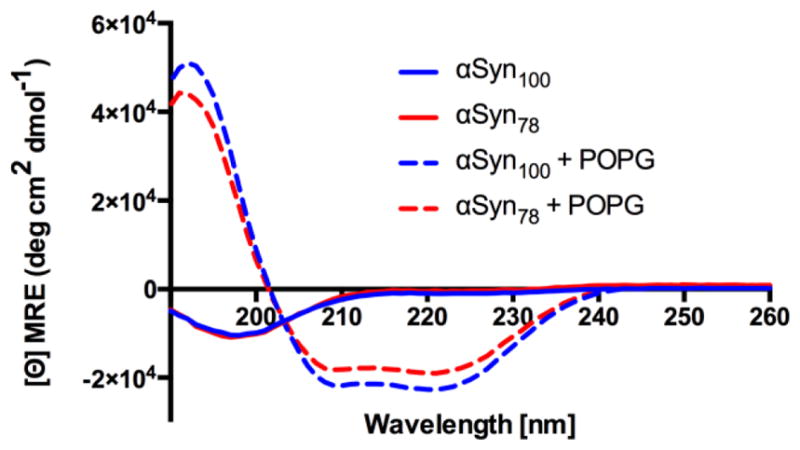
Circular dichroism spectra for αSyn₇₈ (red) and αSyn₁₀₀ (blue) free in solution (solid lines) and incubated with POPG vesicles (dashed lines). Both αSyn₇₈ and αSyn₁₀₀ fold into an α-helical conformation when bound to POPG vesicles.

Figure 3.

(A) FCS traces for αSyn₇₈ and αSyn₁₀₀ in the absence (black or magenta) or presence of POPG (red or blue). (B) Vesicle clearance absorbance traces for POPG + buffer (black), POPG + αSyn₇₈ at equal protein concentration (red), POPG + αSyn₇₈ at equal mass of protein (orange), and POPG + αSyn₁₀₀ (blue). (C) Tubulation capacities for αSyn constructs relative to buffer.

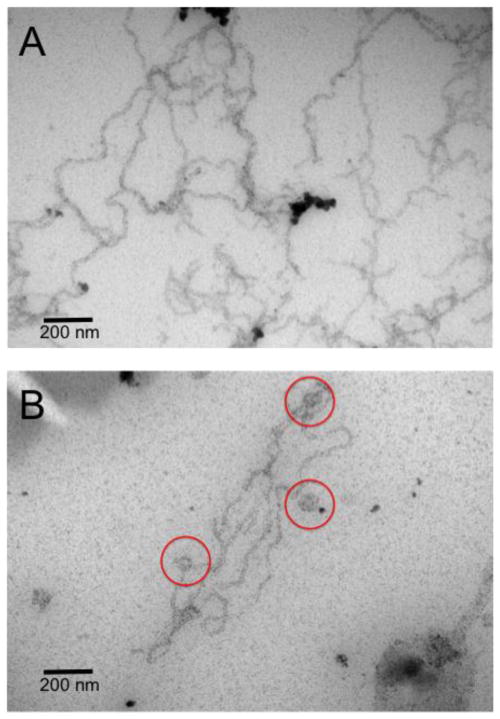
Using electron microscopy (EM) we explored the different membrane structures induced by αSyn remodeling extruded unilamellar POPG vesicles. Both αSyn₁₀₀ and αSyn₇₈ constructs cause tubulation of POPG vesicles (Figure 2). However, images of αSyn₁₀₀ show a dense mesh of tubules, with no evidence of residual vesicles (Figure 2A), whereas the αSyn₇₈ images show fewer tubules which coexist with non-tubulated vesicles indicating incomplete remodeling (Figure 2B). This visual data supports our spectroscopic assay (Figure 3), which showed that the scatter signal arising from tubulation of vesicles plateaus at a higher value for αSyn₇₈ than for αSyn₁₀₀, indicating that it is less effective at tubulating membranes.

Figure 2.

Representative EM images of tubules formed by αSyn₁₀₀ (A) and αSyn₇₈ (B). Scale bar is 200 nm. Red circles highlight vesicles in the αSyn₇₈ system.

In order to quantify this effect, we used a vesicle clearance assay (VCA), following a similar strategy as in our earlier study.¹ In the VCA, large unilamellar vesicles that scatter light are remodeled (cleared) into smaller tubules/vesicles, reducing the amount of scattered light in the sample. Absorbance traces from vesicle clearance assays (Figure 3B) highlight a reduced remodeling capacity for αSyn₇₈ (under both equal bound protein concentration and mass) relative to αSyn₁₀₀. Figure 3C quantifies this remodeling capacity and highlights an ~50% reduction (at equal moles of bound protein) and an ~40% reduction (at equal mass of bound protein) for αSyn₇₈ as compared to αSyn₁₀₀.

To better understand the changes in remodeling capacity between αSyn₇₈ over αSyn₁₀₀ we used coarse-grained MD simulations of planar protein-lipid systems. In total, four MD simulations were run using GROMACS (v4.5.3) with the MARTINI coarse-grain forcefield^19–21; two low-density symmetric systems with 1600:1 lipid to protein ratio (L:P) and two high density asymmetric systems with a 3.77 lipid:protein-residue ratio (comparison of equal lipid:protein-residue ratio for the high-density systems eliminates the trivial lipid dilution effects that a smaller protein at similar concentration would impart). The MARTINI forcefield requires a predefined protein secondary structure. Each αSyn was modeled as an extended α-helix, as per our earlier studies^1,7, where in αSyn₁₀₀ the final seven residues are unstructured. Each system was simulated for a total of 10.5 μs(44 μs, scaled time) with the last 5 μs used for analysis. All systems contained ~3200 POPG lipids with either two αSyn proteins symmetrically bound (one per monolayer for a 1600:1 L:P) or eight αSyn proteins asymmetrically bound (all eight on one leaflet). Area mismatch effects were minimized through removal of excess lipids from the protein leaflet (18-lipids per protein for αSyn₇₈ and 23-lipids per protein for αSyn₁₀₀) to ensure membrane remodeling was not driven by excess lipid area^1,7,9. Although these systems were globally flat, local membrane remodeling recapitulates the macroscopic membrane remodeling characteristics of αSyn⁷.

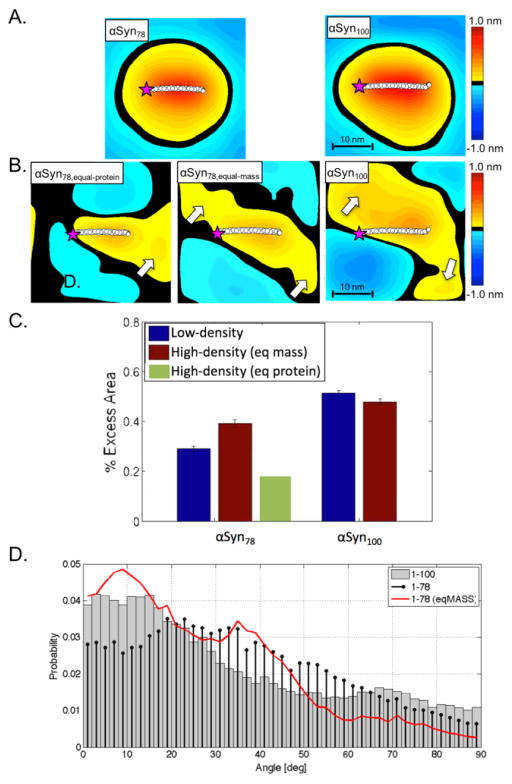
We characterized αSyn’s curvature induction capacity via time-averaged height surfaces, h(x,y), which resolve the stabilized spontaneous curvature near the protein^1,7,22. In the low-density systems (1600:1 lipid:protein), both αSyn constructs induce the same maximum curvature (~1.0 nm membrane deflection, see Figure 4A). However, in the context of tubulation, the total integrated curvature effect is more important than the magnitude of the local maximum. We quantified this total curvature inducing capacity of each protein using the excess lipid area per protein, which describes the total integrated extent to which the induced curvature field varies from the underlying, thermally-driven membrane undulations¹. At low protein-density (Figure 4C) there is significantly reduced curvature induction by αSyn₇₈ than αSyn₁₀₀ (~44% reduction). This value significantly overshoots the expected results based solely on the change in length (16% reduction in AH length), and also is a substantially larger effect than we saw previously with the NAC-null variant (discussed below). To confirm that this surprising result is primarily due to the additional residues in the AH (residues 79–93, and not the seven un-structured residues carrying a net +1 charge), we ran an additional low-density simulation of just the seven heptads (residues 1–93). The results show clearly that the major effect is due to the additional fifteen helical residues in heptad 7 (see Supplemental Figure 1). Comparing the depth of penetration of the AH, the sixth heptad is buried below the headgroups, while the seventh heptad is located within the headgroup region (Figure 5). We previously showed that these kinds of differences in partition depth can have dramatic effects on the induced curvature, and likely explains the unexpected effect on curvature seen here.

Figure 4.

Time-averaged height surfaces, h(x,y), for αSyn₇₈ (left) and αSyn₁₀₀ (right) for low-density (A) and high-density (B) systems. Purple star indicates N-terminus of protein. The white arrows highlight local region of on-average positive curvature suggesting an alignment of proximal proteins. (C) Excess area per protein for αSyn₇₈ (left) and αSyn₁₀₀ (right) systems [low-density, blue; high-density (equal-mass, brown; equal-protein, green)]. (D) Protein angle distributions for αSyn₇₈ and αSyn₁₀₀ high-density systems (αSyn₁₀₀, grey-bars; αSyn_{78,eq-protein}, black-stem; αSyn_78,eq-mass, red-curve).

Figure 5.

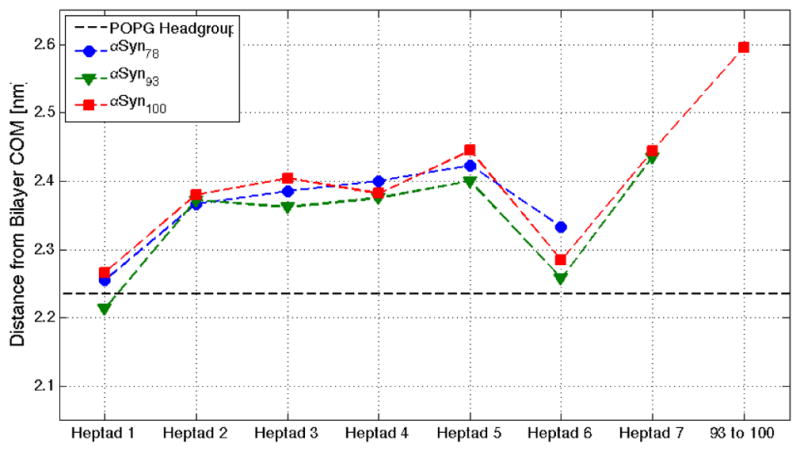
Heptad depth profile for αSyn constructs. Depth profiles for αSyn₇₈ (blue), αSyn₉₃ (green), and αSyn₁₀₀ (red) are parsed by heptad and illustrate differential penetration relative to the POPG headgroup (black dashed-line).

In high-density systems, the curvature maxima for both systems are reduced (~0.6 nm membrane deflection, see Figure 4B), an effect we saw previously that relates to the competition between neighboring curvature fields for limited membrane material¹. The high-density systems were built to most closely mimic the experimental conditions. The same effect of truncation is present but less so (~20% reduction comparing αSyn₇₈ to αSyn₁₀₀, Figure 4C). In both high-density systems there are nearby regions of increased curvature relative to the average protein position in both 1–78 and 1–100, with the 1–78 having a reduced magnitude (see Figure 4B, arrows). These broadened curvature fields suggest curvature field stabilization due to alignment with neighboring curvature fields.

Protein alignment has been shown to be a precursor of macroscopic membrane remodeling²³. We predicted that the lost curvature-reinforcement in the truncated protein would correlate with a shift in the distribution of protein-protein inter-helical tilt angles, specifically that there would be more low-angle alignments in the αSyn₁₀₀ system. This prediction follows our hypothesis that curvature field reinforcement correlates with increased tubulation, not that there is an increase in protein-protein interactions. To understand the degree of curvature field alignment we determined the angle made between nearest neighbor proteins for the high-density systems (Figure 4D). Not surprisingly, at equal molar density, there is a decrease in the population of low-angle (20°) alignments when comparing the αSyn₇₈ and αSyn₁₀₀ simulations. This is a trivial result of there being more space for the shorter AH to sample (higher lipid:protein ratio). On the other hand, and unexpectedly, in the simulations run at equal mass, αSyn₇₈ has a greater percentage of low-angle (<45°) packing states than αSyn₁₀₀.

Discussion and Concluding Remarks

Exactly how the peculiar length of αSyn’s AH impacts its interactions with, and deformations of, membranes remains unknown. Questions still remain about the exact nature of the N-terminal end of the AH where there are an abundance of hydrophobic residues and a net charge of +2 (residues 79–102) before a stretch of unstructured, negatively charged and unbound residues (residues 104–140). NMR relaxometry data showed that in a mixed PG:PC bilayer the residues beyond residue 90 were not alpha helical²⁴. Similarly, NMR results in a 100% PG bilayer from Veglia also suggest that residues 90–100 may not be bound as tightly to the bilayer as the first 89 residues²⁵. Given their strong charge, it is interesting that residues 90–102 do not interact more strongly with a negatively charged bilayer. In all likelihood, the stretch of negatively charged, unstructured residues (residues 104–140) pulls that stretch of the protein out of the bilayer, driven by both an electrostatic repulsion from the negative lipid headgroups and entropic freedom of the disordered chain. We have now shown that the NAC domain sinks the helix deeper into the bilayer (Figure 5), and we previously showed that the NAC domain increases the membrane affinity over a variant in which the sixth-heptad was a repeat of the fifth, less hydrophobic repeat¹. The seventh heptad (residues 79–93) acts a transition between the NAC and the unstructured c-terminal domain, and being more shallow in the bilayer dramatically increases the overall curvature induction of the AH.

In our previous study, we concluded that the major driving force for tubulation is the energy provided by binding. Additionally, we speculated that the binding affinity should correlate with mobility on the membrane surface due specifically to electrostatic interactions between the protein and headgroups. Here, we draw a similar conclusion, further cementing this paradigm for membrane remodeling, though we remain uncertain as to how, or if, the stabilization of curvature fields relates to the geometric alignment of proteins (Figure 4D). The effect on binding affinity reported here regarding truncation of residues 79–100 is slightly less than the effect we saw when we replaced the sixth heptad with a copy of the fifth (compare ~5-fold to an ~6-fold reduction in affinity for the NAC-null variant)¹. In the case of the NAC-null, tubulation was reduced by ~40% as compared to the wild-type sequence. Thus, while a quantitative/theoretical relationship between tubulation and affinity is unknown, if the impact on tubulation is linear in binding energy, one would predict a measured reduction in tubulation of ~30% when comparing αSyn₇₈ to αSyn₁₀₀ at equal moles bound. However, as the binding energy is a per mole measure, we report here an ~50% decrease in tubulation at equal moles bound (Figure 3). This difference (50% observed vs. 30% predicted) strongly suggests that the electrostatic effect of losing a net +1 charge in αSyn₇₈ has a more profound effect on the binding energy and concomitant stabilization of curvature fields than did losing the hydrophobic NAC. Ideally, in order to further understand this finding, we would have experimentally tested the effect of a peptide comprised only of residues 1–93, keeping the charge neutral in the shortening. Presumably, given what would have been a lower binding affinity to the negatively charged bilayer, we would have seen an even more dramatic reduction in tubulation. Unfortunately, the αSyn_1-93 construct proved difficult to purify and therefore produced statistically uncertain results.

The reduced remodeling capacity for the shortened αSyn₇₈ suggests a distinct role for AH length in facilitating curvature field alignment and propagation. The reduced affinity and attenuated membrane remodeling by αSyn₇₈ is similar to our previous results for an engineered, NAC-null protein¹, suggesting that both AH length and hydrophobicity are essential components that drive αSyn’s membrane remodeling capacity. Indeed, all members of the Synuclein protein family possess a long AH, sharing significant homology with αSyn^16,26. The loss of either AH length (βSyn, containing only 6 heptad repeats) or hydrophobic moment (γSyn, lacking the NAC domain) may explain their reduced binding affinities relative to αSyn²⁶, and is consistent with the relaxed membrane remodeling observed tubulation assays with βSyn⁸.

Materials and Methods

Protein expression, purification, and labeling

αSyn₁₀₀ and αSyn₇₈ were generated by introducing a stop codon via QuickChange mutagenesis (Stratagene) after residue 100 or 78 in a full-length αSyn plasmid, as described previously. A S9C mutation was introduced, also by QuickChange, to allow for site-specific fluorescent labeling. The protein was recombinantly expressed in E. coli and purified via ammonium sulfate precipitation followed by cation exchange at pH 4.0 and size exclusion chromatography⁷. Purity and identity of protein was verified by SDS-PAGE and mass spectrometry.

For fluorescence correlation spectroscopy (FCS) experiments, αSyn₁₀₀ and αSyn₇₈ were labeled with Alexa Fluor 488 maleimide (AL488) (Invitrogen) on the cysteine introduced at residue 9. The protein was incubated in Tris buffer (20 mM Tris, 150 mM NaCl, pH 7.4) with 10mM DTT for 30 minutes at room temperature and then DTT was removed by two stacked HiTrap desalting columns (GE Healthcare Life Sciences). Fluorophore was added at 7 to 10× molar excess for 2 hours at room temperature or overnight at 4°C. Unconjugated dye was separated from the labeled protein by two stacked HiTrap desalting columns (GE Healthcare Life Sciences). UV-Vis absorbance at 495 nm was used to quantify the AL488 concentration, and the protein concentration was determined by a modified Lowry assay (Bio-Rad, Hercules, CA). Labeling efficiency (molar ratio of dye to protein) was consistently above 90%.

Vesicles

Liposomes were prepared from 100% 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoglycerol (POPG) lipid. Lipid powder was dissolved in chloroform to make 15–20 mg/mL stock solutions and stored at −20°C. Aliquots of this solution were dried under nitrogen stream and desiccated overnight. The resulting film was resuspended to approximately 4 mM in MOPS buffer (20mM MOPS, 147 mM NaCl, 2.7 mM KCl, pH 7.4) for at least one hour and vortexed. The resulting liposome solutions were used as is for the tubulation assays. For FCS measurements, large unilamellar vesicles (LUVs) were prepared by extruding this suspension 21 times through two stacked membranes of 50 nm pore size (Whatman) in a Liposofast extruder (Avestin). For EM, the suspension was extruded 13 times through 400 nm pore size membranes. LUVs are stored at room temperature for up to several days. Before analyses, all lipid concentrations were determined by assaying for total phosphate content²⁷.

Circular Dichroism

Circular Dichroism (CD) experiments were performed on a Aviv spectrometer, model 215. All samples were prepared in 10 mM sodium phosphate with 0.1mM TCEP, pH adjusted to 7.4. αSyn₁₀₀ or αSyn₇₈ was incubated at 500μM with 1 mM TCEP for 30 minutes on ice, then diluted to 20 μM before measuring, with TCEP 0.1 mM during the measurement. The lipids were not extruded, resuspended to 4mM (approx.) in the phosphate buffer for ~1.5 hours before the measurements, diluted to 400μM for measurement. For the protein+lipid samples, protein and lipid were mixed (20μM αSyn and 400 μM POPG) and allowed to equilibrate for 10 minutes prior to measurement to allow sufficient time for the protein to bind.

Fluorescence Correlation Spectroscopy

FCS measurements were made on a lab-built instrument based around an Olympus IX71 inverted microscope (Olympus, Tokyo, Japan) and a 488 nm DPSS laser (Coherent) as described previously³. Laser power was adjusted to 5μW prior to entering the microscope. Fluorescence emission was collected through the objective and separated from laser excitation using a Z488rdc long-pass dichroic and an HQ600/200m band-pass filter (Chroma) and focused onto the aperture of a 50 μm optical fiber (Oz Optics, Ottawa, Canada) directly coupled to an avalanche photodiode (Pacer). A digital correlator (Flex03LQ-12, correlator.com) was used to generate the autocorrelation curve.

FCS measurements were made in 8-well chambered coverglasses (Nunc). Chambers were plasma treated and passivated by coating with polylysine-conjugated polyethylene glycol to prevent protein adsorption to the surface⁹. Binding studies were carried out at 20°C, mixing 100 nM αSyn₁₀₀ or αSyn₇₈ with concentrations ranging from 1μM to 50μM (1:10 to 1:500 protein:lipid ratio) of 100% POPG LUVs in MOPS buffer in a well (250 μL total volume) and allowing to equilibrate for 8 to 10 minutes before measuring. FCS experiments were performed under conditions where tubulation is not expected (i.e. low protein:lipid ratios). We have previously shown that FCS curves measured after 5-minute incubation are identical to those measured after several hours. For each FCS measurement, 30 traces of 10 seconds each were recorded and averaged together to obtain statistical variations. The average curve was fit to an equation for multiple species of differing brightness (Equation 1) using MATLAB (The MathWorks). Further discussion of this equation can be found in ⁹.

$$G(\tau )=\frac{1}{N}\left(F\ast \frac{1}{1+\frac{\tau }{{\tau }_{D1}}}\ast {\left(\frac{1}{1+\frac{s^2\tau }{{\tau }_{D1}}}\right)}^{½}+Q\ast (1-F)\frac{1}{1+\frac{\tau }{{\tau }_{D2}}}\ast {\left(\frac{1}{1+\frac{s^2\tau }{{\tau }_{D2}}}\right)}^{½}\right),$$ (Eq. 1)

where τ_D1 and τ_D2, the diffusion times for the free protein and vesicle-bound protein, are determined by measurements of samples in the absence of lipid and with very high lipid concentration (all protein is bound), respectively and fixed to within 5% of these values for fitting curves from intermediate lipid concentrations. The structure factors, the ratio of the radial to axial dimensions of the focal volume, was calibrated by measuring a solution of Alexa488 hydrazide and was fixed to 0.17. The only free parameters are: N, the number of fluorescent species; F, the fraction of protein not bound to vesicles; and Q, the average brightness of the vesicles. Binding data were fit with a hyperbolic binding curve (Equation 2) in Origin (OriginLab) to determine the K_D.

$$F\prime =\frac{[\mathit{lipid}]}{K_D+[\mathit{lipid}]},$$ (Eq. 2)

where F′ is the fraction of vesicle-bound protein, determined from fitting the FCS equation, and [lipid] is the molar concentration of accessible lipid, the outer membrane leaflet, calculated as 55% of the total lipid concentration.

Electron Microscopy

αSyn₁₀₀ or αSyn₇₈ were mixed with extruded POPG LUVs (via 0.1μm membranes, Avanti Polar Lipids) in a 1:5 molar ratio in MOPS buffer and incubated overnight at room temperature to ensure remodeling had run to completion. Samples were prepared by pipetting 20 μL onto a carbon/formvar supported copper grid (Electron Microscopy Science, Hatfield, PA) for 2 minutes, followed by blotting with filter paper (Whatman) and rinsing 3 times with MOPS buffer. The sample was stained with 2% (w/v) uranyl acetate for 2 minutes and rinsed 3 times with MOPS buffer. After staining, the grid was left in room temperature to dry for several minutes and then imaged immediately. EM images were taken on a JEM 1011 transmission electron microscope (JEOL, USA). The accelerating voltage was set to 100 kV. Tube diameter analysis was done using Image J (NIH).

Vesicle tubulation

To monitor remodeling of liposomes into tubular structures by αSyn₁₀₀ and αSyn₇₈, the decrease in scattered light at 450 nm was measured as a function of time⁸. The protein was added to non-extruded 100% POPG liposomes at approximately a 1:10 protein:lipid ratio and the absorbance was monitored at 450nm with 1 nm slit width, 1-second response time in a spectrophotometer (Perkin-Elmer). 150 μL of 400 μM lipids in MOPS buffer with 1 mM TCEP was placed in a quartz cuvette and absorbance was measured every 2 seconds for at least 5 minutes to obtain a baseline signal. Appropriate amounts of protein (in MOPS buffer with 1 mM TCEP) were added to achieve equivalent amounts of bound protein as determined by the quadratic binding equation (Equation 3).

$$\frac{[PL]}{[P_{\mathit{tot}}]}=\frac{(K_D+[P_{\mathit{tot}}]+[L_{\mathit{tot}}])-\sqrt{{(K_D+[P_{\mathit{tot}}]+[L_{\mathit{tot}}])}^2-4[P_{\mathit{tot}}][L_{\mathit{tot}}]}}{2[P_{\mathit{tot}}]}$$ (Eq. 3)

where [PL] is the concentration of lipid-bound protein, [P_tot] is the total concentration of protein, [L_tot] is the total concentration of accessible lipid, and KD is the dissociation constant calculated from the FCS measurements. By this calculation, αSyn₁₀₀ was added to 38.4 μM while αSyn₇₈ was added to 40.6 μM, with final concentration of 384 μM POPG in both cases.

Vesicle clearance assays were completed when a plateau in attenuation is achieved. If the assay is monitored for an extended duration, the signal can become erratic as tubules may settle out of the solution. Traces were normalized to the initial lipid-only signal for each sample, and the extent of tubulation was determined by taking the average absorbance of the 50 time points from 2400–2500 sec and subtracting from the initial value. At least three replicates were performed for each lipid composition.

Simulation Methods

All simulations were run using the coarse-grained MARTINI lipid and MARTINI2.2 protein parameters^21,28,29. The MARTINI forcefield applies an ~4:1 (heavy atom:CG bead) mapping, reducing the complexity of the system and allowing the study of larger systems and longer time-scales than typically accessible for all-atom resolution MD. Simulations were run using the GROMACS v4.5.3 program^19,20. All systems were prepared and run in the isothermal-isobaric (NPT) ensemble with barostat and thermostat set to 1 bar and 303K respectively using a 25fs time step. Pressure coupling was performed semi-isotropically with the xy- and z-dimensions independently coupled producing an average zero surface tension. Non-bonded interactions were modeled with the standard MARTINI cut-off scheme with Lennard-Jones interactions shifted to zero between 0.9–1.2nm and electrostatic interactions in the range 0.0–1.2 nm with a uniform screening constant set at 15^21,28,29.

Initial equilibration included 10,000 steps steepest descent minimization followed by 500ns of dynamics using the velocity-rescaling thermostat and a Berendson barostat(Van Der Spoel et al., 2005; Hess et al., 2008). All production runs were simulated using the Nose/-Hoover thermostat and the Parrinello-Rahman barostat^30,31 with a time constant of 2.5ps and 250ps respectively. Pressure coupling was applied semi-isotropically to allow for a tensionless bilayer with uniform x,y-dimensions. All production simulations were 10μs (40μs scaled simulation time) sampled every 1ns with the last 5μs used for analysis (5000 frames).

As with all MARTINI simulations, the protein secondary structure is constrained and must be predefined^21,28,29. This limitation of the MARTINI protein model precludes the direct simulation of αSyn binding, as the binding process induces the transition from intrinsically disordered structure to an AH³². In this study, bound αSyn₁₀₀ (residues 1–100) or αSyn₇₈ (residues 1–78) was modeled as α-helical, except for residues 94–100, which were treated as random-coil.

Starting configurations were symmetric—having identical number of lipids and proteins per monolayer— eliminating potential area-mismatch and allowing the resulting spontaneous curvature to be solely induced by the protein’s perturbation to the local membrane structure. The proteins were positioned on opposite monolayer in remote regions of the periodic cell. Starting configurations were constructed as follows. Two proteins were added (one per monolayer) to a pre-equilibrated 3200-lipid system (100% POPG) with nominal periodic dimensions ~30nm × ~30nm × ~15nm. The protein-lipid system was solvated with a minimum of 70,400 water beads and the appropriate number of counter ions to make a net neutral system.

The 400:1 systems were built with the same random configuration of 8-αSyn on one monolayer. Lipids were inserted into both top and bottom monolayers with 18-lipids per protein and 23-lipids pre protein removed from the αSyn₇₈ and αSyn₁₀₀ leaflets, respectively, to ensure excess lipid area did not drive curvature induction⁷. The system was solvated with 70,400 water beads and the appropriate number of counter ions.

MD Trajectory Data Analysis

Trajectories were manipulated and processed using both the GROMACS v.4.5.3 simulation package^19,20 and the MDAnalysis python library³³. Further data analysis and figure rendering was performed using MATLAB (v.R2012a).

Surface Rendering and Curvature Determination

Curvature analysis to determine 〈h(x,y)〉 was performed without modification as detailed in ⁷. Briefly, PO₄ beads for every lipid were used to define each monolayer. The undulation reference surface (URS) which defines the local mid-plane of the bilayer is rendered using the direct Fourier method with a filter cutoff of q0 = 1.5 nm⁻¹. All surfaces were oriented to center each protein at the origin, aligning the protein’s longitudinal axis with the x-axis. Individual protein h(x,y) were averaged per frame, then subsequent averaged across the production simulation. Analysis of the undulation spectrum indicated convergence of undulation amplitudes with a 5 μs window for simulation times greater than 5 μs.

Surface area for 〈h(x,y)〉, A_h(x,y), was determined using a summation over Fourier coefficients for the surface as described in ²². The percent increase in surface area is determined as (1 − A_h(x,y)/A_xy)×100, where A_h(x,y) is the true area, A_xy is projected area.

Protein-Protein Angle Analysis

For each protein pair the minimum angle between a least-square fit of the backbone beads was calculated for the last 5 μs of simulation and a histogram generated with a 2-degree bin width for 0 to 90 degrees.

Supplementary Material

232_2017_9946_MOESM1_ESM. Supplemental Figure 1.

αSyn’s excess area induction is not dependent on the seven-unstructured C-terminal residues. (A) Curvature fields for αSyn₇₈, αSyn₉₃, and αSyn₁₀₀. αSyn₉₃ induces a consistent curvature field as αSyn₁₀₀. (B) Quantification of the height surfaces in A demonstrates similar curvature induction capacity of αSyn₉₃ relative to that of αSyn₁₀₀.