Using Outcomes to Analyze Patients Rather than Patients to Analyze Outcomes: A Step toward Pragmatism in Benefit:risk Evaluation

Abstract

In the future, clinical trials will have an increased emphasis on pragmatism, providing a practical description of the effects of new treatments in realistic clinical settings. Accomplishing pragmatism requires better summaries of the totality of the evidence in ways that clinical trials consumers---patients, physicians, insurers---find transparent and allow for informed benefit:risk decision-making.

The current approach to the analysis of clinical trials is to analyze efficacy and safety separately and then combine these analyses into a benefit:risk assessment. Many assume that this will effectively describe the impact on patients. But this approach is suboptimal for evaluating the totality of effects on patients.

We discuss methods for benefit:risk assessment that have greater pragmatism than methods that separately analyze efficacy and safety. These include the concepts of within-patient analyses and composite benefit:risk endpoints with a goal of understanding how to analyze one patient before trying to figure out how to analyze many. We discuss the desirability of outcome ranking (DOOR) and introduce the partial credit strategy using an example in a clinical trial evaluating the effects of a new antibiotic. As part of the example we introduce a strategy to engage patients as a resource to inform benefit:risk analyses consistent with the goal of measuring and weighing outcomes that are most important from the patient’s perspective.

We describe a broad vision for the future of clinical trials consistent with increased pragmatism. Greater focus on using endpoints to analyze patients rather than patients to analyze endpoints particularly in late-phase/stage clinical trials is an important part of this vision.

Introduction

With billions of dollars per year spent on evaluating new interventions, one might think that clinical trials would provide doctors with appropriate and practical information to inform clinical decision-making. But they do not. And the serious implications of this deficit are largely absent from public discourse (DeMets and Califf, JAMA, 2011). That is about to change. Increased pragmatism in clinical trials is being urged by many clinical trial leaders including FDA Commissioner, Dr. Robert Califf (Science, 2015).

The goal of a pragmatic (often called effectiveness) trial is practical, to improve clinical practice by evaluating how well an intervention will work in practice. This is in contrast to the goals and foci of the more typical explanatory (efficacy) trials which often focus on biological mechanisms and whether an intervention would work under selected and often less generalizable settings. Characteristics of pragmatic clinical trials include limited restrictions on entry criteria, flexible protocols, flexible intervention application and leniency on concomitant therapy use.

Since the goals and design of pragmatic trials are different from explanatory trials, critical thought regarding the resulting implications to the manner in which data are analyzed is needed to ensure that the goal of pragmatism is met and that analyses appropriately match the design.

Let us see how pragmatic our typical approaches to the analyses of clinical trials are. Suppose one has been diagnosed with a terrible disease and there are three treatment options: A, B, and C. A randomized clinical trial (N=300; 100/arm) was conducted comparing these three treatments with respect to the two major binary outcomes of equal importance: efficacy and toxicity. The summary results of the typical analyses of the endpoints are as follows: A (50% efficacy, 20% toxicity), B (50% efficacy, 50% toxicity), and C (50% efficacy, 50% toxicity). Since all three arms have a 50% efficacy rate but treatment A has the lowest toxicity rate, treatment A is clearly the best choice for use in clinical practice. Or is it? Suppose we are told that treatment C provides the best option. How could this be?

Instead of using the patients to analyze the outcomes, let us use the outcomes to analyze the patients (Table 1). In this scenario, there are four patient outcomes: efficacy without toxicity, efficacy with toxicity, no efficacy without toxicity, and no efficacy without toxicity. In treatment A, efficacy and toxicity were uncorrelated resulting in 10 patients that had efficacy without toxicity. In treatment B, efficacy and toxicity were positively correlated resulting in 0 patients that had efficacy without toxicity. In treatment C, efficacy and toxicity were negatively correlated resulting in 50 patients that had efficacy without toxicity. Clearly this is a fictional example but it illustrates that traditional approaches may not tell the complete story and could be aided by additional analyses. Our culture is to use patients to analyze the endpoints. Should we use endpoints to analyze the patients?

Table 1.

Analysis of Patients by Treatment

		Treatment A Efficacy			Treatment B Efficacy			Treatment C Efficacy
		+	−		+	−		+	−
Toxicity	+	10	10	+	50	0	+	0	50
	−	40	40	−	0	50	−	50	0

Let us consider a more fundamental question regarding generalizability. During analyses of a clinical trial, we define analysis populations. These typically include an efficacy population (e.g., ITT) upon which to conduct an efficacy analysis and a safety population upon which to conduct a safety analysis. We then combine these analyses into what we often term a “benefit:risk analysis”. But these two populations are not the same. To whom does this benefit:risk analysis apply?

The Order of Operations and Within-patient Analyses

Most people likely default to an assumption that benefits and harms are not associated. In the example above they might predict their outcomes by imagining flipping two coins, one appropriately weighted for efficacy and the other for toxicity. With such thinking, the association between benefits and harms is missed. But understanding the nature of the association between benefits and harms is an important part of patient evaluation and for understanding the utility of the intervention. When applying an intervention, some patients may benefit while some may experience harms. If the patients experiencing harm and the patients experiencing benefit are largely disjointed, then it is important to identify ways to distinguish between these 2 groups to guide treatment selection. However, if the 2 groups are largely overlapping, then an assessment of the net effect, i.e., whether the benefits outweigh the harms, is needed. The traditional approaches of separate analysis of each endpoint (even when combined using e.g., typical decision analyses) cannot distinguish between these 2 scenarios, as seen in the inability to distinguish treatment arms B and C in the example above and thus does not optimally evaluate the distribution of the totality of the effects on individual patients.

One approach to addressing these issues is to modify the order of operations during the statistical analyses. While the common practice is to construct separate summary measures of efficacy and safety before integrating the benefits and risks at the population level, a within-patient analysis instead integrates or combines the efficacy and safety outcomes at the patient level and then a summary of the combined benefit:risk outcome is created for each intervention. Interventions can then be compared with respect to the combined benefit:risk outcome. In other words, the traditional approach is to take the first endpoint, summarize results for each treatment arm and then compare the arms with respect to these aggregate results. This process is repeated for each of the other endpoints of interest. The comparative results for all of the relevant endpoints are then put together as part of the so-called “benefit:risk analyses”. In contrast, the within-patient approach first integrates the endpoints (beneficial and harmful outcomes) within patient first, aggregates these data for each intervention, and then compares the interventions. Remember the grade school math lesson: the order of operations is important. This approach may not replace the traditional separate marginal analyses, but should at least be considered as supporting analyses.

Within-patient analysis essentially consists of creating a composite outcome consisting of benefit and risk components. Such composites have been utilized in practice. For example, Schneider et.al. (2006) evaluated the effectiveness of atypical antipsychotic drugs in patients with Alzheimer’s disease using an event-time endpoint of the minimum of the time to treatment discontinuation due to: (i) lack of efficacy, or (ii) toxicity or adverse effects. Mancini and Schulzer (1999) introduced the concept of unqualified success (treatment success without treatment-induced side effects) and unmitigated failure (lack of treatment success with treatment-induced side effects).

Benefit:risk composites incorporate the association between benefits and harms, necessary for understanding the overall effects on individual patients. Analysis of the composite is pragmatic in the sense it provides direct and comprehensive information regarding the overall patient outcomes, resulting in greater utility for patients and clinicians. The benefit:risk composite reflects the totality of outcomes about which patients care.

This perspective aligns with that of the Patient-Centered Outcomes Research Institute (PCORI). One of PCORI’s objectives is to assess the benefits and harms of interventions to inform decision making while highlighting outcomes that matter to people. The idea is to go beyond the traditional paradigm of focusing on individual outcomes and to view the patient’s perspective as integral to relevant research. Choosing appropriate outcomes to measure was declared one of the highest research priorities in trial methodology based on a recent survey (Tudor Smith et.al., 2014).

Other Advantages

Composite benefit:risk endpoints potentially have other important advantages over separate marginal analyses of each endpoint. We highlight two important ones.

Competing risks often distort the interpretation of individual outcomes. For example, the duration of hospitalization may be an outcome of interest in some trials with shorter duration interpreted as a more desirable result. However if a patient dies within the first few days then the duration of hospitalization is short but clearly an undesirable result. Summaries of the duration of hospitalization in isolation without considering survival would be incomplete at best and support use of the inferior therapy at worst. A composite benefit:risk outcome can incorporate the competing risk of death into its definition. The duration of hospitalization can then be interpreted within the appropriate context of survival duration and other outcomes for the individual patient.

Noninferiority (NI) trials have many complexities (Snappin 2000; D’Agostino 2003; Fleming 2008; Evans 2009, 2010; Hamasaki and Evans 2013). Superiority trials are preferred if the option is feasible. Many NI trials are conducted based on the premise that the new intervention has non-efficacy advantages, e.g., less toxic; better quality of life, over the standard of care. The rationale is thus if NI on a primary efficacy outcome is demonstrated then the new intervention may be preferred to the standard of care. In this scenario, the big picture research question is not really one of NI. A broader perspective reveals a superiority research question, i.e., whether the new intervention is globally better than the standard of care when all of the important outcomes are appropriately considered. In this case, a composite benefit:risk outcome may allow for superiority designs.

Limitations

The evaluation of outcomes in clinical trials can be complicated. Interventions often act on a disease pathway and can have myriad downstream effects both on- and off-target. For example, a cardiovascular intervention might lessen the rate of cardiovascular disease as catalogued by strokes, heart attacks, cardiovascular death, and revascularization procedures. A simple and transparent way to describe the complexity of outcomes is by use of a composite where a patient is said to experience an event if any of the above events occur. A fundamental problem with composites is that the components that comprise the composite could have differing levels of importance, and the result on the composite could be primarily driven by components of lesser importance, effectively not providing appropriate weight to the most important component(s). For example, an intervention might have a neutral or even harmful effect on the uncommon event of death but show a substantial benefit on e.g., revascularization so that overall the intervention is deemed to superior to a comparator when using the composite. Furthermore, significance on the composite does not imply significance on the components, and significance on one or more of the components does not imply significance on the composite. Thus a fundamental part of composite endpoint analyses is a careful evaluation of the effects on each component (Neaton et.al., 2005). It is important to rule out a harmful effect on the more important components of a composite endpoint (e.g., death) when a statistically significant effect on the composite endpoint is demonstrated. A strategy that could be employed to address this concern is to specify and evaluate co-primary endpoints (Sozu et.al., 2015), the composite and the most important component, to ensure that effects on the most important component are not hidden by the composition. Even so, there is no panacea and use of a composite involves an acceptance of the implicit weighting of the components that is determined by their relative occurrence.

Methods in the Literature

Several strategies for constructing composite benefit:risk endpoints have been proposed. We briefly summarize them here.

Methods that Involve Weighting

The quality-of-life time without symptoms or toxicity (Q-TWiST) method was originally used to evaluate interventions for the treatment of cancer when survival time was a primary endpoint (Gelber et.al, 1989). Q-TWiST is a two-step process. In the first step, overall survival is partitioned into three clinical disease states: time with toxicity due to therapy (TOX), time without toxicity or progression (TWiST), and time after progression (REL). In the second step, interventions are compared with respect to a survival time where the three clinical disease states are weighted by desirability. The time without toxicity or progression is typically given full weight (w=1) but the toxicity time and the time after progression are down-weighted:

• Q-TWiST = (w_tox × TOX) + (1 × TWiST) + (w_rel X REL) where 0≤ w_tox ≤1 and 0≤ w_rel ≤1.

Noting that the weights may vary depending on patient preference or clinical opinion, sensitivity analysis is then conducted across all possible choices of weights. For example, a patient that treasures every moment of life may select w_tox=w_rel=1, i.e., no down-weighting, whereas a patient that does not wish to endure any suffering may select w_tox=w_rel=0. A threshold utility plot (the vertical axis is w_tox while the horizontal axis w_rel) displays contours of similar treatment effects, e.g., adjusted-months of survival gained or lost, as a function of the selected weights. Individual patients and their clinicians can select their own weights and resulting intervention strategy accordingly.

Chuang-Stein (CCT, 1994) proposed a benefit-less-risk measure that discounts benefits for the presence of harms at a patient-level: BLR_j = B_j – f(R_j), i.e., for any particular patient, the benefit-less-risk score is the benefit score minus a transformation of the harm score, where the transformation puts benefits and harms on a common scale. The measure is intuitive but reducing benefits and harms each to a single score is often challenging as is identifying an appropriate transformation.

Assume that benefits and risks can each be measured on a bounded continuous scale (e.g., 0–10) or can be transformed as such. A scatterplot of patient scores could then be plotted in two-dimensional space. For any particular patient coordinate (i.e., bivariate score), the distance to the ideal outcome (i.e., B (benefit)=10 and R (risk)=0) could be constructed, effectively reducing the patient outcome to a single dimension. The distances could then be summarized by intervention and compared. An extension to this approach could be made to incorporate the potential differential importance of one unit on the benefit vs. risk scale. Thall et.al., (2006) used this approach for dose selection.

Methods that Involve Ranking

Weighting of outcomes, either explicitly as in Q-Twist, or implicitly as in composites are attractive but can be difficult to accomplish. While a specific weight may be controversial, it is often easier to agree upon the ranking of outcomes. A number of methods in the literature have pursued this idea.

Follmann (SiM, 2002) used the idea of multiple outcomes to rank participants’ clinical history in the trial with respect to an overall benefit:risk outcome using a combination of event times. To deal with censoring, pairs of patients are compared over their common follow-up time. As an example pairs are ordered by who lives longer, if both survive, they are then ordered by time to first hospitalization. A logistic regression model is used with the different in treatment indicators for the pairs of patients used as a covariate. The model allows one to estimate the odds that a person on treatment has a better outcome than a person on control.

Pocock et al (2012) introduced the win ratio which is similar to the pairwise ordering method of Follmann (2002). Under his appealing approach all treatment patients are paired with all control patients with a winner being declared if the control patient dies first or, if both survive, if the control patient is hospitalized first. A treatment patient is declared a loser if the opposite happens, if both survive with hospitalization, they are tied. The win ratio is the total number of winners divided by the total number of losers.

Wittkowski et al (SiM 2004) investigated the use of multivariate ranking of pairs of patients. Each patient is scored on a vector of quantitative outcomes. A score between pairs of patients is created by the difference in the number of outcomes on which a patient is superior minus the number of outcomes on which the patient is inferior. The Mann-Whitney-Wilcoxon test can be used to compare scores between groups.

Regulators in Japan historically utilized a composite global utility rating of clinical usefulness. Overall safety for each patient was rated on an ordinal scale (e.g., no, minor, moderate, or major event) while overall effectiveness for each patient was also rated on an ordinal scale (e.g., condition worsened, no change, minor improvement, major improvement). The safety and effectiveness ratings could be viewed in a two-dimensional cross-tabulation. Each cell of the table was then assigned an overall usefulness rating based on desirability (e.g., very useful, slightly useful, not-useful, undesirable for use). Numerical scores could then be assigned to these ratings and interventions could then be compared. Boers et.al. (2010) applied this strategy as part of the Outcome Measures in Rheumatology (OMERACT) initiative.

Chuang-Stein (1991) proposed the global benefit:risk score, a multinomial outcome based on efficacy and safety data. For example, the following ordered categories may be defined in order of desirability: efficacy without serious side effects, efficacy with serious side effects, no efficacy with a lack of serious side effects, no efficacy with serious side effects, toxicity leading to drop-out. An algorithm could be created to objectively classify each patient or a blinded adjudication committee could be used. For analyses, ordinal data methods could be used or weights could be assigned indicating the relative importance of each category. A summary measure could then be computed for each intervention and between-intervention comparisons could be made. Pritchett and Tamura (2008) applied this strategy to define the primary endpoint in a trial comparing two antidepressants by using remission status to categorize benefit and four possible adverse event outcomes to describe risk. Based on these methods, Norton (2011) developed a graphical display that summarizes aggregate treatment effects, within-patient changes longitudinally, and the temporal relationship and association between benefits and harms.

Claggett et.al. (2015) similarly classified each patient’s risk–benefit profile into several clinically meaningful ordinal categories. They then showed how to make inferences when the categorical data are incomplete due to censoring. They presented a systematic procedure to identify patients using baseline characteristics who would benefit from a specific treatment. The procedure consists of cross-validation for model building and evaluation.

If benefits and risks can each be measured on a bounded continuous scale (e.g., 0–10), then regions of plotted scores could also be separated into ordinal regions of desirability, preferably according to pre-specified definitions. Between-intervention comparisons of the proportions of patients that fall into these regions could then be compared using methods that compare ordinal measures.

Operationally another approach is to utilize blinded Adjudication Committees consisting of disease experts to provide an overall ranking for each patient response using an appropriate disease-specific scale defined by benefits and harms. Important data for each patient is sent to the Adjudication Committee for review. Although it is important to clearly and objectively define patient outcomes, the Adjudication Committee approach can be an attractive approach when a clear algorithm for patient response cannot be clearly identified or when there are many unexpected events. However this approach takes considerable planning and can be impractical for very large trials.

Desirability of Outcome Ranking (DOOR)

Evans et.al. (2015) described a strategy using the desirability of outcome ranking (DOOR) that incorporates benefits and harms for the design and analysis of clinical trials.

As the name suggests, DOOR is a ranking of all trial participants with respect to the desirability of their overall outcome. The construction of DOOR begins with defining an ordinal overall clinical outcome. The top and bottom categories are often obvious, e.g., the top category is often a form of efficacy without toxicities and complications whereas the bottom category is death. There are layers in between. The number and definition of categories is tailored to the clinical disease of interest (e.g., more levels could be created based on AE types/severity, or dichotomizing death into early vs. late).

The overall clinical outcome is based on a longitudinal snapshot of the experience, in contrast to measuring outcomes at a single timepoint, of the individual patient during the course of the trial, analogous to a discharge review or exit examination frequently conducted during hospital discharge, but now applied to the clinical trial setting. This provides the opportunity to distinguish with greater granularity between e.g., two patients that meet the definition of “cure”, one that does so without complication vs. one that has several complications along the way. For patients it is not only important where they end-up but how they got there and this can affect how they feel or function in daily life. The overall clinical outcome is based upon the important component outcomes (i.e., benefits, harms, and possibly quality of life) providing a comprehensive synthesis of the results for an individual patient. All trial participants are categorized according to the ordinal overall clinical outcome based on an algorithm constructed from the totality of the experience.

Such ordinal outcomes have advantages over standard approaches. For example in cardiovascular disease, a standard primary analysis is to evaluate the time to the first event where an event may be e.g., stroke, myocardial infarction, or death. However patients may experience more than one event. An ordinal composite outcome could incorporate these multiple events providing a more comprehensive picture of the effects of the intervention.

During analyses, the distributions of DOORs are compared between strategies. The probability that a randomly selected patient will have a better DOOR if assigned to the new strategy vs. the control strategy (plus half of the probability of a tied DOOR) is estimated along with a confidence interval. If there is no difference in DOOR distributions between the 2 strategies, then the probability will be near 50%. This metric may have an intuitive appeal with clinicians as they envision having to select a treatment by comparing treatment alternatives, i.e., what is the probability that this patient will have a probability of a better overall outcome on Treatment A vs. Treatment B?. Hypothesis testing can be conducted to test a null hypothesis, e.g., the probability is greater than e.g., 50%. Trials can be sized using rank-based methods or via simulation. Understanding of the clinical relevance of the metric can be aided by links to common metrics in traditional settings, e.g., differences in proportions/means or hazard ratios. For example, if survival times follow the proportional hazards model and the experimental intervention to control hazard ratio is R, then the probability of living longer on the experimental intervention is 1/(1+R). Thus a survival trial powered to detect a hazard ratio of 0.7 is also a trial powered to detect that the probability of a better outcome on treatment is .59. As another example suppose a continuous outcome is normal with mean 1 and variance 1 in the experimental intervention arm and normal with mean 1 and variance 1 in the control group. Then the probability of a better outcome on the experimental intervention compared to control is the probability a standard normal random variable exceeds 1 over the square root of 2 or 0.76.

Before analyzing several hundred patients, let us understand how to analyze one

One particular challenge is that construction of the ordinal outcome is often novel. Careful deliberation is needed to synthesize the outcomes typically measured in trials of a particular clinical disease. The Antibacterial Resistance Leadership Group (ARLG) is conducting a pre-trial sub-study to develop and validate use of a composite DOOR strategy in a future Staphylococcus aureus bacteremia trial. Twenty representative patient profiles (including benefits, harms, and QoL) were constructed based on experiences observed in completed trials in Staphylococcus aureus bacteremia. The profiles are being independently ranked by each member of a group of expert clinicians. The consensus among the ranks is being examined. Outcome characteristics that guide the average ranks are being evaluated to develop an algorithm for objectively ranking patient outcomes. Future trials could utilize the ranking strategy by comparing the distribution of ranks between randomized therapies. Follmann et.al. (1992) conducted a similar study in cardiovascular disease.

The resulting definition of the overall clinical outcome should be defined clearly in the trial protocol. As the construction may involve subjective components, the use of double-blind designs or blinded adjudication committees should be considered.

Example

We extend the discussion of an example of DOOR recently described in Evans and Follmann (2015).

Colistin is an antibacterial drug that was discovered in the 1940s and largely abandoned for several decades. However it has recently undergone revived use due to activity against several Gram-negative pathogens that cause life-threatening infections and are resistant to multiple other antibiotics (Flagas and Kasiakou, 2005). However, colistin has questionable efficacy (Paul et.al. 2010) and causes nephrotoxicity and neurotoxicity (Koch-Weser et.al. 1970; Wolinsky and Hines, 1962; Hartzell et.al., 2009). A new drug could provide a superior alternative to colistin if it either improves efficacy on major outcomes such as mortality, or has similar efficacy but reduces rates of clinically meaningful adverse effects. In a randomized trial comparing colistin to a new therapy, an ordinal composite clinical outcome may be constructed as follows:

• Survives without a major adverse event (AE)

• Survives with a major AE

• Death

Here it is important to utilize major AEs of unquestionable importance to the patient, e.g., irreversible renal failure or the need for hemodialysis. If the AEs were loosely defined, e.g., reversible creatinine clearance changes that are unnoticed by trial participants, then reductions in less meaningful AEs could result in the perception of overall benefit even if the new drug increases mortality relative to colistin or when neither drug reduces mortality relative to a placebo.

If the new drug reduces major AEs, then a trial comparing trial participants using the ordinal outcome will provide a more comprehensive picture of the overall treatment effects and may have greater power than a mortality trial to detect an overall benefit vs. colistin. Furthermore, examining survival and major AEs marginally, with the implicit assumption of independence, will be incomplete here if survival and major AEs are associated, which is plausible with drugs such as colistin.

Analysis consists of calculating the probability that a randomly selected patient will have a better DOOR if assigned to the new drug vs. colistin plus half of the probability of a tied DOOR. An alternative for dealing with tied ranks is to estimate the probability that a randomly selected patient will have a better DOOR if assigned to the new drug minus the probability that a randomly selected patient will have a better DOOR if assigned to colistin).

To design this trial, one could specify probabilities for the 3 outcomes of death, survival with major AE, and survival without major AE on the new drug and on colistin. Suppose that for colistin, the true probabilities are 0.25, 0.20 and 0.55, respectively (Hartzell et.al., 2009) and that we want to have 90% power to reject the null that the probability that a randomly selected patient will have a better DOOR if assigned to the new drug vs. colistin (plus half of the probability of a tie), i.e., P(DOOR_new> DOOR_colistin)+(1/2)P(DOOR_new= DOOR_colistin) =.5, in favor of the alternative that the probability is 0.59. Under a proportional odds logistic model for ordinal outcomes (McCullagh and Nelder, 1989), this requires that the probabilities of death, survival with major AE, and survival without major AE on the new drug of (0.15, 0.12, 0.73), respectively. A total sample size of 320 is required to achieve 90% power to reject the null hypothesis using an alpha=0.05 two-sided Wilcoxon rank sum test. The P(DOOR_new> DOOR_colistin)+(1/2)P(DOOR_new= DOOR_colistin) could be estimated by appropriately averaging all colistin- new drug pairs of patients and a bootstrap estimate of variance could be used to form confidence intervals.

The rank-based approach has advantages and disadvantages. One advantage is that it does not rely on distributional or other assumptions in contrast to alternative analysis strategies e.g., ordinal logistic regression which relies on the proportional odds assumptions. Another advantage is that it is easier to obtain agreement on ranking outcomes than scoring/grading them.

However a potential concern is that the ranking strategy may not provide the appropriate amount of influence to each specific component. For example in the colistin study, a concern may be that the influence of a major AE is too large compared to survival. The influence of a major AE is not directly assigned and is unknown until after the trial, as it depends on the resulting distribution of the ordinal outcome.

The Partial Credit Strategy

To address this concern, an alternative strategy is to assign the relative importance directly. Envision scoring the 3 categories of the ordinal outcome as if one were scoring an academic test. If a patient survives without a major AE, then a score of 100% is assigned. If the patient dies, then a score of 0 is assigned. If the patient survives with a major AE, then partial credit is given. The natural question is how much partial credit should be provided?

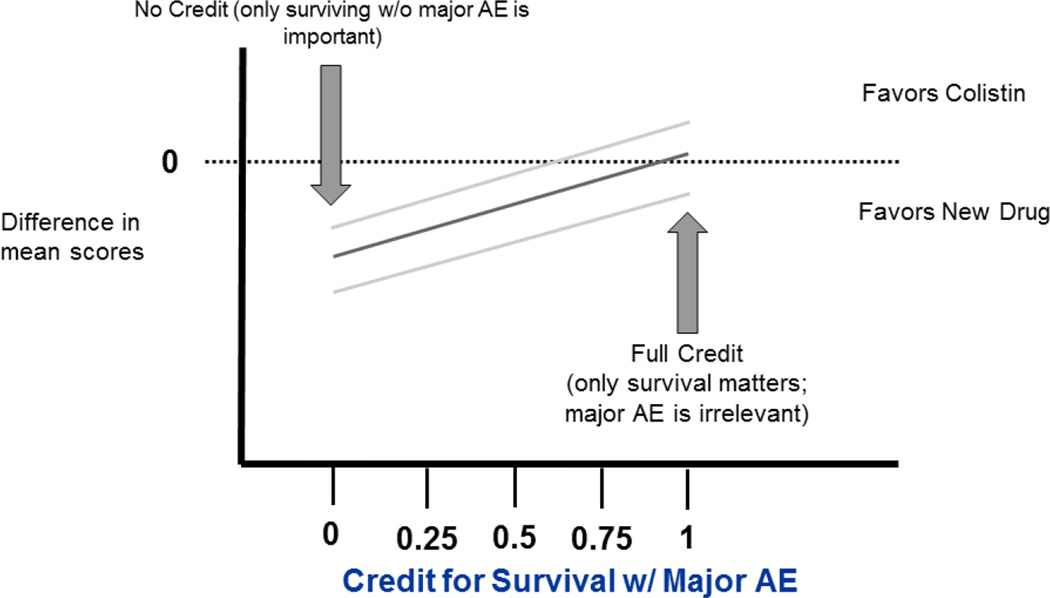
One potentially attractive analysis presentation is to display the estimated magnitude of effect and associated precision for a range (e.g., 0–100%) of possible partial credits as in Figure 1. Such analyses would identify a partial credit tipping point for when the new drug is preferred vs. when colistin is preferred. An attractive feature of this approach is that it allows for patients / clinicians to select therapy based upon their own preferences for partial credit rather than having a partial credit selected for them.

Figure 1.

Estimated magnitude of effect (difference in mean scores) and associated precision as a function of partial credit for survival with major AE

We note features of this plot. The figure displays the difference in mean scores as a function of the partial credit (denoted a) for survival with a major AE. This difference can be described as:

• (P1 – Q1) + a(PA-QA),

where P1 and PA are the rates of survival without AE and survival with a major AE rate in the new drug arm respectively, and Q1 and QA are analogous for the colistin arm. The curve is flat when (PA-QA) = 0, i.e. if there is no difference in the rates of survival with a major AE. If (PA-QA) is relatively small compared to (P1-Q1), then the selection of partial credit (a) has little impact. A partial credit value of 1 corresponds to using survival as a binary outcome while a partial credit value of 0 corresponds to survival without a major AE as a binary outcome.

In principle, individuals could assign different credit scores and make their own conclusions about the trial. However to appropriately size the trial and to provide transparency for the win criterion in a regulatory setting, a specific partial credit could be selected. To help guide choices, several strategies could be taken. One approach is to outreach to patients and calibrate the partial credit for survival with major AE to an external instrument such as a quality of life (QOL) score or an instrument that measures patient function. The QoL instrument could be given at the end or over the course of the trial. Suppose that higher QoL scores indicate a better QoL and the QoL score for death is considered to be zero. Further suppose that the survivors without a major AE have a mean QoL score of A and the survivors with a major AE had a mean QoL score of B. One could assign a partial credit of B/A to the survivors with a major AE. If the AE was as bad as death then the partial credit would be near 0 while if it was irrelevant, then we would have A≈B and the credit would be near 1.

The strategy of engaging patients in this manner may become an increasingly important aspect of trials based on an excerpt from a letter dated February 26, 2016 from FDA Commissioner Rob Califf (Califf, 2016):

“I plan to give special emphasis to further developing the critical role that patients play in our work. When it comes to finding solutions for challenges facing the FDA, there is no greater resource than the one presented through engagement and outreach with patients, as well as their families, caregivers, and advocates. Including their perspectives and voices in our work along the entire medical product continuum, from development to review and evaluation to post-market surveillance, offers opportunities to enhance our knowledge of the benefits and risks of medical products.”

Suppose that a partial credit of >0.5 is expected since survival with a major AE may be viewed as being closer to survival without a major AE than death. Further suppose that we wish to have 80% power (alpha=0.05) to detect a shift from probabilities of 0.25, 0.25 and 0.50 for the 3 outcomes of death, survival with major AE, and survival without major AE for colistin to 0.10, 0.12, and 0.78 for the new drug respectively. The required sample size can be derived assuming use of a t-test. When the partial credit is 0.6 and 0.8, the required sample sizes are 104 and 134. When the partial credit is 1 (equivalent to a binary survival endpoint), the required sample size is 196 (Table 2). Although use of the partial credit strategy reduces the required sample size in this case relative to a binary survival endpoint, the goal of the partial credit strategy is not to choose a partial credit or analysis method that optimizes power. The goal is to fairly and accurately reflect the impact of the major AE on the statistical method of evaluation.

Table 2.

Required Sample Size Using the Partial Credit Strategy for the Colistin Example

Partial Credit	Difference in Means	SD (colistin)	SD (new drug)	Required N (Total)
0.6	0.202	0.40927	0.31192	104
0.8	0.176	0.41231	0.29904	134
1.0	0.15	0.43301	0.3	196

The partial credit determined by using this method will not be available until after the trial is complete and such data are available. Thus for sizing the trial, patient or clinician surveys regarding their perspectives regarding of appropriate partial credit could be conducted before the trial.

Clinical Trials: A Vision for the Future

The increasing need and interest in pragmatism leads to a new vision for the future of clinical trials. This may create a shift in the number of outcomes that will be the focus in late-stage clinical trials as well as the number of treatment effects that will be estimated for each outcome (Table 3).

Table 3.

Clinical Trials: Today and in the Future

	Today	Future
Number of Outcomes	Many (efficacy, safety, QoL)	Few (a global patient outcome)
Treatment Effects per Outcome	Few (often one)	Many (personalized medicine)

Today in clinical trials we often measure several outcomes consisting of a few efficacy outcomes, safety outcomes and perhaps quality-of-life (QoL) outcomes. However improved synthesis of these outcomes is needed. In the future, although we may not measure fewer outcomes, there may be more emphasis on a single (or small group of) synthesized outcome(s) representing a more informative global patient evaluation similar to those described in this paper.

We are also seeing a shift in the number of treatment effects that are estimated for each outcome. Historically we typically estimated a single (population level) treatment effect for each outcome, i.e., we see multiple marginal treatment effects. However the future will have a focus on precision medicine. Instead of estimating a single treatment effect for each outcome, several patient/subgroup-specific treatment effects will be estimated. Focus will be on estimating an overall effect for the patient. The challenge will be to precisely identify subgroups of patients that do best overall while on an investigational intervention vs. those that do best overall on the control intervention.

Summary

The separation of the analysis of efficacy and safety is useful for understanding biological mechanisms but sub-optimal for evaluating the impact on patients. We propose a greater focus on using outcomes to analyze patients rather than patients to analyze outcomes particularly in late-phase/stage clinical trials. Although we have described methodologies such as partial credit within the context of pragmatic trials, such methodologies are equally applicable to explanatory trials where conditions are more tightly controlled. Certainly there is great interest in and need for structured benefit:risk assessment in efficacy trials. Methodologies described within can help fill this gap.

In the future, clinical trials will have an increased emphasis on pragmatism and describing the effects of new treatments in broad clinical settings. Increased pragmatism requires better summaries of the totality of the evidence in ways that clinical trials consumers---patients, physicians, insurers---find transparent and allow for informed choices. Two major themes for such description involve weighting of the multitude of outcomes and by rank-based procedures. Their adoption by the clinical trial community is likely to be incremental as the new methods are applied in settings where they offer clear advantages over existing methods, and then expand more generally as they become reliable and useful tools.