Altered cortical ensembles in mouse models of schizophrenia

Summary

In schizophrenia, brain-wide alterations have been identified at the molecular and cellular levels, yet how these phenomena affect cortical circuit activity remains unclear. We studied two mouse models of schizophrenia-relevant disease processes: chronic ketamine administration (KET) and Df(16)A^+/−, modeling 22q11.2 microdeletions, a genetic variant highly penetrant for schizophrenia. Local field potential recordings in visual cortex confirmed gamma-band abnormalities similar to patient studies. Two-photon calcium imaging of local cortical populations revealed in both models a deficit in the reliability of neuronal coactivity patterns (ensembles) which was not a simple consequence of altered single neuron activity. This effect was present in ongoing and sensory evoked activity and was not replicated by acute ketamine administration or pharmacogenetic parvalbumin-interneuron suppression. These results are consistent with the hypothesis that schizophrenia is an “attractor” disease and demonstrate that degraded neuronal ensembles are a common consequence of diverse genetic, cellular, and synaptic alterations seen in chronic schizophrenia.

ETOC blurb

Hamm et al studied sensory cortical populations in two established mouse models of schizophrenia pathophysiology and risk, chronic ketamine and Df(16)A^+/−. They identify a disorganization of neuronal ensembles, distinct from alterations in neuronal or global activity levels or pairwise correlations, which could constitute the common pathophysiology of the disease.

Introduction

Understanding of the neurobiology of schizophrenia (SZ) has progressed considerably over the past several decades. Research in human subjects with SZ has identified altered neuromodulation, excitatory/inhibitory balance, and neurodevelopmental processes at the molecular, synaptic and single cell levels (Lewis, 2014; Poels et al., 2014). In parallel, altered network connectivity and functional synchrony have been described in SZ at the whole-brain level (Uhlhaas and Singer, 2010; Yang et al., 2014). However, these alterations have not been connected into a coherent pathophysiology, and the heterogeneity and non-specificity of these biomarkers within and across multiple psychiatric diagnostic groups has complicated attempts (Clementz et al., 2016).

Perhaps at the heart of this issue is the possibility that the fundamental neural deviations which set SZ apart from other neuropsychiatric syndromes are best understood not at elemental (proteins, single neuron) or global levels (gross anatomy, fMRI), but at the circuit level (Arguello and Gogos, 2012; Sigurdsson et al., 2010) and within the stable dynamics of intricately connected, local neocortical populations (Rolls et al., 2008; Wang and Krystal, 2014). For instance, recent work in rodents has shown that local populations of neurons in both sensory and association regions exhibit repeating patterns of activity made up of multineuronal “ensembles”, coactive groups of neurons (Hebb, 1946), which are conserved across brain states and stimulation paradigms (Carrillo-Reid et al., 2015, 2016; Harvey et al., 2012; Luczak et al., 2009; Miller et al., 2014). These observations support the hypothesis that neural circuits have evolved to build emergent functional states, such as “attractors” consisting of stable or semistable, recurrent activity patterns which would theoretically underlie thoughts, perception, and action (Hopfield, 1982; Yuste, 2015).

It is therefore plausible that in SZ, a diversity of lower level molecular or synaptic alterations could generate a systematic disorganization of local cortical ensembles, effectively destabilizing otherwise reliable activity patterns present within neocortical networks. In fact, in SZ patients, alterations in the functional dynamics of global networks have been inferred from changes in interregional BOLD signal correlations (fMRI) and oscillatory coherence (EEG) (Lo et al., 2015; Uhlhaas and Singer, 2010; Zhu et al., 2016), providing some evidence for a circuit pathophysiology at the macroscale. Albeit very informative, such whole brain methods provide only a gross estimations of activity within local regions of the cortex, essentially averaging across the activity of tens to hundreds of thousands of neurons in a single measurement and thus lacking the single neuron resolution which may be critically necessary to differentiate and assess the robustness of repeating ensemble activations in local territories. Indeed, a degradation of consistent synchrony among local ensembles could undermine the robustness of signaling within larger brain networks and underlie macro-level network abnormalities. At the behavioral level, spontaneously active and inconsistently stimulus-driven ensembles or “attractor” patterns could explain positive symptoms (perceptual distortions, hallucinations, loose associations) while internally-driven patterns which are unstable and highly susceptible to distraction could account for cognitive deficits (Rolls et al., 2008).

Though theoretically powerful, empirical evidence for this pathophysiological framework at the circuit local level is lacking. To directly study the multineuronal dynamics of cortical microcircuits, we performed two-photon calcium imaging (2P−Ca²⁺), a method enabling stable, long-term observation of single cell spiking activity and patterned coactivations (ensemble activations) across local populations of neurons simultaneously in awake mice (Cossart et al., 2003; Stosiek et al., 2003; Yuste and Katz, 1991). We first induced a schizophrenia-relevant brain state in mice using the well-established ketamine pharmacological approach (Behrens et al., 2007). In humans, acute blockade of N-methyl D-aspartate glutamate receptors (NMDARs; with e.g. ketamine) consistently induces positive, negative, and cognitive symptomology of SZ (Krystal et al., 1994). While neither an acute nor a chronic ketamine model can be said to produce schizophrenia in mice, the chronic ketamine model (KET) recreates numerous schizophrenia-relevant phenotypes at multiple functional levels (Behrens et al., 2007; Phoumthipphavong et al., 2016). Indeed, in mice, chronic (7–14 days) subanesthetic ketamine not only affects NMDAR-neurotransmission, but recapitulates key SZ pathophysiology, including alterations in parvalbumin containing interneurons (Behrens et al., 2007), gamma oscillations (McNally et al., 2013; Sullivan et al., 2015), dopaminergic levels and gene expression (Chatterjee et al., 2012), dendritic spines (Phoumthipphavong et al., 2016), and cognition (Featherstone et al., 2012).

In addition, we also examined neocortical ensemble dynamics in a mouse model of significant genetic risk for SZ. Deletions in the 22q11.2 portion of the human chromosome result in sporadic cases of schizophrenia in 30% of carriers, a penetrance which is among the highest of all known risk genotypes for the disease (Hiroi et al., 2013). Like other high penetrance genetic risk factors, this mutation nevertheless accounts for a small proportion of the SZ population (approximately 1% of cases). But, importantly, individuals with SZ due to this genetic variant are phenotypically identical to the rest of the SZ population (Karayiorgou et al., 2010), sharing not only symptomology but also grey matter alterations (Jalbrzikowski et al., 2013) and functional connectivity impairments (Scariati et al., 2016). This critical section of the genome carries around 25 genes expressed in the forebrain controlling dopamine catabolism (COMT), microRNA production (DGCR8), and axonal growth (RTN4R, ZDHHC8), among others (Karayiorgou et al., 2010). Genetically engineered Df(16)A^+/− mice carry deletions syntenic to 22q11.2 deletions, and recreate a mosaic of SZ pathophysiology, including deficits in cortical parvalbumin interneurons, dendritic spine stability (Fénelon et al., 2013), axonal branching (Mukai et al., 2015) as well as impairments in synaptic plasticity (Fénelon et al., 2013) and hippocampal-prefontal synchrony supported working memory (Sigurdsson et al., 2010). By comparing adult Df(16)A^+/− mice (>P60) to their wild-type (WT) littermate controls, we examined whether and how multineuronal dynamics in sensory cortices are altered in this model of SZ-risk, and how such alterations compare to the KET model.

Our study examined local circuit activity in primary visual cortex. Despite traditional focus on prefrontal cortex, cell- and subcellular-level pathophysiology in psychotic disease is actually cortex-wide (Glantz and Lewis, 2000; Hashimoto et al., 2008; Uhlhaas and Singer, 2010). Moreover, visual processing abnormalities in particular are robustly reported in patients (Spencer et al., 2004; Uhlhaas and Singer, 2010) and visual perceptual disturbances are actually more common than auditory sequelae in first episode patients and prodromal individuals (Javitt, 2009). Given recent progress in understanding functional properties (Niell and Stryker, 2008) and SZ biomarkers in mouse visual cortex (Hamm and Yuste, 2016), we reasoned this cortical area, which can be rigorously studied given its sensory accessibility, could provide potent translational inroads to understanding local cortical circuit dysfunction.

We find that both models produced deficits in stimulus elicited gamma power similar to those reported in sensory cortices of human SZ patients (Spencer et al., 2004; Uhlhaas and Singer, 2010). Increased single neuron activity and background spectral power, a less consistent finding in SZ (Hamm et al., 2014; Moran and Hong, 2011), was only observed in KET mice. But neuronal ensembles were abnormal in both models, with a systematic disorganization wherein the presence of distinct ensembles became less pronounced and recurring ensemble activations became less reliable over time. Importantly, acute NMDAR blockade and pharmacogenetic suppression PV interneurons (using inhibitory hM4D(i) “DREADD” receptors), both components of the chronic KET model, disinhibited neuronal activity but were incapable of recreating higher-order changes. Ensemble-level disorganization in KET and Df(16)A^+/− was present in both ongoing and visually evoked activity, supporting the shallowed neocortical “attractor” landscape hypothesis of SZ (Rolls et al, 2008). Thus, our results show that two distinct chronic manipulations modeling key aspects of schizophrenia-risk and/or synaptic dysfunction generate changes in functional circuit ensembles rather than simple alterations in activity levels or functional connectivity, thus providing a bridge between the pathophysiology of single neurons and networks in a psychiatric disease.

Results

KET and Df(16)A^+/− models reproduce electrophysiological phenotypes of schizophrenia

To explore potentially altered dynamics of cortical circuits in the pathophysiology of schizophrenia, we used mice treated with chronic ketamine or Df(16)A^+/− mutants and performed all measurements in awake animals. Subanesthetic levels of ketamine (KET; 60 mg/kg/day) or an equivalent volume of saline (SAL) continuously (1uL per hour) were administered for 1 week with a subcutaneously implanted osmotic minipump (Alzet, model 2001). Mutant Df(16)A^+/− mice were generated as in (Stark et al., 2008). We first habituated mice to awake head-fixation on a rotating wheel allowing free movement and recorded local field potentials (LFPs) from layer 2/3 of V1. We focused on oscillatory activity at baseline and during the presentation of full field grating stimuli. Frequency and time-frequency spectra were first segregated with principal components analysis into 5 bins (Hamm and Yuste, 2016; Hamm et al., 2014) which conformed well to established neocortical frequency bands (Buzsaki, 2009): low/theta/alpha (1–14Hz), Beta (15–35Hz) Gamma1 (36–58Hz), Gamma2 (62–110Hz), and High (>111Hz).

Relative to saline controls (n=7), KET mice (n=6) exhibited a trend-level broadband increase in baseline spectral power in the high gamma band (PCA-defined gamma-2, 62–110Hz; t(11)= 1.81, p=.09). Df(16)A^+/− (n=8) mice, compared to their WT littermates (n=5), did not show an increase in background spectral power at any frequency (Figure 1A, E; all p>.10; number of mice used is the same for all LFP comparisons for all conditions). But during visual stimulation a significant decrease in sensory elicited gamma power was observed both in KET (first 500ms post-stim onset; gamma1 (36–58Hz), t(11)=2.48, p<.05; gamma2, t(11)= 2.21, p<.05 Figure 1B–D) and Df(16)A^+/− mice (gamma1, t(11)=2.04, p=.06; gamma2, t(11)=3.17, p<.01 Figure 1F–H). Similar trends were observed for gamma-band inter-trial phase coherence (ITC), a measure of phase consistency of stimulus induced oscillations (although ITC values were relatively low above 40Hz; see figure S1 and details in caption). Neither KET nor Df(16)A^+/− mice showed obvious alterations in arousal as evidenced by similar locomotion rates (Figure S1E,F; t^KET(11)= t=−0.12; p<0.90; t^Df16(11)= −1.35, p=0.20) and similar distributions of spectral power across low (<15Hz) and gamma/high frequency bands [>35Hz; Figure 1A,E; S1A,B; ratio: t^KET(11)= −0.14, p=.89; t^Df16(11)= −0.25, p=.81 (Harris and Thiele, 2011; Vinck et al., 2015)]. This held true when spectra were normalized by average overall power (ostensibly; 0.5–120Hz; Figure S1C,D; reflecting “relative” power). Post-hoc examination of these relative power spectra demonstrated a decrease specifically at the theta peak (6.5–7Hz) in Df(16)A^+/− (t(11)=2.21, p<.05) but not KET mice (t(11)= −1.04, p=.32). Alterations in prefrontal-hippocampal theta coherence have been previously reported in Df(16)A^+/− mice (Sigurdsson et al., 2010), and these effects begin to suggest that such abnormalities could extend to other neocortical regions.

Figure 1. Abnormal electrophysiology in KET and Df(16)A^+/− mice.

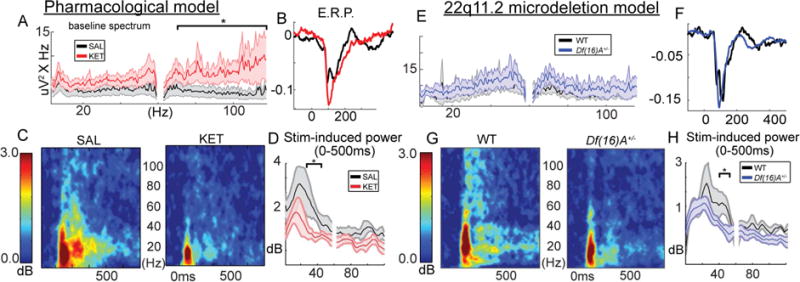
LFP recordings from mouse V1 layer 2/3. (A) Baseline power spectra corrected for 1/f component. (B) The waveform of the initial event related potential (LFP averaged over trials). (C) Stimulus-induced gamma power time-frequency spectra, (D) averaged over the first 500 ms. (E–H) repeated for Df(16)A^+/− mice (*p<.05, 2-tailed; all spectra/lineplots averaged over all mice; n^sal=7, n^ket=6, n^df16=8, n^control=5 mice; Error bars reflect S.E.M across mice).

Deficits in stimulus driven gamma power are relatively consistent in patients (Brenner et al., 2009; Uhlhaas and Singer, 2010) especially when passive, simple paradigms and large samples are studied (Hamm et al., 2014). While alterations in broadband spectral power at baseline have been reported in ketamine models in rodents (Kocsis et al., 2013), such increases are inconsistent across other pharmacological and genetic models of SZ (Featherstone et al., 2015; Sullivan et al., 2015), and similar observations, as well as changes in relative theta power, in SZ are present but variable (Clementz et al., 1994; Hamm et al., 2014; Hirano et al., 2015). In general, dysregulation of gamma-band dynamics and signal to noise ratio, rather than a simple increase or decrease, is a more consistent finding in SZ (Moran and Hong, 2011) and both models recapitulate this deficit in a primary sensory cortex.

KET but not Df(16)A^+/− mice show increased neuronal activity

To measure neuronal population activity with single cell resolution, we virally expressed genetically encoded calcium indicators (GCaMP6) in layer 2/3 of left monocular primary visual cortex (V1) under the synapsin promoter which infects neurons broadly (Figure 2) and imaged populations of 50–150 neurons from V1 in a 500-by-500 um field of view through a surgically thinned skull (≈3.5–4.0 Hz; Figure 2A–B, S2). We first focused on the spontaneous “ongoing” activity in the absence of direct stimulation (i.e. during awake rest). Multineuronal recordings have shown that non-stimulus driven (ongoing) activity is not only abundant in sensory neocortical circuits, but shares a temporal and spatial structure with stimulus evoked activity (Luczak et al., 2009) recapitulating an intrinsic “ensemble” vocabulary of neuronal circuits (Carrillo-Reid et al., 2015; Miller et al., 2014) and potentially supporting intrinsically generated mental states (Ji and Wilson, 2007).

Figure 2. Abnormalities in neuronal activity and correlations in KET and Df(16)A^+/− mice.

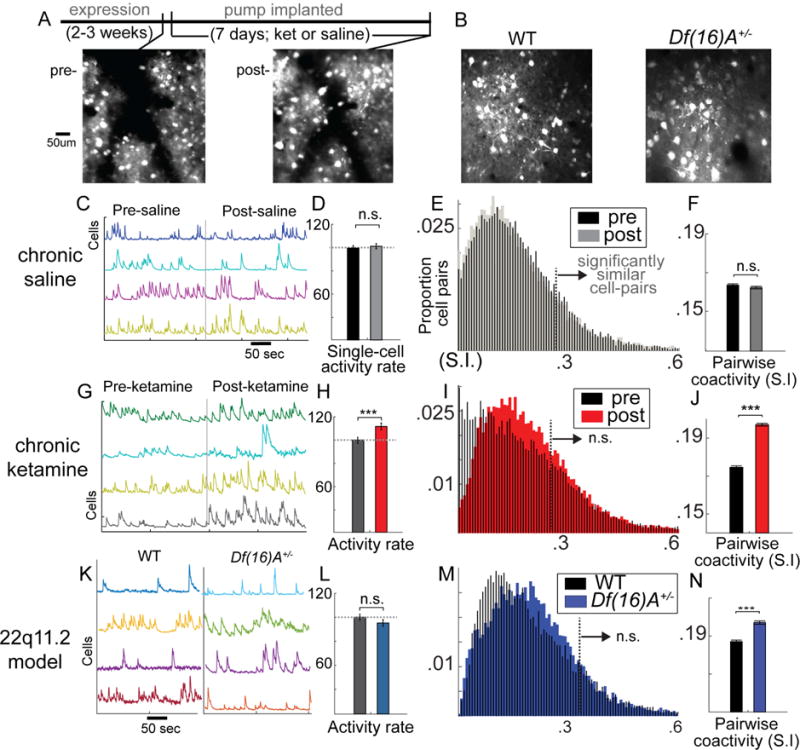
Standard deviation projection frame of virally driven GCaMP6s expression in local V1 populations (A) before after 1 week of minipump delivered ketamine or (B) in 22q11.2 microdeletion model mice [Df(16)A^+/−] or WT littermate controls. (C) Raw florescence traces (f) for single cells recorded during non-locomotive awake rest in a dark room before and after 1 week of saline treatment. (D) Average activity levels across cells (percent of frames showing significant increases in f, a signature of firing; response normalized to mouse-wise mean response pre-treatment). (E) Histograms of pairwise correlated activity (similarity index) with area right of dotted line indicating significantly correlated cell pairs, and (F) a bar plot displaying average correlations over all cell pairs. (G–J) plots repeated for chronic ketamine and (K–N) Df(16)A^+/− (One-way ANOVA, *p<.05, **p<.01, ***p<.001; neuronal populations from n^sal=6, n^ket=6, n^df16=7, n^control=7 mice; Error bars reflect S.E.M across cells/cell-pairs).

Spontaneous calcium transients [putative action potentials bursts (Chen et al., 2013; Smetters et al., 1999); measured by change in fluorescence, Δf/f; Figure S3, Figure 2C,G, K] were quantified in active layer 2/3 neurons before and after 1 week of KET (n=7 mice (6 for rest); 434 cells-pre, 438 cells-post) or saline control (SAL; n=7 mice (6 for rest); ; 436 cells-pre, 443 cells-post; Figure S2) or in Df(16)A^+/− mice (n=7 mice; 336 cells) or their WT littermates (n=7 mice; 408 cells. These animal/cell counts were used for all resting-state analyses, including single-cell, pairwise, and ensemble). When analyses focused on and were pooled across individual neurons, we found that KET increased the average ΔF/F during non-locomotive rest (F^interaction(1,1716)=3.73, p<.05; F^KET(847)=8.17, p<.01; F^SAL(869)=0.22, p=.69). This effect became more dramatic when analyses were limited to cells measured on consecutive weeks (see supplement; Figure S4 A,B; F^KET(146)=20.61, p<.001), and this analysis enabled a direct comparison of absolute florescence values and dynamics (which vary between cells and mice due to natural [i.e., intrinsic firing rate] or artificial reasons [i.e., viral expression, skull thickness, depth of imaging plane]). In KET mice, the frequency of calcium transients did not change (F^interaction (1,264)=0.77, p=.38), but the average size of calcium transients increased (F^interaction (1,264)=42.13, p<.001; F^KET(1,146)=28.51, p<.001). Interestingly, relative baseline activity levels in individual cells did not increase evenly across all neurons (pre-v-post correlation KET; r=.22, p=.04; SAL; r=.52, p<.001; Fisher r-to-z=2.71, p<.01; Figure S4C). This non-uniform increase is consistent with previous reports using acute PCP injection in rats (another NMDAR-antagonist) (Kargieman et al., 2007), but, as others recorded one neuron per animal, they could only infer this population-level effect.

Df(16)A^+/− mice on the other hand did not show a significant change in single neuron activity levels at rest when compared to littermate WT controls (F (1,742)=1.66, p=.19; Figure 2L). These effects showed a similar pattern as analyses of background LFP spectral power, suggesting that increased gamma EEG power observed in SZ visual cortex (Venables et al., 2009) could reflect an increase in neuronal spiking in superficial neocortex. Further, KET mice in our study showed an increase in single neuron calcium transient size but not frequency, echoing again LFP studies in NMDAR-hypofunction mice reporting increased LFP gamma-burst magnitude but not frequency (Carlén et al., 2012).

Disorganization of population activity in KET and Df(16)A+/− mice

Calcium imaging in awake mice enables an examination of the functional relationships and recurrent patterns of activity present in local neuronal populations which are not accessible with LFP (Harvey et al., 2012; Miller et al., 2014). We first sought to determine whether either model showed a simple increase or decrease in coactivity among local neurons by examining the average pairwise “similarity” between all neuron pairs (i.e., estimating the proportion of shared or synchronous calcium events across time; see Methods). In histograms combined across all mice and all cell pairs, both models (but not SAL) appeared to show a positive shift in the distribution towards higher similarity values (Figure 2L–N). However, these differences were not significant: using a frame shuffling procedure (which maintained the activity level and pattern of each individual neuron), we determined that the proportion of “significantly” similar or putatively functionally correlated cell pairs (actual similarity greater than 99% of shuffled values) for each mouse/circuit were neither increased nor decreased after SAL or KET (F^interaction(1,10)=1.92, p=.20), or in Df(16)A+/− (F (1,10)=0.85, p=.37), even though average cell-cell similarity values were increased in both models (F^interaction(1,132762)=284, p<.0001; F^KET(1,65954)=446.4, p<.001; F^SAL(1,66812)=1.90, p=.16; F^d(f16)A+/− (1,44210)=76.0, p<.001, Figure 2F,J,M).

This analysis suggested potential alterations at the ensemble or network level, but it was not clear from average pairwise synchrony alone whether and how ensembles of 3 or more neurons or network activity patterns are affected. For instance, when observed en masse, cortical circuits cycle between relatively quiescent periods and periods of synchronized activity (Miller et al., 2014). The latter consist of distinct groups of coactive neurons, or ensemble activations, which are neither constitutionally random nor perfectly uniform but may reflect the recurrent activity of stable “attractor” states which outline the computational building block of neuronal circuits (Carrillo-Reid et al., 2015; Hebb, 1949; Hopfield, 1982; Luczak et al., 2009; Miller et al., 2014). Thus, to comprehensively examine the effect of any manipulation on cortical circuit dynamics, one needs to measure these population-level dynamics reliably.

To do so, we first identified and defined “ensemble” activations (or high population-coactivity states) statistically for each imaging dataset as population coactivity above chance level (Figure S5 A–C; shuffling within neurons across time). This analysis indicated that the frequency of such population wide events was not altered in either disease model (Figure S6A–C). To determine if ensembles were constitutionally different in these disease models, we also characterized the instantaneous pattern of activity across all recorded neurons for each ensemble activation (i.e. which cells are active/inactive) as an n-dimensional vector (n=number of neurons). We then quantified the consistency of these states across subsequent ensemble activations using a “similarity index”; i.e. a measure of the cosine of the angle between state vectors, bound between 0 and 1 (1=perfect similarity). Smaller angles represent highly similar vectors, and, thus, points in time (or ensembles) with a highly similar constitution or distribution of local population activity (and a high similarity index).

In SAL treated and WT animals we found, as previously reported (Miller et al., 2014), ensemble activations with similarity values far exceeding chance levels (S.I.>.36–.41 based on within-frame shuffling; see experimental methods; Figure 3A,B,E,F; S5D,E). But Df(16)A^+/− and KET mice, however, displayed a significant decrease in state-state similarity, as though ensemble activity was not driven by stable groups of coactive neurons but instead by continuously variable or random activity states (Figure 3C,D,G,H). This was reflected in a ~35% decrease in ensemble “reactivations” across mice/circuits measured (F^interaction(1,10)=4.98, p<.05; F^KET(1,5)=8.01, p<.05; t^SAL(1,5)=0.02, p=.90; F^d(f16)A+/− (1,12)=6.00, p<.05, Figure 3I–K). A comparison of population activity patterns pre- and post-treatment showed that while SAL mice displayed many ensembles (Figure S6D) and/or recurrent population dynamics that repeated even after one week (PCA; Figure S6D,E), KET mice largely did not (Figure S6F,G), suggesting that the local neuronal ensembles which are otherwise stable over time within a circuit (Carrillo-Reid et al., 2016) are disrupted in the KET and Df(16)A^+/− (Figure S6 displays data from one representative SAL mouse and one KET mouse exhibiting a >40 re-identifiable neurons across weeks).

Figure 3. Unreliable ensemble activity in KET and Df(16)A^+/− mice.

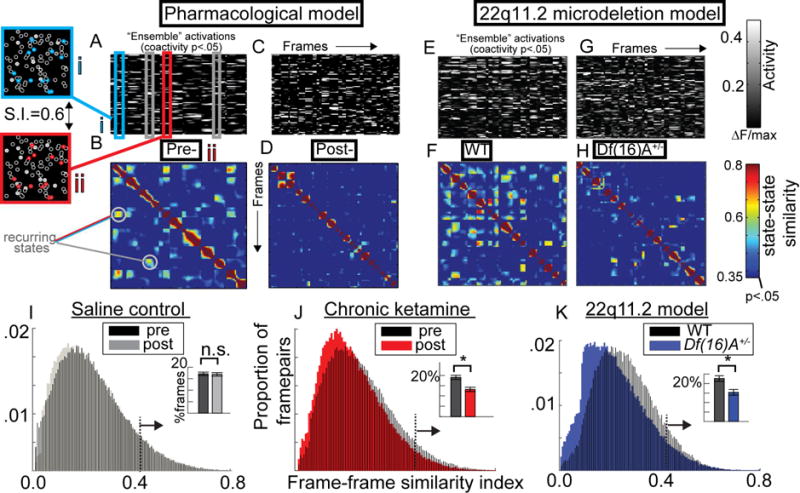
(A) Raster plot of single neuron activity from one mouse during statistically defined ensemble activations and (B) a frame-by-frame matrix of similarity (S.I.; symmetric along diagonal) demonstrating reoccurring population-wide activity patterns (>60% similarity) are depicted alongside the spatial distribution (left) of one repeating ensemble. (C–D) Plots are repeated for chronic ketamine (KET) and (E–H) in the Df(16)A^+/− model. (I) Histograms of S.I. from all state-state pairs along with inset barplots depicting proportion of statistically similar ensemble activations (p<.01) for saline, (J) KET, and (K) Df(16)A^+/− (neuronal populations from n^sal=6, n^ket=6, n^df16=7, n^control=7 mice; Error bars reflect S.E.M across mice; I–J reflect within subjects S.E.M. across mice (i.e. pre- vs post-)).

Further analyses using K-means clustering revealed that, in control animals, ensemble activations appeared to consist of a small number of semi-stereotyped unique “states” (rather than one all inclusive state; Figure 4A–H), suggestive of distinct “basins of attraction” in the cortical network [Figure 4O; (Rolls et al., 2008)] or motifs of activity (Luczak et al., 2009) made up of recurrent patterns coactivation (ensembles) and co-suppression (decorrelated cell pairs). Interestingly, the distinctness of these patterns appeared to be altered after KET and in Df(16)A^+/− (Figure 4B,D,F,H). To quantify this at the group level, we performed a variant of the “gap test” (Clementz et al., 2016; Yan and Ye, 2007) using k-means analyses with k=2 to 15. As the number of fitted cluster centroids (“k”) increases, the within-cluster distances necessarily decreases. The degree to which an added centroid reduces distances approached zero and became linear between 4 and 7, suggesting that in local populations of ~75 neurons, one can expect 4 to 7 distinct patterns of activity to recur during 20 minutes of rest (similar to previous measurements; (Carrillo-Reid et al., 2015)). In general, KET and Df(16)A^+/− mice showed higher within cluster distances (Figure 4 I–K) and significantly smaller reductions of within cluster distances with the inclusion of additional clusters in the models (Figure 3L–N; F^ket(1,10)=5.33, p<.05; F^df(16)A+/− (1,12)=4.40, p<.05).

Figure 4. Disorganized ensemble activity in KET and Df(16)A^+/− mice.

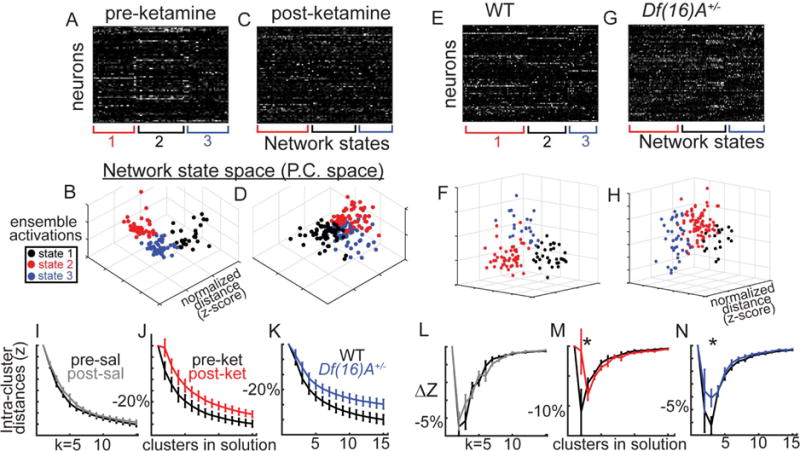
(A) K-means clustering (k=3) on spontaneous ensemble activations, (B) plotted in principal components space (first 3 PCs) from example mice demonstrate internally reliable and externally distinct repeating states, or putative “ensembles”. (C–D) Post KET and (E–H) in 22q11.2 model. K-means was repeated across for k=2 to 15 plotting (I–K) within “cluster” distances and (W–Y) decreases of within cluster distances with added clusters. (neuronal populations from n^sal=6, n^ket=6, n^df16=7, n^control=7 mice; Error bars reflect S.E.M across mice; I–J, L–M reflect within subjects S.E.M. across mice).

Our results are consistent with the hypothesis that both mouse models of SZ demonstrate an essential disorganization of ensemble activity rather than, for instance, an increased number of ensembles or network patterns. This degradation of neuronal ensembles was present in both models of SZ pathophysiology and/or genetic risk despite differences at the LFP, single neuron, or pairwise connectivity levels (Figure 8A).

Figure 8. Summary of effects and model for attractor pathophysiology of schizophrenia.

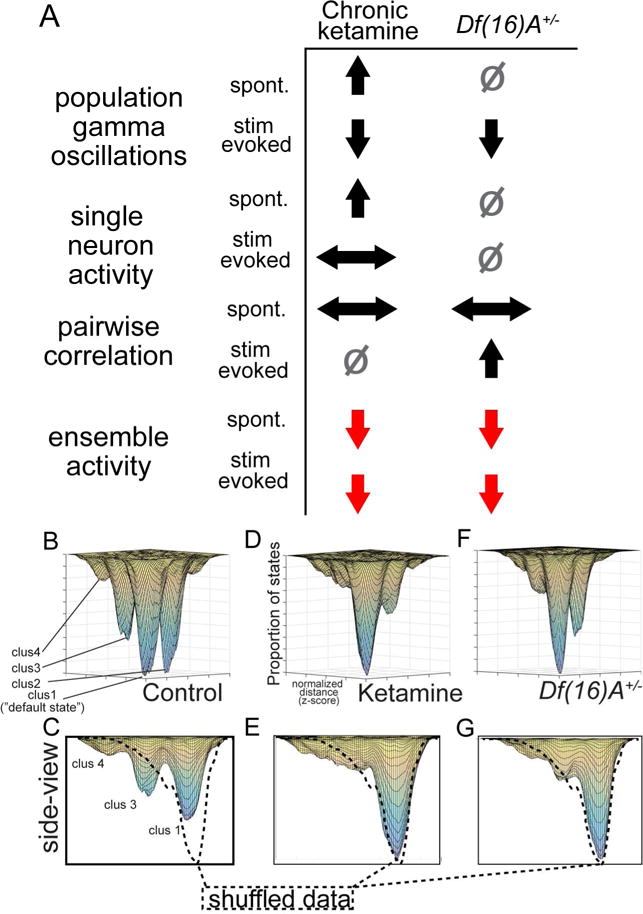
(A) Local field potential, cell-wise, pair-wise, and ensemble-wise effects in both models demonstrate that ensemble-level deficits are the most consistent across models and conditions. Comparing to control animals, up-arrows signify an increase; down-arrows a decrease; left/right a change in distribution; square is no change. (B) Iterative combination of K-means solutions across mice, where spontaneous ensemble activations were assigned to “clusters” based on cluster sizes, and clusters were assigned to a specific location on a 2-d PCA derived map, organized spatially based on average inter-cluster distances within a group. (C) Results after shuffling ensemble-activations (across cells, 1000×) indicate that fully disorganized network activity would result in a single “default state” represented by a single Gaussian peak (dotted line on right). Control mice (pre-treatment/homozygous littermates), (D–G) but not disease model mice showed a number of clear peaks, suggestive of attractors in the network (neuronal populations from n^WT=7, n^ket=6, n^df16=7 mice).

Abnormal ensembles reflect chronic alteration of neocortical circuits

Although psychotic episodes can appear transiently in psychiatrically healthy individuals, due to drug use or sleep deprivation, for example, SZ is a chronic disorder with persistent deficits in cognition and information processing that even precede the first psychotic episode for years (Kahn and Keefe, 2013). Because of this, we next explored whether the disorganization of functional neuronal ensembles identified in KET and Df(16)A^+/− mice could reflect chronic pathological changes to brain function or whether more transient disruptions in neurotransmission could also generate these effects. First, we tested whether a single dose of subanesthetic ketamine could affect ensemble activity. In addition to eliciting transient SZ-like positive, negative, and cognitive symptomology in humans (Krystal et al., 1994), acute subanesthetic doses of ketamine induce hyperlocomotion, electrophysiological, and other behavioral abnormalities in rodents (Amann et al., 2010; Kocsis et al., 2013). To test this, we repeated 2P-Ca²⁺ imaging experiments described above, measuring local neuronal ensembles during awake rest in additional set of mice at baseline, after saline injection, and after 15mg/kg subcutaneous ketamine injection (n=7 mice, 332 cells pre and post; 30 min after injection). As expected, a single treatment of subanesthetic ketamine (but not an equivalent volume of saline) increased locomotion (Figure 5A; F(2,6)=8.92, p<.01; F ^{base vs ket} (1,6)=6.96, p<.05). Although hyperlocomotion is not equivalent to any symptom of SZ or psychosis in humans (which can even involve amotivation, apathy, and reduced engagement in activities), it is a well-replicated effect in acute ketamine studies of mice, and our observation of this effect evinces the effectiveness of our paradigm. Acute ketamine also disinhibited ongoing activity when compared to baseline (during non-locomotive frames; Figure 5B; F(2,662)=14.8, p<.001; F ^{base vs ket} (1,171)=11.56, p<.001), but pairwise correlations (Figure 5C; F(2,6)=1.1, p=.35) and, importantly, the reliability of ongoing ensemble activations were clearly unaltered (Figure 5D; (F(2,6)=2.10, p=.17; KET slightly but non-significantly higher than baseline).

Figure 5. Acute ketamine and interneuron suppression do not affect ensemble reliability.

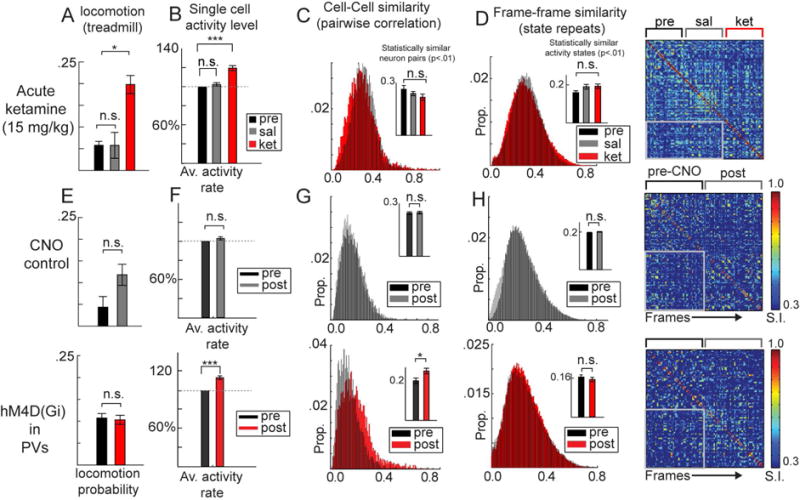
Expected increases in (A) locomotion frequency (percent of frames recorded during locomotion) and (B) single neuron activity was observed after 15 mg/kg acute ketamine compared to saline control (332 cells base, post-sal, post-ket). (C) Functional correlations among all neuron pairs and (D) consistency of ensemble activations were unaltered in after acute ketamine, as population states repeated within and across (gray box) treatment periods (each 20min). (E–H) CNO-control experiments (mice injected only with GCaMP6; above; 356 cells pre, 349 cells post) are compared to DREADD suppression (hM4D(Gi); 429 cells pre, 396 cells post) of parvalbumin containing interneuron (PVs) experiments. (E) locomotion was not affected but (F) single neuron activity and (G) the proportion of significantly coactive neuron pairs increased. (H) Ensemble activations nevertheless maintained reliable patterns of activity across time (*p<.05;***p<.001; One way ANOVA; loco/neuronal populations from n^ket=7, n^pv-hM4D=7, n^cno-control=5 mice; Error bars reflect within subject S.E.M across mice; B/F reflect within cell S.E.M. across cells).

In addition, it has been shown that both the KET and Df(16)A^+/− models induce anatomical alterations in parvalbumin-containing interneurons (PVs, (Behrens et al., 2007; Fénelon et al., 2013)), a well-established cortex wide abnormality in human SZ patients (Hashimoto et al., 2008). GABAergeic pathophysiology is not limited to PV interneurons in SZ [e.g somatostatin-containing and cholesystokinin-containing interneurons also show changes (Fung et al., 2014)], but given their dense local connectivity in neocortical circuits (Fino and Yuste, 2011) and their known role in modulating fast network synchrony (Sippy and Yuste, 2013; Sohal et al., 2009), it has been hypothesized that PV dysfunction in particular may play a primary causal role in disrupting cortical computations underlying sensory processing and cognition (Javitt and Freedman, 2015; Lewis, 2014). In control experiments in the current study, using Pv:Cre∷tdTomato mice, which express a red florescent indicator in PVs enabling stable recording of calcium dynamics (Figure S7A), we confirmed in a subset of mice (n=7; 56 cells) that activity levels in PVs in V1 were stable a week after saline but decreased after chronic ketamine (Figure S7B–E; see supplemental experiments for detailed analyses and results). Because of this, we further sought to address whether transient decreases in local PV activity alone could affect ensemble activity and explain our population level results.

Inhibitory DREADD channel hM4Di functionally silences host cells primarily through the suppression of synaptic current amplitude and release (Designer Receptors Exclusively Activated by Designer Drugs, (Roth, 2016)). Using an awake pharmacogenetic suppression protocol methods (Hamm and Yuste, 2016; Jackson et al., 2016) we virally expressed of hM4Di specifically in PV interneurons using the cre-lox system (Sohal et al., 2009), and recorded LFPs and 2P-Ca2+ dynamics before and after subcutaneous injection of Clozapine N-Oxide (12 mg/kg CNO; a typically inert ligand which activates hM4Di) in PV-hM4DI mice (n=7 mice; 429 cells pre, 396 cells post) or controls (n=5 mice; 356 cells pre, 349 cells post). DREADD suppression of local PVs in the current study did not alter locomotion (Figure 5E) but, as expected, PV suppression generally increased average ΔF/F values in the local population (Figure 5F; (F^PVhM4D(1,824)=18.49, p<.001; F^control(1,706)=0.88, p=.34). The proportion of correlated cell-pairs showed a clear increase after PV suppression, (F ^PVhM4D(1,6) =6.64, p<.05; F^control (1,4) =0.09, p=.77; Figure 5G), a more straightforward change in population coactivity than in the chronic models. It is important to point out that while PVs may facilitate short time scale spike synchrony, organizing spike timing in coactivated neurons by supporting gamma-band oscillations (Sohal et al., 2009), our effect indicates that shared variations in firing rates between neurons over longer time courses (seconds to minutes) is suppressed or modulated by PV interneurons, an effect which converges with previous experiments in thalamocortical slices (Sippy and Yuste, 2013). Further, this increase in pairwise correlations was nevertheless not accompanied by any change in ensemble reliability, as the number of significant framepairs (state repeats) was again unchanged (F ^PVhM4D(1,6) =0.27, p=.62; F^control (1,4) =0.09, p=.77;Figure 5H).

Thus, NMDAR blockade or local PV suppression was sufficient to disinhibit neurons at similar levels as chronic KET, increase locomotion, and/or alter correlations between local neuronal pairs, but neither manipulation disrupted the reliability of local ensemble activity. Altogether this suggests that chronic models of SZ and potentially the disease itself involve a breakdown of stable neocortical activity patterns, and this disruption is beyond the effects that short-term disruptions in local E/I balance have on local circuit function. Further, our results challenge the notion that any disruption of excitatory or inhibitory neurotransmission can disrupt existing ensemble patterns in the cortex, and emphasize that ensemble disorganization is not a simple computational or mechanistic consequence of alterations in single neuron activity or average correlation values. Like our results, past studies have shown acute blockade of NMDA receptors are sufficient to disinhibit brain activity and cause other transient sensory and cognitive disturbances (Kargieman et al., 2007; Yang et al., 2014), perhaps through a suppression of GABAergic cells in the thalamic reticular nucleus (Kargieman et al., 2007). Yet chronic mouse models of KET and genetic mouse models of SZ involve longer lasting changes to dendritic spine stability and local inhibitory interneuron populations (Behrens et al., 2007; Featherstone et al., 2012; Fénelon et al., 2013), and these changes may together give rise to a lasting disorganization of local neuronal ensembles.

Ensemble-level dysfunction during visual stimulation in KET and Df(16)A^+/−

Finally, we inquired whether the functional disorganization of neuronal ensembles we observed in KET and Df(16)A^+/− was specific to ongoing or awake “rest” activity, suggesting a principle abnormality of intrinsic activity (Whitfield-Gabrieli and Ford, 2012), or perhaps also extended to stimulus-elicited brain states, suggesting a more general circuit pathology. If so, this would suggest a deficit in externally driven information processing, possibly accounting for persistent perceptual deficiencies in SZ (Javitt and Freedman, 2015).

As above, we first examined single neuron activity, pairwise correlations, and ensemble-wise functional characteristics in V1 circuits in both models, but not during visual stimulation. We presented awake mice with 3 second, square wave moving gratings (100% contrast, 0.04 cycles per degree, 2 cycles per second, 7–8 second gray screen interstimulus interval) of 6 different orientations (0, 30, 60, 90, 120, 150 degrees; 10–14 repeats each). V1 neurons respond selectively to contours of particular orientations in their visual field and this selectivity can be quantified by the orientation selectivity index, O.S.I. (Niell and Stryker, 2008) (Figure S2 F,H). In our study, neurons showing significant stimulus driven activity (average stimulus induced F greater than 1.67 stdev above baseline fluctuation (Hamm and Yuste, 2016); 70–75% of neurons) maintained the same preferred stimulus orientation prior to minipump insertion and one week after for the SAL or KET treatment (Figure S8), but KET mice showed significantly decreased quantitative O.S.I. values (n^KET=6-mice, 297/299 cells pre/post; n^SAL=6 mice, 320/311 cells; F^interaction(1,1223)=8.4, p<.01; F^sal(1,629)=1.25, p=.26; F^ket(1,594)=9.73, p<.01; Figure 6A–C; S8). Examining stimulus response curves demonstrated significant increases in activity driven across all stimuli (F^week(1,594)=6.01, p<.05; F^{weekBYorientation}(11,594)=0.77, p=.67; Figure 6D), suggestive of a decrease in subtractive inhibition or gain-modulation (Lee et al., 2014), another effect consistent with PV interneuron dysfunction seen in KET mice in the current study (Figure S7). Interestingly, neurons from Df(16)A^+/− mice did not differ from neurons from littermate controls on OSIs (n^Df(16)A+/−=7-mice, 336 cells; n ^WT=7-mice, 246 cells; F(1,580)=0.96, p=.32; Figure 6E) and exhibited equivalent stimulus response curves which did not differ (Figure 6F; F^grp(1,580)=0.94, p=0.33; F^{grpBYorientation}(11,580)=0.66, p=.77). Thus similarly to what was observed during ongoing activity during awake rest, the KET model involved disinhibition at the single neuron level while Df(16)A^+/− mice showed no such abnormality.

Figure 6. Sensory stimulus evoked responses and pairwise variability are altered in KET and Df(16)A^+/− mice.

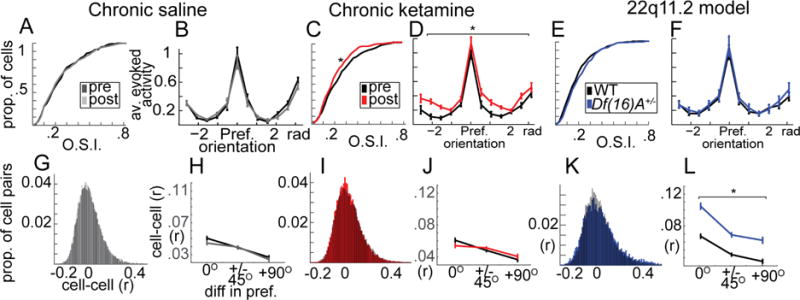
(A) Orientation selectivity (O.S.I) and (B) trial-averaged response curves from visually responsive neurons from saline treated mice (pre vs post, n=631 total cells), (C–D) chronic ketamine treated mice (pre vs post, n=596), (E–F) and Df(16)A^+/− mice compared to littermate controls (n=582). (G) Shared variability among neuron pairs across presentations of the same stimulus (“noise correlations”; same cells from A) (H) varied with respect to the orientation preference similarity of neuron pairs and (I–J) was not affected by KET. (K–L) Df(16)A^+/− mice, on the other hand, showed an increase in noise correlations among all neuron pairs in the local population regardless of whether they shared stimulus preferences. Line plots reflect average cell responses relative to their preferred stimulus (pre-treatment B,D; within mouse F), and/or including only cells with >.1 O.S.I (H,J,L). (*p<.05; one-way ANOVA; n^sal=6, n^ket=6, n^df16=7, n^control=7 mice; Error bars reflect S.E.M across cells/cell-pairs).

During sensory stimulation, neocortical circuits display dynamic changes in correlated activity among neuronal pairs (Averbeck et al., 2006). While correlations arise necessarily due to shared responses to an external stimulus (or “signal correlation”), an additional source of correlations is shared variability across otherwise similar events (Hofer et al., 2011). In other words, individual neurons do not respond identically to the same stimulus over and over, and when this variability is shared among neurons in a local network, it is referred to as “noise correlation.” While the computational consequences of noise correlation are debated and complex (Averbeck et al., 2006), an excess amount of noise correlation could be detrimental to reliable stimulus encoding (Cohen and Maunsell, 2009). Here we focused on noise correlation across stimulus presentations (within the same orientation, then averaged across orientations) within neuron pairs using similar methods as previously reported (Hofer et al., 2011). While neither SAL nor KET affected noise correlations (F^sal(1,26488)=3.26, p=.08; F^ket(1,21004)=0.23, p=.97; Figure 6G–J; pairs^KETpre=12600, pairs^KETpost=9238, pairs^SALpre=13894, pairs^SALpost= 11772; n^KET=6-mice; n^SAL=6 mice), Df(16)A^+/− showed abnormally increased average noise correlations among all neuron pairs (F^group(1,15656)=152.48, p<.001; Figure 6K; pairs^df16= 9442, pairs^WT=6282; n^Df(16)A+/−=7-mice; n ^WT=7-mice). As expected, noise correlations were modulated by the similarity of the preferred orientation of neurons, with neuron pairs sharing the same preferred orientation showing higher noise correlation than pairs with opposite preferred orientations (focusing only on O.S.I.s > .1, (Mazurek et al., 2014); pairs=15724; 14 mice; F(2,15656)=88.79, p<.001). Although a significant group by orientation interaction effect was present (F(2,15656)=3.23, p=.03), it was small relative to the group effect, which was substantial regardless of whether neuron pairs shared orientation preference (Figure 6L). Again, similar to effects seen during ongoing activity, no change was seen in the proportion of significantly noise-correlated neuron pairs present (F(1,11)=1.39, p=.24).

While both KET and Df(16)A^+/− showed some abnormalities in stimulus evoked activity in V1 at single and pairwise neuronal levels, the nature of these effects diverged, with KET showing single neuron disinhibition and Df(16)A^+/− showing augmented noise correlations. We next examined whether a clear deficit in ensemble regularity could again serve as a downstream convergence point for these distinct abnormalities in low-level visual stimulus processing, similar to what we observed during ongoing ensemble activity during awake rest. First we demonstrated that stimulus-evoked ensembles showed relative consistency (significant similarity) during and across repeated presentations of the same stimulus (i.e. grating orientation; Figure 7A–B; left panel). This characteristic was attenuated after KET (Figure 7C–D) and in Df(16)A^+/− mice relative to littermate controls (Figure 7E–H) in representative samples. Figure 7 panels I–L further illustrate this effect using a PCA-derived projection of the multineuronal state-space onto 3 dimensions, showing that the trajectory of the local population activity state during visual stimulation is consistent within and distinct between orientation angles (separate PCA for each condition using average trial data and neurons as variables; each trial is a line; each orientation angle is a different shade of gray). These properties were diminished in the disease models (Figure 7J,L). To quantify this we calculated the relative change in between trial population similarity (similarity index, see above) from baseline (prestim, 1 second), averaging over the stimulus presentation period (3 sec), and normalizing it by the standard-deviation of similarity values derived from a bootstrapped distribution of “random” similarity values derived by shuffling each mouse’s population activity (Figure S5E). This generated a z-score metric for each trial for each mouse.

Figure 7. Stimulus evoked network states are altered similarly in KET and Df(16)A^+/− mice.

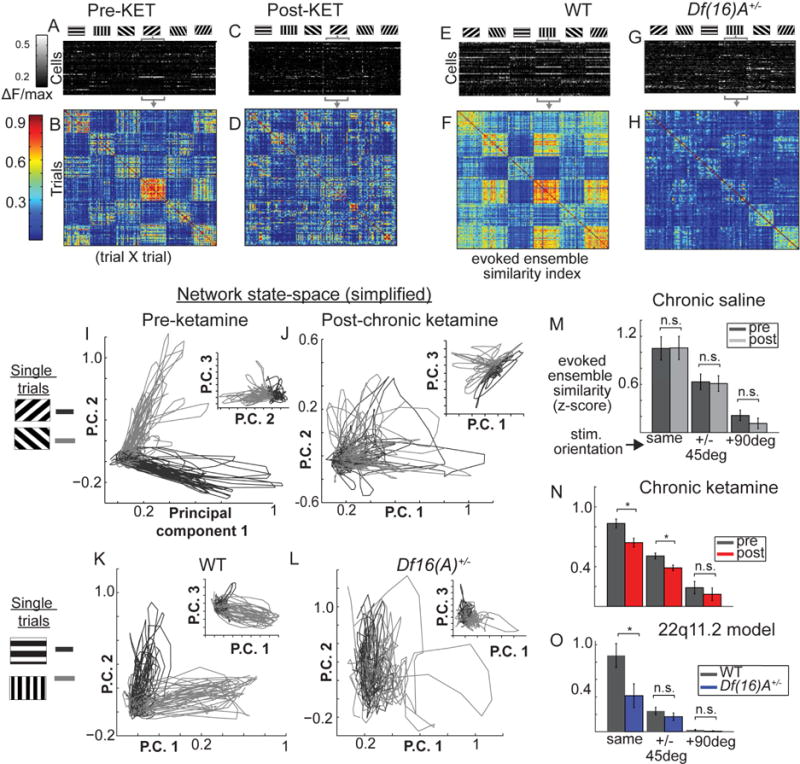
(A) Pre-treatment single trial activity (f) from individual cells (rows), averaged within trials (colums), sorted by stimulus orientation. (B) Cross-trial similarity matrix from trials in (A) (similarity index, S.I.). Same plots (C–D) after KET. (E–F) in littermate controls and (G–H) Df(16)A^+/−. (I–L) Population activity projected with PCA into 3-dimensional space (each line is one trial; shade of gray denotes stimulus orientation). Similar ensemble activations show similar line trajectories from origin. (M–O) Average trial-evoked ensemble similarity (*p<.05, one-way ANOVA; neruonal poplulations from n^sal=6, n^ket=6, n^df16=7, n^control=7 mice; Error bars reflect within subjects S.E.M across mice; O reflects S.E.M. across mice).

As expected, cross trial similarity varied as a function of orientation difference between trials (i.e. trials with the same orientation evoke more similar population states than different orientations; F^orientation(2,12)=22.57, p<.001), yet some similarity above chance 0 was shared even among non-similar orientations. These stimulus evoked population states were stable before and after saline treatment (Figure 7D–G; F^group (1,36)=0.09, p=.77; n^SAL=6 mice) but became less reliable after ketamine treatment (Figure 7D–G; F^group (1,36)=7.58, p<.05; n^KET=6 mice) and in the Df(16)A^+/− mice (F^group(1,41)=5.78, p<.05; n^Df(16)A+/−=7-mice; n ^WT=7 mice). A group by orientation interaction effect did not reach significance for either model (p>.05). Thus activity states in local populations of neurons which encode visual stimuli are unreliably activated by external stimuli in our mouse models, supporting the notion that a generalized disorganization of functional neocortical ensembles could undermine short-term memory processes and/or the stable encoding of the environment (Hopfield, 1982; Rolls et al., 2008), providing a basis to explain the symptomology of SZ.

Discussion

Altered neuronal ensembles in two mouse models of schizophrenia

We examined here the functional dynamics of local cortical circuits in two distinct models schizophrenia-relevant brain pathophysiology: a pharmacological model (ketamine, i.e. KET) and a genetic model, which additionally offered construct validity by recapitulating in mice a strong causal factor for the disease (i.e. 22q11.2 microdeletions).

At the level of local field potentials, which offer a gross-level estimate of cortical activity levels and broad scale synchrony, these models generally recreated one of the most established endophenotypes of SZ (decreased stimulus elicited gamma-band transients), but differed in the degree to which background activity levels were augmented (Figure 8). Further, at the single neuron level, KET disinhibited neurons, leading to larger calcium transients and reduced orientation selectivity, while Df(16)A^+/− did not differ from their littermate controls. Next, at the average pairwise level (correlations), both models showed what appeared to be a dysregulation of synchrony, but the nature of this change was not straightforward, showing no change in strongly correlated neuron pairs despite a change in mean “similarity values”. Correlations among cell-pairs across repeated visual stimulations, or “noise correlations”, also differentiated KET and genetic models, wherein only Df(16)^+/− showed augmentations.

Yet where these models converged was at the ensemble level, when local multineuronal activity patterns were measured across time. Both models showed a systematic decrease in state reliability across ensemble activations at rest and during direct visual stimulation. Importantly, this decrease was not a simple consequence of shared single neuron activity level changes or strengthening/weakening of functional correlations, since neither disinhibition nor orientation selectivity nor pairwise correlations alone could predict the ensemble-level abnormalities apparent only in our chronic models. Instead, our results likely reflect a disorganization of emergent multineuronal dynamics.

Chronic manipulations are necessary for altered ensembles

Acute ketamine blockade of NMDA receptors and pharmacogenetic suppression of PV protocols employed in the current study were sufficient to disinhibit neuronal activity at similar levels as chronic ketamine, yet neither manipulation was sufficient to disorganize ensemble-level activity like in our chronic models. This finding is mechanistically informative in two ways. First, local population activity patterns are stable in a healthy brain state (Figure S6D), but we have recently shown that with persistent and direct perturbation at the microcircuit level, ensembles in adult brains can be programed or “imprinted” (Carrillo-Reid et al., 2016). Thus while acute ketamine may disinhibit neuronal activity, chronic NMDAR blockade or a genetic lesion (22q11.2 microdeletions) additionally result in a persistent destabilization of synapses and dendritic spines (Fénelon et al., 2013), essentially deprogramming local ensembles which are the cortical building blocks necessary for stable cognition. Indeed, many aspects of SZ brain pathology involve deviant developmental trajectories or exacerbation over time (Walterfang et al., 2008), so future work could characterize ensemble organization across various periods of development in relevant mouse models.

Second, it has been previously shown that chronic, but not acute, NMDAR blockade is sufficient to alter local inhibitory interneurons populations (PVs (Behrens et al., 2007)), an effect which we replicate in the functional domain (Figure S7). PVs play a critical role in organizing stimulus elicited local gamma synchrony and pairwise correlations (Figure 5G; (Sippy and Yuste, 2013; Sohal et al., 2009)), yet our results suggest that suppressing PVs alone is again insufficient to produce the ensemble-level deficits seen in both mouse models. This demonstration alone does not exclude a causal role of PVs in SZ. PV dysfunction in the disease could play a developmental role, or, intriguingly, the effect of PVs have on the network may even scale nonlinearly with the degree of their suppression (e.g. partial suppression disinhibits other interneurons more than pyramidal neurons). Further, GABAergic pathophysiology in SZ is not limited to a simple decrease in PV activity, but involves complex changes which may vary at the subecellular level depending on the PV-cell subtype (Lewis et al., 2012) and also involves other subtypes including somatostatin and cholesystokinin interneurons (Fung et al., 2014). Still we provide some evidence that changes, and in particular, long-term changes in excitatory neurotransmission are critical for cortical assembly disorganization, perhaps insofar as synaptic stability and plasticity are affected. So while our chronic KET and Df(16)A^+/− models both alter inhibitory neurotransmission to various degrees, our results together with recently accumulating evidence from large scale genetic studies of SZ (Hall et al., 2015) suggest a critical (if not primary) role of glutamatergic synaptic deficits in the disease etiology (Poels et al., 2014).

Schizophrenia as an attractor disease

These results are consistent with an “attractor” theory of SZ (Rolls et al., 2008), in which the critical pathophysiology of the disease involves altered multineuronal dynamics. The repeating activity patterns described in this report could be naturally interpreted as representing cortical “attractors” (Hopfield, 1982), or the preferred, semi-stable activity patterns in the neocortical network involving recurrently coactive groups of neurons [or ensembles (Miller et al., 2014)]) (Rolls et al., 2008). Our observed lack of reliability in the population-wide activity states observed in both mouse models of SZ pathophysiology, both at rest and during direct visual stimulation, is consistent with an alteration in cortical attractors, resulting in an effective “shallowing” of the cortical attractor landscape, wherein percepts, short-term memories, or computational outcomes become highly unstable (Rolls et al., 2008). To illustrate this possibility quantitatively, we utilized the solutions of the k-means clustering analysis described above, fixing the number of clusters to k=6 (based on Figure 4 L–N), and repeating the analysis 50 times for all multineuronal datasets measured. We iteratively assigned ensemble activations to clusters, and cluster centroids to a specific place in a 2-dimensional plane, arranged by relative size of the cluster groups (largest cluster at the plane origin) and separated by average cluster-to-cluster centroid distances across all mice within a condition (Figure 8B–G). While a bootstrapped fully random distribution of “events” (based on shuffled recorded data from each mouse) resulted in a single Gaussian “valley” centered on the spot of the first “cluster” (the origin), recorded data from healthy circuits showed the emergence of multiple “valleys” (Figure 8B–C), or putative attractors (highly probably patterns in the space of possible activity states). KET and Df(16)A^+/− data can therefore be interpreted, with this demonstration, as showing a shallowing of the attractor landscape in favor of one continuous distribution of possible activity states (Figure 8D–G). Elucidating the exact meaning of observed, repeating population states described herein is a key focus of ongoing work requiring further study and perhaps a substantial advancement in measuring or stimulating neurotechnology, including the ability to record and manipulate all or most of the neurons in an intact, behaving organism (Alivisatos et al., 2012).

In closing, we have established that unreliable and indistinct ensemble activity in sensory cortex is present in two separate mouse models of schizophrenia-relevant pathophysiology and/or risk. Our data suggest that changes affecting ensemble reliability across time may represent a key emergent convergence point for lower level abnormalities. Causally linking local ensemble dysfunction to alterations in global networks like those seen in SZ patient samples (Yang et al., 2014) or to perceptual or cognitive dysfunction fundamental to SZ (Javitt and Freedman, 2015) is a feasible next step given the recently established ability to carry out complex head-fixed behavioral studies in mice (Harvey et al., 2012). Future work with even more diverse disease models will be informative, keeping in mind that the utility of a model rests not necessarily in whether or how well it recapitulates the disease but in how it is employed to test specific hypotheses (Gordon and Moore, 2012). But intriguingly, the ability to selectively activate, reinforce, and imprint neocortical ensembles (Carrillo-Reid et al., 2016) could offer a novel therapeutic approach to SZ via the reprogramming of cortical circuits to restabilize an altered attractor landscape and potentially reversing some of the symptoms of the disease. Finally, our results not only support and refine new computational hypotheses regarding how neuronal circuit dysfunction relates to the phenomenology of the disease, but they also underscore the hypothesis that reliable ensemble activations and attractor states comprise likely building blocks of perception and thought.

STAR methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact Dr. Jordan Hamm (jph2164@columbia.edu or hamm.jordan@gmail.com).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experimental procedures were approved by and carried out in accordance with Columbia University institutional animal care guidelines. Chronic ketamine (KET) or saline (SAL) experiments were performed on adult parvalbumin-Cre or parvalbumin-Cre × LSL-tdTomato transgenic mice, obtained from The Jackson Laboratory (from a C57BL/6 background, 22–32g), at the age of postnatal day (P) P60–P110 (first recording day). Df(16)A^+/− mice (RRID: MGI_3802827) and their wild-type, homozygous littermates/cagemates (WT; P80–P130, 22–32g) were generated on a C57BL/6J background (Stark et al., 2008). All animals were ketamine naïve at the start of testing and were not used for previous or subsequent experimentation. Calcium imaging data are reported on 7 SAL (2 female, 4 PV-cre, 3 PV-cre;;td:tomato), 7 KET mice (2 female, 3 PV-cre, 4 PV-cre;;td:tomato), 7 Df(16)A^+/− mice (all male), and 7 WT (all male). LFP data are reported on 7 SAL and 6 KET treated mice (all PV-cre), and 8 Df(16)A^+/− and 5 WT (all male). Group type was randomly assigned (in pairs for KET/SAL experiments) and blind to the experimenter/analyst throughout experiments, data processing, and analysis. Mice were housed in Allentown ventilated rack caging (IVCs cages) with 1 to 3 cagemates of the same sex on a 12 hour light/dark cycle, and were fed Purina Lab Diet 5053. Sentinel mice tested negative on all major pathogens tested (14 viruses, M. pulmonis, endo/ecto parasites) except murine norovirus (7/8 tested positive; MNV). MNV is by far the most common infectious agent in laboratory mice and is typically asymptomatic (Perdue et al., 2007).

METHOD DETAILS

Animals, Surgery, and Training

Virus injection, head plate fixation, skull thinning, and minipump implantation (KET/SAL only) were carried out in that order over the course of 5 weeks. In the first surgery (virus injection), 3–4 weeks prior to the first imaging session, mice were anesthetized with isoflurane (initially 3% (partial pressure in air) and reduced to 1–2%). A small window was made through the skull above left V1 using a dental drill (coordinates from lambda: X=−250, Y=20 m) taking care not to pierce the dura mater. A glass capillary pulled to a sharp micropipette was advanced with the stereotaxic instrument, and 750nl solution of 1:1 diluted AAV1.Syn.GCaMP6f.WPRE.SV40 (3 KET, 2 SAL) or AAV1.Syn.GCaMP6s.WPRE.SV40 (all other mice; obtained from the University of Pennsylvania Vector Core) was injected into putative layer 2/3 over a 5 min period at a depth of 200–300 m from the pial surface using a UMP3 microsyringe pump (World Precision Instruments).

Approximately 3 weeks after virus injection, mice were anesthetized as previously described and a titanium head plate was attached to the skull centered around the virus injection site using dental cement (Miller et al., 2014). Mice were allowed to recover for at least 5 days in their home cage. In this time, mice were given analgesics (5mg/kg carprofen I.P.) and accustomed to experimenter handling, including brief head-restraint periods, until mice showed non-stressed behavior, which usually began on the second day. Mice then underwent training to maneuver with their head fixed approximately 1 inch above a rotating wheel, beginning with a 30 minute session. This progressed until mice could distribute weight on the wheel evenly and appeared calm (grooming, locomotion) and without signs of distress (tremors, freezing, etc), which generally occurred after the first session (Miller et al., 2014). During training sessions and prior to the first imaging session, mice viewed moving square-wave gratings (see below) for stimulus habituation.

On the first day of imaging, mice were anesthetized again with isoflurane and a small circle (approximately 1 mm in diameter) was thinned with a dental over the left V1 centered just anterior to the injection site or removed (for LFP experiments). The skull was thinned until the bone, moistened with saline, was transparent enough so that the underlying vasculature was visible to the naked eye (usually 20 minutes of drilling). The thin skull preparation prevents exposure of the cortex and meninges and is a minimally invasive method for chronic imaging of cortical changes (Yang et al., 2010). The mouse was then allowed to wake up and was transferred to the wheel. After approximately one hour, imaging began. After the first imaging session, mice were returned to their home cage (SAL/KET) or sacrificed (Df(16)A^+/−/WT). The following day, (for SAL/KET) an osmotic minipump was implanted subcutaneously (Alzet, model 2001) which released approximately 60 mg/kg/day ketamine HCL (KET mice) or an equivalent volume of saline (SAL mice) at 1.0 microliters per hour for 7 days. This dose is within the previous range suggested for mouse chronic ketamine models (Behrens et al., 2007; Chatterjee et al., 2012). The pump was weighed before and after filling to ensure the absence of air bubbles (per manufacturer’s instructions).

To estimate plasma levels of ketamine achieved during this procedure, KET mice were sacrificed at day 4 blood was harvested from a cardiac puncture, centrifuged at 2000 cycles per second at 4C, and the supernatant serum was stored at −20 C. Ketamine in the serum samples was extracted using liquid–liquid extraction and quantitated using liquid chromatography-tandem mass spectrometry (LCMS/MS) using platform comprising Agilent 6410 triple quad mass spectrometer coupled with Agilent 1290 Infinity UHPLC (Agilent Technologies) controlled by MassHunter v 3.1 (Agilent Technologies, Santa Clara, CA). Average plasma levels of ketamine were 135.1 ng/ml (range 129.8–142.4), a concentration at the low end of acute ketamine induced psychotic brain states in human studies (Driesen et al., 2013). As expected, saline treated mice (n=3) did not express detectable levels of ketamine (<2.50 ng/ml). The second imaging day took place one week after implantation of the minipump. Skull thinning was repeated if necessary (about 20% of the time). Animals were sacrificed shortly after the final imaging session, and pumps were removed and inspected to ensure the absence of perforation or clogging.

Genotyping of Df(16)A^+/− mice

Df(16)A^+/− were acquired from a colony maintained by the Gogos (Stark et al. 2008). Mice were genotyped twice from tail samples (stored at −20C for less than 2 weeks) collected before and after experimentation. Samples were screened for the presence of the deficiency (Df(16)A) by using the primers: 5′- ATTCCCCATGGACTAATTATGGACAGG-3′ and 5′ GGTATCTCCATAAGACAGAATGCTATGC 3′, which amplify an 829 basepair band. Primers 5′ CTAGGCCACAGAATTGAAAGATCT 3′ and 5′ GGTGGAAATTCTAGCATCATCC 3′ amplify a 324 bp internal control band. PCR cycling conditions we used were: 94°C for 3 min; 35 cycles of 94°C for 30 s, 60°C for 1min, and 72°C for 1 min; 72°C for 10 min.

Two-Photon Calcium Imaging

The activity of cortical neurons was recorded by imaging fluorescence changes under a two-photon microscope (Bruker Ultima In Vivo; Billerica, MA) excited with a Ti:Sapphire laser (Chameleon Ultra II; Coherent) tuned to 940 nm. The laser beam was intensity modulated with a Pockels cell (Conoptics 350–160BK, with 302 RM driver) and scanned with galvometers through a 20× 0.9 N.A.; (Olympus) water immersion objective (Figure 2A–B). To ensure stability of the imaging meniscus for long duration imaging sessions, a small volume (approx. 1ml) of Aquasonic ultrasound gel (Parker Laboratories Inc.) was centrifuged and dolloped onto a moistened, thinned skull. Scanning and image acquisition were controlled by Prairie View software (3.395 frames per second for 256 × 256 pixels, 1.6 microsecond dwell time per pixel, 200–225 um beneath the pial surface). The Pockels cell blanked the laser outside the imaging field to minimize laser exposure. On both imaging days (before and after treatment) mice were allowed 1 hour on the wheel before imaging began. Imaging consisted of a visual stimulation condition (15 minutes), followed by 20–40 minutes of awake rest in a dark room with the monitor off, followed by a second visual stimulation. Rest sessions were not collected for 1 SAL and 1 KET mouse. Sessions started at the same time of day for both sessions within a mouse (starting between 11am and 4pm). Mice and recordings (LFP, locomotion) were visually monitored by the experimenter to ensure they were awake during data collection. On week 1, at the end of the session, an imaging dataset was recorded in which the field of view was slowly moved systematically in 3 dimensions, thoroughly surveying the cortical area where our calcium indicator was expressed. This movie helped in locating the same cortical region on week 2 (using mainly vasculature landmarks as a guide; e.g. Figure S2A,C). Locomotion was recorded with an infared LED/photodarlington pair (Honeywell S&C HOA1877-003), which consists of a small c-shaped device positioned at the edge of the rotating wheel (striped with black tape) connected to the imaging computer as an analogue input. Locomotion was detected as voltage detections in the photodarlington readout. While previous work has suggested that locomotion enhances visual processing in V1 in mice (Niell and Stryker, 2010), most of our mice did not exhibit enough locomotion to enable thorough examination of this effect in our chronic models (< 10% of frames). Therefore, when detected, frames or trials during locomotion periods were excluded along with the previous and subsequent 12 frames; this did not change the pattern of effects.

Visual Stimulation

Visual stimuli were generated using the Psychophysics Toolbox in MATLAB (MathWorks) and displayed on a liquid crystal display monitor (19-inch diameter, 60-Hz refresh rate) positioned 15 cm from the right eye, roughly at 45° to the long axis of the animal. Stimuli were full-field squarewave gratings (100% contrast, 0.04 cycles per degree, 2 cycles per second) drifting in twelve different directions in random order presented for 3 s, followed by an interstimulus interval of 7–8 s of mean luminescence gray screen (Figure S2E). In each session, mice saw a total of 15 presentations of each stimulus. The timing and identity of gratings played in MATLAB were synchronized with image acquisition by outputting an analogue voltage trigger synchronized with stimulus onset and offset and recorded with the imaging computer using Prairie View 5.2 software (Bruker; Billerica, MA). The timing between actual stimulus onset and recorded voltage traces in Prairie View was confirmed beforehand using a photodiode sensor with a reverse biased voltage output recorded by the software in tandem with the MATLAB output triggers.

Local Field Potential recordings

Local field potentials (LFPs) were recorded as previously reported in our lab (Hamm and Yuste, 2016), using mice that did not undergo virus injection or skull thinning described above. Recordings occurred in Df(16)A^+/− and WT mice or in SAL/KET treated mice only after treatment due to the invasiveness of intracortical LFPs. On the day of recording a small craniotomy was made (less than 1 mm²). LFPs were either recorded with a single AgCl-electrode in a glass pipette filled with saline solution or a single contact from a 16 channel linear silicon probe (spaced at 50 Um intervals; model a1×16–3mm 50–177, Neuronexus Technologies, Ann Arbor MI) inserted perpendicular to and with the top electrode aligned just at the pial surface (visually confirmed with an adjustable miniature digital microscope; Adafruit (New York, NY)). Recordings were made from approximately 250um below the pial surface. Recordings were referenced to the skull above prefrontal cortex and grounded to the headplate. Continuous data were acquired with either a MultiClamp 700B amplifier/software (Molecular Devices, Sunnyvale, CA) or a Plexon MiniDigi amplifier and software (Plexon Inc, Dallas, TX) and analogue filtered from 0.1 Hz to 10 kHz. Mice viewed visual stimuli (described above) of either 1 or 3 seconds in duration. LFP data were manually prescreened for excessive artifact (e.g. signal greater than 8 standard deviations) and deviant trials were removed. Trials during locomotion were also excluded (a total of <10% of trials). Data were then digitally filtered from .5 to 300Hz (bandpass least squares FIR) and with a 60Hz notch filter.

Acute ketamine and pharmacogenetic suppression of PVs

As described above, an additional set of adult parvalbumin-Cre mice were injected with both GCaMP6s and AAV5hsynDIOhM4D(Gi)mCherry (UNC vector core), and underwent headplate implantation, head-fixation training, and imaging (n=7, n=5 GCaMP6 only controls). The efficacy of our methods in successfully targeting PVs have been previously verified in our lab with mCherry and PV immunohistochemistry (Hamm and Yuste, 2016; Jackson et al., 2016; Sippy and Yuste, 2013). On the day of recording, mice ambulated on a treadmill in a dark room as described above while images were recorded at approximately 4-Hz. Then mice each received a subcutaneous injection of Clozapine N-Oxide (12 mg/kg; (Hamm and Yuste, 2016; Perova et al., 2015)), followed by a second set of images recorded starting 30 minutes later. For testing of the effects of acute ketamine, adult Pv-Cre mice (n=3) or wildtype (n=4) underwent a similar set of procedures as CNO injected mice except three recording sessions were acquired, each 30 minutes post-injection and lasting at least 20 minutes: baseline, post-saline injection (subcutaneous), and post-ketamine injection (15mg/kg, subcutaneous; equivalent volumes used for SAL and KET).

Study of Parvalbumin-containing Interneurons

Using transgenic mice expressing cre-recombinase selectively in PVs (PV-cre) crossed with cre-reporting mice expressing the florescent protein td-Tomato (Ai14; B6.Cg-Gt(ROSA)26Sor^{tm14(CAG-tdTomato)Hze/J}), PVs were identified in a subset of mice (PVcre∷tdTomato) by somatic co-localization of GCaMP6s and tdTomato (Figure S7A; 22 PVs across 3 SAL mice; 34 PVs across 4 KET mice; average of 4 neurons per imaged population) (Hofer et al., 2011; Miller et al., 2014). Cells co-expressing tdTomato and GCaMP6s were identified with two-photon stimulation at 940 nm or 1010 nm and using 2 PMTs filtered for green (510/20 nm) and red (607/45); we typically identified 2 to 4 per mouse (at max 8, always less than 8%; Figure S7). Florescent traces from PV ROIs were identified and processed similarly to non-PVs with regard to pixel selection and halo subtraction (see above). Two-photon imaging measured calcium dynamics in PVs are known to differ substantially from pyramidal neurons, with longer decays and more ongoing fluctuation (Hofer et al., 2011). This may be partially due, among other differences, to the higher baseline firing rates and calcium buffering dynamics of PVs. In the present study, we focused on PV calcium dynamics i) evoked by visual stimuli and ii) locked to statistically defined “ensemble activations” (or high activity states of the network).

QUANTIFICATION AND STATISTICAL ANALYSIS

Depending on the question addressed, analyses focused on cell averages (e.g. activity levels, orientation tuning, correlation coefficients) or mouse-wise averages (LFP meausres, locomotion, proportion of significant correlation pairs, ensemble/network-level), from 6–7 mice for each condition per set of experiments (e.g. chronic saline vs ketamine). This report contains no independent replications of any set of experiments. Statistical tests for each experimental condition is described in the following sections and include paired t-tests, independent t-tests, one-way ANOVAs, repeated measures ANOVAs, and mixed ANOVAs (between and within subject factors). As clarified in figure legends, error bars reflect standard errors of the mean (S.E.M), but, when statistical comparisons were mixed ANOVA, repeated measures ANOVA, or paired t-tests, standard error bars reflect within-subjects/within-cells standard error (Loftus, 1994).

Spectral analysis of LFP

Baseline LFP power was measured in 2 second windows (0.5 Hz resolution) between and after visual stimulations. A Fast-Fourier transform (FFT) was carried out, and the spectral power (squared absolute value of the complex output of the FFT) was averaged across all time windows, divided (relative; Figure S1C,D) or not divided (absolute; Figure 1A,E) by the broadband power across frequencies from 1 to 120 Hz, and then multiplied by the frequency (for rescaling for visual presentation only, i.e. correcting for 1/f component).

For analysis of stimulus elicited oscillatory dynamics, LFP data from single trials were segregated into bins −2000ms pre to 5000ms post grating stimulus onset. Data were convolved with a family of modified morlet wavelets from ranging from 2 to 120Hz in 2Hz and 20ms steps with wavelet size increasing linearly from 1 to 20 cycles using code written in MATLAB and EEGLAB 9.0 (Delorme and Makeig, 2004). This approach is ideal for time varying analysis of oscillatory dynamics since it optimizes effective frequency resolution at low frequencies and time resolution at higher frequencies (Hamm et al., 2012). Oscillatory power was expressed in decibels and was averaged over trials. Average power values for each frequency in the baseline period (−1000ms to −100ms pre-grating onset) were subtracted to yield a single time-frequency evoked spectra for each mouse (Figure 1D,H).

Statistical comparisons focused on frequency bins derived via principal components analysis (Hamm and Yuste, 2016; Hamm et al., 2014). Trial averaged time-frequency spectra (including baseline) were converted to z-scores for each mouse, and concatenated in time across all mice. A scree plot indicated that 5 components were present. After varimax rotation, the final frequency bins were 1–14Hz (low/theta/alpha), 15–34 Hz (beta), 35–58 Hz (gamma1; excluding 59–61 Hz), 62–110 Hz (gamma2), and >111Hz (high frequency; excluding 119–121 Hz), highly consistent with traditionally demarcated bin boundaries (Buzsaki, 2009). Baseline absolute power spectra were compared between SAL/KET and Df(16)A^+/−/WT with 2 sample t-tests (df=11) for each frequency band. Stimulus elicited power was averaged across the first 500ms post-grating onset (since this was when the majority of the response was present) for each bin. Two sample t-tests (df=11) were applied for each frequency band, (comparing between SAL/KET and Df(16)A^+/−/WT).

Phase locking (or inter trial phase coherence) assess the consistency of the stimulus elicited LFP waveform without regard to amplitude variations. It is calculated by dividing the complex result of the wavelet analysis by its absolute value for every frequency and timepoint (and normalized for number of trials as previously described (Hamm et al., 2012)). Statistical comparisons were carried out in the same manner as for spectral power, except focusing the first 150 ms where the response is maximal.

For all oscillatory measures, two-tailed significance was used, but trend-level effects were reported since LFP experiments had an a priori directional hypothesis based on the schizophrenia literature (SZ>H for baseline; H>SZ for stimulus evoked; (Hamm et al., 2014; Uhlhaas and Singer, 2010)).

Image Analysis

Imaging datasets were scored similarly to previous reports (Chen et al., 2013; Hamm and Yuste, 2016). The raw images were processed to correct translational brain motion artifacts using the MOCO algorithm and plugin (Dubbs et al., 2016) written in house for ImageJ (Schneider et al., 2012). Then, cell regions of interest (ROIs) were detected semi-automatically for each imaging session and individually confirmed as follows. Mean, standard deviation, and std×skewness projections (pixel-wise) were calculated across all imaging frames (roughly 14000–25000) and plotted for reference (Figure S3A). Then, rectangular sections were selected around the apparent cell bodies using a GUI created in MATLAB. A principal components analysis (PCA) was computed on the pixels contained within the sections, and the pixels with weights at least 80% of the maximum of the first PCA component were defined as the ROI and spatially plotted (Figure S3B) along with the florescence trace averaged across these pixels (e.g. Figure S3C, top). Cells with faint, sparse (<5 events across both weeks), or largely atypical calcium transients were excluded from further analysis at this step [<20%; cells not showing periods of low florescence with intermittent sharp peaks; e.g. Figure S3; (Chen et al., 2013)]. In general, these criteria focused analyses on cells with a bursting profile and firing rate typical of layer 2/3 neocortical neurons (Pyramidal and non-PV pyramidal neurons). PVs, for example, which have higher baseline activity and ostensibly different calcium indicator dynamics (Hofer et al., 2011) were likely excluded at this step, and, when possible (using mice with florescent indicator tdTomato tagged to PVs), we were able directly confirm these differences and exclude PVs from network analyses (Figure S7). This exclusion did not substantively affect the main results (e.g. ensemble reliability F^interaction(1,10)=4.98, p<.05 without PVs; F^interaction(1,10)=5.14, p<.05 with PVs). The average number of active cells used for further analyses did not differ between conditions within experiments (mean/range; SALpre=74 (52/93); SALpost=79 (53/100); KETpre=75 (53/100); KETpost=73 (45/120); F^interaction(1,12)=0.58, p=.28; F^group(1,12)=0.14, p=.71; WT^+/−=66 (31/101); Df(16)A^+/−=51 (25/85); F(1,12)=1.65, p=.22). Florescence of active cells was then calculated as the average across all pixels within this ROI minus the average of the pixels just outside the selected rectangle, termed the “halo”, which excluded pixels from nearby cell bodies (Figure S3C). This subtraction removed background contamination from neuropil and nearby cells. Completing this step ensures maximal correspondence between florescence and actual cell spiking (Chen et al., 2013). The remaining traces were then filtered with a 3-second lowess envelope (Hamm and Yuste, 2016), a regression based smoothing approach which is tolerant of sharply changing values on the edges of the window. Finally, the first discrete derivative was scored either as Δf (within cell/single cell comparisons), or as within-cell maximum normalized Δf (population analyses).

Single cell analyses

For each neuron recorded, we estimated events using thresholds set as 3.1 standard deviations (p<.001) above baseline f for each neuron (lower 8% of values (Carrillo-Reid et al., 2015; Hamm and Yuste, 2016)). We first quantified overall activity levels as the proportion of frames during which a neuron was “active” (i.e. displaying an event). Events/active frames were automatically marked as timeframes with Δf values which exceeded thresholds. Single calcium events normally consist of multiple closely co-occurring action potentials, or “bursts”. For scaling consistency across experiments and conditions and to account for baseline differences across mice, we divided activity levels for each neuron by the mouse-wise average from week 1 only (SAL/KET), or by the global average from WT mice (22q11.2 model). This procedure did not change the pattern of results (i.e. KET still showed an increase when using raw values F^ket(872)=5.76, p<.05; means/std; KET^pre=2.8% active frames/1.7; KET^post=3.1/1.7; WT=2.6/1.2; Df(16)A^+/−=2.5/1.1). For SAL/KET experiments, activity level comparisons were carried out with a 2-by-2 mixed ANOVA on individual cells with TREATMENT as the between subject variable and WEEK as the within subject variable. Follow-up one-way ANOVAs were carried out separately for KET and SAL to interpret interactions. For Df(16)A^+/− experiments, a single one-way ANOVA was carried out on activity levels.

In order to understand the nature of this change in KET, we focused on neurons identifiable pre and post SAL/KET treatment (Figure S2, S4; 4 SAL, 5 KET). Week 2 sessions in which a substantial number of cells (>10) from week 1 could be located precisely, cells were visually matched between weeks by 2 independent scorers for subsequent comparisons. Since the GCaMP6 series has near zero basal florescence, this was a difficult task to do with certainty during the imaging session, and had to be performed post hoc using z-projection plots (see Figure S3). Only regions of interest with agreement between the 2 scorers were counted as the same cell. The average overall activity level (average Δf over all frames), event maximum, and event frequency (contiguous active frame blocks, or “events”, per minute) were quantified for each cell and condition. Again, values were normalized within each mouse using the week-1 event size and event rate, and the same statistical procedures were repeated.

Differences in single neuron disinhibition was one principal difference found between our pharmacological and genetic models. One potential confound is that only the KET/SAL experiments included female mice (n=4; 2 each) and GCaMP6f (n=5; 3 KET, 2 SAL), while the genetic model experiments were on only males and with only GCaMP6s, but additional analyses refute this possibility. First, excluding females from the KET/SAL analysis did not change the effects ((F^interaction(1,1382)=4.79, p<.05; F^KET(765)=5.61, p<.05; F^SAL(617)=0.54, p=.46; n=5 mice KET, 767 cells; n=5 mice SAL, 619 cells). Second, while GCaMP6f has a much shorter decay time than GCaMP6s, our analyses focused only on the rise magnitudes/times (increases in florescence) and were therefore less likely affected by this experimental difference. The data concur with this hypothesis, since excluding GCaMP6f mice from an alternative analyses show that KET still showed disinhibition of ongoing activity (F^interaction(1,1060)=6.11, p<.05; F^KET(468)=7.89, p<.01; F^SAL(892)=0.43, p=.50; n=4 mice KET, 470 cells; n=5 mice SAL, 619 cells).

Pairwise analysis

Pairwise coactivity (or functional connectivity) between single cells was assessed by calculating similarity values between cell pairs. For each cell, the Δf value across all frames was vectorized in n-dimensional space (where n=number of frames). The similarity of each cell/vector pair (Ca, Cb) was calculated as the angle between the vectors in n-dimensional space, or the normalized inner-product (Carrillo-Reid et al., 2015):

$${\text{S-index}}^{\text{Ca,Cb}}={\mathrm{C}}_{\mathrm{a}}·{\mathrm{C}}_{\mathrm{b}}/((|{\mathrm{C}}_{\mathrm{a}}{|}^2+|{\mathrm{C}}_{\mathrm{b}}{|}^2)/2)$$

This metric is bound between 0 and 1 (1 meaning that activity across timepoints is completely identical between cells) and is similar to cosine similarity with the added provision that cell pairs with similar relative magnitudes will have higher values than those with differing relative magnitudes, a step not necessary when cell activities are binary. This similarity metric was chosen to assess cell-cell correlations instead of more traditional methods (e.g. Pearson correlation) since calcium transients (rises in florescence) are relatively sparse (approx. 3% of frames on average) do not show negative values. Detecting a difference between an absence of coactivation between cells (0 correlation) and an inhibitory relationship (negative correlation) would prove difficult to interpret directly. Thus high cell-cell similarities represented high coactivation probabilities between cells across up-states, and low values represented a lack thereof. Since wide distributions of similarity values were observed, and could vary depending on the activity level and the duration of recording, we first sought, within each network, to determine what a “significant” amount of pairwise synchrony was with a bootstrapping procedure. Individual cell time courses were shifted by random amounts in time separately for each cell (holding individual cell activity levels constant at each step) and average pairwise synchrony values were calculated for all cells in these surrogate datasets. This step was repeated 10000 times (Cossart et al., 2003), creating a distribution of similarity indices expected at chance level for each cell pair. Cutoffs were set at the 99^th percentile of the random distributions. For each mouse, we determined the proportion of cell pairs greater than this cutoff, and compared these proportions with a 2-by-2 mixed ANOVA on mice with TREATMENT as the between subject variable and WEEK as the within subject variable. Follow-up one-way RM ANOVAs were carried out separately for KET and SAL to interpret interactions. For Df(16)A^+/− experiments, a single one-way ANOVA was carried out. As we observed obvious changes in the distribution peaks despite no change at the tails (Figure 2I,M), we additionally compared the means of all cell-pairs across all mice with the same statistical approach. Importantly, while traditional tests of distribution differences (e.g. Kolmogorov–Smirnov or Cramer-von Mises tests) both confirmed that KET and Df(16)A+/− pairwise coactivity distributions were deviant, these tests were overpowered in this experiment and were excluded. Even the SAL model, which ostensibly exhibited nearly identical distributions before and after treatments (Figure 2E), elicited a significant effect in both K-S and C-M tests.

Population analysis

Population level analyses of ongoing activity focused on the state similarity of cortical “ensemble” activations, or time-frames with significant levels of coactivity. First, a bootstrap approach was carried out on individual datasets in order to determine what characterized an ensemble as opposed to momentarily high activity states occurring due to uncorrelated variation in firing rates across cells. Δf values were normalized within cells by dividing all values by their maximum Δf across all recorded frames (Figure S5A). Δf values across all cells were then averaged within each frame (Figure S5B), yielding a value for each frame which is bound between 0 and 1, and represents the percentage of total possible network activity (e.g. 0.12 = 12% inferred activity ceiling). Importantly, the relative amount of network-wide coactivity did not differ between conditions (Figure S6A–C). Individual cell time courses were then shifted by random amounts in time separately for each cell (holding individual cell activity levels constant at each step) and average network activity values were calculated for all frames in these surrogate datasets. This step was repeated 10000 times (Cossart et al., 2003), creating a distribution of network activity magnitudes expected at chance level (Figure S5C). Cutoffs were set at the 99^th percentile of the random distributions, which determined that the global “ensemble” definition (i.e. when combining all 38 datasets) was 0.06 or 6% of ceiling. We determined cutoffs on individual datasets, assigning instantaneous “peak” activity frames (local maxima in figure S5B separated by at least 1.5 seconds) which exceeded thresholds as “ensemble activations”. Focusing only on peaks served to exclude the similarity shared by adjacent frames. Each dataset exhibited between 150 and 250 significant ensembles activations during the first 20 minutes ongoing activity, so we focused further analyses on just the highest 150 peaks from each dataset.

The next step was to determine which ensemble activations showed population level patterns of activation which repeated, or had similarity values with subsequent ensemble activity above chance values, suggesting recurrent ensembles or attractor states in the ongoing activity. We calculated between frame “similarity index” as described above on frame-frame pairs (instead of cell-cell activity patterns), yielding 150 by 150 similarity matrices for each mouse (Figure 3B, S5D). We then used a bootstrap method again to determine what constitutes ensemble repeats (Figure S5E), using within-frame shuffling 10000 times, holding overall activity levels constant. The global significant similarity value across all ensemble activity was S.I.=.47, p<.01. Individually derived S.I. cutoffs were derived for each mouse, for each week (when applicable), and used to i) re-adjust histograms for group-wise plotting (Figure 3I–K) and ii) to determine the proportion of significant ensemble repeats, which was between 15% and 25% of frames on average, (15–25 times more likely than chance). The proportion of ensemble repeats for each mouse was compared with the same ANOVA models as described for pairwise comparisons.

Next ongoing data from ensemble activation frames was factorized with Principal Components Analysis (P.C.A; cells as variables) to i) demonstrate that a variety of network patterns were present in the ongoing activity (Carrillo-Reid et al., 2015; Miller et al., 2014) rather than simply one repeated high activity state (Figure 3A, S6D–E), and ii) further confirm that KET reduced overall activity pattern fidelity across time rather than simply increasing the number of distinct states present (Figure 6G). To further address (ii) (Clementz et al., 2016; Yan and Ye, 2007), we reduced ensemble activity into three principal components using a VARIMAX factor rotation after P.C.A for each population imaged. We then carried out k-means clustering (clustering ensemble activations in P.C. space) for four representative datasets using k=3 in order to depict i) the uniqueness of separate, observable ensemble states clusters in control mice and ii) the disruption thereof in disease models. Second, using all datasets, we carried out k-means repeatedly for each population from k=2 to k=15, repeating 100 times for each k to ensure the stability of the solutions, and quantifying the average within cluster distances (i.e. Euclidean distances), dividing by their decrease from the “1-cluster” solution (average distance from the overall mean; Figure 4B–H). Next, we quantified the discrete first-derivative of this plot (Figure 4L–N), estimating the degree to which added clusters parse the ensemble activation variance in P.C. space. Since large decreases in within-cluster distances were seen from k=2 to k=5, we compared these models across mice within experiments (SAL, KET, Df(16)A+/−) with one-way ANOVAs. (Note: “representative” datasets in figure 2A,B; 3A–H, L–S; 6A–L; S2A–D, I–L; S3; S5A,D; S6D–G; S7A,B,D each originate from separate cell populations in order to better represent the breadth of the effects).

Analysis of stimulus evoked activity

Δf values were averaged within trials (free of locomotion +/− 3 sec) from stimulus onset to offset and across trials of the same stimulus (approximately 15 trials per stimulus). Analyses focused on cells exhibiting significant stimulus evoked activity that is, cells for which the average stimulus evoked activity exceeds 1.67 standard deviation of the baseline for at least one stimulus orientation/direction (KET=70%, SAL=72%, Df(16)/WT=75%; (Hamm and Yuste, 2016)). 1 SAL mouse and 1 KET mouse failed to show consistent stimulus elicited activity at week 1 and were excluded from this portion of the study. The orientation selectivity index (O.S.I), which estimates the degree to which a cell prefers lined visual stimuli of a particular angle or orientation, was calculated on average Δf responses (R) across 12 orientations (K; where θ is the angle of the stimulus direction, 0: 2pi radians) as

$$\text{O.S.I}=|{\displaystyle {\sum }_{\mathrm{k}}{\mathrm{R}}_{\mathrm{k}}}·\text{exp}(2{\text{iθ}}_{\mathrm{k}})/{\displaystyle {\sum }_{\mathrm{k}}{\mathrm{R}}_{\mathrm{k}}}|$$

This metric, akin to 1-circular variance, has been demonstrated to be stable and effective at detecting selectivity differences between populations (Mazurek et al., 2014). Although direction selectivity could be detected in some cells, it was sparse overall and weaker than O.S.I., in agreement with previous reports in V1 (Marshel et al., 2011), so analyses focused on O.S.I. Changes in overall O.S.I. for SAL/KET were tested with a 2-by-2 mixed ANOVA on individual cells with TREATMENT as the between subject variable and WEEK as the within subject variable. Significant interactions were followed up by a one way ANOVA.

Average responses across cells displaying orientation selectivity (O.S.I. of at least 0.1 given 30 trials per orientation per week (Mazurek et al., 2014)) were plotted as a function of stimulus direction (x-axis) on the same scale across conditions (Figure 6B,D,F) by dividing responses by the response to their average “preferred” orientation at week 1 (SAL/KET) or the average “peak” across all neurons in DF16/WT (Lee et al., 2014). Cell response curves then were compared for SAL, KET, and DF16/WT with 2-by-12 MIXED ANOVAs with TREATMENT as a between subjects variable and WEEK as within subject variables. In KET, To understand the nature of the O.S.I. changes, additional analyses focused on cells visually identifiable and which showed visually driven activity in week 1 and 2 (n ^SAL=45 cells, n=4 mice; n ^KET=62, n=5 mice). For Figure S8A,C, the preferred angle of each cell was estimated similarly to the O.S.I, but instead of the absolute value, the imaginary component of the log transform of the above expression was calculated (i.e. computational preference).

For assessing noise correlations, we focused on visually active neurons with at least 0.1 O.S.I. (to ensure the reliability of the assessed “preferred orientation”). For each stimulus orientation, for each cell pair, we quantified the pearson correlation coefficient of average responses (stim-on mean minus baseline 1 sec), and then averaged over different orientations. We then grouped pairs into shared preference (difference of computational preference +/−15 degrees), +/−45 (between 30 and 60 deg difference), and opposite (between 75 and 115 degrees). For SAL, KET, and Df(16)^+/−/WT, we computed mixed ANOVAs on the proportion of significantly noise correlated neurons per mouse with ORIENTATION as a within-subjects factor and WEEK (or GROUP) as a between subjects factor (3X2). Next we applied these same statistical models to individual cell pairs.

Population level analyses of visually evoked responses utilized the same similarity metric as for ongoing activity analyses, but focused on average stimulus elicited responses across neurons on individual trials rather than “up-states”. This step quantified whether directly evoked population-wide patterns of activity, without regard to single-cell orientation preferences or baseline levels of activity, were more similar across trials of the same stimulus type compared to different stimulus types. Similarity between all trials was calculated on within trial averages (0–3.5 sec post stim onset to account for offset induced activity), yielding a T by T matrix of similarity values where T= total trials (Figure 7B,D,F,H). Next, bootstrapped similarity distributions described above were used to derive a mean and standard deviation of expected chance level population similarity for each mouse/neuronal-population studied. Individual trials (i.e. matrix cells in Figure 7B) were then rescored as “Z” scores for each trial, and these values were then averaged to yield (i) within-stimulus-type, (ii) cross-stimulus-type (30 and 60deg differences), and (iii) opposite stimulus type intertrial ensemble similarity (barplots in Figure 7M–O). For SAL, KET, and Df(16)^+/−/WT, we then computed mixed ANOVAs on mouse-wise average population similarity z-scores with ORIENTATION difference as a within-subjects factor and WEEK (or GROUP) as a between/within subjects factor (3×2; within for KET/SAL).

For depiction of this effect on single trials (state-space plots in Figure 7I–L), Δf values from −2 to 7 seconds post stimulus onset for all trials and all cells from one representative mouse from each condition were subjected to a PCA (cells as variables) with a VARIMAX rotation applied to the covariance matrix, thereby limiting and optimizing the resulting solution to a minimal number of components (usually 3–6, based on the screeplot). This enabled the n-dimensional network state space (n=number of neurons) in which similarity was computed to be plotted in 2 dimensions (principal component space). In Figure 7, single trials are plotted as continuous trajectories in time and color coded with regard to the stimulus the mouse saw on a given trial.

Acute ketamine and PV-suppression experiments

Calcium imaging data were processed and analyzed with the same methods and statistical comparisons as described above for chronic models. One-way ANOVAs were used for acute ketamine experiments (base vs sal vs KET) and two-way mixed ANOVAs were used for DREADD experiments (base VS CNO-control; base VS CNO-h4MD(Gi)), followed by one-way ANOVAs to follow-up on interactions.

Analysis of PV interneurons

For each interneuron we calculated change in florescence from baseline (2 seconds before each event), divided by the standard deviation of florescence during baseline across all timepoints (z-Δf/f). While this measure does not purely assess the absolute activity of PVs, it reliably indexes the signal to noise ratio of PV responses to visual stimuli and during spontaneous ensemble activations in the local network (Figure S7C) and results in PVs untreated mice conform with previously published properties of PVs (Hofer et al., 2011; Niell and Stryker, 2008). For statistical comparisons, cell responses were normalized within mice (see above). Visually evoked PV z-df/f scores were averaged within the 3 seconds of stimulus presentation and compared with 2-by-2 mixed ANOVAs with TREATMENT as the between subject variable and WEEK as the within subject variable. PV activity locked to statistically identified ensemble activations (above) was averaged within the first 2 seconds after peak network Δf and compared with 2-by-2 mixed ANOVAs with TREATMENT as the between subject variable and WEEK as the within subject variable.

ADDITIONAL RESOURCES

MOCO software for motion correction is available at http://www.columbia.edu/cu/biology/faculty/yuste/Methods/moco.zip.

Highlights.

• -Neuronal ensemble activity is less reliable in mouse chronic ketamine model
• -Ensembles are affected in mouse genetic model of schizophrenia
• -Abnormal ensembles are found in both spontaneous and sensory evoked activity
• -Data is consistent with schizophrenia being a disease of cortical attractors