Local Gradients in Electrotonic Loading Modulate the Local Effective Refractory Period: Implications for Arrhythmogenesis in the Infarct Border Zone

Abstract

Ectopic electrical activity that originates in the peri-infarct region can give rise to potentially lethal re-entrant arrhythmias. The spatial variation in electrotonic loading that results from structural remodelling in the infarct border zone may increase the probability that focal activity will trigger electrical capture, but this has not previously been investigated systematically. This study uses in-silico experiments to examine the structural modulation of effective refractory period on ectopic beat capture. Informed by 3-D reconstructions of myocyte organization in the infarct border zone, a region of rapid tissue expansion is abstracted to an idealized representation. A novel metric is introduced that defines the local electrotonic loading as a function of passive tissue properties and boundary conditions. The effective refractory period correlates closely with local electrotonic loading, while the action potential duration, conduction, and upstroke velocity reduce in regions of increasing electrotonic load. In the presence of focal ectopic stimuli, spatial variation in effective refractory period can cause unidirectional conduction block providing a substrate for reentrant arrhythmias. Consequently, based on the observed results, a possible novel mechanism for arrhythmogenesis in the infarct border zone is proposed.

I. Introduction

INFARCTED hearts are susceptible to spontaneously developing life-threatening reentrant arrhythmias [1]. Heterogeneous tracts of preserved myocytes that surround and penetrate the infarct are thought to provide a structural substrate for reentry, giving rise to tortuous propagation [2], [3] as well as focal conduction delays and unidirectional block [3]. However, reentrant rhythm disturbances are commonly triggered by ectopic electrical activity that also originates in the peri-infarct region [4]. While the mechanisms that give rise to spontaneous depolarization (SD) have been extensively studied at the cellular level [5], [6], it remains unclear how local stimuli of this kind overcome electrotonic loading (EL) and generate propagated activation [7].

In the infarct border zone (BZ), structural and electrophysiological heterogeneities are associated with rapid spatial variations in EL. For instance, the increased EL associated with a region of abrupt tissue expansion gives rise to conduction velocity (CV) slowing immediately distal to the expansion [3], [8], [9]. The corollary to this is that there are regions within the BZ where tracts of preserved myocytes have much reduced cell-to-cell coupling [3]. We hypothesize that the reduced EL in these regions will increase the probability of successful capture by an ectopic stimulus.

In this study, we have characterized regional EL in idealized geometries that are informed by 3-D reconstructions of myocyte organization in the infarct BZ [3]. Local EL is derived from the membrane potential generated passively by a current source at that point. This metric can be evaluated throughout a heterogeneous domain with complex boundary geometry and, in a 1-D semiinfinite cable, is inversely proportional to the space constant λ [10], [11]. Active propagation was simulated in these geometric models and local ERP, CV, and action potential duration (APD) were determined. We demonstrate large spatial gradients in EL in geometric models that correspond to structural remodelling in the infarct BZ with corresponding variation in ERP. In this setting, however, there is no relationship between APD and ERP. Finally, focal stimulation in regions with large ERP gradients is shown to cause unidirectional conduction block, providing a potential mechanism for arrhythmogenesis.

II. Methods

A. Local EL

In this study, the effective local diffusive loading is called the EL. A measurement of the local EL is sought in the presence of structural and electronic heterogeneities, where λ may not be measurable. The solution of the 1-D steady-state cable equation for a point-source in a semiinfinite domain is given by [12]

$$V\left(x\right)=V_0{e}^{-\left|x\right|/\lambda }$$ (1)

where λ is the length constant, V (x) is the transmembrane potential, and V₀ is the transmembrane potential at the origin. From the definition of the axial current density J = −σdV /dx, and given the current density at the source is proportional to the current injected at the point, I₀, we can write

$$V_0\propto \frac{\lambda }{\sigma }{I}_0$$ (2)

where σ is the bulk conductivity. Using $\lambda \propto \sqrt{\sigma }$ allows (2) to be rewritten as

$$V_0\propto \frac{I_0}{\lambda }.$$ (3)

The term V₀ in (3) is inversely proportional to the length constant λ, soa large λ (high conductivity or good cell-to-cell coupling) gives a small V₀ and vice versa. This derivation for V₀ only holds in the 1-D semiinfinite domain. When boundaries are present or the conductivity varies along the cable, V₀ provides a measure of the EL at the point source, or a measure of amount of diffusion due to the surrounding continuum.

Using this concept, it is possible to produce a scalar field of the EL (EL(x)), for point-source stimuli in a multidimensional continuum, provided the source current remains constant. Assuming the conductivity is isotropic, the proximity of boundaries reduces the amount of current diffused at a point due to the zero-flux boundary condition (BC) [13] (in the intracellular domain) so V₀ (x) increases with increasing proximity to the boundary. Consequently, V₀ (x) does not reflect the degree of cell-to-cell electrical coupling that λ describes in the semiinfinite domain. When the conductivity varies as a function of space, V₀ (x) varies commensurately. When both varying conductivity (or varying fiber direction) and boundaries are present, V₀ (x) provides a measure of the local EL. It is important to note that the EL, as defined here, is based on the steady-state variation of the transmembrane potential; thus, transient dynamics are not captured. As V₀ (x) is dependent upon the stimulation current, it is normalized by the minimum of V₀ (x) over the domain and then inverted to give a nondimensional value of EL: EL(x) = (V₀ (x)/ min{V₀ (x)})⁻¹.

In the multidimensional case, the solution to the governing equation [12] diverges at the origin (where the source-term exists). In this study, linear finite elements are used for the numerical solution of the governing equations, with the stimulus current applied at element vertices. The element shape functions effectively distribute the applied current over an area (in 2-D) defined by the element shape, edge length, and connectivity. Thus, the source-term is no longer applied at a point and the solution at the vertex does not diverge. The length scale introduced by the finite discretization necessarily implies that the solution is mesh-dependent. However, by injecting an equivalent current density over the same volume (or area in 2-D), the mesh dependence is removed.

B. Computational Methods

The linear finite-element solver Cardiac Arrhythmia Research Package [14] is used to solve the mono and bidomain partial differential equations (PDEs) for cardiac electrodynamics [15]. The bidomain equations, stated in parabolic form, are written as

$$\begin{array}{l}\nabla \cdot \left({\mathit{\sigma }}_i\nabla {\varphi }_i\right)=\beta I_m\\ \nabla \cdot \left({\mathit{\sigma }}_e\nabla {\varphi }_e\right)=-\beta I_m-I_{ei}\\ I_m=C_m\frac{\partial V}{\partial t}+I_{ion}\left(V,\mathit{\eta }\right)-I_s\\ {\sigma }_b{\nabla }^2{\varphi }_e=-I_{eb}\end{array}$$ (4)

where ϕ_i and ϕ_e are the intra- and extracellular potentials, V = ϕ_i − ϕ_e is the transmembrane potential, σ_i and σ_e are the intra- and extracellular conductivity tensors, β is the membrane surface area to volume ratio, I_m is the transmembrane current density, I_ei and I_eb are the extracellular current stimuli applied to the interstitial and bath space, respectively, I_s is the transmembrane current stimulus, C_m is the membrane capacitance per unit area, and I_ion is the membrane ionic current density, as a function of the transmembrane potential V and the vector of state variables η. As described in [13], the BCs imposed on (4) are motivated by physical arguments and ensure there is no flux of the intracellular current into the bath space surrounding the heart, and that the extracellular and bath potentials are continuous at the boundary of the heart ∂Ω = ∂Ω_t ∪ ∂Ω_tb. The subscript t represents tissue and subscript tb represents the tissue-bath boundary, so that the BCs are

$$\begin{array}{l}\mathit{n}\cdot \left({\mathit{\sigma }}_i\nabla {\varphi }_i\right)=0,\partial {\Omega }_t\\ \mathit{n}\cdot \left({\mathit{\sigma }}_e\nabla {\varphi }_e\right)=\mathit{n}\cdot \left({\sigma }_b\nabla {\varphi }_b\right),\partial {\Omega }_{tb}\end{array}$$ (5)

where n is the outward pointing unit normal to the heart tissue surface. When the anisotropy ratios of the conductivities in the intracellular and extracellular spaces are equal, an effective, or bulk, conductivity may be described by the harmonic mean of the intra and extracellular directional conductivities (in 2-D for illustration):

$${\mathit{\sigma }}_m=\left[\begin{array}{ll}\frac{{\sigma }_i^{\parallel }{\sigma }_e^{\parallel }}{{\sigma }_i^{\parallel }+{\sigma }_e^{\parallel }}\hfill & \hfill 0\hfill \\ 0\hfill & \frac{{\sigma }_i^{\perp }{\sigma }_e^{\perp }}{{\sigma }_i^{\perp }+{\sigma }_e^{\perp }}\hfill \end{array}\right]$$ (6)

where the superscripts ∥ and ⊥ refer to the fiber perpendicular and parallel directions, respectively. The bulk conductivity σ_m allows the bidomain equations (4) to be rewritten as one parabolic PDE for the transmembrane potential V :

$$\nabla \cdot \left({\mathit{\sigma }}_m\nabla V\right)=\beta \left(C_m\frac{\partial V}{\partial t}+I_{ion}\left(V,\mathit{\eta }\right)\right)-I_s.$$ (7)

The condition of equal anisotropy ratios for the intracellular to extracellular conductivities is not observed in nature in general, and many important second-order effects such as virtual electrode formation [16] are not captured by numerical solutions of the monodomain equations. However, when using a harmonic mean conductivity tensor, the monodomain and bidomain models are exactly equivalent for planar wavefronts propagating along an eigenaxis.

The intra- and extracellular conductivity tensors σ_i and σ_e were given experimentally measured values [17] for the directions longitudinal (∥) and transverse (⊥) to the local fiber orientation [with σ_m calculated from (6)]. The prescribed time step for time marching was set to Δt = 25 μs, a value found to be stable and accurate [18] for all simulations when compared against results obtained with a time step of 10 μs. When steady-state solutions were required for passive membrane simulations (when calculating the local EL), iteration was performed until the maximum change of the transmembrane potential at t = t_n ms reduced to less than 1% of its previous value (at t = (t_n − 1) ms) over the domain.

C. Computational Models

1). Funnel Models

Inspection of high-resolution (2-μm voxel size) histology data of the rat infarct BZ [3] revealed contiguous bundles of apparently healthy myocytes surrounded by collagen. The diameter of the myocyte bundles was found to expand and contract through the depth of the tissue (in the apex-base direction) , as shown in Fig. 1. Two-dimensional idealized representations of these histology-informed [3] myocyte fiber-bundle expansions were created; these geometries give rise to source-sink mismatches [6]–[8]. The funnels had base width w = 300 μm (approximately the most frequently observed bundle width in [3]) and length l = 2500 μm, with the expansion occurring half way along the length and the funnel expansion defined by the angle θ, as shown in Fig. 2(a). Four funnels were defined with θ ∈ {0, 30, 60, 90}°. In contrast to the models used in [8], realistic fiber directions were applied to the funnel meshes by taking unit vectors of the gradient of the solution of Laplace’s equation over the domain [19]; Laplace’s equation was solved with Dirichlet BCs applied at the funnel bottom and top with dissimilar values, and zero flux Neumann conditions elsewhere on the boundary. Fig. 2(b) shows the fiber directions obtained using the solution of Laplace’s equation. All of the meshes had uniform triangular elements with constant edge length of 25 μm. In this study, the active ionic currents were described by an established and robust rabbit ventricular cell model [20]. We note that, although the histology data are obtained from a rat infarct, similar variations in electrophysiological properties are to be expected for different ionic models, as (it will be shown that) the variations we observe are driven by the structure and BCs and not the specific ionic model used.

Fig. 1.

Histology (from [3]) showing surviving myocyte bundle expansions through the thickness, encapsulated in collagen.

Fig. 2.

Schematics of the computational domains and imposed fiber directions for the θ ∈ {0, 30, 60, 90}° funnels. (a) Schematic of the computational domains and stimulus locations (note that, although only four locations are shown, the s₂ stimuli were applied at each vertex coinciding with the symmetry line). The reference frame and origin are shown in blue. (b) Example of the imposed fiber directions.

2). Bath-Loading Effects

In order to test the influence of the bath conductivity (in the clinical context the conductivity of the collagen surrounding the healthy myocytes), the strip geometry (θ = 0° funnel) was simulated, with surrounding area (square of side l) representing the bath. The bath conductivity was varied by three orders of magnitude (g_b = {0.01, 0.1, 1.0} S/m) and AP metrics were calculated at all nodes along the vertical axis [see Fig. 2(a)] by solving the bidomain (4) and monodomain equations (7).

D. Stimulation Protocols

Stimulus s₁ and s₂ locations are shown in Fig. 2(a); s₁ stimuli were applied at all vertices lying at the base of the funnels and s₂ stimuli were applied to vertices inside 50-μm squares around points along the vertical axes of the funnels, representing discrete locations undergoing SD. Measurements of refractoriness and excitability were taken at the centroid of the stimulated domain, following activation by a prior s₁ stimulus.

1). ERP

The ERP is defined here as the minimum time following prior local activation from s₁ stimulation (T_s1) at which successful AP propagation from the s₂ stimulus site occurred (T_s2). The ERP was calculated using a bisection search algorithm [21] with a tolerance of approximately 0.1ms, and was calculated using ERP (x) = T_s2(x) − T_s1(x). The funnels had stimuli applied at the s₁ location (along the base of the funnel) at a basic cycle length of 200 ms, with a stimulus duration of 2 ms for ten beats, before capture at the s₂ stimulus locations were attempted. The criterion used for successful propagation was to test that activation had occurred at either of two test points (at the bottom and the top of the funnel domain) after a time sufficient for an AP wavefront to propagate from the point of stimulation to the furthest test point. To remove the functional dependence of the ERP on the stimulus current, I_s at the s₂ locations were equal for all the geometries and set to the minimum current required to elicit successful AP propagation at the point of highest EL for all the domains considered.

2). Computed Electrophysiological Metrics

• a)The max{dV/dt} was calculated as the maximum rate of change of V during depolarization.
• b)The APD was defined as the time interval between the time of crossing the threshold potential (here assumed constant at −20 mV) and the time at which the transmembrane potential reached 90% of its resting potential (−78.1 mV).
• c)The solution for the transmembrane potential was recorded at 0.1 ms increments and the nodal activation time was calculated by a piecewise linear interpolation with a threshold potential of −20 mV. The CV was then calculated using a second-order centered difference, with a space step of 25 μm.

III. Results

As edge (the top and bottom of the funnels) and s₁ stimulation effects contaminated the solution, the results are only shown for −700 ≤ y ≤ 700 μm. The key dynamics occur around the funnel expansions. These are located approximately 3.4 length constants (calculated from the conductivity values [17]) away from the top and bottom edges of the funnels, ensuring that edge effects are negligible. With the exception of the bath-loading studies, all results were calculated by solving the monodomain equations (7).

A. Bath Loading

As the myocyte bundles observed in the histology data [3] are surrounded by collagen, we first investigated the influence of the surrounding bath conductivity on the electrophysiological properties inside the domain by solving the bidomain equations for the θ = 0° funnel as it had the highest perimeter to surface area ratio. Fig. 3 shows the variation in APD (top) and max{dV/dt} (bottom) at points along the centre vertical axis [as shown in Fig. 2(a)], as the bath conductivity is varied from σ_b = 0.01 to 1.0 S/m. The range in variation of APD and max{dV/dt} is small. The monodomain solution corresponds closely with the bidomain results for σ_b = 0.01 S/m. Note that the results shown in Fig. 3 were solved using a higher spatiotemporal resolution (10-μ m edge length and 10-μs time step) than the rest of the results presented to improve the stability of the bidomain solution.

Fig. 3.

Variation in APD and max{dV/dt} for the θ = 0° geometry for large variations in σ_b . The bidomain variations in APD and max{dV/dt}, for different bath conductivities are small and correspond closely with the monodomain results.

B. Electrotonic Loading

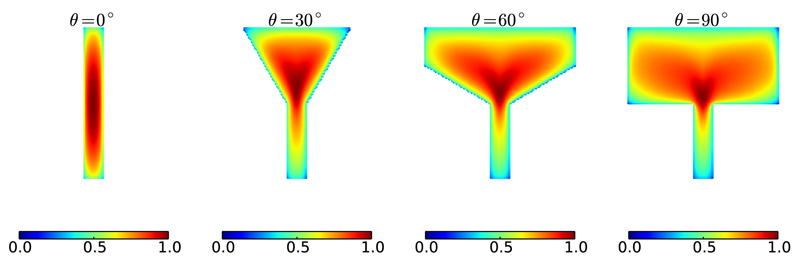
The local EL for the geometries considered was calculated at each vertex in the domain, as shown in Fig. 4.

Fig. 4.

Nondimensional EL(x) for each vertex in the domain. EL(x) reaches a maximum just above the funnel expansion in the θ > 0° funnels. In the θ = 0° funnel the maximum value is located at the centroid of the domain, due to the symmetry.

Fig. 4 shows that points near or coincident with the boundaries of the domain experience the lowest EL; this is due to the no-flux BC [see (5)]. It can be seen from the θ = 0° funnel (the strip) that highest EL occurs at the centroid of the domain; this is due to symmetry and the fact that the fiber-directions do not vary. For funnels with θ > 0°, the highest EL occurs just above the funnel expansion in each case.

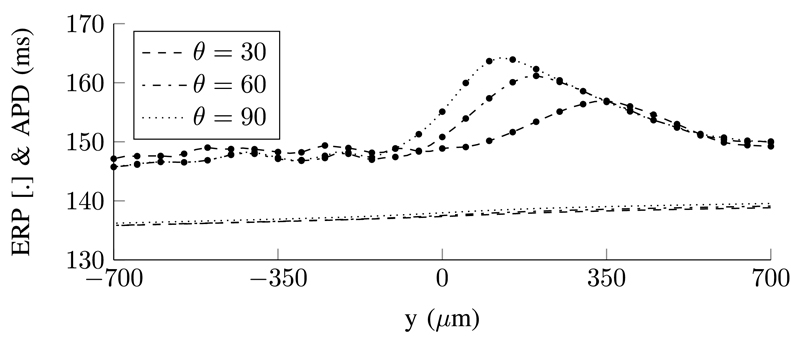
C. Refractoriness, APD, and Local EL

The local ERP and APD were calculated along the symmetry line of stimulus domain (the vertices lying along the vertical axes of the funnels) and shown in Fig. 5 along with the EL at the same locations. The extrema in the ERP and EL are approximately colocated. The magnitude of the variation in ERP (for the θ = 90° funnel) was about 20 ms while the θ = 0° funnel had a maximum variation of 0.5 ms. There is an oscillation in the ERP at a magnitude greater than the tolerance of the ERP bisection search. This is caused by the complex dynamics of the specific ionic model used. We tested a simpler ionic model with fewer ionic currents (the modified Beeler–Reuter [22], [23] model) and did not observe these oscillations. The APD decreases monotonically from the site of activation in each case, with the APD for the strip geometry (θ = 0°) decreasing approximately linearly along the height of the funnel. The APD for the θ = 90° funnel is highest overall with the steepest descent seen just above the funnel expansion. A similar trend is seen in the other funnels.

Fig. 5.

Local variation in ERP (with dotted markers), APD, and EL for points along the vertical (y) axis of the funnels. The ERP reaches a maximum above the funnel expansion for the θ = {30, 60, 90}° funnels, whereas it is maximum at the mid-point of the symmetrical (θ = 0°) funnel. The ERP varies by approximately 20 ms in the θ = 90° funnel and 0.5 ms for the θ = 0° funnel. The maxima in EL(x) is approximately colocated with the maxima in ERP for each funnel.

Unidirectional block was observed in the θ > 0° funnels at sites proximal to a high gradient in ERP, with the direction of propagation favouring the side with a lower ERP. The θ = 0° funnel had a higher average ERP than the θ = 90° funnel. This is due to the smaller domain size—there is a higher perimeter-to-area ratio and due to the no-flux BC (5); there is less area for diffusive redistribution of the transmembrane potential V . Thus, the mean V over the domain is higher after pacing, so the tissue is less repolarized, resulting in a higher ERP. A similar trend can be seen with the other funnels.

D. Propagation Metrics

The wavefront curvature from the first s₁ stimulus is shown in Fig. 6(a). The wavefront remains planar along the θ = 0° funnel but becomes concave just before the funnel expansion in the funnels with θ > 0°. This change in wavefront curvature is induced by the conductivity anisotropy coupled with the varying fiber directions. The action potential (AP) is shown at the point of expansion for each of the funnels in Fig. 6(b). As θ > 0°, the potential at the end of the upstroke is lower and the upstroke velocity is lower; however, the AP traces become similar around the plateau and repolarize at similar times. The CV and max{dV/dt} were calculated at each point along the vertical axis as shown in Fig. 7. The CV dropped from the converged value of approximately 50.6 cm. s⁻¹ along the constant-width part of the funnels to a minimum value of 13.6 cm.s⁻¹ in the θ = 90° funnel. The max{dV/dt} followed a similar trend to the CV, converging to 145.5 mV/ms in the strip geometry and reducing to a minimum of 41.4 mV/ms in the θ = 90° funnel. The extrema in the CV and max{dV/dt} are approximately coincident, as expected. The magnitude of the spatial rate of change of the APD along the vertical axis of the funnels (|∂/∂y(APD)|) is shown in Fig. 8. The rate of change of APD increases sharply just below the funnel expansion to reach a maximum of ≈ 7.9 ms/mm for the θ = 90° funnel (just above the expansion) before decreasing again.

Fig. 6.

(a) Wavefronts for the different funnel geometries shown at t = 3, 4, 5 and 6 ms. When the wavefront approaches the funnel expansion (for the θ > 0° funnels), the anisotropic conductivity coupled with the varying fiber directions causes the wavefront to become concave. (b) Lower plot: APs recorded at the centre of the funnels (x = y = 0). Upper plot: a zoom-in of the AP upstrokes. (a) Activation wavefronts for the different funnels. (b) Lower: APs recorded at point x = y = 0. Upper: zoom-in of AP upstrokes.

Fig. 7.

CV and max{dV/dt} for the different funnels. (a) CV is approximately constant, at 50.6 cm · s⁻¹ for the θ = 0° funnel, but retards at ≈ 525µm below the expansion for the θ > 0° funnels to reach a minimum just above the expansion for each case. (b) max{dV/dt} is approximately constant, at 145.5 mV for the θ = 0° funnel, but reduces at ≈ 525µm below the expansion for the θ > 0° funnels to reach a minimum just above the expansion for each case.

Fig. 8.

Spatial rate of change of APDs for the different funnels. |∂/∂y(APD)| is approximately constant for the θ = 0° funnel at 1.7ms/mm. |∂/∂y(APD)| is slightly lower for the θ > 0° funnels between approximately 700 and 250µm below the funnel expansion before it starts to increase, reaching a maximum just above the expansion for each case.

E. Effect of Fiber Orientation and Pacing Direction

To understand the influence of the fiber field, the ERP and APD were calculated with an isotropic conductivity (the arithmetic mean of the harmonic means of the intra- and extracellular conductivities in the longitudinal and transverse directions). The EL for the isotropic conductivity was also calculated, this is shown in Fig. 9. In the absence of varying fiber directions (scalar conductivity), the magnitude of the variation in ERP (≈ 8 ms for the θ = 90° funnel) is greater than that of the APD (≈ 2.5 ms for the θ = 90° funnel over the same distance); however, the ERP varies more slowly through the funnel expansion in comparison with Fig. 5. The maxima in the ERP and EL again approximately coincide. The variations of the ERP, APD, and EL are due only to the effect of boundaries and wavefront/waveback curvature [24], [25] in the case of an isotropic conductivity. The effects of boundaries on the dispersion of APD in isotropic domains are studied extensively in [26].

Fig. 9.

ERP (marker dots), APD and EL for the θ > 0° funnels with an isotropic conductivity. The maxima in the ERP again roughly correspond to the maxima in EL.

Depending on the specific physiology, the sinus wave may arrive from either direction in the isthmus. To test the effect of the pacing direction, we calculated the ERP and APD, in the same manner as before, but instead applied the s₁ stimulus to all nodes along the top edge of the funnels (with θ > 0°) in Fig. 2. These are shown in Fig. 10. It is clear that the same trend in ERP occurs, however, the mean slope in APD is in the opposite direction and the mean APD is shorter by about 20 ms overall. As in Fig. 5, localized gradients in ERP are sufficient to cause unidirectional block, as discussed in the next section.

Fig. 10.

ERP (marker dots) and APD for the θ > 0° funnels, with the s₁ pacing stimuli applied at the vertices along the top edge of the funnels.

F. Unidirectional Block

In the (θ > 0°) funnels that exhibited large gradients in ERP along the vertical axis, unidirectional block occurred with stimulation between a region of high and low ERP and at a time approximately equal to the local ERP. In each case, an s₂ stimulus was applied to the mid-point of the funnel, colocated with the funnel expansion (see Fig. 5). This is illustrated in Fig. 11. The maximum AP amplitude and CV of the unidirectional wavefront is greater for funnels with a larger expansion angle. This is due to the lower ERP below the expansion for the larger angles (see Fig. 5), as the region below the simulation point has had more time to repolarize so the AP wavefront propagates more rapidly into the more recovered tissue.

Fig. 11.

Unidirectional wavefront propagation from stimuli at the mid-point of the funnel at t = t_ERP for each funnel. (a) θ = 30° funnel. Stimulation is applied at the mid-point at t = 155 ms. (b) θ = 60°. Stimulation is applied at the mid-point at t = 156 ms. (c) θ = 90°. Stimulation is applied at the mid-point at t = 158 ms.

IV. Discussion

A. Bath-Loading Effects

The effects of large variations in bath conductivity on the APD and max{dV/dt} for thin (300 μm wide) bundles of myocytes were shown to be small. This suggests that the uncertainty in the specific value of bath conductivity σ_b (of the surrounding fibrotic tissue) for computational bidomain simulations is of little significance; variations in σ_b of two orders of magnitude around the nominal value of σ_b = 0.01S/m had only a small effect on the APD and max{dV/dt}. In addition, this result suggests that, when the assumption of equal anisotropy ratios for the intra- and extracellular conductivities is reasonable, solving the monodomain equation instead of the full bidomain solution will give acceptable results when simulating the effect of fibrosis as in [3]. In [27], the monodomain equations are shown to be equivalent to the zeroth order term in a perturbation solution of the bidomain equations. Thus, the monodomain equations can be thought of as a first-order approximation to the bidomain equations.

B. Wavefront Propagation, APD and max{dV/dt}

The CV of the wavefront for the θ = 90° funnel [see Fig. 7(a)] was similar to that shown in [8] for the abrupt expansion, despite a different cell model and funnel base-width (200 μm) being used. The wavefront shape after the wave had passed through the funnel expansion was, however, completely different with no concavity in the wavefront observed in [8]. This was due to a constant fiber orientation used [8]. When the fiber orientation is constant (with isotropic or anisotropic conductivity), it is possible to make meaningful predictions about the CV (or APD and refractory period as done in [24]) based on the observation of the wavefront curvature [25], [28]; however, this becomes difficult when varying fiber directions are present. In this study, the CV was shown to reduce while the wavefront became concave. Again, this is due to the presence of varying fiber directions. The θ = 90° funnel was tested with isotropic conductivity and the wavefront became convex at the expansion, in agreement with [28]. The AP morphology, as the excitation wave passed through the funnel expansion, was consistent with those shown in [8], with an increased upstroke duration and a lower plateau potential.

The max{dV/dt} was not explicitly measured in [8]. However, the transmembrane potential was measured at points along the axis of the geometry. In [8], the max{dV/dt} can be seen to decrease from the voltage–time plots of the transmembrane potential shown at points through the expansion to reach a minimum just past the expansion. The same phenomenon was observed in this study [see Fig. 7(b)]. It is important to note that, despite similar computational models being used in [8] and this study, different objectives were sought. In [8], the critical strand diameter required to cause conduction failure at an abrupt expansion was investigated, whereas here we are investigating the effects of structure and BCs in light of possible mechanisms for focal arrhythmogenesis in the BZ.

Fig. 5 shows that the (average) APD increased as the funnel expansion angle increased; this is due to the “feedback” of transmembrane potential from the region above the funnel expansion, in each case. The length constant of excitable tissue during the repolarization phase is generally longer than in passive tissue [29] (as the membrane resistance R_m increases during repolarization and $\lambda \propto \sqrt{R_m}),$ and the APD of a single (diffusively uncoupled) cell is much greater than the time constant for point stimulation in passive tissue. The larger the funnel angle, the more depolarized tissue there is above the expansion to raise the transmembrane potential of the tissue below the expansion through diffusive transport, thus prolonging the APD in the tissue below the expansion. The converse holds true; if the top edge of the funnels are stimulated, the average APD for the θ = 0° funnel is higher than the θ = 90° funnel.

The APD decreased approximately linearly for each funnel before decreasing at a greater rate for the θ > 0° funnels just before the expansion. The magnitudes of the gradients in APD (see Fig. 8), in the y-direction, for the θ > 0° funnels were similar to those observed experimentally, when unidirectional block occurred in a 1.5-mm isthmus in the guinea-pig heart [30]. The APD was also calculated for focal s₂ stimuli, as per the ERP calculations; however, little variation (< 1 ms) in focal APD was observed along the y-axis of the funnels, in comparison with the ERP which varied significantly (≈ 17 ms for the θ = 90° funnel).

C. Focal EL and ERP

The EL, due to structure and proximity of boundaries, at a site of focal stimulation has been shown to significantly modulate the local ERP. Large variations in ERP between neighboring points have been shown to cause unidirectional block, provided the applied stimulus occurred at a point between a region of high ERP and a region of low ERP (see Figs. 5, 10, and 11). This type of unidirectional propagation was observed to occur regardless of the orientation of the initial s₁ wave, demonstrating that the ERP, as we have defined it, is relatively insensitive to gradients in repolarization. This asymmetry in AP propagation is due to stimulation inside the window of vulnerability for the membrane [31], [32].

In regions of high EL, the current density at the s₂ stimulus location, due to the stimulus, is low (due to the diffusive spread of current), resulting in a reduced effective stimulus current. Thus, in regions of high EL, a lower effective stimulus current coupled with the AP phase of nearby points prolongs the refractory period in response to focal stimulations. Conversely, in regions of low EL, the proximity to boundaries acts to confine the s₂ stimulus current, leading to an effectively higher stimulus current and consequent capture at shorter coupling intervals (lower ERP). Although local gradients in repolarization (related to local APD) play a role, we have shown that the ERP is largely driven by the structural effects of a tissue expansion and confinement of stimulus current from the focal s₂ stimulation. The capture of focal ectopics is a complicated phenomenon, with stimulus duration, stimulus strength, existing gradients in repolarization, and the effective diffusivity as factors. This study shows that the ERP, as defined locally, is sensitive to the effects of structure and BCs and correlates closely with the EL.

D. Mechanism for Focal Arrhythmogenesis

A spatial gradient in ERP may explain a potential mechanism for focal arrhythmogenesis in the BZ. This is illustrated in Fig. 12. In Fig. 12, the EL at point p is significantly modulated by the expansion, giving rise to a gradient in ERP. SD at point p causes a unidirectional wavefront which travels in the direction of lowest ERP (to the right). Provided this focal wavefront (blue in Fig. 12) does not collide with the sinus wave, it may circulate around the isthmus and reenter from the left-hand side, setting up a reentrant circuit. Alternatively, the focal wavefront may block the sinus wave (before or after exiting the right-hand side), causing the sinus wave far from the isthmus to enter the left-hand side, setting up a reentrant circuit. In order for the reentrant circuit to be sustained, the path length over which the reentrant wave propagates must be larger than the wavelength of the reentrant wave [31]; this has been demonstrated to be the case in a high-resolution monodomain simulation of the rat infarct BZ [3].

Fig. 12.

Schematic of how unidirectional block may arise due to SD in a region with a spatial gradient in ERP. The symmetry plane implies 2-D symmetry or 3-D cylindrical symmetry. The opacity of the red shading illustrates the magnitude of the local ERP.

We simulated this mechanism by constructing a model based on Fig. 12 and similar to the funnels in the remainder of the study. An initial s₁ stimulus current was applied to nodes along the top edge of the domain and an s₂ stimulus was applied to nodes inside a 50-μm radius centered at the mid-point of the left expansion. The s₂ stimulus was applied at the ERP (≈ 151 ms) at the stimulus location, resulting in unidirectional propagation and a reentrant excitation wave. Fig. 13 shows the transmembrane potential at different times through the domain. The vulnerable window for unidirectional block formation was 150.5–150.9 ms.

Fig. 13.

Emergence of circus movement from stimulation at the local ERP in an idealized isthmus geometry. s₁ stimulation was applied at vertices along the top of the domain and s₂ stimulation was applied at a points corresponding to the s₂ location show in Fig. 12; the stimulus can be seen at t = 200 ms. Unidirectional propagation from the s₂ stimulus occurs due to the large gradient in ERP, resulting in a re-entrant circuit (t > 200 ms). The slowed propagation in the middle of the domain is due to the lower conductivity imposed in that region to replicate slow tortuous conduction through the central isthmus [33].

E. Conclusion and Future Work

It has been demonstrated that the presence of structural remodeling in the infarct BZ provides conditions that facilitate the capture of focal stimulations representing SDs. However, it is important to note that, in order for SDs to cause AP propagation, the EL of surrounding myocardium needs to be overcome so that the membrane potential of surrounding myocytes is raised to the threshold for activation. The source current required to cause activation is modulated by the local EL. Thus, in regions with high EL, it may be less likely that spontaneously depolarizing bundles of myocytes cause AP propagation due to insufficient source current [7]. This source-sink mismatch represents a countering (antiarrhythmic) mechanism which acts to protect the heart. It has been suggested that increased concentrations of myofibroblasts in the infarct BZ could raise the local transmembrane potential [34], reducing the current required from SDs to cause AP propagation. We postulate that SDs in regions of rapid tissue expansions in the BZ of infarct scars may be an important mechanism for arrhythmogenesis.

How the findings from this study relate to the physiological situation in which focal SDs cause AP propagation, perhaps from early or delayed after depolarizations or abnormal automaticity, may be answered by investigating the minimum energy stimulating pulse required for AP propagation. In light of the proposed mechanism for arrhythmogenesis and the ERP as a function of the stimulus current, it is natural to investigate how the ERP varies for minimum energy focal stimulations. There are a number of additional factors that warrant future investigation. Studies suggest that in the BZ, there may be changing myofibroblast concentrations [35], more homogenized distributions of Cx43 [36], and electrical remodelling [37]. These will be the focus of future work.