Failure of the Porcine Ascending Aorta: Multidirectional Experiments and a Unifying Microstructural Model

Abstract

The ascending thoracic aorta is poorly understood mechanically, especially its risk of dissection. To make better predictions of dissection risk, more information about the multidimensional failure behavior of the tissue is needed, and this information must be incorporated into an appropriate theoretical/computational model. Toward the creation of such a model, uniaxial, equibiaxial, peel, and shear lap tests were performed on healthy porcine ascending aorta samples. Uniaxial and equibiaxial tests showed anisotropy with greater stiffness and strength in the circumferential direction. Shear lap tests showed catastrophic failure at shear stresses (150–200 kPa) much lower than uniaxial tests (750–2500 kPa), consistent with the low peel tension (∼60 mN/mm). A novel multiscale computational model, including both prefailure and failure mechanics of the aorta, was developed. The microstructural part of the model included contributions from a collagen-reinforced elastin sheet and interlamellar connections representing fibrillin and smooth muscle. Components were represented as nonlinear fibers that failed at a critical stretch. Multiscale simulations of the different experiments were performed, and the model, appropriately specified, agreed well with all experimental data, representing a uniquely complete structure-based description of aorta mechanics. In addition, our experiments and model demonstrate the very low strength of the aorta in radial shear, suggesting an important possible mechanism for aortic dissection.

Introduction

The ascending thoracic aorta (Fig. 1(a)) supports tremendous hemodynamic loading, expanding (∼11% area change [1]) during systole and elastically recoiling during diastole to augment the forward flow of blood and coronary perfusion [2]. Although it is only about 5 cm long [3,4] (15% of the total length of the thoracic aorta), the ascending aorta is involved in 60% of all thoracic aortic aneurysms [5]. Aneurysm dissection and rupture (resulting in imminent death) are the primary risks associated with ascending thoracic aortic aneurysm (ATAA), occurring when the remodeled tissue is no longer able to withstand the stresses generated by the arterial pressure. Unfortunately, surgical repair of an ATAA also involves considerable risk. Statistically, death from rupture becomes more likely than death during surgery at an ATAA diameter over 5.5 cm, setting the current interventional guidelines [5–8]. Aortic dissection and rupture remain difficult to predict, however, occurring in a significant number of patients with smaller aneurysms [5,7,9] while many patients with ATAA diameters above 5.5 cm do not experience aortic dissection or rupture. New surgical guidelines have been proposed based on aneurysm growth rate [6,8] and normalized aneurysm size [7,10,11], but growth rates can be difficult to determine and require sequential imaging studies [12], and normalizing aneurysm size is still a controversial strategy [13–16]. A better understanding of aortic wall mechanics, especially failure mechanics, is imperative.

Fig. 1.

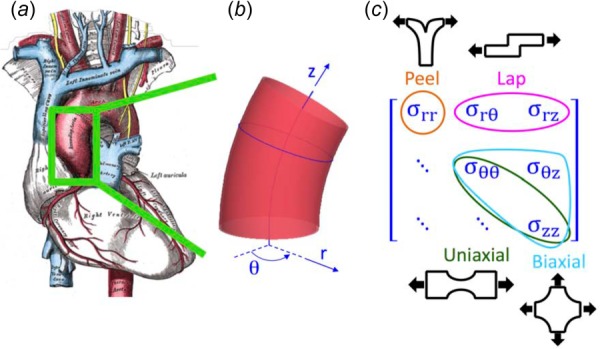
The ascending thoracic aorta. (a) Illustration of the heart with the ascending aorta highlighted [3], (b) Geometry and coordinate system describing the ascending aorta, and (c) The three-dimensional stress tensor for the aorta, marked to show how different testing modes were used to target specific stress components.

Because of the complex geometry of the aortic arch (aggravated in the case of aneurysm) and the complex mechanical environment surrounding an intimal tear, the stress field in a dissecting aorta involves many different shear and tensile stresses. It is therefore necessary to study tissue failure under as many loading conditions as possible. Tissue from the ascending aorta has been tested in a variety of configurations (reviewed by Avanzini et al. [17]), with uniaxial and equibiaxial stretch tensile tests being the most common. In-plane uniaxial [18–20] and biaxial tension tests [21–24] provide information on tensile failure in the plane of the medial lamella $({\sigma }_{\theta \theta },{\sigma }_{\mathit{z}\mathit{z}}),$ and the biaxial tests can provide some additional information on in-plane shear $({\sigma }_{\theta z})$. Although the dominant stresses in these tests may be the primary stresses during vessel rupture, they are not those driving dissection. Stresses near an advancing dissection include a combination of radial tension $({\sigma }_{\mathit{r}\mathit{r}})$ and transmural shear $({\sigma }_{r\theta },{\sigma }_{\mathit{r}\mathit{z}})$ [25], which are more difficult to test experimentally. Peel tests on pieces of artery [26–29] or aneurysm [30] provide insight into the failure behavior of the tissue in radial tension (${\sigma }_{\mathit{r}\mathit{r}}$), loading perpendicular to the medial lamella, as does direct extension to failure in the radial direction [26]. To examine transmural shear stresses $({\sigma }_{\mathit{r}\mathit{z}},{\sigma }_{r\theta })$, the shear lap test, well established in the field of adhesives [31] and used by Gregory et al. [32] to study interlamellar mechanics of the annulus fibrosus of the intervertebral disk, is an attractive option. In the present work, our first objective was to obtain a more complete picture of artery failure mechanics by using a combination of in-plane uniaxial and equibiaxial, shear lap, and peel tests to cover all three-dimensional loading modalities (Figs. 1(b) and 1(c)). To the best of our knowledge, this study was the first to generate data on the interlamellar shear strength of aortic tissue in this manner.

The need for better experiments is complemented by the need for better computational models of tissue failure. Many theoretical models have been utilized to describe ATAAs, but only a few have addressed failure and dissection [33–36]. Volokh [33] used a softening hyperelastic material model and a two-fiber family strain energy density function within the context of a bilayer arterial model to examine the failure of arteries during inflation. This model yields valuable results concerning rupture but does not address dissection. An impressive model of dissection mechanics was put forward by Gasser and Holzapfel [34], employing a finite-element (FE) model with independent continuous and cohesive zones. The Gasser–Holzapfel model combines a nonlinear continuum mechanical framework with a cohesive zone model to investigate the propagation of arterial dissection, and it agreed well with experimental peel test results [26]. However, the reliance on the a priori definition of the location and size of the cohesive zone, the zone in which microcrack initialization and coalescence are confined, limits the model. In addition, the model does not address microscale failure; that is, it does not capture the complex fiber–fiber and fiber–matrix interactions during dissection and does not account for the lamellar structure of the vessel wall. Similar results to those of Gasser and Holzapfel were found by Ferrara and Pandolfi [35], who investigated the impacts of mesh refinement and cohesive strength on dissection. Alternatively, Wang et al. [36] used an energy approach, rather than a cohesive zone, to simulate dissection in two dimensions. In addition to tear propagation, Wang's model was capable of simulating tear arrest, reflecting the clinical observation that dissection often occurs in stages. The energy approach presented, however, requires a priori definition of crack direction, does not allow changes in propagation direction, and does not address microscale failure. Advantages of a multiscale model include its ability to link observed macroscale properties to changes in microscale structure and its allowance of spontaneous failure initiation location and growth.

Recently, we utilized a multiscale model to describe ex vivo testing results of porcine ascending aorta in both uniaxial and equibiaxial extension [21]. The tissue microstructure was idealized as a single network of uniform-diameter fibers functioning in parallel with a neo-Hookean component that accounted for all nonfibrillar contributions. Although that model worked well for in-plane behavior, the lack of an accurate representation of the lamellar structure rendered it inaccurate for out-of-plane data and failed to take advantage of the full capabilities of the multiscale computational framework. It was clearly necessary to modify the simplified microstructural organization of our earlier work and consider the layered structure of the medial lamellae, including in particular the interlamellar connections, in order to capture the tissue's biomechanics in all loading conditions more relevant to dissection. Therefore, the second and third objectives of this study were to generate a tissue-specific microstructure based on the layered structure of the aorta and to utilize the new microstructure to build a multiscale model capable of replicating experimental results from all the mechanical tests (uniaxial extension to failure, equibiaxial extension, peel to failure, and shear lap failure) performed.

Methods

Experiment.

Ascending aortic tissue was obtained from healthy adolescent male swine (∼6 months; 87.4 ± 9.6 kg, mean ± SD) following an unrelated in vivo study on right atrial radio frequency ablation and stored in 1% phosphate-buffered saline (PBS) solution at 4 °C. Tissue specimens were tested within 48 h of harvest while immersed in 1% PBS at room temperature. Per our previous study [21], a ring of tissue was dissected from the ascending aorta and cut open along its superior edge (Figs. 2(a) and 2(b)). The tissue specimen was cut into small samples, both axially and circumferentially aligned, for mechanical testing. Several samples were obtained from each aorta (a typical dissection and testing plan is shown in Fig. 2(c)).

Fig. 2.

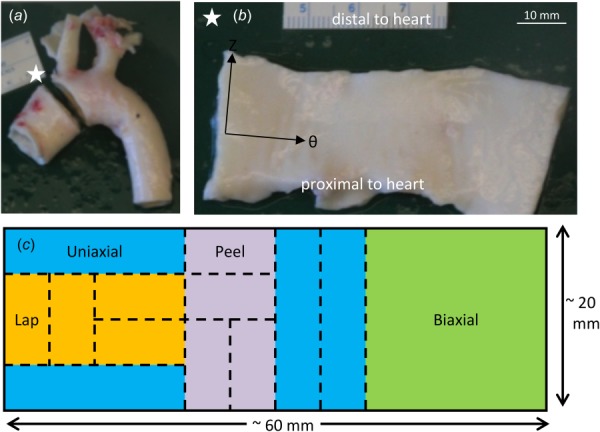
Specimen dissection. (a) Porcine aortic arch with ascending aortic ring removed. The white star represents a marker used to keep track of tissue sample orientation. (b) The ring was cut open along its superior edge and laid flat with the intimal surface up and the axial, Z, and circumferential, θ, directions along the vertical and horizontal directions, respectively. Axial and circumferential directions are shown with black arrows. (c) Schematic showing a typical sectioning and testing plan for an ascending aortic specimen.

Four different loading modalities were utilized to characterize the tissue mechanically: uniaxial, equibiaxial, peel, and lap tests (Fig. 3). Planar uniaxial and equibiaxial tests, which characterized the tissue in tension along the medial lamella $({\sigma }_{\theta \theta },{\sigma }_{\mathit{z}\mathit{z}},{\sigma }_{\theta z})$, were performed and described previously [21]. The intima, adipose tissue, and adventitia were removed from samples tested uniaxially and biaxially. While these testing modalities are relevant to the rupture of the vessel, dissection of the ascending aorta occurs when the medial lamellae separates into two layers and thus is highly dependent on the behavior of the tissue across lamellae. Thus, two additional mechanical testing modes were utilized. Peel tests (cf. [26,27,30]) were performed to quantify the tissues' tensile response perpendicular to the medial lamellae $({\sigma }_{\mathit{r}\mathit{r}})$ and subsequent dissection of the media into two layers. Shear lap tests were performed to quantify the tissues' response when exposed to shear along the medial lamella $({\sigma }_{\mathit{r}\mathit{z}},{\sigma }_{r\theta })$. The two protocols are described in detail below.

Fig. 3.

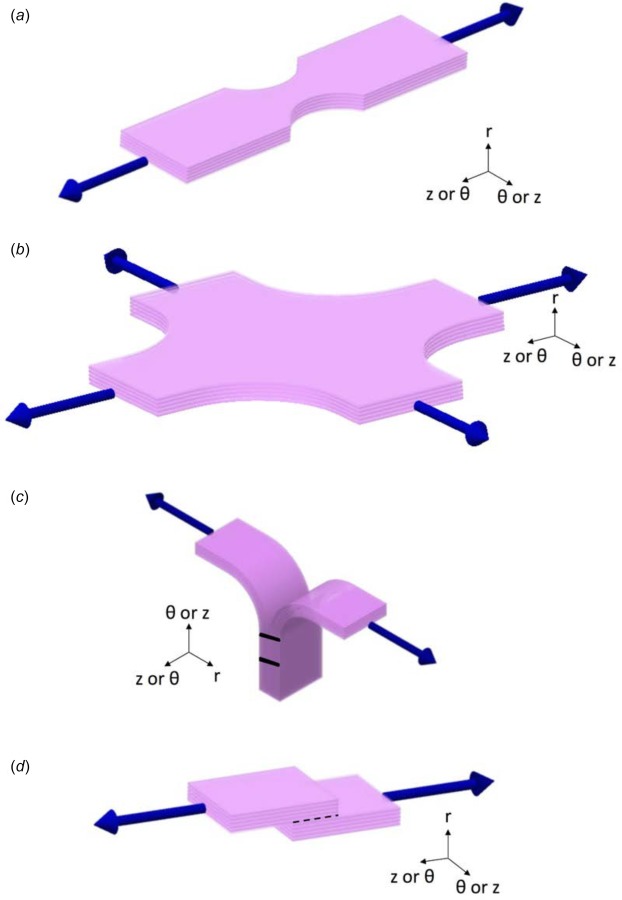
Schematics of all mechanical tests. (a) Uniaxial test: samples were cut and mounted such that the direction of pull corresponded with either the axial or circumferential orientation of the vessel. (b) Equibiaxial test: samples were cut and mounted such that the directions of pull corresponded with the axial and circumferential orientations of the vessel. (c) Peel test: samples were cut and mounted such that the vertical direction corresponded with either the axial or circumferential orientation of the vessel. (d) Lap test: samples were cut and mounted such that the direction of pull corresponded with either the axial or circumferential orientation of the vessel; dotted black line indicates overlap length.

Peel Tests.

The peel test (Fig. 3(c)) measures the adhesive force between two layers as they are pulled apart. For each rectangular sample designated for peel testing, a ∼4 mm incision was made parallel to the plane of the aortic wall to initiate delamination. The incision was made such that the delamination plane was approximately centered within the medial layer, thus separating the sample into two flaps of approximately equal thickness. Images of the sample were taken to determine its initial unloaded dimensions. There was a moderate variation in the exact location of the incision with respect to the center of the media due to sample size and cutting technique. If the delamination plane was outside the middle third of the sample thickness, the sample was discarded. Lines were drawn on the side of the sample with Verhoeff's stain in order to track the progress of failure.

The two flaps of the delaminated section of the tissue sample were then mounted in a custom gripping system with sandpaper on either side to prevent slipping and secured to a uniaxial tester. Samples were cut and mounted on a uniaxial testing machine (MTS, Eden Prairie, MN) such that the vertical direction, as shown in Fig. 3(c), was either axial or circumferential with respect to the vessel. The two flaps were peeled apart, causing the tissue sample to delaminate, at a constant displacement rate of 3 mm/min, and force was measured with a 5 N load cell. Preliminary tests showed no significant dependence on grip speed in the range of 1–10 mm/min, so a single velocity was used for all the subsequent experiments. Images of the side of the sample were recorded every 5 s throughout testing to capture the progression of failure. Peel tension was computed as force divided by undeformed sample width for both axially and circumferentially oriented samples.

Shear Lap Failure.

The shear lap test (Fig. 3(d)) produces large shear stresses in the overlap region. Rectangular samples designated for shear lap testing were specially shaped to test their shear strength. A ∼3.5 mm incision was made on each end of the sample centered within the medial layer and separating each end of the sample into two flaps of approximately equal thickness. The flap containing the intimal surface was removed from one end, and the flap containing the adventitial surface was removed from the other, resulting in the shear lap sample shape with an overlap length (black-dotted line in Fig. 3(d)) of ∼3.0 mm. Images of the sample were taken to determine its initial unloaded dimensions. Again, there was moderate variation in incision location with respect to the center of the media due to sample size and cutting technique; therefore, if either incision surface was measured to be outside, the middle third of the sample thickness the sample was discarded. Verhoeff's stain was used to texture the side of the sample for optical displacement tracking.

The specially cut sample was then mounted in a custom gripping system with sandpaper on either side to prevent slipping and secured to a uniaxial tester (MTS, Eden Prairie, MN). The height of the grips was adjusted such that the overlap surface was along the horizontal, and an image of the sample was taken to determine its initial unloaded dimensions. Each sample was extended to failure at a constant displacement rate of 3 mm/min, and force was measured with a 5 N load cell. During testing, digital video of the side of the sample was obtained at 24 fps, 1080 p HD resolution, and spatial resolution of ∼ 103 pixels/mm. Image analysis and displacement tracking were performed per our previous studies [37,38].

Shear stress was computed as force divided by the undeformed overlap area (sample width multiplied by overlap length). Unlike the peel test, which has been used previously to investigate aortic tissue [26,30], to the best of our knowledge the shear lap test has never been used to investigate aorta or other cardiovascular soft tissues (though Gregory et al. used a similar test to investigate the shear properties of the annulus fibrosus [32]). Therefore, displacement tracking was performed to verify that the shear lap test, as applied to the ascending thoracic aorta, produced large shear strains in the overlap region.

Statistical Analysis and Presentation.

Unless otherwise stated, the p-values are based on unpaired two-tailed t-tests, and p-values less than 0.05 were deemed significant. Values are reported as mean ± 95% confidence interval (CI).

Model.

The multiscale model employed was an extension of the previously presented model of collagen gel mechanics [39–43] applied recently to porcine aortic failure during in-plane tests [21]. It consisted of three scales: the FE domain at the millimeter (mm) scale, representative volume elements (RVEs) at the micrometer (μm) scale, and fibers with radii at the 100 nanometer (nm) scale. Each finite element contained eight Gauss points, and each Gauss point was associated with an RVE. Each RVE was comprised of a discrete fiber network in parallel with a nearly incompressible neo-Hookean component (to represent the nonfibrous material). The governing equations are given in Table 1. The major advance to the model was the implementation of a new tissue-specific network, specifically designed to capture the different components of the aortic wall.

Table 1.

Governing equations applied within the model, as well as the scale at which each equation and its parameters were applied

Equation	Description	Scale	Parameters
${\sigma }_{ij,j}=\frac{1}{V}\underset{\partial V}{\mathrm{\oint }}\left({\sigma }_{\mathit{i}\mathit{j}}^L-{\sigma }_{\mathit{i}\mathit{j}}\right)u_{k,j}{n}_{k}dS$	Macroscale volume-averaged stress balance [44]	Tissue	$\sigma :\text{macroscale}\hspace{0.17em}\hspace{0.17em}\text{averaged}\text{Cauchy}\text{stress}$
			$V:\text{RVE}\text{volume}$
			${\sigma }^L:\text{microscale}\text{stress}$
			$u:\text{RVA}\text{boundary}\text{displacement}$
$n:\text{normal}\text{vector}\text{to}\text{RVE}\text{boundary}$
${\sigma }_{\mathit{i}\mathit{j}}=\frac{1}{V}\int {\sigma }_{\mathit{i}\mathit{j}}^{L}dV=\frac{1}{V}\sum _{\mathit{b}\mathit{c}}\int x_i{f}_j$	Volume-averaged stress of RVE [44]	Network	$bc:\text{boundary}\text{for}\text{all}\hspace{0.17em}\text{the}\hspace{0.17em}\text{RVE}\text{cross}\text{links}$
			$x:\text{boundary}\text{coordinate}$
$f:\text{force}\text{acting}\text{on}\text{boundary}$
$F_f=\frac{E_f{A}_f}{\beta }\left({\mathrm{e}}^{\beta {\epsilon }_G}-1\right)$ $\text{and}{E}_f\approx 0\text{when}{\lambda }_f>{\lambda }_{\text{crit}}$	Fiber constitutive equation [41,45,46]	Fiber	$F_f:\text{fiber}\text{force}$
			$E_f:\text{Young}’\mathrm{s}\text{modulus}\text{of}\text{fiber}$ $\text{at}\text{infinitesimal}\text{strain}$
			$A_f:\text{fiber}$ cross-sectional area
			${\epsilon }_G:\text{fiber}\text{Green}\text{strain}$
			$\beta :\text{fitting}\text{parameter}\text{for}\text{fiber}\text{nonlinearity}$
			${\lambda }_f:\text{fiber}\text{stretch}$
${\lambda }_{\text{crit}}:\text{fiber}\text{stretch}\text{at}\text{failure}$
${\sigma }_{\mathit{i}\mathit{j}}^m=\frac{G}{J}\left(B_{\mathit{i}\mathit{j}}-{\delta }_{\mathit{i}\mathit{j}}\right)$ $+\frac{2G\upsilon }{J\left(1-2\upsilon \right)}{\delta }_{\mathit{i}\mathit{j}}\ln \left(J\right)$	Matrix governing equation [60]	Matrix	${\sigma }^M:\text{matrix}\text{Cauchy}\text{stress}$
			$G:\text{shear}\text{modulus}$
			$J:\text{deformation}\text{tensor}\text{determinant}$
			$B:\text{left}\text{Cauchy}$ -Green deformation tensor
$\upsilon :\text{Poisson’s ratio}$

The aorta is organized into thick concentric medial fibrocellular layers which can be represented by discrete structural and functional units. The lamellar unit, detailed by Clark and Glagov [47], consists of an elastic lamina sandwiched between two sheets of smooth muscle cells. The small-scale network in our computational model was designed to simulate the architecture of this discrete lamellar unit (Fig. 4), as visualized by histological analysis. Portions of unloaded porcine ascending aorta were cut such that the transmural structure was aligned in the circumferential (i.e. horizontal) direction and fixed in 10% buffered neutral formalin solution overnight, embedded in paraffin, and prepared for histological investigation per standard techniques. Sections were stained consecutively with hematoxylin and eosin (HE) stain (Fig. 4(a)) to visualize smooth-muscle cell nuclei, Masson's trichrome stain (Fig. 4(b)) to visualize collagen, and Verhoeff's Van Gieson stain (Fig. 4(c)) to visualize elastin.

Fig. 4.

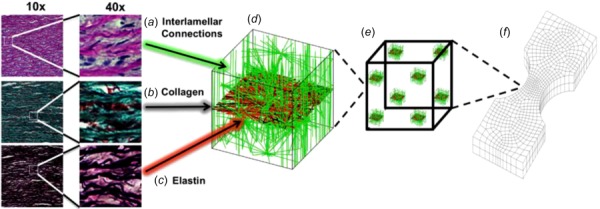
Multiscale model based on aortic media structure. (a) Hematoxylin and eosin stain shows smooth muscle cell nuclei (dark purple) and elastic lamina (pink). (b) Masson's trichrome stain shows collagen (blue) within the lamina and smooth muscle (red). (c) Verhoeff–Van Gieson shows elastin (black/purple). (d) A microstructural model based on the histology contains a layer of elastin (red) reinforced by collagen fibers (black). The collagen fibers are aligned preferentially in the circumferential direction, and the elastin sheet is isotropic. Lamellae are connected by interlamellar connections (green) representing the combined contribution of fibrillin and smooth muscle. The interlamellar connections are aligned primarily in the radial direction but also have some preference for circumferential alignment to match smooth muscle alignment in vivo. (e) An RVE with eight gauss points. (f) FE geometry showing a uniaxial shaped sample (equibiaxial, lap, and peel geometries were also used).

The final network structure is shown in Fig. 4(d), and the network parameters are given in Table 2. The volume fraction for the tissue-specific network was set to 5% per the porcine aorta volume fraction measurements of Snowhill et al. [49]. The elastic lamina was represented by a 2D sheet of elastin and collagen fibers. Collagen fibers within the elastin–collagen sheet were generated such that they exhibited strong circumferential orientation, based on the known tissue structure [47–51]. Histological and compositional studies [2,47–51] show more elastin than collagen within each lamina of the ascending aortic wall. Based on the histological observations of Sokolis et al. [51], the overall ratio of elastin-to-collagen within the 2D sheet was set to ∼1.6. Elastin fibers were generated such that orientation was approximately isotropic within the plane. The radial properties of the aorta are less well established [52,53] but are extremely important because failure of the interlamellar connections dictates delamination and thus aortic dissection. Within the model network, the interlamellar connections were designed to encompass the combined effect of all structural components (smooth muscle cells, fine collagen fibers, and fine elastin fibers) contributing to radial strength. Smooth-muscle cells within the media exhibit preferential circumferential alignment [47,50,54], so interlamellar connections were aligned with circumferential preference. Since the interlamellar connections encompass the combined effect of all the structural components contributing to radial strength (smooth muscle cells, fine collagen fibers, and fine elastin fibers), it is somewhat unclear how to define the proportion of interlamellar connections-to-elastic lamina fibers. Snowhill et al. [49] determined the volume ratio of collagen to smooth muscle to be 1:1 in porcine vessels. While clearly the interlamellar connections encompass some collagen, and the elastic lamina contains large amounts of elastin, we utilized this 1:1 ratio.

Table 2.

Model parameters and sources

Parameters	Value	References
Collagen fibers
Network orientation tensor, $[\begin{array}{ccc}{\Omega }_{\mathit{Z}\mathit{Z}}& {\Omega }_{\theta \theta }& {\Omega }_{\mathit{r}\mathit{r}}\end{array}]$	$[0.1 0.9 0]\pm [0.05 0.05 0]$	[47–51]
Mean ± 95% CI
Fiber stiffness, $A_C$	$340\hspace{0.17em}\text{nN}$	[43]
Fiber nonlinearity, ${\beta }_C$	$2.5$	[43]
Failure stretch, ${\lambda }_{\text{crit}C}$	$1.42$	[43]
Elastin fibers
Network orientation tensor, $[\begin{array}{ccc}{\Omega }_{\mathit{Z}\mathit{Z}}& {\Omega }_{\theta \theta }& {\Omega }_{\mathit{r}\mathit{r}}\end{array}]$	$[0.5 0.5 0]\pm [0.05 0.05 0]$
Mean ± 95% CI
Fiber stiffness, $A_E$	$79\hspace{0.17em}\text{nN}$	[21]
Fiber nonlinearity, βE	2.17	[21]
Failure stretch, ${\lambda }_{\text{crit}E}$	$2.35$	[21]
Interlamellar connections
Network orientation tensor, $[\begin{array}{ccc}{\Omega }_{\mathit{Z}\mathit{Z}}& {\Omega }_{\theta \theta }& {\Omega }_{\mathit{r}\mathit{r}}\end{array}]$	$[0.2 0.6 0.2]\pm [0.05 0.05 0.05]$	[47,50,54]
Mean ± 95% CI
Connection stiffness, $A_{\mathit{I}\mathit{C}}$	$36.4\hspace{0.17em}\text{nN}$	[53]
Connection nonlinearity, ${\beta }_{\mathit{I}\mathit{C}}$	$0.01$	[53]
Failure stretch, ${\lambda }_{\text{critI}C}$	$2.0$	[53]
Matrix
Poisson's ratio, $\upsilon$	$0.49$	[60]
Shear modulus, $G$	$1.7\hspace{0.17em}\text{kPa}$	[21]
Proportions
Total network volume fraction, Φ	0.05	[49,55]
Ratio of elastin-to-collagen, R	8:5	[48,51]
Ratio of interlamellar connections-to-elastic lamina fibers, r	1:1	[49]

Initial estimates of the fiber parameters (fiber stiffness, nonlinearity, and failure stretch) for collagen and elastin were based on our previous works [21,43], and those for the interlamellar connections were specified based on MacLean's experimental stress–strain behavior of the upper thoracic aorta subjected to radial failure [53]. Properties were subsequently adjusted such that a single set of model parameters matched results from the suite of experiments performed herein; the final parameter values are given in Table 2.

In addition to the smooth-muscle cells and connective tissue present within the lamellar unit, there is also fluid, primarily extracellular water [55], that combines with the smooth-muscle cells' cytoplasm to make tissue deformation nearly isochoric. A nonfibrous, neo-Hookean matrix was added to the network to make it nearly incompressible (ν = 0.49). The fiber network and nonfibrous matrix operated as functionally independent until failure, at which point network failure dictated simultaneous matrix failure. Stresses developed by the new tissue-specific network and matrix were treated as additive, as in other constrained mixture models [56–59]. The matrix material was considered homogeneous throughout the global sample geometry; each element, however, was assigned a unique set of fiber networks. New networks were generated for each of the five model simulation replicates for the uniaxial test; the uniaxial simulations showed almost no variability in repeated runs (SD < 1% of value), so no replicates were performed for the other tests.

Macroscale and microscale stress and strain were coupled as described previously [39–41,60]. Briefly, displacements applied to the macroscale model were passed down to the individual RVEs. The tissue-specific network within the RVE responded by stretching and rotating, generating net forces on the RVE boundary. A volume-averaged stress was determined for each Gauss point within the element from the net forces on the network boundary and the nonfibrous resistance to volumetric deformation. The macroscopic displacement field was updated until the global Cauchy stress balance was satisfied. Grip boundaries were enforced using rigid boundary conditions and the remaining sample surfaces were stress-free. All model simulations were run using 256-core parallel processors at the Minnesota Supercomputing Institute, Minneapolis, MN; clock times averaged 10 h per simulation.

Finally, we ran a brief simulation of uniaxial extension in the radial direction to compare with the experimental results of MacLean et al. [53], who performed uniaxial extension to failure of porcine aorta samples in the radial direction as noted earlier. The MacLean study represented an important test for our approach since the experiments were performed on the same tissue (healthy porcine thoracic ascending aorta) but in a mode that we did not use to generate and fit the model (radial extension to failure). Although MacLean did not report the tensile stress at failure, they reported the average tangent modulus at failure as well as the status of different samples at specific values of stretch; these data provided a basis for comparison with the model.

Results

Experiments were performed in four different geometries: uniaxial, biaxial, peel, and lap. In the uniaxial, peel, and lap tests, samples were prepared and pulled in two different directions, with some samples being tested in the axial direction and others in the circumferential direction. The multiscale model was used to describe all of the different experiments; the same set of model parameters was used for all of the experiments, including both prefailure and failure behavior.

Uniaxial Extension to Failure.

Uniaxial samples (Fig. 5(a)) aligned both circumferentially (n = 11) and axially (n = 11) were loaded to failure. In Fig. 5(b), the first Piola-Kirchhoff (PK1) stress, defined as the grip force divided by the undeformed cross-sectional area of the neck of the dogbone, was plotted as a function of grip stretch along with the best-fit tissue-specific model curves for samples aligned circumferentially and axially, respectively. The specified and regressed model parameters of Table 2 allowed the model to match the experimental prefailure and failure results to within the 95% confidence intervals for both orientations, matching the roughly threefold difference in failure stress (2510 ± 979 kPa for samples aligned circumferentially as compared to 753 ± 228 kPa for those aligned axially) and similar to stretch to failure (1.99 ± 0.07 for samples aligned circumferentially as compared to 1.91 ± 0.16 for those aligned axially) in the circumferential case vis-à-vis the longitudinal case. The neck region of the simulated uniaxial samples (both circumferential and axial) experienced the largest stresses (as expected) and also a large degree of fiber reorientation, as can be seen in Fig. 5(b). For the simulated experiments oriented circumferentially, the collagen fibers, which were already preferentially aligned in the circumferential direction, became more strongly aligned and were stretched, leading to the relatively high stresses observed. In contrast, for the simulated experiments oriented axially, the collagen fibers tended to pull apart by stretching the surrounding elastin, leading to a significantly lower stress and more failure of the elastin fibers. In both simulations, the collagen fibers were most likely to fail due to the extremely large extensibility of the elastin fibers, but the tendency of the collagen fibers to break was much higher in the circumferentially aligned simulated experiments (Fig. 5(c)). This shift is attributed to the collagen fibers being aligned in the direction of the pull and thus being forced to stretch more during circumferential extension, whereas there is more elastin and interlamellar connection stretch in the axial extension.

Fig. 5.

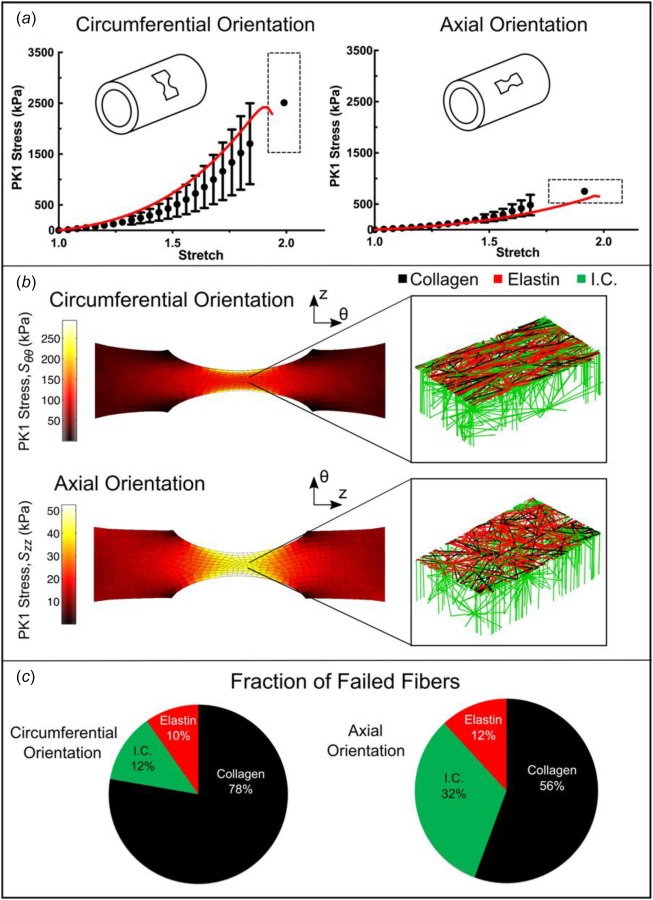
Uniaxial extension to failure. (a) First Piola-Kirchhoff (PK1) stress versus grip stretch for circumferentially (n = 11) and axially (n = 11) orientated samples (dots, mean ±95% CI). Error bars are only shown for stretch levels up to the point at which the first sample failed. The final dot shows the average stretch and stress at tissue failure, and the dashed rectangle indicates the 95% confidence intervals of stretch and stress at failure. The red lines show the model results for PK1 stress as a function of grip stretch. (b) PK1 stress distributions along the axis of applied deformation for both the circumferentially $(S_{\theta \theta })$ and axially $(S_{zz})$ aligned simulations, accompanied by an enlarged view of a network with the upper interlamellar connections removed to make the collagen and elastin visible. (c) Fraction of failed fibers of each type in the simulated experiment. Because the collagen fibers are preferentially aligned in the circumferential direction, more of the failed fibers were collagen for the circumferentially aligned simulation, whereas for the axially aligned simulation more of the failed fibers were interlamellar connections (I.C. = interlamellar connections).

Equibiaxial Extension.

The averaged experimental PK1 stress was plotted as a function of grip stretch (n = 9; also used in our previous analysis [21]) along with the best-fit tissue-specific model curves in Fig. 6(a). The equibiaxial extension test was not performed to failure but instead was stopped at a stretch of 1.4 to ensure that the sample did not fail during testing (based on initial experiments to estimate the safe stretch limit). Thus, the peak circumferential (139 ± 43 kPa) and axial (102 ± 30 kPa) stresses were not failure stresses. The equibiaxial model results (lines) were in good agreement with the experiments in both directions but slightly overpredicted the degree of anisotropy (i.e., the separation between the two lines). In particular, stresses in the circumferential direction were slightly overpredicted but remained within the 95% confidence interval for the experiment. The arms of the sample showed behavior similar to the uniaxial experiments, as can be seen in the stress plots of Fig. 6(b), but our primary interest is in the central region that was stretched equibiaxially. As expected for equibiaxial extension, in-plane fiber orientation of the elements in this region showed little change (Fig. 6(c)); there was, however, a deviation from affinity because the stiffer collagen fibers did not stretch nearly as much as the more compliant elastin fibers. At the final stretch step, for example, the collagen fibers were extended to an average of 13% stretch, but the elastin fibers had an average of 118% stretch.

Fig. 6.

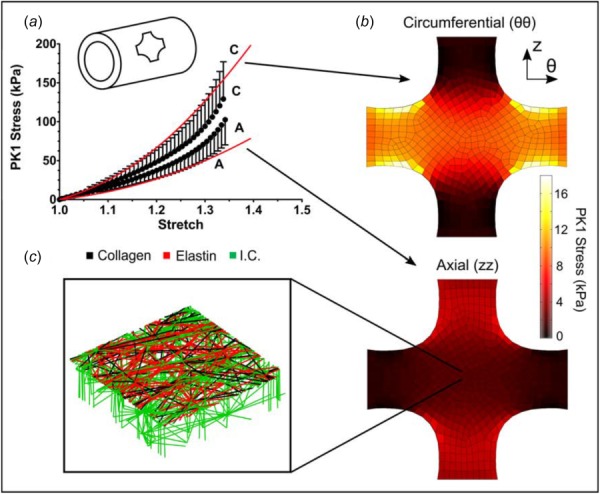
Equibiaxial extension. (a) Mean PK1 stress as a function of grip stretch (dots) for equibiaxial extension. The 95% CI was 30–35% of the measured value but was omitted from the figure to improve visual clarity. The red lines show the model results for PK1 stress versus grip stretch. (b) Circumferential $(S_{\theta \theta })$ and axial $(S_{zz})$ PK1 stress distributions predicted by the model. (c) Enlarged view of a micronetwork with the upper interlamellar connections removed to make the collagen and elastin visible.

Peel to Failure.

Peel samples from both the circumferential (n = 13) and axial (n = 23) orientations were loaded to failure. Peel tension, defined as the grip force divided by the sample width, was used to quantify delamination strength. When plotted as a function of grip displacement, the peel tension rose to an initial peak and then plateaued until total sample failure (Fig. 7(a)); importantly, the rise in each individual experiment was quite steep, but since the rise occurred at different grip stretches in different experiments (because of variation in sample size and initial notch depth), the average data of Fig. 7(a) appear to rise smoothly. The simulation results were thus similar to individual experiments, but we did not introduce the sample-to-sample variation necessary to smooth out initial rise.

Fig. 7.

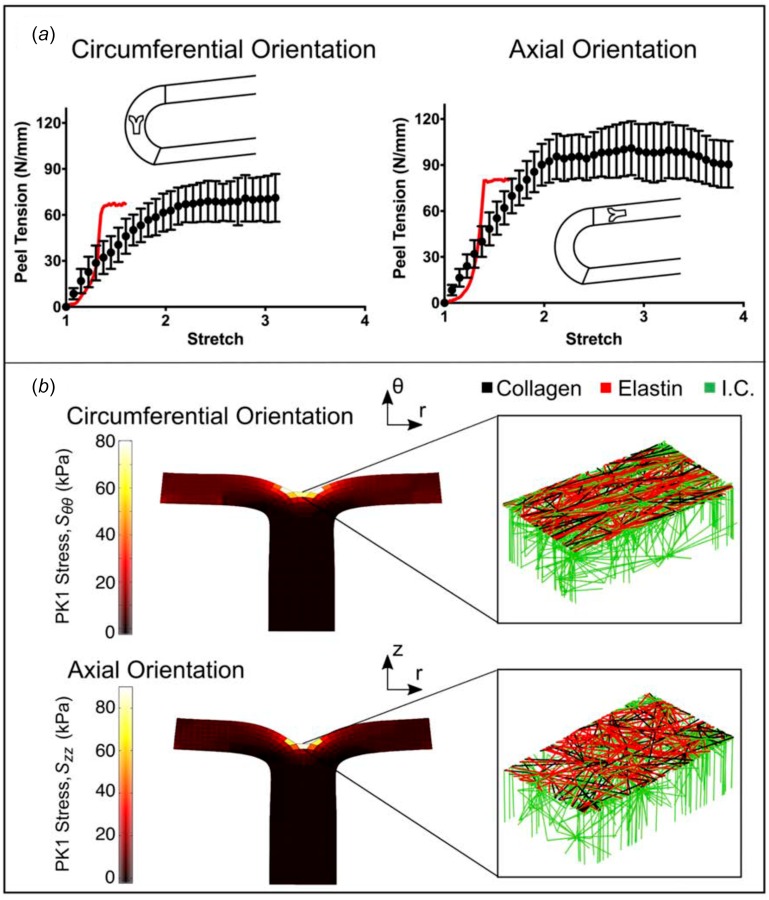
Peel to failure. (a) Peel tension versus grip stretch for both circumferentially and axially oriented samples (dots, mean ± 95% CI). The red lines indicate the model results. (b) PK1 stress (S_rr) distributions along the axis of applied deformation for both the circumferentially and axially aligned simulations, accompanied by an enlarged view of a network with the upper interlamellar connections removed to make the collagen and elastin visible.

The initial point and end point of the plateau region were computed by splining the data into 20 sections and determining where the slope of a linear fit of the points in a section was not significantly different from zero. The value of peel tension in the plateau region was averaged in order to determine the peel strength of each sample. The standard deviation of peel tension within the plateau region was evaluated to assess the degree of fluctuation during the peeling process. The average peel tension was significantly higher (p < 0.01) for samples aligned axially versus circumferentially (97.0 ± 12.7 versus 68.8 ± 14.2 mN/mm, respectively) with an anisotropy ratio of 1.4, similar to the results reported by others [29,30]. The standard deviation of peel tension showed similar anisotropy (p < 0.001) for samples aligned axially versus circumferentially (12.66 ± 2.22 versus 5.78 ± 1.04 mN/mm, respectively). The anisotropic response was present even when the standard deviation was normalized by average peel tension (p < 0.05, 0.145 ± 0.037 versus 0.088 ± 0.017, respectively, for a ratio of 1.65). Simulation results showed similar but less pronounced anisotropy (80.35 versus 67.01 mN/mm, ratio = 1.20). For both the circumferentially and axially oriented simulated experiments, the first Piola-Kirchhoff stress was concentrated around the peel front (Fig. 7(b)), and there was extensive stretching of the interlamellar connections. In sharp contrast to the simulated uniaxial failure experiments (Fig. 5), the vast majority of failed fibers in the simulated peel failure experiments were interlamellar connections; this result highlights the need for a detailed anisotropic model because different physiologically relevant loading configurations impose very different mechanical demands on the tissue's components.

Regional analysis was performed to determine whether sample location (i.e. location along the aortic arch) had an effect on mean average or mean standard deviation of peel tension. First, samples, taken from both the axial and circumferential directions from multiple specimens, were grouped according to their distance from the inner and outer curvature of the aortic arch. No significant difference (all the p-values > 0.10, n > 4 for all groups) was observed. Then, axially oriented samples taken from a single specimen were grouped by where peel failure was initiated (proximal or distal to the heart, n = 4 for both groups). No significant difference was seen in mean average peel tension (paired t-test, p-value = 0.26) or mean standard deviation of peel tension (p-value = 0.84) between the two groups. Pairing was done based on sample location within the specimen.

Shear Lap Failure.

As expected, the displacements were primarily in the pull direction, and shear strain was largest in the overlap region (Figs. 8(a) and 8(b)). In order to investigate the strain behavior of the tissue more fully, a line was drawn at the edge of the overlap surface, and strains tangential and normal to the overlap edge were calculated (n = 15 and n = 19 for axial and circumferential samples, respectively; some samples were not analyzed due to poor speckling). The maximum strain in each direction was determined (Figs. 8(c) and 8(d)). For both the axially and circumferentially aligned samples, the shear strain, E_nt, was large in the overlap region, as desired. For the axially oriented samples, the shear strain was higher than both the normal (p < 0.1) and tangential strains (p < 0.01). For the circumferentially oriented samples it was significantly higher than the tangential strain (p < 0.05) and comparable to the normal strain (p = 0.26).

Fig. 8.

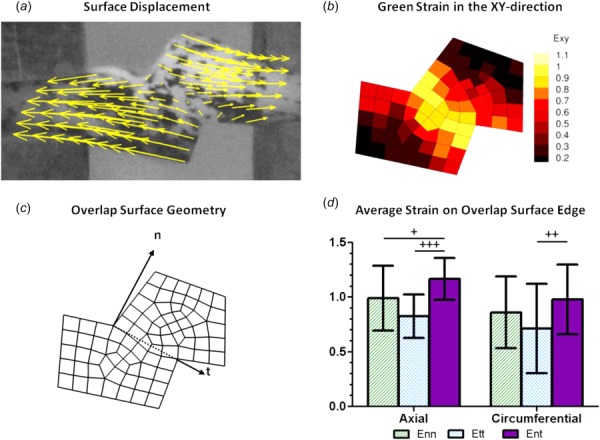
Kinematics of the shear lap test. (a) Displacement of a representative shear lap sample, adjusted to zero displacement at the center. (b) Strain of the representative sample in the xy-direction. (c) Dotted line showing overlap surface edge and vectors with normal and tangential directions. (d) Average strain on the overlap surface edge for both axially (n = 15) and circumferentially (n = 19) oriented samples. Error bars indicate 95% confidence intervals. ⁺p < 0.10, ⁺⁺p < 0.05, and ⁺⁺⁺p < 0.01.

Shear lap samples from both the circumferential (n = 28) and axial (n = 26) orientations were loaded to failure. The nominal (average first Piola-Kirchhoff) shear stress, the force per overlap area (Fig. 9(a)), exhibited catastrophic failure similar to that seen in the uniaxial tests and unlike the steady failure of a peel test. Circumferentially oriented samples exhibited significantly higher (p = 0.013) peak shear stresses than axially aligned samples (185.4 ± 28.4 versus 143.7 ± 16.0 kPa, respectively). In both the axial and circumferential directions, the shear lap failure stress was less than 20% of the failure stress necessary for uniaxial failure, indicating that the tissue is far weaker in shear than in uniaxial tension. The grip strain at failure was used to quantify further the compliance of the tissue. Greater grip strain (p = 0.07) was necessary to fail samples aligned in the axial direction compared with those in the circumferential direction (1.63 ± 0.16 versus 1.43 ± 0.17, respectively). As can be seen in Fig. 9(a), the multiscale model predicted the shear lap behavior of circumferentially oriented samples well (within the 95% CI). It was less successful at predicting the shear lap behavior of axially oriented samples (below the 95% CI), thus overestimating tissue anisotropy. The overlap region edges of the simulated uniaxial samples (both circumferential and axial) experienced the largest stresses and also the largest degree of fiber reorientation (Fig. 9(b)). Interlamellar fibers within the lap region were rotated and stretched strongly by the shearing; the collagen and elastin fibers were stretched more than in the peel test but considerably less than in the uniaxial and biaxial tests. As a result (Fig. 9(c)), the distribution of failed fibers was split more between the different fiber types than during peel or uniaxial failure. Even though the interlamellar connections, being much weaker than the others, were the most common to fail, there was also significant damage to the collagen and elastin fibers, perhaps due to the tangential component of the strain during the test (Fig. 8(d)).

Fig. 9.

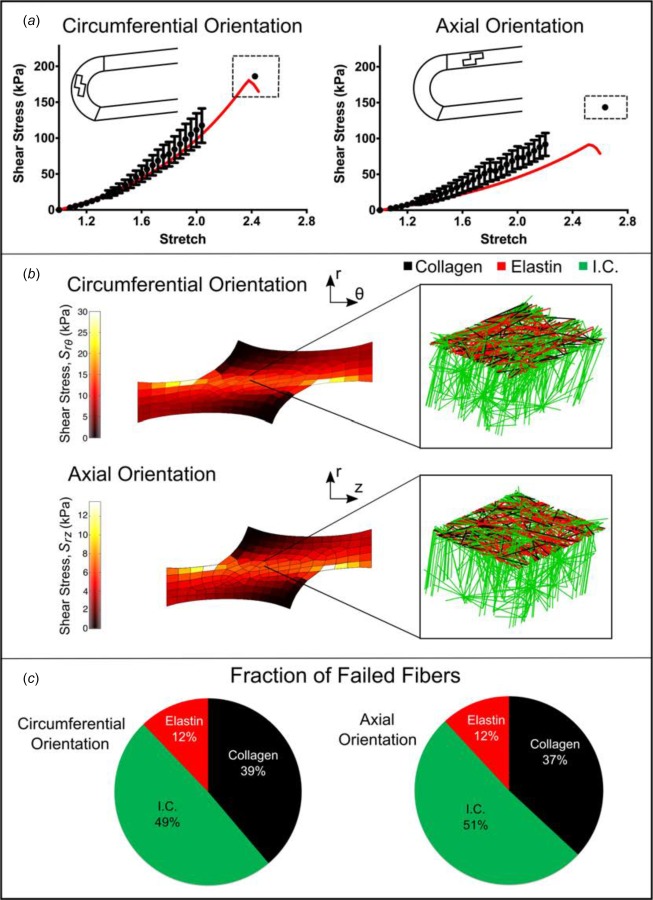
Shear lap failure. (a) PK1 stress versus grip stretch for circumferentially (n = 28) and axially (n = 26) orientated samples (dots, mean ±95% CI). Error bars are only shown for stretch levels up to the point at which the first sample failed. The final dot shows the average stretch and stress at tissue failure and the dashed rectangle indicates the 95% confidence intervals of stretch and stress at failure. The red lines show the model results. (b) Shear stress distributions along the axis of applied deformation for both the circumferentially $(S_{r\theta })$ and axially $(S_{rz})$ aligned simulations, accompanied by an enlarged view of a network with the upper interlamellar connections removed to make the collagen and elastin visible. (c) Fraction of failed fibers of each type in the simulated experiment (I.C. = interlamellar connections).

Summary Comparison of Model and Experiment.

Since a stated goal of this work was construct a multiscale model of aortic tissue mechanics that predicts failure in many different physiologically relevant loading modalities, we present a brief summary of the experimental and model failure results. Figure 10 shows the failure PK1 stress in uniaxial tests, failure tension in peel tests, and failure shear stress in shear lap tests for both the experiments and simulations for samples aligned in both the circumferential and axial directions. A single model with one set of parameters matches all of the experimental results well. It captures both the anisotropy exhibited in the different tests as well as the magnitude of stress or tension. In particular, the model predicts the considerably lower tissue strength observed in shear lap tests than that seen in uniaxial extension.

Fig. 10.

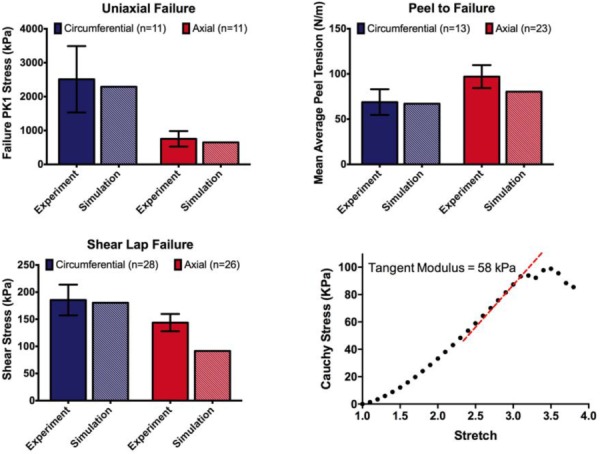
Summary of experimental and model results. (a) Experimental and model failure PK1 stress ($S_{\theta \theta }$ and $S_{zz}$) in uniaxial tension tests for samples oriented circumferentially and axially. (b) Experimental and model failure tension in peel tests for samples oriented circumferentially and axially. (c) Experimental and model failure shear stress ($S_{r\theta }$ and $S_{rz}$) in shear lap tests for samples oriented circumferentially and axially. All the experimental data show mean ±95% CI. (d) The model showed failure at a stretch ratio of 3.1 with a tangent modulus of 58 kPa in the region prior to failure, comparing well to MacLean's reported tangent modulus of 61 kPa.

Uniaxial Extension to Failure in the Radial Direction (Fig. 10(d))

MacLean et al. [53] reported that the average tangent modulus before failure was 61.4 ± 43 kPa. For our simulations, we found that the tangent modulus before failure was 58 kPa, in obvious good agreement with MacLean's experimental result. The stretch ratio at failure in the model was 3.1, and MacLean reported that “there was noticeable elastin layer separation” at a stretch ratio of 2, and that a stretch ratio of 3.5 was “past the value at which the wall can maintain stress.” Although the report of MacLean is obviously vague, the model results all appear to be consistent with MacLean's observations. The ability to make a reasonable prediction of an experiment performed using loading modality different from those used in the creation and specification of the model is a necessary feature for broader application in the future.

Discussion

Two important results came from the current work. First, a more complete picture of the failure behavior of aortic tissue was generated, demonstrating and quantifying the pronounced difference between the relatively high tissue strength in the lamellar plane (longitudinal and especially circumferential directions) and the low strength of the interlamellar connections (radial direction, demonstrated by peel and lap tests). Second, a novel multiscale, microstructural model was presented that, with proper adjustment of the model parameters, was able to reproduce the wide range of experimental observations accurately. This section focuses first on the experiments and then on the model, addressing them in the context of previous work by ourselves and others.

The current study used two novel test methods, the peel test and the shear lap test, to measure material failure in radial tension and transmural shear, respectively. The peel test is relatively new but has been used by others [26,27,30], and our results are consistent with their findings in terms of peel tension as well as the observation that the anisotropy typically expected of arteries in in-plane tests (higher circumferential versus axial stiffness) is reversed in peeling. Sommer et al. [26] suggested that the anisotropic behavior may be a protective mechanism since dissection in the axial direction is often associated with failure across elastic laminae, whereas dissection in the circumferential direction typically propagates between adjacent laminae. Pal et al. [61] suggested based on histology of peeled samples that the anisotropy may be due to stitching of the fibers, with failure in circumferential peeling occurring via a pull-out mechanism, whereas failure in axial peeling occurs via a tearing mechanism. This interesting conceptual description cannot be captured in our current model but clearly merits further investigation.

Although the shear lap test has been used on annulus fibrosus [32], to the best of our knowledge it has not been applied to cardiovascular soft tissues. The loading curve for the shear lap test of ascending aorta showed catastrophic failure similar to that of a uniaxial test rather than the sliding behavior seen by Gregory et al. [32], perhaps attributable to differences in the structure and properties between the annulus fibrosus and the ascending aorta. The failure behavior observed for the shear lap test retained the typical anisotropy expected of arteries, but required a much lower stress than that of uniaxial failure, presumably because the failure did not require as much breaking of collagen and elastin fibers. The shear lap and peel test results directly test the connections between lamellar units, and they are therefore critical in the case of a dissecting ascending aortic aneurysm. As our community moves forward to more patient-based geometries and simulations involving realistic geometries that necessarily lead to complex stress fields, validation of models in multidimensional loading is crucial. For example, it is common [62–66] to report results in terms of principal stresses, which are informative but do not address the fact that a stress acting radially or in shear is more likely to lead to tissue failure than one acting circumferentially. Martin et al. [65] used a potentially generalizable energy-based failure threshold, but they based the failure criterion on uniaxial circumferential tests. Although Martin's work represents a significant advance and demonstrates the potential of the patient-specific FE approach, there is clear need for a more accurate failure model, which could be informed by the current work. Another major challenge is that the tissue properties surely change during aneurysm formation, growth, and remodeling. The current work used only healthy porcine tissue, so our results are useful in guiding thought but should not be considered representative of human aneurysm tissue. There is also great need to develop better tools to estimate tissue mechanical properties in vivo, which would allow the construction of patient-specific constitutive models to match the patient-specific geometries currently in use.

Another goal of this study was to generate a tissue-specific microstructural description based on the layered structure of the aorta. Such a description, when incorporated into our multiscale modeling framework, could replicate mechanical behavior of arteries in lamellar tension, radial tension, and transmural shear, thereby linking microscale failure to the macroscale response. The simplified microstructural organization of our previous work [21] was replaced with a new lamellar model to capture the microstructure more faithfully. The lamella's structure is an essential component in modeling dissection of ATAA since radial and shear loading involve failure of the interlamellar connections rather than the lamina itself. The microstructure design of Fig. 4 mimics the lamellar unit, detailed by Clark and Glagov [47], and visualized here histologically. The unit is represented by a 2D sheet of elastin and collagen fibers (which forms an elastic lamina) attached radially by interlamellar connections (which collectively encompass smooth-muscle cells and fine elastin and collagen fibers). Network parameters were selected to reflect the biological roles of each component and were adjusted to match the experimental results. This approach was successful in matching a wide range of tissue mechanical tests, including one—radial extension to failure—that was not used during the fitting process, and it has the potential to be extended to the more disorganized (and thus more complex) architecture of the aneurysm, especially as better imaging and image-based modeling methods emerge [67,68]. The work of Pal et al. [61] represents an excellent example of this approach, developing a theoretical model of peel failure based on known structure. Pal's approach could be extended to a more general stress field using a strategy similar to ours. Finally, it is important to note that abnormal loading and damage can change tissue structure. For example, Todorovich-Hunter et al. [69] observed the formation of islands of elastin within the pulmonary arteries of rats in which they induced pulmonary hypertension. Thus, moving forward imaging-based alterations to the network design may be necessary to capture the structure of a damaged or diseased aorta.

There are, of course, further opportunities to construct a more realistic micromechanical model of the healthy and the aneurysmal ascending thoracic aorta. As already noted, the work of Pal et al. [61] provides a different and intriguing view of interlamellar failure by tearing versus pull-out effects. Additionally, our current model used collagen orientation tensor with eigenvalues of 0.9 and 1.0, corresponding roughly to collagen aligned within 18 deg of the circumferential axis (sin²(18 deg) = 0.1). That number was based on the observed circumferential alignment of collagen fibers in the vessel wall but is an estimate and could be modified to provide a better match to the experimental data. In fact, the collagen and elastin fiber orientations within the z–θ plane could also be treated as fitting parameters, which would likely improve the model fit, but we chose to use the best estimate from structural data rather than introduce further flexibility to an already highly parameterized model. Finally, the Fung-type model of fiber mechanics (Table 1—Eq. (3)) could be replaced with a recruitment model (e.g., Ref. [70]), which would provide an alternative mechanism to capture the nonlinear behavior associated with fiber waviness [71] and might provide a better fit of the experimental data. All of these modifications are possible and could be implemented as additional data emerge about the arrangement and properties of the components of the arterial wall.

In summary, a microstructurally based multiscale model of prefailure and failure behaviors was able to match the experimentally measured properties of the healthy porcine ascending aorta in four different loading configurations and two different directions, and it was successful when applied to experiments in the literature that were not used during the fitting and specification project. This model could provide new insight into the failure mechanisms involved in aortic dissection and could be incorporated into patient-specific anatomical models, especially if model parameters associated with specific patients or patient groups can be obtained.