The Bonding Situation in Metalated Ylides

Abstract

Quantum chemical calculations have been carried out to study the electronic structure of metalated ylides particularly in comparison to their neutral analogues, the bisylides. A series of compounds of the general composition Ph₃P−C−L with L being either a neutral or an anionic ligand were analyzed and the impact of the nature of the substituent L and the total charge on the electronics and bonding situation was studied. The charge at the carbon atom as well as the dissociation energies, bond lengths, and Wiberg bond indices strongly depend on the nature of L. Here, not only the charge of the ligand but also the position of the charge within the ligand backbone plays an important role. Independent of the substitution pattern, the NBO analysis reveals the preference of unsymmetrical bonding situations (P=C−L or P−C=L) for almost all compounds. However, Lewis structures with two lone‐pair orbitals at the central carbon atom are equally valid for the description of the bonding situation. This is confirmed by the pronounced lone‐pair character of the frontier orbitals. Energy decomposition analysis mostly reveals the preference of several bonding situations, mostly with dative and ylidic electron‐sharing bonds (e.g., P→C⁻−L). In general, the anionic systems show a higher preference of the ylidic bonding situations compared to the neutral analogues. However, in most of the cases different resonance structures have to be considered for the description of the “real” bonding situation.

Introduction

Since the first synthesis of an ylide and their use in Wittig‐type reactions these compounds have been applied in a variety of important reactions, for example, for natural product synthesis.1 The most important class of ylides contains phosphorus ylides (P‐ylides). Their electronic structure has mostly been described by two canonical structures—ylene A and ylide A′ (Figure 1 A). Although computational studies have shown that the contribution of the ylenic structure is minimal, as it requires (d–p)π interaction with the d orbitals at the phosphorus atom, which are too high in energy,2 the canonical structure A′′ with a donor–acceptor interaction between the phosphorus and carbon atoms has found renewed interest.3 The importance of this structure was particularly demonstrated for the description of bisylides,4 above all carbodiphosphoranes (CDPs).5 The unique electronic structure of these compounds has been studied in detail in recent years,6 but is still under debate.7 As for ylides, it has been shown that CDPs cannot be described as heterocumulenes. Instead the central carbon atom features two lone pairs of electrons, which leads either to their description as ylide B′ or as divalent carbon compound with the carbon atom in the formal oxidation state zero (carbone B′′)6d and donor–acceptor interactions between the phosphine and the central carbon atom (Figure 1 B).6 The high electron density and the availability of two lone pairs at the central carbon atom suggest new and unusual ligand properties for the CDPs and related ylidic compounds. In the case of CDPs, initial studies have proven their unique reactivity, which makes them highly attractive as carbon bases. For example, hexaphenylcarbodiphosphorane was found to undergo adduct formation with small molecules, such as CO₂, GeCl⁺, or BH₃,8 or can be used as a ligand in transition‐metal complexes.9 The carbone character of the CDPs was also transferred to other L→C←L′ systems,10 such as carbodicarbenes,11, 12 Ph₃P−C−CO,6 or the heavier Group 14 homologues EL₂ (E=Si–Pb).13

Figure 1.

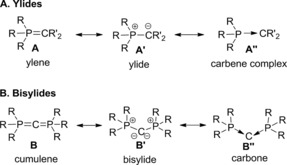
Resonance structures of the P‐ylides and bisylides.

Very recently, we became interested in the properties of metalated P‐ylides [i.e., (R₃P−C−L)⁻M⁺] and their use as potent donor ligands.14 First studies on the isolated metalated ylide [Ph₃P−C−SO₂Tol]Na (1) revealed its unique reactivities and strong donor properties, which for example led to acylation instead of Wittig‐type reactions with aldehydes or the stabilization of borenium cations.15 In a structural sense, metalated ylides—which are also called yldiides—can be regarded as the monoanionic congeners of bisylides, generated by replacement of one phosphine ligand PR₃ (in B′′, Figure 1 B) by an anionic substituent. Consequently, compound 1 showed analogous structural properties to the CDPs, that is, a short P−C bond, a large (but smaller than 180°) P‐C‐L angle and two lone pairs of electrons at the central carbon atom.14 Because of these similarities, we became interested in a detailed study on the electronic structure and bonding situation in metalated ylides of the type Ph₃P−C−L, especially in comparison to the well‐studied CDP 9 and the related bisylides (Figure 2). Our investigations particularly addressed two central questions: how does 1) the nature of the substituent L (anion stabilization vs. charge delocalization) and 2) the total charge of the molecule (neutral vs. anionic) influence the electronics and bonding situation in the system? In order to answer these questions, the ylidic compounds Ph₃P−C−L with the neutral and anionic ligands L depicted in Figure 2 were chosen. Whereas the systems 2, 4, and 6–8 address the influence of the substituent, compounds 1, 3, and 5 are the neutral equivalents to compounds 2, 4, and 6 and thus address the impact of the total charge. The carbodiphosphorane 9 was used for comparison reasons.

Figure 2.

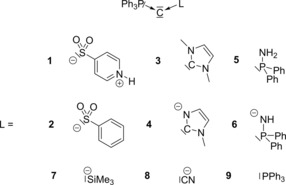
Investigated compounds (moieties L with a net negative charge lead to a negatively charged molecule; the donor lone pair is given for all ligands).

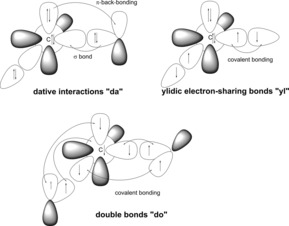
In principal, nine different resonance structures are feasible for the description of the bonding situation in these compounds. These structures result from the different interactions between the central carbon atom, the ligand L, and PPh₃, respectively. Here, either a dative bond (“da”≙C←L), an ylidic electron‐sharing bond (“yl”≙C⁻−L⁺), or a double bond (“do”≙C=L) may be present (Figure 3).16 Double bonds were also included, which—depending on the substituents—can either arise from classical p_π–p_π interactions (e.g., the ligands CN⁻ or NHC) or may arise from negative hyperconjugation effects into low lying σ* orbitals (e.g., the ligands PR₃, SiMe₃). Due to the unsymmetrical substitution pattern at the carbon atom also unsymmetrical bonding situations have to be considered. To evaluate these different structures, we analyzed the molecular orbitals, charges, natural bond orbitals (NBOs), and dissociation energies of these compounds and performed a detailed energy decomposition analysis (EDA). Here we report our findings.

Figure 3.

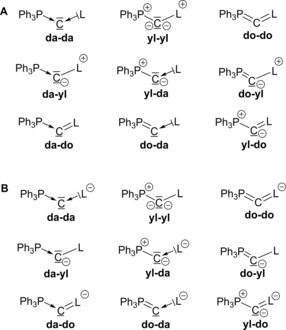
A) Possible bonding situations in bisylides (da=dative bond, yl=ylidic electron‐sharing bond, do=double bond). B) Possible bonding situations in metalated ylides. For B) the whole molecule is negatively charged. Dative bonds are constructed of paired electrons, the fragments are in singlet states, ylidic electron‐sharing bonds are constructed of fragments that are radicals, and double bonds are constructed of fragment in triplet states (compare Figure 7).

Methods

Geometry optimizations without symmetry constraints were carried out with the Gaussian 09 program package17, 18 at the BP8619/def2‐TZVP20 level of theory with Grimme's D3 dispersion correction with Becke–Johnson damping.21 Stationary points were characterized as minima by calculating the Hessian matrix analytically at this level of theory.22 Thermodynamic corrections and Kohn–Sham orbitals were taken from these calculations. The standard state for all thermodynamic data is 298.15 K and 1 atm. Single‐point energies at the BP86/def2‐TZVP‐optimized geometries were calculated with the MP223 method and with the ADF program package at the BP86/TZ2P level. MP2 energies were also calculated with inclusion of the spin‐component‐scaled (SCS) correction proposed by Grimme.24 The NBO25 analyses were carried out with the internal module of Gaussian 09 at the BP86/def2‐TZVP level of theory.

The EDA‐NOCV calculations were carried out with the program package ADF2016.101.26 The BP86/def2‐TZVP geometries were used. BP86 was chosen with uncontracted Slater‐type orbitals (STOs) as basis functions.27 The latter basis sets for all elements have triple‐ζ quality augmented by two sets of polarization functions (ADF basis set TZ2P). Core electrons (i.e., 1s for second‐ and [He]2s2p for third‐row atoms) were treated by the frozen‐core approximation. This level of theory is denoted BP86/TZ2P. An auxiliary set of s, p, d, f, and g STOs was used to fit the molecular densities and to represent the Coulomb and exchange potentials accurately in each SCF cycle.28 Scalar relativistic effects were incorporated by applying the zero‐order regular approximation (ZORA) in all ADF calculations.29

The interatomic interactions were investigated by means of an energy‐decomposition analysis (EDA) developed independently by Morokuma30 and by Ziegler and Rauk31 in conjunction with the natural orbitals for chemical valence (NOCV).32 The bonding analysis focuses on the instantaneous interaction energy ΔE _Int of the bonds A−B, A−C and B−C between the three fragments A, B, and C in the particular electronic reference state and in the frozen geometry of ABC. The interaction is divided into three main components [see Eq. (1)].

$${\displaystyle \Delta E{}_{\mathrm{Int}}=\Delta E{}_{\mathrm{elstat}}+\Delta E{}_{\mathrm{Pauli}}+\Delta E{}_{\mathrm{orb}}}$$ (1)

The term ΔE _elstat corresponds to the quasi‐classical electrostatic interaction between the unperturbed charge distributions of the prepared atoms and is usually attractive. The Pauli repulsion ΔE _Pauli is the energy change associated with the transformation from the superposition of the unperturbed electron densities ρ _A+ρ _B+ρ _C of the isolated fragments to the wavefunction Ψ=NÂ[Ψ ^A Ψ ^B Ψ ^C], which properly obeys the Pauli principle through explicit antisymmetrization (Â operator) and renormalization (N=constant) of the product wavefunction.26a The term ΔE _Pauli comprises the destabilizing interaction between electrons of the same spin on either fragment. The orbital interaction ΔE _orb accounts for charge transfer and polarization effects.33 It is calculated in the final step of the energy partitioning analysis when the Kohn–Sham orbitals relax to their optimal form.

The NOCV method makes it possible to identify those orbitals of a fragment, which contribute most to the bond formation. The NOCVs are defined as the eigenvectors of the diagonalized deformation density matrix, which gives the change in the electron density Δρ(r) that is associated with the bond formation. The total differential density Δρ(r) can be decomposed into individual contributions Δρ_k(r), which can be expressed over pairs of NOCVs ϕ _−k ϕ_k, which are weighted by the eigenvalues λ_k, which come from the diagonalized deformation density matrix [Eq. (2)].

$${\displaystyle \Delta \rho \left(r\right)=\Sigma \Delta \rho {}_k\left(r\right)=\Sigma \lambda {}_{\mathrm{k}}[-\phi {}^2{}_{-k}\left(r\right)+\phi {}^2{}_k\left(r\right)]}$$ (2)

The total orbital interaction term ΔE _orb may now be expressed in a similar fashion by contributions in terms of the eigenvalues of the NOCVs [Eq. (3)]:

$${\displaystyle \Delta E{}_{\mathrm{orb}}=\Sigma \Delta E{}_{\mathrm{orb}\left(\mathrm{k}\right)}=\Sigma \lambda {}_k[-F{}^{\mathrm{TS}}{}_{-k,-k}+F{}^{\mathrm{TS}}{}_{k,k}]}$$ (3)

The terms −F ^TS _−k,−k and +F ^TS _k,k in Equation (3) are the diagonal transition state Kohn–Sham matrix elements corresponding to NOCVs with the eigenvalues −λ_k and λ_k, respectively_.

To obtain the bond dissociation energy (BDE) D _e (by definition with opposite sign to ΔE), the preparation energy ΔE _prep, which gives the relaxation of the fragments into their electronic and geometrical ground states, must be added to ΔE _Int [Eq. (4)].

$${\displaystyle \Delta E(=-D{}_{\mathrm{e}})=\Delta E{}_{\mathrm{Int}}+\Delta E{}_{\mathrm{prep}}}$$ (4)

Further details on the EDA26 and the EDA‐NOCV34 method and their application in the analysis of chemical bonds can be found in the literature.35 Cartesian coordinates and total energies of all compounds discussed in the text are available in the Supporting Information.

Results and Discussion

Geometries and energies

The optimized geometries of compounds 1–9 at the BP86+D3(BJ)/TZVP level are shown in Figure 4. The most important structural parameters are given in Table 1 together with the experimental values of compounds 2 and 9. The calculated geometry of compound 2 is in good agreement with the experimental structure of the tolyl substituted yldiide, obtained from X‐ray diffraction analysis (e.g., P‐C‐S angle: 125.0° compared to 124.3(1)°). It is therefore assumed that the structures for compounds 1 and 3–8, which have not been synthesized yet, are valid as well. Although the P‐C‐P angle of compound 9 is slightly smaller than in the crystal structure (122.2 vs. 131.7(3)°),36 we consider this to be an effect of overestimated dispersion effects in BP8637 and the very shallow bending potential.

Figure 4.

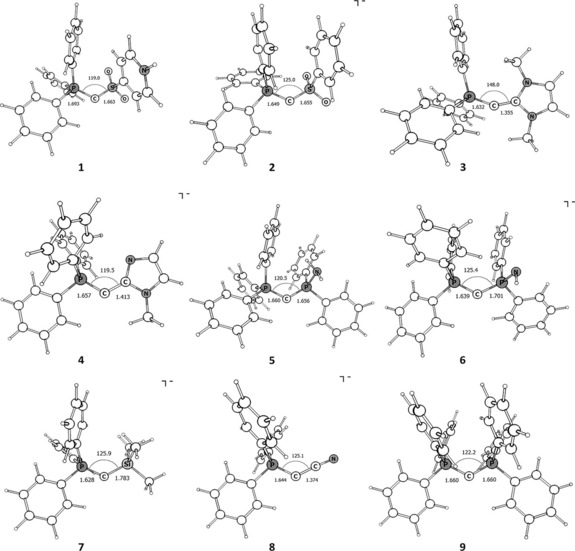
Optimized geometries (bond lengths in [Å], angles in [°]) at the BP86+D3(BJ)/TZVP level of compounds 1–9.

Table 1.

Overview of the bond lengths and angles at the BP86+D3(BJ)/TZVP level. Experimental values are given in brackets.

	L	P‐C‐L [°]	P−C [Å]	C−L [Å]
1	SO2 pPyH	119.0	1.693	1.663
1′	SO2 oPyH	117.5	1.685	1.639
1′′	SO(OH)Py	123.8	1.670	1.573
2	SO2Ph−	125.0 [124.3(1)]	1.649 [1.646(2)]	1.655 [1.626(2)]
3	IMe	148.0	1.632	1.355
4	IMe−	119.5	1.657	1.413
5	PPh2NH2	120.5	1.660	1.656
6	PPh2NH−	125.4	1.639	1.702
7	SiMe3 −	125.9	1.629	1.783
8	CN−	125.1	1.644	1.375
9	PPh3	122.2 [(131.7(3)]	1.660 [1.632(5)]	1.660 [1.638(5)]

It is interesting that the P−C bond length in compounds 1–9 vary significantly (from 1.629 to 1.693 Å) depending on the ligand L. Generally, the P−C bond becomes shorter in the anionic systems compared to the neutral compounds, with the exception of the ligand IMe⁻ (IMe=1,3‐dimethylimidazol‐2‐ylidene) in compound 4, which we will address later. Especially impressive is the shortening of the P−C bond by 44 pm for compound 2 compared to compound 1, thus already suggesting that the introduction of a negative charge also has an important impact on the bonding situation between the phosphorus and carbon atoms.

Naturally, the C−L bond lengths strongly depend on the nature of the donor atom in L. However, some interesting trends can be seen in the related anionic and neutral congeners. In case of the IMe‐functionalized compound 3 and its anionic congener (L=IMe⁻) 4 as well as in the aminophosphine‐substituted systems 5 and 6 with the corresponding iminophosphoryl moiety, the C−L bonds become slightly larger by going from the neutral to the anionic compound. In contrast, the opposite trend is observed for the sulfonyl‐substituted compounds 1 and 2. It should be noted that for the former neutral compounds 3 and 5, the positive charge is located in close proximity to the donor atom, whereas for the sulfonyl moiety in compound 1 the positive charge is shifted into the backbone of the ligand. This suggests that the position of the charge plays an important role. Indeed, shifting the protonated pyridyl unit into the ortho position (i.e., the positive charge in β position to the sulfur donor atom; compound 1′) leads to a shortening of the C−L bond, which is even more pronounced when protonating the oxygen atom of the sulfonyl moiety (i.e., positive charge in α position to the sulfur donor atom; compound 1′′) instead of the pyridyl moiety in compound 1 (Table 1). Generally, the calculated C−L bond lengths are rather in the range of double than of single bonds, suggesting significant double‐bond character despite the acute angles between 119.0 and 148.0° (see the bond lengths according to Ref. 38: C−S=178, C−P=186, C−C=150, C−Si=191 pm; C=S=161, C=P=169, C=C=134, C=Si=174 pm).

All calculated compounds feature bent P‐C‐L structures with angles strongly deviating from an ideal 180° angle in a cumulene‐like structure with a P=C=L linkage. The P‐C‐L angles are similar to those calculated for carbodiphosphoranes that have recently been investigated by Frenking et al.6b The IMe‐functionalized compound 3 exhibits the largest angle (148.0°), which is considerably larger than those of all other compounds (117.5–125.9°). This hints towards a more pronounced double‐bond character in the P‐C‐L linkage of compound 3 compared with all other compounds. This is also in line with the shortening of the P−C bond when going from compound 4 to compound 3 (see above), because the larger angle in compound 3 should also result in an increased double‐bond character. For the other compounds, the P‐C‐L angle does not significantly change upon introduction of the negative total charge. No obvious trend between yldiides and bisylides can be seen here.

Furthermore, we compared the P‐C‐L bending potentials (Table 2) of compounds 1–8 with CDPs and carbodicarbenes.39 The potential well is only slightly deeper for the anionic yldiides than for the neutral bisylides and carbodicarbenes (3.3 to 8.9 kcal mol⁻¹ vs. 0 to 7.7 kcal mol⁻¹).40 It is therefore concluded that these compounds do not distort as easily to their linear forms as, for example, carbon suboxide (O=C=C=C=O). However, this also might result from including dispersion effects, which presumably also explains the relatively high bending potential for the CDP 9. Altogether, the C−P and C−L bond lengths strongly depend on the nature of the substituent and the total charge of the compound (as well as the position of the charges in the ligands), whereas the P‐C‐L angle is only marginally influenced by the ligands.

Table 2.

Calculated relative energies at the BP86+D3(BJ)/TZVP level (in [kcal mol⁻¹]) of compounds 1–9 with different bending angles.

Compound	L	eq[a]	150°	180°
1	SO2PyH	0.0	1.5	5.5
2	SO2Ph−	0.0	3.8	8.9
3	IMe	0.0	0.0	3.8
4	IMe−	0.0	3.7	7.1
5	PPh2NH2	0.0	4.2	6.1
6	PPh2NH−	0.0	4.1	8.2
7	SiMe3 −	0.0	1.6	3.3
8	CN−	0.0	1.4	3.3
9	PPh3	0.0	4.8	7.7

[a] The equilibrium energies correspond to the angles in Table 1.

Next, we investigated the strength of the carbon−ligand bonds. To this end, we calculated the bond dissociation energies (BDEs) according to the following (spin‐symmetry forbidden) Equation (5).

$${\displaystyle \mathrm{C}\left(\mathrm{PPh}{}_3\right)\mathrm{L}\to \mathrm{C}\left({}^3\mathrm{P}\right)+\mathrm{PPh}{}_3+\mathrm{L}}$$ (5)

The results are summarized in Table 3.41 Due to the already mentioned impact of the ligand L on the C−P bond length (see above), we refrain from interpretation of estimated C−L bond strengths because this requires the assumption of constant C−P bond strengths, which is certainly not correct for the compounds 1–9. Thus, only total dissociation energies (disruption of the C−P and C−L bond) will be discussed. In general, one can expect a decreasing bond strength with a decreasing bond order, that is, in the series BDE(C=L)>BDE(C−L)>BDE(C←L). In general, the investigated compounds 1–8 exhibit dissociation energies comparable to similarly sized bisylides, such as the carbodiphosphorane 9, hinting to similar bonding situations. Particularly, compounds 4 and 7 exhibit high dissociation energies (170.8 and 176.9 kcal mol⁻¹, respectively). However, the bond strengthening is not a general phenomenon for the anionic systems. For example, the bond dissociation energy for the cyanido‐functionalized compound 8 is very similar to the isoelectronic carbonylcarbophosphorane Ph₃P−C−CO, (144.7 vs. 145.4 kcal mol⁻¹, respectively).6b Similarly, introduction of a negative charge into the compounds 3 and 4 as well as 5 and 6 increases the dissociation energy significantly (>15 kcal mol⁻¹), whereas a reverse trend is seen for compounds 1 and 2. Here, the BDE decreases by 6 kcal mol⁻¹ in the anionic compound 2, which agrees well with the changes in the bond lengths (see above). We suppose once again that this effect is strongly dependent on the location of the positive charge, which of course influences the stability of the formed fragments. It is interesting to note that the highest BDE is not found for the IMe‐functionalized compound 3, which showed the largest P‐C‐L angle as well as short P−C and C−L bond lengths, and thus presumably the highest double‐bond character (Table 1), but for compound 7 with a strong σ‐donating ligand. This—together with the low bending potential—suggests that the P‐C‐L angles do not provide any significant information about the bond strengths in these types of compounds. The small differences in the angles also suggest that either all compounds exhibit similar bonding situations or that the angle is little meaningful regarding the bonding situation because sterics and dispersion effects might surpass orbital interactions within the P‐C‐L linkage.

Table 3.

Dissociation energies D _e and energies including thermal and vibrational contributions D ₀ ²⁹⁸ for the dissociation reaction C(PPh₃₎L→C(³P)+PPh₃+L_. Geometries were optimized at the BP86+D3(BJ)/TZVP level of theory.

Compound	L	TZVP		MP2		SCS‐MP2
		D e [kcal mol−1]	D 0 298 [kcal mol−1]	D e [kcal mol−1]	D 0 298 [kcal mol−1]	D e [kcal mol−1]	D 0 298 [kcal mol−1]
1	SO2PyH	150.2	146.4	155.3	151.5	141.3	137.5
2	SO2Ph−	150.1	146.7	149.3	145.9	134.5	131.1
3	IMe	169.6	166.8	162.5	159.7	150.2	147.4
4	IMe−	189.6	186.6	183.1	180.1	170.8	167.9
5	PPh2NH2	161.3	157.6	160.4	156.6	146.0	142.2
6	PPh2NH−	173.0	169.5	174.1	170.6	159.4	155.8
7	SiMe3 −	188.6	185.7	189.1	186.2	176.9	174.0
8	CN−	167.7	165.3	156.2	153.9	144.7	142.4
9	PPh3	159.9	156.2	158.7	155.4	142.4	139.1

Bonding analysis

At first, we examined the molecular orbitals of the compounds. The two highest canonical molecular orbitals, HOMO and HOMO−1, are shown exemplarily for compounds 1, 3, and 8 in Figure 5. These molecular orbitals of compound 1 are mainly localized at the central carbon atom and indicative for two lone‐pair orbitals, one of σ and one of π symmetry, which means that the interpretation of two “localized” pairs of electrons at the central carbon atom is certainly valid. This is also the case for the systems 2, 5–7, and 9 (see the Supporting Information). For the IMe‐ and cyanido‐functionalized compounds 3, 4, and 8, however, the situation is somewhat different. In compounds 3 and 4 the molecular orbitals suggest the presence of only one lone‐pair orbital at the central carbon atom (HOMO−1), whereas the other “lone pair” is delocalized over the carbene ligand. Thus, the HOMO represents an antibonding combination with the π system of the IMe moiety. This indicates a double‐bond character in the C−C bond or a dative bond with strong π‐back‐bonding. The molecular orbitals of compound 8 even show the delocalization of both lone pairs into the CN ligand. Both, the HOMO and the HOMO−1 represent non‐bonding combinations with the π system of the CN moiety, whereas the HOMO−3 and HOMO−5 are the corresponding bonding analogues. Of course, the HOMO and the HOMO−1 of all other compounds also show small contributions of other atoms, which can be attributed to negative hyperconjugation effects rather than π delocalization as found for compounds 3 and 8. This is, for example, also the case for the sulfonyl‐substituted system 1 (Figure 5).

Figure 5.

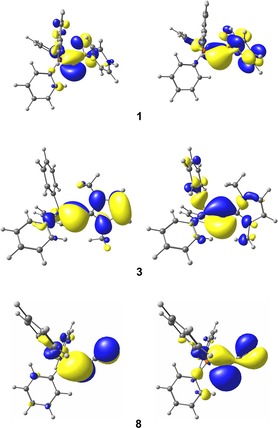
HOMO (left) and HOMO−1 (right) of compounds 1, 3, and 8 at the BP86/TZVP level of theory.

The bonding situation in compounds 1–9 was next investigated by NBO analysis. The numerical results of these analyses are given in Table 4. Both the regular NBO and the enforced NBO analysis (with two lone pairs fixed at the central carbon atom in accordance with the molecular orbitals) were performed. Independent of the method the residual densities stayed around 3 % for either option, indicating that both bonding situations are suitable for the description of the electron distribution within the molecule. As shown in Table 4, the calculated negative charge at the central carbon atom differs significantly depending on the ligand L and varies between q(C)=−0.96 in the IMe‐substituted compound 3 and q(C)=−1.50 in the silyl system 7. Most interestingly, however, a comparison of the neutral and anionic compound pairs (i.e., compounds 1 and 2, 3 and 4, and 5 and 6) shows that the negative charge of the central carbon atom does not change significantly upon introduction of the negative charge. The sulfonyl systems only show a small increase from q(C)=−1.13 to −1.29 upon introduction of the negative charge. Because the charges of the adjacent atoms remain unchanged (1.50 to 1.48 for P and 2.07 to 2.07 for S), the major part of the negative charge must ultimately be delocalized mostly within the backbone of the ligands, thus also reflecting the strong electron‐withdrawing ability of the sulfonyl moiety. For compounds 3 and 4 as well as 5 and 6 this effect is even more pronounced, because neither the charge of the central carbon atom nor the charge of the donor atoms experience a significant change (q(C)=−0.96 to −0.97, and q(C)=−1.43 to −1.42, for compounds 3 and 4 as well as 5 and 6, respectively). Instead, the most pronounced change of the negative charge is found for the nitrogen atoms in the ligand backbone (compare q(N)=−0.33 and −0.54 for compounds 3 and 4, respectively, and q(N)=−1.15 and −1.33 for compounds 5 and 6, respectively).

Table 4.

NBO results (BP86/TZVP) for compounds 1–9. E refers to the atom of the ligand L that is adjacent to the central carbon atom. Partial charges q and orbital populations are given in electrons. Values in parenthesis correspond to Lewis structures with two lone pairs at the central carbon atom, which have been enforced in the NBO calculation.

Compound	L	Charges			WBI[a]		LP(C)σ [b]		LP(C)π	Residual density
		q(C)	q(P)	q(E)	C−P	C−E	Occ[c]	[%s‐Orbital]	Occ	[%]
1	SO2PyH	−1.13	1.50	2.07	1.23	1.08	1.72	46.5	1.22	3.3
2	SO2Ph−	−1.29	1.48	2.07	1.42	1.13	1.64	42.8	(1.45)	3.2 (3.2)
3	IMe	−0.96	1.51	0.33	1.37	1.54	1.55	16.5	(1.31)	2.9 (3.2)
4	IMe−	−0.97	1.47	0.26	1.40	1.34	1.68	35.8	1.26	3.3
5	PPh2NH2	−1.43	1.55	1.68	1.32	1.34	1.62	36.7	(1.49)	3.3. (3.3)
6	PPh2NH−	−1.42	1.51	1.70	1.45	1.13	1.62	36.2	(1.46)	3.2 (3.1)
7	SiMe3 −	−1.50	1.45	1.60	1.58	1.01	1.59	41.0	(1.43)	2.8 (2.8)
8	CN−	−0.99	1.46	0.18	1.43	1.41	(1.57)	(34.9)	1.33	3.9 (3.6)
9	PPh3	−1.39	1.55	1.55	1.32	1.32	1.61	38.6	(1.49)	3.4 (3.4)

[a] WBI=Wiberg bond indices. [b] LP=lone pair. [c] Occ=occupancy.

The second main observation from the NBO analysis concerns the charges of the donor atoms of the ligand L. Only the carbon‐based donor ligands IMe, IMe⁻, and CN⁻ exhibit small positive charges between q(E) 0.18 and 0.33. This suggests that these ligands are capable to a more pronounced π‐back‐bonding due to the orbital orientations of the adjacent carbon atom, which reduces the negative charge at the central carbon atom as well as the positive charge of the ligand bridge head atom. This is particularly interesting for the cyanido ligand, which—despite of its negative charge—behaves similar to the neutral compounds with L=IMe or CO.6b The increased contribution of π‐back‐bonding in the carbon‐based donor ligands is also in line with the π delocalization observed in the molecular orbitals of these compounds (see above). In contrast, the silyl, sulfonyl, and phosphorus ligands show high positive charges at the donor atom of L and a high negative charge at the central carbon atom. Consequently, these ligands strongly donate electron density towards the central carbon atom (strong σ donors), but are only poor π acceptors. The negative partial charge at the carbon atom together with the positive charges of q(P) and q(E) nicely reflect an ylidic bonding situation, although the partial and formal charges do not necessarily correlate with each other.

The Wiberg bond indices (WBI) of the C−P bonds differ significantly depending on the ligand L.42 This is in line with the aforementioned differences in the C−P bond lengths. Accordingly, the decrease of the C−P bond length from compound 1 to 2 and from compound 5 to 6 leads to a higher WBI (1.23 to 1.42, and 1.32 to 1.45, respectively), whereas the increase of the C−P bond length from compound 3 to 4 leads to a slightly lower WBI (1.40 to 1.37). The highest WBI of the C−P bond is observed for the trimethylsilyl (TMS)‐functionalized system 7 with a value of 1.58, which agrees well with the high dissociation energy in this system. Assuming a dative interaction between the PPh₃ ligand and the central carbon atom, this may be explained by stronger π‐back‐bonding due to the higher negative charge at the carbon atom connected with the strong σ‐donor properties of the silyl ligand. An alternative explanation would be the higher Coulombic attraction in case of an ylidic P⁺−C⁻ bond.

The regular NBO analysis of all compounds delivers the Lewis structures shown in Figure 6. In most cases the NBO calculations revealed unsymmetrical bonding situations with a central P−C=L or P=C−L linkage, whereas for compounds 1 and 4 a P−C−L linkage with single bonds was obtained. It should be noted that the NBO analysis cannot distinguish between dative and electron‐sharing bonds. Thus, a single bond can also be interpreted as a dative bond and a double bond can also be interpreted as a dative bond with strong π‐back‐bonding. Figure 6 only depicts the interpretation as electron‐sharing bonds. It is also worth mentioning that enforced structures with two lone pairs of electrons at the central carbon atom (i.e., compounds 2, 3, and 5–9) showed equally high residual densities suggesting that the sole interpretation of the Lewis structures given by the NBO analysis is too simple (see Table 4). This is also indicated by the high polarization of the C−P π bonds towards the C end, which is consistently above 80 %. Here, one always has to keep in mind that the transition between a true lone pair and a strongly polarized double bond is gradual. Similarly, for compound 5, the π bond between C and PPh₂NH₂ is strongly polarized towards the C atom with 88.9 %. The only “true” double bond is found in compound 3, where the C−C bond is polarized towards the central carbon atom with only 61.9 %. Nevertheless, based on the residual density (r.d.), the Lewis structure of compound 3 with an ylidic C−C single bond (3.2 % r.d.) as well as the structure with a doubly bonded P=C=C linkage (3.0 % r.d.) seem to be equally accurate to describe the bonding situation than the structure shown in Figure 6.

Figure 6.

Lewis structures according to the NBO analysis (note that single bonds may also be dative bonds and double bonds can also be considered as dative bonds with strong π‐back‐bonding).

Thus, simple NBO analysis is ambiguous in the description of the bonding situation. Compared to the C−P π bond, the σ bond does not undergo significant changes upon variation of L (55–60 % polarization towards the carbon end, s character of about 30 %), which is surprising regarding the changes in the bond lengths and the WBI. In contrast to the P−C σ bond, the C−L σ bond shows much bigger differences depending on the nature of L. Although the s character does not change considerably when going from a neutral to an anionic compound, the bond polarization varies significantly. For compounds 1–4 and 8, a non‐polarized σ bond was calculated. In contrast, the aminophosphane 5, the phosphaneamide 6, and the silyl compound 7 show a bond that is at least slightly polarized towards the central carbon atom (58.2, 59.4, and 70.4 % respectively). This is consistent with the high charges found at the central carbon atom.

It should be noted that in contrast to carbodiphosphoranes, carbon suboxide, and carbodicarbenes, the s character of the σ lone pair is always quite pronounced (>35 %) except for compound 3 (16.5 %), which is most likely due to the more acute angle for these compounds.6b It is also worth mentioning that the σ lone pair always possesses a higher occupancy (>1.5 electrons) than the π lone pair, if the latter is present. This is particularly interesting for the use of these compounds as donor ligands in metal complexes, presumably leading to a stronger σ donation and a weaker π donation. Especially compounds 2 and 5–7 have a high occupation for the π lone pair (>1.4 electrons), hinting towards their significant double lone pair character, whereas compounds 1, 3, 4, and 8 show lower occupations (1.2–1.3 electrons).

Finally, an extensive energy decomposition analysis (EDA) of all compounds was performed by using the ADF program package. In this method, the electronic structure of molecular fragments is compared with the final electronic structure of the molecule. The quality of different fragmentation possibilities of a molecule can then be estimated by means of the orbital interaction term ΔE _orb. This term reflects the degree of how much the orbitals of the fragments have to relax compared to the orbitals in the whole molecule. Thus, a low absolute ΔE _orb value indicates that the fragment orbitals match the molecular orbitals well, that is, that the electronic structure of the fragments is similar to the electronic structure of the final molecule. Consequently, the best fragmentation pattern is the one with the lowest ΔE _orb value. This method has been found very useful in recent work to distinguish between electron‐sharing bonds A−B and dative bonds A→B.43 As outlined in Figure 3, nine different fragmentation patterns are possible for all calculated compounds. Figure 7 exemplarily depicts the orbital interactions of the three symmetric bonding modes (“da–da”, “yl–yl”, “do–do”) together with the occupations of the corresponding orbitals. The orbital occupations of the central carbon atom were chosen by chemical intuition. Except for the quintet state, double occupation of the 2s orbital was chosen. Earlier investigations have shown that a non‐occupied 2s orbital leads to hybridization and therefore donation from the occupied 2p orbitals into the 2s orbital. A doubly occupied 2s orbital represents the carbon ground state much better due to the energy difference between 2s and 2p orbitals. The p orbitals of the central carbon atom were occupied in such a way to allow for the bonding in the desired Lewis structures. For the unsymmetrical bonding modes, combinations of the interactions in Figure 7 were used. Thereby, the coordinate system was chosen in such a way that the dative bond always directly points towards the empty p orbital of the carbon atom, whereas the second bond points slightly between two orbitals. This arrangement was found to give the lowest ΔE _orb values compared to other orientations.

Figure 7.

Orbital occupations for two dative (“da”), two single ylidic electron‐sharing (“yl”), and two double (“do”) bonds.

A further criterion to estimate the importance of a resonance structure/fragmentation pattern is the preparation energy ΔE _prep. ΔE _prep is the energy which is required to “excite” the fragments from their electronic and geometric ground state to the state in the molecule. Thus, high ΔE _prep values indicate that the relaxed fragments are very different from the fragments in the molecules and hence only poorly reflect the electronic situation in the total molecule. Thereby, the BDE values given in Table 5 either correspond to a homolytic or heterolytic bond cleavage depending on the bonding mode. According to the procedure reported by Haaland, a rupture of a dative bond proceeds heterolytically, whereas the electron‐sharing single and double bonds are cleaved homolytically.44 This differentiation between homolytic and heterolytic bond dissociation results, for example, in high BDEs for the ylidic electron‐sharing bonds. This high BDE results from the formation of charged, radical fragments, which are naturally high in energy in gas‐phase calculations. The high BDE in turn leads to a lower preparation energy for the system [compare Eq. (2)], which thus seems to be favorable compared to other resonance structures. For example, the symmetric bisylidic bonding situation “yl–yl” in compound 1 shows a BDE of 594.8 kcal mol⁻¹ and a low ΔE _prep of only 15.9 kcal mol⁻¹ (Table 5). Alternatively, the heterolytic bond rupture would lead to a lower dissociation and higher preparation energy due to the additional electron transfer required to form the charged “yl” fragments in the molecule.

Table 5.

Results of the energy decomposition analysis for all possible fragmentation patterns of the molecules 1 and 2 (da=dative bond, yl=ylidic electron‐sharing bond, do=double bond), energies [given in kcal mol⁻¹] are taken from the ADF program package at the BP86/TZ2P level.

1 (SO2PyH)	da–da	do–do	yl–yl	yl–do	do–yl	da–yl	yl–da	da–do	do–da
ΔE Int	−172.8	−487.0	−613.3	−391.4	−388.5	−301.1	−306.2	−257.0	−259.2
ΔE Pauli	703.8	574.7	1064.5	955.4	929.5	828.1	760.7	776.5	697.1
ΔE elstat	−303.3	−379.4	−974.4	−656.3	−658.1	−541.5	−492.5	−369.0	−320.8
ΔE Orb	−573.2	−682.3	−703.4	−690.6	−659.9	−587.7	−574.5	−664.5	−635.5
ΔE prep(PPh3)	1.8	127.5	11.1	11.1	127.5	1.8	11.1	1.8	127.5
ΔE prep(L)	2.7	127.7	4.8	127.7	4.8	4.8	2.7	127.7	2.7
ΔE prep(C)	43.5	100.8	0.0	0.0	0.0	41.0	41.0	0.0	0.0
ΔE prep	48.1	356.0	15.9	138.8	132.2	47.6	54.8	129.5	130.1
BDE	125.0	125.0	594.8	249.6	251.8	251.8	249.6	125.0	125.0

2 (SO2Ph−)	da–da	do–do	yl–yl	yl–do	do–yl	da–yl	yl–da	da–do	do–da
ΔE Int	−168.7	−464.7	−507.9	−375.2	−277.1	−192.4	−305.3	−237.5	−252.3
ΔE Pauli	761.7	608.6	1107.7	1005.6	988.4	835.6	816.4	790.6	766.5
ΔE elstat	−336.3	−403.7	−870.9	−649.2	−594.0	−444.6	−486.1	−362.9	−365.4
ΔE Orb	−594.1	−669.6	−744.7	−731.7	−671.5	−583.4	−635.6	−665.2	−653.4
ΔE prep(PPh3)	0.0	122.0	12.9	12.9	122.0	0.0	12.9	0.0	122.0
ΔE prep(L)	3.0	112.6	4.2	112.6	4.2	4.2	3.0	112.6	3.0
ΔE prep(C)	43.5	100.8	0.0	0.0	0.0	41.0	41.0	0.0	0.0
ΔE prep	46.5	335.4	17.1	125.5	126.1	45.2	56.9	112.6	124.9
BDE	122.3	122.3	488.6	246.9	145.6	145.6	246.9	122.3	122.3

In this context, it is also important to distinguish between the electronic structure of the individual fragments prior to bond formation and after the bond is formed. A low preparation energy of the fragments is not necessarily a reliable indicator for the final nature of the chemical bond and the definition of Haaland may sometimes fail when it comes to distinguish between dative and electron‐sharing bonds. A striking example is tetrafluoroethylene F₂C=CF₂, which has a classical electron‐sharing C=C double bond. Rupture of the double bond in F₂C=CF₂ gives two CF₂ fragments in the ¹A₁ singlet state and a bond dissociation energy of D _e=73.3 kcal mol⁻¹, which is less than the BDE of the C−C single bond in F₃C−CF₃ (D _e=87.3 kcal mol⁻¹).45 A faithful description of the C=C double bond in F₂C=CF₂ is only found when the CF₂ fragments are considered in the ³B₁ triplet state, which requires a total preparation energy of 114.0 kcal mol⁻¹, but gives an intrinsic interaction energy of ΔE _int=187.3 kcal mol⁻¹ that is in agreement with the bond strength.45

Table 5 gives an overview of the results of the energy decomposition analysis of compounds 1 and 2. For the neutral compound 1, three fragmentation patterns were obtained with similarly low ΔE _orb and ΔE _prep values. These correspond to a “carbone‐like” structure with dative bonds between the carbon atom and PPh₃ as well as SO₂PyH (“da–da”), and two unsymmetrical bonding situations with a combination of an ylidic electron‐sharing single bond towards the PPh₃ and a dative bond towards the sulfonyl, and vice versa (“da–yl” and “yl–da”, respectively). All other fragmentation patterns possess by at least 50 kcal mol⁻¹ less favored orbital interactions and higher preparation energies. Sole exception is the electron‐sharing bonding mode “yl–yl”, which shows a low ΔE _prep value, but the highest ΔE _orb value in the whole series. Hence, the EDA for compound 1 suggests that the bonding situation is best described by three resonance structures, that is, the carbone structure and two structures with dative/ylidic bonds, thus indicating that the C−L and C−PPh₃ interactions possess a dative as well as an ylidic electron‐sharing bonding character (Figure 8). This is also consistent with the molecular orbitals (two lone pairs at the carbon atom) and the high negative charge at the central carbon atom, the WBI, and the NBO analysis.

Figure 8.

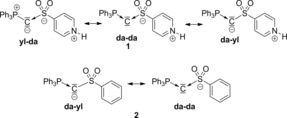
Most favored resonance structures for compounds 1 and 2 according to the EDA.

For the anionic compound 2, only two combinations show equally low ΔE _orb and ΔE _prep values, that is, 1) the carbone structure with dative bonds to both ligands and 2) the combination of a dative bond to PPh₃ and an ylidic electron‐sharing bond to the sulfonyl group (Figure 8). Thus, only these two structures seem to have a significant contribution for the description of the bonding situation. Consequently, by introduction of a negative charge in compound 1 to form compound 2 the C−S bond possesses a less pronounced dative character and a more pronounced ylidic electron‐sharing character (note that both the fragmentation patterns “yl–da” and “da–da” become less favorable). This can be explained by the stronger σ‐donating property of the anionic sulfonyl group and likewise by its weaker π‐accepting ability. This results in a stronger transfer of electron density towards the carbon atom, which is consistent with the higher negative charge calculated for the central carbon atom in compound 2 compared to compound 1 whereas the positive charges of the sulfur atoms are equally high (see the NBO analysis in Table 4). It is interesting to note that the total interaction energy ΔE _int between the carbon atom and the two ligands in the two most favored resonance structures of compound 2 only differs by 23 kcal mol⁻¹. This is in contrast to compound 1, where ΔE _int is much higher for the structures with an ylidic bond. The small difference in compound 2 results from the fact that the fragmentation pattern in both structures (i.e., “da–yl” and “da–da”) leads to the formation of charged fragments or radical species with a high contribution of electrostatic interactions and Pauli repulsion to the overall bonding situation. This is in contrast to compound 1, where the dative interaction (“da–da”) solely leads to neutral, diamagnetic fragments and thus to an overall smaller interaction energy.

The results of the EDA studies for compounds 3–9 are given in Table 6. Here, only the most favored fragmentation patterns are listed. Figure 9 shows the most favored Lewis structures obtained from the EDA. For more details, see the Supporting Information. For compound 3 with the carbene ligand, the combination of two double bonds is the only relevant description of the binding mode according to the ΔE _orb value. This was already suggested by the NBO analysis (see above) and is also in line with the large P‐C‐C bonding angle of 150°, which already suggests a pronounced allene‐like structure for compound 3 compared to other compounds with more acute angles. However, the high ΔE _prep value for this interaction suggests that although the orbital interaction is favorable, the electronic structure of the fragments is highly different to that in the final molecule. Together with the lone‐pair character of the HOMO in compound 3 (see above), this suggests that one also has to consider the unsymmetrical bonding modes with a dative bond to PPh₃ and either an ylidic electron‐sharing or a double bond to the carbene ligand despite their higher ΔE _orb values. Upon introduction of a negative charge into the ligand backbone, the unsymmetrical bonding modes again become more favorable. Although there is still a high contribution of the allene‐like structure with the lowest ΔE _orb value of −604.6 kcal mol⁻¹, the ylidic electron‐sharing bond to L shows an almost equally low ΔE _orb value of −618.5 kcal mol⁻¹, but requires a considerably lower preparation energy ΔE _prep. This suggests that this structure has a much more significant influence on the electronic structure, which is consistent with the smaller P‐C‐C angle in compound 4 compared to compound 3.

Table 6.

Results of the energy decomposition analysis for the most favored fragmentation patterns of compounds 3–8. Energies are given in kcal mol⁻¹.

	3 (IMe)			5 (PPh2NH2)
	“do–do”	“da–yl”	“da–do”	“da–da”	“da–yl”	“yl–da”
ΔE Int	−482.0	−352.7	−250.2	−181.4	−314.4	−316.3
ΔE Pauli	476.4	785.4	747.5	786.3	818.5	841.5
ΔE elstat	−380.4	−457.5	−307.7	−357.0	−548.9	−550.2
ΔE Orb	−578.0	−680.6	−690.0	−610.7	−584.0	−607.6
ΔE prep(PPh3)	128.1	0.9	0.9	1.0	1.0	11.9
ΔE prep(L)	91.4	10.1	91.4	4.2	10.2	4.2
ΔE prep(C)	100.8	41.0	0.0	43.5	41.0	41.0
ΔE prep	320.3	52.0	92.3	48.7	52.2	57.1
BDE	152.5	297.2	152.5	133.0	260.4	257.6

	4 (IMe−)			6 (PPh2NH−)
	“do–do”	“da–yl”	“da–do”	“da–da”	“da–yl”	“yl–da”
ΔE Int	−487.1	−232.6	−258.1	−190.5	−197.0	−328.2
ΔE Pauli	517.6	797.3	761.3	776.6	798.7	822.9
ΔE elstat	−400.0	−411.3	−367.3	−351.7	−437.6	−507.7
ΔE Orb	−604.6	−618.5	−652.0	−615.5	−558.2	−643.4
ΔE prep(PPh3)	127.4	0.7	0.7	0.3	0.3	14.3
ΔE prep(L)	75.3	7.6	75.3	3.2	3.8	3.2
ΔE prep(C)	100.8	41.0	0.0	43.5	41.0	41.0
ΔE prep	303.5	49.3	76.0	47.1	45.2	58.5
BDE	174.4	179.4	174.4	143.5	149.7	268.1

	7 (SiMe3 −)	8 (CN−)		9 (PPh3)
	“da–yl”	“do–do”	“da–yl”	“da–da”	“da–yl”
ΔE Int	−202.7	−526.3	−256.0	−170.6	−304.9
ΔE Pauli	680.2	509.4	753.6	770.4	820.1
ΔE elstat	−388.0	−396.4	−387.4	−341.4	−532.8
ΔE Orb	−494.9	−639.2	−622.2	−599.6	−592.2
ΔE prep(PPh3)	1.3	127.5	0.6	1.1	1.1
ΔE prep(L)	3.0	131.0	0.4	1.1	11.5
ΔE prep(C)	41.0	100.8	41.0	43.5	41.0
ΔE prep	45.3	359.2	42.1	45.7	53.6
BDE	155.3	161.5	211.4	124.9	249.5

Figure 9.

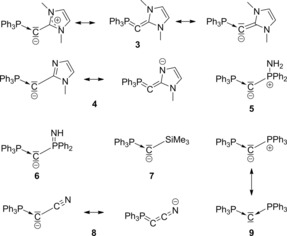
Lewis resonance structures according to EDA.

Furthermore, it is interesting to note—as already discussed above—that the bonding mode of the ligand L significantly affects the bond between the central carbon atom and the PPh₃ ligand. Overall, the N‐heterocyclic carbene (NHC)‐type ligands favor a C−C bond with significant double‐bond character and at the same time considerably increase the double‐bond character of the P−C bond. Here, the combination of a dative and a double bond (Ph₃P→C=L) is significantly disfavored (ΔE _orb=−652.0 kcal mol⁻¹) over the allene‐like structure. It is surprising that apparently the NHC ligand IMe, which—by itself—is a singlet carbene and a strong σ‐donor as well as a weak π‐acceptor ligand, prefers a triplet state to form a double bond rather than a singlet state to form a dative bond.

For both compounds 5 and 6 the structure with a dative bond to the PPh₃ and a electron‐sharing single bond to the phosphorus atom is the most important resonance structure, which is also consistent with the NBO analysis. Again, it should be noted that the introduction of a negative charge increases the importance of the ylidic electron‐sharing bond compared to other fragmentation patterns, which can clearly be deduced from the difference between the ΔE _orb value of this and other bonding modes. As such, the aminophosphane 5 shows only a preference of 26.7 kcal mol⁻¹ for the unsymmetrical bonding mode Ph₃P→C⁻−L, whereas in case of the anionic phosphanamide 6 this structure is preferred by 57.3 kcal mol⁻¹. This further confirms that the introduction of a negative charge into the molecule (i.e., the change from a bisylide to a metalated ylide) leads to a higher contribution of the ylidic electron‐sharing bond and thus to a lower importance of dative interactions.

As for compounds 5 and 6, the only relevant structure for the TMS‐functionalized compound 7 is the structure “da–yl” with an ylidic electron‐sharing single bond towards the ligand L. This is in line with the NBO charges, the molecular orbitals and the WBI. The high WBI for the P−C bond in compound 7 can be explained by the strong σ‐donor ability of the silyl ligand, which results in a stronger π‐back‐bonding to the phosphine ligand and a short P−C bond length.

For the cyanide‐substituted compound 8, both the combination of a dative bond to the PPh₃ group and an electron‐sharing single bond to the cyanide ligand (“da–yl”) and the all‐double‐bonded structure (“do–do”) are relevant. Although the former suggests that the negative charge is located at the central carbon atom, the latter favors the negative charge at the terminal nitrogen atom. The latter is also consistent with the high Wiberg bond index of 1.41 for the C−C bond as well as with the calculated NBO charges. However, the “da–yl” structure agrees with the NBO analysis, which favored a P=C⁻−C structure, in which the P=C bond can also be interpreted as a dative bond with a strong σ‐donor and π‐acceptor ligand.

Applying the unsymmetrical fragmentation pattern to the hexaphenylcarbodiphosphorane 9 also reveals two competing bonding modes. The carbone structure Ph₃P→C←PPh₃ possesses a low ΔE _orb value, which however, is also obtained for the unsymmetrical structure with a dative and an ylidic electron‐sharing single bond. It has to be kept in mind that due to symmetry reasons this does not mean that the bonds are truly different, but simply that both bonds have a significant ylidic electron‐sharing character. We would assume that in this case both notations have their validity, although for the most other discussed structures the most favored structure is the unsymmetrical bonding mode P→C⁻−L⁺ with an ylidic electron‐sharing single bond to L. The fact that the carbone structure and the P→C⁻−L⁺ bonding mode are similarly relevant for the description of compound 9, whereas the latter is more favored in compound 5, probably results from the fact that the aminophosphine ligand in compound 5 is more electron‐rich than PPh₃ and thus favors an electron‐sharing interaction.

Conclusion

An extensive computational analysis of bisylides and metalated ylides of the type Ph₃P−C−L was performed to study the impact of the substitution pattern and the total charge on the electronic structure as well as on the bonding situation in these compounds. The charge at the central carbon atom as well as the dissociation energies, bond lengths, and Wiberg bond indices strongly depend on the nature of the ligand L. Here, not only the charge of the ligand (L=anionic or neutral) but also the position of the charge within the ligand backbone and its distance from the donor atom play an important role. Despite their negative total charge, metalated ylides do not necessarily feature the highest negative charges at the central carbon atom. The NBO analysis mostly reveals unsymmetrical bonding situations—above all P=C−L and P−C=L linkages—independent of the substitution pattern and the total charge of the molecule. However, Lewis structures with two lone‐pair orbitals enforced at the carbon atom and two single bonds to the ligands show equally high residual densities. Thus, simple NBO analysis is not suitable to differ between different bonding situations in these types of compounds. The energy decomposition analysis shows also no clear‐cut picture on the bonding situation. In general, several fragmentation patterns are feasible, all showing equally low orbital interaction energies. However, for all structures the unsymmetrical bonding situation P→C⁻−L⁽⁺⁾ with a dative bond between the carbon atom and the phosphine ligand PPh₃ and an ylidic electron‐sharing bond to the ligand L contributes to the bonding situation. This bonding mode is more important for the negatively charged yldiides, whereas the carbone‐like bonding situation P→C←L is only relevant for the neutral compounds. A contribution of C=L double bonds was only observed for the carbon‐based ligands CN⁻ and IMe, for which also the molecular orbitals showed partial delocalization of the lone pairs into the ligand backbone.

Overall, these studies demonstrate that the bonding situation in metalated ylides and related bisylides is complex. Dative, ylidic, and double bonds can be formed depending on the substitution pattern, whereat mostly several resonance structures have to be considered for the description of the “real” bonding situation. In general, stronger σ‐donor ligands seem to favor an ylidic C⁻−L⁺ bond over a dative C←L interaction. Thus, ylidic structures are more important in the anionic systems than in the neutral bisylides. This bonding situation however, can also be manipulated by the position of the charge and the distance to the donor atom in the ligand L. This indicates that bonding situations—and with that reactivities and donor properties of these compounds—can be tailored by a careful design of the ligand L.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

L. T. Scharf, D. M. Andrada, G. Frenking, V. H. Gessner, Chem. Eur. J. 2017, 23, 4422.