Nearest neighbor imputation using spatial–temporal correlations in wireless sensor networks

Abstract

Missing data is common in Wireless Sensor Networks (WSNs), especially with multi-hop communications. There are many reasons for this phenomenon, such as unstable wireless communications, synchronization issues, and unreliable sensors. Unfortunately, missing data creates a number of problems for WSNs. First, since most sensor nodes in the network are battery-powered, it is too expensive to have the nodes retransmit missing data across the network. Data re-transmission may also cause time delays when detecting abnormal changes in an environment. Furthermore, localized reasoning techniques on sensor nodes (such as machine learning algorithms to classify states of the environment) are generally not robust enough to handle missing data. Since sensor data collected by a WSN is generally correlated in time and space, we illustrate how replacing missing sensor values with spatially and temporally correlated sensor values can significantly improve the network’s performance. However, our studies show that it is important to determine which nodes are spatially and temporally correlated with each other. Simple techniques based on Euclidean distance are not sufficient for complex environmental deployments. Thus, we have developed a novel Nearest Neighbor (NN) imputation method that estimates missing data in WSNs by learning spatial and temporal correlations between sensor nodes. To improve the search time, we utilize a kd-tree data structure, which is a non-parametric, data-driven binary search tree. Instead of using traditional mean and variance of each dimension for kd-tree construction, and Euclidean distance for kd-tree search, we use weighted variances and weighted Euclidean distances based on measured percentages of missing data. We have evaluated this approach through experiments on sensor data from a volcano dataset collected by a network of Crossbow motes, as well as experiments using sensor data from a highway traffic monitoring application. Our experimental results show that our proposed 𝒦-NN imputation method has a competitive accuracy with state-of-the-art Expectation–Maximization (EM) techniques, while using much simpler computational techniques, thus making it suitable for use in resource-constrained WSNs.

1. Introduction

Wireless Sensor Networks (WSNs) are widely used in environmental monitoring applications, in which sensor nodes transmit raw sensor signals, processed signals, or local decisions to each other. Oftentimes, some of these sensor values are lost during wireless communication, due to synchronization problems, sensor faults, sensor power outages, communication malfunctions, malicious attacks, packet collisions, signal strength fading, or environmental interference (due to, for example, a microwave, walls, or human blockage). For highly dense WSNs used primarily for data collection, this may not be a problem. However, in many applications, the WSN processes data locally within the network in a hierarchical fashion in order to extract useful information, such as the detection of anomalies in the environment. In such applications, it can be useful to employ machine learning algorithms distributed across the network to automatically learn to recognize normal and abnormal modes of operation. However, most autonomous learning techniques are not robust to incomplete data, and will generate incorrect results (such as false positives) when there is missing data. One solution would be to use a reliable transport protocol, which requires nodes to re-transmit their data until successful. But since sensor nodes are usually battery-powered, data re-transmission can cost significant additional energy. In addition, the re-transmission process could delay the decision time when the processing algorithms are embedded in the network. While additional nodes could be added to create a dense WSN that relies on data redundancies to compensate for the missing values, the extra hardware is more costly, and also adds to the computational cost of routing path discovery.

A better technique for many applications is to estimate and replace missing sensor values using a well-suited statistical imputation technique. We believe that properly estimating the missing data should improve the performance of localized reasoning algorithms (such as machine learning techniques) and the overall system in general. Such an approach would also be useful in WSNs in which every sensor reading is critical and the system cannot afford to lose any information.

Our work is based on the observation that, in most applications of WSNs, sensor data in the environment tends to be highly correlated for sensors that are geographically close to each other (spatially correlated), and also highly correlated for a period of time (temporally correlated). Using this observation, we present a novel imputation technique for WSNs that takes advantage of the spatial and temporal correlations in the sensor data. After reviewing the literature on missing data imputation techniques in Section 2, we illustrate in Section 3 that utilizing spatial and temporal information to replace missing values yields high accuracies with low computational complexity, compared to other imputation strategies that do not use spatial–temporal correlation. However, this first study presumes that sensor data correlation is a linear function of the Euclidean distance between sensors. In practical applications, this assumption may not be valid, such as WSN deployments in complex environments in which sensors have environmental features between them, such as walls, obstacles, hills, and so forth. Thus, Section 4 presents a novel Nearest Neighbor (NN) imputation method that learns the spatial–temporal correlations among sensors. This technique does not require an offline analysis of the temporal and spatial sensor data correlations. The proposed method organizes the temporally and spatially correlated data into a kd-tree data structure [1]. When estimating missing sensor values, the NN imputation technique uses the nearest neighbors found from the kd-tree traversal. Rather than use the Euclidean distance metric in the kd-tree construction and search, a weighted Euclidean metric is developed to compensate for missing data by considering the percentage of missing data for each sensor, in a manner that is more suitable for WSNs. We present results of applying this technique to a volcano dataset and a traffic monitoring dataset. We compare our NN imputation technique to an Expectation–Maximization (EM)-based imputation technique. The experimental results show that our technique achieves a similar solution quality to the EM-based imputation, but with much lower computational complexity, making our technique more suitable for use in WSNs.

Our imputation approach is expected to work for both dense and sparse sensor networks. In dense networks, designers hope to use additional hardware to compensate for lost information. When analyzing data, techniques like majority vote or averaging can be used. Including additional nodes in the network is equivalent to adding more features to a classifier. The “Ugly Duckling” theorem [2] states that adding more features may not necessarily improve classification performance. With more features, one still has to decide which (subset) of features to use. Our proposed kd-tree approach offers a systematic way of finding the useful features automatically regardless of network densities.

The rest of the paper is organized as follows, we first review the existing literature in Section 2. In Section 3, we illustrate spatial temporal imputation correlations. We present our novel Nearest Neighbor (NN) imputation method and our experimental results for wireless sensor networks in Section 4. Finally, we conclude our study in Section 5.

2. Related work

Many researchers working with WSNs (e.g., [3–5]) have encountered problems with missing sensor data. It is common to have as much as 40% of the sensor readings to be missing in a one-hop network and 85% of the sensor readings to be missing in a multi-hop sensor network [6]. Several solutions have been suggested to tolerate this error at the communication level, such as link quality profiling [3] or reliable data transportation protocols [7]. As previously noted, this type of solution usually requires retransmitting the lost data, which costs additional transmission power that is unavailable in resource-constrained WSNs. Moreover, the retransmission process can cause delays in the local sensor node processing algorithms (such as an anomaly detection decision).

Higher-level algorithms have been developed to estimate missing sensor data, such as Fletcher et al. [4], who have estimated missing sensor data using a jump linear system and Kalman filtering. However, these regression models usually require extensive computation and an offline training process, in addition to large storage capabilities. Werner-Allen et al. [5] built a simple linear Autoregressive model to estimate missing values based on collected historical sensory readings.

Although missing data is not a well-studied area in WSNs, many missing data imputation methods have been developed outside of the WSN research area, including Nearest Neighbors (NN) imputation [8,9], Bayesian-based imputation [10,11], and regression-based imputation [12]. Missing data in general is a well-studied subject in statistics. Little and Rubin [13] provide an introduction to statistical missing data imputation techniques, such as Least Squares Estimates, Bartlett’s ANCOVA, and likelihood-based approaches. However, these techniques for general missing data imputation are not suitable for WSNs, due to their high space and/or time complexities.

Nearest Neighbor (NN) classifiers were first introduced by Fix and Hodges [14]. Cover et al. have proven that NN classifier risk is less than twice the Bayes risk for all reasonable distributions and for any number of categories [15]. Since we use sensor data that are correlated in space and time, we would expect performance better than the worst case scenario.

The NN methods gained popularity in machine learning through the work of Aha in [16], who showed that instance-based learning can be combined with attribute-weighting and the pruning of noisy instances. The resulting methods perform well in comparison with other learning methods. The use of the kd-tree to improve nearest-neighbor classification time was introduced by Friedman et al. [17]. The approach used in this article was directly modified from the algorithm given by Andrew Moore [18] and Friedman et al. [17]. Moore, along with Omohundro [19], pioneered kd-tree usage in machine learning. However, these existing kd-tree data structures do not consider missing data when constructing the tree. Furthermore, existing approaches assume all sensors in the network are the same. Our approach makes the traditional kd-tree more suitable for WSNs by introducing weighted variance and weighted Euclidean distance measures, which take into account the missing data as well as the possible uniqueness of each sensor in the network.

3. Using spatial–temporal correlation for missing data imputation

There are two main roles for a sensor node in a WSN: (1) sense the environment, and (2) gather information from other nodes in the network. Our missing data imputation techniques are primarily designed for nodes that gather data from other nodes (i.e., clusterheads, data hops, or a sink); such methods are needed for these nodes, since re-transmitting the missing values via wireless communication costs too much battery life. In addition, re-transmissions may take more time and create synchronization issues.

The formulation of the missing data imputation problem in a WSN is as follows. Let $a_i^t$ denote the observation vector made by sensor node i at time t. When $a_i^t=“\mathrm{N}\mathrm{A}”$, it means the observations of node i at time t are missing. The missing data imputation problem is to determine a substitute value for each missing data that is as close a match to the likely true value as possible. Note that the missing data problem in WSNs is Missing At Random (MAR), which means that the probability of the data being missing is independent of the data values. However, this assumption does not mean that the pattern itself is random.

We hypothesize that if the sensor data are correlated in time and space, this correlation can be used to replace missing values, and should yield high accuracy. This section investigates the potential of using spatial–temporal correlations for missing data imputation. Section 3.1 presents our spatial–temporal imputation technique that is based on the assumption that spatial–temporal correlation is a linear function of Euclidean distance. For comparison, Section 3.2 discusses several alternative simple strategies for imputation in WSNs that are not based on spatial–temporal correlations. Section 3.3 presents experimental results that compare our approach with the alternative approaches, showing that using a spatial–temporal correlation approach to imputation is highly beneficial. Following this discussion, the next section (Section 4) relaxes the assumption that the sensor data correlation is a linear function of the Euclidean distance between sensors, and presents a new technique that can learn the spatial and temporal correlations.

3.1. Spatial–temporal imputation technique

We have previously designed a simple online algorithm to estimate missing data based on spatial–temporal correlations, as a function of Euclidean distance between the sensors. (The detailed algorithm can be found in [20].) The missing data algorithm first checks if a neighbor sensor node is within the missing sensor’s sensing range. The observations from the neighbor are used for filling in the missing values if there are neighboring sensors within the cluster. This generates a spatially correlated replacement. If there are multiple neighbors within the sensor’s range, and they do not have the same readings, the majority reading is chosen. Otherwise, the last seen sensor reading is used, resulting in a temporally correlated replacement.

The computational space complexity for this simple approach is O(1), since only one previous observation needs to be stored. The computational time complexity is O(k), where k is the number of nodes within the communication range, since the computational requirement for a sensor node to estimate missing data using this algorithm is a linear function of the number of nodes, k. Assume the sensing range is the same as the communication range and all sensors have the same communication/sensing range. Let r denote the radius of the WSN, c denote the communication range or sensing range of each sensor, and l denote the number of nodes in a WSN. If r is much larger than a node’s communication range c, then k is much smaller than l. The worst-case scenario is when k = l. In typical WSN applications, the sensor nodes are divided into clusters; each cluster covers a local region, and together they cover the entire environment. Hence, searching within a local cluster of k nodes is typically not computationally intensive.

3.2. Alternative imputation techniques for WSNs

Due to the constrained resources on the sensor nodes, any appropriate missing data imputation technique should be simple and require only limited memory. However, there are many possible simple strategies for imputation, and it is not clear in advance which strategy might be best. We have listed several possible alternative missing data replacement strategies in the following list. These imputation strategies have been used to improve the performance of localized algorithms for information fusion in WSNs; a detailed study can be found in [20]. Section 3.3 summarizes some of the key techniques and experimental findings to illustrate that using temporal and spacial correlations to estimate missing values in WSNs yields high performance, and is thus feasible for resource-constrained WSNs. It is important to note that these simple strategies (strategies 1–5, and 7) have many limitations. They are hard to adapt to different network topologies and/or different applications. Therefore, we propose an improved imputation technique in Section 4.

• Strategy 1 uses the most recent available data to fill in the missing values (we also refer to this strategy as “do nothing”). The computational complexities for both time and space of this imputation strategy are O(1) for each node.

• Strategies 2 and 3 replace the missing data by a fixed constant. Specifically, the minimum non-existing value (e.g., 0) and the maximum non-existing value (e.g., 1) are used for strategies 2 and 3, respectively. The computational time and space complexities of these strategies are O(1) for each node.

• Strategies 4 and 5 replace missing values by a moving average. Specifically, strategy 4 uses the mean of the past 5 used sensor values, including the estimated missing values; strategy 5 uses the mean of the past 5 observed values, but excluding the processed missing values. The computational time and space complexities of these strategies are O(1) for each node.

• Strategy 6 is an Expectation Maximization (EM)-based imputation technique (explained in more detail below). The computation time complexity for EM-based imputation is O(nk), where n is number of observations made by a sensor node. The space complexity is O(n).

• Strategy 7 fills in missing data by a neighbor sensor node’s readings. If there are no readings available from sensor nodes within the cluster, the last seen sensor reading is used. The computational time for this algorithm is O(n), and the space complexity is O(1).

Strategy 6 is the Expectation Maximization (EM)-based imputation technique, which is the standard missing data imputation strategy from the literature of statistics. However, the EM-based imputation method is computationally intensive both in space and time. Therefore, it is not practical for resource-constrained WSNs. We nevertheless include this technique for comparison purposes. A detailed explanation of EM-based imputation is given in [13]. We summarize the technique as follows. The EM algorithm is an iterative procedure that finds the Maximum Likelihood (ML) estimation of the parameter vector by repeating the following steps:

• The Expectation step (E-step): Given the mean vector and covariance matrix for a multivariate normal distribution, the estimation step calculates the conditional expectation of the complete-data log-likelihood given the observed data and these parameter estimates. Specifically, let θ^(t) be the current estimate of the parameter θ. The E-step of EM finds the expected complete data log-likelihood if θ were θ^(t):

  $$Q(\theta |{\theta }^{(t)})=\int L(\theta |y)f(Y_{\mathit{\text{mis}}}|Y_{\mathit{\text{obs}}},\theta ={\theta }^{(t)})d{Y}_{\mathit{\text{mis}}}$$ (1)

  where observation Y = (Y_obs, Y_miss), Y_obs represents the observed part of Y, and Y_mis represents the missing part of Y.
• The Maximization step (M-step): Given the complete-data log likelihood, this step finds the parameter estimates to maximize the complete data log-likelihood from the estimation step. The M-step of EM determines θ^(t+1) by maximizing the expected complete-data log likelihood:

  $$Q({\theta }^{(t+1)}|{\theta }^{(t)})\ge Q(\theta ={\theta }^{(t)}),\text{ for all }\theta$$ (2)

  These two steps are iterated until convergence, i.e., the log-likelihood does not exceed a threshold value. Note that there is an initialization step before the EM procedure, which fills in a guess for each missing value. Typically, this initialization step directly impacts the performance of the EM-based imputation.

3.3. Experimental evaluation of spatial–temporal imputation

To determine the extent to which spatial–temporal information can improve performance, we have conducted physical experiments to compare these imputation strategies. To fully study the impact, we must evaluate the approaches both for data that truly is spatially–temporally correlated, and for data that is not correlated. The following section first discusses common techniques for determining if a particular set of data is spatially or temporally correlated. We then discuss, in Section 3.3.2, the performance metrics used to evaluate the alternative approaches. Section 3.3.3 presents results for experimental data that is spatially–temporally correlated.

3.3.1. Testing for spatial and temporal correlations

To determine whether the sensory values are correlated in space and time, standard techniques can be used from statistics. For time correlations, two time-series tests can be used—the Durbin–Watson (DW) test and the Partial AutoCorrelation Function (PACF). The DW test determines whether or not the data set is time correlated, and the PACF gives information on how the sensor data are correlated with each other in time. The value of the DW statistic lies in the range of [0, 4]. A value of 2 indicates that there appears to be no autocorrelation. If the DW statistic d is substantially less than 2, there is evidence of positive serial correlation. On the other hand, large values of d indicate that successive error terms are, on average, much different in value from one another, or are negatively correlated.

For space correlation testing, the Pearson correlation coefficients and R² testing are used. The Pearson correlation coefficient is a common measure of the correlation between two random variables X and Y. Pearson’s correlation reflects the degree of association between two variables, yielding values in the range from −1 to +1. A correlation of +1 means that there is a perfect positive association between variables, while a correlation of −1 means that there is a perfect negative association between variables. A correlation of 0 means there is no linear relationship between the two variables. R² is a statistical measure of how well a regression line approximates data points. R² is a descriptive measure between 0 and 1, where a value of 1.0 indicates a perfect fit. Thus, the closer the R² value is to 1, the better the model.

3.3.2. Performance metrics

In these studies, accuracy is used as the performance metric. Since we are applying these techniques to localized learning algorithms in WSNs, we supply a machine learning classifier¹ with the imputed data, and measure the mismatch between the classifier’s categorization and the true category. Accuracy is defined as the number of correct categorizations divided by the total number of observations. To ensure a fair comparison, the parameters of the classifier were readjusted for each replacement strategy until the best performance is obtained.

In the conducted experiments, our spatial–temporal imputation technique is compared against the other techniques. To determine the significance of the differences in the results, the Student’s t-test is applied. The assumption of the test is that the underlying distributions of accuracies/errors are Gaussian, because of the Central Limit Theorem—as the number of testing sets approaches infinity, the distribution of the mean of accuracy/error approaches a Normal distribution.

3.3.3. Experiment with spatially–temporally correlated physical sensor data

Our wireless sensor network consists of six Crossbow Motes [21], in which five serve as cluster members and one serves as a clusterhead that receives data from the cluster members. We distribute the five cluster members uniformly around the clusterhead in a typical office environment. All sensor nodes are within communication range of each other. The cluster members use light and microphone sensors as input to an on-board learning algorithm that classifies the current environmental state into classes. All learned classes from the cluster members are transmitted to the clusterhead through wireless communication. The clusterhead uses the class labels as input to its own localized learning algorithm. Like most existing classifiers, these localized learning algorithms on each cluster member and clusterhead are sensitive to missing data. While we only present results from a two-layered WSN in this experiment, we believe our approach is scalable to many clusters in a hierarchical fashion, since the localized learning would take place at each level, based on the class labels transmitted from the next lower layer.

The following experimental results are obtained from three sets of trials. In each trial, each sensor node has made 6500 observations. For testing time and space correlations, only the first trial of collected data is used, since the other two trials repeat the first trial and the environment settings do not change. For the purposes of correlation testing, samples with missing values are removed. All testing results have been made from a data set of approximately 1500 samples with no missing values.

The sensory data under the lab setting passed the Durbin–Watson test with a value of 0.0059 with 99.5% confidence level. A DW value of less than 2 indicates there is a high correlation in time. The DW value obtained from the lab setting is near 0, which is evidence that the sensory data does have time correlation. The partial autocorrelations results show that the sensor data has high correlation with one previous data point, i.e., the lag 1 value is close to 1; however, there is little association with 2 or more sensory observations made in the past, i.e., low lag 2–5 values (refer to [22] for more details on the test results).

To determine space correlation, the correlation coefficients between the sensors at each observation as well as R² are calculated. The Pearson correlation coefficients between nodes show that the correlation coefficients between sensor nodes are close to 1, meaning that there are high positive associations between sensor nodes. This study further tested the goodness of fit of the model of one sensor’s observations replaced by other sensor’s observations. As an example, the entire observations made by sensor 1 are used to against the entire observations made by sensor 2 to obtain the R² value. The R² value is almost perfect (close to 1), which means if sensor 1’s reading is used to replace sensor 2’s reading when sensor 2’s observation is missing, it should result in high accuracy, due to the model fitness being high. The sensory data under this setting passed both the time and space correlation tests; therefore, the sensory data is highly correlated in time and space.

Fig. 1 shows the averaged accuracies and standard deviations of the different imputation techniques. We applied the Student’s t-test to the accuracy results for the spatial–temporal strategy compared against other imputation strategies. The Student’s t-test confirmed that the differences in these results are statistically significant, with a confidence level of 99.5%. The spatial–temporal imputation strategy (strategy 7) outperformed the other strategies. This is due to the fact that the sensory data in this experiment have high correlation both in time and space. If the nodes are densely deployed, the readings from nearby nodes are likely to be highly correlated. The system is able to achieve good performance with relatively low computational costs.

Fig. 1.

Accuracies of different imputation techniques, with the x axis indicating the strategy number. Error bars indicate one standard deviation. (Refer to the list in Section 3.2 for the definitions of the strategies.)

The experimental results show that the “do nothing” (strategy 1) has a better performance than a moving average of 5 (strategies 4 and 5), since the sensory data is highly correlated with the past 1 data point, not 5 data points (a high lag 1 value). It is important to use the correct time model, since it directly affects the imputation performance. Strategies 2 and 3 just use a fixed value for missing data, which should not be expected to perform well. The EM-based imputation technique tries to find the best distribution for the observations in terms of likelihood; therefore, it has a relatively high accuracy. However, since the EM-based imputation is computationally expensive in both time and space compared to other strategies, the performance gain does not have a clear advantage. In summary, the proposed simple imputation algorithm (strategy 7) works the best because the correct temporal and spatial models were used.

In previous work [22], we also explored the use of a spatial–temporal imputation technique for data that is not spatially or temporally correlated. Our findings showed that all of the possible imputation techniques perform poorly (around 30–40% accuracy) when the data have no correlations in time or space. Thus, since the proposed spatial–temporal imputation approach performs well with data that is time/space correlated, and no worse when the data is not correlated, it is the preferred method for imputation among the methods listed thus far.

Of course, as previously noted, this simple method is based on the assumption that the sensor correlations are proportional to the Euclidean distance between sensor nodes—an assumption that often does not hold. The results from this section show the importance of using the correct time and space models for the given application. An alternative approach would be to change the localized decision algorithm (e.g., learning classifier) to learn the pattern of missing data; however, we have shown that this approach does not result in satisfactory performance [22], primarily due to the fact that the missing data pattern varies too much. An ideal approach, then, is to enable the network to learn an accurate time and space correlation model for the current application. The next section discusses our approach for learning the correct time and space correlation model.

4. Nearest neighbor missing data imputation for WSNs

As shown in the previous section, environmental data tends to be correlated in space and time. Therefore, searching among nearest neighbors whose values are spatially and temporally correlated yields good performance. In the previous spatial–temporal missing data technique, the system makes use of the spatial property of the WSN to impute the missing sensor value with the most common sensor reading within the same cluster. If no spatial data is available at the current time instance, the algorithm uses the missing sensor’s latest known value (using the temporal correlation assumption of the environment). However, the previous spatial–temporal imputation approach possesses some shortcomings. First, the correct time and space models have to be used in order for this technique to have good performance. Additionally, the time and space correlation tests must be performed offline. Further, it requires a brute-force search on available time and space correlated data, which can be expensive as the data size increases. Finally, the approach assumes sensors within a cluster have the same sensor readings, and the sensor value correlations are proportional to the Euclidean distances between the sensors. However, these assumptions may not be true in certain environments. For example, Fig. 2 shows sensors 1, 2 and 3 deployed in two offices. Even though the Euclidean distance between sensors 1 and 2 is less than the distance between sensors 2 and 3, the sensor correlation between sensors 2 and 3 is higher than the sensor correlation between sensors 1 and 2, since sensors 2 and 3 are located in the same room while sensors 1 and 2 are located in two different rooms.

Fig. 2.

Correlations between sensors are not necessarily proportional to their Euclidean distance. Sensors 1, 2 and 3 are deployed into two offices. Even though the Euclidean distance between sensors 1 and 2 is smaller than that between sensors 2 and 3, the sensor correlation between sensors 1 and 2 is lower than the correlation between sensors 2 and 3.

This section presents an automatic and efficient Nearest Neighbor (NN) imputation technique for missing data in WSNs that learns the correct time and space correlations between sensor nodes. The 𝒦-Nearest Neighbor (𝒦-NN) method is a common imputation method, in which 𝒦 candidates are selected from the neighbors such that they minimize some similarity measure [22]. The 𝒦-NN imputation approach has many attractive characteristics [24]: (1) it is a non-parametric method, which does not require the creation of a predictive model for each feature with missing data; (2) it can handle both continuous and categorical values; (3) it can easily deal with cases where there are multiple missing values; and (4) it takes into account the correlation structure of the data. The most important characteristic is its capability of using auxiliary information, such as space and/or time correlation between sensor node values. As already shown, using spatial correlations to impute missing data can yield high performances.

In WSN applications, to is important to find the closest match for missing values efficiently. Thus, our approach uses an efficient data structure for nearest neighbor imputation—the kd-tree [25]. The kd-tree is one of the earliest and most popular data structures used for NN retrieval. The kd-tree improves the previous spatial–temporal missing data imputation method by automatically learning the sensor data correlations in time and space. The advantages of using a kd-tree to store the sensor data are that the tree building process is data-driven, and the search process for each observation vector is localized, with a computation time of O(lg n), where n is the size of the training data. In the designed WSN sensor imputation process, a kd-tree is able to capture the spatial–temporal correlations automatically without human supervision; hence, human operators do not need to have any initial knowledge of the environment or of the sensor network deployment.

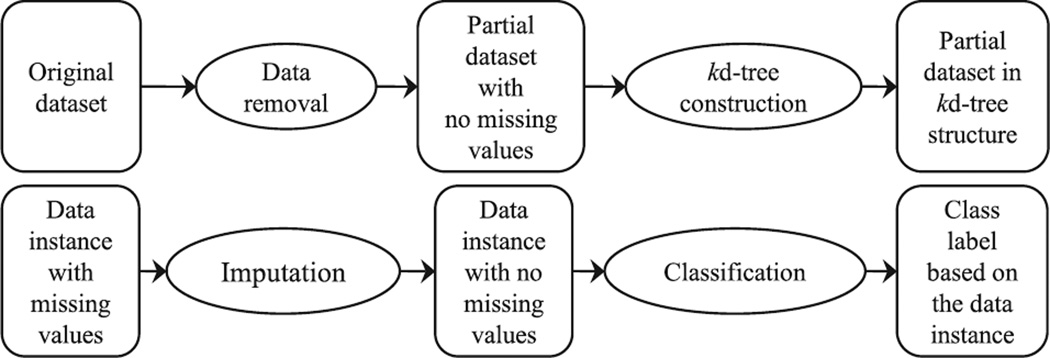
As illustrated in Fig. 3, the overall imputation procedure works as follows. First, there is an initial training period in which each data gathering node constructs a kd-tree using an initial dataset. Traditional approaches to kd-tree construction use variance and Euclidean distance to split k-dimensional data, with the underlying assumption that all dimensions have equal weights. However, in WSNs, some parts of the region may have more missing values than others, resulting in computed variances not correctly representing the true distribution. Therefore, the system should also consider the missing rates in building the kd-tree. To address this problem, we propose the use of weighted variances and weighted Euclidean distance measures, which are calculated as a function of the missing data rate for each dimension. These weight factors are then used to control the order of dimensions to be searched.

Fig. 3.

Overall view of the NN imputation approach. Top: The training procedure for constructing the kd-tree. Bottom: The imputation process when part of the current observation values are missing. The imputation procedure is a NN kd-tree search.

After the kd-tree is fully constructed, it can be used for online imputation. When the current sensor node data has missing values, the algorithm searches for its nearest neighbor(s) by traversing the kd-tree and replacing the missing values in the current sensor node data with the nearest neighbor values. The kd-tree search uses a weighted Euclidean distance that we develop to find the nearest neighbor values. Finally, the observation instance with no missing values can be used in the localized reasoning algorithm (such as a machine learning classifier).

The main contributions of this imputation method are twofold. First, a 𝒦-NN missing data imputation technique is developed that enables the system to take advantage of space and/or time correlations in the sensor data. Second, a weighted dimension ranking procedure is defined to make the kd-tree data structure more suitable for missing data in WSNs. The following sections describe this approach in more detail.

4.1. The kd-tree construction

The kd-tree is a multidimensional data structure that decomposes a multidimensional space into hyper-rectangles. The constructed tree is a binary tree in which each node of the tree corresponds to a hyper-rectangle. Stored with each node are the following fields: splitting dimension number, splitting value, left kd-tree, and right kd-tree.

The procedure for constructing the kd-tree takes as input a training set Ω, where Ω contains n observation vectors made by k sensor nodes from time 1 to time t_n. Each vector has k-dimensions, and each dimension corresponds to one sensor node in the WSN. The kd-tree construction procedure then returns a kd-tree storing the training data Ω.

One caveat to this construction process is that the training set Ω does not contain all training instances, but only those training instances that contain complete (i.e., no missing) data. Since incomplete data is not useful for imputation, adding them into the tree would slow the search time. Therefore, only complete data instances are used during construction of the kd-tree. This approach assumes some reasonable upper bound on the percentage of missing data.

The conventional kd-tree data structure is constructed by splitting the dimension with the largest variance first, based on the training data. This is justified by realizing that, in general, the sensor with the largest variance may have the most influence on the classification process. Since the tree search time can be greatly reduced by starting from the dimension that varies the most (i.e., the largest variance) and skipping dimensions that do not change much, the typical kd-tree is built so that dimensions with the largest variance are at the top of the tree. The variance σ2 is defined as follows:

$${\sigma }^2=\frac{{\sum }_{n=1}^N{x}_n^2-{\left({\sum }_{n=1}^N{x}_n\right)}^2/N}{N-1}$$ (3)

where x is a sensor’s readings and N is the size of the dataset. However, with missing values in a WSN, the kd-tree construction process also needs to account for missing values in a particular dimension. If the system uses an inaccurate estimation of the variance to construct the kd-tree data structure, then searching for the nearest neighbor takes longer. Our approach accomplishes this by weighting the variances of the sensor node data according to the percentage of missing data. These percentages are determined by analyzing the original training input that contains both complete and missing data.

The weighted variance of dimension k can be viewed as a scoring function for dimension k, in which the score is proportional to the variance and inversely proportional to the percentage of missing data. Thus, as the variance increases, the score increases as well; and, as the amount of missing data increases, the score decreases. Our approach is to set the weight of dimension k to:

$$w^{(k)}=(1-M_k)$$ (4)

with the score of that dimension set equal to σ_k × w_k, where σ_k is the variance and M_k is the percentage of missing data for sensor k. This score function automatically accounts for both missingness and variance values. Note that the actual function may depend on the application; system designers can choose a different weight function if desired.

After choosing the split dimension, the system needs to determine the splitting value. Generally, it is good to choose the split to be in the middle of the points along the splitting dimension. There are many ways to accomplish this. Splitting at the median ensures a balanced tree. Splitting at the mean results in square hyper- rectangles, but may lead to an unbalanced tree. An unevenly distributed tree can result in long and skinny hyper-rectangles. Our approach chooses the splitting value to be the mean, µ_s, of the training observations of the splitting sensor, since it can be easily determined by the distribution of the data. Thus, during the training process, the training vectors in Ω are recursively split into two subsets. One subset contains observations smaller than the splitting value µ_s, the other contains the observations larger than or equal to the splitting value µ_s. The splitting value µ_s is stored at the root and the two subsets are stored recursively in the two subtrees.

We now give an example to illustrate the importance of using weight factors for missing data in a WSN during kd-tree construction. Suppose there are two sensor nodes observing the environment. The system collects a set of 2-dimensional data points over time (shown in Fig. 4a), where dimension/sensor x has a variance of 4.62 and dimension/sensor y has a variance of 1.64. Sensor x has a larger variance than sensor y. Therefore, the kd-tree first splits dimension x, then dimension y when no weights are used. Suppose sensor y has approximately 52% missing values at both the beginning and the end of the data collection period. A new kd-tree constructed by using the remaining data instances with no weights included is shown in Fig. 4b. With no weights included, the new variances become 0.39 and 0.58 for sensors x and y, respectively. The new kd-tree first splits dimension y, then dimension x. However, this split is not consistent with the complete data case. This is because sensor y has missing values and its variance obtained from incomplete data is different from the complete data. By adding weights (i.e., w₁ = (1–0%) = 1 and w2 = (1–52%) = 0.42), and reconstructing the tree, the splitting order of the kd-tree is changed back to its original form (see Fig. 4c). The final scores (weighted variances) are 0.39 × 1 = 0.39 and 0.42 × 0.58 = 0.28 for dimensions x and y, respectively. In this manner, the constructed kd-tree is more likely to resemble the true distribution of the sensor data.

Fig. 4.

An example illustrating the use of the weight function. See text for details.

The detailed kd-tree construction algorithm is given in Algorithm 1. The developed implementation closely follows the algorithm that is presented by Friedman in [17], except for the added CHOOSESPLIT function. The developed CHOOSESPLIT function chooses the splitting order based on weighted variances instead of unweighted variances.

Algorithm 1.

BUILDKDTREE (Ω)

Input: A set of observations Ω, and a weight vector w.
Output: a kd-tree storing Ω.
1:	if Ω is empty
2:	return NULL.
3:	end if
4:	if Ω contains one observation
5:	return a leaf storing this observation.
6:	end if
7:	s ← CHOOSESPLIT (Ω, w), where s is the splitting dimension.
8:	µs←mean of dimension s.
9:	pLeft ← {x ∈ Ω : xs < µs}.
10:	pRight ← {x ∈ Ω : xs ≥ µs}.
11:	kdLeft ← BUILDKDTREE(pLeft).
12:	kdRight ← BUILDKDTREE(pRight).
13:	return kd-tree with fields [s, µs, kdLeft, kdRight]
CHOOSESPLIT (Ω, w)
1:	σ ← get variances of all dimensions in Ω.
2:	score ← apply weights to all variances (i.e., σi × wi).
3:	return j ← dimension of the max score.

4.2. Nearest neighbor imputation

When the current observation has missing values, the developed NN imputation algorithm is activated. The imputation works as follows: First, find the current observation’s closest match in the built kd-tree by using a NN search algorithm. Then, fill in each missing value with the corresponding value in the best match found. This approach is called a hot-deck imputation technique [24], and is one of the most commonly used missing data imputation techniques, in which missing values of incomplete records are filled in using values from similar, but complete records of the same dataset.

To find nearest neighbors, a NN search algorithm makes use of a pre-specified distance metric. The conventional distance used is Euclidean distance, defined as follows:

$$d(x_i,x_j)=\sqrt{{\sum }_{k=1}^K{(x_i^{(k)}-x_j^{(k)})}^2}$$ (5)

where, x_i and x_j are two data vectors with K-dimensions. The average squared distance between objects across all K-dimensions is given by:

$$\hat{D}=\frac{1}{N^2}\sum _{k=1}^K\sum _{i=1}^N\sum _{j=1}^N{(x_i^{(k)}-x_j^{(k)})}^2$$ (6)

However, in the presence of missing data, it is preferred to choose the splitting dimension in the kd-tree by using a weighted Euclidean distance, defined as follows:

$$\hat{d}(x_i,x_j)=\sqrt{{\sum }_{k=1}^K{w}^{(k)}{(x_i^{(k)}-x_j^{(k)})}^2}$$ (7)

where w^(k) is the weight factor previously defined (i.e., a function of the percentage of missing data for the kth dimension). The average squared distance between objects for all K-dimensions is given by:

$${\hat{D}}_w=\frac{1}{N^2}\sum _{k=1}^K{w}_i^{(k)}\sum _{i=1}^N\sum _{j=1}^N{(x_i^{(k)}-x_j^{(k)})}^2$$ (8)

The following are some well-known properties of a weighted Euclidean distance:

• If the w^(k) for each dimension is set to be the identity matrix, then the weighted Euclidean distance is equivalent to the conventional Euclidean distance.

• If the w^(k) is set to be the inverse of the variance squared at dimension k, then the weighted Euclidean distance is proportional to the Mahalonobis distance with the diagonal covariance matrix.

If the system sets the weight to be two times the inverse of the variance squared at dimension k, then the system has demoted the importance of dimension k by half.

The developed kd-tree search algorithm closely follows the conventional NN search implementation [17] with slight modifications. First, the algorithm uses the weighted Euclidean distances given in Eq. (8) instead of the Euclidean distance to determine the closeness of previously-seen sensor data. When there are missing values from the current dimension, the algorithm needs to search both sides of the subtree, since, without any information on that dimension, the nearest neighbors could reside on either side of the (sub)tree. This is why keeping the dimensions with the most missing values towards the bottom of the tree during tree construction can help the system localize the search, which can improve the search time. Once the closest match to the current observation is found, the missing values can be filled in.

4.3. Complexity analysis

Our kd-tree construction and search algorithms are direct modifications of the algorithms presented in [17], and thus the algorithm complexities are not changed from the original. That is, for tree construction, the algorithm time complexity is O(kn lg n), where k is the number of sensor nodes that the data gathering node is listening from and n is the number of training instances.

The kd-tree search time is constrained by the amount of data that the algorithm can eliminate in each dimension. As shown in Fig. 5, based on the distance and mean (split point) for each dimension, the tree search algorithm decides to traverse the left or right side of the kd-tree; hence, at each iteration, one side of the subtree can be eliminated. It is important to choose the top levels of the kd-tree wisely, since they determine the tree search order and can help the system limit the amount of search early on. For complete data, the search time is O(lg n). In the 𝒦-NN missing data imputation approach, each missing value corresponds to a data point in a dimension. If the dimension is at the top of the tree, the traversal can be expensive, since the search algorithm must continue to search both sides of the tree. If the missing value dimension is towards the bottom of the built kd-tree, the NN search is faster, since the system searches both sides of the subtree with fewer data points. Therefore, by using weights to lower the dimensions that have high missing rates toward the bottom of the kd-tree, the system can speed up the nearest neighbor search process. The assumption made here is that if sensor nodes tend to miss values during the training period, they are likely to have similar missing rates online. The more one can constrain the search to part of the subtrees, the faster the system can find the NNs for the missing values.

Fig. 5.

An example of a kd-tree search. At each level/dimension, eliminate some part of the tree based on the distance.

This approach can be compared to a brute-force NN search method (like the previous spatial–temporal imputation method in Section 3); if we assume no sorting is performed, then the search may require that each data vector be examined. To find the nearest neighbor of each point in a data set of n vectors requires O(n²) time using a brute-force method. With k sensor nodes, and an O(n lg n) sorting algorithm, the brute-force search therefore has a total search time of O(kn²).

We note that the kd-tree construction can be performed online as well. The simplest way of constructing the kd-tree online works as follows: for each complete data instance, add the new instance to the tree as in other search trees. Then, use the kd-tree construction algorithm as shown in Algorithm 1. This is a simple modification to the existing algorithm. If we assume that there are j complete instances in the kd-tree, then the online construction algorithm takes O(lg j) time to traverse and add the new instance to the tree. Reconstructing the kd-tree takes O(j lg j) time.

The space complexity of storing a kd-tree is linear, i.e., O(kn) where k is the number of sensors in a cluster and n is the number of observations in the past history. A system designer can always trade off space for time. Suppose one tree is constructed for each combination of missing sensor values. When an observation has a missing pattern in it, the tree with only that missing pattern can be searched. The total possible number of trees for k sensors is $({𝒦}_k^1+\cdots +{𝒦}_k^k)\times k!$. Storing data into different trees may limit the search time; however, the space grows quickly with this method.

These computation and space requirements are considered to be acceptable, since they help to save communication costs in WSNs. If the developed missing data algorithm were not in place, the WSN would need to continue to broadcast and query the data transmitting sensor nodes repeatedly until all data are received. The extra energy requirements for these repeated messages are not acceptable in our resource-constrained WSNs.

Since we compare our approach (in the next section) with an EM-based imputation technique, we also include the time and space complexity analysis for EM in Table 1. The time and space complexities are calculated based on a single sensor node, and for finding one imputation value, where n is the number of observations made from time 1 and k is the number of sensor nodes within proximity (dimensions).mis the number of Gaussian mixtures used for the EM-algorithm. Like our spatial–temporal kd-tree approach, the EM imputation strategy also uses space linear in k and n. However, the time complexity for EM-based imputation is much more than our kd-tree based imputation technique. If the EM-based imputation assumes m mixtures of Gaussian models are used, this results in O(mkn) computation time for the E-step, and O(mkn) computation time for the M-step. The EM procedure continues until convergence, so these steps are repeated many times. The space cost for EM-based imputation is O(kn + 2m + m²), which includes storing all data points and Gaussian mixture models.

Table 1.

Comparison of EM and kd-tree imputations.

Imputation	Time	Space
kd-tree	Construct: O(kn lg n)	O(kn)
	Search: O(lg n)
EM-based	E-step: O(mkn)	O(kn + m2)
	M-step: O(mkn)
	Iterate E and M steps until convergence

4.4. Experimental evaluation of NN imputation technique using Volcano Monitoring Application

One objective of our research is to design a flexible NN imputation technique for resource constrained WSNs that is applicable to a wide range of applications. Thus, to validate our approach, we illustrate it in two applications—volcano monitoring and highway traffic monitoring. In the volcano monitoring application we show the system using a network of 16 seismic sensors with a high sampling rate and a large volume of data, while in the highway traffic monitoring application, we show a network of 5 sensor nodes with a very sparse sampling rate and small amounts of data.

A volcano monitoring dataset was collected by Werner-Allen et al. at the Volcano Reventador. The detailed data collection process can be found in [5]. The data used in these experiments was obtained from a network of 16 Crossbow sensor motes. Each of the sensors continuously sampled acoustic data at 100 Hz over a 19-day deployment. Motes used an event-detection algorithm to trigger on interesting volcanic activity and initiate data transfer to the base station. Each data collection event is “triggered” when the event-detection algorithm exceeds a threshold. The 60 s download window contains approximately 30 s before the trigger and 30 s after the trigger. Note that the trigger may not be exactly centered at the intended event within the download window.

Our implementation of the kd-tree imputation approach with weighted variances and distances uses an adaptation of the kd-tree implementation in the WEKA [26] open source machine learning software. All of the following experiments have been conducted on a PC with an Intel Core duo processor E6320 running at 1867 MHz, with 2 GB of main memory.

4.4.1. Preprocessing the sensor data

During the deployment, the network recorded 229 earthquakes, eruptions, and other acoustic events; however, only eight events have complete readings from all 16 sensor nodes. After discarding the data that does not have all 16 sensor readings, only 8 min of data are left; this data is selected as the training and testing data. With this complete data and all 16 sensors’ readings, the ground truth can be obtained for the following missing data experiments.

Two 1-min events are chosen (one minute as training and one minute as testing data) to evaluate the developed imputation method in the following experiments. The training and testing data sets from the 16 sensor nodes’ acoustic signals are plotted in Fig. 6. The training data contains 7950 observations, and the testing data contains 4415 observations. To determine the impact of the developed 𝒦-NN missing data technique on a localized machine learning classifier,² we trained this unsupervised classifier using the training data and the testing data, to determine the best classification performance that could be achieved with complete data. This process resulted in the identification of 16 discrete categories.

Fig. 6.

Acoustic sensor readings from all 16 sensors: (a) shows the training data to build kd-trees, and (b) shows the testing data.

We then removed data from the complete testing set to create new testing sets with missing sensor data. Based on observing the volcano dataset, if a sensor has missing values at the beginning of the fetch procedure, the values in that sensor would stay missing during the entire procedure. Therefore, 15 missing datasets are generated from the testing data by randomly removing sensors. That is, the first missing dataset is created by randomly removing the data of one sensor from the original testing data; the second missing dataset is created by randomly removing the data from two sensors, and so on. The last missing dataset is created by removing the data from 15 sensors. Thus, the percentage of missing data for the newly generated testing cases are chosen to be one of the following percentages: 1/16, 2/16, …, 15/16. We also generated 9 other missing datasets with different missing data percentages (i.e., 10%, 20%, …, 90%) for each sensor. The missing data are removed at random for each sensor based on the missing percentage.

We compare the accuracies of the developed NN missing data imputation technique to two EM-based imputation software packages. The first EM-based software is the state-of-the-art missing data imputation software Amelia II [11]. Amelia II makes use of a bootstrapping-based EM-algorithm, which is a parametric approach to estimate missing values that assumes the complete data (that is, both observed and unobserved) is modeled by a multivariate Gaussian distribution. Note that our NN imputation is a nonparametric approach, which makes no assumption of the data distribution.

To compare the run times of the approaches, we found it difficult to use Amelia II as a comparative approach, since it is installed under R (a free software environment for statistical computing that runs under Linux). Instead, we compare our technique’s run time to that of another EM-based imputation software available in WEKA. For the EM imputation procedure, we used default parameter settings of the threshold for convergence in Expectation Maximization. That is, if the change in the observed data log-likelihood across iterations is no more than 0.0001, then convergence is considered to be achieved and the iterative process is ceased.

4.5. Performance metrics

To measure the quality of the imputed volcano data sets, micro-average accuracy and macro-average accuracy metrics are used. Micro-average accuracy is defined as the ratio of the observations that have been correctly categorized (A), to the total number of instances that have been categorized (T). Macro-average accuracy is defined as the average accuracy for each class—that is, the ratio of the number of correctly categorized observations in category i to the number of observations in category i.

These two averaging procedures bias the results differently—micro-averaging tends to over-emphasize the performance on the largest categories, while macro-averaging over-emphasizes the performance of the smallest categories. Both of the averaging results are often examined simultaneously to get a good idea of how the developed algorithm performs across different categories.

To ensure a fair comparison, the parameters of the classifier have been readjusted for each replacement strategy until the best performances are obtained.

4.6. NN imputation accuracies

As shown in Fig. 7, the performance of the developed nearest neighbor technique is competitive with that of the Amelia II missing data imputation software in terms of micro-averaging accuracies. The kd-tree is constructed using approximately 8000 observations with 500 splits. The Amelia II missing data imputation software’s performances are averaged over 30 trials.

Fig. 7.

Micro-averaging of 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9}) vs. Amelia II.

As shown in Fig. 8, the macro-average accuracies of the developed NN imputation technique are about the same as Amelia II. A shortcoming of Amelia II is that it assumes the underlying distribution is Gaussian. However, when the underlying distribution is not Gaussian, parametric approaches have a model mismatch problem. Additionally, parametric based approaches generally require large numbers of training instances to estimate the parameters of the models accurately. If the training instances are not sufficient to train the model, the imputation results would not be accurate. The developed NN approach is a non-parametric approach, with no assumptions of the data distribution. Therefore, its performances could be better than the parametric approach in some applications. Note that instead of replacing missing data with a single estimated value, 𝒦-NN imputation can also replace the missing value with 𝒦 different values, for 𝒦 greater than one. This technique is generally referred to as a Multiple Imputation (MI) method. MI-based approaches replace each missing value with a set of plausible values that represent the uncertainty about the correct value to impute. In this situation, the Amelia II imputation procedure has to iterate over patterns of missingness (that is, all the possible ways that a row has missing cells). Thus, the complexity grows quickly with the number of these patterns. On the other hand, for the developed kd-tree imputation approach, the cost remains linear when searching more nearest neighbors.

Fig. 8.

Macro-averaging of 𝒦 − NN(𝒦 ∈ {1, 3, 5, 7, 9}) vs. Amelia II.

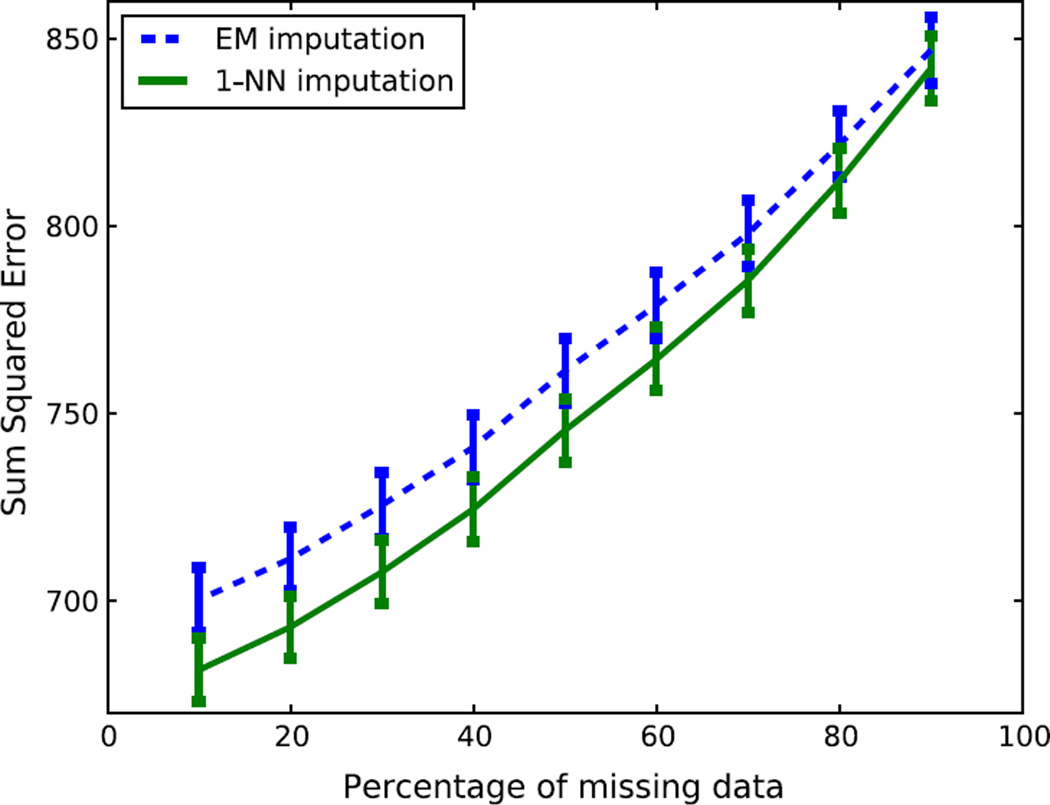
To determine the statistical significance of the comparison between our imputation technique and the EM approach, 10-fold cross-validations are performed on the training data. The EM imputation technique used in the following experiments is from the WEKA machine learning software. Rather than determining missing data accuracy in terms of the learning classifier’s performance, in this experiment, the Sum Squared Error performance is used to compare the imputation results between the NN imputation and the EM-based imputation algorithm. The Sum Squared Error is defined as ∑ (Y − Ŷ)², where Y denotes the ground truth and Ŷ denotes the imputation value. Fig. 9 plots the mean and standard deviations of Sum Squared Errors of 1-NN imputation and EM imputation over different percentages of missing data. The mean and standard deviations are obtained from 10 sets of testing data. The 1-NN imputation has a better performance than the EM imputation technique in most cases except when 90% of the data is missing. To determine the significance of these results, the Student’s t-test is applied to the Sum Squared Error results for the 1-NN imputation technique compared against WEKA’s EM imputation strategy. This test confirms that the differences are statistically significant (except for the 90% missing data case), with a confidence level of 99.5%. The NN imputation strategy performed better than EM-imputation in most cases because the training data set is correlated in time and space, whereas the EM-based imputation technique assumes there is only one Gaussian distribution in the training data. When there is too much data missing (e.g., 90% missing data), 1-NN imputation and the EM-based imputation technique perform about the same because it is hard to find solutions when only a few sensors are available. In general, the distance error increases as the percentage of missing data increases.

Fig. 9.

The Sum Squared Error of 1-NN vs. EM-based imputations. The averaged Sum Squared Error and standard deviations are obtained from 10-fold cross-validation on the training data. 1-NN imputation has less Sum Squared Errors than the EM-based imputation method except in the case of 90% missing data.

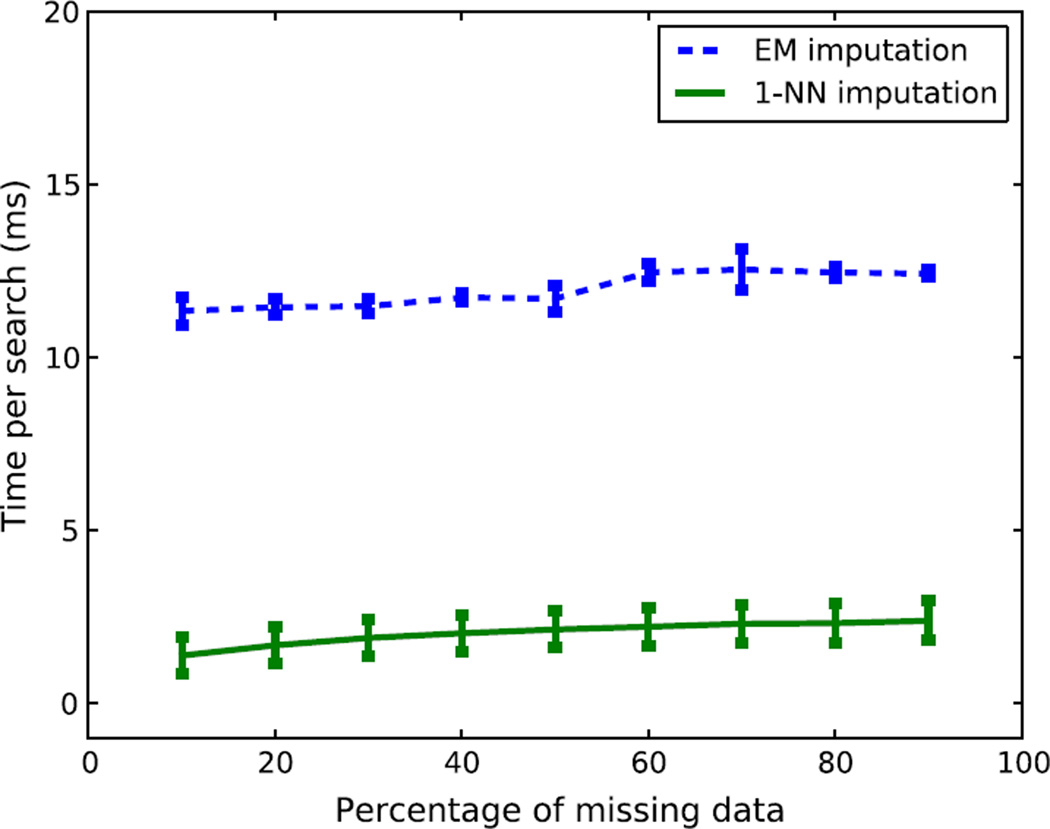
The imputation times for each data instance of different imputation techniques are averaged over 10 sets of data and the results are shown in Fig. 10. Nearest neighbor imputation uses less time compared to the EM imputation method, due to the fact that NN imputation does not have to iterate through all the data until convergence. To determine the significance of these results, the Student’s t-test is applied to the time performances for the 1-NN imputation scheme compared against the EM-based imputation strategy. This test confirms that the differences in these results are statistically significant, with a confidence level of 99.5%. Combining these results with those of Fig. 9, we can conclude that the 𝒦-NN imputation is preferred over the EM-based imputation technique for solving the missing data problem in WSNs.

Fig. 10.

The imputation times of 1-NN imputation vs. EM-based imputation for estimating each data instance. The average time and standard deviations are obtained from 10-fold cross-validation on the training data. For all missing percentages, 1-NN imputation has much better imputation time than the EM-based imputation method.

4.7. Timing comparisons for searching different NNs

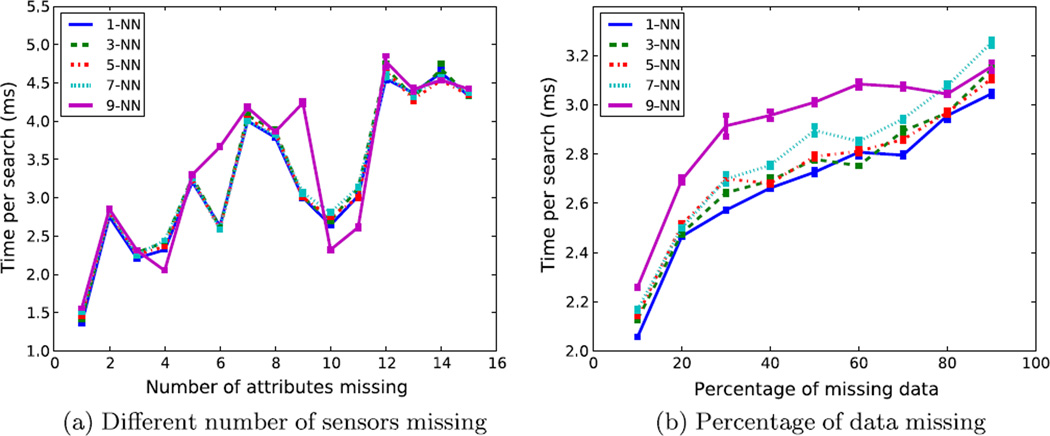
Fig. 11 shows the average search time for 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9}) per observation on the pre-built kd-tree; specifically, Fig. 11a plots the search time for a different number of missing sensors, and Fig. 11b plots the search time for a different percentage of missing data. Note that the combinations of sensors missing are randomly selected in Fig. 11a, and that the missing data is randomly selected for different percentages in Fig. 11b. The search times for each nearest neighbor are averaged over 10 trials, and the variances of the search times are plotted as error-bars. In most of the cases, the variances are too small to notice. All search times per observation are between 1 and 5 ms. In general, the search time shows an upward trend as the volume of missing data increases. This is true for varying numbers of sensors missing and for varying percentages of data missing. The search time for finding 9 nearest neighbors is usually slightly longer than the rest in both missing data cases. The search time for finding 1, 3, 5, and 7 NN are approximately the same. The search time curves in Fig. 11a are not as smooth as the curves in Fig. 11b. This is due to the combinations of missing sensors that are selected at random. Different combinations of the missing sensors create different search patterns for the kd-tree approach. Fig. 11b shows much smoother curves than Fig. 11a because the missing sensors for all the testing sets are selected at random. Depending on the sensor and combinations of sensors missing, some may take longer to traverse than others.

Fig. 11.

Average search time per observation for 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9}), where (a) shows the search time for different numbers of sensors missing. The missing sensors are selected at random. (b) Shows the search time for different percentages of missing data. The search times are averaged over 10 trials. Error bars plot the standard deviations of search time. The missing data are selected at random.

4.8. Timing comparisons after adding weights

To test the effect of the weight factor, the variances for all 16 dimensions (sensors) are evaluated. The sensor with the most variance (sensor 12) is selected, a very small weight is applied to its variance, and a kd-tree is built with the weighted variance. This selection is empirical and is intended to demonstrate the importance of the designed weight factor. In the original kd-tree, sensor 12 has the highest rank; however, by adding the weight factor, sensor 12 ranks the last among all 16 dimensions in the new weighted kd-tree construction. The hypothesis is that the system uses more time to traverse the non-weighted kd-tree to find the nearest neighbors.

Fig. 12 shows the average search time and standard deviation per observation for different percentages of missing data (although most of the standard deviations are too small to see). The solid lines denote the average search time for traversing kd-trees with added weights, while the dashed lines denote the average search time for traversing regular kd-trees with no weights added. The search times are averaged over ten trials. The performances are evaluated based on finding 1-NN with tree size d, where d ∈ {50;,500, 1000}. The weighted kd-trees take less search time than non-weighted kd-trees, because sensor 12 has the largest variance during training time; however, the testing data has missing values and the distributions are changed from the training data. It takes the system less time to localize its searches, because the system is able to eliminate more data as compared to the non-weighted kd-tree. Therefore, if the weights are used correctly, the system can localize the search faster.

Fig. 12.

Search time per observation for finding 1-NN from kd-tree sizes. The regular kd-trees are plotted using dashed lines and the weighted kd-trees are plotted using solid lines. Standard deviations are also shown, although most of them are too small too see.

The average search times for search 1-NN on regular kd-trees are 2.9 ms, 3.8 ms, and 4.2 ms for tree sizes of 50, 500 and 1000 splits, respectively. The average search times for search 1-NN on weighted kd-trees are 2.8 ms, 3.4 ms, and 4.1 ms for tree sizes of 50, 500, and 1000 splits, respectively. Thus, the percentage that the search time differs between the regular kd-trees and the weighted kd-trees are approximately 3%, 10%, and 2% for tree sizes of 50, 500, and 1000 splits, respectively. Note that the weight of only one dimension is changed (out of a total of 16 dimensions). Depending on the data distribution, re-ranking more dimensions may have more influence on the search time. The ranking of the dimensions in kd-tree construction according to the missing percentage is likely the most influential factor in the search time.

This experiment shows that using weights are very important to retrieve nearest neighbors from the kd-tree data structure. The weight factors require some knowledge of the environment’s and sensors’ behaviors. For example, if a sensor constantly misses values, or transmits noisy data, the system can re-rank the search tree by applying small weights to the noisy sensor, saving search time. The designed weighted variance and Euclidean distance offer an automatic way of changing the importance of each sensor in the network. With changes in the environment and sensor nodes (i.e., power outage, replacements of new sensors, etc.) the system designers can choose any functions to calculate weights as desired. The weighted variance of dimension i should be proportional to the variance of dimension i and inversely proportional to the missing percentage of dimension i. Therefore, using a weight parameter allows the system to control the ranking of the kd-tree. As the environment or the network structure changes, the system can re-evaluate the weights and construct a new kd-tree easily without re-programming all sensor nodes in the WSN.

4.9. Traffic monitoring application

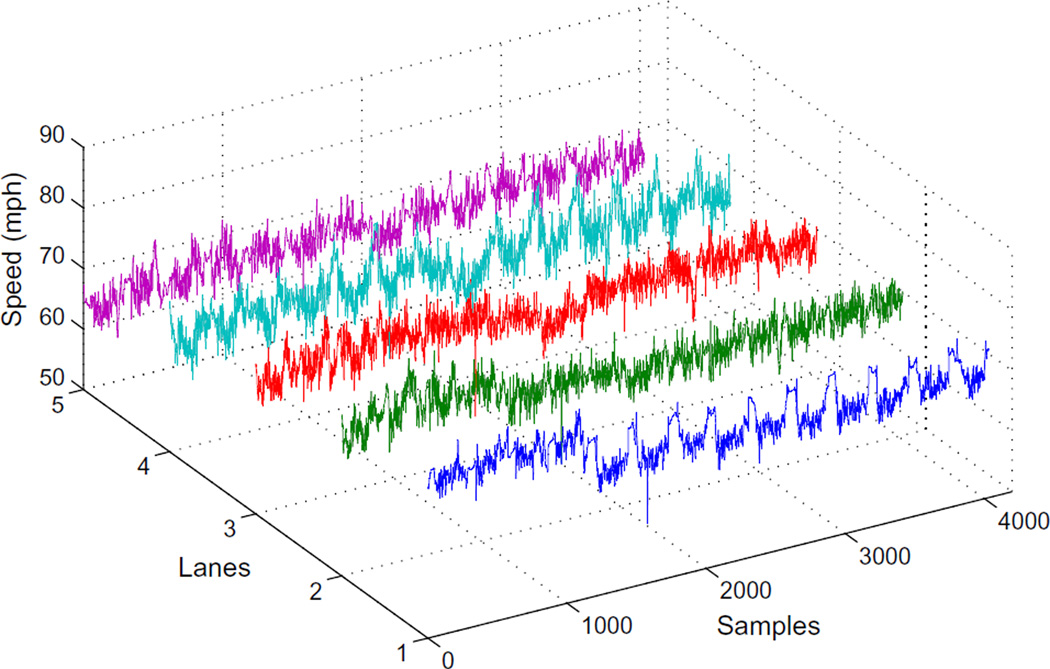
To further evaluate the flexibility and effectiveness of our NN imputation technique for WSNs, we have evaluated our framework in the application of highway traffic monitoring using data from the Caltrans Performance Measurement System (PeMS) project. The traffic data of the PeMS system is collected in real time from over 25,000 sensors that span the freeway system across all major metropolitan areas of the State of California [27]. In a typical highway sensor deployment under PeMS, a single sensor is positioned in each highway lane, as illustrated in Fig. 13. While the PeMS system often has missing data, it is difficult to compare our approach with other techniques if we do not have ground truth data. Thus, we chose a highway segment of PeMS sensor data that happened to not have any missing data, as well as being one of the most congested segments of the highway; we then simulate missing data (as described below), and compare it to the actual ground truth data. Specifically, for our study, we chose a highway segment on highway I-5 with speed flow sensor readings. This Vehicle Detector Station (VDS) is located at the CA PM = 6.284 marker, San Diego County, Chula Vista, and the VDS is 1114748 in District 11. The chosen highway segment has five lanes, with each lane having one detector (as shown in 13b). The lane detection IDs are 1114737 to 1114741 for lanes 1 to 5, respectively.

Fig. 13.

The Vehicle Detector Station 1114748 is located in District 11, San Diego County, Chula Vista, I5-North CA PM = 6.284 (a); (b) shows sensor displacements. Both figures are from the PeMS website [27].

We treat sensor data collected from each lane as an individual cluster member sensor node. We obtain data from the PeMS over a period of 14 days, from July 26, 2010 to August 8, 2010. This dataset gives us 4032 data samples per detector, totaling 20,160 samples across the five sensor nodes. The sampling rate is once every five minutes (i.e., 12 samples per hour), and the unit for speed feature is mph. This data also includes ground truth labels that indicate when traffic incidents occur; this information is used to determine the accuracy of the algorithms we are comparing. To illustrate our proposed approach in a hierarchical sensor network, we simulated an additional clusterhead sensor node for these five traffic lane sensors. Thus, each of the five cluster member nodes would use the traffic data as input to our missing data imputation module to estimate missing values.

As previously mentioned, since there are no missing values from the chosen traffic monitoring highway segment, we simulate the missing data scenario by removing observations at random from the dataset for different percentages of missing data—i.e., 10%, 20%, …, 90% missing observations from each sensor node. The complete dataset serves as the ground truth for the following missing data experiments. Fig. 14 shows the raw speed readings from the five sensors over a 14 day period.

Fig. 14.

The raw traffic data from the VDS 1114748. There are five sensor nodes collecting speed readings over a period of 14 days.

To ensure the robustness of our approach, we split our data evenly into three parts and performed a 3-fold cross-validation. Each part of data has 1344 samples. Each part has a chance to be the training data, the validation data and the testing data. We have normalized the training & validation and training & testing data pairs between 0 and 1. Next, we process the validation sets and the testing sets by randomly removing data by specified missing percentages (e.g., 10%, 20%, …, 90%). We have generated 9 missing data sets with 10%, 20%, …, 90% missing data from each sensor. The missing data are removed at random for each sensor based on the missing percentage.

We compare our NN imputation technique with the EM imputation algorithm from the WEKA software package. The EM imputation algorithm stopping criteria is when the log-likelihood value is converged (i.e., less than 0.0001). Our NN imputation algorithm stops growing the kd-tree at 950 splits and only searches for 1 nearest neighbor. Fig. 15 shows the averaged Sum Squared Errors (SSE) of our 1-NN imputation vs. the EM-based imputation for different missing percentages. The errors were averaged over 3-folds of testing data. To determine the significance of these results, the student’s t-test is applied to the averaged Sum Squared Errors for the 1-NN imputation and the EM-based imputation. This test confirms that the differences are statistically significant, with a confidence level of 85%. From these experimental results, our NN imputation technique performs slightly better than the EM imputation technique with an 85% confidence interval. Both techniques become less stable as the missing percentages increase. In this experiment, the EM-based imputation becomes unstable when the missing percentages are high, compared to our technique.

Fig. 15.

The averaged Sum Squared Errors of the proposed NN imputation vs. the EM imputation for different missing percentages of the traffic monitoring dataset. The Sum Squared Errors were averaged over 3-folds of testing data.

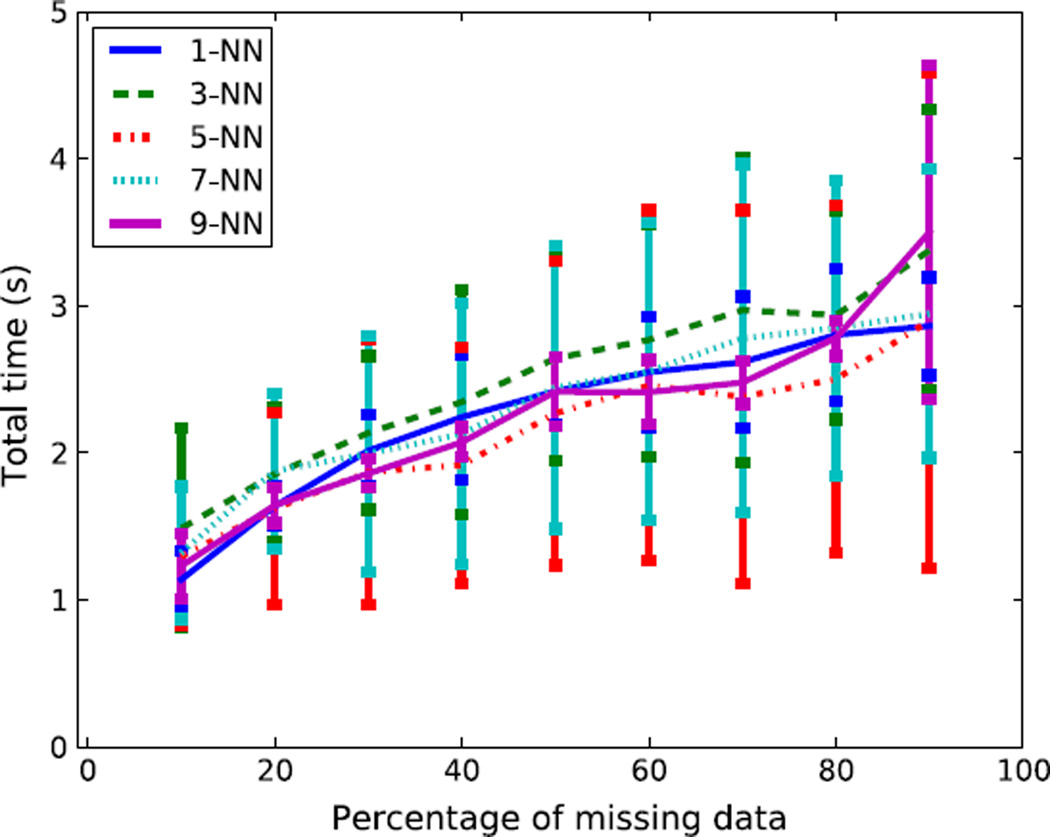
To determine the efficiency of our NN algorithm, we have calculated the total running time for imputation of all missing values in each testing trial. Then, the averaged total running times are computed for different missing percentages. Fig. 16 plots the averaged total running times of our NN imputation technique (green³) and the EM-based imputation technique (blue). The error bars indicate one standard deviation of time in seconds. Note that our developed algorithm is more efficient than the EM imputation technique, making it much more suitable for resource-constrained WSNs.

Fig. 16.

The average running time of the proposed NN imputation vs. the EM imputation for different missing percentages of the traffic monitoring dataset. The running times are averaged over 3-folds of testing data.

Next, we have analyzed our NN imputation performances by varying the number of nearest neighbors found. Fig. 17 shows the average SSE of 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9}). These experimental results show that the average SSEs of 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9} are about the same. In addition, as the missing percentage increases, the average SSE also increases.

Fig. 17.

The average Sum Squared Errors of the 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9} for different missing percentages of the traffic dataset. The Sum Squared Errors are averaged over 3-folds of testing data.

To determine the computational efficiency of finding different numbers of nearest neighbors, we have collected the statistics of average total running time. Fig. 18 shows the average total running time of searching 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9}). We have applied the student’s t-test to each pair of nearest neighbor imputations’ average total running times. These tests confirm that the differences are statistically significant between 3-NN imputation and 5-NN imputation with a confidence interval of 80%; and the differences are statistically significant between 1-NN imputation and 3-NN imputation with a confidence interval of 60%. Since the searching time for finding different NNs for traffic monitoring data are almost about the same, 1-NN should be used for the traffic monitoring application because it has less computational steps compared to multiple-NNs.

Fig. 18.

The average total time of the 𝒦-NN (𝒦 ∈ {1, 3, 5, 7, 9} for different missing percentages of the traffic dataset. The Sum Squared Errors are averaged over 3-folds of testing data.

In summary, we believe that the experimental results from the traffic monitoring application, combined with the volcano application, have illustrated that our proposed nearest neighbor imputation technique is flexible enough to be applied in very different application domains in WSNs, and can achieve a high performance. In both applications, we have used the state-of-the-art EM-based imputation technique as the baseline in comparison to our proposed nearest neighbor imputation technique. Our experimental results have shown that the NN-imputation techniques have comparable (sometimes better) performances with the EM-based imputation techniques in terms of micro/macro accuracies, and Sum Squared Errors. In addition, our NN-imputation technique out-performs the EM-based imputation technique in terms of computational time and space. This is mainly because our technique uses a online kd-tree that takes the advantage of the fact that the sensor network data tends to be correlated with time and space. We further improve the search performances of the existing kd-tree by adding a weighted Euclidean distance metric to consider both variations in sensor values and the missing data percentage of sensor nodes. These results also show that EM-based imputation techniques are not appropriate for WSNs for 2 main reasons: (1) the EM algorithm is expensive for resource-constrained sensor nodes, both in computational time and space; and, (2) the EM imputation technique is an offline method, which does not suit our online monitoring needs in environmental applications. Therefore, our NN imputation technique is more suitable for resource-constrained WSNs.

5. Conclusion

The environments that WSNs operate in tend to be both time and space correlated. A novel spatial–temporal missing data imputation technique has been developed that takes advantage of such correlations. We studied several alternative missing data imputation strategies to illustrate the potential of spatial–temporal missing data imputation. The experimental results show that making use of time and space information to estimate missing values allows the system to achieve high accuracy. However, the results also show that using the correct spatial–temporal model is important to achieve high performance. Thus, we developed a nearest neighbor imputation technique that learns the true temporal and spatial correlations among the sensor nodes. The NN imputation approach organizes a set of temporally and spatially correlated data into a kd-tree. To impute missing values, the system traverses the constructed kd-tree to find the nearest neighbor(s) of the querying data instance and replaces the missing values with the nearest neighbors. Unlike traditional kd-trees, a weighted Euclidean metric is developed that considers the probability of missing values during tree construction and search. We compared our technique with state-of-the-art EM-based imputation approaches, showing that our approach achieves similar accuracy while requiring much less computation, and achieving faster search times. These characteristics of our approach result in an imputation technique that is highly suitable for resource-constrained WSNs. Since our approach is a non-parametric technique that makes no assumptions of the underlying distribution of the data, it should be expected to achieve good performances in a wide variety of WSN applications.