miSTAR: miRNA target prediction through modeling quantitative and qualitative miRNA binding site information in a stacked model structure

Abstract

In microRNA (miRNA) target prediction, typically two levels of information need to be modeled: the number of potential miRNA binding sites present in a target mRNA and the genomic context of each individual site. Single model structures insufficiently cope with this complex training data structure, consisting of feature vectors of unequal length as a consequence of the varying number of miRNA binding sites in different mRNAs. To circumvent this problem, we developed a two-layered, stacked model, in which the influence of binding site context is separately modeled. Using logistic regression and random forests, we applied the stacked model approach to a unique data set of 7990 probed miRNA–mRNA interactions, hereby including the largest number of miRNAs in model training to date. Compared to lower-complexity models, a particular stacked model, named miSTAR (miRNA stacked model target prediction; www.mi-star.org), displays a higher general performance and precision on top scoring predictions. More importantly, our model outperforms published and widely used miRNA target prediction algorithms. Finally, we highlight flaws in cross-validation schemes for evaluation of miRNA target prediction models and adopt a more fair and stringent approach.

INTRODUCTION

MicroRNAs (miRNAs) are small, non-coding RNA molecules that regulate the expression of protein-coding genes at the post-transcriptional level. Since many important developmental and physiological processes are strictly regulated by miRNAs, it is not surprising that deregulation of miRNA function has been implicated in the pathogenesis of many human diseases (1). Understanding miRNA function has therefore been a major focus of biomedical research in the past decade.

In the canonical pathway, miRNAs guide a protein complex, named miRISC, to binding sites that most often reside in the 3΄ untranslated region (3΄ UTR) of target mRNA molecules. Subsequently, miRISC initiates inhibition of translation, deadenylation and decay of the target mRNA (2). Knowledge of target mRNAs is imperative to understand the role of a particular miRNA in both normal cellular processes and pathogenesis. Similarly, knowing the full complement of miRNAs regulating a particular mRNA is essential to comprehend its dynamic regulation that is tightly linked to its function.

Multiple experimental techniques are available to identify miRNA–mRNA interactions (3,4), but all of them share major disadvantages in that they are laborious, costly, technically challenging and have limited throughput. Therefore, considerable effort has been put into elucidating miRNA–mRNA pairing rules and model building for in silico miRNA target prediction, bypassing or preceding wet-lab tests (5,6). Predictive models enable researchers to prioritize interactions for experimental validation and to generate large-scale interaction information for biological network creation. Initially, published algorithms lacked an underlying statistical model and their predictions were based on scanning for the presence of features known or speculated to be important for an effective miRNA–mRNA interaction. More recent models are based on machine learning and do provide a statistical basis (5,6).

Here, we apply machine learning methods, in particular logistic regression (LR) (7) and random forests (RF) (8), to a unique data set of 7990 miRNA–mRNA combinations, probed for interaction in a high-throughput 3΄ UTR reporter screen. The data set includes interaction information for 470 miRNAs, which is the largest number of miRNAs included in algorithm training to date. We tackle the complex training data structure, inherent to the miRNA target prediction problem, with a unique stacked model approach that allows us to model both information on the number of potential miRNA binding sites, and the genomic context of binding sites. Modeling both levels of information has proven challenging in a single model structure, and has therefore been either ignored or poorly addressed in the past. Attempts to address this include simple summation of binding site scores (9,10), restricting training instances to those containing single sites (11) or considering the binding site as the training instance and adding binding site counts in the target as a feature (12).

Performances of stacked models are compared with those of models of lower complexity. The latter only model information on binding site counts or attempt to model both site counts and context in a single, non-stacked model structure. We highlight flaws in cross-validation schemes for performance assessment of miRNA target prediction models and adopt a more fair and stringent approach. Applying this approach, a particular stacked model outperforms lower-complexity models, and displays a higher general performance and equal or higher precision of high-scoring predictions when comparing with four published and widely used algorithms. Predictions of this model, named miSTAR (miRNA stacked model target prediction), can be queried online (www.mi-star.org). Altogether, the presented findings underscore the potential of the newly presented stacked model structure for improved miRNA target prediction.

MATERIALS AND METHODS

Training data set

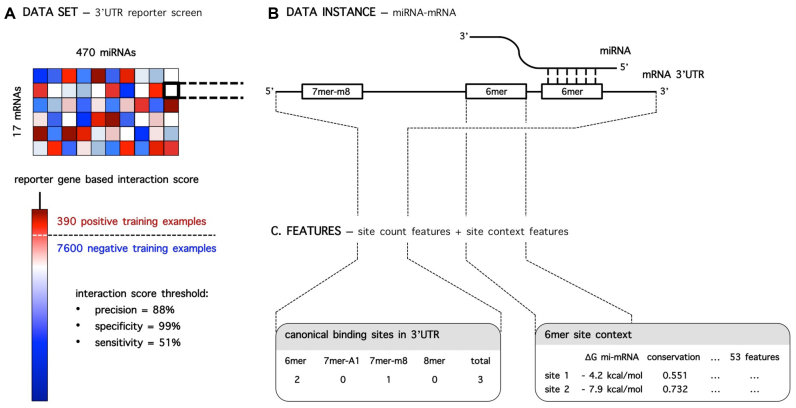
Training data was obtained from a 3΄ UTR reporter miRNA library screen, in which 7990 potential interactions between 17 human mRNAs and 470 miRNA mimics (miRBase release 9.2) were probed (Figure 1A; Supplementary Data). Interactions are identified with 88% precision, 99% specificity and 51% sensitivity, apparent from ROC-curve analysis on a set of positive and negative control interactions included in the screen (Supplementary Data). The data set contains 390 positive and 7600 negative training examples.

Figure 1.

(A) 3΄ UTR reporter screen data set: interaction information on 7990 miRNA–mRNA combinations. The data set contains 390 positive and 7600 negative training examples, identified with 88% precision, 99% specificity and 51% sensitivity. (B) Schematic representation of an example miRNA–mRNA data instance: three canonical binding sites are present in the 3΄ UTR. (C) Two levels of information are modeled: information on site counts and site specific genomic context information.

Potential canonical miRNA binding sites (13) in all probed miRNA–mRNA combinations were detected by alignment of miRNA sequences with 3΄ UTR sequences, resulting in five site count features: individual counts for 6mer, 7mer-A1, 7mer-m8 and 8mer sites and the total site count (Figure 1B and C; Supplementary Data).

The genomic context of each potential binding site was characterized by calculating 53 features (Figure 1C). Among others, they involve features describing the evolutionary conservation of the site, the accessibility of the site and the thermodynamic stability of the miRNA–mRNA duplex upon binding. A description of all calculated site context features can be found in Supplementary Data.

The training data set is available in Supplementary Data.

Model structure

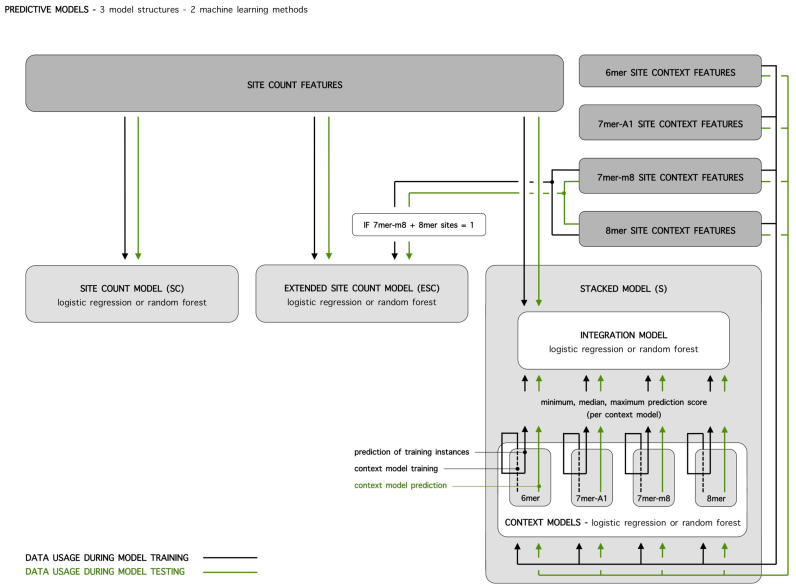
Since a miRNA can have a variable number of potential binding sites in a 3΄ UTR, the number of descriptive features calculated for each miRNA–mRNA combination varies greatly (i.e. it is a multiple of the number of binding sites). However, traditional machine learning algorithms, such as logistic regression and random forests, are designed to handle feature vectors of equal length and have difficulties handling complex data structures, such as the one presented. Therefore, we propose a two-layered, stacked model structure in which information on binding site context is separately modeled. For any miRNA–mRNA combination, the contribution of each potential binding site to effective interaction is predicted by models that only consider context information. Predictions for all sites present are subsequently summarized in a fixed number of context features that are combined with binding site count features to train the final model. In this way, the problem of feature vectors of unequal length is circumvented. We compare the performance of stacked (S) models with lower-complexity models that only model information on binding site counts—site count (SC) models—or that attempt to model both site counts and context in a single, non-stacked model structure—extended site count (ESC) models—and with four publicly available and widely used algorithms.

The SC model is the simplest model built in this work. The only predictive features taken into account are the counts of potential binding sites (five features). No additional information on binding site context is incorporated in the model (Figure 2).

Figure 2.

Overview of model structures and machine learning methods applied for the site count (SC), extended site count (ESC) and stacked (S) model. Data usage and information flow for model training and testing are indicated with black and green lines, respectively.

The ESC model is an extension of the SC model. Next to information on binding site counts, it incorporates context information for the two most potent canonical binding site types: 7mer-m8 and 8mer sites (referred to as potent sites below). The structure of this model is partly based on that of the MirTarget2 algorithm (11). MirTarget2 handles the complex data structure, with feature vectors of unequal length, by restricting training instances to instances with a single potent site, and thus an equal number of features. An approach like this, however, ignores a great part of available training data (91% of instances in our data set). Furthermore, it only models site context, and not the influence of the presence of multiple binding sites and possible co-operative interactions between them. Moreover, with 6mer and 7mer-A1 sites, it ignores other well-established, canonical binding sites. Here, we modified this approach and focus on single potent site instances to model site context influence, but contrary to MirTarget2 we do not filter out instances with no or multiple potent sites, as they still hold information on the importance of canonical site counts. More specific, in case a single potent site is present (726 of 7990 training instances), the site's context features are added to the canonical site count features in the feature vector of this particular miRNA–mRNA combination. If no or multiple potent sites are present, the site context features are set to zero. Training instances are thus characterized by feature vectors of equal length that capture information on the number of all types of canonical binding sites and the site context for single potent sites (Figure 2).

Finally, the S model uses all information available. Since the data obviously has two levels of information—information on the number of binding sites and on binding site context—the idea of using a single prediction model is abandoned. Instead, a two-layered, stacked model structure is applied. The S model consists of a layer of context models, that take into account the genomic context of sites, and a second layer with an integration model, that combines information received from context models with site count information (Figure 2). For each type of binding site, the influence of binding site context on effective interaction is modeled separately, resulting in 4 context models. Training instances for these context models are no longer miRNA–mRNA combinations, but individual binding sites. The feature vectors of these training instances only contain site context information and are all equal in length. In case a miRNA–mRNA combination has multiple binding sites (818 of 7990 instances), these represent multiple training instances in the context models and we attribute the label of the interaction to each of its sites. For any miRNA–mRNA combination, context model prediction scores for the binding sites present are added as additional features to feature vectors of the integration model that already contain site count features. However, to account for the fact that miRNA–mRNA combinations display varying numbers of binding sites (31% of the probed combinations have potential binding sites, of which 33% have more than one), predictions from each context model are summarized in a fixed number of context features: the minimum, median and maximum score. In this way, feature vectors of the integration model are of equal length, regardless of the number of binding sites present. The integration model has five features on the number of binding sites, and 12 features (3 features from each of the 4 context models) on site context.

Machine learning techniques

All models are built in the R statistical programming environment (version 3.0.2). LR with lasso regularization (glmnet package version 1.9-5 (14); λ with minimal cross-validated mean squared error) and RF (randomForest package version 4.6-7 (15); number of trees = 500; number of variables sampled per split = square root of the total number of variables) are alternately used to construct SC, ESC and both the integration and context models of the S model.

Performance estimation

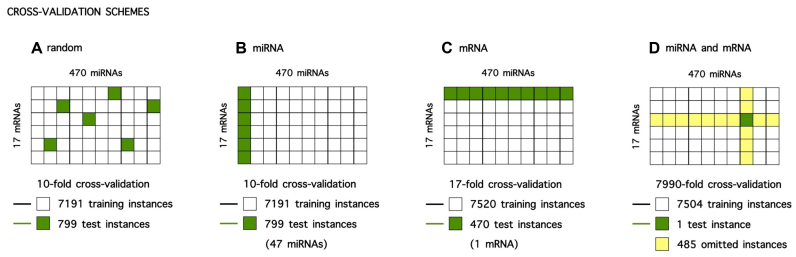
The performance of models based on a learning process is typically estimated using cross-validation, in which the data set is split up in a training data set for model building and a test set for performance estimation. In case a predictive model tries to model the interaction between two molecules, as with miRNA target prediction, a training instance consists of two objects, here a miRNA and a mRNA. The model may have learned from either both objects, only one object or none of the objects of the test instance during training, depending on how training and test instances were selected. Subdivision of data in a training and test data set can be either random or systematic, with selective inclusion of instances involving particular miRNA and/or mRNA specimens in the latter case. Four different cross-validation schemes are possible (Figure 3).

Figure 3.

Overview of (systematic) sampling of training and test instances in different cross-validation schemes. (A) Random cross-validation scheme. (B) miRNA cross-validation scheme. (C) mRNA cross-validation scheme. (D) miRNA and mRNA cross-validation scheme.

In random cross-validation, randomly selected miRNA–mRNA instances are omitted for model training and included in the test set for performance estimation. When predicting a test instance, the exact miRNA–mRNA combination is new to the model, but information on how both molecules interact with other mRNAs and miRNAs respectively, was most likely included in model training. Performance estimated with this cross-validation setting is therefore the most optimistic. In every fold of the k-fold cross-validation (k = 10) a random selection of 799 mRNA–miRNA instances is omitted from training data (Figure 3A).

In miRNA cross-validation, instances involving particular miRNAs are omitted for model training and included in the test set for performance estimation. In every fold of the k-fold cross-validation (k = 10), a model is trained on the data of all but 47 miRNAs (7191 instances) and performance is estimated on predictions for the instances involving these unseen miRNAs (799 instances) (Figure 3B).

In mRNA cross-validation, instances involving one particular mRNA are omitted for model training and included in the test set for performance estimation. Since there are only 17 mRNAs present in our data set, we apply a leave-one-out cross-validation. In every fold of the k-fold cross-validation (k = 17), a model is trained on the data of all but one mRNAs (7520 instances) and performance is estimated on predictions for the instances involving this unseen mRNA (470 instances) (Figure 3C).

In miRNA and mRNA cross-validation, instances involving either one particular miRNA or one particular mRNA are omitted for model training, and the single combination of this miRNA and mRNA is used for performance estimation. When predicting the single test instance, both the miRNA and the mRNA are unseen by the model, making performance estimation in this cross-validation scheme the most stringent. Note that performance estimation in this leave-one-out cross-validation is very computationally intensive, since the number of folds equals the total number of miRNA–mRNA combinations in the data set (k = 7990) and a new model has to be trained for every instance (Figure 3D).

For the SC and ESC models, data usage and information flow during cross-validation are straightforward: the model is trained on training instances, after which test instances are predicted and performance measures are calculated (Figure 2). For the S model data usage is more complicated. Site context features from training instances are used to train context models. Site count features of training instances are subsequently used to train the integration model, together with summarized site context features, received from trained context models. However, to provide these summarized context features for a given data instance, we exceptionally rely on prediction scores of context models that were trained on the same training instances (Figure 2).

General performance of a model is typically assessed using receiver operating characteristic (ROC) curves (16). A ROC curve plots the true positive rate as a function of the false positive rate for every possible prediction score threshold. The area under the ROC curve (AUC ROC) is a measure for the ability of the model to rank true interactions higher than non-interactions independent of prediction score threshold. Alternatively, the area under the precision-recall curve can be evaluated. A PR curve plots the proportion of predicted positives that are actual positives as a function of the true positive rate for every possible prediction score threshold. In unbalanced data sets with relatively few positive instances, PR curves have the advantage over ROC curves that they better capture the effect of increases in false positive classifications on model performance (17).

Performance of top scoring predictions is assessed using precision. Precision represents the fraction of positive predictions that are true interactions when applying a prediction score threshold for binary classification. Tailored to the application of miRNA target prediction algorithms as prioritization tools of interactions for wet-lab validation, we here consider the precision of the top 10 scoring predictions, a realistic number to pursue. In addition, we evaluate the mean precision of top 10 scoring predictions evaluated per mRNA, only considering mRNAs with at least 10 true interactions (15 out of 17 mRNAs).

Publicly available models

Performance of our models is compared to that of four models described in literature: miRanda (version August 2010) (18), TargetScan (version 6.2) (13,19), PITA (20) and MirTarget2 (11). These are three models without and one model with a machine learning basis, respectively. The selection of these algorithms is based on frequency of use in the research community and ability to perform custom predictions for our data set.

Statistics

All statistical analyses are performed using the R statistical programming environment (version 3.0.2). AUC ROC and area under the precision-recall curve values are calculated using the packages ROCR (version 1.0-5) (21) and pracma (version 1.7.0; http://cran.r-project.org/package=pracma), respectively. Comparison of AUC ROC values is performed with the pROC package (version 1.7.3) (22) according to Delong's method for the analysis of correlated ROC curves (23). Assessment of the influence of cross-validation schemes on the estimated performances is done by comparing AUC ROC or precision values, grouped according to the cross-validation scheme applied, using the Friedman test (24). Post-hoc analysis is performed with the Wilcoxon–Nemenyi–McDonald–Thompson test (24), using the coin (version 1.0-23) (25) and multcomp (version 1.3-4; http://cran.r-project.org/package=multcomp) packages.

RESULTS

Depending on the research question, the use of a predictive model that either displays a good overall performance or a high precision of top scoring predictions is desirable. High overall performance is desirable in case a ranked list of total predictions is used—for instance for enrichment analyses and in silico network building—and the ranking throughout the entire list should be as accurate as possible. High precision of top scoring predictions, on the other hand, is preferred in situations where the goal is to identify a limited number of interactions with high confidence, for instance when using target prediction for prioritization of interactions for wet-lab validation, where one is often limited in throughput and can only focus on the most likely candidates. Here, we assess different measures of model performance for stacked (S) and lower-complexity (SC and ESC) models, and compare them with non-cross-validated performances of four published models.

Pair-input cross-validation schemes influence performance estimation

Performances of models based on a learning process are typically estimated using cross-validation. An important, often overlooked aspect of cross-validation when predicting the interaction between two objects is the impact of training and test instance selection. Information on both objects of the test instance has to be systematically omitted from training data in order for the instance to be completely unseen by the model during model testing. If this requirement is not met, performances are systematically overestimated. However, just as for single-input modeling problems, for this kind of pair-input modeling, training instances are often randomly selected (26).

Hence, for a miRNA target prediction model, information on both the miRNA and the mRNA constituting a test instance has to be systematically omitted from training data. Alternatively, systematically omitting information on either the miRNA or the mRNA during training can assess the model's ability to generalize miRNA- and mRNA-related aspects of interaction, respectively. Models here were trained on data containing interaction information on a relatively high number of miRNAs, but on only few mRNAs. Since a model can learn more if more examples are presented to it, models trained on this data set are therefore expected to perform well at generalizing results when predicting instances involving unseen miRNAs, while it should have more difficulties handling unseen mRNA specimens. Including the often and erroneously applied non-systematic, random sampling of test instances, four possible cross-validation schemes can thus be applied in miRNA target prediction (Figure 3) (26).

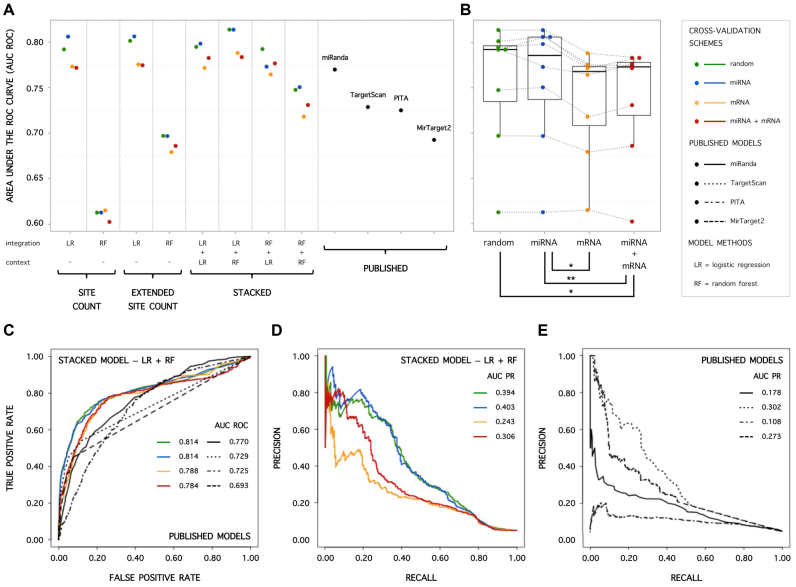
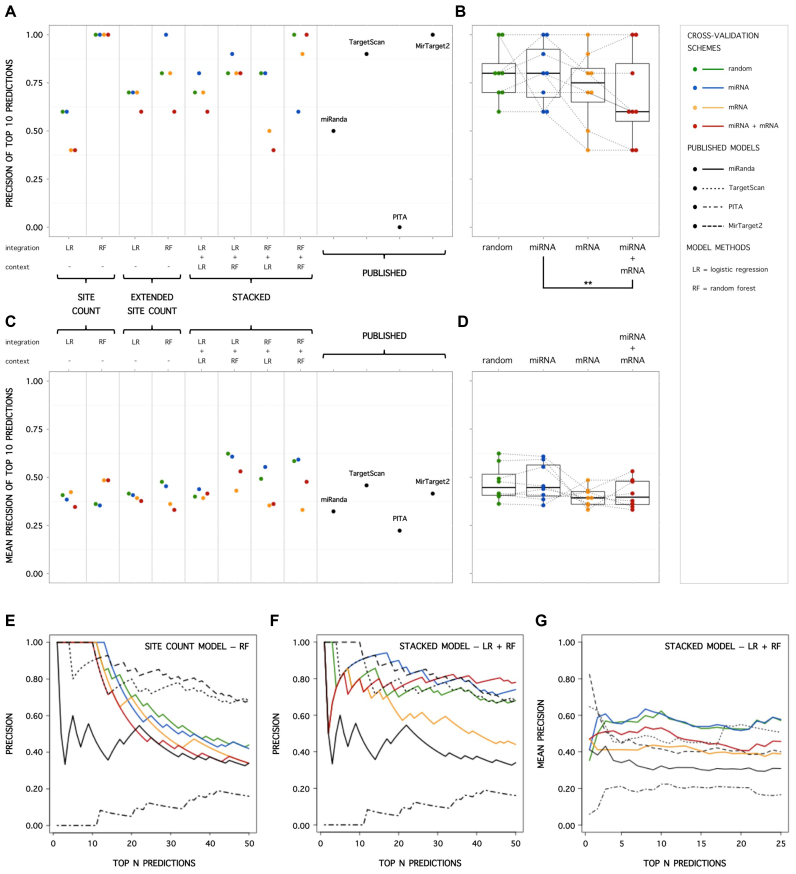
As expected, the estimated general performance of our models, calculated as the area under the ROC curve, is on average highest when we do not systematically omit instances involving particular miRNAs and/or mRNAs from training data, but randomly select miRNA–mRNA combinations as test instances (random cross-validation scheme) (Figure 4B). Selectively omitting instances involving particular miRNAs (miRNA cross-validation scheme) does not significantly lower the estimated performances (Figure 4B). Although the trained models have not seen the exact miRNAs presented in performance estimation, they received information on a high number of miRNAs during training and are good at generalizing miRNA-related aspects of constituting an effective interaction. In contrast, selectively omitting instances involving a particular mRNA during training, and subsequently predicting interactions involving this mRNA (mRNA cross-validation scheme) proves to be more difficult and results in lower estimated general performances (Figure 4B). Since the models only received information on a relatively limited number of mRNAs during training, the possibility of overfitting on specific traits of a mRNA is high, and generalization is hampered. Application of the most stringent cross-validation scheme (miRNA and mRNA cross-validation scheme) (Figure 4B), hardly has any influence on estimated performances compared to the mRNA cross-validation scheme, again showing that our models cope very well with unseen miRNAs. When estimating the model performances using the different cross-validation schemes, but considering the precision of top 10 scoring predictions instead of general performance, similar trends can be appreciated (Figure 5B and D).

Figure 4.

(A) Area under the ROC curve (AUC ROC) for SC, ESC and S models, applying different cross-validation schemes. (B) Influence of cross-validation scheme on AUC ROC values (Friedman test with post-hoc analysis; ** significant difference: P < 0.05; * borderline significant difference: P < 0.055). AUC ROC values of models with the same structure and machine learning techniques applied are interconnected. (C) ROC curves for the S-LR+RF model applying different cross-validation schemes and for non-cross-validated published models. (D) Precision recall curves for the S-LR+RF model applying different cross-validation schemes. (E) Precision recall curves for non-cross-validated published models.

Figure 5.

(A) Precision of top 10 scoring predictions for SC, ESC and S models, applying different cross-validation schemes. (B) Influence of cross-validation scheme on precision of top 10 scoring predictions (Friedman test with post-hoc analysis; ** significant difference: P < 0.05). Precision values of models with the same structure and machine learning techniques applied are interconnected. (C) Mean precision (per mRNA) of top 10 scoring predictions for SC, ESC and S models, applying different cross-validation schemes. (D) Influence of cross-validation scheme on mean precision (per mRNA) of top 10 scoring predictions (Friedman test with post-hoc analysis; no significant differences). (E) Precision as a function of the range (N) of top scoring predictions considered for the SC-RF model applying different cross-validation schemes, and for non-cross-validated published models. (F) Precision as a function of the range (N) of top scoring predictions considered for the S-LR+RF model applying different cross-validation schemes, and for non-cross-validated published models. (G) Mean precision (per mRNA) as a function of the range (N) of top scoring predictions considered for the S-LR+RF model applying different cross-validation schemes, and for non-cross-validated published models.

Highest general performance for a stacked model

Applying any of the cross-validation schemes, including the most stringent one, a stacked model that applies logistic regression in the integration model and random forests in the context models (S-LR+RF) systematically displays a higher general performance than lower-complexity SC and ESC models (Figure 4A; P-values ΔAUC ROC < 0.05). In addition, it significantly outperforms non-cross-validated published models (Figure 4C; P-values ΔAUC ROC < 0.05). Similar conclusions can be drawn when assessing the area under the precision-recall curves (Figure 4D and E).

Highest precision of top scoring predictions for a stacked model

A lower complexity model, applying random forests to site count information (SC-RF), displays the highest precision of top 10 scoring predictions, independent of the cross-validation scheme (Figure 5A). Maximum precisions are reached, just as for the published MirTarget2 algorithm. However, estimated precisions are strongly dependent on the range in which high precision is demanded. While being very precise in a narrow (and in practice often considered) range of 10 top scoring predictions, precisions rapidly decrease for the SC-RF model when further expanding the range (Figure 5E). Although scoring lower on the very narrow top of 10 predictions, the stacked S-LR+RF model obtains higher and more stable precisions when expanding the desired range (Figure 5F), producing similar precisions as MirTarget2 and TargetScan. This partly reflects the high general performance, independent of prediction score threshold, of the S-LR+RF model.

Furthermore, in realistic situations where high precision of top scoring predictions is desired, e.g. when prioritizing interactions for wet-lab validation, predictions are often obtained on a per mRNA or per miRNA of interest basis. Therefore, assessing the average precision of a model per mRNA or per miRNA is often more relevant, compared to assessing the precision of predictions for all possible miRNA–mRNA combinations. Considering the mean of precisions of top 10 scoring predictions estimated per mRNA entity, the S-LR+RF model again stands out compared to SC and ESC models (Figure 5C). Furthermore, even when stringently cross-validated, it reaches similar to better mean precisions when comparing with published models (Figure 5C and G).

DISCUSSION

In this work, we tackle the complex training data structure inherent to the miRNA target prediction problem. Using a two-layered, stacked model approach, we circumvent the problem of feature vectors of unequal length, as a consequence of the two levels of information that need to be modeled: the number of potential miRNA binding sites present in a target mRNA and the genomic context of each individual site. We apply the stacked model approach to a unique data set of 7990 probed miRNA–mRNA interactions, hereby including the largest number of miRNAs in model training to date.

Compared to lower-complexity models, a stacked model that uses random forests to model the contribution of individual sites and their genomic context, and logistic regression to combine individual contributions with site count information (S-LR+RF), displays a higher general performance and mean precision on top scoring predictions. More importantly, it outperforms currently available algorithms in general performance and reaches equal or better precisions. Transcriptome-wide, human target predictions of this new model, named miSTAR, can be queried online (www.mi-star.org).

In performance estimation, we apply more fair and stringent cross-validation schemes than typically done, acknowledging the fact that in pair-input prediction problems, information on both objects constituting the test instance has to be systematically omitted during model training in order for the instance to be completely unseen by the model. Hence, we avoid systematic overestimation of model performance. Furthermore, cross-validation schemes applied here uncover both the strength and weakness of our models, which are tightly linked to the training data set. Models trained on our data set obviously perform well predicting instances involving new miRNAs, while performance is lower when predicting new mRNAs. This is in contrast with most current machine learning-based algorithms that are expected to be particularly weak at handling unseen miRNA specimens, since they are typically trained on data sets containing interaction information on a large number of mRNAs and only one or few miRNAs (microarrays, mass-spectrometry and AGO CLIP-seq after exogenous miRNA modulation). Prediction databases, however, often offer target predictions for the full complement of miRNAs and mRNAs annotated in genomic databases, and ignore this limitation in generalization of the algorithms applied. Since models built here have opposite strengths and weaknesses to current machine learning-based algorithms with respect to generalization, they provide complementary information. However, the most performant model trained here still outperforms a machine learning-based algorithm trained on a high number of mRNAs (MirTarget2), when cross-validated probing its potential to generalize mRNA-related aspects of the miRNA–mRNA interaction.

In conclusion, we show that applying a stacked model approach can improve miRNA target prediction and recommend best practices in cross-validation for the performance assessment of miRNA target prediction models. The predictions of the best performing stacked model, named miSTAR, are available online (www.mi-star.org).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Multidisciplinary Research Partnership ‘Bioinformatics: From Nucleotides to Networks’ Project of Ghent University; Belgian Foundation against Cancer (Stichting Tegen Kanker) [SCIE 2010-177 to J.V.]; Emmanuel van der Schueren research grant from the Flemish League against Cancer (Vlaamse Liga tegen Kanker) [to G.V.P.]; a PhD grant from Ghent University [BOF 01D35609 to G.V.P.]. Funding for open access charge: Ghent University.

Conflict of interest statement. None declared.