How accurate are accurate force-fields for B-DNA?

Abstract

Last generation of force-fields are raising expectations on the quality of molecular dynamics (MD) simulations of DNA, as well as to the belief that theoretical models can substitute experimental ones in several cases. However these claims are based on limited benchmarks, where MD simulations have shown the ability to reproduce already existing ‘experimental models’, which in turn, have an unclear accuracy to represent DNA conformation in solution. In this work we explore the ability of different force-fields to predict the structure of two new B-DNA dodecamers, determined herein by means of ¹H nuclear magnetic resonance (NMR). The study allowed us to check directly for experimental NMR observables on duplexes previously not solved, and also to assess the reliability of ‘experimental structures’. We observed that technical details in the annealing procedures can induce non-negligible local changes in the final structures. We also found that while not all theoretical simulations are equally reliable, those obtained using last generation of AMBER force-fields (BSC1 and BSC0_OL15) show predictive power in the multi-microsecond timescale and can be safely used to reproduce global structure of DNA duplexes and fine sequence-dependent details.

INTRODUCTION

Since the first prototypes published in the seventies, DNA force-fields have been under continuum refinement (1–6). The accessibility of an increasing amount of experimental data and the possibility to perform high-level quantum mechanical calculations has provided the required reference data for force-field refinement, but the real engine behind the improvement of force-fields has been the continuum increase in hardware and software capabilities. Thus, as a new generation of hardware and software allowed the access to larger trajectory time scale, errors in the force-field emerged, forcing a community effort to solve them. In this sense, problems in twist emerging in sub-nanosecond scale parm94 (7) simulations led to the development of parm99 (8), which was the dominant force-field until multi-nanosecond trajectories reported the presence of artifactual α/γ transitions, which accumulated in time, corrupting the entire duplex (9). These issues were solved by the parmbsc0 (BSC0 from now on) revision (10), which became the ‘gold standard’ for almost a decade, until microsecond scale trajectories highlighted the existence of other errors, which required further recalibration of the force-field (1,2), leading to parmbsc1 (BSC1 from now on) (11) and to the Czech's family of force-fields (12–14) based on BSC0. A similar type of error-driven refinement happened for the CHARMM family of force-fields leading to the development of its latest two-body (15) and polarized versions (16).

There is little doubt that last generation of force-fields provides improved pictures of regular DNA duplexes (1–2,10–11). However, how accurate is really the global and local information derived from the MD trajectories? Are MD structures comparable in quality to the experimental models? Can theoretical ensembles be safely used in parameterization of lower-resolution models? Despite the optimism on last generation of force-fields, there is still little evidence on their predictive power, as large benchmark studies are rare (11,17–18) and often go in detail only for a prototypical duplex (the Drew-Dickerson dodecamer; DDD (19)). This is very risky, as DDD has been the standard test system in force-field refinement, which means that an agreement between theory and experiment for this duplex might be related to an overtraining artifact. Furthermore, the few extensive benchmarks performed to date (11) were typically based on the comparison of MD trajectories with reference ‘experimental models’, some of which have clear limited accuracy to reproduce details of the helical structure. Theoreticians tend to consider the experimental model in PDB as the ‘truth’, but any DNA structural biologist knows that the PDB has shown significant inconsistency in the quality of models (20), leading to structural artifacts in several of the deposited structures. For example, DNA often crystallizes in the A-form, as a left handed Z-DNA helix, or as an H-like conformation (21,22), while none of these structures is significantly populated in physiological conditions. Similarly, nuclear magnetic resonance (NMR)-derived structures can be dependent not only on the quality of the spectra, but on fine details in spectra acquisition and processing. Although frequently ignored, all experimental physical observables reflect temporal averages and when multiple conformations are present, the NMR observables quantities reflect an average over the different exchanging conformations. Moreover, most structural determinations of DNA derived from NMR methods rely mainly on two observables, NOE intensities (nuclear Overhauser effect) and J-coupling constants, which average over time in different ways. Due to this different kind of averaging, both types of constraints may represent contradictory information. DNA structures are usually determined through restrained molecular dynamics methods, which search for one single structure that satisfies all the constraints simultaneously. In flexible molecules as DNA, the attempt to fit all this information simultaneously may lead to artifacts that do not represent real structural features. Overall, caution is needed when using experimental structures as reference.

We present here a systematic unbiased validation of the last-generation force-fields for DNA. Firstly, we collected ‘de novo’ NMR data for DDD (labeled as SEQ1), which we used in different refinement protocols to determine the impact of spectra processing in defining NMR-derived structural models. The quality of these NMR-derived models can then be checked by comparison with a myriad of ultra-high resolution X-Ray structures, a very-accurate NMR model (1NAJ, (23)) and accurate wide angle scattering data (WAXS; (24)). This preliminary study provides information on the expected accuracy on the best NMR models that can be refined from typical NMR-data, and suggest an optimal refinement protocol. We focused then our attention in two other duplexes, for which no experimental information was available: d(GCTAGCGAGTCC)·d(GGACTCGCTAGC) (referred to as SEQ2) and d(GGAGACCAGAGG)·d(CCTCTGGTCTCC) (SEQ3), for which we have collected solution NMR data, solved their structures and compared them with previously obtained unbiased MD simulations.

The global structure of DNA is very well defined from the NMR spectra, and is quite robust to changes in the refinement procedure. However, sequence-dependent structural details are very dependent on details of the refinement procedure. Commonly used protocols result in unrealistically sharp distributions of local parameters due to compensatory variations along the duplex that can lead to sample extreme values of the expected distribution of helical parameters at the base-pair step resolution. Not all force-field derived trajectories are equally reliable, and some of them revealed structural artifacts in the sub-microsecond timescale. Considering the results presented herein, which extend the ones published recently, last generation AMBER force-fields, particularly BSC0_OL15 (14) and BSC1 (11) provide structural data (both global and local) of very high quality. In fact, our analysis suggest that expected quality of the ensembles obtained with last-generation AMBER force-fields is not worse than that of the NMR-derived structures and theoretical models derived from these force-fields can be safely used to describe DNA duplexes.

MATERIALS AND METHODS

Force-field selection

We evaluate here the most prominent AMBER and CHARMM families of DNA force-fields. From the AMBER family we test the default BSC0 (10), the BSC0_OL1 (13), refined in ε/ζ backbone dihedrals; BSC0_OL4 (12), refined in χ torsion, coupled with BSC0_OL1 (noted as BSC0_OL1+OL4); recently published BSC0_OL15 (14), refined in β backbone dihedral and coupled with previous corrections BSC0_OL1 and BSC0_OL4, as well asBSC1 (11). All these force-fields share the same non-bonded part of the force-field that comes from the old parm94 force-field (7). Lastly, we tried a DNA adapted version of Chen and Garcia's force-field for RNA (25,26) (noted as CG), which follow AMBER definitions, with refined χ torsion, as well as scaled vdW terms to reproduces weaker stacking interactions. From CHARMM force-field we benchmarked latest C36 for DNA (27) (noted as C36) and recent polarized version of the same force-field based on classical Drude-particle oscillators (16) (labeled as C36pol from now on).

System preparation

Simulations done with the AMBER14 suite of programs (BSC0, BSC1, BSC0_OL1, BSC0_OL1+OL4, BSC0_OL15, CG) were prepared using leap (28). C36 simulations were prepared using grompp from the GROMACS 4.5 simulation package (29), while simulations with polarized C36pol force-field were prepared using Drude Prepper from CHARMM-GUI server (30). NMR derived structures were used as starting points for the simulations. All the systems started from a canonical Arnott B-DNA structure (31), solvated in a TIP3P box of water molecules (32) with a minimum of 10 Å beyond the solute and neutralized with Na+ ions with additional 150 mM of NaCl. Ion parameters from Smith and Dang (33) were used for AMBER family simulations, while the default CHARMM ion parameters (34) were considered for that family. Several test calculations in the group (data not shown) discard the existence of bias in the results related to the MD engine used to collect trajectories (11).

Molecular dynamics simulations

We have performed 2 μs simulations of the three duplexes for each force-field, except for computationally demanding C36pol force-field for which we have performed 1.2 μs simulation of SEQ1 and 100 ns of SEQ2 and SEQ3 (use of the polarized force-field increases, using our computer resources, around 10 time the cost of the simulation). We have use Particle Mesh Ewald (35) as implemented in the programs AMBER14 (28) or GROMACS (29), with the default grid settings and tolerance. For C36pol simulations we used a special NAMD code (36). Unless otherwise noted NPT conditions with T = 300 K and P = 1 atm were used. All pair-wise additive simulations used an integration step of 2 fs in conjunction with SHAKE (37) or LINCS (38) (C36 simulations) to constrain bonds containing hydrogen atoms with default tolerance. We used default settings coming from CHARMM-GUI server for all C36pol simulations, which is mainly different to other simulations in using 1 fs time step and dual-Langevin thermostat scheme (30). For the simulations with CHARMM and the C36 force-field a 12 Å cutoff with a smoothing over 10 to 12 Å was used to treat Lennard-Jones (LJ) interactions. In contrast, for the AMBER simulations (all the tested force-fields) we used a hard truncation of the LJ interactions at 10 Å. All structures were first optimized, thermalized and pre-equilibrated for 1 ns using our standard equilibrium protocol (39,40) and were later re-equilibrated for 10 ns.

NMR structure determination

NMR spectroscopy studies were performed to obtain experimental geometrical constraints and the associated ‘structural models’ that can be then used to benchmark unbiased simulations.

NMR experiments

Samples of DDD (SEQ1), SEQ2 and SEQ3 duplexes (∼1.5 mM duplex concentration) were suspended in 500 μl of either D₂O or H₂O/D₂O 9:1 in 25 mM sodium phosphate buffer, 125 mM NaCl, pH 7. NMR spectra were acquired in a Bruker Advance spectrometer operating at 800 MHz, and processed with Topspin software. DQF-COSY, TOCSY and NOESY experiments were recorded in D₂O and H₂O/D₂O 9:1. The NOESY spectra were acquired with mixing times of 75, 100, 200 and 300 ms, and the TOCSY spectra were recorded with standard MLEV 17 spin lock sequence, and 80 ms mixing time. NOESY spectra were recorded at 5 and 25°C. The spectral analysis program Sparky (41) was used for semiautomatic assignment of the NOESY cross-peaks and quantitative evaluation of the NOE intensities.

NMR assignments and experimental constraints

Sequential assignments of exchangeable and non-exchangeable proton resonances were performed following standard methods for right-handed, double-stranded nucleic acids, using DQF-COSY, TOCSY and 2D NOESY spectra. Complete assignment could be carried out with the exception of some H5΄/H5΄ protons, and some guanine amino resonances which are not observed (see Supplementary Tables S1 and 2, for DDD see Hare et al. (42)). Spectral assignment pathways are shown in Supplementary Figures S1–3. Quantitative distance constraints were obtained from NOE intensities by using a complete relaxation matrix analysis with the program MARDIGRAS (43). Error bounds in the inter-protonic distances were estimated by carrying out several MARDIGRAS calculations with different initial models (standard fiber A- and B-forms), mixing times (100, 200 and 300 ms) and correlation times (2.0, 4.0 and 6.0 ns). Final constraints were obtained by averaging the upper and lower distance bounds in all the MARDIGRAS runs. No solvent exchange effects were taken into account in the analysis of NOE intensities in H₂O. Therefore, only upper limits were used in the distance constraints involving labile protons. In case of severe overlapping between cross-peaks, the NOE intensities are not considered reliable enough for the complete relaxation analysis and the only qualitative upper distance limits were set according to a visual classification of NOEs in strong, medium and weak. J-coupling constants were estimated from DQF-COSY cross-peaks. In all cases, DQF-COSY cross-peaks were consistent with South-type puckerings.

Refinement of the experimental structures

Two different approaches were used to derive ensembles of structures using atomistic force-fields based on the distance constraints obtained experimentally. The first approach, labeled as Standard in this work, refers to the classical and usual annealing procedure similar to that used to refine most NMR structures (32,33). Accordingly, ideal fiber B-DNA and A-DNA structures are thermalized (298 K) and equilibrated for 100 ps each (using the same options described previously), applying harmonic restraints of 100 kcal/mol·Å² on the DNA. Then, a 500 ps MD simulation is performed where the global restraints are replaced by the specific NMR distance constraints obtained experimentally (each represented by a harmonic restraint of 20 kcal/mol·Å²). To obtain the final ensemble, 50 structures (one every 10 ps) were chosen and minimized individually in vacuo at 0 Kelvin, keeping the NMR constraints. In a second approach different starting structures were used (using the three reference force-fields: BSC0, BSC1 and BSC0_OL15), as well as a different annealing protocol. The same thermalization and equilibration procedures were used but starting from equilibrated structures (taken after 1 μs of simulation time) obtained from the unbiased MD simulations described previously. Then structural ensembles were obtained in a three-stage procedure: first the NMR constraints were smoothly applied (from 0 to 500 ps) scaling linearly the harmonic restraints from 2 to 20 kcal/mol·Å², then the system cooled down during 50 ps from 298 to 50 K maintaining the restraints, and finally 500 ps of MD simulation at 50 K with the NMR constraints (20 kcal/mol·Å²) were used to generate the ensemble of 50 structures used to represent the experimental ensemble. Depending on the origin of the initial structures, and the force-field used in the refinement these ensembles were labeled in this work as: BSC0-NOE, BSC1-NOE and BSC0_OL15-NOE. It's worth nothing that we repeated our second refinement protocol for DDD using as starting conformations pre-equilibrated structures from the unbiased MD, but taken at 100 and 500 ns (more affordable simulation times for the general reader). As shown in Supplementary Table S3, changing the initial conformation in our new NMR protocol leads to a different set of structures with helical parameters slightly different, but still compatible with the previous results. Nevertheless, the ensemble obtained with a structure pre-equilibrated during 1 μs is still closer to 1NAJ and was chosen as the default in this work.

Analysis of trajectories

During production runs, data was typically collected every 1 ps, which allowed us to study infrequent, but fast movements. Geometrical analysis were carried out with AMBERTOOLS 14 (28), GROMACS tools, MDWeb (44,45,46), NaFlex (47) and the Curves+ package (48). As in our recent work (18), the 3D-RISM model (37, for details see 11) was used to compute the SAXS-WAXS spectra (Small-Angle and Wide-Angle X-ray Scattering) of the experimental structures 1BNA (X-ray, (19)), 1NAJ (NMR, (23)), 1GIP (NMR, (49,50)), the NMR structures derived in-house and the average structure from the unbiased MD simulations (computed with cpptraj from the last 200 ns of simulation). Even not experimentally available for comparison, we predict also the SAXS-WAXS spectra for SEQ2 and SEQ3 using the last-generation force-fields and the NMR models. The statistical analyses were obtained with the R 3.0.1 statistical package (51) and the ggplot2 library (52), or with MATLAB version 2014a (53). The molecular plots were generated using either VMD 1.9 (54), or the UCSF Chimera package version 1.8.1 (55).

RESULTS AND DISCUSSION

Are ‘experimental structures’ accurate?

As discussed above, ‘experimental structures’ are in reality models which fulfill a series or geometrical retrains derived from the processing of some experimental observables. In particular, most ‘NMR-experimental structures’ in solution are derived from MD simulations that incorporate three types of experimental restraints: (i) the interchangeability of protons which provide a direct information on the hydrogen bonding scheme, (ii) the J-couplings which provide direct information on certain torsional angles and (iii) the NOE intensities, which after processing yield average inter-proton distances. Additional restraints, such as the residual dipolar couplings (RDC) can be incorporated, but this is still not a common practice, and very few structures in PDB were refined considering RDC restraints. Fortunately for our purposes, DDD was used as a model for a tour-of-force of NMR refinement and structural ensemble at PDB entry 1NAJ was refined considering all possible NMR-derived restraints, leading to what is arguably the most accurate model of DDD in solution (23). Comparison of our ‘de novo’ NMR structure with 1NAJ provides us direct information on the errors expected in NMR-derived models obtained using the current standards for NMR structural refinement. Additional information on the accuracy of our new experimental structure of DDD can be obtained by comparing with high resolution X-Ray data (excluding terminal bases to reduce lattice artifacts), with other NMR-refined models (50) and finally with low resolution data derived from wide angle scattering spectroscopy in solution (WAXS; (24)). DDD is then an optimum model to evaluate the accuracy of NMR structural models.

We used two different procedures to derive structures from the NOEs collected in the NMR experiments. The first one, which can be considered as the standard in the field (also labeled standard in our work), starts from a fiber model of the double helix which is solvated, thermalized (at room temperature), and equilibrated imposing the experimental restraints. An ensemble of structures is finally obtained by minimizing in vacuo at 0 Kelvin a selected number of snapshots collected from the equilibration step (see Methods). In the second approach, structures previously equilibrated using unbiased MD simulations are used as starting points for the refinement procedure. In addition, the restraints are applied smoothly and the final ensemble of structures is collected from a restrained-MD cooled at 50 Kelvin (see Methods for more details). For DDD the standard procedure leads to a fast convergence of all trajectories to the B-basin, and to a narrow set of B-like structures which reproduce well the experimental restraints (Tables 1 and 2). The refined geometries are globally similar to previously reported ‘experimental structures’ for DDD (Table 1), but looking in detail disturbing differences become evident. For example, (Figure 1) twist of central d(ApT) step is very low in ensembles obtained using the standard refinement procedure compared with 1NAJ, with crystal structures and with the expected values derived from database analysis (Supplementary Figure S4). The under-twisting is corrected in neighboring d(ApA) steps, which adopt unusually large twist values (Figure 1 and Supplementary Figure S4) leading to an overall correct helix, but to probably unrealistic local geometries. Very interestingly, this sharp twist profile is not directly supported by specific NOEs in this region and it is not due to errors in the force-field (see below), but it is mostly related to potential equilibration artifacts probably produced by the sharp cooling of the system. In fact, when a more elaborated refinement procedure is used (second approach mentioned above, see ‘Materials and Methods’ section, Table 1 and Figure 1) with exactly the same experimental restraints, more realistic helical profiles are obtained for all the force-fields (Tables 1, 2, Figure 1 and Supplementary Table S4). Note that while the refinement procedure seems to have a significant impact on the final local structure of the double helix, changing the force-field appears to be not very relevant as the NMR-structures refined using BSC0, BSC1 and BSC0_OL15 are quite similar (Tables 1, 2 and Supplementary Table S4). Finally, a few words of caution are needed on the generalized use of the NOE violations as a direct undisputable measure of the quality of structural ensembles. Actually, NOE violations reflect the quality of the global fitting of all the distance constraints to a single structure and not the quality of the structures themselves. Thus, NMR-refined ensembles in PDB codes 1NAJ or 1GIP, or X-Ray structures lead to a non-negligible number of violations of our NMR data, while these experimental structural models are geometrically very close to our NMR model (Figure 1 and Table 2). On the contrary, the structural model refined from the standard procedure shows excellent NOE violation metrics, while local geometry is most likely unrealistic (Figure 1 and Table 2).

Table 1. Comparison of average RMSd values (in Å) of the NOEs-restrained MD simulations calculated in reference to NMR or X-RAY structures of the DDD sequence.

Structure	Standardc	BSC1-NOEd	BSC0-NOEd	BSC0OL15-NOEd
1NAJa	1.32	1.07	1.20	1.22
1GIPa	1.09	1.14	1.15	1.23
XRAYb	1.72	1.39	1.43	1.49
1JGR	1.64	1.35	1.35	1.46
4C64	1.67	1.37	1.39	1.48

^aThe RMSd calculations were done against an average structure obtained from NMR conformations with PDB code 1NAJ and 1GIP.

^bThe averages were obtained combining the X-Ray structures with PDB codes: 1BNA, 2BNA, 7BNA and 9BNA. Note that the capping base-pairs were not considered.

^cNMR structures obtained by using the standard refinement process with annealing and optimization using the default BSC0 force-field (see ‘Mials and Methods’ section).

^dNMR structures obtained by using the mild annealing procedure described in the ‘Materials and Methods’ section using 3 force-fields: BSC1, BSC0 and BSC0_OL15.

Table 2. Summary of NOE distances violation and energy penalties for the DDD sequence using the NMR data obtained in-house (see ‘Materials and Methods’ section)^a.

Structure	N° of violations	Energy penaltyb (kcal/mol)	Average violation (Å)	Largest violation (Å)
BSC1-NOE	8	20.4	0.35	0.46
BSC0-NOE	9	22.7	0.35	0.43
BSC0OL15-NOE	14	35.0	0.35	0.47
Standard NMR	5	11.3	0.33	0.40
1NAJc	35	159.2	0.47	0.63
1GIPc	50	265.4	0.51	1.06
X-RAYc	46	332.1	0.60	1.58

^aTaking T as 298.15 K, the kT constant has a value of 0.5924812 kcal mol⁻¹. We considered an experimental restraint violated when its average penalty energy was above 3·kT. Given the force constant used to apply the distance restraints (k_res = 20 kcal/Ų), 3·kT is equivalent to set a tolerance of ±0.3 Å on the experimental range to consider that a specific distance has been violated.

^bFor each distance the energy penalty (E_pen) was computed as: E_pen = k_res(dist_calc-dist_obs)². Note that we simply reported the sum of each individual E_pen.

^cA single-point calculation in vacuo was performed on the average experimental structure applying our NMR restraints.

Figure 1.

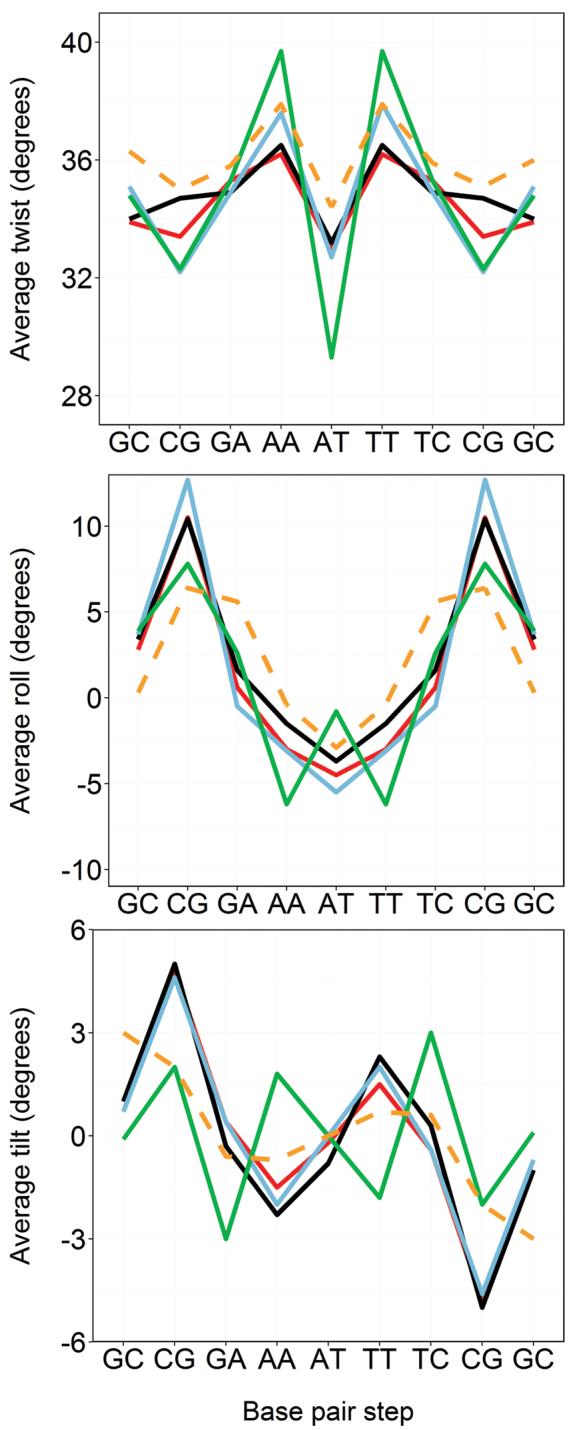
Average values of the average three rotational base-pair step helical parameters of DDD computed from NMR-biased MD simulations. BSC0-NOE (red), BSC1-NOE (black) and BSC0_OL15-NOE (blue). The standard procedure for refinement, based on fast annealing and optimization with the default BSC0 force-field is shown in green. The rest of profiles were obtained by implementing the mild annealing procedure described in the ‘Materials and Methods’ section. Profiles are compared with the highest quality NMR structure deposited in the PDB: 1NAJ (orange dashed line). Note that capping base-pair steps were excluded from the analysis.

In summary, our systematic analysis of the DDD duplex, strongly suggests that while global structure can be safely recovered by usual NMR-restrained models, some caution is needed when going to details, since they are dependent on the quality of the experimental data and on the way in which such data are processed. Also, it must be noted that the standard procedures for structural determination from NMR data try to fit all the experimental constraints to a single structure, which may lead to artifacts in cases when multiple conformations co-exist in equilibrium. This means that: (i) we should treat simulations results with some indulgence, as significant local deviations between NMR-derived models and theoretical results are not always signaling a poor quality of the later, and (ii) transferring helical parameters derived at the base-pair step level from NMR-data into coarse-grained models to reproduce structural properties of other DNA duplexes should be validated with care.

Do force fields corrupt duplex structure?

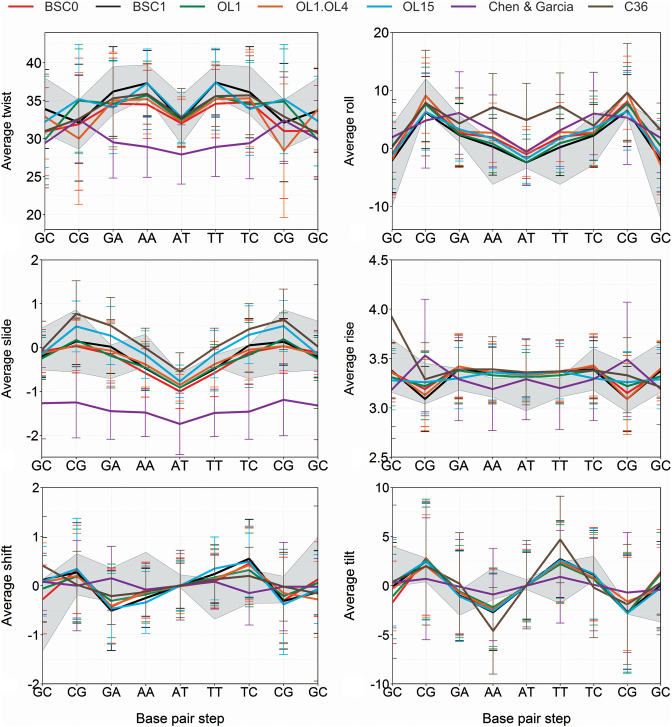
As described above, we have collected accurate NMR observables for three very different DNA duplexes, which in all the cases are found as stable B-type structures. We can then compare the structural models derived by imposing NMR restraints (using the mild refinement procedure outlined above) with unbiased μs-scale simulations performed with the different force-fields. As shown in Figures 2–4, not all the force-fields provide samplings consistent with the experimental data. For example, the scaling down of van der Waals interactions in CG force-field leads to structures which are far from those expected for a B-DNA duplex. C36 provides reasonable structures for the central portion of the duplex (perhaps with the exception of roll), but terminal fraying is too large, distorting the geometry at neighboring pairs (Figure 3 and discussion below). The newly polarizable C36pol force-field represents, in our opinion, a milestone in the development of a new generation of force-fields, as it is able to maintain the duplex integrity for around 100 ns, which should be considered a major success for this type of force-fields. However, there is room for improvement in the balance of the interactions, as all the duplexes simulated with this force-field are extremely distorted in the sub-μs scale (Figure 3). Trajectories obtained with BSC0, the different patches added to this force-field by Jurečka et al., and the new BSC1 force-field provide stable helices belonging in all the cases to the B-family (Figures 2–4).

Figure 2.

Averages and standard deviations of the 6 base-pair step helical parameters of DDD. All the tested force-field are compared with an experimental range (gray zone defined by the average ± standard deviation) obtained by taking the NMR structures 1NAJ, Standard (in-house data) and the X-ray structures with PDB codes: 1BNA, 2BNA, 7BNA, 9BNA, 1JGR and 4C64. The C36polforce-field leads to corruption of the helix for μs-scale simulation and results are not shown. See Figure 3 for structural models.

Figure 4.

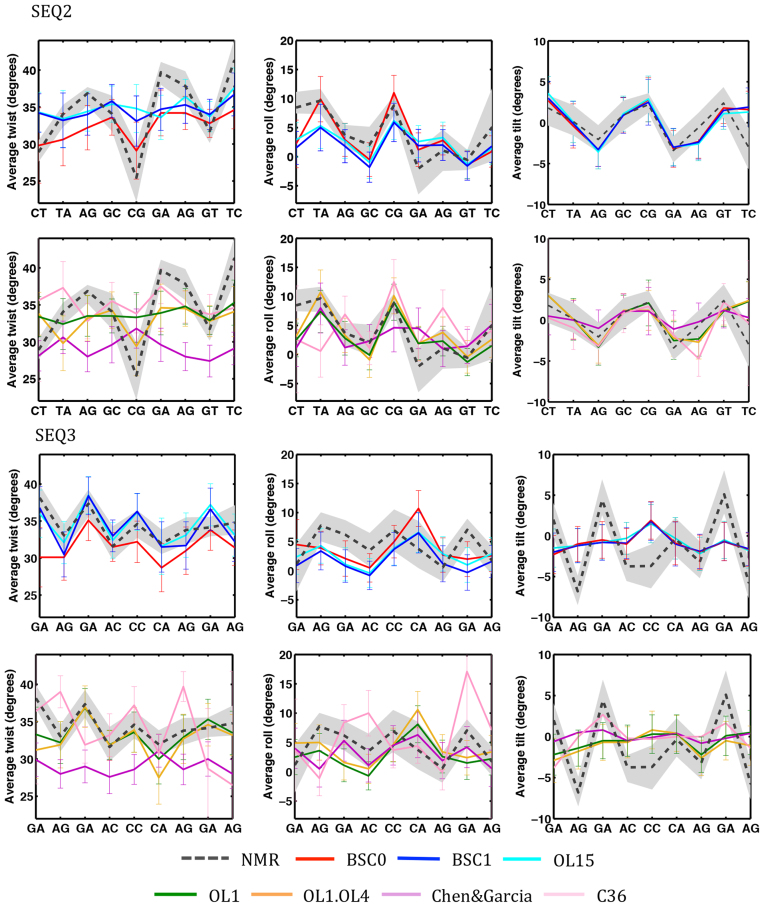
Averages and standard deviations of twist, roll and slide of SEQ2 and SEQ3. All the tested force-field are compared with the range of NMR structures refined using BSC1BSC0_OL15 (average in black dotted line) force-fields. The C36polforce-field leads to complete corruption of the helix in the μs-scale simulation and results are not shown. See Figure 3 for structural models.

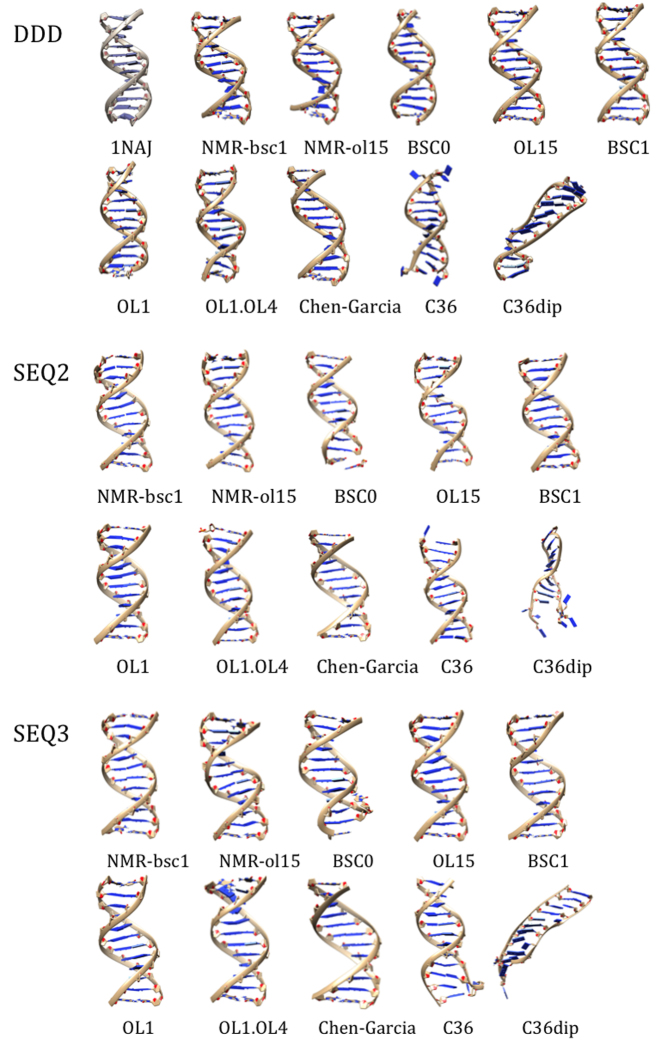
Figure 3.

Comparison of MD simulated (colored) structures with NMR obtained (top left; grayish) structures of the three sequences. The MD structures illustrated are average conformations taken from last 20 ns of the trajectory.

What is the global quality of theoretical DNA ensembles?

Unbiased MD trajectories obtained from BSC1 and BSC0_OL15 simulations provide samplings of the DDD conformational space that are globally hard to distinguish from the experimental models, as noted in RMSd in the range 1.3–1.7 Å (Table 3) to the different experimental structures, values which are not far from the range 1.0–1.5 Å found between the different experimental models (Table 1). Similarly, average helical parameters obtained from unbiased MD trajectories of DDD using BSC1 or BSC0_OL15 force-fields are within the experimental range of variability for this duplex (Table 4 and Figure 2). All other BSC0-based force-fields behave also reasonably well in terms of general structure for DDD, while significantly larger RMSd and worse helical parameters are found for the rest of the tested potentials (see also Figure 2). As discussed above, it is important to not only evaluate the similarity between unbiased MD samplings and experimental structural models, but also the ability of unbiased ensembles to reproduce direct experimental observables. Not surprisingly, unbiased BSC1 simulations reproduce very well NMR observables used to solve 1NAJ and encouraging, also the new NMR observables collected here (Table 5). In fact, the BSC1 unbiased trajectories for DDD seem to be more consistent with NMR observables than many of the experimental models deposited in PDB (compare Tables 2 and 5). Furthermore, BSC1 trajectories reproduce also very well the challenging WAXS spectrum, which is not well reproduced for most of the experimental models deposited in PDB (Supplementary Table S5). As expected from the previous sections the new BSC0_OL15 functional provides also good estimates of experimental observables, while slightly worse results are derived from BSC0, BSC0_OL1 and BSC0_OL1+OL4 force-fields. Large deviations between predicted and detected experimental observables are found in simulations performed with the other force-fields considered in this work (Table 5).

Table 3. Comparison of average RMSd values (in Å) calculated in reference to NMR or X-RAY structures of the DDD sequence.

Force-field	1NAJa	NMRb	X-RAYc	1JGR	4C64
BSC1	1.39	1.61 | 1.81	1.68	1.63	1.69
BSC0	1.77	1.87 | 2.04	2.78	2.06	2.17
BSC0OL1	1.65	1.72 | 1.87	1.90	1.83	1.91
BSC0OL1+OL4	1.85	1.74 | 2.00	2.06	1.94	2.03
BSC0OL15	1.46	1.67 | 1.83	1.66	1.65	1.70
CG	4.12	3.50 | 3.88	4.32	4.15	4.22
C36	3.29	3.27 | 3.40	3.40	3.37	3.40
C36pol	10.36	10.27 | 10.28	10.01	10.10	10.03

^aThe RMSd calculations were done against an average structure obtained from NMR conformations with PDB code 1NAJ.

^b de novo NMR data for the DDD sequence were obtained in our labs (see ‘Materials and Methods’ section). First row of numbers correspond to the NMR ensemble refined with BSC1, and the second row with BSC0_OL15.

^cAs in (a), the averages were obtained combining the X-Ray structures with PDB codes: 1BNA, 2BNA, 7BNA and 9BNA. Note that the capping base-pairs were not considered in RMSd calculations.

Table 4. Comparison of global twist and roll values (in degrees) and average canonical WC hydrogen bond count (HB%) with (all) or without (no ends) terminal base pairs.

		DDD			SEQ2			SEQ3
		Twist	Roll	HB %	Twist	Roll	HB %	Twist	Roll	HB %
BSC1	All	35.23	2.66	96.2	34.06	3.28	99.1	33.89	2.53	99.2
	No ends	34.39	1.47	99.7	34.65	2.13	99.2	34.09	2.05	99.4
BSC0	All	32.99	16.65	83.4	29.85	10.44	89.2	30.09	1.87	89.4
	No ends	32.81	2.41	99.6	32.34	3.22	98.7	31.54	3.78	98.1
BSC0OL1	All	34.16	15.85	84.8	32.75	3.88	95.5	31.52	3.71	90.6
	No ends	33.59	2.26	99.6	33.67	2.89	99.3	33.29	2.81	97.8
BSC0OL1+OL4	All	33.45	7.00	93.7	31.8	5.80	93.5	31.67	12.25	90.1
	No ends	33.12	2.71	99.5	32.94	3.80	99.1	32.64	4.04	98.4
BSC0OL15	All	35.01	2.97	98.7	34.62	2.30	99.1	34.27	2.90	97.7
	No ends	34.49	2.11	99.6	34.84	2.46	99.4	34.47	2.74	99.1
CG	All	28.05	5.42	87.2	29.62	3.12	99.9	29.2	3.39	97.6
	No ends	29.87	3.49	92.6	29.13	3.24	99.9	28.98	3.16	99.9
C36	All	30.06	19.00	85.2	30.56	13.14	79.2	30.57	9.26	78.4
	No ends	33.61	5.36	95.4	35.06	4.33	91.2	33.71	5.92	92.3
C36pol	All	30.72	1.47	49.4	29.11	0.63	52.8	18.46	3.43	68.4
	No ends	31.01	3.37	57.2	26.27	1.27	53.1	15.09	3.87	81.6
Standard a	All	34.46	4.71		34.38	3.36		34.51	5.65
	No ends	34.85	2.29		34.1	2.59		34.36	3.66
BSC1-NOE b	All	34.10	4.22		34.89	4.24		34.79	5.38
	No ends	34.85	2.37		35.14	4.12		34.63	4.68
BSC0OL15-NOE c	All	34.27	4.57		33.25	4.29		34.33	4.16
	No ends	34.69	2.29		33.72	3.91		33.97	3.58
1NAJ	All	35.71	3.27
	No ends	36.07	2.12
X-rayd	All	35.69	-0.31
	No ends	35.24	-0.73
1JGR	All	35.30	0.95
	No ends	35.36	-0.63
4C65	All	35.37	0.56
	No ends	35.44	-0.68

^aNMR values are averages derived from 10 NMR structures per sequence obtained in the group using standard refinement protocol.

^bNMR values correspond to the NMR ensemble refined with BSC1.

^cNMR values correspond to the NMR ensemble refined with BSC0_OL15.

^d The values were obtained combining the X-Ray structures with PDB codes: 1BNA, 2BNA, 7BNA and 9BNA.

Table 5. Summary of NOE distance violations from unrestrained MD simulations of the three duplexes using the NMR data obtained in-house (see Materials and Methods’ section) and 1NAJ (only for DDD)^a.

Force-field	N° of violations	Largest violation (Å)	Average violation (Å)
DDD
BSC1	40 | 2b	0.94 | 0.76	0.51 | 0.76
BSC0	37 | 6	2.11 | 1.35	0.66 | 0.83
BSC0OL15	46 | 4	0.94 | 0.79	0.48 | 0.77
BSC0OL1	32 | 4	1.98 | 1.17	0.65 | 1.00
BSC0OL1+OL4	35 | 5	1.27 | 0.87	0.54 | 0.63
CG	50 | 42	1.50 | 1.40	0.65 | 0.60
C36	124 | 93	6.86 | 6.44	2.63 | 2.57
SEQ2
BSC1	45	1.25	0.54
BSC0	53	4.15	0.83
BSC0OL15	46	1.37	0.54
BSC0OL1	42	1.53	0.64
BSC0OL1+OL4	46	1.56	0.61
CG	61	1.92	0.78
C36	66	2.42	0.87
SEQ3
BSC1	51	1.19	0.59
BSC0	51	2.18	0.78
BSC0OL15	56	1.30	0.55
BSC0OL1	81	4.73	1.89
BSC0OL1+OL4	84	5.52	1.84
CG	78	5.37	1.86
C36	86	3.37	0.94

^aWe considered an experimental restraint violated when its average penalty energy was above 3·kT. See the footnote comment to Table 2 and the ‘Materials and Methods’ section for additional details.

^bNumber reported in italic were computed using the NMR restraints from PDB code 1NAJ.

In summary, last generation of AMBER family of force-fields (BSC1 and BSC0_OL15) reproduces extremely well the general structure of DDD. However, this sequence has always been the guinea pig in force-field development and accordingly this good agreement might just reflect over-training in the force-field. We could argue that such over-training cannot explain agreement with WAXS spectra, or with the new NMR data presented here. However, to have a complete unbiased estimate of the quality of recent force-fields we collect trajectories for SEQ2 and SEQ3 duplexes for which no experimental information was available at the time of running the simulations. Results in Table 6 confirm the ability of BSC1 and BSC0_OL15 to sample conformations globally close to the refined NMR ones (RMSd around 1.6–1.8 Å; see Table 3), providing average helical coordinates which are very close to the experimental ones for both duplexes (see Table 4 and Figure 3). Furthermore, NOE violations (Table 5 and Supplementary Figure S3) obtained from BSC1 and BSC0_OL15 samplings are in the range of those found for DDD when NOEs were predicted from high quality experimental models (Table 2). In summary, ability of unbiased trajectories for SEQ2 and SEQ3 to predict experimental structures, rules out the over-training hypothesis, and demonstrates the accuracy of these force-fields in terms of global structure in solution (Supplementary Table S6). We cannot evaluate here the ability of BSC1 and BSC0_OL15 ensembles to reproduce WAXS spectra for SEQ2 and SEQ3 as we did for DDD, but we provide estimates for future experimental testing (Supplementary Table S7).

Table 6. Comparison of average RMSd values (in Å) calculated in reference to de novo NMR data collected in our lab refined using BSC1 (top value in the cell) or BSC0_OL15 (bottom value in cell) force-fields for SEQ2 and SEQ3^a.

	BSC1	BSC0	BSC0OL1	BSC0OL1+OL4	BSC0OL15	CG	C36	C36pol
SEQ2	1.69	2.10	1.69	1.80	1.72	3.36	3.41	7.39
	1.68	1.93	1.63	1.70	1.71	3.27	3.42	7.23
SEQ3	1.85	2.45	2.04	2.09	1.88	3.57	4.95	4.14
	1.79	2.35	1.96	2.02	1.86	3.34	4.92	4.07

^aNote that the capping base-pairs were not considered in RMSd calculations.

As expected from DDD results, previous BSC0-based force-fields behave reasonably well (Tables 3–6 and Figure 3). Structures obtained using the C36 force-field show some moderate distortions related to massive fraying (see below) and CG force-field yield to largely under-twisted structures (Tables 3 and 4) which are far from what is experimentally observed. Finally, as discussed for DDD the polarized C36 behaves very well for dozens of nanoseconds, but later the helical structure is lost (Figure 3 and Table 4), highlighting again on one hand the potential of this new force-field, but also the need for further refinements.

Are helix ends well represented by current force-fields?

The breathing of central base pairs is a very rare event, as it requires breaking dual stacking interactions, something very unlikely in microsecond-long simulations for coding bases ((56) and references cited therein), but stacking interactions are less intense for terminal base pairs, which are then expected to open more frequently. However, in the three duplexes considered here the helices are caped with C·G pairs, which means that in the simulated time we should expect slight breathing, but rare opening events (11,18). This hypothesis was confirmed experimentally, looking to the sequential NOEs collected herein, some of which provide direct information on local stacking. Indeed, as shown in Supplementary Figures S1–3 in the Supporting Information, central and terminal base pair steps appear to have very similar intensities, evidence of few or even inexistent fraying. Although our NMR data cannot provide a quantitative estimate of the opening frequencies, the experimental spectra are inconsistent with a massive opening of the terminal pairs, in disagreement not only with C36, C36pol, but also with BSC0, BSC0_OL1, BSC0_OL1+OL4 and CG simulations which provides an excessive fraying of terminal bases (Table 4 and Figures 3 and4). Trajectories collected with the last generation of AMBER force-fields are in much better agreement with NMR data, reporting a conservation of terminal hydrogen bonding above 96% of the simulation time and a low RMSd of the terminal bases respect to the closed conformation (Supplementary Figures S5–7). Similar conclusions about low fraying can be obtained from the data mining of crystal structures determined by X-ray and deposited in the Protein Data Bank. From a total of 318 structures (to date, considering only X-ray with a resolution better than 2.5 Å), only 5 duplexes in the PDB had at least one terminal base pair broken (we considered that a base pair was broken when the opening angle was lower than −10° or higher than 10°, which actually can be considered as a small structural distortion), representing 1.6% of the B-DNA structures analyzed. In addition, we noted by visual inspection, that in those 5 cases the open pairs showed hydrogen bond or stacking interactions with other nucleobases from other DNA molecules in the crystal lattice. Accordingly, the conservation of terminal pairing is an important improvement of BSC1 and BSC0_OL15 force-fields, since previous MD showed that the opened bases often interacted through the grooves with other regions of the DNA leading to a propagation of the structural distortion over the central portion of the duplexes (11,18,57–58).

Are sequence-dependent properties of DNA well reproduced by force-fields?

Massive initiatives, such as the Ascona B-DNA consortium (59) are using MD simulations on representative duplexes to trace sequence-dependent properties of DNA, providing parameters that can be then implemented in coarse-grained helical models to simulate long DNA segments (60). Unfortunately, except for a few cases (11,14,61), the validity of sequence-dependent geometrical parameters derived from MD simulations has not been yet demonstrated. Figure 2 shows that all BSC0-based force-field are able to provide reasonable profiles of helical properties along the central 10 bp part of the DDD sequence, but a detailed analysis shows the presence of some systematic biases that cannot be ignored. For example, BSC0 and BSC0_OL1+OL4 generate good relative profiles, but underestimate the twist (see above). The BSC0_OL1 and BSC0_OL15 simulations lead to good helical profiles in the entire duplex (Supplementary Tables S8 and 9; Figure 2) except for a certain over-twist at the d(CpG) step, which generates compensatory under-twist at the neighboring d(GpA) and d(GpC). An apparently incorrect balance in low/high twist populations at d(CpG) step seems to be the responsible of this effect (Supplementary Figure S8), which was also present in more extended BSC0_OL15 simulations by Cheatham and coworkers (17). BSC1 provide helical profiles, which are in practice, indistinguishable from the experimental ones for the entire DDD duplex (Figure 2 and Supplementary Tables S8 and 9). The C36 helical profiles deviate from the experimental one mostly because of the large fraying at the ends (Supplementary Tables S8 and S9), but if terminal base pairs are removed from the study the C36 helical profiles are reasonable except for some problems with roll. Globally (Supplementary Table S8 and S9) the CG helical profiles benefit from a better representation of helix termini, but systematic errors in some of the parameters are very clear (Figure 2), which warns against the use of this variant of BSC0. Finally, as commented above the C36pol force-field has problems to define properly the helical structure and helical profiles are unrealistic (Figure 3).

As largely discussed above, it can be claimed that the good ability of recent AMBER force-fields to reproduce DDD helical profiles might be a simple overtraining artifact. However, both BSC1 and BSC0_OL15 behave well in reproducing the helical profiles of two previously unknown structures SEQ2 and SEQ3 (Figure 4 and Table 7), and there are only a few, but interesting cases, where unbiased estimates disagree from the range of NMR solutions. For example, for SEQ2 both BSC1 and BSC0_OL15 trajectories suggest a smoother twist profile than that found in NMR-biased calculations, which suggest a very low twist (around 25°) at the central d(CpG) step which leads to a compensatory increase in twist the neighboring steps, with the d(GpA) step sampling twist values above 40 degrees. For SEQ3 the most significant difference between unbiased BSC1/BSC0_OL15 and NMR-restrained simulations are found for tilt, and at lower extend in roll, in both cases MD-unbiased profiles are quite flat, while they show sharp and compensatory variations along the sequence in the NMR-biased simulations.

Table 7. Global accumulated root mean square deviations (RMSd; first row in each cell) and mean signed error (MSE; second row in each cell) forthe six inter base-pair parameters (translations and rotations)^adetermined from MD simulations and those obtained from the same sequences using NMR-restrained ensembles^b.

Seq/FF	BSC1	BSC0	BSC0OL1	BSC0OL1+OL4	BSC0OL15	CG	C36
DDD	0.34	1.07	0.99	0.52	0.42	0.65	1.29
	0.00	0.26	0.26	0.06	0.06	−0.24	0.08
SEQ2	0.37	0.80	0.49	0.55	0.44	0.68	1.05
	−0.02	0.00	−0.09	−0.05	−0.01	−0.31	−0.13
SEQ3	0.39	0.84	0.65	1.02	0.57	0.71	1.11
	−0.02	−0.05	−0.09	0.06	0.04	−0.24	-0.17

^aWe used the normalization between translational and rotational parameters proposed by Lankas and coworkers (57).

^bValues considered here are the average of BSC0_OL15-NOE and BSC1-NOE simulations.

The analysis of DDD for which very accurate experimental structures were available warned us against too sharp profiles in NMR-refined structures (see above), as they can emerge as the result of the refinement procedure, rather than from direct experimental observables. Thus, we compared NMR-biased and unbiased helical values with equivalent distribution found at PDB (62). Interestingly, the low twist at the central d(CpG) step in NMR-derived structure of SEQ2 is consistent with 100% population in ‘low twist’ state, something that is uncommon in previous experimental structures of the same step (Supplementary Figure S9), which seems to favor a twist population similar to that obtained BSC1 and BSC0_OL15 simulations. The low twist at the d(CpG) step triggers the generation of twist values around 40 at d(GpA), which is rather unusual in other experimental structures, which align better with our BSC1 or BSC0_OL15 simulations (Supplementary Figure S9). The sharp compensatory tilt variations found for SEQ3 in the NMR-restrained simulations have not impact in the overall duplex structure, but lead to local tilt values very uncommon in other experimental structures (Supplementary Figure S10). Finally, large roll values (which compensate each other) found in NMR-restrained, but not in MD unbiased simulations for SEQ3 are again rather unusual in previously determined structures (Supplementary Figure S10). It is worth noting that these discrepancies found between unbiased and NMR-biased structures cannot be justified from the force-field used in NMR-refinement, as results obtained with BSC0_OL15-NOE and BSC1-NOE are very similar (Figure 4). Considering the lessons learnt from DDD it is not clear that discrepancies NMR-restrained and unbiased MD ensembles mean necessarily force-field errors, but can be related to technical details in the NMR refinement, in particular, the premise that a single structure can satisfy all the experimental constraints.

Are MD structures better than extrapolated models?

Very often structural studies of DNA use an average representation of DNA derived from fiber diffraction data by Arnott et al. (31). More elaborated models introduce sequence-dependence by using average helical parameters derived at the base-pair step assuming the near neighbor model and experimental data in PDB (63). More recent approaches average helical parameters at the base-pair level but in the tetramer context using then MD ensembles (9,59,62,64) as not many tetramers are well covered in PDB (2). The last question we try to answer here is whether atomistic MD simulations provide better results than those that can be obtained by using these simple extrapolated models. To investigate this point we used NAFlex (47), and ‘in house’ scripts, to create expected models using average helical parameters from Arnott-B (31) and average base pair step parameters from naked-DNA structures in the PDB (62). Additionally, we extracted from the μABC dataset (59) and BiGNaSim database (65) average helical parameters, at the tetramer level, which represent MD ensembles generated with BSC0 or BSC1 force-fields respectively. We compare all the models computing the RMSd of each bps in the helical space (Supplementary Figure S11 and Table 8) respect to the experimental NMR structures. The ensembles collected by last-generation AMBER force fields are clearly more accurate than the structures derived from Arnott's parameters, and to the structures that can be built (assuming perfect reconstitution of the backbone) by transferring helical parameters of other naked DNA duplexes in the PDB. Very interestingly, DNA models built using average values in stored BSC1 trajectories in BigNasim are quite reasonable, suggesting that structures generated from MD-averaged helical parameters can become an excellent starting points for structural studies of DNA.

Table 8. Global accumulated root mean square deviations for the six inter base-pair parameters (translations and rotations)^a determined for each model respect to the experimental NMR structures^b.

Seq/source	BigNaSim BSC1	μABC BSC0	X-ray naked-DNA	Fiber Arnott-B
DDD	0.46	0.62	0.53	0.93
SEQ2	0.74	0.70	1.35	1.42
SEQ3	0.74	0.70	1.35	1.26

^aWe used the normalization between translational and rotational parameters proposed by Lankas et al. (57).

^bValues considered here are the average of BSC0_OL15-NOE and BSC1-NOEresults. Note that the capping base pairs were not considered in the calculations.

CONCLUSIONS

We present here an evaluation of the predictive power of last generation force-fields to reproduce the structure and dynamics of two new DNA duplexes in aqueous solution. Our results show that not all recent DNA force-fields are equivalent in terms of accuracy, and in some cases force-field derived results are not of enough quality to correctly reproduce the structure of B-DNA. Last force-fields from the AMBER family (BSC0_OL15 and BSC1) provide without doubt the best results when comparing MD results with direct NMR observables. In addition, our results suggest that the procedures used to refine structures from NMR data can produce non-negligible noise in the fine details of DNA duplexes. Our study, still limited to only three duplexes, seems to indicate that unbiased MD simulations produced with BSC1 or BSC0_OL15 are not necessarily of poorer quality than those obtained by usual restrained-NMR MD refinement approaches that the scientific community end naming ‘experimental structures’.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Spanish Ministry of Science [BFU2014-61670-EXP, BFU2014-52864-R]; Catalan SGR, the Instituto Nacional de Bioinformática; European Research Council (ERC SimDNA); European Union's Horizon 2020 research and innovation program [676556]; European Union's Horizon 2020 research and innovation program under a Marie Sklodowska-Curie grant [654812 to G.P.]; Biomolecular and Bioinformatics Resources Platform (ISCIII PT 13/0001/0030) co-funded by the Fondo Europeo de Desarrollo Regional (FEDER); MINECO Severo Ochoa Award of Excellence (Government of Spain) (awarded to IRB Barcelona). Funding for open access charge: European Research Council (ERC SimDNA).

Conflict of interest statement. None declared.