The impact of base stacking on the conformations and electrostatics of single-stranded DNA

Abstract

Single-stranded DNA (ssDNA) is notable for its interactions with ssDNA binding proteins (SSBs) during fundamentally important biological processes including DNA repair and replication. Previous work has begun to characterize the conformational and electrostatic properties of ssDNA in association with SSBs. However, the conformational distributions of free ssDNA have been difficult to determine. To capture the vast array of ssDNA conformations in solution, we pair small angle X-ray scattering with novel ensemble fitting methods, obtaining key parameters such as the size, shape and stacking character of strands with different sequences. Complementary ion counting measurements using inductively coupled plasma atomic emission spectroscopy are employed to determine the composition of the ion atmosphere at physiological ionic strength. Applying this combined approach to poly dA and poly dT, we find that the global properties of these sequences are very similar, despite having vastly different propensities for single-stranded helical stacking. These results suggest that a relatively simple mechanism for the binding of ssDNA to non-specific SSBs may be at play, which explains the disparity in binding affinities observed for these systems.

INTRODUCTION

Single-stranded DNA (ssDNA) is essential to many key cellular functions (1–3). In most cases, protein partners bind to protect these vulnerable elements when they are exposed during DNA processing (4–7). Due to the multitude of sequences present in the cell, many ssDNA binding proteins (SSBs) must bind non-specifically to ssDNA targets. Given this task, we may expect these SSBs to bind with roughly equivalent affinity to all ssDNAs. However, this affinity is known to vary significantly across strand sequences (8–10). For example, the equilibrium binding constant of free poly dT single strands is orders of magnitude higher than that of poly dA in numerous SSBs within the same binding mode (11,12). What differences drive such disparity? To understand the interplay between these proteins and ssDNA, details of the conformations adopted by both molecules in free and complexed states are required. Unfortunately, the high flexibility of ssDNA limits our knowledge of its molecular conformations and associated electrostatic properties, especially in solution. Such information, which dictates the modes of interaction with proteins, is central to creating models of binding, which range from conformational capture through induced fit (13,14).

Most of what is known about DNA structure is derived from measurements on double-stranded duplexes and higher order structures such as nucleosomes and chromatin. Due to their size, propensity to crystallize and overall rigidity, these systems are amenable to study with high resolution methods such as crystallography, electron-microscopy (EM) and atomic force microscopy (AFM) (e.g. (15–20)). ssDNA is small and highly flexible by comparison, making it far more challenging to characterize. Crystal structures of ssDNA bound to SSB complexes can be obtained (21,22); however, only a small number have been solved, and they are restricted in salt conditions and strand sequences probed. Both EM and AFM have been applied to image unbound ssDNA over a range of ionic conditions (23,24), but (non-physiological) long strand lengths must be used. While nuclear magnetic resonance can examine intricate details of the bound ssNA–SSB complex (25), application to free single-strands remains limited to short sequences (26). Most studies of ssDNA are solution investigations that provide mean, global chain properties, such as persistence lengths in pulling experiments, end-to-end distances in Förster resonance energy transfer (FRET) measurements and radii of gyration in small angle X-ray scattering (SAXS) (e.g. (27–32)). These variables describe average solution structures, but are uninformative on chain to chain variations and on structural details at the short-length scales of relevance to biology.

Despite the limitations of solution-based approaches, key insights into ssDNA properties have been gleaned. Notably a connection is found between sequence and conformation (28,29,33,34). This association stems from the strong base-stacking observed in polypurines relative to polypyrimidines. In pulling experiments, stacking increases the mechanical stiffness and decreases the effective length of the former, and seeds a preconception that polypurine chains exhibit distinct conformations (32,35). For these flexible systems however, a description in terms of mean statistics can be misleading, and may obscure the richness of ssDNA conformations that are likely pertinent in biological systems.

In addition to base stacking, electrostatic effects determine the conformation of nucleic acids and affect their interactions with partner molecules. Ion association to the negatively charged phosphate backbone drives chain collapse, while positively charged pockets on protein partners can offer favorable binding sites. The electrostatic character of highly-charged polyions such as ssDNA can be revealed by measurements of the diffuse cloud of counter-ions that are attracted to the macromolecule. Anomalous SAXS (ASAXS) provides both the spatial distribution of ions around DNA, as well as a count of the number of excess ions attracted relative to the number present in the surrounding bulk solution (36). These measurements have primarily been performed on double-stranded DNA and RNA, where the known structure of duplexes facilitates comparison with computational and theoretical models (37,38). Although ASAXS has been used to count the number of ions around dT₃₀ (27), it is challenging to extract information about their spatial distribution, due to the range of ssNA conformations present. Finally, ASAXS is limited in application to heavy ions such as Rb⁺ or Sr²⁺ in place of the more physiological K⁺, Na⁺ or Mg²⁺.

Characterization of the electrostatic and conformational properties of ssNAs has thus proven difficult. Recently, two techniques have emerged to (partially) resolve these issues. The first pairs SAXS with ensemble optimization (EOM) (39–41). From a large pool of possible candidates, a genetic algorithm selects sets of model structures that best recapitulate the experimental scattering curve and therefore yield a detailed structural decomposition of the data. Distributions of global statistics such as the radius of gyration and end-to-end distance can be calculated from the selected states, providing an unparalleled picture of the underlying conformations. The second uses buffer exchange atomic emission spectroscopy (BE-AES) to probe the ion atmosphere (42). This approach exploits equilibrium dialysis to count the number of excess ions attracted to the nucleic acid. It reports not only the number of physiological relevant ions present, but also quantifies the effects of competing ions in mixed monovalent-divalent atmospheres. This technique has recently been extended to ssNAs, revealing the number of positively charged ions preferentially attracted to long chains of poly rU and poly dT at a variety of Na concentrations (43).

To gain new insight into the role of sequence in the conformational and electrostatic properties of ssNAs, we carried out SAXS-EOM and inductively coupled plasma AES (ICP-AES) studies on homopolymers consisting of nucleotides containing either T or A bases. These sequences were chosen to maximize differences in stacking interactions (44), and therefore represent extremes in ssDNA conformations and properties. This approach overcomes the difficulties associated with global averaging, obtaining representative solution structures and incisive short length scale parameters relating to the phosphate backbone and associated ion atmospheres. Despite dramatic microscopic differences of each chain in terms of base-stacking, these measurements show the effect of this interaction on conformation space is much subtler than previously thought. Furthermore, the conformations and electrostatic properties of dT₃₀ and dA₃₀ in solution are found to be surprisingly similar around physiologically-relevant ionic strengths. These findings have important implications for rationalizing the observed differences in ssDNA binding affinities to SSBs.

MATERIALS AND METHODS

SAXS experiments

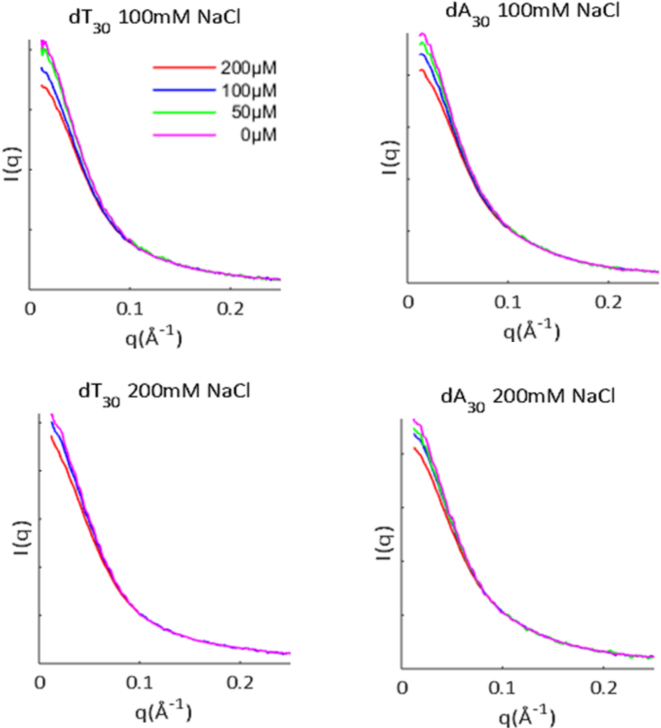
HPLC-purified DNA oligomers of dT₃₀ and dA₃₀ were purchased from Integrated DNA Technologies (Coralville, IA, USA). Lyophilized powders were resuspended in STE buffer (10 mM TRIS, 50 mM NaCl, 1 mM ethylenediaminetetraacetic acid (EDTA), pH 8.0) and dialyzed four times with either 100 mM NaCl or 200 mM NaCl, 1 mM Na MOPS pH 7 using Amicon Ultra-0.5 10kDa concentrators (EMD Millipore, Billerica, MA, USA). SAXS profiles were measured at Cornell High Energy Synchrotron Source (CHESS) beamline G1, at three DNA concentrations: 200, 100 and 50 μM. Buffer subtracted curves were matched in the range 0.10 < q < 0.25Å⁻¹, for accurate concentration normalization, and were linearly extrapolated to zero-concentration to remove any inter-particle interference effects observed at low scattering angle or q (see Figure 1 caption for definition). The zero-concentration curves were stitched at q = 0.10Å⁻¹ to the high concentration curve to provide the final, structure-factor free SAXS profiles. Due to a slight over-estimation of errors during the SAXS integration step, a rescaling of the uncertainties was performed. The inverse Fourier transform (IFT) of the experimental data was calculated with GNOM (45), after which the uncertainties on the experimental curves were rescaled so that the chi-square for the IFT fits were equal to 1. All data analysis was performed with MATLAB (MathWorks, Natick, MA, USA) using in-house code. Second virial coefficients were calculated as in (27).

Figure 1.

Extrapolation to infinite dilution of SAXS data for ssDNAs. SAXS profiles of ssDNAs were acquired at a minimum of two different sample concentrations (as shown in the legend), in solutions containing 100–200 mM NaCl. Intensity is shown as a function of q = 4πsinθ/λ, where θ is one half the scattering angle and λ is the X-ray wavelength. Interparticle interference results from like-charge repulsion between molecules, and was removed by linearly extrapolating to the zero concentration limit. The SAXS data and additional analysis can be found on SASBDB through accession codes: SASDB39, SASDB29, SASDB49 and SASDBZ8. Guinier and Kratky plots are reproduced in Supplementary Figure S1.

Ensemble optimization

A detailed method is prescribed in a companion paper (Ref. (41)). For each experimental condition, 15 refinement rounds were performed. In each round, a pool of 1000 structures was generated. For every member in the pool, SAXS profiles were calculated with CRYSOL (46), using a maximum harmonic order of 15, Fibonacci grid of order 18 and default hydration parameters. EOM was then performed with GAJOE 1.3 (39) to fit the experimental SAXS curves to those calculated from the pool of models, using an ensemble size of 20 and with repeat selections allowed. The algorithm was run for 50 generations and repeated 50 times. After the refinement rounds, a final selection round was performed. This differed from the previous rounds in that 10 000 models were generated in the pool, while 500 generations and repetitions of GAJOE were utilized. The structures selected in this final round were interpreted to give the final results. This process was repeated for each experimental condition independently.

ICP-AES sample preparation

Four DNA oligonucleotides were synthesized and HPLC purified by Integrated DNA Technologies (Coralville, IA, USA); sequence GCATCTGGGCTATAAAAGGGCGTCG (S1), its complement (S2), a 30-mer of deoxythymidine (dT₃₀) and a 30-mer of deoxyadenosine (dA₃₀). Lyophilized strands S1 and S2 were re-suspended in STE buffer (10 mM TRIS, 50 mM NaCl, 1 mM EDTA, pH 8.0) at a concentration of 0.5 mM. To generate a 25-base pair DNA duplex (ds25), strands S1 and S2 were mixed together in an equimolar ratio in a microcentrifuge tube, placed in a 95°C heat bath for 5 min and allowed to cool on the bench. ssDNA homopolymers were re-suspended in TE buffer (10 mM TRIS, 1 mM EDTA, pH 8.0).

Samples were equilibrated using centrifugal concentrators with buffers containing 10 mM Na-MOPS pH 7 and added NaCl ([Na⁺] = 20 mM) and either 0, 0.5, 1, 2, 5, 10, 15 or 20 mM MgCl₂. Eight dilution and concentration cycles were carried out with the volume of the concentrate kept above 100 μl. After the final concentration cycle, the concentrate and flow-through were immediately diluted 500- to 750-fold to concentrations appropriate for the ICP-AES instrument: for each dilution, 20–30 μl was added to 15 ml of 10 mM high purity ammonium acetate (Sigma-Aldrich) to promote solubility of trace metal ions (47). For all samples with bulk Mg concentrations between 0 and 10 mM, the DNA concentration pre-dilution (determined by ICP-AES) was 0.39–0.46 mM for dT₃₀, 0.45–0.53 mM for dA₃₀ and 0.16–0.32 mM for ds25. Higher DNA concentrations were used for the 15 and 20 mM Mg conditions to improve the single-to-background ratio: 1.1–1.2 mM for dT₃₀, 1.5–1.9 mM for dA₃₀ and 0.78–1.2 mM for ds25. Sources of uncertainty in the ion-counting experiment include pipetting error in the dilution step and detection noise or instability of the ICP-AES instrument. Therefore, 2–4 separate ICP datasets with independent calibration were acquired; several atomic emission lines were recorded for each element (3 for P, 2 for Na and 4 for Mg); and 3–4 separate dilutions were performed when feasible (excluding the DNA-containing samples with 15 and 20 mM Mg, where sample quantity limited the number of dilutions to 1).

Ion-counting with ICP-AES

Concentrations of the counterions and DNA were determined using an Optima 7300DV ICP-AES (Perkin Elmer, Waltham, MA, USA) within the linear detection range of the instrument: emission lines for elements P, Na and Mg were monitored (Cl⁻ anions were not detected) and integrated intensities were converted to concentration units by calibrating the instrument with standard solutions. The number of excess ions per phosphate was determined for each sample using:

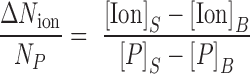(1)

Where the subscripts S and B, refer to the DNA-containing sample and the corresponding buffer flow-through, respectively. The competition curves were fit using a four-parameter phenomenological model from Ref. (42) (Hill-equation):

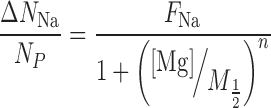(2)

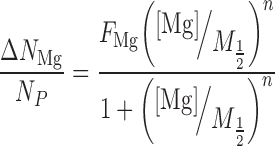(3)

Where [Mg] is the bulk concentration, M_1/2 is the competition constant, n is the Hill coefficient, F_Na is the excess Na/P ratio at [Mg] = 0 and F_Mg is the Mg/P ratio in the limit [Mg] → ∞. When analyzing the data, each ICP-AES reading was considered an independent measurement. Equations (2) and (3) were simultaneously fit to the data using the lsqnonlin function in MATLAB, where the points were weighted according to the standard deviation of all measurements for that sample, and errors in the fit parameters were estimated by boot-strapping (48). For presentation purposes, data points for each sample were averaged, and the error bars were computed as the standard deviation divided by the square root of the number of measurements.

RESULTS

SAXS experiments and pool generation

To probe dT₃₀ and dA₃₀ conformations under near-physiological ionic conditions, SAXS experiments were performed in solutions containing 100 and 200 mM NaCl. To remove any potential effects of inter-particle interference in the scattering data, SAXS profiles were acquired at a minimum of two sample concentrations for each solution condition. Linear extrapolation of these curves to the zero concentration limit ensures removal of concentration dependent artifacts (Figure 1).

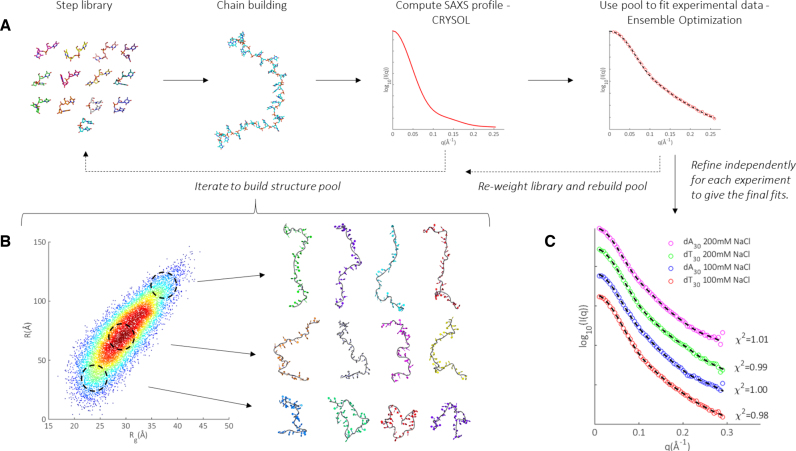
To analyze the data, we exploit a unique pool generation and iterative refinement scheme based on multiple rounds of fitting with EOM. This strategy is explained in Ref. (41), and illustrated in Figure 2A. In brief, we build ssDNA chains in a series of discrete dinucleotide steps, where the steps are derived from both DNA and RNA backbone consensus surveys (49–52). By drawing each step probabilistically from a library of representatives (tailored for a specific base), many distinct chains can be built to generate a large pool consisting of thousands of structural models. After calculating the theoretical SAXS profiles for each model using CRYSOL, EOM is performed to select sets of structures from the pool that best fit the experimental data. We then examine the selected structures to identify preferences for certain dinucleotide steps, and re-weight the library accordingly. A new pool of models is subsequently constructed from this updated library, after which another round of fitting and refinement follows. This process is repeated until the solution converges, at which point a final round of selection is performed with a fully refined pool. This dynamic pool generation and EOM led refinement is employed independently for each experimental condition, custom tuning the fully refined pools for each molecule and salt condition.

Figure 2.

Overview of pool generation and refinement for ensemble modeling. (A) We build chains from a library of representative steps, calculate the theoretical SAXS profile of each model and select ensembles from the pool that collectively fit the scattering data. The library is iteratively refined to improve pool quality. (B) Refined pool for dT₃₀ in 100 mM NaCl, visualized as a heat map in R_g and R space. Each structure in the pool contributes one point, located by its (R_g, R) value and heat corresponds to local density of points. For each region indicated by a dashed circle, example structures are shown to the right. Similar pools were generated for dT₃₀ and dA₃₀ and refined against the SAXS data in each salt condition (heat maps not shown). (C) Using this dynamic pool generation and iterative refinement scheme, excellent fits (dotted lines) to experimental SAXS data (circles) can be achieved. An enlarged version of this panel with experimental uncertainties and fit residuals is shown in Supplementary Figure S2. Structures were rendered using Pymol version 1.2 (DeLano Scientific LLC).

An example of a fully refined pool is illustrated in Figure 2B for data acquired on dT₃₀ in 100 mM NaCl. To visualize the distribution of chains, we represent each structure as a point in a two-dimensional space of the radius of gyration (R_g) and end-to-end distance (R). These complementary parameters capture the rough size and extension of the generated chains. Each model contributes one point to the plot. To represent the density of structures, the number of points within a 2Å radius centered about each point in the space is computed and shown as heat/color on the map. Red (hot) areas are more densely populated than blue (cold) areas. To demonstrate the breadth of chains constructed with this approach, structures at varying locations in this space are shown. Those at the smallest end of R_g-R space are tightly wound and compact: these conformations might be expected at high salt conditions. At the opposite extreme, near fully extended, straight chains exist, as might be expected in lower salt conditions. The middle region of space, containing the bulk of structures in the pool, comprises a rich vein of intermediate conformers with varying global sizes and shapes. At this stage, the range of conformations available in the final pool is vast. While the steps comprising the chains are correctly weighted, we have yet to select the subset of these structures that best represent the size and shape of the conformers in solution. This selection occurs in the final round of EOM, where 500 sets of 20 member ensembles are selected from the fully refined pools, with each ensemble independently reconstructing the experimental SAXS data. The fits achieved using this approach, shown in Figure 2C, illustrate the power of such a dynamically varying pool: the value of χ² is close to 1.

Ensemble optimization reveals conformational distributions

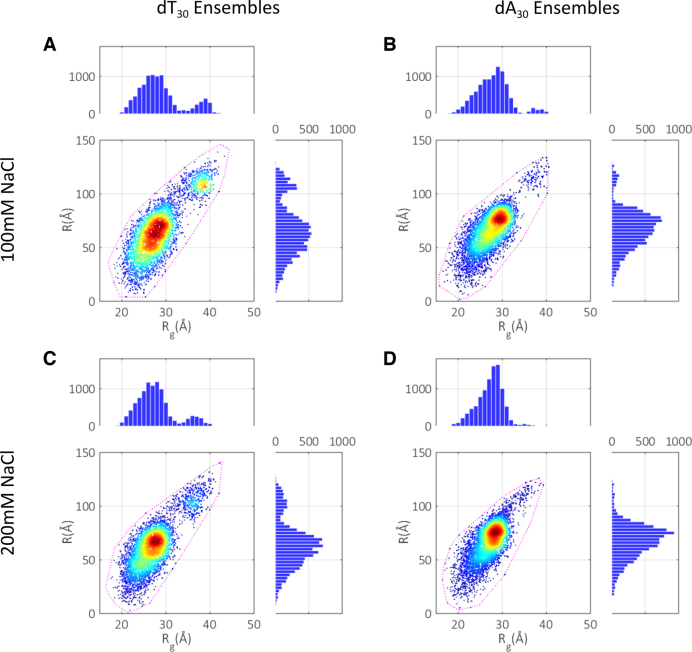
The final selection reduces the pool to reflect the subset of structures present in solution. These refined spaces for each experimental condition are shown in Figure 3, together with the projections of each ensemble onto R_g and R spaces. Most striking is the range of chain conformations sampled; all types of structures are included in the ensembles: small and compact, long and extended as well as a wide array of intermediate sizes. This striking conformational flexibility is further emphasized by comparing the selected models to the bounding states of the pool (illustrated by the dashed purple contours), with almost the full span of available structures utilized. The similar overall extent of both dT₃₀ and dA₃₀ in R_g and R space indicates a surprisingly similar range of accessible conformations. Some notable differences are observed: the conformational landscape is slightly broader for dT chains, displaying a lower density of structures near the central region of the R_g/R maps than is seen in the dA maps. This point is emphasized when examining the widths of the projected distributions (Table 1). While both dA₃₀ and dT₃₀ chains display large standard deviations in both distributions, the purine sequences are in general slightly more constrained than the pyrimidines. This restriction suggests a greater preference for certain sized conformers in dA₃₀ compared to dT₃₀. In addition, the dT₃₀ maps appear to have a more exaggerated secondary population at high R_g and R. We hesitate to interpret this feature however, as this may be an artifact caused by noise in the SAXS curves in the mid-q range.

Figure 3.

Conformation spaces selected in the final round of ensemble optimization. (A) dT₃₀ at 100 mM NaCl. (B) dA₃₀ at 100 mM NaCl. (C) dT₃₀ at 200 mM NaCl. (D) dA₃₀ at 200 mM NaCl. The bounding contour of the fully refined pools (the outline of Figure 2B for each experimental condition) are indicated by the dashed lines. The selected distributions are also projected onto the R and R_g axes, and visualized as histograms. Mean values and standard deviations of the projected distributions are given in Table 1.

Table 1. Mean values of R_g and R calculated from the distributions in Figure 3 (± one standard deviation).

	dT30 100 mM	dA30 100 mM	dT30 200 mM	dA30 200 mM
Mean Rg (Å)	28.8 ± 5.0	27.9 ± 3.9	27.7 ± 4.4	27.3 ± 3.0
Mean R (Å)	67.1 ± 25.6	67.5 ± 19.8	64.3 ± 22.1	67.2 ± 16.9

With increasing salt, reduced repulsion between segments of the charged phosphate backbone permits closer contact of chain elements, resulting in a shift of the populations to the low R_g, low R corner of conformation space. This shift coincides with an increase in the density of structures and corresponding decrease in standard deviations in R_g and R at higher salt concentrations for both sequences. A slight constraining of accessible states and a decrease in conformational flexibility therefore occurs for both molecules. Finally, the mean statistics reveal that on average, dA chains are slightly more extended than dT chains, but paradoxically more compact.

Iterative refinement gives representative structures

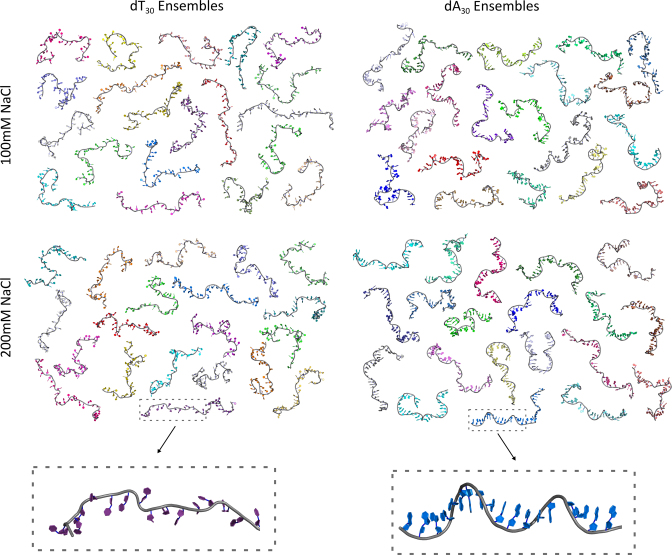
The use of an iteratively refining pool allows us to view a representative ensemble of structures selected for each condition, as shown in Figure 4. Upon visual inspection, it is clear that a variety of chain geometries are selected from a broad range of conformational space. Interestingly, no common theme or global structural motifs are observed in chains of like sequence or salt. However, a distinction can be seen in the shape of the dA₃₀ backbone relative to dT₃₀. While the latter are generally random-coil like and straight, the former are tortuous in nature and feature a number of stacked bases.

Figure 4.

Ensembles of representative structures. Four 20-membered ensembles whose theoretical SAXS profiles sum to reconstitute the experimentally measured curve for each solution condition are shown. A close-up view of one structure from the dT and dA ensembles is also shown to exemplify the differences in backbone style for each sequence. These structures can be accessed via SASBDB through codes: SASDB39, SASDB29, SASDB49 and SASDBZ8.

Once an ensemble of structures has been identified, any number of backbone parameters can be derived, including persistence lengths, orientation correlation functions and contour lengths. Given the expectation that base-stacking and electrostatics are important for chain conformations and binding, we concentrate on quantifying these interactions. The stacking character of each polymer can be easily assessed by calculating both the mean number and length of the stacked bases per chain for all models in each ensemble. Due to the limited resolution of SAXS, we are not sensitive to isolated instances of stacked bases. Therefore, to obtain a reasonable estimate of the mean number of stacked bases, only stacked runs that persist for at least three bases are counted in subsequent analysis. Both A and B-form stack steps are represented in our chain building algorithm, however those with B-form conformations are overwhelmingly selected. Little if any A-form is present. A stacked base therefore implies B-form. For electrostatic interactions, the location of negatively charged phosphates on the backbone is an important parameter that quantifies the linear charge density of the chain. To assess this, we calculate the mean phosphate–phosphate distance (L_pp), defined as the contour length divided by the number of bases averaged over all models in the ensembles. These metrics are reported in Table 2.

Table 2. Summary of base-stacking statistics and interphosphate distances (L_pp) for each experimental condition.

	dT30 100 mM	dA30 100 mM	dT30 200 mM	dA30 200 mM
Mean stacked bases	4.7 ± 3.5	17.8 ± 4.5	5.0 ± 3.5	24.1 ± 3.3
Mean stacked length	N/A	3.7 ± 1.0	N/A	5.6 ± 2.0
Lpp (Å)	6.7 ± 0.1	6.8 ± 0.1	6.6 ± 0.1	6.8 ± 0.1

Values reported are the mean ± one standard deviation. Due to the lack of stacking character within poly dT, we refrain from providing an estimate of the average stacked length.

In both salt conditions, dT₃₀ displays minimal base-stacking: roughly a sixth of all bases in the chain participate in these interactions. In contrast, dA₃₀ stacks considerably, involving a significant fraction of the backbone in helical or partially helical winds. The nature of this stacking is distinct in both sequences. In poly dA, persistent stacks of moderate length (3–6 bases) are frequent, leaving only short stretches of free-bases between them. On the other hand, poly dT chains contain long stretches free of any stacking. These differences account for the variations in backbone shape in the ensemble structures, and explain how dA₃₀ can appear longer yet more compact than dT₃₀. As the base-stacking motif is helical, a greater number of electrons are closer to the scattering center than an equivalent end-to-end length of a straighter backbone. With added salt, the number of stacking interactions increases for dA₃₀, but remains stable for dT₃₀. In spite of this increase, a few dA bases remain unstacked at the higher salt condition. Combining the relatively large standard deviations in the mean stacked bases with the structures shown in Figure 4, we conclude that poly dA is not a rigid single-helix locked in a fixed conformation. Instead, it contains ‘free’ unstacked bases which can aid in chain collapse and exploration. In terms of mean inter-phosphate distances, no significant change is seen for either molecule with increased NaCl concentration. These distances appear to be weakly correlated with the number of stacked bases, with the highly stacked dA ensembles displaying slightly larger inter-phosphate distances than their dT counterparts. These differences are however subtle, as the inter-phosphate distances for all four cases considered are the same within a standard deviation (Table 2).

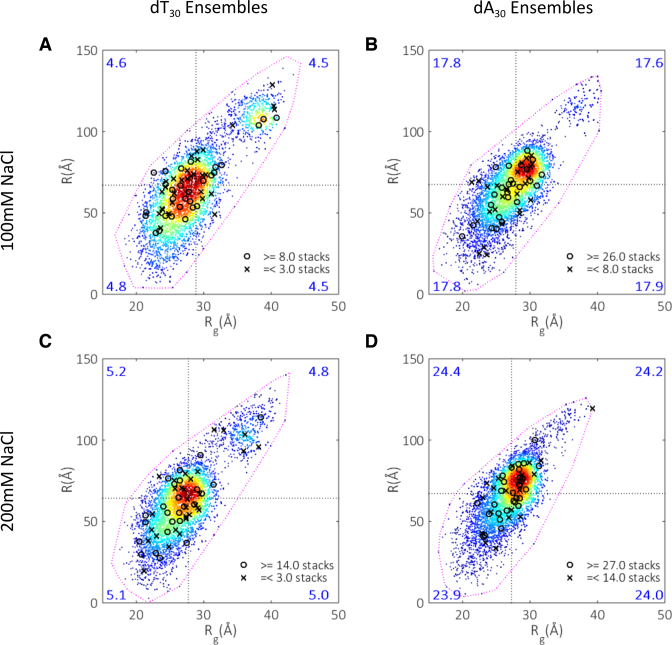
To understand how stacked bases affect global chain conformations, we divide each ensemble into four groups (quadrants) according to a member's value of R and R_g, and calculate the number of stacked bases for each quadrant (Figure 5). Surprisingly, the largest extended quadrant and the smaller compact one share roughly equal mean stack composition for both molecules and salt conditions. In fact, there is no strong correlation between the mean number of stacked bases per structure with the quadrant in which a given model falls. Additionally, there is no definite location for the structures that display extreme stacking behavior; both minimally and maximally stacked examples are found at a range of global conformations.

Figure 5.

Stacking maps. Each space is divided into four quadrants, with the divisions marked by the mean R_g and R for each ensemble. The mean number of stacked bases per structure is calculated for each quadrant and displayed in the relevant corners (large numbers). Extreme examples of stacked structures are located by circles (highly stacked) and crosses (least stacked). The specific number of stacked bases defining these extreme structures is shown in the legend accompanying each panel. (A) dT₃₀ at 100 mM NaCl. (B) dA₃₀ at 100 mM NaCl. (C) dT₃₀ at 200 mM NaCl. (D) dA₃₀ at 200 mM NaCl.

ICP-AES reports on electrostatics

As a probe of the electrostatic properties of these ssDNAs, we used ICP-AES to count the number of Na⁺ and Mg²⁺ ions around dT₃₀ and dA₃₀, relative to the number in the buffer. A 25-bp DNA duplex was included in these measurements as a control, as the ion atmosphere(s) around DNA duplexes have been extensively characterized (42). To maximize our sensitivity, we adopted the conditions reported in Ref. (42): 20 mM Na with added Mg ranging from 0 to 50 mM. The low monovalent ion concentration is crucial for measuring Na concentration differences with sufficient signal-to-noise. To ensure that these data can be reasonably well compared with the SAXS data reported above, we first counted the number of ions around dT₃₀ in a solution containing 20 mM NaCl. The number of excess ions we count, 19.7 ± 0.6, is consistent with the ASAXS reported number in 100 mM RbCl (27). Furthermore, Ref. (43) reports only a small change in the number of excess ions when the NaCl concentration increases from 20 to 200 mM. A second check ensures that the electrostatic properties of the NA system in this mixed ion solution are close to those in 100 or 200 mM NaCl. We computed the second virial coefficient (B₂) from the SAXS data which quantifies the electrostatic repulsion between different chains, using dT₃₀ as a model system for direct comparison with the results in monovalent-only and mixed ion solutions (27). At 100 mM NaCl, B₂ = (0.99 ± 0.13) × 10⁶ ų, which is the same as measured in a solution containing 20 mM NaCl and 1 mM MgCl₂. At 200 mM NaCl, B₂ = (0.42 ± 0.04) × 10⁶ Å ³, which is similar to a solution containing 20 mM NaCl and 5 mM MgCl₂.

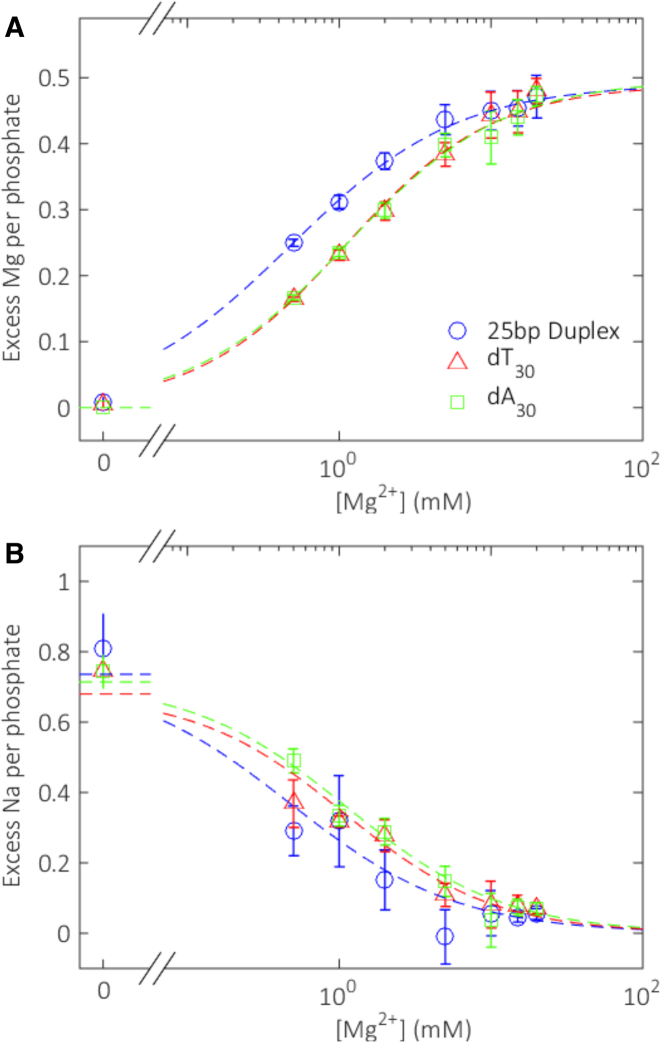
Figure 6 shows the results of the Na-Mg competition experiments, reporting the number of excess ions present around each of the three constructs. For the double-stranded sample, we measure a competition constant M_1/2 = 0.48 ± 0.01 mM, in agreement with earlier BE-AES measurements on DNA duplexes with a differing base sequence, but comparable length (42). Turning next to the single-stranded molecules, two features of these curves are important. First, a larger number of Mg ions per phosphate group are attracted to the (more charge dense) duplex than to the single strands at a given solution condition. Second, there is no significant difference in the number of ions around dA₃₀ and dT₃₀ in any condition tested. Thus, the relative affinity of dA₃₀ and dT₃₀ for either Na⁺ or Mg²⁺ over a large range of divalent ion concentrations is equivalent. Both homopolymers appear to be electrostatically identical when probed at near-physiological ionic strengths.

Figure 6.

Ion counting results. (A) Number of excess magnesium ions and (B) sodium ions per phosphate attracted to three different constructs as a function of magnesium ion concentration. Dashed lines show Hill-equation fits to the data points, as described in the ‘Materials and Methods’ section. Fit parameters are given in Supplementary Table S1.

DISCUSSION

Base stacking effect on conformations

By pairing SAXS with EOM, we obtained representations of highly flexible polymers of poly dA and poly dT at salt conditions at near-physiological ionic strength. The use of an iteratively refined pool provides previously inaccessible information about conformations, such as the number and distribution of stacked bases in each molecule. Most generally, and in good agreement with results reported by other techniques (e.g. (32,35)), this in depth analysis reveals that poly dA has a high propensity to form stacked bases. Although much less pronounced in poly dT, stacking is present in the refined structures. These stacked bases, however, are sparse, and have little effect on the overall conformations and short-range ordering of the chains. In contrast, segments of stacked bases appear frequently in dA, and this base-stacking clearly impacts the local chain structure over consecutive bases. The relatively short mean stack length observed in both salt conditions for dA₃₀ indicates that the stacking interaction for this base is weakly cooperative, and only marginally energetically favorable over the unstacked conformation. This behavior has recently been shown in theoretical calculations (53), where base-stacking was found to be weakly stabilizing for purines and destabilizing for pyrimidines. These points can be easily rationalized through visualization of the representative structures (Figure 4).

In addition, we find that the stacking interactions of dA are promoted at higher salt concentration. An increase in the mean number and length of stacked bases acts to oppose the entropically-driven collapse expected when screening is more efficient. This result appears to be inconsistent with a thermodynamic analysis of force-extension measurements (32), where the free-energy of stacking was found to be independent of salt concentration over a wide range of conditions. This discrepancy could be due to tethers or other surfaces influencing the conformations adopted by ssNAs, as we have found in our earlier work (30), thus making comparison to techniques that require special sample preparations difficult. If however, we consider our statistics more coarsely, with their associated standard deviations, we arrive at the same conclusion. In either case, both works agree that fewer bases are free to facilitate chain collapse in poly dA. This results in smaller conformational changes under more efficient screening conditions when compared to the poly dT ensembles. The net result is seen as smaller changes in mean R and R_g in dA₃₀ compared to dT₃₀ in higher screening conditions. While our data only provides coverage of two salt points, this trend has been found to hold over a wide-range of salt concentrations (28). Thus, base-stacking can play a large role in determining the salt response of these polymers when assayed by average measurements.

Despite the high mean number of stacked bases, poly dA displays a range of stacking interactions, as is evident from the relatively large standard deviation on this metric. When coupled with the variation of ensemble structures, this finding challenges the expectation that stacking constrains the accessible conformation space. Instead, we propose that stacked molecules are more fluid, with stacks continually breaking and reforming in solution. This idea is further supported by the absence of correlations between the degree of base-stacking in a given structure and its location in conformation space. This finding may not be surprising for dT₃₀, as the diminished propensity for stacking leaves a large fraction of the chain free to explore space unrestrained. However, it is also true for the highly stacked dA₃₀, with chains differing by many bases being found in the same regions of conformation space. In conjunction with the length of the unstacked regions observed in poly dA, it appears that only a few short regions of ‘free’ bases are required to contort the chain into a large variety of shapes and extents. An overall picture emerges where base-stacking does little to influence conformations on a structure-by-structure basis, but instead affects the average properties of the ensemble.

Electrostatics of dT₃₀ and dA₃₀

Results of ICP-AES experiments illustrate that dA₃₀ and dT₃₀ support identical ion atmospheres, with fewer ions per phosphate attracted relative to a DNA duplex. This is found to hold over a large range of mixed mono- and di-valent ionic conditions, and shows that the relative affinity of dA₃₀ and dT₃₀ for Na⁺ vs Mg²⁺ is identical. This result runs counter to expectation, because both the macroscopic and microscopic response of each chain to increased salt concentration is base-dependent: the change in R_g is smaller and there is a promotion in the mean number and length of stacked bases in dA₃₀. These chain-dependent effects have also been observed in water release experiments (54), where magnesium association distinctly alters the molecular hydration of dT₃₀ compared to dA₃₀. We find the unusual situation where a specific sequence can respond distinctly to a given ion, while maintaining the bulk composition of the ion atmosphere.

A potential explanation for this observation is that there is no specific ion coordination or binding to either sequence, and that the attraction of an ion atmosphere depends largely on the linear charge density of each chain. This idea is borne out by EOM-based computations of the mean interphosphate distances, where no significant difference is observed between all four experimental conditions. In this case, the distinct response of each polymer to salt may reflect the preferred conformations of each molecule in higher screening environments. While this concept seems attractive, we must be cautious in interpreting L_pp. Given the limited resolution of SAXS, extraction of details on such short length scales requires extrapolation from large-scale features (the contour length); L_pp may not truly represent the real interphosphate distance. Despite these caveats, there are no large-scale differences between dA and dT in terms of inter-phosphate distances or charge density.

Similarity of dT₃₀ and dA₃₀

Given the above discussion, we pose the following question about dT₃₀ and dA₃₀: how similar are these supposedly distinct molecules at physiologically relevant ionic strength? Their ion atmospheres (assayed by ICP-AES) are identical and global examination of the range and distribution of conformations open to each molecule, enabled through the ensemble visualizations we report here, suggests that they are conformationally similar. Both molecules span the farthest corners of conformation space and have equivalently broad distributions, thus appear equally flexible. At the salt concentrations we probed, the populated conformational spaces overlap significantly, with the densest regions intersecting (Supplementary Figure S3).

While similar in terms of the range of accessible conformations and location of the densest regions in conformational space, differences between poly dA and poly dT arise in the number of states populating these regions. For example, the density of dA₃₀ conformers is lower at the smaller end-to-end distances than dT₃₀. Thus while dA₃₀ can access the same global conformations as dT₃₀, it does so with a slightly lower probability. This finding agrees with work on DNA hairpins containing dA₃₀ or dT₃₀ homopolymer strands, with the former showing longer closing times than the latter (33). Both constructs may access the same extreme structures, albeit dA fluctuates into these states less frequently. Since hairpin-closing experiments are sensitive to only this extreme of conformational space, they exaggerate sequence-dependent conformational preferences, and fail to report directly on the detailed size and shape of all other accessible states. With this understanding, our conclusion that dA and dT are more similar than previously thought is consistent with such experiments.

Implications for ssDNA recognition by SSB's

Due to the previous lack of experimental information on single-strand conformations and electrostatics, discussion of ssDNA-SSB binding has largely focused on the role of the protein. However, the conformational and electrostatic similarity of single-stranded chains with different sequences may have important implications for non-specific SSB's. These proteins are involved in general DNA maintenance and require non-sequence-specific binding of ssDNA both to function correctly and to reject nonconforming ligands such as dsDNA (5). Recent theoretical work highlights the importance of electrostatics, flexibility and aromatic interactions in the association of ssDNA to SSBs (55). Using a coarse-grained parameterization of ssDNA to prescribe both the flexibility and overall conformations of the chains, the authors conclude that all three factors are comparable in stabilizing and guiding binding to varying SSBs.

Given our finding that dT₃₀ and dA₃₀ are basically indistinguishable in terms of electrostatics, global conformation and flexibility, one would expect non-specific SSBs to bind with equal affinity to either sequence. However, as previously mentioned, the equilibrium binding constant for free poly dT single strands is orders of magnitude higher than poly dA across varying SSBs. The disparity in stacking propensities between dA and dT is an obvious source for this discrepancy. However, our ensemble statistics show that on average, even at the highest salt concentration, a sixth of all dA bases remain unstacked in the chains. It seems difficult to motivate an orders-of-magnitude difference in binding affinity based solely from the presence of additional base stacks, which are likely transiently breaking and reforming. Furthermore, many SSB's such as replication protein A (RPA) and Escherichia coli (Eco) SSB can melt DNA secondary structure while diffusing on long strands of poly dT (56,57). These results appear to be inconsistent, suggesting on the one hand that base stacking can hamper binding, while on the other, these proteins show behavior that is unaffected by DNA structure.

The visualization of structural ensembles, described here, suggests that a conformational capture of ssDNA drives its association to SSBs. Prior to binding, any candidate ligand must spontaneously fluctuate into a stack-free structure, whose length matches the size of the binding pocket. As an important example, the binding of Eco SSB to ssDNA on average occludes ∼30 nt of single-strand, distributed across two binding pockets in most of its binding modes (21,58). Experiments on this system are most often performed on 30-mer single strands, the same length as we study here. In our sample size of 10 000 structures, the ratio of poly dT structures to poly dA that would make a suitable candidate for an initial SSB binding event to one of the subunits (∼10 nt length of unstacked bases) equals two orders of magnitude. Thus, within the ligand conformational capture framework, the presence of even a small fraction of stacked bases in poly dA would dramatically alter single-strand binding affinities. Further support for this picture can be found in measured heat-capacity changes (11) and pulling experiments on single-strand SSB complexes (24), which suggest that all long range ordering (i.e. stacked bases) is removed from single-strands when in complex with protein partners. Additionally, crystal structures of ssDNA bound to SSBs display unstacked phosphate backbones (e.g. (9,21,22)), akin to those found in the poly dT ensembles, and distinct from the highly tortuous motifs found for poly dA.

CONCLUSION

By pairing SAXS and ICP-AES, we have been able to characterize the solution properties and conformations of free single-strands of DNA. Using ensemble methods to probe states away from the mean, we have found that, despite the large differences in stacking propensities, disparate sequences are similar in most regards. Thus, although this work supports the long held view that base stacking is the most significant difference between chains of differing sequence, what is surprising are the dramatic biological consequences due solely to the stacked arrangement, rather than the secondary influence of stacking on backbone shape, global size or electrostatics.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health (to L.P.) [R01-GM085062]; NSF and NIH/NIGMS via NSF Award (to CHESS) [DMR-1332208]; Funding for open access charge: National Institutes of Health [R01-085062].

Conflict of interest statement. None declared.