Linking economic activities to the distribution of exotic plants

Abstract

The human enterprise is flooding Earth's ecosystems with exotic species. Human population size is often correlated with species introductions, whereas more proximate mechanisms, such as economic activities, are frequently overlooked. Here we present a hypothesis that links ecology and economics to provide a causal framework for the distribution of exotic plants in the United States. We test two competing hypotheses (the population-only and population-economic models) using a national data set of exotic plants, employing a statistical framework to simultaneously model direct and indirect effects of human population and ecological and economic variables. The population-only model included direct effects of human population and ecological factors as predictors of exotics. In contrast, the population-economic model included the direct effects of economic and ecological factors and the indirect effects of human population as predictors of exotics. The explicit addition of economic activity in the population-economic model provided a better explanation for the distribution of exotics than did the population-only model. The population-economic model explained 75% of the variation in the number of exotic plants in the 50 states and provided a good description of the observed number of exotic plants in the Canadian provinces and in other nations in 85% of the cases. A specific economic activity, real estate gross state product, had the strongest positive effect on the number of exotics. The strong influence of economics on exotics demonstrates that economics matter for resolving the exotic-species problem because the underlying causes, and some of the solutions, may lie in human-economic behaviors.

Humans are noteworthy in their ability to alter landscapes and drastically change the distribution and abundance of species (1–3). Biological invasions, the establishment and spread of nonnative species into new environments, have substantial economic and environmental costs and are now considered a leading component of human-accelerated environmental change (3, 4). Two of the most pressing issues of the exotic-species problem are to predict which areas are most susceptible to invasion and to identify what causal factors can be modified to reduce further species introductions. In some recent studies, human population size has been correlated with the distribution of exotic fish and plants in the United States (U.S.) and the United Kingdom (5–8). However, enormous human-induced environmental change can occur even in sparsely populated areas if per capita impacts are high (3, 9). Human-induced environmental change may result from interactions among human population size, economic activity, political institutions, and attributes of the surrounding ecological system (10–12). Yet, quantitative information on the relative importance of economic, ecological, and human-demographic factors to the distribution of exotic species remains elusive (2). Here we build on previous studies by developing and testing the synergistic effects of human population size, economic activity, and ecological factors on the proliferation of exotic plant species. If we agree that the exotic-species problem is due to human actions (3, 13), then we need to develop theories that include those human behaviors that are the major driving forces. Lacking from our current theories of human-induced species invasions is the explicit integration of ecological and economic causal pathways.

As a first step toward quantifying the effects of economics on exotics species, we hypothesized that economic activities closely linked to the establishment of exotics should include mechanisms that have been theoretically and empirically shown to increase the likelihood of invasion. For example, economic parameters associated with land use patterns and the introduction of new species may provide explanatory predictions of the distribution of exotic species (14). In particular, land use change has been linked to species invasions and is often a prerequisite (15–17). In a classic example, exotic birds were able to invade New Zealand islands only after forest clearing by humans and introduced herbivores (18). Similarly, land clearing by fire has allowed fire-promoting grasses (e.g., European cheatgrass) to successfully invade many areas (19). Moreover, the supply rate of new propagules is a necessary link in the invasion process that has been shown to be important in small-scale experiments (20) and is widely recognized as having increased globally, in large part, because of economic activities associated with trade (13, 21). From an economic and ecological perspective, real estate gross state product (GSP) is a measure of the intensity of economic activities that have the potential to disturb natural landscapes, increase the import and dispersal of exotic propagules, and thereby facilitate the establishment of exotic plants. Our estimate of real estate GSP includes the construction of new buildings, clearing and excavation of land, the landscaping industry, and the operators, owners, and lessees, as well as buyers, sellers, and developers, engaged in development, exchange, and ownership of property (U.S. Bureau of Economic Analysis, www.bea.gov). Monetary exchanges associated with real estate GSP result in various forms and rates of energy transfer either as commodities or as land use change. Indeed, real estate GSP is highly correlated with a State's urban land area (r = 0.91, P = 0.0001), most of which was forest, pasture, and range-land that has now been converted into households, schools, office buildings, and other commercial and industrial sites (U.S. Department of Agriculture, Economic Research Service, www.ers.usda.gov/data/majorlanduses). Furthermore, introductions of exotic plants are included in real estate GSP as purchases of exotics for aesthetic and utilitarian purposes by the landscaping industry, resulting in many of the deliberate and accidental introductions of our most pernicious plant invaders (15).

Here we used an ex post approach (i.e., postintroduction) to test the causal factors that determine the number of established exotic plant species in the 50 states. We tested two competing models: (i) the population-economic model (Fig. 1a), which included the direct effects of real estate GSP and ecological factors and the indirect effects of human population on number of exotics; and (ii) the population-only model (Fig. 1b), which included the direct effects of human population and ecological factors on the number of exotic species. We used path analysis and structural equation modeling (SEM) to evaluate which model provided a better fit to the observed data. We then used the model that provided the better fit to quantitatively compare the relative importance of different causal pathways to the number of established exotic plants in the U.S. Finally, we tested the utility of the model for predicting the number of exotic plant species in other nations.

Fig. 1.

Two alternative casual structures for predicting the number of exotic plants by using ecological, economic, and human demographic parameters. (a) The population-economic model. (b) The population-only model. The variable union is the year that each state was admitted to the U.S. Latitude is the geographic center of each state. Natives and exotics are the number of native and exotic plant species in each state. Dashed lines indicate negative effects, solid lines indicate positive effects, and lines with double-headed arrows are modeled intercorrelations. The path from U to each variable is the variation unexplained by the causal structure. The width of each line is proportional to the standardized path coefficient. *, P < 0.05 paths.

Methods

The Data. We obtained data on the number of exotic and native plant taxa in the 50 states from the Biota of North America Program (BONAP) (22), using the unique taxa classification, which includes species, subspecies, and varieties. For simplicity, we refer to these taxa as species. Plants were classified as exotic if they occurred outside North America and had been accidentally or intentionally introduced and escaped as a result of human activity. Agricultural crop plants were not counted as exotics (22). We obtained the 2001 human population size for the 50 states from the U.S. Census Bureau (www.census.gov) and 2001 economic data from the U.S. Bureau of Economic Analysis (www.bea.gov).

Hereafter, we distinguish between real estate GSP (the variable used in the population-economic model, described below) and per capita real estate GSP, which is real estate GSP divided by the number of people in a state. Per capita real estate GSP was not used in the population-economic model but, rather, was used in a separate analysis to demonstrate that the effects of real estate GSP on exotic species were independent of population size (see Results).

There was no logical a prior reason to suspect that total state GSP would influence exotic plants, because total state GSP includes many activities that are irrelevant to the exotics species problem. Moreover, although we recognize that there may be a variety of more proximate causal mechanisms for which real estate GSP merely serves as a proxy, data on these processes either do not exist (e.g., propagule pressure) or are measured infrequently, which is surprising, especially for such key factors as land use change (23). In contrast, real estate GSP is measured more frequently and precisely than most proximate factors. In addition, a major advantage of using an economic variable is that existing theory and empirical information can be used to model the interrelationships among human demographic, economic, and ecological systems. Finally, we fully realize that real estate GSP may be one of many economic activities linked to invasive species. However, that does not detract from our major premise, namely that human-economic activity is positively linked to the distribution of exotic plants.

In both the population-economic model and the population-only model (described below), we included two ecological variables: latitude and number of native species. Latitude was included in the models because of well established gradients in species diversity (24). Latitude was measured at the geographic center of each state (U.S. Geological Survey, www.usgs.gov). We included the number of native plant species in the models because native species diversity has been implicated in invasion resistance (16, 25) or correlated with the number of exotics species (20, 26). Finally, the year that each state was admitted into the union was included as an estimate of settlement and disturbance by Europeans (6). Species introductions spread rapidly along an east–west axis because at the same latitude, species have fewer environmental conditions to adapt to than along a north–south axis (27). Thus, there was no a priori reason to suspect that longitude should predict the number of exotic species, and it was not included in the models. We also did not include distance to the nearest coastline in the models because the effects of distance to coastline on the number of exotics are likely a synthetic measure of the timing of human arrival, population density, and economic activities along coastlines, variables which are already included in the models.

Population, union date, real estate GSP, and number of native and exotic plant species were log₁₀-transformed to adjust for heteroscedasticity and nonlinearity. We normalized population, real estate GSP, and the number of native and exotic plants for state area by dividing by the log₁₀-transformed area (28). Although the standardization for area had little effect on the model results, we chose to present standardized estimates because of well known species–area relationships (28).

Statistical Methods. We used path analysis combined with SEM to test the fit of two competing a priori hypotheses, the population-economic and population-only models (Fig. 1), by evaluating the relationships among human population and ecological and economic variables on the number of exotic plants. Path analysis and SEM offer several advantages over multiple regression. Path analysis allows for the examination of multiple causal relationships among variables, both direct and indirect, and allows for the estimation and comparison of effect sizes for different pathways (29, 30). Moreover, parameters for the structural equations that make up the path analysis can be estimated and used for prediction. SEM combines an econometric perspective focusing on prediction with statistical tests of a priori hypotheses by confronting models with empirical data (29). Furthermore, SEM circumvents problems with intercorrelations among variables by explicitly modeling them, tests multivariate causation, and provides tests of goodness-of-fit between the model and the data (29).

Model description. In both the population-economic model and the population-only model, we included direct effects of union, native species, and latitude on the number of exotic species because these variables may be associated with the number of exotic plants (5, 20, 26, 31). We also included an indirect effect of latitude on exotics through the number of native plant species. In the population-economic model, we included the indirect effects of human population on the number of exotic species mediated through human actions, in particular, real estate GSP. In this model, a change in human population results in a multiplicative change in real estate GSP, and a change in real estate GSP directly affects exotics. The form of this set of paths in the model is similar to the I = PAT framework (12), where I is environmental impact, P is human population size, A is affluence, and T is technology, and economic activity in the population-economic model provides a synthetic measure of the product of affluence and technology. We did not model population and real estate GSP (or per capita real estate GSP) as separate direct effects on exotics because the major premise of the model is that population size indirectly affects exotics through changes in economic activities. Support for the population-economic model would suggest that human-economic activity is an important predictor of the number of exotic plant species. In the population-only model, we removed the effect of real estate GSP and modeled the direct effect of human population on the number of exotic plants. If we find support for the population-only model, this would suggest that explicit modeling of human actions is not necessary for predicting the number of exotic plant species.

Model testing. We used SEM to statistically test which competing hypothesis, the population-economic model or the population-only model, provided the better fit to the observed data. Before evaluating the path models, we screened for collinearity among predictor variables by using variance inflation factors (VIFs). All VIFs were <10, suggesting that collinearity did not strongly affect the precision of the path models (32). We compared the fit of competing models by using goodness-of-fit tests, Akaike's information criterion (AIC), and Schwarz's Bayesian information criterion (BIC) (32, 33). A nonsignificant goodness-of-fit test (i.e., P > 0.10) suggests that the expected correlation structure of the path model does not differ significantly from the observed correlation structure of the data (i.e., the model provides a good fit to the observed data). AIC and BIC allow for comparison of nonnested models with different numbers of parameters by adding a penalty (i.e., 2 × the number of estimated parameters) to the negative log-likelihood for each additional parameter. In the case of BIC, an additional penalty is imposed for sample size (33). In general, each goodness-of-fit statistic provides a measure of the information gained from additional parameters relative to the penalty incurred due to increasing the model's complexity. To determine the more parsimonious model, we chose the model that did not differ from the observed data and that minimized the AIC and BIC values by at least 2 units (33). A sample size of at least five observations per estimated parameter is recommended for path analysis and SEM (29). With 50 states, our sample size is within the acceptable range.

For the model that provided the better fit to the observed data, we calculated standardized partial regression coefficients and significance levels by using the maximum-likelihood estimation method in proc calis of sas (32). We then used the structural equations parameterized from the model that provided the better fit to predict the number of exotic species in other nations. We chose developed and developing nations (see Table 1) that spanned a wide range of ecological and economic values and for which the observed number of native and exotic plants was available. We used data sets for nations that we think classified taxa as being exotic to the continent or island, which made them comparable to the U.S. data set on which the model was based.

Table 1. Predicted and observed number of exotic plant species in the Canadian provinces and other nations.

Country and province (ref.)	Predicted no. of exotic plant species (prediction interval)	Observed no. of exotic plant species
Australia (14)	2,490 (1,908-3,249)	1,952
Canada (22)
Alberta	426 (326-555)	301*
British Columbia	763 (585-996)	691
Manitoba	363 (278-474)	321
New Brunswick	540 (414-704)	469
Newfoundland	402 (308-525)	371
Nova Scotia	580 (444-756)	522
Ontario	1,017 (779-1,327)	914
Prince Edward Island	367 (281-479)	312
Quebec	899 (689-1172)	703
Saskatchewan	340 (260-444)	281
New Zealand (45)	1,231 (943-1,606)	1,570
Puerto Rico (22)	997 (764-1,301)	758*
United Kingdom (15)	1,383 (1,060-1,804)	1,169

We obtained the predicted number of exotic species and prediction intervals by using standardized parameters and variables from Eq. 4:

For Canadian provinces, the union date was the date that provinces were admitted to Canada. For other nations, the union date was the date that countries gained independence and were self-governing. Population values were obtained from the U.S. Census Bureau International Database. We provide the mean and standard deviation based on the 50 U.S. states, which were used to standardize the input and output variables in Eq. 4.

^*Observed values not within the model's 95% prediction intervals.

Results and Discussion

Overall, the population-economic model provided a more parsimonious fit to the observed data (Fig. 1a; χ² = 4.74, df = 5, P = 0.45, AIC = –5.26, BIC = –14.81) than the population-only model (Fig. 1b; χ² = 0.78, df = 1, P = 0.38, AIC =–1.22, BIC = –3.13). The two different measures of goodness-of-fit, AIC and BIC, used for comparing nonnested models with different numbers of parameters (32, 34) show that the population-economic model provided the better fit to the observed data because it minimized the AIC and BIC (34).

The population-economic model explained 75% of the variation in number of exotic plants compared with only 68% of the variation explained by the population-only model. Real estate GSP had the strongest direct positive effect on the number of exotics (Fig. 1a). The magnitude of the effect of real estate GSP on number of exotic plant species was 2-fold greater than any other direct effect on exotics in the model (Fig. 1a). Although human population is a positive driver of real estate GSP, in a separate regression analysis we found that the number of exotic plant species was also a positive function of per capita real estate GSP (Fig. 2a; r² = 0.44, t₄₈ = 6.19, P < 0.0001). This result demonstrates that the effect of real estate GSP on the number of exotics is not solely a function of population size but is due to the amount of economic activity of the population. Interestingly, the states that had more exotic plant species than predicted by per capita real estate GSP (e.g., California, New York, Florida, and Massachusetts; Fig. 2a) also had the highest real estate GSP (Fig. 2b; r² = 0.58, t₄₈ = 8.10, P < 0.0001), lending further support that economics are important in accounting for introduced species. The number of exotics also increased as a function of per capita real estate GSP standardized for the per capita GSP purchasing power parity, an exchange rate that normalizes the price of goods and services among each state's local economy (r² = 0.47, t₄₈ = 6.48, P < 0.0001). Thus, the relationship between exotics and real estate GSP was not the result of systematic differences in market value among states. Moreover, there was no relationship between the number of native plants and per capita real estate GSP (r = 0.11, P = 0.45), suggesting that the findings from the population-economic model were not the result of spurious correlations between real estate GSP and species richness.

Fig. 2.

The number of exotic plant species increases as a linear function of per capita real estate GSP (a) and total real estate GSP (b). The equation for the line in a is number of exotics species per km² = 67.7 + 0.09(per capita real estate GSP per km²). The equation for the line in b is number of exotics species per km² =–587.8 + 77.2[log₁₀(real estate GSP) per km²]. All values are based on the log₁₀ of state area in km².

To understand whether economic factors, in general, give added insight into the distribution of exotic plants in other nations, we compared predictions of exotic plants from the population-economic model (parameterized with U.S. data) with the observed number of exotic plants from developed and developing nations by using the structural equations that are synonymous with Fig. 1a:

[1]

[2]

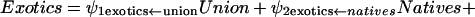[3]

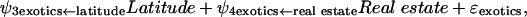where the notation (e.g., real estate ← population) after each estimated coefficient is the hypothesized structural relationship. After redesignation of the coefficients, Eqs. 1–3 simplify to

[4]

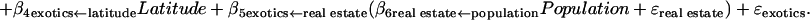Using Eq. 4 (see Fig. 1), we found that the model predictions encompassed the observed number of exotics within the 95% prediction intervals for 85% of the cases (Table 1). Although this particular population-economic model, parameterized with U.S. data, will require modification before it is applicable across broad sociopolitical and socioeconomic gradients, it suggests that consideration of economic activities is likely to provide additional insight into the distribution of exotic species. The population-economic model overpredicted the number of exotic plants in one country, Puerto Rico. However, this was not completely unexpected because the coefficient for real estate GSP was estimated by using U.S. data, and the U.S. has a higher real estate GSP than Puerto Rico. However, this overprediction may be a forecast of the consequences of growing economies to the exotic-species problem in developing nations. One caveat is that surprisingly few countries have up-to-date estimates of the number of native and exotic plants. Moreover, even fewer countries have directly comparable data sets with similar classification schemes for exotic species (i.e., species classified as exotic to the country versus the continent). Such data are desperately needed to further evaluate the population-economic model. Furthermore, risk assessment models should consider the economic and ecological characteristics of the invaded ecosystem, as well as the invader (35, 36), when predicting where exotic species pose serious environmental and economic impacts.

Surprisingly, the number of exotic plant species did not increase with state area. In fact, the number of exotic species tended to decrease with increasing state area (r² = 0.12, t₄₈ = –2.50, P = 0.02). This pattern was not the result of larger states at higher latitudes (r² = 0.03, t₄₈ = 1.29, P = 0.21). The negative relationship between log-transformed exotics and log-transformed area may indicate that larger states have been systematically undersampled or that they are not saturated with exotic species. We have no evidence to suggest that the species lists are incomplete for larger states; however, undersaturation may be a likely explanation that deserves further examination. Evidence from oceanic islands, where saturation should be more rapid, shows that islands with positive species–area curves continue to accumulate species at a rapid rate (37).

The population-economic model also sheds light on a current dispute in invasion biology. Recent studies argue that biodiversity hotspots are more prone to plant invasion than species-poor habitats (38), counter to the biotic resistance hypothesis (25). Although the numbers of exotic and native plants in the 50 states are correlated (r = 0.35, P = 0.01), they both change systematically with latitude, as is typical for most organisms (24). Using a similar data set as Stohlgren et al. (38), we found no effect of the number of native species on the number of exotic species after statistically controlling for other factors in the model by using SEM analysis (Fig. 1a; t_1,44 =–0.34, P = 0.6 for the natives to exotics partial regression coefficient). Similarly, a multiple regression analysis with the number of exotics as the response variable and the number of natives, latitude, and real estate GSP as predictors indicated no effect of native plant richness on exotic plant richness (t_1,46 = –0.74, P = 0.4617) after statistically controlling for the effects of latitude and real estate GSP (latitude: t_1,46 = –2.54, P = 0.01; real estate GSP: t_1,46 = 7.59, P < 0.0001). Hence, our results provide no support for the hypothesis that species-rich areas are more or less susceptible to invasion due to causal effects of native species richness at the scale of the 50 states. What mechanisms might explain the covariance between exotic and native species? One possibility is that extrinsic factors affecting the establishment of exotics (e.g., population and economic activities) and intrinsic factors affecting native species diversity (e.g., latitude) may covary. For example, population and latitude are correlated (Fig. 1a). Thus, our findings are consistent with a recent scale-dependent competition model that predicts a positive correlation between natives and exotics at large spatial scales (39) and with an experimental study which showed that exotic propagule pressure and disturbance covary with native diversity (20). The effects of extrinsic factors, such as economic activity, on exotic species warrant further attention at larger spatial scales, given the distinct latitudinal patterns in exotic species diversity (40) and human-economic activities (41).

In a recent study, international trade gross domestic product (GDP) was related to establishment rates of exotic species for the continental U.S. (21); however, the per capita effects of trade GDP on exotics were not quantified. Without standardizing trade GDP for human population, the effects of trade GDP on exotics could not be disentangled from population effects. Furthermore, the number of exotic species in 26 countries was not related to international trade adjusted for population size (14). The population-economic model presented here links economic and ecological parameters and accounts for indirect effects of human population density to predict the number of exotic species. Inasmuch as exotic species cause economic losses (4), economic behavior can be a major driver of the proliferation of exotics.

By blending ecological and economic variables, we were able to develop an intuitive model and practical method to statistically measure direct and indirect effects of human population and economics on the distribution of exotic species. We explicitly modeled total human impacts on exotics from the indirect and direct effects of population density and economic activities. The causal structure of population and economic effects is fundamental because the environmental consequences of an increasing population are highly sensitive to the economic conditions of that population [sensu I = PAT (12)]. Even more alarming are potential synergistic effects of higher per capita real estate activity associated with reductions in household size (42). More housing units may increase land alteration, resulting in higher per capita real estate GSP, even when population size declines (42). If the population-economic principle applies to most nations, then future increases in exotic species will be enormous in areas with rapidly growing economies and may affect many of the world's biodiversity hotspots (9). For both practical and socioeconomic reasons, there is a critical need for a multidisciplinary effort to identify the specific economic components that are the most proximate causes of the exotics species problem. Just as policy makers cannot ignore economic activity, ecologists cannot ignore the chain of effects stemming from human population and economic activity (43, 44) when testing causality and predicting the distribution of exotic species. Lastly, our findings suggest that economic practices or incentives could be powerful policy tools to reduce future invasions. Unfortunately, neoclassical economics present a major stumbling block for ecological-economic models because costs associated with externalities, such as exotics species, positively influence overall economic growth and, thus, are considered to benefit societal welfare.