Abstract
Recent theoretical and experimental results point to the existence of small barriers to protein folding. These barriers can even be absent altogether, resulting in a continuous folding transition (i.e., downhill folding). With small barriers, the detailed properties of folding ensembles may become accessible to equilibrium experiments. However, further progress is hampered because folding experiments are interpreted with chemical models (e.g., the two-state model), which assume the existence of well defined macrostates separated by arbitrarily high barriers. Here we introduce a phenomenological model based on the classical Landau theory for critical transitions. In this physical model the height of the thermodynamic free energy barrier and the general properties of the folding ensemble are directly obtained from the experimental data. From the analysis of differential scanning calorimetry data alone, our model identifies the presence of a significant (>35 kJ/mol) barrier for the two-state protein thioredoxin and the absence of a barrier for BBL, a previously characterized downhill folding protein. These results illustrate the potential of our approach for extracting the general features of protein ensembles from equilibrium folding experiments.
Keywords: experimental analysis, free energy barrier, downhill folding, two-state folding, phenomenological model
In contrast to the situation in many fields of modern physics, experimental results in protein folding are seldom directly interpretable by analytical theory or computer simulations. The interpretation typically involves a simple phenomenological model with which experimental results are analyzed, and the outcome of such ad hoc analysis is used to extract conclusions regarding experiments. A paradigm of this principle is the two-state model, in which protein-folding reactions are analyzed in terms of a chemical equilibrium between two independent species, native (N) and unfolded (U):
 |
[1] |
In Eq. 1, species with intermediate degree of structure are ignored, and the transition from one state to the other is of the first order. The use of a two-state model and its obvious generalization (i.e., a series of chemical equilibria between n structurally defined macrostates) is deeply rooted in the tradition of describing chemical transformations of small molecules as reaction schemes.
Despite the obvious limitations of comparing protein folding with simple chemical reactions, the two-state protein-folding model enjoys tremendous popularity. One of the reasons is that this model seems to accommodate the folding behavior of a large set of single-domain proteins (1). Two-state folding could also provide proteins with a significant biological advantage by conferring upon them kinetic stability in vivo (see ref. 2 for a recent discussion). However, to make sure that the two-state character of proteins is not a self-fulfilling prophecy (3), it is important to analyze experimental data with a procedure that does not make assumptions about the existence of a free energy barrier. A more general procedure would also provide an opportunity to extract information about protein-folding ensembles that is discarded in the traditional two-state analysis.
The need for better procedures to analyze folding experiments has become more urgent in light of recent developments. Theory predicts that folding free energy barriers arise from the nonsynchronous compensation between energy and entropy (4, 5), and are small in the chemical sense (6). Accordingly, protein-folding transitions are expected to be of the first order (i.e., type I scenario in the energy landscape language) or continuous (i.e., type 0 scenario, or downhill) depending on experimental conditions (4). Kinetic experiments in very fast-folding proteins (7) and thermodynamic analysis of the folding kinetics of several two-state-like proteins (8) suggest that for many natural proteins folding barriers are, indeed, rather small. Computer-designed proteins fold faster than their natural templates, although no selection for folding efficiency was included in the design strategy (9). Therefore, the higher folding barriers of the natural proteins might be the result of natural selection, rather than an intrinsic feature of protein folding. The theoretical analysis of protein polymer models also indicates that it might be harder for proteins to achieve cooperativity (i.e., a large free energy barrier) than a stable folded structure (10). Furthermore, folding barriers can be reduced by mutations resulting in a populated “activated” complex (11) or can even disappear when mutations are combined with extrinsic stabilizing agents (12). In fact, in some proteins the folding free energy barrier can be altogether absent in thermodynamic terms, resulting in global downhill folding and continuous unfolding transitions (13, 14). Proteins with such features could even have an important biological role as molecular rheostats (14).
The problem of describing processes that, depending on conditions, behave either as first-order or continuous transitions arises in a well known branch of thermodynamics: the theory of critical transitions. In the classical Landau theory of critical transitions (see chapter 10 in ref. 15), this phenomenon is described with a free energy functional expressed as a series expansion in powers of an “order parameter” (the property that exhibits large fluctuations near critical conditions) and truncating the expansion at the quartic level. The truncated expansion produces a free energy functional with one or two free energy minima, depending on the sign of the coefficient of the quadratic term.
Here, using the Landau free energy as a starting point, we introduce a simple phenomenological model for the analysis of equilibrium protein-folding experiments. The great advantage of this model is that the height of the free energy barrier and the general properties of the folding ensemble are not preassumed but are obtained directly from the experimental data. We have used this variable-barrier model to analyze differential scanning calorimetry (DSC) experiments of protein unfolding. Because DSC data are directly related to the relevant protein partition function (16), their analysis with the model highlights the potential of this approach for investigating equilibrium folding ensembles. The model produces a large barrier when used to analyze the DSC thermogram of the two-state protein thioredoxin (17) and a barrierless free energy profile when used to analyze the DSC thermogram of the downhill folding protein BBL (14).
Theory
We are interested in describing protein-folding/unfolding transitions as a continuous distribution of protein states. Therefore, we write the partition function (Q) as
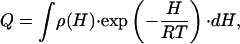 |
[2] |
in which the system is described as an ensemble of enthalpy microstates, H is a suitably defined enthalpy scale, and ρ(H) is the density of enthalpy microstates. The enthalpy scale and ρ(H) are taken strictly independent of temperature. In other words, microstates are assigned constant energy (enthalpy) values. Other properties such as entropy and heat capacity arise from the characteristic probability distribution of the ensemble of microstates, and the heat capacity defines the temperature dependence of the average enthalpy. We also note that Eq. 2 for the partition function is a continuous analogue of the well known Freire–Biltonen expression (16), in which the system is divided in a series of discrete macrostates,
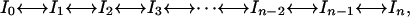 |
[3] |
and the partition function is expressed as
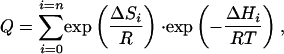 |
[4] |
where the native state (I0 = N) is taken as reference and, therefore, ΔHi = H(Ii) - H(N) and ΔSi = S(Ii) - S(N). The term exp(ΔSi/R) in Eq. 4 is equivalent to the density of states in Eq. 2.
From Eq. 2, the probability of finding the protein in a microstate of enthalpy H at a given temperature T is given by
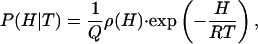 |
[5] |
where P(H|T) is a probability density, its precise meaning being that P(H|T)dH gives the probability of finding values of enthalpy within the infinitesimal range {H, H + dH} at the temperature T. The relationship between the probabilities at the temperature T and at a “characteristic” temperature T0 is determined by
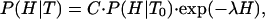 |
[6] |
where
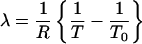 |
[7] |
and C is a constant determined by the normalization condition [∫P(H|T)·dH = 1].
It follows that first- and higher-order enthalpy moments (i.e., 〈Hn〉 with n = 1, 2,...) can be expressed as
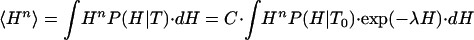 |
[8] |
and that the excess heat capacity (with reference to the native state) can be expressed as
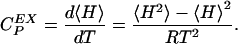 |
[9] |
Eqs. 6–9 allow us to calculate the excess heat capacity as a function of temperature provided that the probability density at the characteristic temperature (P(H|T0)) is known. In principle, the probability density could be directly extracted from the DSC data by calculating the inverse Laplace transform of the partition function. However, calculation of the inverse Laplace transform of experimental data is a notoriously ill-defined problem, as is discussed in the context of protein folding by Kaya and Chan (18). Instead of attempting a model-free inversion, we seek to describe the probability density in terms of a simple and physically reasonable free energy functional that is defined with a few parameters and can be used in a standard fitting process. Particularly, we define P(H|T0) as
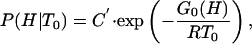 |
[10] |
where G0(H) is a free energy functional and C′ is a constant resulting from application of the normalization condition [∫P(H|T0)dH = 1] once G0(H) has been obtained. Inspired by the classical Landau theory of critical transitions (see chapter 10 in ref. 15), we now expand G0(H) as a power series of H, truncate the expansion in the quartic term, and assume that the coefficients of the odd powers are zero at the characteristic temperature
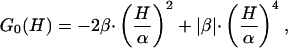 |
[11] |
where we have expressed the coefficients of H2 and H4 in terms of two parameters, α and β, which (as we show below) have a clear and intuitive meaning. The symmetry of Eq. 11 implies that the excess enthalpy (Eq. 8 with n = 1) at the temperature T0 is zero. This only means that the enthalpy scale has been shifted (by adding a constant value), a fact of no physical consequence because any constant added to 〈H〉 will vanish in the derivative that defines the excess heat capacity, CP = d〈H〉/dT. It is important to note that, in contrast with the classical Landau theory, the coefficients of the H2 and H4 terms are taken to be independent of temperature in our model. Therefore, our model is not meant to predict the transition from a scenario with two macrostates to a scenario with a single macrostate as temperature changes (see chapter 10 in ref. 15), and discussion of critical exponents is not relevant here.
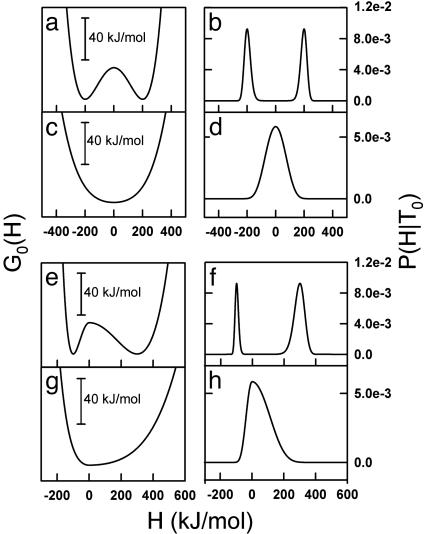
The parameter β in Eq. 11 may be a positive or a negative number, but the coefficient of H4 is always positive (i.e., the absolute value of β, |β|). A positive coefficient in the quartic term is required to guarantee stability with respect to large enthalpy fluctuations. It can be easily shown (by solving dG0/dH = 0 and evaluating d2G0/dT2 at the roots) that, for β > 0, G0(H) has a maximum at H = 0 and two minima at H =±α (see Fig. 1a). Thus, for β > 0, there are two macrostates (Fig. 1b) with an enthalpy difference of ≈2α. β corresponds in this case to the height of the barrier separating the two minima at the characteristic temperature (G0(0) - G0(±α) = β) (Fig. 1a). For β < 0, G0(H) shows only a minimum at H = 0 (Fig. 1c), and there is only one macrostate (Fig. 1d). In this case, α and β are just convenient parameters that describe the shape of the free energy functional. Therefore, in this model the sign of the parameter β determines the observation of two macrostates or a single macrostate at the characteristic temperature T0. Of course, very small positive β values will be essentially equivalent to the barrierless case.
Fig. 1.
Plots of free energy [G0(H)] vs. enthalpy (a, c, e, and g) and probability distributions [P(H|T0)] vs. enthalpy (b, d, f, and h) at the characteristic temperature (T0). (a and c) Free energy profiles calculated with an asymmetry factor of 1 and with positive (a) or negative (c) β values. (b and d) The probability distributions corresponding to the free energy profiles in a and c. (e and g) Free energy profiles calculated with an asymmetry factor of <1, and with positive (e) or negative (g)β values. (f and g) The probability distributions corresponding to the free energy profiles of e and g.
To better attune this phenomenological variable-barrier model to the specific properties of protein-folding reactions, we introduce an additional modification. The inherent symmetry of Eq. 11 implies that, for large and positive β values, the two resulting free energy wells must have the same enthalpy fluctuations (i.e., the same heat capacity). A free energy profile with two wells of the same shape is a desirable property when dealing with systems that have intrinsic symmetry, such as Ising ferromagnets. However, symmetry between the two free energy minima is at odds with the typical situation in protein-folding/unfolding transitions in which the high-enthalpy macrostate (i.e., thermal unfolded state) has a significantly larger heat capacity than the low-enthalpy macrostate (i.e., native state). To account for the asymmetry of protein folding, we introduce one α parameter for negative values of H (αN) and another α parameter for positive values of H (αP). The effect of this modification is illustrated for the high-barrier scenario (β > 0; Fig. 1 e and f) as well as for the barrierless, one-state scenario (β < 0, Fig. 1 g and h).
Fitting Procedure
The model defined in the previous section has only four parameters: T0, β, αN, and αP. These four parameters allow for the calculation of the first and second enthalpy moments by numerical integration of Eq. 8 with n = 1 and n = 2 [and use of Eq. 10 for P(H|T0)]. Substitution of the calculated first and second enthalpy moments into Eq. 9 provides the excess heat capacity, which can be directly compared with the results of DSC experiments. For convenience in the fitting, we express αN and αP in terms of the parameters Σα and f defined by the following relationships:
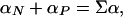 |
[12] |
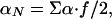 |
[13] |
and
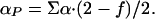 |
[14] |
Σα roughly corresponds to the difference in enthalpy between the minima found at low and at high temperature. For the two-macrostate scenario (i.e., β >> 0), Σα is a good estimate of the transition enthalpy at T0 (Fig. 1e). f is an “asymmetry factor.” If f = 1, then the heat capacity is the same for both minima at T0, whereas if f < 1, then the heat capacity of the low-enthalpy macrostate (i.e., native) decreases with respect to that of the high-enthalpy macrostate (i.e., unfolded).
Therefore, Σα and T0 are the two main parameters for describing the general thermodynamic properties of the transition. The shape of the free energy functional, which is mainly defined by β and f, determines the enthalpy fluctuations associated with the unfolding transition. The DSC data also include enthalpy fluctuations arising from the intrinsic heat capacity of proteins. To eliminate this contribution, we perform a native baseline subtraction (see below), which should result in an infinitely narrow distribution function for a fully native protein (i.e., f → 0 and T0 → ∞). In practice, we have not observed significant differences once f < 0.25, which probably reflects the existence of a limit in the resolution of the procedure and experimental data. Here, we have used a constant f = 0.1 because it is well within the appropriate range and is still large enough to facilitate numerical integration and produce a T0 not much higher than the temperature at which both macrostates are equally populated, Tm. The critical parameter β determines the height of the barrier and affects the magnitude of the enthalpy fluctuations in the transition region for unfolding.
In our fitting procedure we fit (in the least-squares sense) T0 and Σα to DSC data using fixed β values and a constant f = 0.1. This procedure is repeated for a set of β values in an exhaustive grid search to generate plots of σ (the standard deviation between the experimental and predicted excess heat capacity values) vs. β. Such exhaustive analysis is tedious and time-consuming, but it gives us some degree of confidence that the fitting is not trapped in local minima. Furthermore, the σ/β plots facilitate the classification of the unfolding transition as one dominated by crossing a free energy barrier (β >> 0, two macrostates) or as a barrierless transition (β ≤ 0, downhill) by simple visual inspection.
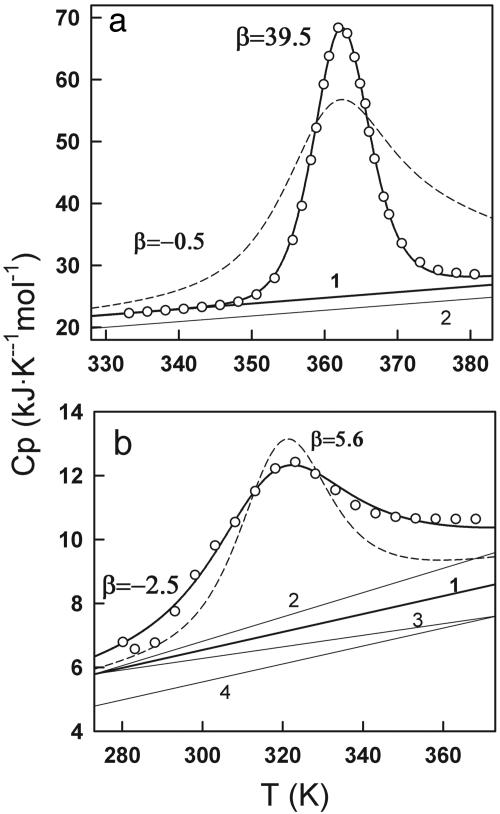
Application of the Model to the Thermal Unfolding of Thioredoxin. The DSC thermogram for the thermal unfolding of thioredoxin from Escherichia coli shows a single calorimetric transition (“peak”) (Fig. 2a). These results have been previously interpreted as a first-order transition (i.e., two macrostates separated by a barrier) on the basis of the analysis with a chemical two-state model (17). At pH 7.0, the chemical two-state model produces a Tm of 362 K, a ΔHm of 431 kJ·mol-1, and a ΔCP of 6.5 kJ·K-1·mol-1 (17).
Fig. 2.
Experimental and theoretical DSC profiles for E. coli thioredoxin (a) and BBL (b). The experimental DSC data (open circles) were taken from refs. 17 (thioredoxin) and 14 (BBL). The curves traced with continuous lines are the best fits to the variable-barrier model. The β value is shown along the lines of the fit. Curves traced with dashed lines show a fit with a β value of opposite sign to that of the best fit. The different native baselines (1–4) are shown as continuous lines.
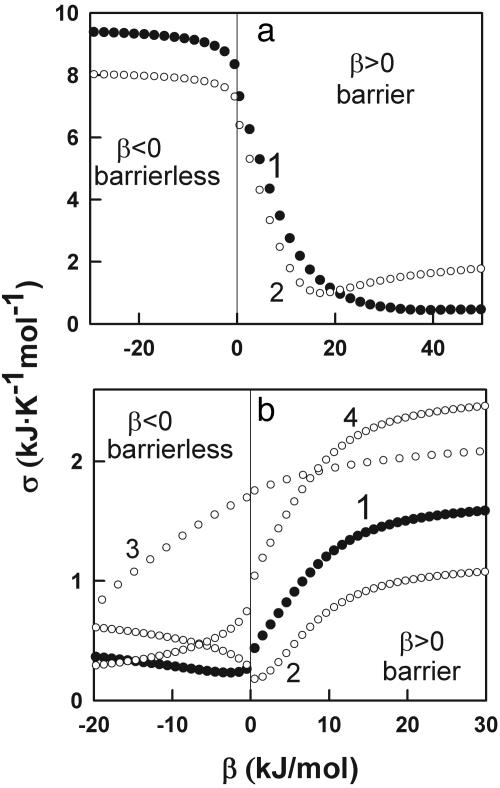
Fig. 3a shows plots of σ vs. β for the fitting of our model to the experimental excess heat capacity data for thioredoxin unfolding. The fitting has been carried out by directly taking the heat capacity values in the 333–343 K range to trace the native baseline (baseline 1 in Fig. 2a) and by downshifting this baseline by 2 kJ·K-1·mol-1 to test the sensitivity of the analysis to native baseline tracing (baseline 2 in Fig. 2a). Inspection of Fig. 3a reveals that low values of σ (good fits) can only be obtained for positive and large β values. Baseline 1 produces lower σ values than baseline 2, which is not surprising because, for a protein with a DSC thermogram such as the one shown in Fig. 2a, tracing the native baseline directly from the data is straightforward. The best overall fit produces the parameters β = 39.5 kJ/mol, T0 = 96.6°C, and Σα = 451 kJ/mol. The result of this fit is shown in Fig. 2a together with the experimental data and a fit with a slightly negative β value for comparison. The fitted parameters indicate that there is a free energy barrier separating two distinct macrostates in the unfolding of thioredoxin. This conclusion still holds when the native baseline is downshifted, which results in artificially broader transitions.
Fig. 3.
Plots of standard deviation vs. β value for the fits of the variable-barrier model to the experimental data shown in Fig. 2 for thioredoxin (a) and BBL (b). Numbers 1–4 labeling the profiles refer to the baselines used in the calculation of the excess heat capacity profiles (see Fig. 2). All calculations used an asymmetry factor of 0.1.
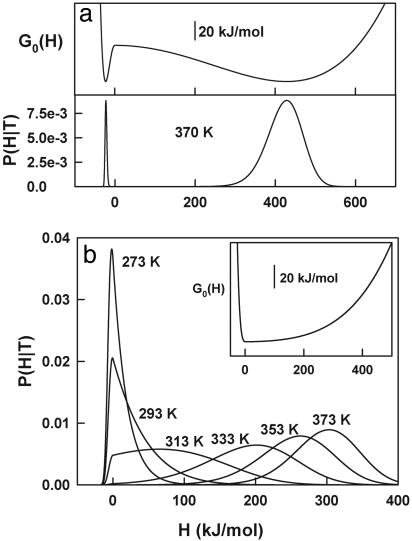
The free energy functional and the probability distribution as a function of H calculated at T0 with the parameters of the best fit are shown in Fig. 4a. The free energy functional has one sharp minimum at low-enthalpy values (i.e., native state) and a much broader minimum at high-enthalpy values (i.e., unfolded state) separated by a large free energy barrier. The probability distribution shows a very sharp peak for the native state and a broad distribution centered at ≈410 kJ/mol for the unfolded state. A straightforward calculation yields 362 K for the temperature at which both macrostates are equally populated, Tm, and 430 kJ/mol for the unfolding enthalpy at the Tm(ΔHm), in excellent agreement with the parameters derived from the chemical two-state analysis.
Fig. 4.
Plots of free energy [G0(H)] vs. enthalpy and probability distributions [P(H/T)] for thioredoxin (a) and BBL (b) calculated with the parameters from the best fits described in the text. For the sake of clarity, only the P(H|T) vs. H profile corresponding to the characteristic temperature is shown for thioredoxin. Probability profiles for other temperatures differ from the one shown, mainly in the heights of the two “peaks.”
Application of the Model to the Thermal Unfolding of BBL. The equilibrium unfolding transition of the small protein BBL has been investigated in great detail as a function of temperature (14) and urea (19). The analysis of these experiments with a simple statistical mechanical model indicated that BBL folds without crossing free energy barriers (14). The absence of a free energy barrier results in a conformational ensemble in which the degree of order decreases gradually with protein stability (13, 14). BBL seems like an ideal candidate to test the performance of our model and investigate the characteristics of its folding ensemble.
BBL has a DSC thermogram that shows a broad transition (Fig. 2b). In this condition BBL is well above its cold denaturation temperature (19), so the broadening is not a consequence of overlapping heat- and cold-induced unfolding transitions. If analyzed individually, this DSC thermogram can be fitted to a chemical two-state model, producing a ΔHm of 92 kJ·mol-1, a Tm of 320 K, and a van't Hoff ratio close to unity (data not shown). However, there are several indications that this fitting is unphysical: the temperature dependence obtained for the native state heat capacity is >2 times higher than that expected for proteins of this size (20); the absolute heat capacity recorded at the lowest temperatures is higher than that expected for the fully native protein [i.e., 1.5 J·K-1·g-1 recorded vs. 1.3 J·K-1·g-1 expected (20, 21)], and the obtained ΔCP changes from positive to negative in the middle of the transition because the two baselines cross. These observations indicate that the transition is clearly not two-state. In fact, the three outlined features have also been observed in leucine zippers and interpreted as indicative of a non-two-state transition (22). The importance of the heat capacity tails has also been discussed in the context of comparing experimental data and polymer models (18).
Therefore, for BBL, and possibly for most of the very small proteins, the native baseline cannot be directly extrapolated from the DSC thermogram, as we have done for thioredoxin. As an alternative to direct extrapolation, we use the empirical equation proposed by Freire (23), in which the heat capacity as a function of temperature is directly calculated from the molecular mass of the protein,
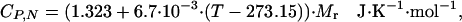 |
[15] |
where T is the temperature in K and Mr is the molecular mass of the protein in g/mol. For DSC experiments reporting absolute heat capacities, this equation should provide a reasonable approximation of the native baseline (see Appendix 1 and Fig. 5, which are published as supporting information on the PNAS web site). The native baseline calculated for BBL with this equation is baseline 1 in Fig. 2b, which is in good accordance with the DSC thermogram (i.e., close to the data at low temperatures and not crossing the thermogram at higher temperatures). We have carried out calculations with other possible native baselines in an effort to test the influence of the native baseline in the performance of the variable-barrier model. Particularly, we have used baselines with a higher temperature slope (baseline 2) and lower temperature slope (baseline 3) and baselines that are parallel but downshifted (baseline 4). This range of baselines constitutes a generous estimate of the uncertainty involved in estimating the heat capacities for native proteins from Eq. 15 (see Appendix 1).
The results of the analysis of BBL's DSC thermogram with the variable-barrier model are summarized in Figs. 2b and 3b. In this case, the plots of σ vs. β (Fig. 3b) clearly indicate that good fits (low values of σ) are only obtained for small absolute β values (see also Fig. 2b). Actually, the best fit with baseline 1 is obtained with a slightly negative β value (T0 = 308.8 K, Σα = 235 kJ/mol, β =-2.5 kJ/mol). Baselines with a lower temperature slope or downshifted baselines (i.e., baselines 3 and 4) produce best fits with even more negative β values. The baseline with the highest temperature slope (i.e., baseline 2) produces best fits with β values very close to zero, which still correspond to a barrierless scenario. Fig. 2b also shows a fit with a β value that results in a marginal free energy barrier (i.e., ≈2 RT) to illustrate the sensitivity of the method. Therefore, the analysis with the variable-barrier model detects the absence of a global free energy barrier for folding in BBL from just the enthalpy fluctuations measured in equilibrium by DSC. Furthermore, the result is largely independent of the tracing of the native baseline, as long as this baseline is constrained within a physically reasonable range.
Fig. 4b shows the probability distribution as a function of H for BBL as obtained from the best fit with baseline 1. The free energy functional at T0 is shown in Fig. 4b Inset. The shape of the free energy functional is clearly downhill, and it is quite similar to free energy profiles previously obtained from a global analysis of experimental data and a statistical mechanical model that uses the number of native peptide bonds as order parameter (14). The probability distribution changes as expected for a one-state transition. The distribution is clearly unimodal at all temperatures, with the maximum probability shifting from low-enthalpy values at low temperature to high-enthalpy values at high temperature. At intermediate temperatures the width of the probability distribution is maximal, in agreement with the observation of a “peaked” DSC thermogram.
A Critical Assessment of the Phenomenological Variable-Barrier Model. The phenomenological model presented here is a simple adaptation of the Landau theory of critical transitions to protein folding. We have formulated this model to be a new tool for the analysis of experimental data. The model is extremely simple, with only three to four adjustable parameters. Yet, as we have shown above, it is a powerful tool for the study of protein-folding ensembles and should prove very useful in the identification of new cases of barrierless folding. However, formulating such a simple model implies that some approximations had to be made. Here we discuss the most important ones and their implications.
Procedures for deriving the shape of the free energy surface for a particular process typically require the definition of an order parameter. In this case, the order parameter should provide a structural scale directly connected to the degree of protein unfolding. We have used the excess enthalpy with respect to the native state as our order parameter mainly because it is directly related to the DSC measurements; by using it we also avoid making specific assumptions about folding mechanisms. However, it is our contention that the excess enthalpy is also a reasonable approximation of a real structural scale for protein folding.
As originally noted by Cooper (24), the enthalpy fluctuations calculated from the heat capacity of native proteins with the equation 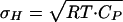 are of the same order of the unfolding enthalpy. For example, for thioredoxin (CP of ≈22 kJ·K-1·mol-1; Fig. 2a) the enthalpy fluctuations of the native state amount to ≈150 kJ/mol at 333 K. Most of these fluctuations in the structurally well defined native state are probably associated with soft vibrational modes and the hydration of polar and apolar groups. Therefore, to obtain an enthalpy scale that is a reasonable order parameter for folding, it is important to reduce the contribution of enthalpy fluctuations with a nonstructural origin.
are of the same order of the unfolding enthalpy. For example, for thioredoxin (CP of ≈22 kJ·K-1·mol-1; Fig. 2a) the enthalpy fluctuations of the native state amount to ≈150 kJ/mol at 333 K. Most of these fluctuations in the structurally well defined native state are probably associated with soft vibrational modes and the hydration of polar and apolar groups. Therefore, to obtain an enthalpy scale that is a reasonable order parameter for folding, it is important to reduce the contribution of enthalpy fluctuations with a nonstructural origin.
To correct for this problem, we analyzed the excess heat capacity obtained after subtracting the native baseline, which is equivalent to assuming that all of the enthalpy fluctuations on the native state are of nonstructural origin. In principle, native baseline subtraction should produce an infinitely narrow probability distribution for the native state. Although it is not feasible to obtain an infinitely narrow peak from the analysis of real experimental data, our variable-barrier model with an asymmetry factor of 0.1 does yield a very narrow peak for native thioredoxin (Fig. 4a). This procedure should also eliminate the largest fraction of nonstructural enthalpy fluctuations in all of the significantly populated nonnative species. Given that unfolded proteins are ensembles of conformations of varying structure (ref. 25 and references therein), it is reasonable to assume that the enthalpy fluctuations remaining in the unfolded state after native baseline subtraction arise from the coupled structural reorganizations of the nonnative polypeptide chain and surrounding solvent. Because these fluctuations are relevant to protein-folding reactions, an enthalpy scale so defined should be as close to a true structural scale as a phenomenological approach permits.
It is also important to restate that our variable-barrier model has been formulated for the analysis of first-order and continuous protein-folding transitions. The analysis of suitable experimental data with this model should indicate whether the protein has a two-state-like transition (i.e., a large barrier separating two minima) or is better described as a one-state transition with varying degrees of heterogeneity in the ensemble. The latter includes transitions with very small barriers and purely downhill transitions. However, the model is not intended to analyze DSC thermograms showing several distinct transitions, because in its current formulation the free energy functional only accommodates one or two macrostates (see Eq. 10). Cold denaturation and unfolding processes involving the accumulation of structurally defined intermediates are beyond the current capabilities of the model. In the context of a chemical two-state model, cold denaturation is equivalent to heat denaturation and arises simply from the parabolic shape of the ΔG for unfolding. At high temperatures the unfolded state has high enthalpy and entropy, and at very low temperatures it has low enthalpy and entropy. Our model uses enthalpy as order parameter, so the cold denatured state should actually be a distinct state at lower enthalpy values from the native state. Therefore, the model requires a more complex free energy functional with two possible barriers and three possible minima to describe cold denaturation. The potential advantage of an explicit treatment of cold denaturation is that it will allow the analysis of transitions in which heat and cold denatured states are symmetric (i.e., as predicted by the chemical two-state model) and nonsymmetric (i.e., heat and cold denatured states with different properties). These two scenarios are illustrated by recent work on ubiquitin (26, 27). In the presence of guanidine, the heat denatured and cold denatured states of ubiquitin populate in a similar temperature range, and the symmetric scenario holds (26). Without denaturants, heat and cold denaturation are separated by >100 K, and the two processes appear fundamentally different (27). Our phenomenological model can certainly accommodate both situations by using a more complex expression for the free energy functional. The general approach could also be extended to chemical denaturation by defining the sensitivity to chemical denaturant (m value) as a continuous variable and defining a suitable G0(m) free energy functional.
Finally, we would like to emphasize that we do not attribute a kinetic meaning to the free energy barriers found in the analysis with the variable-barrier model (at least, at this stage). Within the context of our model, the role of a barrier of height β is simply to reduce the population of intermediate microstates, as required by the properties of the protein-folding ensemble under study. It is not yet clear that folding/unfolding rate constants can be calculated from the β value: this would imply that protein-folding reactions can be described with a single reaction coordinate and that our enthalpy scale is a reasonable approximation of such reaction coordinate.
Concluding Remarks
Theoretical work carried out in the last 20 years emphasizes that protein folding is best envisioned as motion of the polypeptide chain in search of its native structure in a hyperdimensional free energy surface (4, 5, 28–34). Thus, each protein molecule is expected to follow a distinct folding trajectory, whereas bulk experiments provide information about the ensemble-averaged behavior. To connect theory and computer simulations (performed in single molecules) with experiment, the energy landscape approach asserts that is possible to describe protein folding as diffusion on a projection of the free energy hypersurface onto a few order parameters (4). In recent years efforts have been made in this direction by analyzing the folding of a β-hairpin (35) and, later, of the small protein BBL (14) with simplified statistical mechanical models. Inevitably, the use of these models involves making assumptions about molecular mechanisms (36).
To date, there have not been phenomenological alternatives that could allow for a detailed analysis of protein-folding ensembles without assuming particular folding mechanisms. It is perhaps for this reason that most of the experimental results are still interpreted in terms of chemical models. The variable-barrier model that we introduce here is intended to fill this gap. The model is rooted in Landau's phenomenological theory of critical transitions and is operationally as simple as the chemical models. We show that the analysis of equilibrium protein-(un)folding experiments can be performed by using the enthalpy as order parameter and a phenomenological free energy functional with adjustable shape. The shape of the free energy is directly obtained from the experimental data and provides the general thermodynamic properties of the protein-folding ensemble. The extended application of this approach to the analysis of equilibrium protein unfolding data should result in a wealth of new information on folding ensembles and in a more precise evaluation of the thermodynamic barriers to folding.
Supplementary Material
Acknowledgments
V.M. is a recipient of a Dreyfus New Faculty Award, a Packard Fellowship for Science and Engineering, and a Searle Scholarship. This work was supported by National Institutes of Health Grant RO1-GM06680-01 (to V.M.) and Spanish Ministry of Education and Science Grant BIO2003-0229 and Feder Funds (to J.M.S.-R.).
This paper was submitted directly (Track II) to the PNAS office.
Abbreviation: DSC, differential scanning calorimetry.
Note Added in Proof. While this paper was in press, Fersht and coworkers published a report (37) that questions our previous work on downhill folding of BBL. They contend that doubly labeled BBL behaves anomalously and aggregates. However, it is important to note that most of our previously published data (14, 19), as well as the DSC data analyzed in this work, have been obtained on a BBL variant with a single fluorescent label, not on the doubly labeled protein. The singly labeled protein does not aggregate even at millimolar concentrations and exhibits reversible thermal unfolding transitions by DSC (see the supporting materials of ref. 14). We used the doubly labeled BBL only for fluorescence measurements and at protein concentrations that do not result in aggregation (14).
References
- 1.Jackson, S. E. (1998) Folding Des. 3, R81–R91. [DOI] [PubMed] [Google Scholar]
- 2.Plaza del Pino, I. M., Ibarra-Molero, B. & Sanchez-Ruiz, J. M. (2000) Proteins Struct. Funct. Genet. 40, 58–70. [DOI] [PubMed] [Google Scholar]
- 3.Zhou, Y. Q., Hall, C. K. & Karplus, M. (1999) Protein Sci. 8, 1064–1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bryngelson, J. D., Onuchic, J. N., Socci, N. D. & Wolynes, P. G. (1995) Proteins Struct. Funct. Genet. 21, 167–195. [DOI] [PubMed] [Google Scholar]
- 5.Onuchic, J. N., LutheySchulten, Z. & Wolynes, P. G. (1997) Annu. Rev. Phys. Chem. 48, 545–600. [DOI] [PubMed] [Google Scholar]
- 6.Portman, J. J., Takada, S. & Wolynes, P. G. (1998) Phys. Rev. Lett. 81, 5237–5240. [Google Scholar]
- 7.Kubelka, J., Hofrichter, J. & Eaton, W. A. (2004) Curr. Opin. Struct. Biol. 14, 76–88. [DOI] [PubMed] [Google Scholar]
- 8.Akmal, A. & Muñoz, V. (2004) Proteins 57, 142–152. [DOI] [PubMed] [Google Scholar]
- 9.Scalley-Kim, M. & Baker, D. (2004) J. Mol. Biol. 338, 573–583. [DOI] [PubMed] [Google Scholar]
- 10.Chan, H. S., Shimizu, S. & Kaya, H. (2004) Methods Enzymol. 380, 350–379. [DOI] [PubMed] [Google Scholar]
- 11.Yang, W. Y. & Gruebele, M. (2003) Nature 423, 193–197. [DOI] [PubMed] [Google Scholar]
- 12.Yang, W. Y. & Gruebele, M. (2004) Biophys. J. 87, 596–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Muñoz, V. (2002) Intern. J. Quantum Chem. 90, 1522–1528. [Google Scholar]
- 14.Garcia-Mira, M. M., Sadqi, M., Fischer, N., Sanchez-Ruiz, J. M. & Muñoz, V. (2002) Science 298, 2191–2195. [DOI] [PubMed] [Google Scholar]
- 15.Callen, H. B. (1985) Thermodynamics and an Introduction to Thermostatistics (Wiley, New York).
- 16.Freire, E. & Biltonen, R. L. (1978) Biopolymers 17, 463–479. [DOI] [PubMed] [Google Scholar]
- 17.Perez-Jimenez, R., Godoy-Ruiz, R., Ibarra-Molero, B. & Sanchez-Ruiz, J. M. (2004) Biophys. J. 86, 2414–2429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kaya, H. & Chan, H. S. (2000) Proteins Struct. Funct. Genet. 40, 637–661. [DOI] [PubMed] [Google Scholar]
- 19.Oliva, F. Y. & Muñoz, V. (2004) J. Am. Chem. Soc. 126, 8596–8597. [DOI] [PubMed] [Google Scholar]
- 20.Makhatadze, G. I. & Privalov, P. L. (1995) Adv. Protein Chem. 47, 307–425. [DOI] [PubMed] [Google Scholar]
- 21.Makhatadze, G. I. & Privalov, P. L. (1996) in Physical Properties of Polymers Handbook, ed. Mark, J. E. (Am. Inst. of Physics, Melville, NY), pp. 91–100.
- 22.Dragan, A. I. & Privalov, P. L. (2002) J. Mol. Biol. 321, 891–908. [DOI] [PubMed] [Google Scholar]
- 23.Freire, E. (1995) Protein Stability and Folding (Humana, Totowa, NJ).
- 24.Cooper, A. (1976) Proc. Natl. Acad. Sci. USA 73, 2740–2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Guzman-Casado, M., Parody-Morreale, A., Robic, S., Marqusee, S. & Sanchez-Ruiz, J. M. (2003) J. Mol. Biol. 329, 731–743. [DOI] [PubMed] [Google Scholar]
- 26.Ibarra-Molero, B., Makhatadze, G. I. & Sanchez-Ruiz, J. M. (1999) Biochim. Biophys. Acta 1429, 384–390. [DOI] [PubMed] [Google Scholar]
- 27.Babu, C. R., Hilser, V. J. & Wand, A. J. (2004) Nat. Struct. Mol. Biol. 11, 352–357. [DOI] [PubMed] [Google Scholar]
- 28.Hinds, D. A. & Levitt, M. (1995) Trends Biotechnol. 13, 23–27. [Google Scholar]
- 29.Shakhnovich, E. I. (1997) Curr. Opin. Struct. Biol. 7, 29–40. [DOI] [PubMed] [Google Scholar]
- 30.Chan, H. S. & Dill, K. A. (1998) Proteins Struct. Funct. Genet. 30, 2–33. [DOI] [PubMed] [Google Scholar]
- 31.Pande, V. S., Grosberg, A. Y., Tanaka, T. & Rokhsar, D. S. (1998) Curr. Opin. Struct. Biol. 8, 68–79. [DOI] [PubMed] [Google Scholar]
- 32.Dobson, C. M., Sali, A. & Karplus, M. (1998) Angew. Chem. Int. Ed. 37, 868–893. [DOI] [PubMed] [Google Scholar]
- 33.Brooks, C. L. (1998) Curr. Opin. Struct. Biol. 8, 222–226. [DOI] [PubMed] [Google Scholar]
- 34.Thirumalai, D. & Klimov, D. K. (1999) Curr. Opin. Struct. Biol. 9, 197–207. [DOI] [PubMed] [Google Scholar]
- 35.Muñoz, V., Thompson, P. A., Hofrichter, J. & Eaton, W. A. (1997) Nature 390, 196–199. [DOI] [PubMed] [Google Scholar]
- 36.Muñoz, V. (2001) Curr. Opin. Struct. Biol. 11, 212–216. [DOI] [PubMed] [Google Scholar]
- 37.Ferguson, N., Schartau, P. J., Sharpe, T. D., Sato, S. & Fersht, A. R. (2004) J. Mol. Biol. 344, 295–301. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.