Gene-based Segregation Method for Identifying Rare Variants in Family-based Sequencing Studies

Abstract

Whole-exome sequencing using family data has identified rare coding variants in Mendelian diseases or complex diseases with Mendelian subtypes, using filters based on variant novelty, functionality, and segregation with the phenotype within families. However, formal statistical approaches are limited. We propose a GEne-based SEgregation Test (GESE) that quantifies the uncertainty of the filtering approach. It is constructed using the probability of segregation events under the null hypothesis of Mendelian transmission. This test takes into account different degrees of relatedness in families, the number of functional rare variants in the gene, and their minor allele frequencies in the corresponding population. In addition, a weighted version of this test allows incorporating additional subject phenotypes to improve statistical power. We show via simulations that the GESE and weighted GESE tests maintain appropriate type I error rate, and have greater power than several commonly used region-based methods. We apply our method to whole-exome sequencing data from 49 extended pedigrees with severe, early-onset chronic obstructive pulmonary disease (COPD) in the Boston Early-Onset COPD Study (BEOCOPD) and identify several promising candidate genes. Our proposed methods show great potential for identifying rare coding variants of large effect and high penetrance for family-based sequencing data. The proposed tests are implemented in an R package that is available on CRAN (https://cran.r-project.org/web/packages/GESE/).

Introduction

Advancements in sequencing technology have allowed examination of rare coding variants associated with disease. In contrast to large studies in complex disease, a “filtering”-based approach focusing on variant segregation with phenotype, predicted variant functionality and novelty has been used to identify causal variants/genes for Mendelian diseases[Bamshad, et al. 2011; Chong, et al. 2015; Ionita-Laza, et al. 2011; Ng, et al. 2010]. Some complex diseases are also known to have Mendelian or near-Mendelian variants, such as alpha-1 antitrypsin deficiency in Chronic Obstructive Pulmonary disease (COPD)[Dahl, et al. 2001], BRCA1 and BRCA2 for breast and ovarian cancer[Aida, et al. 1998; Miki, et al. 1994; Szabo and King 1995], and TARDBP for Amyotrophic Lateral Sclerosis (ALS)[Daoud, et al. 2009]. Therefore, filtering-based methodologies for exome-sequencing data may also be applicable to identify disease genes in subsets of complex disease with Mendelian features.

However, the number of families recruited for these studies are generally small, which creates challenges for traditional variant-based or gene-based association methods. Typical filtering-based methods do not quantify the uncertainty of the results, nor do they account for different degrees of relatedness or background variations in the gene. To overcome these limitations, several other solutions have been proposed. MendelScan [Koboldt, et al. 2014] is a ranking scheme that incorporates segregation information, variant rarity and predicted functionality. However, it does not differentiate between family structures, and it gives only a variant-based ranking without providing confidence statements. A variant-based approach is likely to be less powerful due to the rarity of the causal variants and the potential for different variants in the gene to contribute to disease susceptibility in different families. Collapsing the information from multiple variants within a gene may be more likely to capture key genes[Dering, et al. 2011; Price, et al. 2010; Sun, et al. 2011]. This is one of the advantages of the methods described in Ionita-Laza et al [Ionita-Laza, et al. 2011], in which the authors designed a gene-based test for segregation events in pairs of affected relatives. It considers background variation in the gene and degrees of relatedness between the affected relatives. However, only pairs of the same relationship can be incorporated in this test, whereas many studies include different family structures. A method based on the exact probability of sharing between affected relatives proposed by Bureau et al [Bureau, et al. 2014] has the advantage of relying on a formal statistical approach that can incorporate different family structures. It computes the sharing probability of each variant in the affected subjects conditioning on the presence of the variant in the family and gives an exact test based on the segregation events across families. However, it is also variant-based and cannot collapse information across a gene. Our method is motivated by this approach, but computes the marginal probability of segregation events within a gene, in the case where a reference database or control set from the same population exists, with the following goals: (1) the method should collapse segregation information of all selected variants in the gene; (2) it should also take into account background variations in the gene, such as the number of variants and variant frequencies in the gene; and (3) it should differentiate different degrees of relatedness in the families. Our method differs from traditional haplotype sharing methods[Allen and Satten 2007; Beckmann, et al. 2001] as we utilize reference database to combine population-based signal with segregation information and consider each rare variant separately.

In this paper, we propose a GEne-based SEgregation test named GESE, which quantifies the uncertainty of segregation events for rare variants and is designed to identify genetic variants of high penetrance in sequencing studies using multiple pedigrees of any family structure with at least one affected individual. It is constructed using estimated segregation probabilities of the gene in the families under the null hypothesis that no variant in the gene is associated with disease status. It achieves the goals listed above, and it gives statistically valid p-values. Our method also allows weighting of families, for example, higher weights for families with more severe cases. We show using simulations that our gene-based tests are valid under the null hypothesis and perform better than other methods for identifying causal variants of large effect and high penetrance. We apply our methods to whole-exome sequencing data from pedigrees in the Boston Early-Onset Chronic Obstructive Pulmonary Disease study (BECOPD) [Aida, et al. 1998; Qiao, et al. 2016a; Silverman, et al. 1998]. Our approaches are implemented in an R package GESE that is publicly available on CRAN (https://cran.r-project.org/web/packages/GESE/). We also implemented a Python pipeline for the preprocessing of data and application of the GESE package using the annotations provided by WGS Annotator[Liu, et al. 2016] (Supplemental Material). It is publicly available at http://scholar.harvard.edu/dqiao/gese. Some of the results of this study have been previously reported in the form of abstracts[Qiao, et al. 2016b].

Materials and Methods

The Gene-based segregation test

Our gene-based segregation test (GESE) is based on segregation events in sequenced pedigrees. A segregation event of a variant in a pedigree refers to the scenario where among all of the sequenced subjects in the family, all those affected carry the variant and all those unaffected subjects do not carry the variant. By obtaining the probability of segregation events across a gene for multiple families, we can compute the p-value of such events considering the entire sample space of segregation events for all families in the data. Since we are looking for rare variants with large effects, we assume that only one founder in the family introduced a causal variant in the gene (as shown below) into the family. We can further limit the test variants to a single class of variants, e.g. variants with high functional impact.

For a gene of interest, say gene G, assume that X_f represents the event that at least one variant in gene G segregates in family f. Then X_f follows a Bernoulli distribution with parameter p_f, where p_f is the probability that at least one variant in gene G segregates in family f, for families f = 1, …, F This probability is computed under the assumption of no association between any variant in the gene and affection status, and is based only on the allele frequencies of the variants in the gene, and the family relatedness. Then GESE is based on computing the probability of segregation events of families, assuming independence, using the formula:

$$S_{(X_1,\dots ,X_F)}=P(X_1,\dots ,X_F)={\mathrm{\Pi }}_{f=1}^F{p_f}^{X_f}{(1-p_f)}^{1-X_f}$$ (1)

With the estimates of the segregating probabilities p_f, we can compute the p-value of this test, which is the sum of the probability of events that are as or more extreme (less likely) than the observed events. The probabilities can be estimated using simulations from the Bernoulli distribution.

To estimate p_f – the probability that at least one variant in gene G segregates in family f, we extend the calculation of variant-sharing probabilities by affected relatives described in Bureau et al[Bureau, et al. 2014] and compute the marginal probability of segregation events for the gene. Let indicator variable V_if, i = 1, …, m indicate whether variant i in gene G segregates in family f. Then:

$$\begin{array}{l}{p}_f=P\left(V_{1f}+\cdots +V_{mf}>0\right)=1-P\left(V_{1f}=\cdots =V_{mf}=0\right)\\ \le 1-{\mathrm{\Pi }}_{i=1}^{m}P\left(V_{if}=0\right)=1-{\mathrm{\Pi }}_{i=1}^m(1-P\left(V_{if}=1\right))\end{array}$$ (2)

Eq. 2 is valid with equality under the assumption of marginally independent segregation events between these rare variants within the gene. Since we are considering only rare variants, the linkage disequilibrium (LD) between these variants is likely to be small. Therefore, the probability of finding multiple rare variants (RVs) with a MAF < 0.001 in the same gene in the same family is also small. From our simulation, the average number of RVs in the same gene with 100 variants is about 1.1 in our simulated dataset of 50 families of approximately 200 samples under the null (Supplemental Table S7). With the small probability of observing multiple RVs in the same gene in the same family, the marginal gene-based segregation probability can be approximated under the assumption of independent segregation events between the variants within the gene. We performed gene-dropping algorithm assuming no recombination within genes in the simulation, and evaluated the effect of LD using simulated data.

To obtain the probability that variant i segregates in family f, which is P(V_if = 1), let R_if indicates whether variant i is present in any founders in family f. Then:

$$\begin{array}{l}P\left(V_{if}=1\right)=P\left(V_{if}=1|R_{if}=1\right)P(R_{if}=1)\\ \text{since}P\left(V_{if}=1|R_{if}=0\right)=0.\end{array}$$ (3)

The probabilities in (Eq. 3) can be computed analytically assuming that only one founder introduced the rare variant into the family, with equal probability for any founder (Supplemental Material). The conditional probability in (Eq. 3) distinguishes different degrees of relatedness between different families. In P(R_if = 1), we assume that all founders are unrelated with the same probability of introducing the variant to the pedigree under the null hypothesis. This probability can be estimated using unrelated controls from a large sample, or a reference genome database with a matching population. Therefore, p_f summarizes the different genetic background variations based on the number of variants in the gene and their minor allele frequencies (MAFs) in the population. With the estimation of these segregating probabilities p_f under the null overall families, we can compute the marginal probability of any segregation events, and obtain the p-value for the GESE test by summarizing the probability of any segregating events with probability less than the probability of the observed segregating event. Using the definition of the test statistic S defined in (Eq. 1), we can obtain the p-value using:

$$p-\mathit{value}=\sum _{({\mathit{X}}_{\mathbf{1}},\dots ,{\mathit{X}}_{\mathit{F}})\in {\{\mathbf{0},\mathbf{1}\}}^{\mathit{F}}}P\left(S_{({\mathit{X}}_{\mathbf{1}},\dots ,{\mathit{X}}_{\mathit{F}})}\le S_{({\mathit{x}}_{\mathbf{1}},\dots ,{\mathit{x}}_{\mathit{F}})}\right)$$

Weighted GESE test

Individual families may not have equal probability of harboring the same causal rare variant; for example, one may choose to increase the contribution of more extreme phenotypes. Therefore, we propose a weighted GESE test by weighting the families on additional information with the goal of maximizing the power to detect the causal genes:

$$S_w={\sum }_{f=1}^F{w}_f(X_{f}log{p}_f+\left(1-X_f\right)log(1-p_f))$$ (4)

where w_f indicates the weight of family f for one gene, which can be a function of the phenotypes or covariates of subjects in the family, with constraint ${\sum }_{j=1}^F{w}_f=1$. For example, for the application to the BEOCOPD exome data, we gave higher weights to families with more severe cases (severity defined using the residuals obtained by regressing lung function to other covariates, including age, sex, pack-years, and height). Note that w_f should be independent of the genetic data to maintain the correct type I error rate for the weighted test. We can again compute the p-value for this test using simulations based on the estimated segregating probabilities p_f

Results

We investigated via simulations the performance of the tests proposed here. We also applied GESE to whole exome sequencing data from 49 pedigrees ascertained through severe, early-onset chronic obstructive pulmonary disease (COPD) patients from the Boston Early-Onset COPD study, with a goal of identifying candidate genes with rare variants of large effect on risk to COPD.

Simulating sequencing data for ascertained families

To simulate a phenotype due to a rare, highly penetrant variant, we simulated sequencing data for 50 families ascertained on a value of an extreme quantitative trait with different family structures. We generated families with structure shown in Supplemental Figure S1, and generated a quantitative phenotype. We defined affecteds to be subjects with phenotype above 99^th percentile under the null, and unaffecteds to be subjects with phenotype below the 30^th percentile. We selected only families with at least two affected subjects. All of the affected subjects and a randomly generated number of unaffected subjects (between 0 and 3) in these families were ascertained to be in the simulated dataset. This resembles the ascertainment process for selecting subjects to undergo sequencing in real projects. For the founders of the families, we generated haplotypes using a multivariate normal distribution[Schaid, et al. 2013] for genes of size 10, 100, or 1000 variants with MAFs from the Beta(1, 25) distribution between 0 and 0.001 (Supplemental Material). The multivariate normal distribution allows us to change the linkage disequilibrium (LD) between variants to examine the effect of LD on the performance of the test. We consider ρ (specified correlation structure[Schaid, et al. 2013]) of 0, 0.3, and 0.7 between adjacent variants, and let the LD decay with an autoregressive model of order 1 between further variants. The genotypes of the non-founders were generated using gene-dropping algorithms under Mendelian transmission, where we assumed no recombination or mutation events during the transmission of the haplotypes from the parents to the offspring.

Type I error rate of the GESE test

To evaluate the validity of our test, we randomly generated a quantitative response variable independently from the simulated genotypes, with heritability equal to 50%. Suppose there are n individuals in the simulated dataset, the phenotype vector of size n × 1 follows

$$y=\delta +\epsilon$$ (4)

where δ is a n × 1 vector from $N(0,{\sigma }_G^2\mathrm{\Phi })$ representing the familial correlation, and ε is a n × 1 vector from $N(0,{\sigma }_E^{2}I)$ representing the independent random error. Here Φ is twice the kinship matrix of size n × n, and I is the identify matrix of size n × n. At least 100,000 simulations were ran to estimate the type I error rates in each scenario.

Table 1 shows the type I error rate of our GESE methods when all variants in the gene are transmitted together without recombination or mutation events, from the parents to the offspring. We assume that we have complete information about all the variants in the gene and their true MAFs in the population. For genes with a small number of variants, this test is conservative due to the rarity of the events. As the number of variants increases, the probabilities of no segregation events computed under independent segregation becomes smaller than the real probabilities due to inequality (Eq. 1); therefore, the type I error rate becomes less conservative as the number of variants increases. As the LD between variants increases, the type I error rate does not vary much. Table 2 shows the type I error is well maintained at different significance levels for both the GESE and weighted GESE test.

Table 1. Type I error rate of the GESE tests.

Type I error rate for genes with number of variants 10, 100, and 1000, at three different LD levels specified by ρ = 0.3, and 0.7. The significance level is 0.05.

ρ	GESE			Weighted GESE
	10	100	1000	10	100	1000
0	0.007	0.046	0.047	0.007	0.049	0.048
0.3	0.007	0.044	0.047	0.007	0.048	0.047
0.7	0.007	0.042	0.041	0.007	0.045	0.041

Table 2. Type I error rate of the GESE test at different significant levels.

Type I error rate of the GESE test and the weighted GESE test for genes of various sizes (10, 100 or 1000 variants) with LD=0, at different significance levels.

Significance	GESE			Weighted GESE
	10	100	1000	10	100	1000
5 × 10−2	7.1 × 10−3	4.6 × 10−2	4.7 × 10−2	7.1 × 10−3	4.9 × 10−2	4.8 × 10−2
10−2	6.6 × 10−3	8.5 × 10−3	9.3 × 10−3	6.9 × 10−3	9.5 × 10−3	9.4 × 10−3
10−3	7.6 × 10−4	1.0 × 10−3	9.0 × 10−4	9.1 × 10−4	1.1 × 10−3	8.5 × 10−4
10−4	7.3 × 10−5	1.2 × 10−4	7.8 × 10−5	8.8 × 10−5	1.2 × 10−4	8.9 × 10−5

Evaluating the effect of the reference genome database

In reality, since we do not have complete information about the variants and their true MAFs, the approach requires estimates of MAFs of the variants in the gene, which could be obtained from reference genome database. However, reference databases consist of limited numbers of genomes, and variants with small MAFs are likely to be missed. Therefore, the calculation of the probability of observing a variant in a given gene for the family using the reference database is only an approximation. In our implementation, we included variants that are present in the study but absent in the reference database in the calculation, and assigned an estimated MAF based on the size of the reference database (Supplemental Material). This ensures that the probabilities of observing the genes present in the study but absent in the reference genome database are nonzero. We evaluated the effect of the size of the reference database in our method using the same simulation procedure as above, assuming that only a subset of variants in a gene could be found in the reference database.

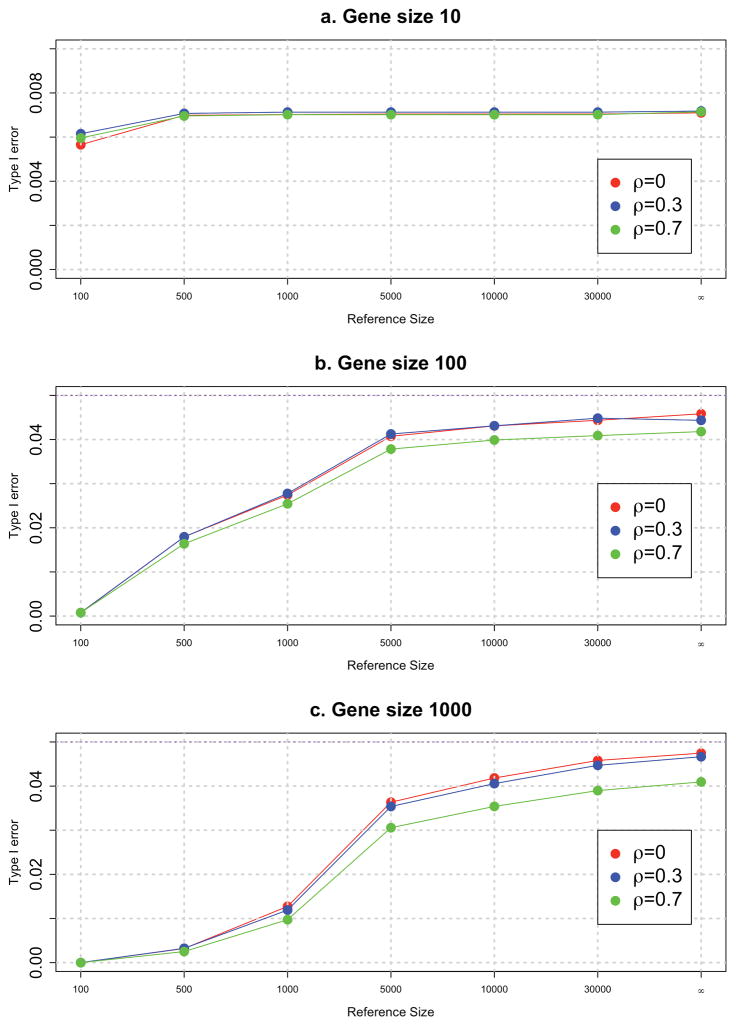
Specifically, we assume that the reference database contains N subjects (N=10, 100, 500, 1,000, 5,000, 10,000, 30,000) randomly selected from the population. The type I error rate for different sizes of the reference database is shown in Figure 1. We observed that when the reference database is small, the test is conservative and approaches the type I error rate of the test using the true population MAF. Therefore, we recommend using a population-appropriate reference database (as large as possible) to obtain accurate estimates of background variations in the gene; but a population-appropriate reference database of at least 5,000 subjects will give an appropriate type I error rate.

Figure 1. Type I error of the GESE tests.

Type I error of the GESE tests using reference genome databases of various sizes (number of subjects = 10, 100, 500, 1000, 5000, 10000, and 30000), for genes with 10, 100, and 1000 variants and three different LD values: 0, 0.3, and 0.7.

Power of the GESE tests

To assess the power of our test, we considered different levels of genetic heterogeneity by simulating 2 or 10 causal genes; 10% of the rare variants in the causal genes were assumed to be functional and all of these were assumed to be deleterious.

We generated a quantitative phenotype based on the same model in (Eq. 4), with an additional genotype term:

$$y=X\beta +\delta +\epsilon$$

where X is an n × m genotype matrix with m variants and n subjects, We set the coefficients β to be fixed for the causal variants under the alternative hypothesis. Few methods are directly comparable to our tests. While our method is fundamentally different from association tests, such methods are often applied for identifying causal genes in family-based exome sequencing studies. We compared GESE with two association tests, famSKAT[Chen, et al. 2013] and PedGene[Schaid, et al. 2013] burden-based test. Both tests were designed to collapse variants to identify causal genes. In our simulation, the weighted GESE test used the average of the underlying quantitative phenotype of the cases in the family (i.e. families with more severe cases were weighted higher). 2,000 simulations were ran to obtain the power estimates for the tests using the true MAF population for each scenario, and 10,000 simulations were ran to obtain the power estimates for the tests using reference genome database.

One important note is that since GESE considers all possible genes in the genome, the p-value of the GESE test should be corrected using the total number of genes in the reference genome database instead of the genes in the study. Since we compute the marginal probability of segregation event using the MAFs in the population and not the conditional probability given at least one rare variant is present, we cannot consider only the genes present in the study. For a fair comparison, we utilized significance levels of 2.5 × 10⁻⁶ for GESE and 1.0 × 10⁻⁵ for famSKAT and PedGene since we considered only the rare and functional set of variants. The significance levels were chosen based on our experience with the BEOCOPD whole exome sequencing data (shown below). The average heritability explained by each gene under each scenario is reported in Supplemental Table S6, and the average number of variants observed in each gene is reported in Supplemental Table S7.

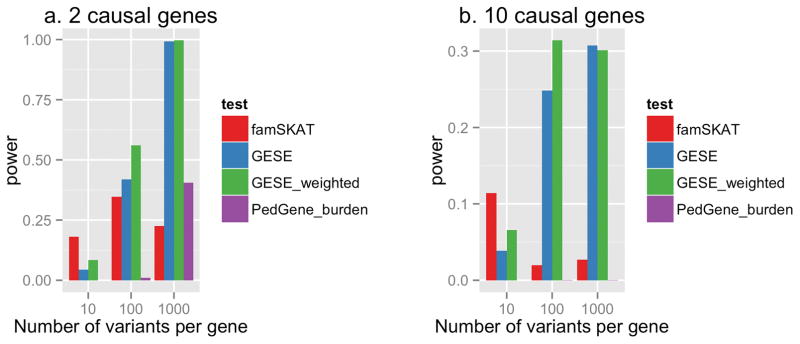
Figure 2 shows the power of the GESE test, weighted GESE test, famSKAT, and PedGene burden-based test at the LD level of ρ = 0.3 for 2 and 10 causal genes. Since famSKAT was designed for quantitative phenotypes, we used the underlying quantitative phenotype. The power of these tests at other LD levels is very similar to these results (Supplemental Table S1 and S2). A similar trend is observed for an affected-only analysis; when no unaffected subjects were included in the data (Supplemental Figure S3, Supplemental Table S4 and S5), the power is slightly lower.

Figure 2. Power comparison.

Power for GESE and other tests when there are (a) two causal genes and (b) 10 causal genes, with 100 variants each, at the LD level of ρ = 0.3, and 10% of the variants are deleterious. Significance levels are set to 2.5e-06 for GESE and 1e-05 for famSKAT and PedGene.

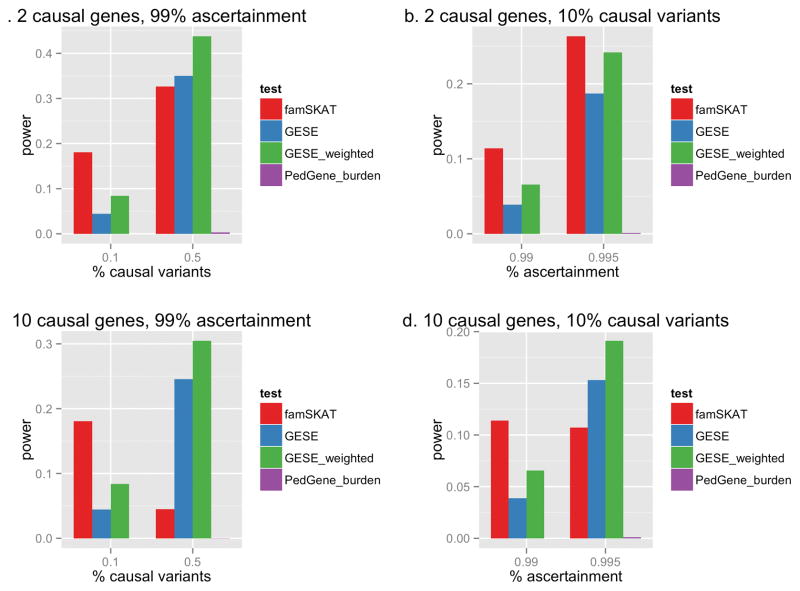
When the number of variants in the gene is 10, the power of GESE is small due to the rarity of the events. In this scenario, famSKAT performed well since there is only one causal variant and a small number of non-causal variants in the gene. However, as we increase the percentage of causal variants in each gene, the power of GESE increases (Figure 3a, 3c). In addition, if we consider more extreme ascertainment (for example, from the 99% to 99.5% percentile for the situation of 10 causal genes), we observe dramatic increase in the power of GESE (Figure 3d). With a larger number of variants in the gene (100 and 1000 variants per gene, Figure 2), GESE performs better than PedGene and famSKAT (which uses the quantitative trait). It has been shown that asymptotic tests can be conservative at extreme significance levels[Schneiter, et al. 2005], which may be one of the reasons that these association methods do not perform as well. In general, as the number of causal genes increases, the power to detect any of the causal genes is reduced due to increased genetic heterogeneity (Figure 2b). However, a similar pattern is observed where GESE tests perform better than the other association methods as the number of variants increases.

Figure 3. Power comparison for genes with 10 variants.

Power for genes each with 10 variants of interest at the LD level of ρ = 0.3 with 2 (a and b) or 10 (b and d) causal genes, showing the effect of increasing the percentage of causal variants (a and c) and increasing the ascertainment threshold (b and d).

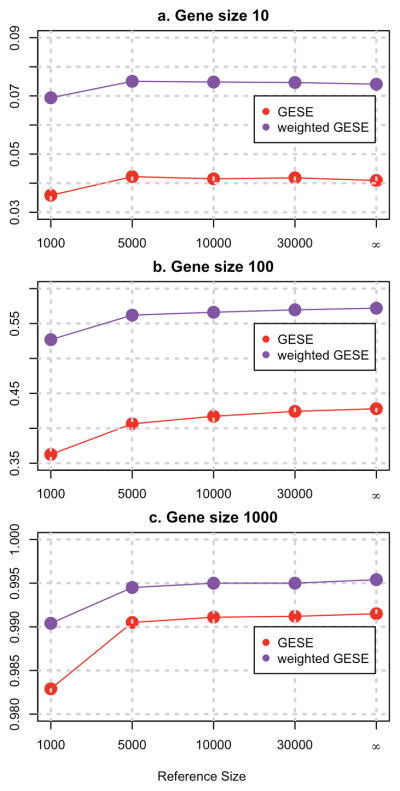
We also looked at the power estimates for different sizes of the reference database. Figure 4 clearly shows that as the size of the reference database increases, the power of the GESE tests increases and approaches the power of the tests computed using the true population MAFs. More detailed results can be found in Supplemental Table S8 and S9.

Figure 4. Power estimates of the GESE tests.

Power estimates of the GESE tests using reference genome databases of various sizes (number of subjects = 1000, 5000, 10000, and 30000) and using the true population MAF (indicated by symbol ∞ ), for genes with 10 (panel a), 100 (panel b), and1000 (panel c) variants at LD level ρ = 0.3. There are 2 casual genes in the simulation.

Application to the BEOCOPD dataset

We selected 107 affected subjects with severe and very severe COPD, and 34 unaffected current or former smokers with normal lung function from the whole exome sequencing data of 347 subjects from 49 pedigrees ascertained through severe, early-onset COPD patients[Qiao, et al. 2016a; Silverman, et al. 1998]. Details on exome sequencing, including subject selection and quality control, have been previously described [Qiao, et al. 2016a]. Compared to the previous filtering-based approach[Qiao, et al. 2016a] using ExAC r0.1 [Lek, et al. 2016] and CADD[Kircher, et al. 2014] version 1.0) and different filtering criteria (including SnpEff[Cingolani, et al. 2012], Condel[Gonzalez-Perez and Lopez-Bigas 2011] and CADD for annotation score), here we used ExAC r0.3 and CADD 3.0 for first step filtering. We included variants with selected consequence categories (missense, stop gained, stop lost, start lost, splice acceptor and donor variants), MAF < 0.1% in Europeans in UK10K[Muddyman, et al. 2013] and 1000 Genomes Project[Genomes Project, et al. 2015] and in non-Finnish Europeans in ExAC r0.3 dataset, MAF < 1% in the controls in the BEOCOPD dataset, and CADD score >15. There are 5,761 variants in 4361 genes in the filtered set of variants, and 14 of these genes segregate in at least 3 families. Only 4 individual variants in 4 different genes segregate in more than one family (2 families for all 4 variants). Applying a naive filtering approach, the top genes that segregated in 5 and 4 families were TTN and MLL2 respectively. Since these are large genes with many variants, it is likely that they are false positives. Therefore, we applied GESE, which considers the genetic background variation and the family structures to prioritize genes. We used the estimated MAFs from the 33,370 non-Finnish Europeans in the ExAC r0.3 database[Lek, et al. 2016] in the computation of the tests. We also applied the weighted GESE test by incorporating additional phenotypic information. We weighted the families using w_f which is the average residual of the cases obtained by regressing each individual’s lung function (forced expiratory volume in 1 second, or FEV₁) on height, age, sex and number of pack-years of smoking, to increase the contribution of the most extreme subjects. No genes were significant after Bonferroni correction. The top 10 genes identified using the weighted GESE test are shown in Table 3. Six of these genes were in the 69 segregating in more than one family in previous analyses using different filtering criteria[Qiao, et al. 2016a]. We also applied famSKAT and PedGene; the smallest p-value obtained using famSKAT was 0.016, using PedGene burden was 0.00024).

Table 3.

Top results from the weighted GESE test applied on the BEOCOPD data.

GENE	GESE p-value	Weighted GESE p-value	# simulations	# segregating families	# segregating variants
PALM2	7.1×10−5	2.0×10−5	106	3	3
SPINT1	5.2×10−5	1.0×10−4	106	3	3
PLCB1	1.5×10−4	1.0×10−4	106	3	2
OR4K13	3.4×10−4	1.1×10−4	106	2	2
PLEKHG1	1.1×10−3	1.6×10−4	105	3	3
ZNF256	3.7×10−4	3.0×10−4	105	2	2
RXFP1	4.5×10−3	3.0×10−4	105	2	2
HSPA5	3.7×10−4	3.2×10−4	105	2	2
ZUFSP	2.1×10−3	4.4×10−4	105	2	2
OR6A2	4.1×10−3	5.0×10−4	105	2	2

Comparing to simple filtering approach, the weighted GESE test takes into account the family structure, phenotype information, and the number of variants and their frequencies in the gene in the corresponding population. Our top-ranked genes, PALM, SPINT1 and PLCB1, all segregate in three families. For example, PALM2 segregates in one uncle-niece pair (CADD score for the segregating variant 26.3) and two sibling pairs (CADD 26 and 25.8). SPINT1 segregates in one sibling pair family with a unaffected second-degree aunt (CADD 22.9), and two parent-offspring families with at least one unaffected subjects (CADD 33 and 23.9). Genes such as OR4K13, which segregates in two families, are ranked higher than other genes segregating in three families (14 genes segregating in at least 3 families). In fact it is segregating in a family with a sibling pair (both in their thirties) with extremely low FEV₁% predicted values (20 and 23). We note that among our top genes are several of potential biologic interest, including SPINT1, part of a pathway CFTR-dependent regulation of ion channels in airway epithelium; HSPA5, which encodes GRP78, autoantibodies to which were found in emphysema; and RXFP1, which may protect against airway fibrosis in murine models[Samuel, et al. 2009].

Eight of the top 10 genes (all except OR4K13 and OR6A2), showed evidence for expression in the lung by RNA-Seq (FPKM > 0.5 in more than 50% of samples) in the Lung Genomics Research Consortium (http://www.lung-genomics.org/)[Uhlen, et al. 2015] (p-value for enrichment = 0.51). In lung tissue from 111 subjects with severe COPD and 40 unaffected subjects with normal spirometry, 1 of the top 10 genes showed significant differences in expression in COPD (HSPA5, also known as CRP78 [Morrow 2015]; adjusted differential expression p = 0.0487 for HSPA5, enrichment p-value of the top 10 genes = 0.00474).

Discussion

An approach looking for segregation of rare, deleterious variants has been utilized frequently in Mendelian or near-Mendelian disease studies. While a few methods have attempted to apply inference testing to these studies, most previous approaches lack the ability to expand to multiple pedigrees with more complex relationships, and they do not allow formal statistical testing. We propose a gene-based test constructed using the probabilities of variant-segregation events within the family, and aggregates variant-based information over a gene. We recognize the sample size for such studies could be very small; our method requires only sequencing extremely affected subjects and a population-appropriate reference database with summary statistics (MAFs). Our method also allows the incorporation of family-specific weights. In simulation studies, we demonstrate that our method has preserved type I error, and improved power compared to two previously reported family-based methods. The power improvement of GESE comes from the fact that we combine the association signals (using reference data) and linkage signals (segregation probability) in calculating the marginal probability of segregation, and also that we assumed that the rare variants have only deleterious effects. In addition, for data with small sample size, GESE maintains the appropriate type I error rate by obtaining MAFs from the reference database rather than the data under study, and is not conservative at extreme significance levels (1e-05 for example) as other asymptotic methods. We also applied our methods to whole-exome sequencing data from the Boston Early-Onset COPD study. Due to the nature of our approach, we were limited in our ability to compare our approach with other methods in simulations. The most applicable approaches mentioned previously[Bureau, et al. 2014; Ionita-Laza, et al. 2011; Koboldt, et al. 2014] do not perform gene-based tests, or do not allow a flexible pedigree structure. One additional method that we were unable to directly test against in simulations was pVAAST [Hu, et al. 2014]. Though we have applied this method to the BECOPD data[Qiao, et al. 2016a], since pVAAST applies its own set of filtering criteria to a set of individually genotyped controls and utilizes genomic annotation in the test, and our simulated data were based on multivariate normal distribution instead of haplotypes sampled from a reference database, we were unable to create a comparable scenario in simulations.

Our method makes several simplifying assumptions. For the calculation of segregation probability, we made the assumption that at most one founder introduced the rare causal variant into the family; however, this is a common assumption for identifying rare causal variants for Mendelian disease. We also assume independent transmission of deleterious and rare variants in the gene between generations. These assumptions limit the set of variants included in the analysis to rare variants predicted to be deleterious in the genes. If less rare variants (MAF > 1%) were included, it is likely to violate the assumption that only one founder introduced variant[Bureau, et al. 2014], and the assumption of independence between variants may also be violated. Therefore, we recommend filtering down to a set of rare and predicted functional variants. Our test implicitly assumes a dominant mode of inheritance for the disease of interest and a shared causal variant within the family. Families with different causal variants would not provide additional information and would reduce the power of the test. Further work is needed to extend this model in these situations. One approach to extend the method could be to consider different sets of subjects to compute the segregation probabilities. Similarly, under the assumption of complete penetrance, unaffecteds could be included (but this is not required). Our method also relies on an accurate and well-matched reference database to obtain background variation for maintaining appropriate type I error rates. Batch effects or population structure could affect the validity of these tests, therefore a matching reference database and well-curated subset of variants need to be selected carefully. In the scenario where no reference database is present or only one family is present, the variant-based sharing method of Bureau et al[Bureau, et al. 2014] would be more appropriate. Fortunately, thanks to important collaborative efforts, such datasets with increasingly large sample sizes are becoming publicly available.