Phylogeny of protein-folding trajectories reveals a unique pathway to native structure

Abstract

To scrutinize how a protein folds at atomic resolution, we performed 200 molecular dynamics simulations (each of 50 ns) of the miniprotein Trp-cage on the computational grid. Within the trajectories, 58 folding and 31 unfolding events were identified and subjected to extensive comparison and classification. Based on an analogy with biological sequences, the folding and unfolding trajectories (arrays of sequential snapshots of structures) were aligned by dynamic programming allowing gaps. A phylogenetic tree derived from the alignments revealed four distinct groups of the trajectories, characterized by the Trp side-chain motions and the main-chain motions. It was found that only one group attained the native structure and that the other three led to pseudonative structures having the correct main-chain trace but different nonnative Trp side-chain rotamers, indicating that those four folded structures were each attained through a unique folding pathway.

Protein molecules rapidly fold into a unique, native structure despite the vast size of conformational space in the unfolded state (1). To resolve the paradox between the large space and the fast process, the folding pathway (2) and folding funnel (3) models have been proposed. The pathway model emphasizes narrow pathways in the conformational space, whereas the funnel theory focuses on quick folding on a funnel-like potential surface. A number of experimental results, particularly for small proteins, have been interpreted in terms of either the pathway or funnel model (4–11). However, these views do not necessarily present a comprehensive picture explaining in detail how a specific protein folds into the native structure. Recently, folding simulation at atomic resolution has become a realistic possibility to study the folding process of small proteins (12–18) in spite of the extremely large computational burden. An atomically detailed picture of the folding process could explain how a specific protein folds and complement the generic theories.

The difficulty in simulating folding lies not only in the relatively short simulated time scale but also in two other issues. The first is the representation of the highly stochastic nature of protein motion. A single observation of the folding event cannot be a representative of various trajectories in the folding process. An ensemble comprising a diversity of folding trajectories is indispensable to develop a rigorous understanding. The second problem is how to analyze the complicated folding trajectories in a high-dimensional space. Projection of the motions onto two- to three-dimensional space has been used for small peptides (19, 20), but it does not have high enough resolution to depict detailed dynamical features in a larger system. We need a more sophisticated technique to analyze large sets of trajectory data.

In this study we calculated an ensemble of folding trajectories of a small protein, a 20-residue miniprotein Trp-cage [TC5b; NLYIQ WLKDG GPSSG RPPPS; PDB ID code 1l2y (21)]. Trp-cage is already known to fold quickly into the native structure (22) and has been regarded as the best object for the folding study in silico (23–27). We carried out a total of 10 μs of simulation (200 simulations of 50 ns, each starting from the fully extended structure) and captured 58 folding and 31 unfolding events. They were subjected to classification to determine how similar or different they are. For the classification of the trajectories in 3N-dimensional space (N being the number of atoms), we developed an analytical method for comparing many atomic trajectories, “trajectory alignment,” by which the trajectories are analyzed as if they were biological sequences. The dendrogram of the trajectories shows at atomic resolution how the native structure is achieved by funneling the unfolded protein through a narrow, specific pathway.

Methods

Folding Simulations. Molecular dynamics simulations of Trp-cage were performed at 325 K by using the AMBER99 force field (28) with a small modification (23) and the generalized Born implicit solvent model (29). The trajectories were recorded every 20 ps. For the computations, we used the Titech grid (30), developed at the Tokyo Institute of Technology, in which many cluster machines (totaling 800 CPUs) are connected in a network to work as if they were a single machine. Jobs were scheduled by using the condor system (31).

Definition of Folding/Unfolding. A folding event was defined in a trajectory according to the following criteria. The rms deviation (rmsd) for the main-chain atoms from the NMR structure (21), after smoothing with a window of 400 ps, decreases from 2.7 to <2.0 Å and then remains <2.0 Å during the subsequent 200 ps. During the last 200 ps, the molecule is regarded to be in the folded state. The fragments of the trajectories before (1.8 ns) and after (200 ps) folding were extracted for comparison (total of 2 ns composed of 101 snapshots). It is also required that the rmsd value averaged over 1.8 ns before folding is >3.0 Å so that we can clearly distinguish the folding events from other types of structural fluctuations. For the unfolding events, we applied the same definition to the reverse time series.

Trajectory Alignment. Each pair of folding trajectories and the reversed-unfolding trajectories was aligned on the basis of analogy with biological sequence comparison, i.e., “a snapshot in the trajectory” corresponds to “an amino acid residue in the sequence,” “the rmsd of corresponding atoms” corresponds to “a blosum-like scoring function (32),” and “a roundabout route” corresponds to “insertion/deletion.” According to this interpretation, we can use dynamic programming (33) to make an alignment of two trajectories.

Similarity Scores and Distance Scores. Given two structures a and b from two trajectories, respectively, the similarity score between a and b, s(a, b), was defined by s(a, b) = 1 – rmsd(a, b)/R_N, where rmsd(a, b) is the rmsd value in Å between the structures a and b, R_N = max[rmsd(NMR, a), rmsd(NMR, b)], and R_N = 2.5 (if right-hand side < 2.5) or 3.5 (if right-hand side > 3.5), with rmsd(NMR, a) being the rmsd value between the NMR structure (21) and the structure a. This score gives unity for the identical structures with rmsd(a, b) = 0, and zero for the structures with rmsd(a, b) = R_N. Gap penalties for open and extension are –0.2 and –0.01, respectively (34). Gap at the termini was not penalized, i.e., the alignment is global-local. The side-chain atoms of Trp-6, as well as the main-chain atoms, were included in the calculation of the rmsd values to emphasize the position of the Trp side chain. The alignment score S of two trajectories was obtained by dynamic programming. The distance scores D to make the dendrogram was calculated by D = S_max – S (if S < 10) or D = S_max – (0.8S + 2) (if S > 10), where S_max is a certain constant to make D positive. In this definition, the difference in dissimilar trajectories is more stressed than that in similar trajectories. The form of the scoring functions was confirmed not to affect the resultant feature of the dendrogram sensitively.

Structural Characteristics: Ring, Front/Back, and Left-Handed/Right-Handed. Trp-cage was defined as having a ring-shaped loop structure when any pair of C_α atoms separated in the sequence by ≥13 residues are located within 7 Å (35). A trajectory was defined as having a ring in the unfolded state when ≥60 snapshots among the first 90 have the ring structure.

When Trp-cage is in the ring form, it is possible to define whether the Trp side chain is at the front or back side of the ring. The ring plane was defined by three C_α atoms, two at the ring termini and one at the middle. The definition of front and back uses the distance d from the ring plane to the midpoint of C_ζ2 and C_η2 of the Trp side chain, the positive direction of which is according to the corkscrew rule along the sequence. The Trp side chain is regarded to be at the front of the ring when the average value, d, is more than 1.0 Å for the first 90 snapshots and at the back when d is less than –1.0 Å.

The shape of the main chain in the unfolded state was characterized by the handedness of the main-chain trace, either right-handed or left-handed. After superimposing the main chain at a snapshot to that of the 90th frame (the onset of the folding), we calculate the projection of the vector from C_α of Asn-1 to C_α of Ser-20 onto the normal vector of the ring defined at the 90th frame. The handedness of the main-chain trace was defined to be right-handed when the average of the projection, dt, was >3.0 Å for the first 90 snapshots and left-handed when dt was less than –3.0 Å.

Results and Discussion

Two hundred molecular dynamics simulations, each of 50 ns, were carried out on the Titech grid (30) with the job-scheduling system condor (31). A job visited 33 host machines on average, repeating migration, check-pointing, and eviction, and finished within 2–4 weeks.

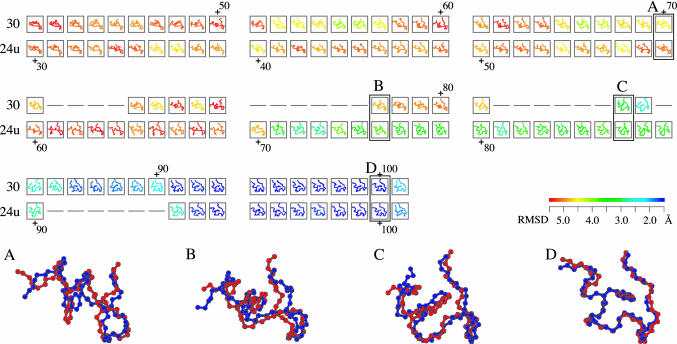
Exploring the 10-μs trajectories, we found that Trp-cage stayed in the folded structure [whose main-chain rmsd from the NMR structure (21) is <2.0 Å] for 704 ns in total, and the smallest rmsd value was 0.92 Å. Eventually, we identified 58 folding and 31 unfolding events that satisfy the conditions described in Methods and compared their trajectories by the trajectory alignment. Fig. 1 shows an example of the alignment of folding trajectory 30 and time-reversed-unfolding trajectory 24 (24u; “u” stands for unfolding). These trajectories align up to the 71st frame of 30 and the 60th frame of 24u (see the superimposed snapshots A in Fig. 1). They evolved simultaneously for ∼60 frames (1.2 ns; the first 30 frames are not shown). In the second and third rows of the alignment, several gaps, inserted successfully as we intended, represent the mismatch of the speed in approaching the folded state (B and C). Finally, at the 92nd frame, both 30 and 24u reached the folded state (D). It is noted that the time scale in the trajectories is not necessarily equal to the real scale, because the implicit solvent model discounts the viscosity of water (36), and the force field currently available may be inadequate to estimate the exact potential barrier.

Fig. 1.

A part of the alignment of folding trajectory 30 and the time-reversed-unfolding trajectory 24u. All structures are colored according to rmsd of the NMR structure (21). The color gradient from red to blue indicates a decrease in rmsd from >5.5Åto <1.5 Å (see color bar). The similarity score S of the alignment is 27.3. The average rmsd between aligned 84 pairs of the snapshots is 2.2 Å. The magnified views of the aligned snapshots (A–D) show how similar these two folding pathways are; the blue and red chains are of trajectories 30 and 24u, respectively, whose rmsd values of A–D are 1.9, 2.2, 2.0, and 0.7 Å, respectively. Model 32 of PDB ID code 1l2y was used as the experimental structure, because it is closest to the average structure of the 38 models in 1l2y (21).

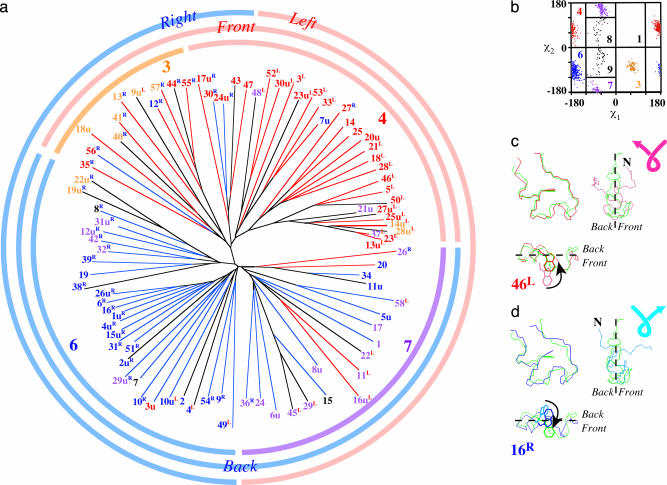
The alignment scores thus obtained indicate the similarity between the trajectories. After the transformation of the similarity scale to distance, a dendrogram of the folding pathways was constructed by the neighbor-joining method (Fig. 2a) (37). First, it is seen that the reversed-unfolding trajectories are scattered almost randomly among the folding trajectories. This means that we cannot discriminate the time-reversal of the unfolding pathways from the folding pathways (38).

Fig. 2.

Classification of the folding and unfolding trajectories. (a) Phylogenetic tree. Colors of the trajectory numbers indicate the rotamer states of the Trp side chain in the folded state, i.e., the native structure or rotamer 4 (red) and three pseudonative structures, rotamer 3 (orange), rotamer 6 (blue), and rotamer 7 (violet). Red- and blue-colored branches of the tree represent the positions of the Trp side chain in the unfolded state, the front side of the ring structure, and the back side, respectively. The superscript letters on the trajectory numbers indicate the handedness of the main-chain trace in the unfolded state; blue “R”s and red “L”s represent the right-handed and left-handed screw shape, respectively. Those with no superscript letters are close to planar. (b) The plot of χ₁ and χ₂ angles of Trp-6 in the folded state and the definition of the rotamers mostly according to Dunbrack and Karplus (39). (c) The folded form of trajectory 46 (red) defined to be native; both the main-chain trace and the Trp side chain (rotamer 4) are similar to those of the NMR structure (green). In the unfolded state, the Trp side chain is at the front side of the ring (pink in the lower left), and the main-chain shape is left-handed (pink in the upper right). (d) The folded form of trajectory 16 (blue), showing that the main-chain trace is similar to the NMR structure (green), but the rotamer state of the Trp side chain is apparently different, i.e., rotamer 6, and thus defined to be pseudonative (24). In the unfolded state, the Trp side chain is at the back (sky blue in the lower left) and the main-chain shape is right-handed (sky blue in the upper right).

More significantly, this tree classifies the 89 folding/unfolding pathways into four distinct groups. Notice that only one group of the folding trajectories correctly lead to the native structure (Fig. 2a, red-numbered trajectories), whereas the other three groups fold into pseudonative structures (orange, blue, and violet numbers), which have the correct main-chain conformation but wrong side-chain rotamers of Trp-6 (24), judged from χ₁ and χ₂ angles (Fig. 2b) (39). The upper-right branch of the tree contains mostly the native structure of rotamer 4 [|χ₁|> 120 and χ₂ > 0]. The other branches encompass the pseudonative structures, i.e., the upper-left, the lower-left, and the lower-right branches are those of rotamers 3 (orange), 6 (blue), and 7 (violet), respectively (see Fig. 2b). The one-to-one correspondence between the trajectory and the rotamer state indicates that each rotamer state is reached by a specific folding pathway.

What characteristics of the trajectories discriminate these four groups? First, let us focus on the motions of the Trp side chain. From the early stage of the folding process, Trp-cage forms a ring-shaped loop characterized by the proximity of the N and C termini (35). In fact, a majority of the snapshots in the trajectories contain the ring-shaped structure in the main chain; 6,587 snapshots (73%) of a total of 101 × 89 snapshots exhibit the ring structure (see Methods for the definition). The plane defined by the ring structure separates the atomic positions into those at the front of the plane and those at the back, and thus the structures can be classified into two categories depending on whether the Trp side chain is at the front or back of the ring. The red and blue branches of the tree indicate that the Trp side chain stays at the front and back during the folding process, respectively. It is noted that the groups of rotamers 3 and 4 have the Trp side chain at the front, and those of rotamers 6 and 7 have the side chain at the back. The side-chain motions in two representative cases are shown in Fig. 2 c and d. Trajectory 46 attains the native structure (rotamer 4) and shows the Trp side chain diving into the pocket of the “ring” from the front (Fig. 2c). On the other hand, trajectory 16 shows the side-chain motion from the back to finish the pseudonative structure with rotamer 6 (Fig. 2d).

The main-chain motions are characterized by the handedness of the ring shape. The ring-shaped loop in the unfolded state can be classified into either left-handed or right-handed screws (see Fig. 2 c and d and Methods for the definition). The handedness vanishes at the folded state, at which the main chain attains the planar ring (green). The handedness in the unfolded state is designated by the superscript letter after the trajectory number (“L” for left-handed and “R” for right-handed). Fig. 2a shows that the groups of rotamers 4 and 7 are classified mostly as left-handed, and those of rotamers 3 and 6 are right-handed. Fig. 2 c and d show that trajectories 46 and 16 are classified as left-handed and right-handed, respectively.

It was confirmed that these pseudonative structures were off-pathway intermediates. We examined whether the folding and unfolding events are connected directly without the intervening unfolded state. Because one of the criteria for folding/unfolding, the average rmsd before folding >3.0 Å (see Methods), is inappropriate for this examination, we redefined 222 folding and 167 unfolding events by ignoring this criterion and identified 155 pairs of consecutive folding and unfolding events. We observed only four parts of the trajectories in which the native state (rotamer 4) is connected to either of the three pseudonative states (rotamers 3, 6, and 7), three times to rotamer 6 and one time to rotamer 7. All four cases accompanied slight expansion of the molecule as well as an exposure of the Trp side chain to the solvent, which means that there exists a large potential barrier preventing a direct link between the native and pseudonative states.

The residence time of Trp-cage staying at each rotamer state could be a measure of its stability. We evaluated the average residence time by using the 155 folding and unfolding pairs defined above. As expected, the residence time of the native state was found to be much longer (4.1 ns) than those of the pseudonative states (2.1, 1.3, and 0.6 ns for rotamers 6, 7, and 3, respectively). It is noted that there are 34 trajectories in which Trp-cage kept the native state until the end of the simulation after it folded in the middle of the simulation, whereas there are only 15 such trajectories for the pseudonative states (1, 9, and 5 trajectories for rotamers 3, 6, and 7, respectively). Apparently, the native structure having rotamer 4 is the most stable among the folded states.

In summary, the native state is achieved by a pathway along which the Trp side chain enters into the pocket from the front of the ring, and the main chain changes its structure from the left-handed screw to the planar ring. The pseudonative structures are formed through pathways characterized by the other three possible combinations of these two parameters [front/right (rotamer 3), back/right (rotamer 6), or back/left (rotamer 7)], and they are not on-pathway intermediates leading to the native structure. Characteristic features of each trajectory are listed in Table 1. The table also shows the classification based only on the main-chain atoms, which is consistent with the one taking into account the Trp side chain.

Table 1. Character of each trajectory before and after folding.

	Before						After
Trajectory	Nr	d	dt	Rg	F/B	L/R	Rt	Mc
13u	87	2.1	-3.8	O	F	L	4	A
23	88	2.1	-8.1	O	F	L	4	A
37	90	1.5	-8.0	O	F	L	7	A
28u	88	1.0	-8.2	O		L	3	A
14u	83	1.4	-6.6	O	F	L	3	A
25u	86	2.0	-6.4	O	F	L	4	A
27u	83	0.7	-5.1	O		L	4	A
21u	77	-0.5	2.9	O			7	A
50	85	0.5	-7.5	O		L	4	A
5	86	1.4	-7.1	O	F	L	4	A
46	87	1.7	-6.6	O	F	L	4	A
28	76	2.4	-8.4	O	F	L	4	A
18	74	3.0	-3.7	O	F	L	4	A
21	65	1.6	-6.9	O	F	L	4	A
20u	61	1.7	-1.1	O	F		4	A
25	89	2.6	1.0	O	F		4	B
14	68	2.6	-2.6	O	F		4	B
27	72	2.6	4.3	O	F	R	4	B
7u	74	1.8	-2.2	O	F		6	A
33	88	2.7	-6.8	O	F	L	4	A
53	58	4.1	-12.2		F	L	4	A
23u	46	0.1	-4.3			L	4	A
3	23	1.7	-9.0		F	L	4	A
30u	72	3.7	-15.0	O	F	L	4	A
52	70	2.2	-11.9	O	F	L	4	A
48	78	0.6	-9.7	O		L	7	D
47	19	1.1	-0.4		F		4	E
43	17	-0.2	-2.1				4	E
24u	41	-2.2	9.2		B	R	4	E
30	29	-1.1	7.2		B	R	4	E
17u	28	2.3	3.3		F	R	4	E
55	75	1.6	3.8	O	F	R	4	B
44	71	0.7	6.5	O		R	4	B
57	83	3.7	8.1	O	F	R	3	B
12	58	1.8	6.0		F	R	6	B
9u	60	0.6	-7.4	O		L	3	B
13	81	1.4	8.9	O	F	R	3	A
41	35	2.6	3.2		F	R	3	A
40	54	0.8	4.0			R	3	B
18u	59	3.0	-1.2		F		3	D
56	53	-2.2	4.0		B	R	4	B
35	80	1.8	7.2	O	F	R	4	B
22u	61	-0.8	9.0	O		R	3	E
19u	72	-0.7	7.7	O		R	3	E
8	73	-2.4	5.6	O	B	R	9	E
31u	73	-3.1	7.8	O	B	R	7	E
12u	39	-2.2	6.2		B	R	7	E
42	33	-3.2	7.0		B	R	7	E
32	57	-2.0	4.5		B	R	7	E
39	40	-2.3	6.7		B	R	6	E
19	70	-3.3	3.0	O	B		6	E
38	57	0.3	3.5			R	6	E
26u	79	-1.8	7.6	O	B	R	6	C
6	84	-1.4	3.1	O	B	R	6	C
16	74	-2.4	3.2	O	B	R	6	C
1u	80	-2.5	8.6	O	B	R	6	C
4u	71	-2.9	4.2	O	B	R	6	C
15u	46	-2.6	6.5		B	R	6	C
31	38	-2.8	3.0		B	R	6	C
51	49	-1.5	5.8		B	R	6	C
2u	83	0.7	6.1	O		R	6
29u	57	-3.5	3.2		B	R	8	C
7	80	-3.5	2.4	O	B		8	D
10	69	-2.7	4.6	O	B	R	6	D
3u	50	-2.8	0.7		B		4	B
10u	32	-1.8	-3.1		B	L	6	A
2	68	0.4	2.7	O			6	A
4	37	-0.6	-5.2			L	6	A
54	49	-2.7	5.2		B	R	6	E
9	69	-2.3	7.3	O	B	R	6	E
49	11	-2.2	-10.5		B	L	6	E
36	60	-1.9	6.1	O	B	R	7	E
24	67	-2.0	0.2	O	B		7	D
6u	74	-2.8	-1.4	O	B		7	D
45	68	-0.2	-4.9	O		L	7	D
29	68	-0.9	-4.5	O		L	7	D
15	74	-2.1	-2.2	O	B		9	D
8u	80	-2.4	2.4	O	B		7	D
16u	46	1.6	-8.1		F	L	9	A
11	71	1.4	-10.3	O	F	L	7	A
22	64	0.9	-5.1	O		L	7	A
1	33	-3.1	1.0		B		7	E
17	34	-2.2	1.2		B		7	D
5u	79	-2.4	-1.7	O	B		6	D
58	62	-2.7	-6.2	O	B	L	7	D
11u	82	-0.5	1.6	O			6	E
34	70	-1.6	2.2	O	B		6	E
20	78	1.2	-2.9	O	F		6	E
26	83	2.0	8.9	O	F	R	7	E

Each of 89 trajectories is characterized by various features. Nr is the number of the snapshots exhibiting the ring shape (35) among the first 90 frames of the unfolded state. A trajectory is marked by O if Nr ≥ 60 in the column Rg. d is the average distance from the ring plane to the midpoint of C_ζ2 and C_η2 of Trp-6. If d > 1 Å (less than -1 Å), the Trp side chain is regarded to be at the front (back) of the ring, and the symbol F (B) is assigned in the column F/B. dt is the mean distance between the terminal residues (see Methods). If dt > 3 Å (less than -3 Å), the main-chain shape is defined to be left-handed (right-handed) and marked L (R) in the L/R column. The column Rt assigns the rotamer type of the folded state. In the column Mc, the cluster indices of the phylogeny calculated by using only the main-chain rmsd are given: A, B, C, and D roughly correspond to the upper-right, upper-left, lower-left, and lower-right branches in Fig. 2a, respectively. E is the cluster of anomalous trajectories, most of which do not form the ring shape in the unfolded state. The order of the trajectories follows Fig. 2a counterclockwise, starting from the right side of the upper-right branch (trajectory 13u).

This clear distinction of the folding pathways should be attributed to the partitioning of the conformational space by the ring structure at an early stage of folding. The ring divides the position of the Trp side chain into the front and back and prevents the side chain from changing sides. Looking at the folded structures, we notice that the C_α–C_β vector of Trp-6 is parallel to the ring plane irrespective of the rotamer state. Accordingly, the rotamer state has a clear correspondence with the direction of the indole ring, i.e., the indole ring points toward the front when the rotamer state is 3 or 4 and toward the back for rotamer 6 or 7. Such folded structures can only be achieved through each specific pathway; rotamers 3 and 4 were formed by the pathways from the front, and rotamers 6 and 7 were from the back (Fig. 2 c and d).

The relation between the side-chain position and the handedness is explained simply by the fact that the side chain of Trp-6 moves together with the N-terminal part of the main chain (residues 1–8). Such collective motions are observed in the trajectories of rotamers 4 (front/left or both the side chain and the N terminus are at the front) and 6 (back/right or both are at the back) but not in those of rotamers 3 (front/right) and 7 (back/left). In fact, those of rotamers 3 and 7 show odd pathways; the trajectories of rotamer 3 distort the α-helix (Leu-2–Lys-8), which forms simultaneously with the ring [(φ,ψ) = (–118 ± 38, –50 ± 11) for Trp-6 with rotamer 3, but (φ,ψ) = (–71 ± 20, –40 ± 12) with the other rotamers], and the χ angles of rotamer 7 become nonstandard, as shown in Fig. 2b (39).

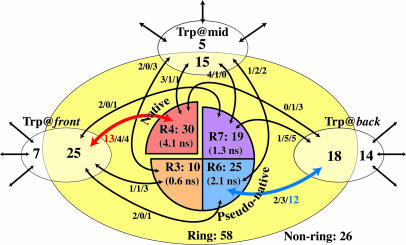
Fig. 3 delineates the classification of the trajectories. The major pathways are the front/left, leading to the native structure (rotamer 4), and the back/right, leading to a pseudonative structure of rotamer 6. As seen in the residence time in the folded states, the native structure is the most stable, followed by rotamer 6. It is seen also that the clear distinction of the pathways requires the formation of the ring-shaped structure. The fact that there is no pathway directly connecting those rotamer states indicates that the pathway to the native structure is highly exclusive. In other words, the landscape of Trp-cage is far from the ideal funnel but is extremely rugged and even contains a “false funnel,” possibly because Trp-cage is not a naturally occurring protein but a small artificial protein produced from a moiety of the wild-type extendin-4 (21, 40) and because the simulations were done at a rather high temperature (23).

Fig. 3.

Diagram of the folding and unfolding pathways of Trp-cage. The numbers in the enclosed areas correspond to the number of trajectories in the folding simulations. A trajectory is named “Ring” when more than two-thirds of the snapshots in the unfolded state have the ring structure; otherwise, the trajectories are named “Non-ring.” The average residence time of the folded states is shown in the parentheses. The arrows connecting the boxes represent the pathway. The handedness of the trajectories is indicated by the three numbers on the arrow (left-handed/neutral/right-handed). Five trajectories folding into the structures with the Trp rotamers 8 and 9 (see Fig. 2a) are not included in the diagram.