Protein Folding, Binding, and Droplet Formation in Cell-Like Conditions

Abstract

The many bystander macromolecules in the crowded cellular environments present both steric repulsion and weak attraction to proteins undergoing folding or binding and hence impact the thermodynamic and kinetic properties of these processes. The weak not nonrandom binding with bystander macromolecules may facilitate subcellular localization and biological function. Weak binding also leads to the emergence of a protein-rich, droplet phase, which has been implicated in regulating a variety of cellular functions. All these important problems can now be addressed by realistic modeling of intermolecular interactions. Configurational sampling of concentrated protein solutions is an ongoing challenge.

Graphical Abstract

Introduction

Proteins and other macromolecules are present at high total concentrations in all cells, a situation that is now known as macromolecular crowding [1]. Macromolecular crowding can affect protein folding and binding reactions (Fig. 1), typically studied in a dilute solution, in small and large ways. Even when the net effect of crowding is small, it does not mean that the bystander macromolecules, or crowders, exert no influence on direct participants, or test proteins, in the reactions. Instead, the crowders generate opposing effects that often cancel to a large extent. Accurate modeling of protein-crowder interactions and efficient computation are thus necessary to complements experiments in untangling the various effects of crowding.

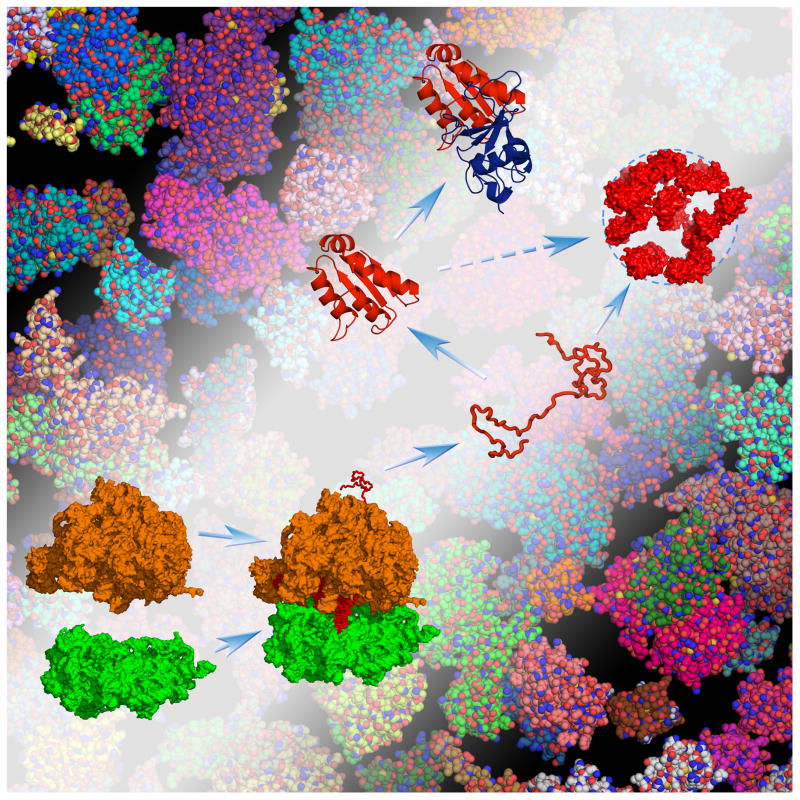
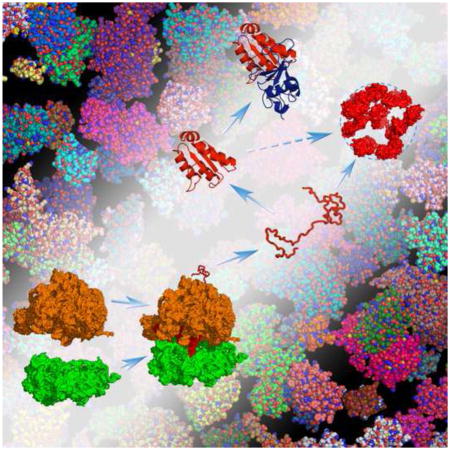
Fig. 1.

Protein folding, binding, and droplet formation inside a cell. “Test” proteins are volume-excluded from but also weakly bind to bystander macromolecules in the cellular environment, and these interactions can steer folding and binding stability in complex ways. Test proteins (either unstructured or structured) can also weakly interact among themselves, and form a new, droplet phase in the cellular environment.

Recent years have seen continued growth of interest in protein folding and binding in cell-like conditions [2–11]. Injecting new interest in modeling cell-like conditions and posing new challenges to computation are experiments demonstrating intriguing or emergent behaviors that arise from nonspecific protein-crowder and protein-protein interactions. In particular, experimental evidence has indicated preference for specific sites on proteins in forming weak binding with crowders [12,13]. The implication is that proteins can bind weakly but nonrandomly with bystander macromolecules in their subcellular environments, and such nonrandom binding facilitates subcellular localization as well as biological function.

There is great excitement about a new phase, which is increasingly referred to as protein droplet (Fig. 1), that emerges in concentrated protein solutions under the right conditions of temperature, pH, salt concentration, etc. [14,15]. Cell biologists have for some time identified some of these membraneless intracellular “bodies” and associated them with regulating various cellular functions [16,17]. The physical nature of protein droplets has come into focus in recent years [18–21]. It is now known that these droplets represent a high-density phase of protein solutions, and their formation is similar to the condensation of water vapor into the liquid phase; the former corresponds to the ordinary low-density dissolved phase of protein solutions whereas the latter the droplet phase. Much like the vapor-liquid phase transition of water, the liquid-liquid phase separation of protein solutions is reversible and this reversibility is well suited for regulating cellular functions. The liquid-liquid phase boundaries are exquisitely sensitive to molecular details including phosphorylation, and can be significantly shifted by adding crowding agents [22]. Computational methods are now beginning to enable accurate calculations of liquid-liquid phase equilibria [23].

Below we review the major developments and challenges in modeling macromolecular crowding since the last time Curr. Opin. Struct. Biol. covered this topic [3]. Complementary coverage of the experimental literature can be found in two recent surveys in this journal [4,9,10].

Approaches to modeling protein folding and binding under crowding

Computation of crowding effects on protein folding and binding faces the twin challenges posed by the significant size of the protein-crowder systems and by the enormous amount of sampling over both the folding or binding reaction of the protein(s) and the reconfiguration of the crowders [5,8]. A number of groups have carried out direct simulations where test proteins are mixed with crowders [24–37] (horizontal paths in Fig. 2a). In most cases, a coarse-grained representation was used for the proteins and crowders to ensure adequate sampling. Others used an all-atom representation to study folding stability under crowding but whether an equilibrium conformational ensemble of the protein was generated and whether protein-crowder interactions were adequately sampled were not assessed [28,29].

Fig. 2.

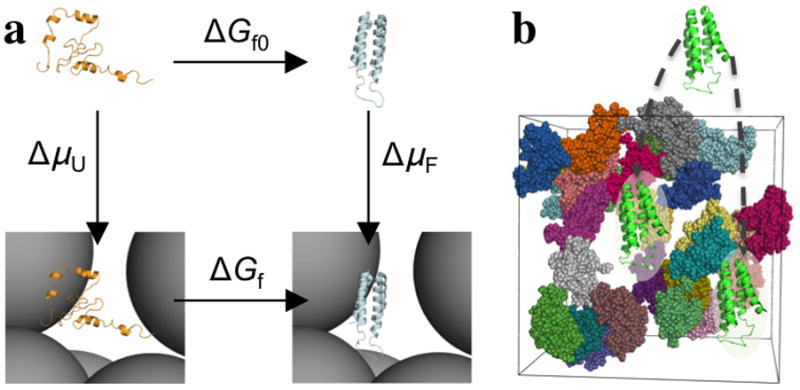
Direct simulation versus postprocessing approach, illustrated on the folding of cytochrome b₅₆₂. (a) Direct simulation follows the vertical paths, whereas postprocessing follows the vertical paths. The former approach yields the folding free energies in the absence (ΔG_f0) and presence (ΔG_f) of crowders, whereas the latter approach yields the transfer free energies of the unfolded (Δμ_U) and folded (Δμ_F) states from a dilute solution to the crowder solution. By closing a thermodynamic cycle, they lead to the same effect of crowding on the folding free energy, ΔΔG_f. Taken from ref [38]. (b) To calculate Δμ(X), one has to fictitiously place the protein with conformation X into different positions and evaluate the protein-crowder interaction energy at each position. Taken from ref [5].

To resolve the conflict between realistic representation and adequate sampling, we introduced the postprocessing approach [5,38,39] (vertical paths in Fig. 2a). Here the test protein and the crowders are separately simulated. Moreover, for the test protein, only the end states (e.g., folded and unfolded states) are simulated, not their transitions, which are rare events and hence hard to sample. Each protein conformation (denoted by X) is then weighted by the Boltzmann factor of the of the transfer free energy Δμ(X),

$$exp[-\beta \mathrm{\Delta }\mu (\mathrm{X})]=<exp[-\beta U_{int}(\mathrm{X},\mathrm{R})]{>}_{\mathrm{R},\mathrm{c}}$$ (1)

where U_int(X,R) is the protein-crowder interaction energy for protein conformation X placed at position R inside the crowder solution; β = 1/k_B T in which k_B is the Boltzmann constant and T the absolute temperature; and < … >_R,c signifies averaging over R and crowder configuration. The calculation of Δμ(X) entails probing the test protein at different positions inside the crowder solution (Fig. 2b), according to the Widom insertion [40]. Further averaging over protein conformations in an end state then yields Δμ_U or Δμ_F in the case of protein folding. The difference, Δμ_F − Δμ_U, yields ΔΔG_f, the effect of crowding on the folding free energy.

Because the simulations of the test protein are performed for the end state only and without crowders, adequate sampling of protein conformations can be achieved even with an all-atom representation. Separate simulations of the crowders are needed but, once done, can be reused for the study of many test proteins. Lastly placing the protein in many positions and averaging over many crowder configurations [eq (1)] assure exhaustive sampling of protein-crowder interactions.

The sampling over protein-crowder interactions prescribed in eq (1) can make the calculation of Δμ(X) quite expensive. A direct implementation of the Widom insertion indeed incurred “very significant computational expense” [41]. We were able to develop efficient methods for atomistic proteins interacting with hard-sphere crowders [38,42]. Applications to folding and binding stability of single-domain proteins predicted modest effects of crowding (up to ~1 kcal/mol) [5,38,42,43], in line with magnitudes observed in many experimental studies [44–65]. In contrast, using simple protein models, much more dramatic effects of crowding were predicted [66].

In theory the postprocessing approach is rigorous, but in practice its accuracy depends on the extent to which the conformational ensemble of the test protein in the absence of crowders overlaps with the counterpart in the presence of crowders. We have validated the postprocessing approach against direct simulations in cases where coarse-grained test proteins interacted with hard-sphere crowders. One validation study [67] was motivated by a paper by Mittal and Best [26], who used replica-exchange umbrella sampling to generate folding free energy surfaces of three small proteins in the absence and presence of crowders. By postprocessing the crowder-free protein conformations, we were able to closely reproduce the folding free energy surfaces over a range of crowder concentrations (up to a volume fraction of 35%). Consequently the postprocessing approach, using the crowder-free protein conformations alone, was able to accurately predict the effects of crowding on the folding stability. Importantly, with assumptions or information about how crowding affects motions along reaction coordinates, the postprocessing approach can also predict folding and binding kinetics [67–69].

In a second validation study [70], the conformational ensembles of an intrinsically disordered protein (IDP) represented at the coarse-grained level in the presence of hard-sphere crowders at a range of concentrations, obtained from direct simulations, were used for benchmarking predictions of the postprocessing approach. Up to a crowder volume fraction of 31%, the postprocessing approach faithfully predicted the crowder-present conformational ensembles from the crowder-free conformational ensemble. The contraction of the IDP (as measured, e.g., by the mean radius of gyration) with increasing concentration of a repulsive crowder obtained in this study presaged similar observations in subsequent experimental [71] and computational [34,36] studies. However, the predicted conformational ensemble of the IDP at an even higher crowder volume fraction of 49% was discernibly skewed due to an under-sampling of the most compact conformations in the crowder-free simulations. In addition, if the crowders are not purely repulsive and the protein-crowder attraction has a sufficient strength, postprocessing predictions can be erroneous even at intermediate crowder volume fractions (Qin and Zhou, unpublished). This is in line with all-atom simulations showing that a partially denatured protein in the presence of crowders had only partial conformational overlap with the urea denatured state [29]. On the other hand, all-atom simulations of protein-crowder systems presently can reach only sub-microsecond times, during which test proteins can easily be trapped in local crowder environments. Continued cross-validation between direct simulation and postprocessing approaches is thus called for.

Recently we cleared a remaining hurdle for realizing the full potential of the postprocessing approach, by developing a practical method for calculating Δμ(X) when both the test protein and the crowders are represented at the all-atom level and the protein-crowder interactions have both hard-core repulsion and soft components [72,73]. To do so, we expressed these interactions as correlation functions and evaluated them via fast Fourier transform (FFT). A 40,000-fold speedup was gained over brute-force Widom insertion, without losing accuracy.

This FFT-based method for Modeling Atomistic Proteins-crowder interactions, or FMAP, has the unique advantage that its computational cost remains the same whether the crowder solution consists of a single species of macromolecules or is a heterogeneous mixture of many different macromolecules, as in cellular compartments. That is because all the crowder molecules are mapped to a grid, which circumvents the need for atomic identities in the expensive calculations. With FMAP, the postprocessing approach is poised to make quantitatively predictions of crowding effects and pair with in vitro and in vivo experiments to uncover the physical basis of complex and emergent behaviors of biomacromolecules in cellular environments.

Varying effects of protein-crowder hard-core repulsion and soft attraction

Intermolecular interactions generally comprise both hard-core repulsion and “soft” components, which are attractive in the case of van der Waals and hydrophobic interactions and either attractive or repulsive depending on the signs of charges in the case of electrostatic interactions. The effects of protein-crowder hard-core repulsion, also termed excluded-volume, have long been recognized [2,74]. They favor more compact conformations of test proteins over more open or extended conformations, i.e., favor those presenting less excluded volume to crowders. As a consequence, both folding and binding stability would be enhanced, and compaction of IDPs would be expected.

It is now widely recognized that hard-core repulsion alone does not dictate the outcome of crowding effects. Soft attraction typically oppose and can reverse the qualitative trend expected from hard-core repulsion. For example, the more open conformations of a protein in the unfolded state are expected to allow it to experience stronger attractive interactions with crowders than in the folded state. Accordingly the soft attraction would favor the unfolded state over the folded state, thereby further moderating or even reversing the already modest effect on folding stability expected of hard-core repulsion. This expectation is supported by exquisite experimental data of Pielak’s laboratory using NMR-detected hydrogen/deuterium exchange [50,52–54,59] and by other studies [60,64]. In cells, soft attraction manifests as weak binding with cellular components (see below), and exerts complex effects on folding stability [57,58,62–65].

For an IDP in the presence of protein crowders, the compaction expected from hard-core repulsion was not supported by small-angle neutron scattering data [75]; soft attraction was offered as a possible counteracting factor [76]. Similar subtle effects of hard-core repulsion and soft attraction can be expected for protein binding stability under crowding. As for binding kinetics, these subtle effects on thermodynamics are further muddied by crowding effects on inter- and intra-protein dynamics [77]. All these complications highlight the importance of accurate modeling of protein-crowder interactions for capturing both the trends and the magnitudes of crowding effects on protein folding and binding.

The dependence of crowding effects on temperature potentially brings out another level of complexity. Surprisingly, a simple prediction regarding folding stability was made: for any kind of crowders there exists a crossover temperature, at which the effect of crowding switches from destabilizing to stabilizing [78]. This prediction is based on the assumption that crowding decreases both the unfolding entropy (due to conformational compaction of the unfolded state) and the unfolding entropy (due to stronger attractive interactions of the unfolded state, relative to the folded state, with the crowders). Reanalysis of the temperature-dependent data from the Pielak’s laboratory [53,54] provides support for the existence of a crossover temperature, and more such data will be required to settle this issue. If proven, the existence of a crossover temperature has broad implications. In particular, macromolecular crowding might have provided some of the stabilization to proteins in the very early cells in thermophilic environments, such that the pressure on evolution to produce stably folded proteins was lessened. One also wonders whether the dependences of crowding effects on solvent properties other than temperature, e.g., pH or salt concentration, have their own crossover points.

Blurring the divide between specific and nonspecific binding

The high concentration of bystander macromolecules in the cellular environment of any given protein provides ample opportunities for chance encounters. Researchers have long focused on “specific” binding, i.e., interactions between proteins and their partners that are direct participants of biochemical processes, such as interactions between enzymes and activators or inhibitors. Many of the resulting complexes are stable and can be captured for structure determination by X-ray crystallography, NMR spectroscopy, and cryo-electron microscopy. In contrast, “nonspecific” binding with bystander macromolecules in the past was either ignored or viewed as harmful.

High-throughput techniques such as yeast two-hybrid and affinity purification-mass spectrometry have now enabled the identifications of many protein interaction partners [79–82]. The notion of a cardinal divide between specific and nonspecific interactions has given rise to the classification of protein pairs as binders and non-binders, and likely accounts for the branding of at least some portions of high-throughput results as false positives. Is there a physical basis for classifying proteins pairs into binders and non-binders? The physiochemical property that measures the strength of protein association is the binding constant. Statistical thermodynamic theory [83] predicts and numerous experimental measurements confirm that the magnitudes of binding constants span a wide, continuous range, and therefore there is no obvious demarcation for classifying proteins pairs into binders and non-binders. It can be stated that the divide between specific and nonspecific binding is a matter of degree not type. Instead of the binding constant, weak nonspecific binary interactions are often measured by the second virial coefficient, which appears in the expansion of the osmotic pressure of a protein solution in terms of the protein concentration. The second virial coefficient can be determined by techniques including static light scattering [84].

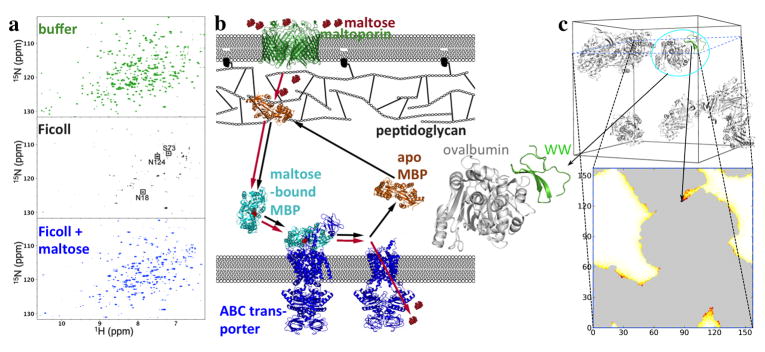
Recently, many in-cell NMR studies [13,63–65,85–92] have shown that, in both bacterial and eukaryotic cells, nearly all proteins participate in weak, nonspecific binding with cellular components, resulting in disappearance of NMR peaks. Interestingly, the nonspecific interactions observed are not random. In some cases, injected proteins were found to bind with particular cellular components. For examples, the neural protein tau when injected into X. laevis oocytes bound to microtubules [86]. In E. coli the MetJ repressor formed extensive nonspecific interactions with genomic DNA [87]. In other cases, there was evidence implicating a specific site of a protein for the nonspecific interactions. The Pin1 WW domain used the substrate recognition site for nonspecific interactions; nonspecific interactions were apparently abrogated when either the substrate recognition site was phosphorylated or a substrate peptide was bound [13]. Similarly, MBP formed nonspecific interactions with protein and polymer crowders, but this ability was weakened or lost when maltose was bound [12] (Fig. 3a).

Fig. 3.

Nonrandom weak binding of the maltose-binding protein (MBP) and the Pin1 WW domain with bystander macromolecules. (a) Competition of Ficoll and maltose for interaction with MBP, shown by NMR spectroscopy. In buffer, apo MBP shows well-resolved ¹H-¹⁵N TROSY spectra. With 200 g/l Ficoll, most of the TROSY peaks are broadened beyond detection, indicating MBP-Ficoll binding. Upon further addition of 1 mM maltose, the peaks are recovered, indicating that the ligand has competed out the weakly bound Ficoll. (b) Shuttling of MBP in the E. coli periplasm for transport of maltose into the cytoplasm. The apo form may be weakly bound to the outer membrane-attached peptidoglycan; upon binding maltose, MBP is released from the peptidoglycan and diffuses toward the inner membrane, where it hands over the ligand to the ABC transporter for translocation into the cytoplasm. Red and black arrows indicate the flow of maltose and the shuttling of MBP, respectively. (a)and (b) taken from [12]. (c) Protein-crowder interaction energies calculated by FMAP. Top panel: the test protein (green) is the Pin1 WW protein, and the crowder is ovalbumin, with 8 copies present in a cubic box with a 157.4-Å side length (corresponding to a concentration of approximately 150 mg/mL). The crowder configuration was a snapshot taken from molecular dynamics simulation in explicit solvent. Note that the crowder molecules formed clusters. Bottom panel: in the FMAP calculation, both the protein and crowder molecules were represented at the all-atom level, and the energy function consisted of Lennard-Jones terms for modeling steric, van der Waals, and hydrophobic interactions and Debye-Hu ckel terms for modeling electrostatic interactions [73]. The energy map on a slice through the crowder box is shown according to a color scale from white to dark red; the gray regions are occupied by the crowder molecules. The placement of the test protein shown in the top panel has the minimum interaction energy, in which the substrate recognition site of the WW domain forms close contacts with one of the ovalbumin molecules (enlarged view on the left).

In many of the cases cited above, nonspecific interactions can be inferred to impart biological function. In particular, the binding of tau to microtubules is thought to be important for the latter’s stability. Nonspecific binding of the MetJ repressor to genomic DNA may facilitate the search for a specific site. Nonspecific binding with endogenous proteins via the substrate recognition site of the WW domain may contribute to Pin1’s subcellular localization. For MBP, it has been proposed that nonspecific binding with the outer membrane-attached peptidoglycan primes the protein for receiving maltose; binding of maltose releases the protein, allowing it to diffuse to the inner membrane-bound ABC transporter and hand over the ligand for translocation into the cytoplasm [12] (Fig. 3b).

It is remarkable that nonspecific binding can be tuned out by phosphorylation or substrate binding [13], or by ligand binding [12]. Apparently, nonspecific binding can be regulated by some of the same biochemical signals, e.g., phosphorylation or ligand or substrate binding, as those for specific binding. So in many respects the divide between specific and nonspecific binding is becoming blurred.

The nonrandom nature of weak protein-crowder binding and its sensitivity to biochemical signals can only be recapitulated by realistic models of protein-crowder interaction energies. An atomistic energy function consisting of Lennard-Jones and Debye-Hu ckel terms exhibit the desired features (Fig. 3c). The energy map is highly non-uniform, with multiple minima corresponding to particular orientations and positions of the test protein (the Pin1 WW domain) relative to the crowder (ovalbumin) molecules. In many of these minima, the substrate recognition site of the WW domain faces the crowder molecules, consistent with experimental observations [13]. Such nonrandom protein-crowder weak binding has also been observed in direct simulations of trp-cage crowded by bovine pancreatic trypsin inhibitor [33]. The crowder molecules also weakly bind among themselves, forming various transient clusters (Fig. 3c). Cluster formation reduces the magnitude of volume exclusion to and affects the soft attraction for test proteins, and thereby impact their folding and binding.

Protein droplet formation and regulation of cellular functions

At sufficiently high concentrations and under appropriate solvent conditions, weak interactions of protein molecules result in the co-existence of the droplet phase with the low-density dissolved phase. Experimentally, many purified proteins, mostly components of intracellular bodies but also engineered constructs, have been shown to undergo the liquid-liquid phase separation [19,22,93–101]. These proteins typically contain disordered regions and/or bind RNA. Droplet formation can facilitate the assembly of multi-component complexes for biochemical reactions, but the concentration of disordered proteins is also inductive to fibrillization and degenerative diseases.

Liquid-liquid phase separation of globular protein solutions has been studied theoretically and computationally in the past by representing proteins as spheres (with either centrosymmetric or site-specific interactions) or by other simple shapes [102–110]. FMAP, the FFT-based method for modeling atomistic intermolecular interactions, has now opened the door to accurate calculation of liquid-liquid phase equilibria for protein(/RNA) mixtures in cell-like conditions [23]. The co-existence of two phases requires equality in chemical potential. Using FMAP, we can calculate chemical potentials over a range of protein concentration (Fig. 4a). The concentration dependence of the chemical potential can then be used to identify the concentrations of the dissolved and droplet phases (Fig. 4b). The first such results, for γII-crystallin (a globular protein in the eye lens), are shown in Fig. 4c. Compared to the experimental data [111], the broadness of the phase diagram on the high-concentration side is underestimated. This discrepancy was attributed to under-sampling of cluster formation [23]. While FMAP enables accurate calculation of the chemical potential once the configurations of a protein solution at given concentrations are properly sampled, achieving this configurational sampling at high protein concentrations is an ongoing challenge [112].

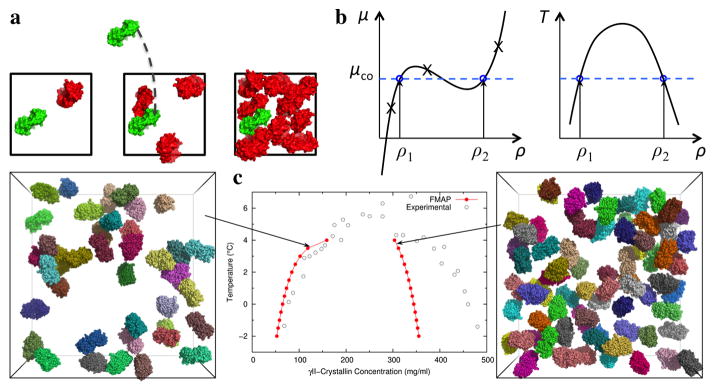
Fig. 4.

Calculation of liquid-liquid coexistence curves [23]. (a) By the Widom insertion, such as implemented by FMAP, the chemical potentials of a protein over a range of concentrations are obtained. (b) Left: the phase co-existence condition is located by applying the Maxwell equal-area rule on the isotherm in the chemical potential (μ) – concentration (ρ) plane. The blue horizontal dash (at μ = μ_CO) crosses the isotherm with equal areas enclosed above and below. The concentrations (ρ₁ and ρ₂) at the low and high crossing points are those of the dissolved and droplet phases, respectively. Right: by repeating the process over a range of temperature, the full phase diagram is constructed. (c) Liquid-liquid phase diagram for γII-crystallin calculated by FMAP, compared to the experimental data. In the calculation, γII-crystallin molecules were represented at the all-atom level, and their interactions were modeled by Lennard-Jones and Debye-Hu ckel potentials. Snapshots of protein configurations at 123 and 307 mg/mL in an 81-Å thick slab are shown to the left and right, respectively.

In regulating cellular functions, cells apparently use a variety of means, including pH change and phosphorylation/dephosphorylation, to modify the liquid-liquid phase boundary and thereby control droplet formation. An in vitro study has shown that the phase boundary can be significantly shifted by adding crowding agents [22]. Some protein components are selected into the droplet phase while others are excluded. These critical issues can now be addressed by computational methods.

Highlights.

• Proteins and other macromolecules weakly bind in cell-like conditions

• Weak binding has many consequences, including the formation of protein droplets

• Computation is positioned to accurately capture the many effects of weak binding