Xe NMR lineshapes in channels of peptide molecular crystals

Abstract

To further an understanding of the nature of information available from Xe chemical shifts in cavities in biological systems, it would be advantageous to start with Xe in regular nanochannels that have well known ordered structures built from amino acid units. In this paper, we report the experimental observation of Xe NMR lineshapes in peptide channels, specifically the self-assembled nanochannels of the dipeptide l-Val-l-Ala and its retroanalog l-Ala-l-Val in the crystalline state. We carry out grand canonical Monte Carlo simulations of Xe in these channels to provide a physical understanding of the observed Xe lineshapes in these two systems.

Self-assembling structures with nanochannels have been of increasing interest (1, 2). A subset of these (peptide-based nanochannels) have demonstrated applicability as transmembrane pores and ion channels, as well as size-selective ion sensors (1). Görbitz and coworkers (3, 4) have described peptide nanochannels formed by the aggregation of dipeptides in a head-to-tail hydrogen-bonded network, forming a channel with a hydrophobic interior. Two such systems, the dipeptide l-Val-l-Ala (3) (VA) and its retroanalog, l-Ala-l-Val (4) (AV), form two distinct channels, which have been demonstrated to act as supramolecular hosts for organic molecules. These dipeptide systems are the subject of the present study.

Binding of Xe within cavities in proteins is common because of several favorable factors. The Xe atom has a large electric dipole polarizability; cavities within proteins are about the correct size to hold one or more Xe atoms, and the unfavorable entropic term related to the need to orient the ligand in the binding site is absent for Xe atom. The affinity of Xe for hydrophobic cavities in the interiors of macromolecules (5–10) coupled with the development of techniques for hyperpolarization of Xe nuclear spins have inspired an array of NMR studies of Xe in proteins (11), cells, (12, 13), and tissues (14–16). For example, hyperpolarized (HP) ¹²⁹Xe has been developed as a tool for the characterization of protein cavities which bind Xe, by using its nuclear spin polarization to enhance the signals of the protons in the cavity (10, 17), by using the Xe chemical shift itself as a reporter of cavity structure in both solution and the solid state (11), and in applications to biomolecular assays (18, 19).

Xe adsorbed into nanochannels and cavities gives rise to an anisotropic lineshape in the NMR spectrum. Such lineshapes have been observed experimentally in 1D channels in various crystalline materials (20–23), with the observed lineshape varying with changing Xe occupancy within the channel. A theoretical understanding, using the dimer tensor model in grand canonical Monte Carlo (GCMC) simulations (24), permits the prediction of the average Xe chemical shift tensor and the lineshapes that are observed in the Xe NMR spectrum of a polycrystalline sample (24, 25) or of a single crystal (26), with no adjustable parameters. The lineshapes calculated for a uniform distribution of crystallite orientations in the sample reproduces typical Xe lineshapes observed experimentally. These simulations demonstrated that, for static nanochannels, the characteristics of the observed line (the number of singularities; that is, the number of unique nonvanishing tensor components, and the relative magnitudes of tensor components) provide a signature of the channel architecture, whereas the magnitude of the isotropic chemical shift and the span of the anisotropic line are signatures of the electronic structure of the atoms of the host channel. Furthermore, the simulations demonstrated that the systematic behavior of the average tensor components with increasing Xe occupancy provides additional information about the architecture of the channel (24, 26).

Biological cavities that bind Xe vary widely in structure and constitution, making the modeling of Xe in such environments difficult. Furthermore, the assumption of a static, rigid architecture may be questionable in these cases. For example, diffraction studies show that in the binding of Xe within engineered cavities in T4 lysozyme, the binding event tends to expand the volume of the cavity (9). For an understanding of the nature of information available from Xe chemical shifts in biological cavities, it would be advantageous to start with Xe in regular nanochannels that have well known ordered structures built from amino acid units. In this paper, we report the experimental observation of Xe lineshapes in peptide channels, specifically the self-assembled nanochannels of the dipeptide VA and its retroanalog, AV, in the crystalline state. We then apply the aforementioned GCMC methodology to provide a physical understanding of the observed Xe lineshapes in these two systems.

Methods

Experimental Methods. Materials. The VA and AV dipeptides obtained from commercial sources (ICN) were used in all experiments. The crystal structures of both dipeptides at low temperatures are reported in refs. 3 and 4. To elucidate the details of the crystal structures at the conditions at which NMR experiments were performed, both dipeptides were characterized by single-crystal XRD at room temperature. Suitable specimens were obtained as colorless prisms by evaporation of 0.3 M aqueous solutions of the dipeptides. A summary of the crystal structure parameters is given in Table 1. Full crystallographic data have been deposited with the Cambridge Crystallographic Data Centre as supplementary publications 238398 (VA) and 238397 (AV). The details of the room-temperature XRD study are reported elsewhere (45). Powder XRD analyses of the bulk dipeptides used in NMR experiments indicated total correspondence of these materials to the specimens studied with single-crystal XRD.

Table 1. Crystal structure parameters for the studied dipeptides.

Dipeptide	VA	VA	AV	AV
Temperature of study, K	120	293	150	293
Crystal system space group	Hexagonal, P61	Hexagonal, P61	Hexagonal, P61	Hexagonal, P61
a, Å	14.424(4)	14.461(2)	14.296(1)	14.462(2)
c, Å	9.996(6)	10.083(1)	9.908(1)	10.027(1)
V, Å3	1,801(1)	1,826.1(4)	1,753.5(3)	1,816.2(4)
Ref.	3	This work	4	This work
CCDC refcode or deposition number	WIRYEB	238398	XUDVOH	238397

CCDC, Cambridge Crystallographic Data Centre.

NMR experiments. All ¹²⁹Xe NMR measurements were made on a Bruker (Billerica, MA) DSX-400 instrument operating at 110.8 MHz (magnetic field of 9.4 T). Two types of ¹²⁹Xe NMR experiments were performed in this work: (i) with samples in a continuous flow of hyperpolarized ¹²⁹Xe and (ii) with samples sealed in glass tubes (NMR spectroscopy with thermally polarized ¹²⁹Xe). A modified probe with a 5-mm solenoid coil from Morris Instruments was used for all static experiments (π /2 pulse was 3.5 μs) with sealed samples. The experiments with a continuous flow of HP Xe were carried out in a modified Bruker 7-mm BL magic angle spinning (MAS) probe similar to that used in ref. 27. The continuous-flow polarizer for production of HP Xe was of a design similar to that reported in ref. 28 and operated with an 80-W diode laser from Coherent Radiation (Palo Alto, CA) (effective wavelength and linewidth were 795 nm and 1.2 nm, respectively). A Xe–He–N₂ mixture with a volume composition of 1%/98%/1% was used in all continuous-flow HP experiments. The flow rate was monitored with a Vacuum General flow controller (Model 80-4) and kept constant in the range of 80–100 scc/min (scc/min, gas flow normalized to standard conditions). In the continuous-flow HP experiments a flow of HP Xe was delivered directly into the coil region of an NMR probe through 1.5-mm-i.d. plastic tubing. The reported ¹²⁹Xe NMR chemical shifts were referenced to Xe gas extrapolated to zero pressure.

Sealed samples were prepared by placing a known amount of material (0.02–0.05 g) into a 5-mm-o.d. glass tube ≈40 mm long, evacuated at 100°C for 4–5 h. Isotopically enriched Xe gas (Cambridge Isotope Laboratories, Cambridge, MA; ¹²⁹Xe enrichment of 99.1%) was frozen into the sample tube, and the tube was sealed. The packed materials occupied about half the length of the tube. With this sample geometry, we are able to perform quantitative measurements of the Xe distribution between the adsorbed and the gas phases. First, we position the sample tube so that all of the solid is inside the NMR coil. After the measurement is completed, the tube is shifted, and only the signal from the gas phase is recorded. The amount of adsorbed Xe was determined by comparison with the signal of a known quantity of Xe adsorbed in NaY zeolite. The density of Xe in the gas phase is found by comparing its signal with that of a Xe gas sample at known pressure. Relaxation times (T₁) of the adsorbed Xe were estimated experimentally for both the gas and adsorbed phases and were found to be ≈400 and 100 s, respectively. Sufficiently long delays between the pulses were used to ensure quantitative measurements. The adsorption uptake measurements with pressure <1.5 bar were performed on a custom-built vacuum system equipped with digital pressure gauges. The reported uptakes at higher Xe pressures are from the quantitative NMR measurements as described above.

Theoretical Methods. Models. For the present work, we model the experimental system in two steps. First, we investigate how the average Xe chemical shift tensor in the dipeptide channels distinguishes between the two (AV and VA) channel architectures. Next, we consider how the electronic structure of the channel atoms affects the Xe shielding response. For the first quest, we make the assumption that the Xe shielding response functions that describe the Xe shielding tensor in the Xe@CH₄ system (model I) can be applied unchanged to Xe in the dipeptide channels, because the nanochannel walls are lined with CH₃ groups that constitute the alanine and valine side chains.

As a second avenue of investigation, we seek the magnitude of the difference in the Xe shielding response arising from the difference in electronic structure of a CH₃ group in the dipeptide crystal and in a CH₄ molecule. First, we do shielding calculations for Xe approaching an isolated dipeptide in vacuum (model A). Next, we do shielding calculations for Xe approaching a dipeptide with its full complement of hydrogen bonding interactions, which are provided by six dipeptide molecules: two on the sides in the same level in the channel, plus two above and two below (model B). The change in Xe shielding response tensors due to the differences in electronic structure of the CH₃ group in models A and B provides us with information about the magnitudes of the corrections provided by a more complete model than the Xe@CH₄ shielding model that was used to carry out all of the GCMC simulations in this work.

Quantum mechanical calculations. For the quantum mechanical calculations of Xe shielding, we use gauge-including atomic orbitals (GIAO) that have been shown to provide an advantage when used with any size of basis set, but especially for modest sized ones, because they provide the correct first-order wavefunctions for an atom in the presence of an external magnetic field (29). We used both Hartree–Fock and density functional (DFT) methods. We employ 240 basis functions for Xe, as described in our previous work, starting from the compilation of Partridge and Faegri (30) and augmented with polarization functions according to the recipe of Bishop et al. (31). This basis set was specifically constituted to describe the shielding response of Xe under the influence of a static electric field. It is so well balanced for this purpose that full counterpoise corrections (32), even with 1,200 additional basis functions on the neighboring atoms, amount to mere hundredths of ppm at the typical distances of interaction. The Pople-type 6-311G** basis set is used for all other atoms, except where explicitly stated. All calculations in the present work were carried out by using the pqs 3.0 software developed by Pulay et al. (Parallel Quantum Solutions, Fayetteville, AK).

Geometry optimization was carried out on dipeptide molecules captured directly from the x-ray crystal structure. The cluster was chosen such that the dipeptide was surrounded by all of its hydrogen-bonding partners (six other dipeptide molecules). The optimization of the proton positions in the seven-dipeptide cluster was done in steps. The first optimization step used the combined quantum mechanics–molecular mechanics QMMM/ONIOM method of Morokuma (33), where the quantum mechanical entity was the core dipeptide (at DFT/B3LYP/6-311G**) with the surrounding six dipeptides treated at the semiempirical AM1 level, in the absence of the Xe atom. Upon convergence, the proton positions in the seven dipeptide cluster were then quantum mechanically optimized in the presence of a Xe atom. The full quantum mechanical optimization started at the STO-3G level for all entities. The basis sets of the core dipeptide and the Xe atom were then increased, resulting in a locally dense basis set, with the outer six dipeptides having a STO-3G basis, whereas the core dipeptide was at 6-31G*, and the Xe atom had the 240 basis functions of Bishop et al. (31). Finally, the core dipeptide basis was increased to 6-311G**. The final converged geometry for the seven dipeptide cluster (model B) was used for Xe shielding response calculations at the final basis set size (6-311G** basis for the dipeptides and 240 basis functions on the Xe atom). The shielding response calculation for Xe with a single dipeptide molecule (model A) used the same basis sets, except that the six surrounding dipeptides were removed.

GCMC simulations. The methods used in the GCMC simulations of Xe NMR lineshapes are described in refs. 24 and 34. Briefly, the method relies on the dimer tensor model (24) that considers the contributions to intermolecular Xe shielding as additive and derived from the parallel and perpendicular tensor components of the Xe-A dimer, which are assumed to be known for each A atom. We therefore require the atomic coordinates of the dipeptides in the crystal.

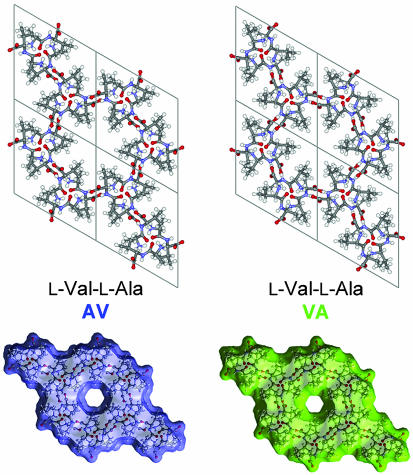
The crystal structures of the dipeptides studied are illustrated in Fig. 1. The channel results from an assembly of H-bonded molecules spiraling about a sixfold screw axis. Fig. 1 also shows the effective dimensions of the nanochannels that are obtained by rolling a spherical particle with a diameter of 4 Å over the internal surface of the channel. The van der Waals diameter of the VA channel is smaller than that of the AV channel. The diameter of the channel changes only slightly (within 0.15 Å), with average values of 4.90 Å and 5.13 Å for VA and AV, respectively. The channel is chiral; the center of the channel is displaced from the 6₁ axis by 1.05 Å and 0.60 Å for VA and AV, respectively, and rotates around the axis in a right-handed fashion. This geometry accounts for the greater “length” of the channel period as compared with the c crystallographic translation. Therefore, three Xe atoms (diameter of 4.4 Å) may be placed in the channel per one c translation.

Fig. 1.

The molecular crystals of VA and AV are assemblies that form one-dimensional channels running parallel to the c axis of the dipeptide crystals. Also shown are the surfaces accessible to a sphere4Åin diameter.

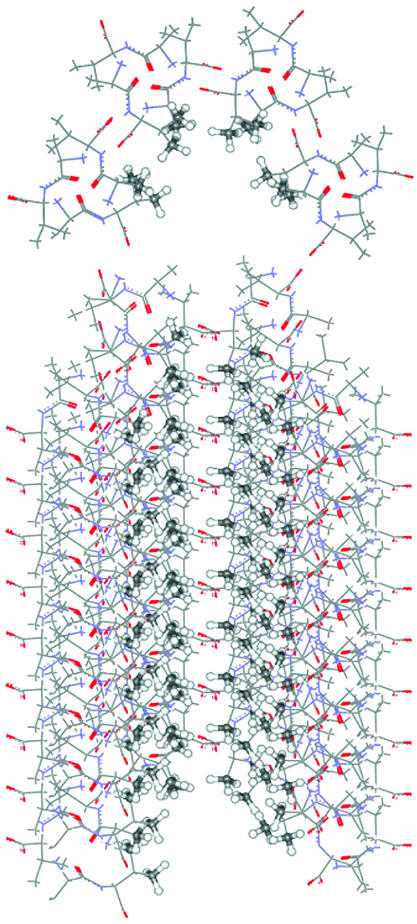
Fig. 2 shows the VA channel as seen by a Xe atom. The nanochannel walls in the dipeptide crystals of the present study are lined with CH₃ groups, which constitute the alanine and valine side chains. Although the peptide plane is involved in the stacking of the dipeptide molecules that constitute the channel, only the CH₃ groups are close enough to elicit the local Xe shielding response. The magnitude of the Xe shielding response is known to fall off rapidly with increasing distance, then, in a pairwise scheme, we need to include only the sums over the Xe shielding responses from the C and H atoms of CH₃ of alanine and CH(CH₃)₂ of valine.

Fig. 2.

The channel walls of the VA crystal, as seen by a Xe atom, are comprised largely of ordered CH₃ groups.

Comparison of the structures derived at different temperatures shows a distinct behavior of the VA and AV architectures with changing temperature (see Table 1). The VA structure reveals relatively low flexibility, with very small changes in the unit cell parameters. The crystal structure stays the same, slightly expanding upon heating, mostly in the c direction. In contrast, the AV structure reveals a high flexibility, with an almost three times greater unit cell expansion upon heating to room temperature. The expansion occurs in both a and c directions and affects the geometry of the channel. Inspection of the room-temperature structure reveals changes that allow for disorder of the isopropyl fragments (the side chain of valine) lining the channel walls. This disorder, experimentally observed in the crystal structure only at room temperature, was taken into account in our calculations. Starting with the fractional coordinates from the x-ray diffraction results, we carried out molecular dynamics simulations by using a supercell of 2 × 2 × 3 unit cells under 3D periodic boundary conditions to find robust positions for the H atoms and also to generate the disordered AV channel for simulations at room temperature. Molecular dynamic simulations were carried out by using the cerius² 4.2 (Accelrys, San Diego) software package with the CVF91 force field parameters. Additional details are given in Supporting Text, which is published as supporting information on the PNAS web site.

The equations that relate the parallel and perpendicular components of the dimer shielding to their contributions to the xx, xy, etc. components of the Xe shielding tensor in situ have been derived previously (24, 34). We employ parallel and perpendicular Xe–C and Xe–H dimer shielding response functions. The xx, xy, yy, etc. components of the Xe shielding tensor for a given Xe atom within the channel can be calculated for any arbitrary positions of any number of Xe atoms, because the Xe–Xe dimer tensor functions are also known from quantum mechanical calculations (35). Pairwise additive potential functions are used for both Xe–Xe and Xe–channel interactions. The Xe–Xe potential is the same one used in previous simulations (36). The same Xe–C and Xe–H potential functions are used throughout the present work as were used in calculations of the Xe chemical shifts in mixtures of Xe and CH₄ in the gas phase (35). The binning of the Xe resonance frequencies (or their equivalent shielding values) for various directions of magnetic field relative to the crystal frame, under fast or slow diffusion, is described in ref. 24. The GCMC scheme itself, as implemented in our work, is described in ref. 36.

Results

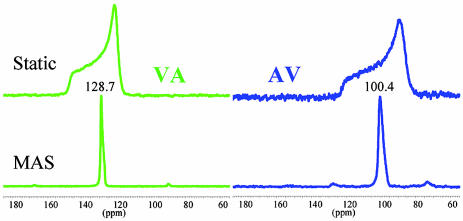
The adsorption isotherms obtained at 298 K are given in Fig. 6, which is published as supporting information on the PNAS web site. Because a single unit cell contains one channel and six dipeptide molecules, the ideal compositions for the fully saturated inclusion compounds would be Xe_1/2VA and Xe_1/2AV, which are in excellent agreement with experiment. The remarkable difference between sorption constants for the two dipeptides reflects a better complementarity toward the Xe atom in the VA channel. Taking the volume of one Xe atom at 44.6 ų, the packing efficiency of Xe atoms in the channels are 70.4% and 64.6% for VA and AV, respectively. The total gas storage capacity of the materials is ≈60 ml/g. The observation that Xe adsorbs easily is in agreement with the single-crystal XRD data, which suggest that the crystals are indeed microporous. The static and corresponding magic angle spinning ¹²⁹Xe NMR spectra obtained with HP Xe gas under continuous-flow conditions are shown in Fig. 3. Because the Xe–N₂–He mixture used in these experiments contains only 1% Xe (a partial pressure of only 10 mbar), the spectra correspond to very low Xe loadings and represents a situation where Xe–Xe interactions are negligible. The isotropic chemical shifts found from the magic angle spinning experiments were 128.9 ppm and 98.7 ppm for Xe in VA and AV, respectively. The anisotropies Δδ and asymmetry parameters η were determined by fitting the static spectra. Both of these parameters were found to be somewhat smaller for VA than for AV, with Δδ of 18.0 ppm and 23.0 ppm and η of 0.15 and 0.2, respectively.

Fig. 3.

Hyperpolarized ¹²⁹Xe NMR spectra at the low occupancy limit in VA and AV crystals.

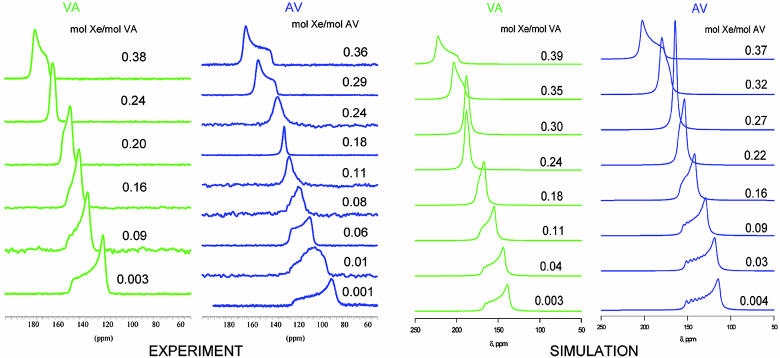
The results of the GCMC simulations using model I are shown in Table 2 in the limit of zero occupancy and in Fig. 4 as a function of occupancy. The trends observed in the simulations agree with all of the trends observed in experiment, although the absolute numbers do not accurately match experimental data. The series of Xe NMR lineshapes in Fig. 4 were calculated (before the experimental Xe lineshapes became available) in a simulation box of 2 × 2 × 3 unit cells under periodic boundary conditions, using a nanochannel of CH₃ groups that are electronically indistinguishable (as far as the Xe chemical shift functions and the Xe–C and Xe–H potential functions are concerned) from the CH₃ groups of CH₄. The GCMC simulations clearly show an axially symmetric chemical shift tensor at near-zero loading, with the component parallel to the channel axis being larger than the component perpendicular to the channel in both AV and VA. The primary difference in Xe tensors in the AV and VA channels lies in the tensor components perpendicular to the channel axis; the perpendicular components are larger for VA than for AV. This difference leads to Xe in the larger diameter channel (AV) having a smaller calculated isotropic Xe chemical shift compared with VA. We find a larger span for AV than for VA. Comparison with experimental lineshapes in Fig. 4 reveals agreement with experiment in all visible trends such as relative isotropic shifts and spans in AV and VA, and change of lineshapes with increasing Xe occupancy. The component of the Xe chemical shift tensor parallel to the channel axis does not stay constant but, rather, increases upon increasing Xe occupancy.

Table 2. The Xe chemical shift tensor (ppm) in dipeptide channels.

	VA		AV
	Experiment	Simulation	Experiment	Simulation
δiso	128.7 (MAS)	147.7	100.4 (MAS)	128.1
δ∥	146.9	169.4	121.7	158.1
δ⊥	121.2, 118.6	136.9	89.7, 84.7	112.2, 114.2
Span	28.4	32.6	37.0	46

Comparison of experiments and simulations at the low-occupancy limit.

Fig. 4.

The experimental thermally polarized Xe NMR spectra at room temperature, at various Xe occupancies in VA and AV crystals, are compared with the Xe NMR spectra calculated by GCMC simulations.

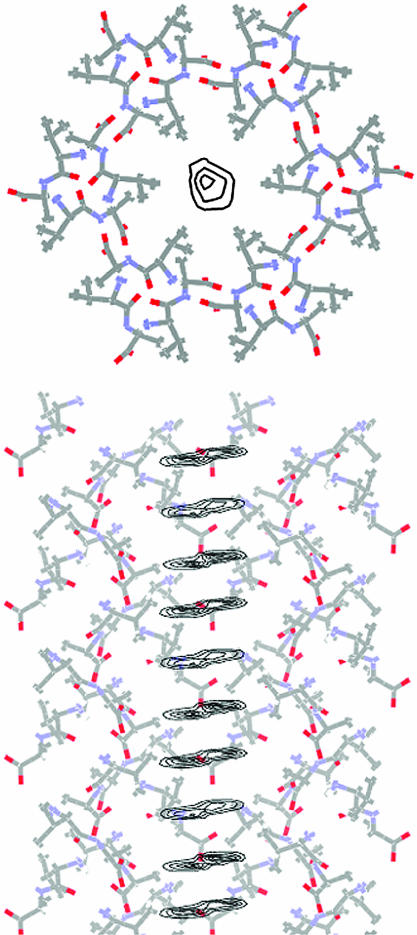
These peptide crystals have chiral channels, and the Xe distribution throughout the channel (Fig. 5) shows the helical nature of the inside walls. The upper contours show the probability of finding the Xe at various points on a plane perpendicular to the axis of the channel, and the lower contour shows the probability of finding the Xe at various points on a plane passing through the axis of the channel and normal to the a crystal axis. The helical nature of the inside of the channel is hinted at by the contours on this plane.

Fig. 5.

The one-body distribution function for Xe in the VA channel; the contours indicate the regions of highest probability. Shown as the top view is the probability of finding the Xe atom on a plane normal to the axis of the channel. Below that is the probability of finding a Xe atom on a plane passing through the axis of the channel and normal to the a axis of the crystal.

Discussion: The Xe Chemical Shift as a Probe of Small Differences in Channel Architecture

Effects of Lattice Expansion and Disorder. By examining the results of simulations using the Xe@CH₄ model in the low- and room-temperature structures of VA and AV, we demonstrate the sensitivity of the Xe chemical shift tensor components to the structure of the channel and its dimensions. A major difference between AV and VA is the appearance of the isopropyl disorder in the AV crystal at room temperature; the VA structures have no disorder of the CH₃ groups, at room temperature or below. The crystal structure of the AV crystal significantly expands upon heating to room temperature in both the a and c directions (Table 1). We investigated the effect of both of these factors. To investigate the effect of the expanded lattice parameters in AV, we used the fractional coordinates of the low-temperature structure and merely expanded the crystal structure to the room-temperature lattice parameters. The simulations show the extreme sensitivity of the Xe chemical shift tensor to the dimensions of the channel. For the nearly empty channel, upon expansion of the lattice, the average Xe chemical shift tensor components change as follows: δ_∥ = 170 ppm goes to 156 ppm, and δ_⊥ = 122 and 123 ppm go to 112 ppm. On the other hand, the differences between the average Xe tensors in the disordered structure and those for the merely expanded lattice are small. The average Xe chemical shift tensor components change as follows: δ_∥ = 156 ppm and δ_⊥ = 112 ppm in the expanded lattice may be compared with δ_∥ = 158 ppm and δ_⊥ = 112 and 114 ppm in the disordered crystal. The average Xe tensor in disordered AV reveals a slight deviation from axial symmetry of 1–2 ppm for all occupancies. GCMC simulations with the VA structure obtained at room temperature revealed the following changes at near-zero occupancy. Upon going from low to room temperature, δ_∥ = 159 ppm goes to 169 ppm, and δ_⊥ = 125.5 ppm goes to 136.9 ppm. The direction of the change upon slight expansion of the lattice parameters was predictable on the basis of previous work; however, how large the differences can be upon small changes in lattice parameters had not been documented previously. By examining the results of simulations in the ordered crystalline structures of both AV and VA, using the low temperature structure for both, we find the essential differences arising from the head-to-tail or the tail-to-head arrangement of the amino acids. We find that Xe is able to tell the difference between the two channels, even when the differences in electronic structures are not taken into account at all. Furthermore, by comparing the results for the ordered and disordered channels of AV, we discover the slight sensitivity of the Xe to the flip disorder of the CH₃ groups of the side chains of the AV dipeptide.

The Xe–Xe contributions themselves are different in the two cases, as might be expected on the basis of the channel dimensions. When the Xe has the opportunity to explore the channel in the cross-sectional plane, the smaller the channel, the larger the Xe–Xe contributions to the chemical shift tensor, because the average Xe–Xe distances are smaller. The invariability of the parallel component of the tensor, found in nanochannels such as ALPO-11 (24), is a consequence of the channel architecture and depends on the manner in which the Xe atoms registers into suitable sites along the channel walls. In the case of the AV and VA dipeptides, the Xe–Xe contributions are not that different, but the nature of the channel architecture is such that the Xe–Xe contribution to the tensor component parallel to the channel axis changes with increasing occupancy, although the Xe atoms do not pass each other in the channel. The Xe–Xe contribution is responsible for the overall increase in value of the parallel component found in both the simulations and the experiments.

One more factor that might influence the experimentally observed shifts and lineshapes is a possible change in the dipeptide crystal structure upon inclusion of the guest in the channels. The dipeptide architectures built on hydrogen-bonding interactions present an example of a previously uncharacterized class of “soft” sorbents that have a micropore structure that is sensitive to the presence, concentration, and properties of the guest species (2, 37–40). Only a few detailed investigations have been directed at understanding the sorption behavior of such materials (41–44), and similar studies on the materials studied here likely will be quite helpful.

Effects of Differences in Electronic Structure. Next, we examine those electronic aspects that had been completely neglected in using the Xe@CH₄ shielding response model. With the coordinates of the XeH₃C fragment being completely preserved in the comparisons, we find a systematic decrease in the Xe shielding response in going from Xe@H₃CH to Xe@H₃CCH₃ to Xe@dipeptide. (Shielding values at various separations for these three cases are given in Table 3, which is published as supporting information on the PNAS web site.) Including the electronic factors by providing the entire dipeptide molecule (model A) leads to a smaller deshielding than for Xe@CH₄ at all distances. The Xe shielding response in model B (in which the Xe is interacting with a dipeptide that has the full set of hydrogen bonding partners in the crystal) is smaller yet (per C or per H) than that found in model A. The quantum mechanical calculation for Xe@(VA)₇ in model B gives a chemical shift of 47.8 ppm, whereas the sum over Xe–C and Xe–H methane-like shieldings is 52.1 ppm. This finding suggests that the absolute magnitudes of the average chemical shifts would have been much closer to experiment had we used shielding response tensors from model B in the averaging. Additional factors contributing to the discrepancies between calculated and experimental absolute Xe shifts are mentioned in Supporting Text.

Conclusions

The experimental observation of the anisotropic Xe lineshapes in peptide channels along with simulations of the Xe chemical shifts will be of fundamental importance in understanding applications of Xe NMR spectroscopy to biological systems. Using the Xe@CH₄ shielding response functions, we have found that the signature Xe lineshapes characteristic of the near-zero occupancy nanochannels in the dipeptide crystals are very sensitive to (i) the dimensions of the channel and (ii) the arrangement of alanine and valine as either head or tail in the dipeptide, and only slightly sensitive to (iii) the presence or absence of disorder in the CH₃ groups that form the internal walls of the channel. The changes of the lineshapes with loading are well understood in terms of the progressively increasing Xe–Xe contributions to the Xe chemical shift tensor, as imposed by the confinement the Xe atoms experience in the slightly different AV and VA dipeptide channels. All of the experimental trends are reproduced by the simulations; the absolute magnitudes of the calculated Xe chemical shifts are greater than experiment, however. A more complete description of the Xe shielding response function using a dipeptide with its full complement of hydrogen bonding partners (6 other dipeptides) leads to smaller absolute magnitudes of Xe chemical shifts than those afforded by the Xe@CH₄ shielding response and to closer agreement with experiment.

The physical understanding of the Xe chemical shift tensors in these crystalline systems with well established structures will enlighten investigations into chemical shifts of Xe in protein cavities lined with various amino acid side chains, and in polymer voids with various pendant functional groups. The present work informs us about pores having pendant side chains consisting entirely of CH₃ groups. Investigations of channels with other functional groups (aromatic, phenolic, etc.) are of immediate interest toward the goal of simulating Xe chemical shifts in biological nanocavities, where HP ¹²⁹Xe could be used as a probe to detect ligand-binding events and to distinguish changes in protein structure upon ligand binding.