Abstract
We demonstrate that a “brute force” quantum chemical calculation based on an ab initio multiconfigurational second order perturbation theory approach implemented in a quantum mechanics/molecular mechanics strategy can be applied to the investigation of the excited state of the visual pigment rhodopsin (Rh) with a computational error <5 kcal·mol-1. As a consequence, the simulation of the absorption and fluorescence of Rh and its retinal chromophore in solution allows for a nearly quantitative analysis of the factors determining the properties of the protein environment. More specifically, we demonstrate that the Rh environment is more similar to the “gas phase” than to the solution environment and that the so-called “opsin shift” originates from the inability of the solvent to effectively “shield” the chromophore from its counterion. The same strategy is used to investigate three transient structures involved in the photoisomerization of Rh under the assumption that the protein cavity does not change shape during the reaction. Accordingly, the analysis of the initially relaxed excited-state structure, the conical intersection driving the excited-state decay, and the primary isolable bathorhodopsin intermediate supports a mechanism where the photoisomerization coordinate involves a “motion” reminiscent of the so-called bicycle-pedal reaction coordinate. Most importantly, it is shown that the mechanism of the ∼30 kcal·mol-1 photon energy storage observed for Rh is not consistent with a model based exclusively on the change of the electrostatic interaction of the chromophore with the protein/counterion environment.
Keywords: photoisomerization, quantum mechanics, molecular mechanics, retinal, vision
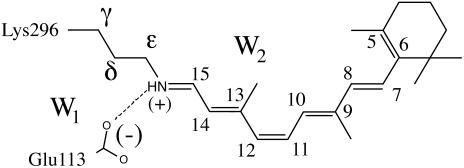
The visual pigment rhodopsin (Rh) (1, 2) is a G protein-coupled receptor containing an 11-cis retinal chromophore (PSB11) bounded to a lysine residue (Lys-296) via a protonated Schiff base linkage (see Scheme 1). While the biological activity of Rh is triggered by the light-induced 11-cis → all-trans isomerization of PSB11, this reaction owes its efficiency (e.g., short time scale and quantum yields) to the protein cavity (1). Accordingly, investigation of the environment-dependent properties of PSB11 is a prerequisite for understanding the Rh “catalytic” effect. The equilibrium geometry, absorption maxima (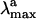 ), and fluorescence maxima (
), and fluorescence maxima (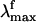 ) are indicators of the environment effect. In fact, whereas the geometry of PSB11 is nearly planar in a crystal (3), in bovine Rh it has a helical conformation (4). Similarly, the 445-nm
) are indicators of the environment effect. In fact, whereas the geometry of PSB11 is nearly planar in a crystal (3), in bovine Rh it has a helical conformation (4). Similarly, the 445-nm 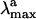 observed for PSB11 in methanol (5) is red-shifted to 498 nm in Rh (1, 2): an effect known as the opsin shift.
observed for PSB11 in methanol (5) is red-shifted to 498 nm in Rh (1, 2): an effect known as the opsin shift.
Scheme 1.
The rhodopsin chromophore.
The Rh fluorescence band ranges from 530 to 780 nm (6). The 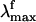 has been reported (6) to be excitation wavelength-dependent, shifting from 595 to 704 nm when the excitation wavelength is shifted from 472 to 568 nm. This observation is consistent with the idea that the emission arises from a nonstationary unrelaxed excited-state population. In methanol solution the PSB11
has been reported (6) to be excitation wavelength-dependent, shifting from 595 to 704 nm when the excitation wavelength is shifted from 472 to 568 nm. This observation is consistent with the idea that the emission arises from a nonstationary unrelaxed excited-state population. In methanol solution the PSB11 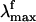 observed after 444-nm irradiation is 660 nm (7) and falls in the
observed after 444-nm irradiation is 660 nm (7) and falls in the 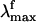 range measured for the protein.
range measured for the protein.
Preliminary studies (8) on the properties of different reduced models of PSB11 embedded in the Rh cavity suggested that the level of theory required for a correct description of its geometrical and electronic structure must include the treatment of electron dynamic correlation. In particular, the use of a CASPT2//complete active space self-consistent field (CASSCF)/amber quantum mechanics (QM)/molecular mechanics (MM) strategy allowing for geometry optimization and excited-state property evaluation in proteins yields reasonable values for the retinal backbone geometry, absolute 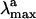 value, and change in dipole moment (Δμ) when compared with the available experimental data.
value, and change in dipole moment (Δμ) when compared with the available experimental data.
The target of the present contribution is 2-fold. On one hand, we show that CASPT2//CASSCF/amber computations can be successfully used to evaluate the structural and spectroscopic parameters of full (i.e., comprising the entire retinal chromophore) models of Rh and N-methyl-PSB11 in methanol solution. On the other hand, we show that the same level of theory can be used to get realistic information on the excited-state and ground-state relaxation of PSB11 in the Rh cavity. Indeed, the initial relaxation leads to a loose nonfluorescent intermediate (i.e., an excited-state energy minimum)∥ featuring a chromophore structure with a 20–30° twisted C11 C12 double bond and an S1-S0 energy gap falling in the near IR region. To improve our understanding of the mechanisms driving the excited-state decay and photon energy storage in Rh, we also locate the structure of a 90°-twisted low-lying S1/S0 conical intersection and that of the primary S0 intermediate bathorhodopsin (bathoRh). These structures demonstrate that the isomerization involves a component of bicycle pedal-type motion and that the ∼30 kcal·mol-1 photon energy stored in bathoRh does not involve extensive charge separation.
C12 double bond and an S1-S0 energy gap falling in the near IR region. To improve our understanding of the mechanisms driving the excited-state decay and photon energy storage in Rh, we also locate the structure of a 90°-twisted low-lying S1/S0 conical intersection and that of the primary S0 intermediate bathorhodopsin (bathoRh). These structures demonstrate that the isomerization involves a component of bicycle pedal-type motion and that the ∼30 kcal·mol-1 photon energy stored in bathoRh does not involve extensive charge separation.
Methodology
Although a number of QM/MM studies have been reported (9) for Rh proteins only a few used ab initio QM. Yamada et al. (10) used a restricted Hartree-Fock/6–31G/amber scheme to investigate the ground-state (S0) stability of PSB11 protonated state in Rh. Hayashi et al. (11) reported a CASSCF//HF/double ζ valence/amber computation of the λmax of the related pigment bacteriorhodopsin (bR). Although those authors correctly predicted the λmax changes among different bR photocycle intermediates, the λmax absolute values were strongly blue-shifted. More recently, a molecular dynamics simulation of the photoisomerization of bR has been reported by Hayashi et al. (12) who used a CASSCF/amber force field with a truncated active space (six electrons in six π-orbitals). These calculations have illustrated the role of bR in the high selectivity of the photoisomerization: protein blocks alternative isomerization paths and funnels them into isomerization, leading to the 13-cis product.
Our QM/MM scheme is fully described in ref. 8. Briefly, the method is based on a hydrogen link-atom scheme (13) with the frontier placed at the Cδ—Ce bond of the Lys-296 side chain (see Scheme 1). The ab initio QM calculations are based on a CASSCF/6–31G* level. The active space comprises the full π-system of PSB11 (12 electrons in 12 π-orbitals). The MM segments (we used the amber force field) and QM segments interact in the following way: (i) all QM atoms feel the electrostatic potential of the MM point charges, (ii) stretching, bending, and torsional potentials involving at least one MM atom are described by the MM potential, and (iii) QM and MM atom pairs separated by more then two bonds interact via either standard or reparametrized (14, 15) van der Waals potentials. CASSCF/6–31G*/amber geometry optimization was carried out with the gaussian98 (16) and tinker (17) programs.
The protein framework used in the computation is derived from monomer A deposited in the Protein Data Bank archive as file 1HZX (4). With the exception of the Glu-113 counterion [forming a salt bridge with NH(+)] the Rh cavity is set to neutral, consistent with the experiment (18). While the protein is kept frozen during the optimizations, the Lys-296 side chain, the position/orientation of two TIP3P water molecules (W1 and W2 in Scheme 1), and the chromophore are relaxed. The optimizations have been stopped when the maximum force is <0.003 a.u./bohr and the rms is <0.0005 bohr. Because of the excessive computational cost no second derivative computations could be performed to rigorously determine the nature of the stationary point. At the equilibrium geometries a three-root state average CASPT2 computation is carried out by using the molcas-5 (19) program to evaluate the λmax and the oscillator strength (f) of the S0 → S1 and S0 → S2 transitions. The amber charges account for S0 polarization effects in a mean-field way (20). The same charges are used for the excited-state computations with no ad hoc dielectric constant. The computation of the 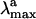 for PSB11 in solution has been carried out by embedding the QM chromophore in a box of 385 MM methanol molecules by using periodic boundary conditions and choosing Cl- (treated at the MM level) as the counterion. The average ground-state configuration of the solvent has been determined according to the approximate scheme described in Supporting Appendix, which is published as supporting information on the PNAS web site. More specifically, the solvent was minimized for 2000 steps by using the steepest descent method and keeping the N-methyl-PSB11 solute fixed in its gas-phase configuration. During the optimization the partial charges of PSB11 atoms used in our QM/MM simulations were determined with gaussian98, using a restrained electrostatic potential (21) procedure at the HF/6–31G* level of theory. The next step was to perform CASSCF/6–31G*/amber geometry optimization to relax the coordinates of the QM chromophore and the counterion while the positions of solvent molecules were kept frozen. One has to be aware of the simplicity of this procedure as the fluctuations of the solvent molecules around the solute are not taken into account. The van der Waals parameters for PSB11 in solution are the same as those chosen for PSB11 in the protein. The ultimate goal was to obtain
for PSB11 in solution has been carried out by embedding the QM chromophore in a box of 385 MM methanol molecules by using periodic boundary conditions and choosing Cl- (treated at the MM level) as the counterion. The average ground-state configuration of the solvent has been determined according to the approximate scheme described in Supporting Appendix, which is published as supporting information on the PNAS web site. More specifically, the solvent was minimized for 2000 steps by using the steepest descent method and keeping the N-methyl-PSB11 solute fixed in its gas-phase configuration. During the optimization the partial charges of PSB11 atoms used in our QM/MM simulations were determined with gaussian98, using a restrained electrostatic potential (21) procedure at the HF/6–31G* level of theory. The next step was to perform CASSCF/6–31G*/amber geometry optimization to relax the coordinates of the QM chromophore and the counterion while the positions of solvent molecules were kept frozen. One has to be aware of the simplicity of this procedure as the fluctuations of the solvent molecules around the solute are not taken into account. The van der Waals parameters for PSB11 in solution are the same as those chosen for PSB11 in the protein. The ultimate goal was to obtain 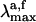 and oscillator strengths for S0 → S1 and S0 → S2 transitions of PSB11 in the protein and solution environments. In all cases the excitation energies and wavelengths were evaluated in terms of the energy gap between the corresponding electronic states.
and oscillator strengths for S0 → S1 and S0 → S2 transitions of PSB11 in the protein and solution environments. In all cases the excitation energies and wavelengths were evaluated in terms of the energy gap between the corresponding electronic states.
Details of the QM/MM scheme, protein and solvent models, coordinates of all optimized structures, S1 forces of PSB11 in S0-Rh and S0-PSB11+Cl-, energies, and charge distribution, Δμ and f, are in Supporting Appendix.
Results and Discussion
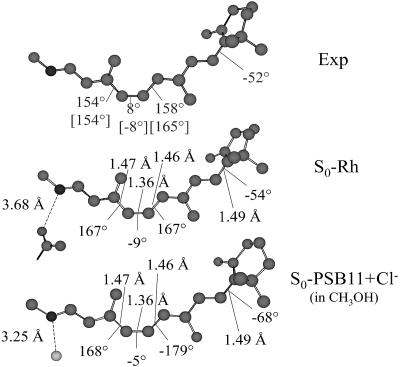
As shown in Fig. 1 the S0-Rh optimized structure shows a chromophore conformation remarkably close to the one observed in bovine Rh (4, 22, 23). [This structure is similar to the one obtained by Sugihara et al. (24) via self-consistent-charge–density-functional tight-binding computations on a reduced Rh model comprising the entire PSB11 unit.] The same conformation is also consistent with that of a simplified Rh model including a chromophore that does not explicitly include the β-ionone ring (8). In fact, the S0-Rh chromophore has a spiral-like structure with the correct negative (counterclockwise) helicity. The detailed chromophore geometry can be compared with that obtained for PSB11 in methanol solution (S0-PSB11+Cl-). It is evident from Fig. 1 that, in solution, the central segment of PSB11 is close to planarity. However, the β-ionone ring is (for this conformer) 14° more twisted than in the protein.
Fig. 1.
CASSCF/amber-optimized structures for S0-Rh and S0-PSB11+Cl- compared with the crystallographic (4) and NMR (22) (values in square brackets) structure Exp. More recent NMR measurements yield a -65° C5 C6—C7
C6—C7 C8 torsion and 150° C11
C8 torsion and 150° C11 C12—C13
C12—C13 C14 torsion (23).
C14 torsion (23).
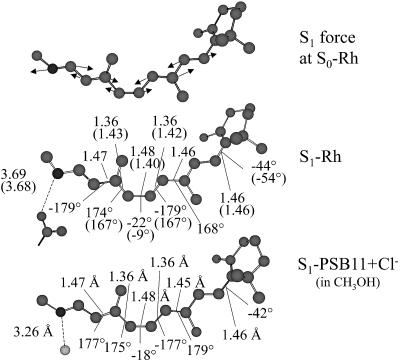
State-average geometry optimization on S1 yields structure S1-Rh that is located ∼10 kcal·mol-1 below the vertical excitation point.†† The geometry of S1-Rh is dramatically different from S0-Rh. The main change regards the bond lengths of the central part of the PSB11 backbone. Indeed, a complete inversion of the double-bond, single-bond character is observed in the –C9 C10—C11
C10—C11 C12—C13
C12—C13 C14- moiety. This inversion is somehow more limited in the terminal parts of the chromophore. In particular, the –C5
C14- moiety. This inversion is somehow more limited in the terminal parts of the chromophore. In particular, the –C5 C6—C7
C6—C7 C8- moiety shows bond lengths closer to the corresponding ground-state values.
C8- moiety shows bond lengths closer to the corresponding ground-state values.
The torsional deformation of the chromophore upon the initial excited-state relaxation is of great interest in connection with the 11-cis → all-trans photoisomerization. Notice that, upon relaxation the central C11 C12 torsion increases by 13°, whereas the C10—C11 and C12—C13 torsions become more planar. The β-ionone ring undergoes a torsional reorientation of the same magnitude of that occurring in the central part of the molecule but in the inverse direction. Indeed, the C6—C7 torsion shifts from -54° to -44°. Thus, the initial torsional relaxation can be described as a clockwise rotation of the part of the π-plane hosting the -C7
C12 torsion increases by 13°, whereas the C10—C11 and C12—C13 torsions become more planar. The β-ionone ring undergoes a torsional reorientation of the same magnitude of that occurring in the central part of the molecule but in the inverse direction. Indeed, the C6—C7 torsion shifts from -54° to -44°. Thus, the initial torsional relaxation can be described as a clockwise rotation of the part of the π-plane hosting the -C7 C8—C9
C8—C9 C10—C11- pentadienyl fragment.
C10—C11- pentadienyl fragment.
To characterize the initial relaxation of PSB11 we have computed the QM/MM S1 forces at S0-Rh. The components displayed in Fig. 2 show that, despite the protein chiral environment, the force field prompts a double-bond expansion, single-bond contraction along the chromophore backbone. No major torsional component is detected at this initial stage. Indeed, comparison of the structures S1-Rhstretch (where only the bond lengths have been optimized) and S1-Rh reveals that 90% of the excited-state stabilization originates from bond length relaxation. This result is consistent with the previously proposed (25, 26) two-mode (first stretching, then torsion) isomerization coordinate. On the other hand, stretching and torsions must be highly coupled in Rh as no intermediate could be detected between S0-Rh and S1-Rh. Furthermore, the magnitude of the bond lengths at S1-Rhstretch suggests that only a partial stretching relaxation is achieved in this torsionally constrained structure. In other words, S0-Rh must relax directly to S1-Rh through a barrierless but highly “curved” path sequentially dominated by stretching and stretching plus unidirectional (clockwise with respect to the –C10—C11 C12—C13–dihedral angle) twisting. In Fig. 2 we also show the relaxed structure determined for PSB11 in methanol solution- S1-PSB11+Cl- (the remarks in †† also apply in this case). It can be clearly seen that the general behavior found in the protein environment is reproduced in solution where there is single-bond, double-bond inversion and an ∼20° planarization of the β-ionone ring.
C12—C13–dihedral angle) twisting. In Fig. 2 we also show the relaxed structure determined for PSB11 in methanol solution- S1-PSB11+Cl- (the remarks in †† also apply in this case). It can be clearly seen that the general behavior found in the protein environment is reproduced in solution where there is single-bond, double-bond inversion and an ∼20° planarization of the β-ionone ring.
Fig. 2.
CASSCF/amber S1 forces at S0-Rh (Top) and optimized structure for S1-Rh (Middle) and excited-state retinal chromophore in methanol solution S1-PSB11+Cl- (Bottom). The values in parentheses are relative to the torsionally constrained structure S1-Rhstretch (see text).
The quality of our approach can be assessed by comparing the 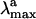 computed in terms of vertical excitation energies with the observed
computed in terms of vertical excitation energies with the observed 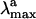 . Consistently with the data in Fig. 3, the computed S0-Rh
. Consistently with the data in Fig. 3, the computed S0-Rh 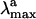 (479 nm) is only 3 kcal·mol-1 off from the experimental value (498 nm), whereas the computed solution
(479 nm) is only 3 kcal·mol-1 off from the experimental value (498 nm), whereas the computed solution 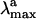 (429 nm) is only 1 kcal·mol-1 off the observed value (440 nm). Thus, the opsin shift of Rh is reproduced with a 2 kcal·mol-1 error. To reproduce the observed 595-to 704-nm range of wavelength-dependent
(429 nm) is only 1 kcal·mol-1 off the observed value (440 nm). Thus, the opsin shift of Rh is reproduced with a 2 kcal·mol-1 error. To reproduce the observed 595-to 704-nm range of wavelength-dependent 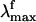 we assume that the structures responsible for the emission correspond to the part of S1 energy surface comprised between the S1-Rhstretch and S1-Rh structures. In other words, we assume that the experimentally proposed nonstationary fluorescent state corresponds to the vibrationally excited population generated immediately after the initial stretching relaxation (see discussion above) and undergoing energy redistribution to the other molecular modes (including the reactive torsional mode). As shown in Fig. 3, the observed
we assume that the structures responsible for the emission correspond to the part of S1 energy surface comprised between the S1-Rhstretch and S1-Rh structures. In other words, we assume that the experimentally proposed nonstationary fluorescent state corresponds to the vibrationally excited population generated immediately after the initial stretching relaxation (see discussion above) and undergoing energy redistribution to the other molecular modes (including the reactive torsional mode). As shown in Fig. 3, the observed 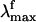 range (i.e., the gray band in Fig. 3) falls right in the middle between the computed S1-Rhstretch and S1-Rh S1-S0 energy gaps consistently with the above hypothesis. Notice that, recently, Schenkl et al. (27) demonstrated that the excitation wavelength-dependent
range (i.e., the gray band in Fig. 3) falls right in the middle between the computed S1-Rhstretch and S1-Rh S1-S0 energy gaps consistently with the above hypothesis. Notice that, recently, Schenkl et al. (27) demonstrated that the excitation wavelength-dependent 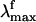 observed for the bR pigment is not detected when a more accurate time-integrated fluorescence technique is used (27). This result raises the question of the possible existence of a wavelength-independent
observed for the bR pigment is not detected when a more accurate time-integrated fluorescence technique is used (27). This result raises the question of the possible existence of a wavelength-independent 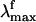 value of Rh that, according to our computations, should fall near 770 nm.
value of Rh that, according to our computations, should fall near 770 nm.
Fig. 3.
S0 → S1 (circles) and S0 → S2 (triangles) excitation energies computed at the CASSCF (open circles) and CASPT2 (filled circles and triangles) QM levels. The energy gap “a” indicates the computed range of excitation energy-dependent emission maxima, and the energy gap “b” indicates the computed opsin shift. The energy values in italics refer to experimental quantities.
It is established (25) that, in vacuo, the S1 state of PSB11 has a dominant hole-pair (ionic) character as originally proposed by Michl and coworkers (28, 29). Indeed, upon S0 → S1 excitation, approximately half of the positive charge initially located on the -N = C15- moiety moves away along the π-skeleton, leading to large values of Δμ and f. In contrast, the S2 state has a dominant dot-dot (covalent) character, the charge remains on -N = C15-, leading to low Δμ and f values for the S0 → S2 transition. Consistently with the previous results on reduced PSB11 models (25, 30), the magnitude of Δμ and f in Table 1 indicates that the S1 state of the isolated PSB11 chromophore, taken with its S0-Rh geometry, has indeed a larger ionic character with respect to S2.
Table 1. Oscillator strength and vertical change in dipole moment (Debyes) in parentheses.
| Structure | S0 → S1 | S0 → S2 |
|---|---|---|
| PSB11 | 0.77 (14.2) | 0.32 (3.6) |
| PSB11+Glu113 | 0.13 (3.7) | 0.86 (7.4) |
| S0-Rh | 0.51 (11.1) | 0.40 (3.1) |
| S1-Rh | 0.59 (8.2) | 0.43 (3.7) |
| S0-PSB11+Cl- in CH3OH | 0.42 (5.6) | 0.60 (3.4) |
| S1-PSB11+Cl- in CH3OH | 0.32 (3.4) | 0.65 (8.5) |
In complete contrast, the PSB11+Glu-113 chromophore-counterion system, again taken with its S0-Rh geometry, displays an S2 state with a large ionic character and an S1 state with a covalent character. The inversion of the electronic nature of these states is readily rationalized by the fact that the negative Glu-113 group stabilizes the positive charge on the -C15 NH-fragment, therefore stabilizing the original S0 and S2 covalent states with respect to S1 [where charge translocation occurs (28); see also below]. However, in S0-Rh where the chromophore-counterion system is surrounded by the protein matrix, the character of the S1 and S2 states is more similar to that seen in the isolated chromophore.
NH-fragment, therefore stabilizing the original S0 and S2 covalent states with respect to S1 [where charge translocation occurs (28); see also below]. However, in S0-Rh where the chromophore-counterion system is surrounded by the protein matrix, the character of the S1 and S2 states is more similar to that seen in the isolated chromophore.
The results above suggest that the protein matrix is specifically designed to offset or counterbalance the effect of the counterion (31). This is also consistent with the analysis of the excitation energies. In fact, to disentangle the contribution of the protein cavity to the Rh 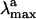 we have determined the S1-S0 energy gap for PSB11+Glu-113. In Fig. 3 we show that the S1-S0 energy gap increases, leading to a strongly blue-shifted
we have determined the S1-S0 energy gap for PSB11+Glu-113. In Fig. 3 we show that the S1-S0 energy gap increases, leading to a strongly blue-shifted 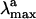 . On the other hand, the isolated PSB11 chromophore displays a
. On the other hand, the isolated PSB11 chromophore displays a 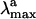 value much closer to that of the protein. (The recovery is more complete at the CASPT2 level, suggesting that dynamic correlation is more important in the protein or in solution than in vacuo.) Most likely, this is an effect of the suitably designed (by the biological evolution!) charge distribution of the protein cavity. This result is in line with the opsin-shift mechanism proposed by Sheves et al. (32) provided that a negative point charge is replaced by a cloud of partial charges. As apparent from Table 1 and Fig. 3 the solvent environment is much less effective in offsetting the counterion effect.
value much closer to that of the protein. (The recovery is more complete at the CASPT2 level, suggesting that dynamic correlation is more important in the protein or in solution than in vacuo.) Most likely, this is an effect of the suitably designed (by the biological evolution!) charge distribution of the protein cavity. This result is in line with the opsin-shift mechanism proposed by Sheves et al. (32) provided that a negative point charge is replaced by a cloud of partial charges. As apparent from Table 1 and Fig. 3 the solvent environment is much less effective in offsetting the counterion effect.
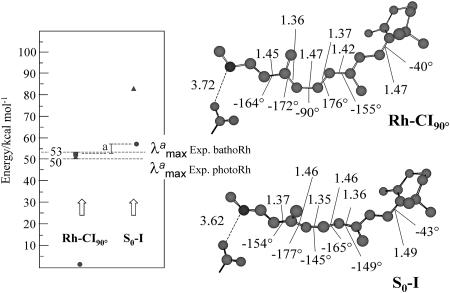
To provide information on the geometry and energy changes associated with the Sn → Sp decay, as well as with the generation of a stable ground-state intermediate, we discuss the structure and excitation energies of the S1/S0 conical intersection Rh-CI90°. This structure has been previously reported (33) and corresponds to both the lowest energy conical intersection and absolute S1 minimum of Rh. (We would like to stress that higher-energy conical intersection points at less or more twisted structures also have been located and may be involved in the excited-state decay.) Starting at Rh-CI90° we have then located, via standard geometry optimization, a stable S0 intermediate (S0-I) displaying an all-trans-like chromophore.
As shown in Fig. 4, Rh-CI90° displays a highly helical structure characterized by large structural changes in the –C9 C10—C11
C10—C11 C12—C13
C12—C13 C14- moiety. Comparison with S1-Rh indicates that the motion leading to S1 → S0 decay involves torsion about the C11
C14- moiety. Comparison with S1-Rh indicates that the motion leading to S1 → S0 decay involves torsion about the C11 C12 reactive double bond that increases by 68°, as well as about the C9
C12 reactive double bond that increases by 68°, as well as about the C9 C10 and C13
C10 and C13 C14 bonds that increase by 37° and 15°, respectively. All of the other bonds remain substantially unchanged, including the β-ionone C6—C7 bond. Thus, these preliminary results indicate that the S1 reaction coordinate has a “double” bicycle-pedaling (34) nature where the reactive motion is accompanied by changes in the torsional angle of the two adjacent C
C14 bonds that increase by 37° and 15°, respectively. All of the other bonds remain substantially unchanged, including the β-ionone C6—C7 bond. Thus, these preliminary results indicate that the S1 reaction coordinate has a “double” bicycle-pedaling (34) nature where the reactive motion is accompanied by changes in the torsional angle of the two adjacent C C bonds (mainly of the C9
C bonds (mainly of the C9 C10 bond). Since the C10—C11 and C12—C13 bonds remain substantially untwisted (due to the fact that during excited-state evolution these are, effectively, double bonds) the involvement of a hula-twist coordinate (35) is fully excluded at the CASSCF/amber level.
C10 bond). Since the C10—C11 and C12—C13 bonds remain substantially untwisted (due to the fact that during excited-state evolution these are, effectively, double bonds) the involvement of a hula-twist coordinate (35) is fully excluded at the CASSCF/amber level.
Fig. 4.
CASSCF/amber-optimized structure and S0 → S1 (circles), S0 → S2 (triangles), and S1 → S2 (squares) CASPT2//CASSCF/amber excitation energies for Rh-CI90° and S0-I. “a” indicates the difference between the corresponding S1 → S2 (Rh-CI90°) and S0 → S1 (S0-I) computed excitation energies. The energy values in the frame refer to experimental quantities.
Comparison of the Rh-CI90° and S0-I structures indicates that the ground-state relaxation must involve, quite unexpectedly, further twisting deformation together with the expected double-bond, single-bond back inversion. Indeed, whereas the C11 C12 reactive double bond is now -145° twisted (yielding a 55° torsional deformation toward the all-trans form), the twisting about the C13
C12 reactive double bond is now -145° twisted (yielding a 55° torsional deformation toward the all-trans form), the twisting about the C13 C14 bond decreases by an additional 10° (i.e., from -164° to -154°) despite its reconstituted double-bond character (i.e., the C13
C14 bond decreases by an additional 10° (i.e., from -164° to -154°) despite its reconstituted double-bond character (i.e., the C13 14 bond length is now 1.37 Å). In contrast, the torsional deformation about the C9
14 bond length is now 1.37 Å). In contrast, the torsional deformation about the C9 C10 bond is limited.
C10 bond is limited.
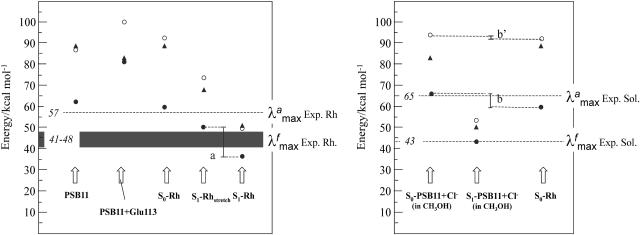
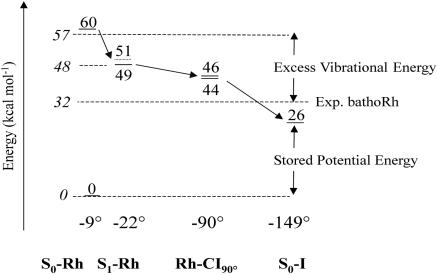
The results seen above can be tentatively validated by computing the excitation energy and thermodynamic stability of S0-I and comparing their values with those observed for the primary isolable photoproduct bathoRh. It is apparent from Fig. 4 that the experimental 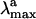 is reproduced with <5 kcal·mol– error when compared with the S0 → S1 excitation energy. Notice, however, that the relative difference between the computed S0-Rh and S0-I
is reproduced with <5 kcal·mol– error when compared with the S0 → S1 excitation energy. Notice, however, that the relative difference between the computed S0-Rh and S0-I 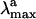 is reproduced with an even more limited 2 kcal·mol 1 error as the computed quantities are both blue-shifted with respect to the experiment. The thermodynamic stability of bathoRh with respect to WT Rh has been determined by Schick et al. (36) using time-resolved calorimetry. This is an important biophysical quantity that provides information about the fraction of the photon energy that has been actually stored in the distorted protein structure. As shown in Fig. 5 the differences between the CASPT2//CASSCF/amber ground-state energy at S0-Rh and S0-I yield a 26 kcal·mol-1 value for such a stored energy, yielding a 7 kcal·mol-1 difference with respect to the experimental value. Given the complexity of the molecular system under investigation and the approximations made (e.g., no side-chain relaxation for the residues in the cavity and no explicit protein charge polarizabilities) we are convinced that our results indicate that the S0-I structure corresponds to bathoRh. A similar (but slightly better) energy difference between S0-Rh and S0-I has been obtained on the basis of an ONIOM (Our own N-layered Integrated molecular Orbital and molecular Mechanics) method (37) that combines B3LYP (Becke three-parameter hybrid functional combined with Lee–Yang–Parr correlation functional) and the amber force field and takes into account the electrostatic interaction between the two layers. However, the predicted bathoRh structure appears to be rather different from ours. A prediction of the bathoRh structure that yields torsional parameters consistent with the ones documented above has been reported by Sugihara et al. (38), who used a QM/MM strategy based on the density-functional tight-binding method.
is reproduced with an even more limited 2 kcal·mol 1 error as the computed quantities are both blue-shifted with respect to the experiment. The thermodynamic stability of bathoRh with respect to WT Rh has been determined by Schick et al. (36) using time-resolved calorimetry. This is an important biophysical quantity that provides information about the fraction of the photon energy that has been actually stored in the distorted protein structure. As shown in Fig. 5 the differences between the CASPT2//CASSCF/amber ground-state energy at S0-Rh and S0-I yield a 26 kcal·mol-1 value for such a stored energy, yielding a 7 kcal·mol-1 difference with respect to the experimental value. Given the complexity of the molecular system under investigation and the approximations made (e.g., no side-chain relaxation for the residues in the cavity and no explicit protein charge polarizabilities) we are convinced that our results indicate that the S0-I structure corresponds to bathoRh. A similar (but slightly better) energy difference between S0-Rh and S0-I has been obtained on the basis of an ONIOM (Our own N-layered Integrated molecular Orbital and molecular Mechanics) method (37) that combines B3LYP (Becke three-parameter hybrid functional combined with Lee–Yang–Parr correlation functional) and the amber force field and takes into account the electrostatic interaction between the two layers. However, the predicted bathoRh structure appears to be rather different from ours. A prediction of the bathoRh structure that yields torsional parameters consistent with the ones documented above has been reported by Sugihara et al. (38), who used a QM/MM strategy based on the density-functional tight-binding method.
Fig. 5.
CASPT2//CASSCF/amber energy profile for the Rh → S0-I photochemical reaction. The energy values in italics refer to experimental quantities.
A more delicate problem is related to the assignment of the primary transient intermediate photo Rh (39) that is formed only 200 fs after photon absorption. This species cannot be isolated even at low temperature, and it is identified through a red-shifted, 570-nm 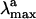 . Furthermore, the excited-state or ground-state nature of photo Rh is still a matter of debate (40–42). Given the limited knowledge provided by our computations on the structure of the S1 reaction path and S0 relaxation path we cannot presently assign such an entity. Nevertheless, it must be noticed that the S1 → S2 excitation energy computed at Rh-CI90° yields a 53 kcal·mol-1 energy gap and therefore close to the experimental quantity of 50 kcal·mol-1 detected for photo Rh. Whereas the S1 → S2 transition features a small 0.016 f value, the alternative S0 → S2 transition is found to be completely forbidden. Despite these observations it is important to stress that, at a conical intersection, one usually expects a fully efficient S1 → S0 decay inconsistently with the existence of a transient, but spectroscopically detectable, species. Clearly, a better understanding of the topography of the S1 and S0 energy surfaces and the relaxation dynamics in the region surrounding Rh-CI90° is needed.
. Furthermore, the excited-state or ground-state nature of photo Rh is still a matter of debate (40–42). Given the limited knowledge provided by our computations on the structure of the S1 reaction path and S0 relaxation path we cannot presently assign such an entity. Nevertheless, it must be noticed that the S1 → S2 excitation energy computed at Rh-CI90° yields a 53 kcal·mol-1 energy gap and therefore close to the experimental quantity of 50 kcal·mol-1 detected for photo Rh. Whereas the S1 → S2 transition features a small 0.016 f value, the alternative S0 → S2 transition is found to be completely forbidden. Despite these observations it is important to stress that, at a conical intersection, one usually expects a fully efficient S1 → S0 decay inconsistently with the existence of a transient, but spectroscopically detectable, species. Clearly, a better understanding of the topography of the S1 and S0 energy surfaces and the relaxation dynamics in the region surrounding Rh-CI90° is needed.
Conclusions
The computational investigation of a photochemical reaction in the protein environment is currently considered to be a formidable research target. A primary requirement to be fulfilled is the accurate mapping of the force field (i.e., of the potential energy surface) driving the reaction. Here, we have provided evidence that a brute force CASPT2//CASSCF/6–31G*/amber strategy can be used to study the structure and spectroscopy of the visual photo-receptor Rh with a limited (<5 kcal·mol-1) computational error, opening the way to a more quantitative investigation of the early transient species involved in the vision photocycle.
In particular, it has been possible to trace the entities and factors responsible for the absorption and emission spectroscopy of Rh and the large-scale energetics of the photochemical transformation. Accordingly (see Fig. 5) upon S0 → S1 excitation the Rh chromophore acquires, with respect to the bottom of S1, at least 15 kcal·mol-1 of vibrational excess energy. Approximately 10 kcal·mol-1 of this energy is initially located in stretching modes and, most likely, get partially redistributed before the fluorescent region is left. Approximately 5 kcal·mol-1 of vibrational excess energy should accelerate the system toward a reactive, but rather complex (i.e., involving more than a single torsion), torsional coordinate. Ground-state relaxation from the decay channel Rh-CI90° to S0-I (i.e., to bathoRh) provides an additional 20 kcal·mol-1 excess energy, which populates a relaxation coordinate with a large component of bicycle pedal-like motion of the C11 C12—C13
C12—C13 C14 moiety.
C14 moiety.
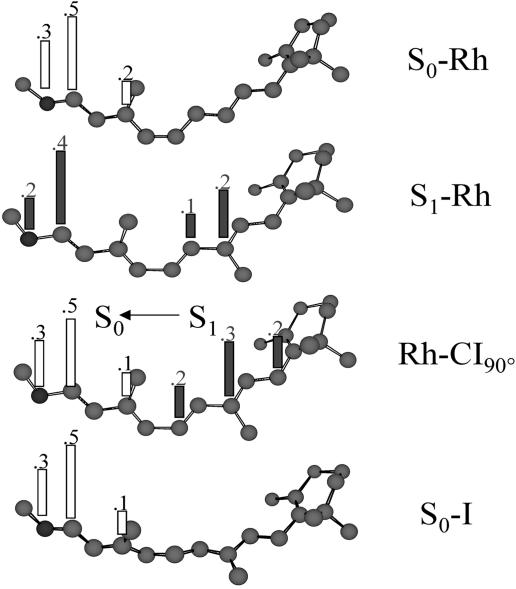
As mentioned above, the bathoRh intermediate represents an isolable S0 species of the Rh photocycle. It is therefore often described as the locus of the photon energy storage. To help understand the nature of this storage process we show in Fig. 6 the distribution of the positive charge along the chromophore backbone for the key structures of Fig. 5. It is apparent that after photoexcitation about half of the charge migrates from its original position on the  C13—C14
C13—C14 NH- moiety to the -C8
NH- moiety to the -C8 C9-fragment (in S1-Rh). Further excited-state evolution leads to a complete translocation of the charge that in Rh-CI90° is fully localized on the -C6—C7
C9-fragment (in S1-Rh). Further excited-state evolution leads to a complete translocation of the charge that in Rh-CI90° is fully localized on the -C6—C7 C8—C9
C8—C9 C10- moiety (this assumes an electronic and geometrical structure very close to that of a pentadienyl cation). S1 → S0 decay immediately restores the original S0 charge distribution. In fact, the change in wavefunction at Rh-CI90° prompts a substantially complete charge transfer to the
C10- moiety (this assumes an electronic and geometrical structure very close to that of a pentadienyl cation). S1 → S0 decay immediately restores the original S0 charge distribution. In fact, the change in wavefunction at Rh-CI90° prompts a substantially complete charge transfer to the  C13—C14
C13—C14 NH- moiety. (This moiety acquires a radical cation character whereas the -C6—C7
NH- moiety. (This moiety acquires a radical cation character whereas the -C6—C7 C8—C9
C8—C9 C10- moiety becomes a pentadienyl radical.) The reconstituted charge distribution is then maintained during the structural relaxation to S0-I.
C10- moiety becomes a pentadienyl radical.) The reconstituted charge distribution is then maintained during the structural relaxation to S0-I.
Fig. 6.
Ground-state (open bars) and excited-state (filled bars) Mulliken charges along the backbone (charges of the hydrogen atoms and the alkyl substituents are summed to that of the C atom) of different points of the reaction coordinate of Rh.
Inspection of Fig. 6 demonstrates that the charge distribution of S0-Rh and S0-I are substantially identical. On the other hand, inspection of the relevant geometrical parameters in Figs. 1 and 4 shows that the distance and relative orientation between the locus of the positive charge (i.e., of the –N-C14—C13—C12- moiety) and the Glu-113 carboxylate are basically unchanged in S0-Rh and S0-I. This finding leads to the conclusion that the photon energy storage mechanism in Rh cannot be based on a change of the electrostatic interaction of the chromophore with its protein/counterion environment. This idea is supported by a decomposition of the 26 kcal·mol-1 stored photon energy in terms of (i) the change in the electrostatic interaction between the chromophore and the protein cavity (including the Glu-113 counterion), (ii) steric (nonbonding) interaction between the chromophore and the protein cavity, and (iii) chromophore strain (including bond, angle, and torsional strain). The result indicates that the change in electrostatic interaction contributes for only 6.1 kcal·mol-1. On the other hand, the change in steric interaction contributes for 6.6 kcal·mol-1. Thus, the largest amount (∼51%) of the stored photon energy must “reside” in the highly strained chromophore of bathoRh (i.e., in the S0-I structure). Since both the bond lengths and angles appear to have values close to the (S0-Rh) equilibrium structure, the strain must be related to the distorted π system of the (all-trans) S0-I chromophore. In other words, we conclude that the photon energy is stored mainly in terms of torsional (i.e., Pitzer) strain. Similar conclusions have been reported by Rohrig et al. (43), who used a restricted open-shell Kohn–Sham and density functional theory computations.
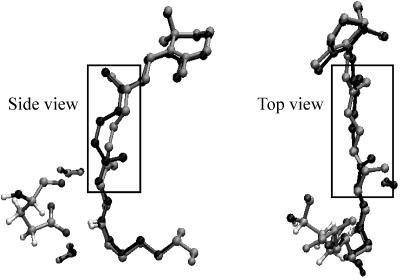
The fact that only 6.6 kcal·mol-1 are attributed to the increased steric (nonbonding) interaction between the chromophore and the protein cavity in S0-I is consistent with the idea that the photoisomerization of PSB11 occurs with only little displacement/reorientation of the retinal backbone. To better understand the structural nature of such “space-saving” displacement, we show in Fig. 7 a superposition of the S0-Rh and S0-I chromophore frameworks. It can be seen that the position of the β-ionone ring and that of the protonated Schiff base region remain substantially unchanged (including the integrity of the Glu-113-chromophore salt bridge). This finding is consistent with the fact that the β-ionone ring is hosted in a tight protein pocket (mainly formed by Thr-265, Phe-212, and Glu-122) and that the acidic hydrogen of the Schiff base is hydrogen-bounded to the Glu-113 counterion. This last conclusion is supported by recent time-resolved Raman measurements demonstrating that the C N bonds of Rh and bathoRh have substantially the same frequency (44). In contrast, it is the central moiety (see the framed fragment in Fig. 7) that undergoes the structural change required by the isomerization. This change, which results in a reorientation of the π-system of the C11
N bonds of Rh and bathoRh have substantially the same frequency (44). In contrast, it is the central moiety (see the framed fragment in Fig. 7) that undergoes the structural change required by the isomerization. This change, which results in a reorientation of the π-system of the C11 C12 bond on a plane orthogonal to the original one (see the side view in Fig. 7), involves (mainly) the auxiliary twisting of the C13
C12 bond on a plane orthogonal to the original one (see the side view in Fig. 7), involves (mainly) the auxiliary twisting of the C13 C14 bond. Such deformation can be described more accurately in terms of a clockwise change in the C10—C11—C12—C13 dihedral angle coupled to a much more limited counterclockwise change in the C12—C13—C14—C15 dihedral, yielding a kind of asynchronous bicycle-pedaling motion. Accordingly, although this motion allows for an effective space-saving coordinate, only the isomerization of the C11—C12 double bond is actually achieved in bathoRh.
C14 bond. Such deformation can be described more accurately in terms of a clockwise change in the C10—C11—C12—C13 dihedral angle coupled to a much more limited counterclockwise change in the C12—C13—C14—C15 dihedral, yielding a kind of asynchronous bicycle-pedaling motion. Accordingly, although this motion allows for an effective space-saving coordinate, only the isomerization of the C11—C12 double bond is actually achieved in bathoRh.
Fig. 7.
The gray and black frameworks correspond to S0-Rh and S0-I retinal, respectively. The structure on the left corresponds to the frozen Glu-113 counterion. The frame indicates the position of the central  C9H—C10H
C9H—C10H C11H
C11H C12H—C13H
C12H—C13H C14H- moiety.
C14H- moiety.
Supplementary Material
Acknowledgments
We thank A. Warshel for valuable comments and Consorzio Interuniversitario per il Calcolo Automatico dell' Italia Nord Orientale and Consorzio Interuniversitario Nazionale per la Scienza e Tecnologia dei Materiali for granted calculation time. Funds have been provided by the Università di Siena (Progetto di Ateneo 04/06) and the Human Frontier Science Program (Grant RG 0229/2000-M). N.F. and T.A. are grateful for Marie Curie Fellowships HPMF-CT-2001-01769 and HPMF-CT-2002-01769, respectively.
Author contributions: T.A., N.F., and M.O. designed research; T.A. and N.F. performed research; T.A., N.F., and M.O. analyzed data; and M.O. wrote the paper.
Abbreviations: CASSCF, complete active space self-consistent field; Rh, rhodopsin; bathoRh, bathorhodopsin; bR, bacteriorhodopsin; QM, quantum mechanics; MM, molecular mechanics; CASPT2, multiconfigurational second order perturbation theory.
Footnotes
Because it is currently impossible to run frequency calculations for the full protein, the excited-state energy minimum has been assigned only on the basis of its stability with respect to different geometry optimization attempts after distorting the located molecular structure.
The optimization of S1-Rh has been carried out with the loose criteria indicated in Methodology. Therefore, this structure is better described as a representative of a flat region of the S1 energy surface. The evaluation of the barrier restraining the evolution of S1-Rh out of this region requires the computation of the excited-state isomerization path.
References
- 1.Mathies, R. A. & Lugtenburg, J. (2000) in Handbook of Biological Physics, eds. Stavenga, D. G., de Grip, W. J. & Pugh, E. N. (Elsevier, Amsterdam), Vol. 3, pp. 55–90. [Google Scholar]
- 2.Kandori, H., Schichida, Y. & Yoshisawa, T. (2001) Biochemistry (Moscow) 66, 1197–1209. [DOI] [PubMed] [Google Scholar]
- 3.Santarsiero, B. D. & James, M. N. G. (1990) J. Am. Chem. Soc. 112, 9416–9418. [Google Scholar]
- 4.Teller, D. C., Okada, T., Behnke, C. A., Palczewski, K. & Stenkamp, R. E. (2001) Biochemistry 40, 7761–7772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Freedman, K. A. & Becker, R. S. (1986) J. Am. Chem. Soc. 108, 1245–1251. [Google Scholar]
- 6.Kochendoerfer, G. G. & Mathies, R. A. (1996) J. Phys. Chem. 100, 14526–14532. [Google Scholar]
- 7.Kandori, H., Katsuta, Y., Ito, M. & Sasabe, H. (1995) J. Am. Chem. Soc. 117, 2669–2670. [Google Scholar]
- 8.Ferré, N. & Olivucci, M. (2003) J. Am. Chem. Soc. 125, 6868–6869. [DOI] [PubMed] [Google Scholar]
- 9.Rajamani, R. & Gao, J. (2002) J. Comp. Chem. 23, 96–105. [DOI] [PubMed] [Google Scholar]
- 10.Yamada, A., Kakitani, T., Yamamoto, S. & Yamato, T. (2002) Chem. Phys. Lett. 366, 670–675. [Google Scholar]
- 11.Hayashi, S., Tajkhorshid, E. & Schulten, K. (2002) Biophys. J. 83, 1281–1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hayashi, S., Tajkhorshid, E. & Schulten, K. (2003) Biophys. J. 85, 1440–1448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Singh, U. C. & Kollman, P. A. (1986) J. Comp. Chem. 7, 718–730. [Google Scholar]
- 14.Ferré, N. & Olivucci, M. (2003) J. Mol. Struct. (Theochem) 632, 71–82. [Google Scholar]
- 15.Ferré, N., Cembran, A., Garavelli, M. & Olivucci, M. (2004) Theor. Chem. Acc. 112, 335–341. [Google Scholar]
- 16.Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Zakrzewski, V. G., Montgomery, J. A., Stratmann, R. E., Burant, J. C., et al. (1998) gaussian 98 (Gaussian, Pittsburgh).
- 17.Ponder, J. W. & Richards, F. M. (1987) J. Comp. Chem. 8, 1016–1024. [Google Scholar]
- 18.Fahmy, K., Jager, F., Beck, M., Zvyaga, T. A., Sakmar, T. P. & Siebert, F. (1993) Proc. Natl. Acad. Sci. USA 90, 10206–10210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Andersson, K., Blomberg, M. R. A., Fülscher, M. P., Karlstöm, G., Lundh, R., Malmqvist, P.-A., Neogrády, P., Olsen, J., Roos, B. O., Sadlej, A. J., et al. (2002) molcas (Lund University, Lund, Sweden), Version 5.5.
- 20.Besler, B., Merz, K. & Kollman, P. (1985) J. Comp. Chem. 11, 431–439. [Google Scholar]
- 21.Bayly, C. I., Cieplak P., Cornell, W. D. & Kollman, P. A. (1993) J. Phys. Chem. 97, 10269–10280. [Google Scholar]
- 22.Verdegem, P. J. E., Bovee-Geurts, P. H. M., De-Grip, W. J., Lugtenburg, J. & De-Groot, H. J. M. (1999) Biochemistry 38, 11316–11324. [DOI] [PubMed] [Google Scholar]
- 23.Salgado, G. F. J., Struts, A. V., Tanaka, K., Fujioka, N., Nakanishi, K. & Brown, M. F. (2004) Biochemistry 43, 12819–12828. [DOI] [PubMed] [Google Scholar]
- 24.Sughihara, M., Buss, V., Entel, P., Elstner, M. & Frauenheim, T. (2002) Biochemistry 41, 15259–15266. [DOI] [PubMed] [Google Scholar]
- 25.Gonzalez-Luque, R., Garavelli, M., Bernardi, F., Merchan, M., Robb, M. A. & Olivucci, M. (2000) Proc. Natl. Acad. Sci. USA 97, 9379–9384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhong, Q., Ruhman, S. & Ottolenghi, M. (1996) J. Am. Chem. Soc. 118, 12828–12829. [Google Scholar]
- 27.Schenkl, S., Portuondo, E., Zgrablic, G., Chergui, M., Haacke, S., Friedman, N. & Sheves, M. (2002) Phys. Chem. Chem. Phys. 4, 5020–5024. [Google Scholar]
- 28.Bonačić-Koutecký, V., Schöffel, K. J. & Michl, J. (1987) Theor. Chim. Acta 72, 459–474. [Google Scholar]
- 29.Bonačić-Koutecký, V., Köhler, K. & Michl, J. (1984) Chem. Phys. Lett. 104, 440–443. [Google Scholar]
- 30.Garavelli, M., Vreven, T., Celani, P., Bernardi, F., Robb, M. A. & Olivucci, M. (1998) J. Am. Chem. Soc. 120, 1285–1288. [Google Scholar]
- 31.Sugihara, M., Buss V., Entel, P. & Hafner J. (2004) J. Phys. Chem. B 108, 3673–3680. [Google Scholar]
- 32.Sheves, M., Nakanishi, K. & Honig, B. J. (1979) J. Am. Chem. Soc. 101, 7086–7088. [Google Scholar]
- 33.Migani, A., Sinicropi, A., Ferré, N., Cembran, A., Garavelli, M. & Olivucci M. (2004) Faraday Discuss. 127, 179–191. [DOI] [PubMed] [Google Scholar]
- 34.Warshel, A. (1976) Nature 260, 679–683. [DOI] [PubMed] [Google Scholar]
- 35.Liu, R. S. H. & Asato, A. E. (1985) Proc. Natl. Acad. Sci. USA 82, 259–263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schick, G. A., Cooper, T. M., Holloway, R. A., Murray, L. P. & Birge, R. R. (1987) Biochemistry 26, 2556–2562. [DOI] [PubMed] [Google Scholar]
- 37.Gascon, J. A. & Batista, V. S. (2004) Biophys. J., 87, 2931–2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sugihara, M., Buss, V., Entel, P., Hafner, L., Elstnere, M. & Frauenheim, T. (2004) Phase Trans., 77, 31–45. [Google Scholar]
- 39.Kandori, H., Matuoka, S., Shichida, Y. & Yoshizawa, T. (1989) Photochem. Photobiol. 49, 181–184. [DOI] [PubMed] [Google Scholar]
- 40.Kim, J. E. & Mathies, R. A. (2002) J. Phys. Chem. A 106, 8508–8515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yan, M., Manor, D., Weng, G., Chao, H., Rothberg, L., Jedju, T. M., Alfano, R. R. & Callender, R., H. (1991) Proc. Natl. Acad. Sci. USA 88, 9809–9812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jager, F., Lou, J., Nakanishi, K., Ujj, L. & Atkinson, G. H. (1998) J. Am. Chem. Soc. 120, 3739–3747. [Google Scholar]
- 43.Rohrig, U. F., Guidoni, L., Laio, A., Frank, I., Rothlisberger, U. (2004) J. Am. Chem. Soc. 126, 15328–15329. [DOI] [PubMed] [Google Scholar]
- 44.Pan, D., Ganim, Z., Kim, J. E., Verhoeven, M. A., Lugtenburg, J. & Mathies, R. A. (2002) J. Am. Chem. Soc. 124, 4857–4864. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.