Abstract
Odor recognition encompasses both clustering and fine discrimination. Clustering joins together sets of odors, and fine discrimination distinguishes between odors belonging to the same cluster. We hypothesize that these two aspects of odor recognition are encoded in parallel by two brain areas of the insect olfactory system. Population activity of neurons in the lateral horn encodes the odor cluster, and population activity of neurons in the mushroom body encodes the fine identity of the odor. Our mechanism is based on the hypothesis that the underlying network of the insect olfactory system consists of a repetitive, hard-wired substructure whose anatomy we describe. We show that these suggested mechanisms and circuitry explain not only the observed numbers and connections of neurons in the system, but also the observed activity of these neurons, and why oscillations are critical for fine discrimination but not for clustering of odors.
Keywords: antennal lobe, lateral horn, mushroom body, olfaction, oscillation
The antennal lobe (AL), the first relay of the insect olfactory system, is a network of excitatory projection neurons (PNs) and inhibitory local neurons (1), which generates odor-evoked oscillatory firing. The oscillations have been found in various species and are believed to be a general phenomenon (see, for example, refs. 2 and 3). Stopfer et al. (3) showed that honey bees can distinguish between two chemically dissimilar odors even when these oscillations are blocked by applying picrotoxin onto the AL. In this case however, the honey bees could not distinguish between two chemically similar odors (for details, see ref. 3). This finding supports the idea that the insect brain is capable of both clustering and fine discrimination of odors, and that these two aspects of odor recognition are achieved by different underlying mechanisms.
Another indication of the existence of two separate mechanisms comes from the anatomy of the insect olfactory system. The PNs of the first relay extend their axons into two distinct regions in the insect brain, the lateral horn (LH) and the mushroom body (MB) (4, 5), suggesting the existence of two pathways. In Drosophila, the connectivity between the MB and LH to higher brain regions was further mapped (6), and it was found that they are connected to different regions and thus form distinct parallel pathways. Moreover, it was shown that, in Drosophila, when the MB is completely abolished, some odor recognition abilities are maintained (7-9), suggesting that the LH and MB are involved in different aspects of odor recognition.
A mechanism that was suggested for coding fine identity of odors in the locust (10-14) is based on the slow patterning seen in the firing activity of PNs when odor is presented (1). Accordingly, each odor generates a unique spatiotemporal firing activity in the PNs. Moreover, these firing activities have a tendency to decorrelate in time, so that even two similar odors that initially generate a similar response in the PNs drift apart over time, generating a less similar response (15), and thus enhancing the differences between them. This slow patterning activity of the PNs is read by the Kenyon cells (KCs), a group of neurons in the MB that act as coincidence detectors. Each KC in the locust is connected to ≈10 PNs (2, 5) and, at each cycle of the underlying oscillations, detects the coactivity of these PNs (5). Consequently, the cycle-by-cycle activity of the KCs encodes the fine identity of the odor. In line with this suggested mechanism, we also assume that the fine identity of an odor is encoded by the KC activity.
This suggested mechanism for fine discrimination, however, poses a problem for a clustering mechanism. The decorrelation of similar odors helps to distinguish between them, but it makes their clustering harder (10). A few clustering mechanisms have been suggested to overcome this problem (see Discussion). Here, we completely bypass this problem by introducing a clustering mechanism that is parallel to the activity of the KCs and therefore does not have to deal with regrouping the encodings of the odors in the cluster. We suggest that a different group of inhibitory neurons in the LH (denoted LHIs) encodes the cluster of the odor and creates a different pathway that conveys this information to higher brain areas. As we show, this parallel mechanism also fits the known data regarding the circuitry of the insect olfactory system.
Methods
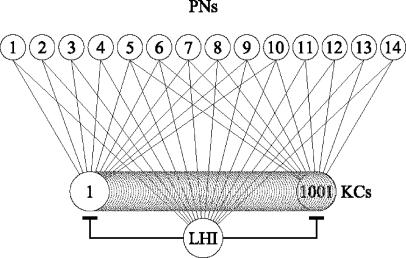
Network Simulation. The simulated network used to generate Table 1 includes 14 PNs, 1 LHI, and 1001 KCs as presented in Fig. 1. Both KCs and LHIs are modeled as “integrate-and-fire” neurons. They generate an action potential at time T when N (denoted “threshold”) excitatory inputs arrive between times T - Δt and T, where Δt = min(summation window, T - last generated action potential time). Summation window was set to be 30 ms in both KCs and LHI. The threshold N was set to be 10 in both KCs and LHI [in line with work showing that the number of simultaneous PN inputs that are required to activate a KC is around 8 (16)].
Table 1. Firing probabilities and mean firing of the LHI and KCs.
| PN inputs oscillate
|
No underlying oscillations
|
Without LHI inhibition
|
Inhibited PNs fire at 1 Hz
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| Cell type | No. of cells | Firing prob. | Mean firing | Firing prob. | Mean firing | Firing prob. | Mean firing | Mean firing | Firing prob. |
| LHI | 1 | 1.0 | 11.99 | 1.0 | 6.194 | 1.0 | 12.12 | 1.0 | 12.15 |
| 10 match KC | 66 | 0.665 | 1.514 | 0.58 | 1.398 | 0.971 | 2.936 | 0.595 | 1.436 |
| 9 match KC | 440 | 0.02 | 1.014 | 0.197 | 1.08 | 0.094 | 1.043 | 0.092 | 1.018 |
| 8 match KC | 495 | 0.001 | 1.0 | 0.048 | 1.019 | 0.004 | 1.02 | 0.074 | 1.0 |
A 1,000-ms odor presentation was simulated by activating 12 PNs and inhibiting the remaining 2 PNs. The 1,001 KCs were grouped according to the number of activated PNs connected to them. The 10 match KCs are those connected to 10 activated PNs, 9 match KCs are those connected to 9 activated PNs and one inhibited PN, and 8 match KCs are those connected to 8 activated PNs and 2 inhibited PNs. The firing probability and mean firing of the LHI and KCs occur as follows. (i) The PN input displays 20-Hz oscillations. The fact that not all 66 10 match KCs fire is not critical. Even the firing of a single KC narrows the possible combinations from 91 to 6, and the firing of 12 KCs is enough to uniquely identify the odor. (ii) The PN input is random. (iii) The KCs are not inhibited by the LHI. (iv) The PN input displays 20-Hz oscillations, and the inhibited PNs fire at 1 Hz.
Fig. 1.
The connectivity between the PNs of an average FS with its related LH inhibitory neuron and the KCs in the MB. Fourteen PNs excite a single LHI in the LH, and each combination of 10 PNs excites a different KC in the MB. The LHI inhibits the KCs.
The action potentials of the PNs that were used as the excitatory input to both the KCs and LHI were generated in the following way. First, the number of action potentials that each PN fires was determined. If a PN was activated by an odor, a random number between 16 and 20 was selected (in line with ref. 5); this number was set to 0 if the PN was inhibited. If the PN remained at its resting level, the number was taken from a normal distribution of mean = 3.87 and SD = 2.23 (5). Next, the action potentials were distributed along the 1,000-ms trial duration by using the following procedure: the 1,000-ms trial duration was binned to 50-ms bins. The bins in which an action potential was generated were then randomly chosen (except the first bin of an activated PN, in which case an action potential was always generated). At most one action potential per bin was permitted. In the underlying oscillation trials, the exact time the action potential occurred within a bin was normally distributed around the middle of the bin (SD = 10 ms), thus simulating the observed 20-Hz oscillations in the AL of the locust (2). In the nonoscillating trials, the action potential time was randomly distributed within a bin.
The LHI inhibition of the KCs was introduced in the following way. If the LHI generated an action potential at time T, PN inputs onto the KCs were ignored between times T + delay and T + delay + inhibition duration. We set delay to be 4 ms and inhibition duration to be 25 ms.
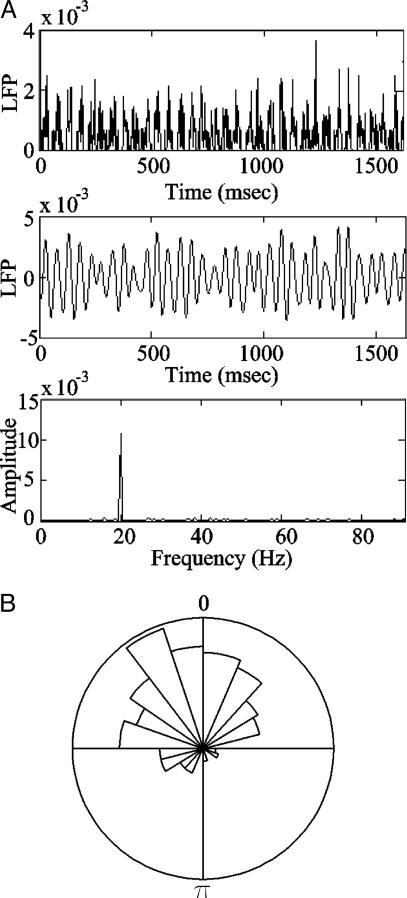
Model Local Field Potential (LFP). The model LFP seen in Fig. 3 is derived from the action potentials generated by the PNs during the simulation. Each PN action potential is assumed to travel along an axon and, at the terminal, change the fraction of open synaptic channels; the model LFP is the sum of all synaptic conductances activated by the action potentials of all PNs:
 |
1 |
Fig. 3.
Local field potentials display oscillations correlated with PN spiking. (A Top) The LFP generated from 350 action potentials of 14 PNs at the first 1,600 ms of one simulation trial (see Methods for details). (Middle) The same LFP filtered to frequencies between 5 Hz and 60 Hz. (Bottom) LFP spectrum (unfiltered but truncated at ≈95 Hz). Notice that the experimentally observed 20-Hz oscillations are reproduced. (B) The PN-LFP phase. The action potentials in the trial used to generate the LFP in A were also used here. The distribution of the action potentials along the underlying LFP cycle is similar to that of a “vigorously” activated PN in figure 1C in ref. 13.
Here gmax, the maximal conductance, is 1 μS, and the fraction of open channels, [O], is described by (17)
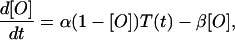 |
2 |
where α is 10 ms-1 and β is 0.16 ms-1. T(t) is described by
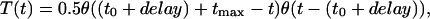 |
3 |
where θ(t) is the Heaviside (step-) function, tmax = 0.3 ms, t0 is the time of the action potential pick, and the axonal conductance, delay, is 6 ms.
PN-LFP Phase. The phase of the PN action potentials relative to the LFP (denoted PN-LFP phase) seen in Fig. 3B is calculated as follows. For each PN, P, the phase of its Nth action potential, ϕPNspike, is given by (17)
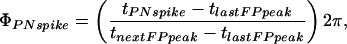 |
4 |
where tPNspike is the time the Nth action potential occurred, tnextFPpeak is the time of the LFP closest peak right after the action potential time, and tlastFPpeak is the time of the LFP closest peak just before the spike time.
Network simulation was done in Microsoft visual j#; the LFP and PN-LFP phase were done in matlab 6.5.1. All code sources are available upon request from E.S.
Results
“Functional Subsets”: A Conceptual Framework. The connectivity of the locust olfactory system presents an intriguing puzzle. There are ≈830 PNs in the AL, providing input to ≈50,000 KCs in the ipsilateral MB (18). Each KC receives input from ≈10 PNs (2, 5), and it was suggested that each KC acts as a coincidence detector for activity of these inputs (10-14). However, the number of KCs (i.e., “detectors”) is negligible compared with the number of combinations of 10 PNs, which is 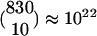 (the number of different combinations of 10 PNs one can pick from a group of 830 PNs). What is special about the few combinations of PNs that enable the KCs to encode the fine identity of the odor represented by the spatiotemporal activity of the PNs? No answer has yet been given for this question. We address it by introducing the notion of a functional subset (FS), which constrains the possible combinations of PNs. Fig. 1 depicts an example of such an FS. Each FS is associated with a unique LHI and distinct nonoverlapping subsets of PNs and KCs, as follows. (i) All of the PNs project to the associated LHI (e.g., all 14 PNs in Fig. 1). (ii) Each KC is connected to a different subset of such PNs (e.g., a different combination of 10 PNs in Fig. 1). (iii) The LHI project to all of the KCs and inhibit them (as we show below, this inhibition may be required in some species and not in others). These substructures (i.e., FSs) constrain the combinations of PNs that are being detected because a KC has input only from PNs that are part of the same FS. Also note that the FSs may differ in size. The FS connectivity is in line with known data (4-6). Moreover, the finding that PNs in Drosophila can be grouped into classes according to their morphological structure and their distinct innervations in both the LH (4) and the MB (6) suggests that these morphological classes are related to our functional subsets so that all PNs of a specific FS are part of the same morphological structure.
(the number of different combinations of 10 PNs one can pick from a group of 830 PNs). What is special about the few combinations of PNs that enable the KCs to encode the fine identity of the odor represented by the spatiotemporal activity of the PNs? No answer has yet been given for this question. We address it by introducing the notion of a functional subset (FS), which constrains the possible combinations of PNs. Fig. 1 depicts an example of such an FS. Each FS is associated with a unique LHI and distinct nonoverlapping subsets of PNs and KCs, as follows. (i) All of the PNs project to the associated LHI (e.g., all 14 PNs in Fig. 1). (ii) Each KC is connected to a different subset of such PNs (e.g., a different combination of 10 PNs in Fig. 1). (iii) The LHI project to all of the KCs and inhibit them (as we show below, this inhibition may be required in some species and not in others). These substructures (i.e., FSs) constrain the combinations of PNs that are being detected because a KC has input only from PNs that are part of the same FS. Also note that the FSs may differ in size. The FS connectivity is in line with known data (4-6). Moreover, the finding that PNs in Drosophila can be grouped into classes according to their morphological structure and their distinct innervations in both the LH (4) and the MB (6) suggests that these morphological classes are related to our functional subsets so that all PNs of a specific FS are part of the same morphological structure.
Such circuitry provides a substrate for both clustering and fine discrimination of odors. Because the LHI is connected to all of the PNs, it is insensitive to the exact subset of PNs activated by the odor. Each KC, on the other hand, is connected to a specific subset of those PNs and will thus be activated only if that subset is activated. Thus, we hypothesize that two odors are “clustered” when they activate the same subset of FSs†; and they can be “finely discriminated” when they activate different subset of PNs in at least one of those FSs. (Here, a PN is an “activated PN” if the odor presentation increases the PN firing rate; and an FS is an “activated FS” if the number of activated PNs in the FS exceeds a certain “activation threshold” such that the LHI and some of the KCs in the FS increase their firing rate too, i.e., are activated.) Accordingly, odors belonging to the same cluster will activate the same subset of FSs (and hence LHIs) and therefore will have the same cluster-identity code; because they activate different PNs within some FSs, they will activate somewhat different KCs and will thus differ in their fine identity code (see, for example, Fig. 2). Note that this definition of odor clustering does not attach any conceptual or chemical meaning to a cluster.
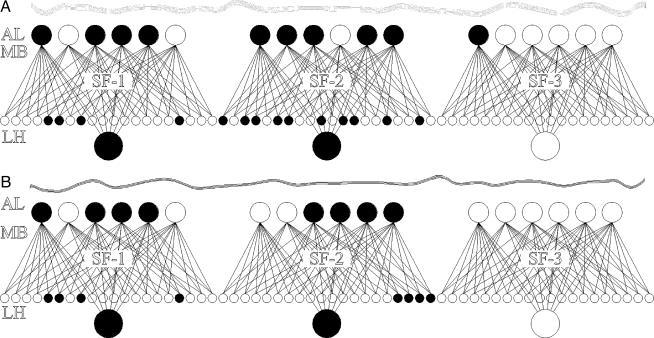
Fig. 2.
Two similar odors, A and B, are presented to a simplified olfactory system. The system consists of three identical functional subsets (FS-1, FS-2, and FS-3) where each FS contains six PNs in the AL and each combination of three PNs is connected to a different KC (giving rise to 20 KCs in the MB). In addition, all of the PNs of an FS are connected to a unique LHI in the LH. The neurons activated by the odors are filled (we assume that the threshold of the KCs and LHIs is three). In this example, both odors activate PNs in FS-1 and FS-2 and thus activate the LHIs in these FSs. Consequently, these two odors have the same clustering code. The odors differ, however, in the subset of PNs that they activate in FS-2 and therefore activate somewhat different KCs there, giving rise to a different fine identity code. (Note that the single PN activated by odor A in FS-3 is ignored.)
Size and Connectivity of Average FS Matches Locust Data. The central insight of this model is that it helps explain why oscillations might be critical in fine discrimination coding, but not in clustering coding [as seen in the honey bee experiment (3)]. We explain this idea in the context of a simulation, considering a single FS (out of all of the activated FSs). For the simulation, we will work with an “average” FS; but there is nothing in the theory that requires all of the functional subsets to be of the same size or the same connectivity. Estimates on the numbers of cells and inputs to them in the locust enable us to derive a rough average size of an FS for that insect. With ≈60 LHIs in the LH (5) and 830 PNs in the AL, on average, each one of the 60 FSs would have ≈14 (≈830/60) PNs. Based on estimates that each KC gets inputs from ≈10 PNs (2, 5) and that each combination of 10 PNs is connected to a different KC, there would be 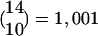 KCs in an average FS (see Fig. 1). Note that this result implies that the total number of KCs is ≈60,060, a number very close to current estimates (18). Within an FS, each PN is (on the average) a part of
KCs in an average FS (see Fig. 1). Note that this result implies that the total number of KCs is ≈60,060, a number very close to current estimates (18). Within an FS, each PN is (on the average) a part of 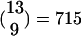 groups of 10 PNs, and hence is connected in this hypothesized circuitry to approximately that number of KCs. This result is also very close to the estimated number of 600 connections from a single PN to different KCs (18). Note that the number 600 was only a rough estimation reached by multiplying the number of synaptic varicosities per PN axon (≈30) by the number of synaptic contacts with different KC per varicosity, (≈20) (18). A 10% increase in those numbers gives the same number of connections (22 × 32.5 = 715). Thus, by using numbers of LHIs, PNs, and inputs to KCs from the literature, the hypothesis that there are FSs gives an explanation for the number of detectors (KCs) seen in the MB, i.e., what combinations of PNs are used to encode the fine identity of the odor.
groups of 10 PNs, and hence is connected in this hypothesized circuitry to approximately that number of KCs. This result is also very close to the estimated number of 600 connections from a single PN to different KCs (18). Note that the number 600 was only a rough estimation reached by multiplying the number of synaptic varicosities per PN axon (≈30) by the number of synaptic contacts with different KC per varicosity, (≈20) (18). A 10% increase in those numbers gives the same number of connections (22 × 32.5 = 715). Thus, by using numbers of LHIs, PNs, and inputs to KCs from the literature, the hypothesis that there are FSs gives an explanation for the number of detectors (KCs) seen in the MB, i.e., what combinations of PNs are used to encode the fine identity of the odor.
Effects of Oscillations on Coding: A Simulation. The central goals of the simulation were to illustrate the following. (i) When the population activity of the PNs is oscillatory and the FS is activated, KC activity can distinguish among different combinations of activated PNs. (ii) When the PN population activity is not oscillatory, the LHI of the activated FS fires; however, the KCs that are supposed to fire are silent, or are joined by other KCs so specificity is lost. Thus, the FS in question continues to play an appropriate role in cluster coding, but not in fine discrimination.
Assumptions and methods. In the simulation, we assume that the number of activated PNs in our chosen FS is 12 of its 14 PNs. (In the smaller example of Fig. 2, we activated 4 PNs of the 6 PNs in FS-1.) We also set the KCs (and LHI) threshold to be 10, assuming that a KC is to be activated only if all of the 10 PNs connected to it are activated (in line with ref. 16). These assumptions allow a single average FS to code up to 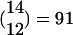 activation combinations (i.e., 91 different fine odors), where each combination consists of the activation of
activation combinations (i.e., 91 different fine odors), where each combination consists of the activation of 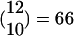 KCs. Because there are 60 independent FSs, the total number of odors that can be discriminated is 9160.
KCs. Because there are 60 independent FSs, the total number of odors that can be discriminated is 9160.
In each trial, we simulated a 1,000-ms-long presentation of the odor by setting the activity of 12 PNs (denoted “activated PNs”) to the observed firing rate of PNs activated by odors, i.e., 16-20 Hz (5), and reducing the activity of the remaining 2 PNs (denoted “inhibited neurons”) to 0. This simulation was done in two paradigms: for the “oscillatory” paradigm, the inputs to the KCs from the PNs were distributed to arrive around a specific time of a 20-Hz cycle (SD = 10 ms; see Methods for details). This distribution, which is similar to that observed experimentally in a “vigorously” activated PN (13), also gives rise to 20-Hz oscillations in the LFP (see Fig. 3). For the nonoscillatory regime, the inputs from the PNs to the KCs were spread uniformly in time and thus showed no underlying oscillations.
Fine discrimination is accomplished only in the presence of oscillations. The results of 1,000 trials are presented in Table 1. Note that, when the PN inputs are oscillatory, only a negligible number of KCs (≈2%) connected to <10 activated PNs are themselves activated (Table 1, “PN inputs oscillate”). This simulation result satisfies our first goal, because it ensures that different odors activate different subsets of KCs and, hence, fine discrimination is achieved. When oscillations are removed this specificity is lost. KCs with input from 10 activated PNs now fire at lower probability (58%) and KCs with inputs from <10 activated PNs now fire with higher probability (≈ 20% of the 440 KCs connected to only nine activated PNs and ≈5% of 495 KCs connected to only eight KCs also fire; see Table 1, “No underlying oscillations”). That outcome can explain the result of the honey bee experiment where the removal of oscillations caused the bee to lose its ability to distinguish between two similar odors (3). The crucial role of the oscillation for the activation of the KCs is that it synchronizes the PN inputs onto the KCs and thus ensures that all of them arrive in a short enough time frame so that just the correct subset of KCs is pushed over the threshold.
The LHIs are believed to play a critical role in the ability of the KCs to separate between spatially and temporally integrated inputs (5, 10). The LHI inhibits the KCs at the end of each oscillation cycle, resetting their membrane potential (5). It is believed that this membrane reset enables the KCs to separate PN inputs, arriving at different oscillation cycles (5). Indeed, it can be seen in Table 1 (“PN inputs oscillate” and “No underlying oscillations”) that KCs connected to only nine activated PNs fire at higher probability when oscillations are removed as the inhibition from the LHI is not correctly timed. Also, as can be seen in Table 1 (“Without LHI inhibition”), when we remove the LHI inhibition, KCs with only nine activated inputs also have a relatively high firing probability (≈10%). Our proposed connectivity ensures the precise timing of the input of the LHI and PNs onto the KCs, as the input to the LHI and the KCs come from the same set of PNs (see Fig. 1).
However, this LHI role of resetting the KC membrane potential becomes redundant when we considerably tighten the PN action potential distribution (SD = 2 ms; see Methods for details). Consequently, we were also able to reduce the KC and LHI summation window (from 30 ms to 8 ms) as their input arrived in a more synchronized fashion. In this case, we achieved fine discrimination (i.e., only KCs connected to 10 activated PNs fired) even without any LHI inhibition onto the KCs (data not shown). This result suggests the hypothesis that, in the locust, as the action potentials of the PNs are not finely tuned to the underlying oscillations, a longer summation window of the KCs is required (to sum the widely distributed action potentials along the cycle). Consequently, one needs the LHI inhibition to achieve cycle-by-cycle summation. Therefore, if in other species the inputs from PNs are more synchronized, the LHI inhibition might not be necessary. [This might be the case in Drosophila, where the track between LH and MB seems to be missing (6).]
One surprising result was our inability (despite a very broad search) to find a set of parameters that allows a firing frequency of 1 Hz or higher for the inhibited PNs within an activated FS, and still allow the KC population to reliably distinguish among different combinations of PNs; whenever the KCs receiving input from 10 of the activated PNs fired with high probability, the KCs receiving input from only 9 or 8 activated PNs fired with a probability of >5% [see, for example, Table 1 (“Inhibited PNs fire at 1 Hz”)]. Thus, the model suggests that the inhibited activity seen in some PNs during odor presentation (e.g., figure 2A of ref. 13) is important to ensure that only the appropriate subset of KCs within an FS is activated.
The results presented in Table 1 are in line with many experimental results. The increase in KC firing probability when LHI inhibition is removed (Table 1, “Without LHI inhibition”) was seen experimentally (5). Moreover, the experimentally observed increase in the number of spikes when LHI inhibition is removed (5) was also reproduced (Table 1, “Without LHI inhibition”). It was recently shown that, when the LFP is absent, KCs that are silent under normal conditions start to fire (14). This behavior is also consistent with our results (Table 1, “No underlying oscillations”).
Odor clustering does not require oscillations. In contrast to fine discrimination, clustering (coded by the activity of the LHIs) is almost unaffected by the removal of the underlying oscillations (only the mean firing of the LHI is reduced; compare “PN inputs oscillate” and “No underlying oscillations” in Table 1). This finding is consistent with the results of the honey bee experiments regarding the two very different odors that the bee was able to distinguish even when oscillations were removed (3). In our model, oscillations are not important for activation of the LHI because the LHI gets inputs from more PNs than do the KCs; thus, it passes the threshold even without oscillations to synchronize its inputs. Indeed, when we set the number of activated PNs to be 10 or 11 (instead of 12), which effectively lowered the number of inputs to the LHI, the LHI firing probability was reduced.
If the clustering is to be done by a population code of LHIs, it is important that they fire only when there are an adequate number of inputs from PNs. Thus, we simulated a nonactivated FS by leaving all 14 PNs at resting firing rate [3.87 ± 2.23 (5)]. In this case, the LHI (or the KCs) did not fire with or without underlying oscillations. Even when we activated up to 4 PNs (leaving the remaining 10 at resting firing rate) we got only a negligible response (<5% firing probability of the LHI and none of the KCs fired). This result may indicate that some partial activation of the PNs in a nonactivated FS may occur, but that activity is filtered out and does not affect activity in the LH or MB.
Discussion
In this article, we introduced the idea that the insect olfactory system is constructed of repetitive, hard wired substructures that we denoted functional subsets (FS, see Fig. 1). We showed that these FSs provide a substrate for mechanisms of both clustering and fine discrimination of odors. Accordingly, the LHIs that are connected to all of the PNs in their related FS are not sensitive to the exact subset of PNs activated by the odor and, therefore, code a coarse representation of the odor. Each KC, on the other hand, is connected to exactly one combination of activated PNs, and, therefore, the KC population represents the fine identity of that odor. We also showed that the known connectivity between the AL, MB, and LH of insects matches well the connectivity predicted by our model. In particular, the fact that only combinations of PNs belonging to the same FS are detected by some KC provides an explanation to the puzzle of why only a very small percentage of combinations are detected. Finally, we were able to explain why oscillations are critical for fine discrimination but are not so critical for clustering [as seen in the honey bee experiment (3)].
Our model is also consistent with the amount of spiking activity observed in the various regions of the locust olfactory system when an odor is presented. It was shown that an odor presentation can activate as many as 70% of the 830 PNs. In this case, an even higher percentage of the 60 LHIs is activated, whereas only a very small percentage (<10%) of the 50,000 KCs seemed to respond (5). To show that our model is consistent with these data, let us first calculate the number of FSs that are activated when 70% of the PNs are activated. In the following, we neglect the activated PNs in nonactivated FSs; including them requires a more complicated calculation that gives a lower estimate to the number of activated FSs and does not change the qualitative picture. Because we assumed that 12 PNs are activated in each activated FS, the number of activated FSs is ≈47[≈0.7(830/12)]. This result would also be the approximate number of LHIs (out of 60) that will fire when the odor is presented (because there is one LHI in each FS), hence predicting that almost 80% of the LHIs will be activated in this case. [Notice that, even with such a high number of activated LHIs, the number of different odor clusters that can be coded is huge, 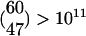 .] The number of activated KCs according to our model is also in line with the known data. It predicts that the percentage of activated KCs as a result of the odor presentation would be only ≈6% [≈66(47/50,000)], because only 66 KCs are activated in each FS. We want to emphasize, however, that our model does not imply that each odor activates 70% of the PNs nor does it imply that all odors activate the same percentage of the PNs. On the contrary, the number of FSs activated by an odor may vary, and some odors may activate only one or two FSs whereas others may activate many more.
.] The number of activated KCs according to our model is also in line with the known data. It predicts that the percentage of activated KCs as a result of the odor presentation would be only ≈6% [≈66(47/50,000)], because only 66 KCs are activated in each FS. We want to emphasize, however, that our model does not imply that each odor activates 70% of the PNs nor does it imply that all odors activate the same percentage of the PNs. On the contrary, the number of FSs activated by an odor may vary, and some odors may activate only one or two FSs whereas others may activate many more.
Although the assumption that 12 PNs are activated in each FS fits experimental data (see previous paragraph), it is not critical for the mechanisms to work; if 13 are activated by each odor, the total number of activation combinations would be 1460 (rather than 9160), which also provides more than enough odor codes. However, assuming that the number of activated PNs is 10 or 11 leads to a small number (<12) of activated KCs for each pattern and also lowers the probability of activating the LHI in the absence of oscillations (see simulation results). The assumption that the KC threshold is 10 is also not critical; however, it ensures a relatively small overlap between the activated KCs of two different odors. A combinatorial calculation (not given here) shows that, for any two odors, at most 11 KCs of their 66 activated KCs are the same. If, for example, we assume that the KC threshold is 9, the number of activated KCs would be 506 and two odors may have as many as 341 overlapping activated KCs in each FS.
More generally, we believe that our findings do not depend on any specific numbers used above; the fact that the experimental data suggest that, on average, the FS will be the one depicted in Fig. 1 does not rule out the possibility that different FSs will have different sizes. Indeed, one would expect that FSs participating in odors that are critical to the animal will differ from FSs of other odors. Also, the numbers of PNs, KCs, and LHIs differ between species, and it is highly improbable that even the averaged number of PNs within an FS or the number of FSs is retained. It would be interesting, however, to see whether the connectivity between the AL, LH, and MB is consistent with the existence of FSs in other species as well.
We suggest that the population activity of the KCs encodes the fine identity of an odor, and we claim that the FSs provide the infrastructure that enables the KCs to do so. As such, our model is in full compliance with the already suggested mechanism that is based on the spatiotemporal activity of the PNs (10-14). In particular, a recent article by Stopfer et al. (13) showed that the evolving slow pattern activity of the PNs in the AL (19) contains enough information to discriminate between various odor intensities. Moreover, they found (using clustering techniques) that the evolving slow patterning activity generated by different intensities of the same odor is similar (or at least more similar than slow patterning activity of two different odors). In line with this finding, our theory indeed suggests that different (but similar) intensities of the same odor belong to the same cluster (i.e., they activate the same subset of FSs). Within each FS, both the exact PNs and their slow patterning are different for different intensities. Nevertheless, because different odor intensities will activate a relatively large number of shared PNs, their overall activity will be similar.
It is not known what odor features are encoded by the spatiotemporal activity of the PNs; we believe that it includes not only its molecular structure and concentration (13), but also time-related aspects like onset, offset, concentration change, duration, and direction change. We further speculate that the slow patterning seen in the PNs activity (19) is a result of these time-related features that change along the odor presentation, and not the molecular structure of the odor that is encoded by the population activity of the PNs. Supporting evidence is the finding that a single cycle during the odor presentation can contain enough information to identify both the molecular structure and the intensity of the odor (figure 6 of ref. 13). Thus, the slow patterning in the activity of the PNs does not add information regarding the molecular structure (and concentration) of the odor. Also, these temporal features probably do not affect the clustering of an odor; we thus predict that slow patterning will not affect the activity of the LHIs, which, according to our model, encode the odor cluster.
Our mechanism for clustering of odors bypasses two problems that were encountered by other suggested mechanisms. We denote the first problem “the sequential problem”: i.e., the declustering of similar odors enables downstream regions to uniquely identify each odor. But such declustering makes odor grouping difficult. The more different they are, the harder it is to group them. A few mechanisms have been suggested to overcome this problem. (i) Clustering is a high level learned ability that groups arbitrary odors according to the animal experience and is done somewhere downstream. (ii) As two similar odors initially generate somewhat similar activity in the PNs (15), this initial activity is used to define the cluster. (iii) Although the activity of the PNs decorrelates in time, the differences between different concentrations of the same odor are smaller than the difference between different odors (13), and thus a grouping of all these not so different representations can be made downstream. Our suggested mechanism solves this problem by introducing a parallel pathway for the coding of the odor cluster, a pathway that was found to exist anatomically in the Drosophila. Furthermore, some evidence shows that this parallel pathway is capable of doing coarse odor recognition (6-9). The second problem our mechanism bypasses is that it is not yet known the principles by which odors are joined in a cluster. Does it relate to meanings of odors in addition to molecular structure? We bypassed this problem by providing a precise definition of a cluster based on the subset of FSs it activates; i.e., two odors belong to the same cluster if they activate the same set of FSs.
The basic connectivity suggested here does not take into account any interaction between the various FSs. Such connectivity probably exists, because the oscillations in the local field potential recorded in the MB indicate that the activity of the PNs (and the LHIs) oscillates synchronously (2). This synchrony is probably achieved by cross-FS connectivity by means of the LNs in the AL. It was shown that LNs are critical for the generation of the LFP (19) and that their processes extend across a huge percentage of the AL (1); thus, they probably inhibit PNs of different FSs. This cross-FS synchrony is also consistent with our suggested mechanism, because it synchronizes the activity of LHIs and KCs of all FSs, and thus facilitates the readout of the cluster and fine coding by higher brain regions. Cleland and Linster (20) suggest a related idea for the honey bee olfactory system: higher concentration of odorants may lead, by means of network interactions, to higher amplitude oscillations, which then lead to more synchrony and hence a better readout. Other cross-FS connectivity may also exist although no connections are currently known among the KCs in the MB (19).
A completely random network can also account for fine discrimination. However, in a mechanism built on top of such a network, the size of the population of KCs that is activated by an odor depends exponentially on the size of the population of PNs activated by the odor. For example, if an odor activates 70% of the PNs and the KC threshold is still 10, in a random network the probability of a KC to be activated is 0.710 ≈ 0.028 (i.e., on average, ≈1,400 KCs will be activated). If the odor, however, activates “only” 50% of the PNs (rather than 70%), the probability of activating a KC drops to 0.510 ≈ 0.001 (i.e., on average, ≈50 KCs will be activated). This feature of the random model not only suggests that a high percentage of the PNs should respond to any odor (at any concentration), it also poses a challenge to higher brain regions that are to read this encoding (having to deal with codes of sizes different in orders of magnitude). In our model, on the other hand, the ratio between the number of activated PNs and the number of activated KCs is fixed (i.e., 12/66).
Our hypothesis may be tested by extending to other species the following two types of experiments: (i) the experiments in the locust where the number of neurons in each group (PNs, KCs, and LHIs) together with the number of connections between them were counted (2, 5, 18) and (ii) the experiments in Drosophila where the overall axons tracks were mapped (of these groups of neurons as well as higher brain regions) (4, 6). We predict that evidence for the repetitive substructure hypothesized here will be found.
Acknowledgments
We thank Leslie M. Kay, Mark Stopfer, Henry Greenside, Matt Wachowiak, and Gilles Laurent for discussions and comments. This work was supported by Burroughs Wellcome Fund Award 1001749 and by National Institutes of Health Grant 1 R01 NS46058.
Author contributions: E.S. and N.K. designed research; E.S. performed research; E.S. contributed new reagents/analytic tools; E.S. and N.K. analyzed data; and E.S. and N.K. wrote the paper.
Abbreviations: MB, mushroom body; KC, Kenyon cells; LH, lateral horn; LHI, LH inhibitory neuron; AL, antennal lobe; PN, projection neuron; FS, functional subset; LFP, local field potential.
See Commentary on page 17569.
Footnotes
One can relax this definition by defining two odors to be clustered if the subset of FSs activated by one odor is contained in the subset of FSs activated by the other.
References
- 1.Laurent, G. (1996) Trends Neurosci. 19, 489-496. [DOI] [PubMed] [Google Scholar]
- 2.Laurent G. & Naraghi, M. (1994) J. Neurosci. 14, 2993-3004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Stopfer, M., Bhagavan, S., Smith, B. & Laurent, G. (1997) Nature 390, 70-74. [DOI] [PubMed] [Google Scholar]
- 4.Marin, E. C., Jefferis, G. S., Komiyama, T., Zhu, H. & Luo, L. (2000) Cell 109(2), 243-255. [DOI] [PubMed] [Google Scholar]
- 5.Perez-Orive, J., Mazor, O., Turner, G. C., Cassenaer, S., Wilson, R. I. & Laurent, G. (2002) Science 297, 359-365. [DOI] [PubMed] [Google Scholar]
- 6.Tanaka, N. K., Awasaki, T., Shimada, T. & Ito K. (2004) Curr. Biol. 14, 449-457. [DOI] [PubMed] [Google Scholar]
- 7.de Belle, J. S. & Heisenberg, M. (1994) Science 263, 692-695. [DOI] [PubMed] [Google Scholar]
- 8.Heimbeck, G., Bugnon, V., Gendre, N., Keller, A. & Stocker, R. F. (2001) Proc. Natl. Acad. Sci. USA 98, 15336-15341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kido, A. & Ito K. (2002) J. Neurobiol. 52, 302-311. [DOI] [PubMed] [Google Scholar]
- 10.Laurent, G. (2002) Nat. Rev. Neurosci. 3, 884-895. [DOI] [PubMed] [Google Scholar]
- 11.Laurent, G., Stopfer, M., Friedrich, R. W., Rabinovich, M. I., Volkovskii, A. & Abarbanel, H. D. (2001) Annu. Rev. Neurosci. 24, 263-297. [DOI] [PubMed] [Google Scholar]
- 12.Rabinovich, M., Volkovskii, A., Lecanda, P., Huerta, R., Abarbanel, H. D. & Laurent, G. (2001) Phys. Rev. Lett. 87, 068102. [DOI] [PubMed] [Google Scholar]
- 13.Stopfer, M., Jayaraman, V. & Laurent, G. (2003) Neuron 39, 991-1004. [DOI] [PubMed] [Google Scholar]
- 14.Perez-Orive, J., Bazhenov, M. & Laurent, G. (2004) J. Neurosci. 24, 6037-6047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Friedrich, R. W. & Laurent, G. (2001) Science 291, 889-894. [DOI] [PubMed] [Google Scholar]
- 16.Bäcker, A. (2002). Ph.D. thesis (California Institute of Technology, Pasadena).
- 17.Bazhenov, M., Stopfer, M., Rabinovich, M., Huerta, R., Abarbanel, H. D. I., Sejnowski, T. J. & Laurent, G. (2001) Neuron 30, 553-567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Leitch, B. & Laurent G. (1996) J. Comp. Neurol. 372, 487-514. [DOI] [PubMed] [Google Scholar]
- 19.Wehr, M. & Laurent, G. (1996) Nature 384, 162-166. [DOI] [PubMed] [Google Scholar]
- 20.Cleland, T. A. & Linster, C. (2002) Behav. Neurosci. 116, 212-221. [DOI] [PubMed] [Google Scholar]