How attention influences perceptual decision making: Single-trial EEG correlates of drift-diffusion model parameters

Abstract

Perceptual decision making can be accounted for by drift-diffusion models, a class of decision-making models that assume a stochastic accumulation of evidence on each trial. Fitting response time and accuracy to a drift-diffusion model produces evidence accumulation rate and non-decision time parameter estimates that reflect cognitive processes. Our goal is to elucidate the effect of attention on visual decision making. In this study, we show that measures of attention obtained from simultaneous EEG recordings can explain per-trial evidence accumulation rates and perceptual preprocessing times during a visual decision making task. Models assuming linear relationships between diffusion model parameters and EEG measures as external inputs were fit in a single step in a hierarchical Bayesian framework. The EEG measures were features of the evoked potential (EP) to the onset of a masking noise and the onset of a task-relevant signal stimulus. Single-trial evoked EEG responses, P200s to the onsets of visual noise and N200s to the onsets of visual signal, explain single-trial evidence accumulation and preprocessing times. Within-trial evidence accumulation variance was not found to be influenced by attention to the signal or noise. Single-trial measures of attention lead to better out-of-sample predictions of accuracy and correct reaction time distributions for individual subjects.

1. Introduction

There are many situations on the road when the driver of a vehicle must decide to stop or accelerate through an intersection by observing a traffic light. The presence of a green arrow for an adjacent lane (i.e. the distractor or “noise”) can be distracting for the driver whose light is red (i.e. the “signal”). The presence of the distractor affects the reaction time and choice of the driver. However the driver can suppress their attention to the green arrow and/or attend to the correct red light in their lane. The decision to stop or accelerate is an example of a perceptual decision. Perceptual decision making is the process of making quick decisions based on objects’ features observed with the senses. As shown in the stoplight example, attention is highly influential in the perceptual decision making process. When distracting objects exist in visual space, one must attend only to the relevant objects and actively ignore distracting objects. Each time an individual reaches a stop light, they will be more likely to make a safer decision if they suppress distracting visual input and enhance relevant visual input.

The goal of this study was to evaluate whether attention could predict different components of the decision making process on each trial of a visual discrimination experiment. We make use of high-density electroencephalographic (EEG) recordings from the human scalp to find single-trial evoked potentials (EPs) to the onset of visual signal and to the onset of a distractor (mask) to measure the deployment of attention to task-relevant features. We found that on each trial, modulations of the evoked potentials by attention were predictive of specific components of a drift-diffusion model of the decision making process.

1.1. Visual attention and decision making

Attention is beneficial for decision making because relevant features of the environment can be preferentially processed to enhance the quality of evidence. During visual tasks individuals may deploy different attention strategies such as: enhancing the signal, suppressing external noise (distractors), or suppressing internal noise (Lu and Dosher, 1998; Dosher and Lu, 2000). These strategies are thought to change based on the signal to noise ratio of the stimulus, such that individuals will enhance sensory gain to both signal and noise during periods of low noise and sharpen attention to only signal during periods of high noise (Lu and Dosher, 1998), although specific strategies have been shown to differ across subjects (Bridwell et al., 2013; Krishnan et al., 2013; Nunez et al., 2015). Multiple groups have proposed models of visual attention and decision making that yield diverse reaction time and choice distributions dependent upon attentional load (Spieler et al., 2000; Smith and Ratcliff, 2009). Attention can be deployed to the features and/or location of a stimulus, and attention can benefit decision making when the subject is cued to the location or features of the stimulus (Eriksen and Hoffman, 1972; Shaw and Shaw, 1977; Davis and Graham, 1981).

Event-related potentials (ERPs) are trial-averaged EEG responses to external stimuli. Visual ERPs (also labeled Visual Evoked Potentials; VEPs) have been shown to track visual attention to the onset of stimuli (Harter and Aine, 1984; Luck et al., 2000). That is, amplitudes of the peaks of the ERP waveform (i.e., ERP “components”) within certain millisecond-scale time windows are shown to be larger when subjects encounter task-relevant stimuli in the expected location in visual space. Two components of particular interest are the N1 (or N200) and P2 (or P200) components. The terms N1 and P2 refer the order of negative and positive peaks in the time series respectively, and the more general alternative names N200 and P200 refer to their approximate latencies in milliseconds. Changes in N200 latencies have been shown to correlate with attentional load (Callaway and Halliday, 1982), and N200 measures have even been used in Brain-Computer Interfaces (BCI) that make use of subjects’ attention to specific changing stimuli, such as letters in a BCI speller (Hong et al., 2009). Findings in these trial-averaged EEG (ERP) studies suggest that information is also available in single-trials of EEG that can be used to evaluate the relationship between attention and decision making. In this paper we will use the alternative names P200 and N200 because 1) the exact time windows of components vary across studies, 2) components in this study were both localized to around 200 milliseconds, and 3) components in this study were found on single-trials as opposed to in the trial-average.

1.2. Behavioral models of decision making

Drift-diffusion models are a widely-used class of models used to jointly predict subjects’ choices and reaction times (RT) during two-choice decision making (Stone, 1960; Ratcliff, 1978; Ratcliff and McKoon, 2008). “Neural” drift-diffusion models have also successfully incorporated functional magnetic resonance imaging (fMRI) and EEG recordings into hierarchical models of choice-RT (e.g. Mulder et al., 2014; Turner et al., 2015; Nunez et al., 2015). In this study, we use a hierarchical form of the diffusion model (Vandekerckhove et al., 2011), allowing variability between participants and across conditions, to predict and describe single-trial reaction times and accuracy during a visual decision making task. While other similar models of choice-RT have successfully predicted behavior during visual decision making, such as the simpler linear ballistic accumulator model (Brown and Heathcote, 2008) or a more complicated drift-diffusion model that intrinsically accounts for trial-to-trial variability in parameters within subjects (Ratcliff, 1978; Ratcliff and McKoon, 2008), we have chosen a diffusion model that allows us to test specific predictions from models of attention (i.e. Smith and Ratcliff, 2009; Lu and Dosher, 1998) while being simple-enough to fit in reasonable time periods given the hierarchical form.

In the drift-diffusion model it is assumed that subjects accumulate evidence for one choice over another (or a correct versus incorrect response, as in this study) in a random walk evidence accumulation process with an infinitesimal time step. That is, evidence E_t accumulates following a Wiener process (i.e. Brownian motion) with drift rate δ and instantaneous variance ς² (Ross, 2014) such that

$$\frac{d{E}_t}{dt}\sim \mathcal{N}(\delta ,{\varsigma }^2)$$ (1)

Thus the drift rate δ describes mean rate of evidence accumulation within a trial and the diffusion coefficient ς influences the variance of evidence accumulation within one trial, with the true variance of the current evidence at any particular time t being ς²t. A graphical representation of the diffusion model is provided in the middle panel of Figure 1.

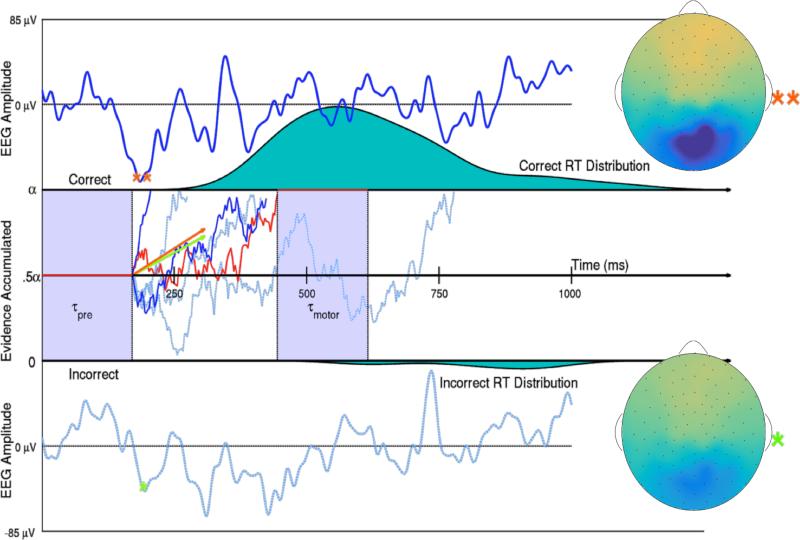
Figure 1.

Two trials of Subject 10's SVD weighted EEG (Top and Bottom with bounds −85 to 85 μV) and representations of this subject's evidence accumulation process on 6 low noise trials (Middle). Evidence for a correct response in one example trial (denoted by the red line) first remains neutral during an initial period of visual preprocessing time τ_pre. Then evidence is accumulated with an instantaneous evidence accumulation rate of mean δ (the drift rate) and standard deviation ς (the diffusion coefficient) via a Wiener process. The subject acquires either α = 1 evidence unit or 0 evidence units to make a correct or incorrect decision respectively. After enough evidence is reached for either decision, motor response time τ_motor explains the remainder of that trial's observed reaction time. The 85^th and 15^th percentiles of Subject 10's single-trial drift rates δ_i,10,1 in the low noise condition are shown as orange and green vectors, such that it would take 253 and 299 ms respectively to accumulate the .5 evidence accumulation units need to make a correct decision if there was no variance in the accumulation process. The larger drift rate is a linear function of the larger single-trial N200 amplitude (**), while the smaller drift rate is a linear function of the smaller N200 amplitude (*). The scalp activation (SVD weights multiplied by one trial's N200 amplitude) of this subject's response to the visual signal ranges from −13 to 13 μV on both trials. The two dark blue and red evidence time courses were randomly generated trials with the larger drift rate. The three dotted, light blue evidence time courses were randomly generated trials with the smaller drift rate. True Wiener processes with drifts δ_i,10,1 and diffusion coefficient ς_10,1 were estimated using a simple numerical technique discussed in Brown et al. (2006).

A few other parameters describe a diffusion model. The boundary separation α is equal to the amount of relative evidence required to make choice A over choice B (or make a correct decision over an incorrect decision), and the boundary separation has been shown to be manipulated by speed vs. accuracy strategy trade-offs (Voss et al., 2004). The parameter that encodes the starting position of evidence β reflects the bias towards one choice or another (equal to .5 when modeling correct versus incorrect choices as in this study). The non-decision time τ is equal to the amount of time within the reaction time of each trial that is not dedicated to the decision making process. Typically non-decision time is assumed to be equal to the sum of preprocessing time before the evidence accumulation process and motor response time after a decision has been reached. The relative contribution of these two non-decision times is not identifiable from behavior alone and therefore is rarely explicitly modeled.

All three of the parameters related to evidence accumulation are not identifiable with behavioral data alone (i.e. drift rate δ, the diffusion coefficient ς, and the boundary separation a). Only two of the three parameters can be assumed to vary across subjects and trials (e.g. multiplying ς by two and dividing both a and δ by two would result in the same fit of choice-RT) (Ratcliff and McKoon, 2008; Wabersich and Vandekerckhove, 2014). Previous studies have typically chosen to fix the diffusion coefficient ς to 1 or 0.1 (Vandekerckhove et al., 2011; Wabersich and Vandekerckhove, 2014). However due to the predictions made by Dosher and Lu (2000), in that internal noise is suppressed by attention to the signal, we choose to leave ς to vary. The boundary separation α was fixed at 1 for all trials and subjects. Our primary analysis focused on the trial-to-trial variability in the evidence accumulation process due to fluctuations in attention from trial-to-trial within individuals. Although trial-to-trial speed-accuracy trade-offs can be experimentally introduced to find neural correlates of the boundary separation (e.g. van Maanen et al., 2011) or may exist due to per-trial performance feedback (Dutilh et al., 2012), we have no reason to believe that the boundary separation will vary considerably from trial-to-trial within a subject due to changes in attention. Moreover, all subjects were given the same accuracy instruction to maintain similar accuracy vs. speed trade-offs across subjects.

1.3. Single-trial EEG measures of attention

EEG correlates of attention and decision making have been found using classification methods. One group has shown that the amplitude of certain EEG components in the time domain track type and duration of two-alternative forced choice responses and then showed that these components’ amplitudes tracked evidence accumulation rate (Philiastides and Sajda, 2006; Ratcliff et al., 2009). However the EEG components in these studies were found by finding the maximum predictors of the behavioral data and thus had no a priori interpretation. Another group has found that that single-trial amplitude in a few frequency bands, especially the 4-9 Hz theta band, predicts evidence accumulation rates (van Vugt et al., 2012). However these oscillations were found using canonical correlation analysis (CCA; Calhoun et al., 2001), a data driven algorithm that found any EEG channel mixtures that contained correlations with the drift diffusion model parameters. While the results were confirmed using cross validation, the set of EEG identified by this method also did not have an a priori explanation. These studies point us in directions of exploration and perform well at prediction, but we have little information as to whether the EEG information reflected attention, the decision process itself, or some other correlate of evidence accumulation. In this study, we introduce a simple procedure that is informed by ERPs known to be related to attention, and we make use of single-trial ERP estimates to model behavior on single trials.

1.4. Hypothesized attention effects

An integrated model of visual attention, visual short term memory, and perceptual decision making by Smith and Ratcliff (2009) predicts that attention operates on the encoding of the stimulus, and that enhanced encoding increases drift rate during the decision making process. Furthermore, the model predicts that visual encoding time (i.e. visual preprocessing) will be reduced by attention which is reflected in the non-decision time parameter. However, this model of visual attention only considers the detection of a stimulus in an otherwise blank field—that is, a field with no visual noise. Thus, it does not have predictions for the distinct processes of noise suppression and signal enhancement, as in the Perceptual Template Model (Lu and Dosher, 1998). Signal enhancement during the evidence accumulation process is predicted to reduce the diffusion coefficient ς because the mechanism by which signal enhancement takes place, according to the Perceptual Template Model, is additive internal noise reduction¹ (Dosher and Lu, 2000); this mechanism is predicted to be most effective in low noise conditions since decreasing internal noise will lead to better processing of both the visual signal and external visual noise. External noise suppression, on the other hand, is expected to reflect the encoding of the stimulus by manipulation of a perceptual template, increasing the average rate of evidence accumulation δ by improving the overall quality of evidence on a trial. The Perceptual Template Model predicts this mechanism is most effective in high noise conditions.

In a previous study we showed that individual differences in noise suppression predicts individual differences in evidence accumulation rates and non-decision times (Nunez et al., 2015). We also showed that differences across individuals in signal enhancement predict individual differences in non-decision times and evidence accumulation variance (i.e. the diffusion coefficient), which we assume tracks internal noise in the subject. The findings of signal enhancement effects on evidence accumulation variance and noise suppression effects on evidence accumulation rate seem to correspond closely to predictions made by the Perceptual Template Model. However the Perceptual Template Model does not make explicit predictions about attention effects on non-decision times. The previous study did not explore how trial-to-trial variation in attention affected trial-to-trial cognitive differences. Individual differences in attention could be found that are not detected to be changing within a subject, and/or trial-to-trial variability in attention could occur that does not change across individuals. In this study, we show that within-subject, trial-to-trial variability in attention to both noise and signal predict variability in drift rate and non-decision times, corresponding closely to predictions made by the model of Smith and Ratcliff (2009) that predicts speeded encoding time and increased evidence accumulation rate due to enhanced attention. The two studies together suggest that within-trial evidence accumulation variances ς varied across individuals, but we did not find evidence that this measure varied within individuals due to changes in trial-to-trial attention.

2. Methods

2.1. Experimental stimulus: Bar field orientation task

Reported in a previous study, behavioral and EEG data were collected from a simple two-alternative forced choice task to test individual differences in attention during visual decision making (Nunez et al., 2015). Here, we reanalyze these data to explore per-trial attention effects on the decision making process. Subjects were instructed on each trial to differentiate the mean rotation of a field of small bars that were either oriented at 45 deg or 135 deg from horizontal on average. Two representative frames of the display and the time course of a trial are provided in Figure 2. The circular field of small bars was embedded in a square field of visual noise that was changing at 8 Hz. The bar field was flickering at 15 Hz. These frequencies were chosen to evoke steady-state visual evoked potentials (SSVEPs), stimulus frequency-tagged EEG responses that were useful in the previous study but will not be used in this study. Stimuli were built and displayed using the MATLAB Psychophysics toolbox (Psychtoolbox-2; www.psychtoolbox.org).

Figure 2.

The time course of one trial of the experimental stimulus. One trial consisted of the following: 1) 750 ms of fixation on a black cross on a gray screen, then 2) visual contrast noise changing at 8 Hz for 750 ms while maintaining fixation (dubbed the cue interval) and 3) a circular field of small oriented bars flickering at 15 Hz overlaid on the changing visual noise for 1000 to 2000 ms while maintaining fixation (dubbed the response interval). The subjects’ task was to indicate during the response interval whether the bars were on average oriented towards the “top-right” (45° from horizontal; as in this example) or the “top-left” (135° from horizontal). It was assumed that subjects’ decision making process occurred only during the response interval but could be influenced by both onset attention to the visual noise during the cue interval and onset attention to visual signal during the response interval.

Subjects viewed each trial of the experimental stimulus on a monitor in a dark room. Subjects sat 57 cm away from the monitor. The entire circular field of small oriented bars was 9.5 cm in diameter, corresponding to a visual angle of 9.5°. Within each trial subjects first observed a black cross for 750 ms in the center of the screen, on which they were instructed to maintain fixation throughout the trial. Subjects then observed visual noise for 750 ms. This time period of the stimulus will henceforth be referred to as cue interval, with the onset EEG response at the beginning of this interval being the response to the noise (or “distractor”) stimulus. Subjects then observed the circular field of small oriented bars overlaid on the square field of visual noise for 1000 to 2000 ms and responded during this interval. Subjects were instructed to respond as accurately as possible while providing a response during every trial. Because evidence required to make a decision only appeared during this time frame, the decision process was assumed to take place during this interval. This interval is referred to as the response interval, and attentional onset EEG measures during this time period are referred to as responses to the signal stimulus. After the response interval the fixation cross was again shown for 250 ms to alert the subjects that the trial was over and to collect any delayed responses.

Three levels of variance of bar rotation and three levels of noise luminance were used to modulate the task difficulty. However only the noise luminance manipulation is relevant for the analysis presented here. Average luminance of the noise was 50% and the luminance of the bars was 15%. In the low noise condition, that luminance was drawn randomly at each pixel from a uniform distribution of 35% to 65% luminance. In the medium and high noise conditions, noise luminance was drawn randomly at each pixel from a uniform distribution of 27.5% to 72.5% and 20% to 80% luminance respectively. Each subject experienced 180 trials from each noise condition, interleaved, for a total of 540 trials split evenly over 6 blocks. The total duration of the visual experiment for each subject was approximately one hour and 15 minutes including elective breaks between blocks. More details of the experiment can be found in our previous publication (Nunez et al., 2015).

Behavioral and EEG data were collected concurrently from 17 subjects. Subjects performed accurately during the task. The across-subject mean, standard deviation, and median of accuracy were 90.1% ± 5.8% ỹ = 91.6%, while the across-subject mean, standard deviation, and median of average reaction time were 678±106 , t̃ = 670 ms. Individual differences in behavior existed across subjects with the most accurate subject answering 98.3% of trials correctly and the least accurate subject answering 78.5% of trials correctly. Two different subjects were the fastest and slowest with mean RTs of 502 ms and 866 ms respectively.

2.2. Single-trial EEG predictors

Electroencephalograms (EEG) were recorded using Electrical Geodesics, Inc.'s high density 128-channel Geodesic Sensor Net and Advanced Neuro Technology's amplifier. Electrical activity from the scalp was recorded at a sampling rate of 1024 samples per second with an online average reference using Advanced Neuro Technology software. The EEG data was then imported into MATLAB for offline analysis. Linear trends were removed from the EEG data, and the data were band pass filtered to a 1 to 50 Hz window using a high pass Butterworth filter (1 Hz pass band with a 1 dB ripple and a 0.25 Hz stop band with 10 dB attenuation) and a low pass Butterworth filter (50 Hz pass band with 1 dB ripple and a 60 Hz stop band with 10 dB attenuation).

EEG artifact is broadly defined as data collected within EEG recordings that does not originate from the brain. Electrical artifact can be biological (e.g. from the muscles-EMG or from the arteries-EKG) or non-biological (e.g. temporary electrode dislocations, DC shifts, or 60 Hz line noise). Contribution of muscle and electrical artifact was reduced in recordings by using an extended Infomax Independent Component Analysis algorithm (ICA; Makeig et al., 1996; Lee et al., 1999). ICA algorithms are used to find linear mixtures of EEG data that relate to specific artifact. Components that are indicative of artifact typically have high spatial frequency scalp topographies, high temporal frequency or a ¹/_f frequency falloff, and are present either in only a few trials or intermittently throughout the recording. These properties are not shared by electrical signals from the brain as recorded on the scalp (Nunez and Srinivasan, 2006). Using these metrics, components manually deemed to reflect artifact were projected into EEG space and subtracted from the raw data. Components deemed to be a mixture of artifact and brain activity were kept. More information about using ICA to reduce the contribution of artifact can be found in Jung et al. (2000).

Event-related potential (ERP) components have been shown to index attention (Callaway and Halliday, 1982; Harter and Aine, 1984; Luck et al., 2000), in particular the P200 and N200 latencies and amplitudes, and these values were used as independent measures of attention in the following analyses. Event-related potentials (ERPs) are EEG responses that are time-locked to a stimulus onset and are typically estimated by aligning and averaging EEG responses across trials. They usually cannot be directly measured on each trial from single electrodes. Raw EEG signals could be used as a single-trial measures but typically have very low signal-to-noise ratios (SNR) for task-specific brain responses. Since the goal of this analysis was to explore single-trial effects of attention on visual decision making, a single-trial estimate of the ERP was developed.

Because the signal-to-noise ratio (SNR) in ongoing EEG increases when adjacent electrodes of relevant activity are summed (Parra et al., 2005), we anticipated that the SNR of the response to the visual stimulus would be boosted on individual trials by summing over the mixture of channels that best described the average visual response. Traditional ERPs at each channel (represented by a matrix of size T × C where T is the length of a trial in milliseconds and C is the number of EEG channels) were calculated separately for each subject. One ERP was calculated for the response to the visual signal and another was found for the response to the visual noise by averaging a random set of two-thirds of the trials across all conditions for each subject in each window. This random set of trials was the same set used as the training set for cross validation, to be discussed later. The test sets of trials were not used to calculate the traditional ERPs.

Singular value decomposition (SVD; analogous to principal component analysis) of the trial averages were then used to find linear mixtures of channels that explained the largest amount of the variance in the ERP data (i.e. the first right-singular vectors v, explaining a percentage of variance from 39.4% to 91.9% and 45.0% to 93.2% across subjects in the cue and response intervals respectively). The first right-singular vectors were then used as weights to mix the raw EEG data into a brain response biased toward the maximum response to the visual stimuli, yielding one time course of the EEG per trial for both the cue and response intervals. A visual representation of the simple procedure for a single trial is provided in Figure 3. The raw data matrix E of dimension N × C was multiplied by the first right singular vector v (a C × 1 vector of channel weights) to obtain a N × 1 vector Ev = e, which could then be split up into epochs of length T × 1 representing the response to the stimulus on each trial. Note that the voltage amplitudes of the ERP measures calculated based on this method will differ from traditional single electrode ERP amplitudes since the single-trial estimates are a weighted sum of potentials over all electrodes.

Figure 3.

A visual representation of the singular value decomposition (SVD) method for finding single-trial estimates of evoked responses in EEG. The EEG presented here is time-locked to the signal onset during the response interval, such that the single-trial ERP encoded the response to the signal onset. A single trial of EEG from Subject 16 (Left) can be thought of as a time by channel (T × C) matrix. The first SVD component explained the most variability (79.9%) in Subject 16's ERP response to the signal across all trials in the training set. SVD weights v (C × 1) are obtained from the ERP response (i.e. trial-averaged EEG; T × C) and can be plotted on a cartoon representation of the human scalp with intermediate interpolated values (Middle). This specific trial's ERP (Right) was obtained by multiplying the time series data from each channel on this trial by the associated weight in vector v and then summing across all weighted channels.

Not only did this method boost the SNR of the EEG measures, but this method also reduced EEG measures of size T × C on each trial to one latent variable that varies in time of size T × 1. Thus the correlation of the EEG as inputs to the model was drastically reduced and the interpretability of model parameters was increased compared to analyses with highly correlated model inputs. The weight vector v for each subject in both the cue and response intervals also yields a scalp map when the values of the weights are interpolated between electrodes. Channel weights calculated using SVD on subject's ERPs to the noise onset (during the cue interval) are shown in topographic plots for each subject in Figure 7. Channel weights calculated using SVD on subject's ERPs to the signal onset (during the response interval) are shown in topographic plots for each subject in Figure 6. While raw EEG on single trials from single electrodes may have large enough SNRs to be informative for our analysis, we would not obtain an idea of the locus of activation or the pattern of activation over the scalp.

Figure 7.

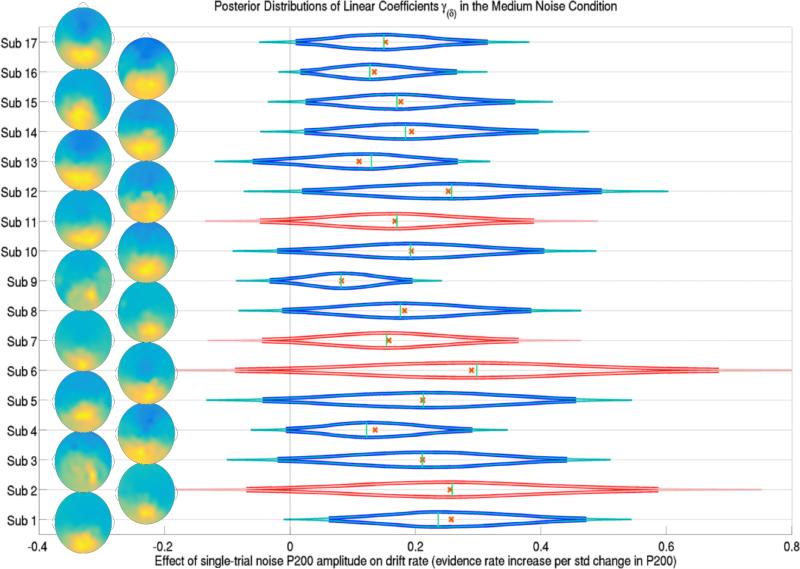
The posterior distributions of the effect of a trial's P200 amplitude during the cue interval (onset of attention to the noise stimulus) on trial-specific evidence accumulation rates δ_ijk for each subject j in the medium noise condition k = 2. Subjects 2, 6, 7 and 11 were left out of the training set, their predicted posterior distributions are shown in red. Thick lines forming the distribution functions represent 95% credible intervals while thin lines represent 99% credible intervals. Crosses and vertical lines represent posterior means and modes respectively. Also shown are the topographic representation of the channel weights of the first SVD component of each subject's cue interval ERP, indicating the location of single-trial P200s over occipital and parietal electrodes. Evidence suggests that the effect of the attention to the noise, reflected in P200 amplitudes, positively influenced the drift rate of each subject in each trial, in the medium and high noise conditions.

Figure 6.

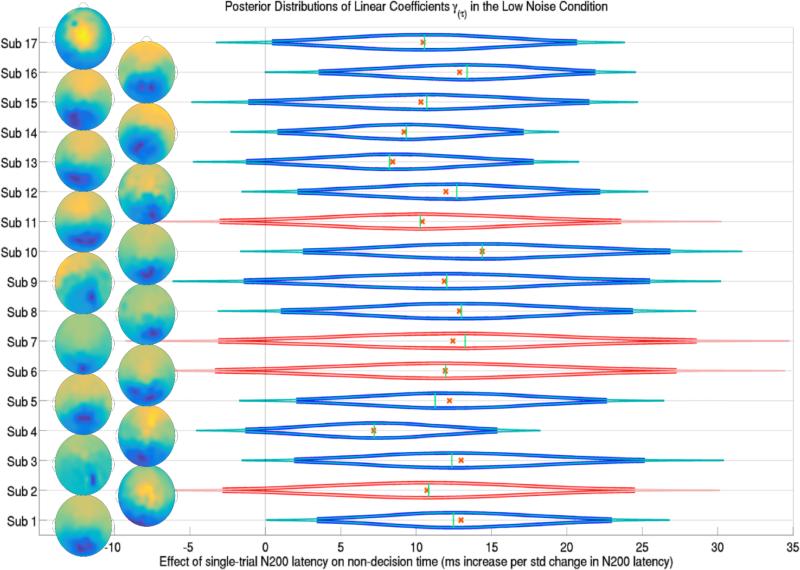
The posterior distributions of the effect of a trial's N200 latency during the response interval (onset attention latency to the signal stimulus) on trial-specific non-decision times τ_ijk for each subject j in the low noise condition k = 1. Subjects 2, 6, 7 and 11 were left out of the training set and their predicted posterior distributions are shown in red. Thick lines forming the distribution functions represent 95% credible intervals while thin lines represent 99% credible intervals. Crosses and vertical lines represent posterior means and modes respectively. Also shown are the topographic representations of the channel weights of the first SVD component of each subject's response interval ERP, indicating the location of single-trial N200s over occipital and parietal electrodes. Evidence suggests that longer attentional latencies to the signal, N200 latencies, are linearly correlated with longer non-decision times in the low noise condition.

We focused our analysis on the windows 150 to 275 ms post stimulus-onset in the cue and response intervals. These windows were found to contain P200 and N200 ERP components. On each trial, we measured the peak positive and negative amplitudes, and the latency at which these peaks were observed. We used these 8 single-trial measures to predict single-trial diffusion model parameters. However in this paper we will focus only on the results of models with 4 single-trial measures: the amplitude and latency of the peak positive deflection (P200) during the cue interval and the amplitude and latency of the peak negative deflection (N200) during the response interval, because very weak evidence, if any, was found for the effects of the other attention measures on diffusion model parameters in models with all 8 single-trial measures. It should be noted that single-trial measures of EEG spectral responses at SSVEP frequencies (see Nunez et al., 2015) were briefly explored but future methods must be developed to increase signal-to-noise ratios of SSVEP measures on single-trials.

2.3. Hierarchical Bayesian models

Hierarchical models of visual decision making were assumed and placed into a Bayesian framework. Bayesian methods yield a number of benefits compared to other inferential techniques such as traditional maximum likelihood methods. Rather than point estimates of parameters, Bayesian methods provide entire distributions of the unknown parameters. Bayesian methods also allow us to perform the model fitting procedure in a single step, maintaining all uncertainty about each parameter through each hierarchical level of the model.

One downside of Bayesian methods is that creating sampling algorithms to find posterior distributions of Bayesian hierarchical models can be time consuming and cumbersome. However Just Another Gibbs Sampler (JAGS; Plummer et al., 2003) is a program that uses multiple sampling techniques to find estimates of hierarchical models, only requiring the form of the model, data, and initial values as input from the user. In order to find posterior distributions, we have used JAGS with an extension that adds a diffusion model distribution (without intrinsic trial-to-trial variability) as one of the distributions to be sampled from (Wabersich and Vandekerckhove, 2014). Similar software packages to fit hierarchical diffusion models have been developed independently in other programming languages such as Python (Wiecki et al., 2013).

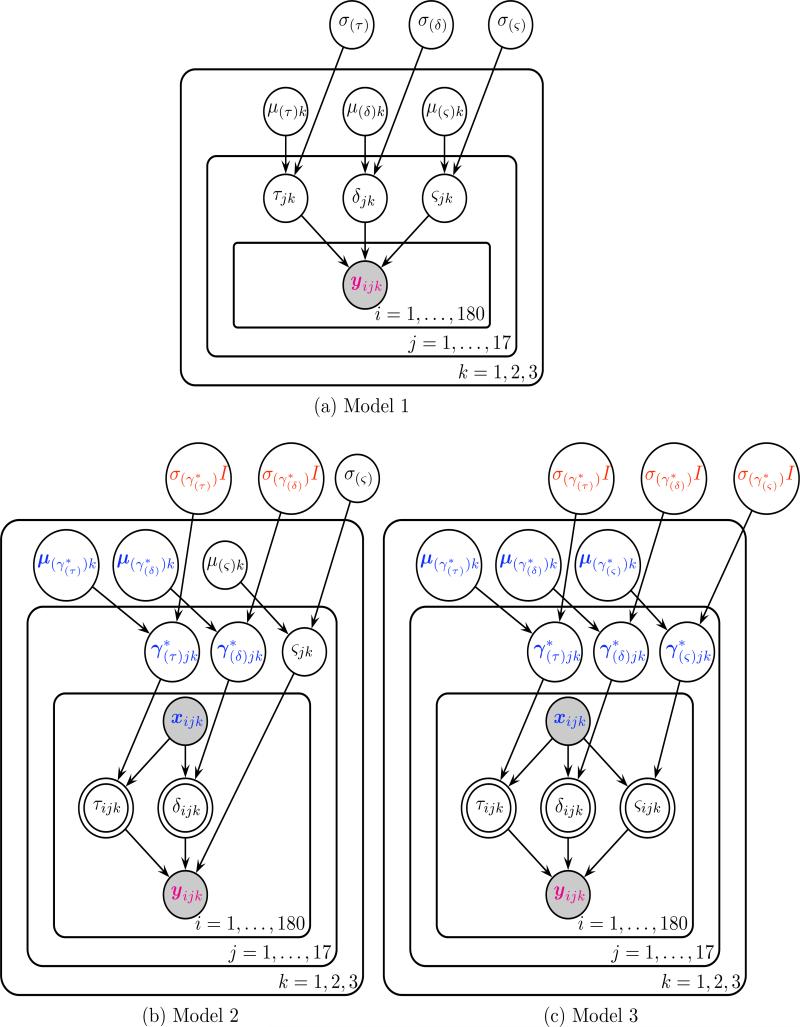
In order to evaluate the benefit to prediction of adding EEG measures to hierarchical diffusion models, three different models were compared. Model 3 assumed that evidence accumulation rates, evidence accumulation variances, and non-decision times were each equal to a linear combination of EEG measures on each trial. Because we found no effect of the observed single-trial EEG measures on single-trial evidence accumulation variances, we also fit Model 2, where single-trial evidence accumulation rates and non-decision times were influence by EEG, but single-trial evidence variances were not. Model 1 did not assume any EEG contribution to any parameters. This model assumed that parameters not varying with EEG would change based on subject and condition, drawn from a condition level distribution. Graphical representations of the hierarchical Bayesian models are provided in Figure 4 following the convention of Lee and Wagenmakers (2014).

Figure 4.

Graphical representations of the three hierarchical Bayesian models following the convention of Lee and Wagenmakers (2014). Each node represents a variable in the model with arrows indicating what variables are influenced by other variables. The magenta 2 ∗ 1 vector of reaction time and accuracy y_ijk and the blue (p + 1) ∗ 1 vector of p EEG regressors (+1 intercept) x_ijk are observed variables, as indicated by the shaded nodes. Bolded blue variables indicate (p + 1) ∗ 1 vectors, such as the subject j level effects ${\gamma }_{jk}^{\ast }$ of each EEG regressor and the condition k level effects μ_(γ∗)k of each EEG regressor. In Model 3 for each trial i, values of non-decision time τ_ijk, drift rate (evidence accumulation rate) δ_ijk, the diffusion coefficient (evidence accumulation variance) ς_ijk are deterministic linear combinations of single-trial EEG regressors x_ijk and the effects of those regressors ${\gamma }_{jk}^{\ast }$ that vary by subject and condition.

For Model 1 (Figure 4a), prior distributions were kept mostly uninformative (i.e. parameters of interest had prior distributions with large variances) so that the analyses would be data-driven. The prior distributions of parameters for each subject j and condition k free from EEG influence had the following prior and hyperprior structure

$$\begin{array}{ccc}({\delta }_{jk}\mid {\mu }_{\left(\delta \right)k},{\sigma }_{\left(\delta \right)})\sim \mathcal{N}({\mu }_{\left(\delta \right)k},{\sigma }_{\left(\delta \right)}^2),\hfill & {\mu }_{\left(\delta \right)k}\sim \mathcal{N}(1.5,4^2)\in (-9,9),\hfill & {\sigma }_{\left(\delta \right)}\sim \Gamma (5,0.20)\hfill \\ ({\tau }_{jk}\mid {\mu }_{\left(\tau \right)k},{\sigma }_{\left(\tau \right)})\sim \mathcal{N}({\mu }_{\left(\tau \right)k},{\sigma }_{\left(\tau \right)}^2),\hfill & {\mu }_{\left(\tau \right)k}\sim \mathcal{N}(0.3,1^2)\in (0,3),\hfill & {\sigma }_{\left(\tau \right)}\sim \Gamma (5,0.05)\hfill \\ ({\varsigma }_{jk}\mid {\mu }_{\left(\varsigma \right)k},{\sigma }_{\left(\varsigma \right)})\sim \mathcal{N}({\mu }_{\left(\varsigma \right)k},{\sigma }_{\left(\varsigma \right)}^2),\hfill & {\mu }_{\left(\varsigma \right)k}\sim \mathcal{N}(0.6,2^2)\in (0,4),\hfill & {\sigma }_{\left(\varsigma \right)}\sim \Gamma (5,0.05)\hfill \end{array}$$

Where the normal distributions $\mathcal{N}$ are parameterized with mean and variance respectively and the gamma distributions Γ are parameterized with shape and scale parameters respectively.

In Models 2 (Figure 4b) and 3 (Figure 4c), to ensure noninterference by the prior distributions, uninformative priors were given for both the effects γ_jk of EEG on the parameters of interest and the linear intercepts η_jk. Note that the effect of EEG γ_jk is a vector with one element per EEG regressor and each effect of EEG is assumed to be statistically independent from the others. If a drift-diffusion model parameter was assumed to be equal to a linear combination of EEG inputs then the following two lines replaced the priors of the respective parameter above.

$$\begin{array}{ccc}({\eta }_{jk}\mid {\mu }_{\left(\eta \right)k},{\sigma }_{\left(\eta \right)})\sim \mathcal{N}({\mu }_{\left(\eta \right)k},{\sigma }_{\left(\eta \right)}^2),\hfill & {\mu }_{\left(\eta \right)k}\sim \mathcal{N}(0,{100}^2),\hfill & {\sigma }_{\left(\eta \right)}\sim \Gamma (5,5)\hfill \\ ({\gamma }_{jk}\mid {\mu }_{\left(\gamma \right)k},{\sigma }_{\left(\gamma \right)})\sim \mathcal{M}\mathcal{V}\mathcal{N}({\mu }_{\left(\gamma \right)k},{\sigma }_{\left(\gamma \right)}^{2}I),\hfill & {\mu }_{\left(\gamma \right)k}\sim \mathcal{M}\mathcal{V}\mathcal{N}(0,{100}^{2}I),\hfill & {\sigma }_{\left(\gamma \right)}\sim \Gamma (5,5)\hfill \end{array}$$

In Models 2 and 3, the parameter on each trial was assumed to be equal to a simple linear combination of the vector of single-trial EEG inputs x_ijk on that trial i with η_jk and γ_jk as the intercept and slopes respectively:

$$\begin{array}{cc}\hfill {\delta }_{ijk}=& {\eta }_{\left(\delta \right)jk}+{\gamma }_{\left(\delta \right)jk}^{⊺}{\mathbf{x}}_{ijk}\hfill \\ \hfill {\tau }_{ijk}=& {\eta }_{\left(\tau \right)jk}+{\gamma }_{\left(\tau \right)jk}^{⊺}{\mathbf{x}}_{ijk}\hfill \\ \hfill {\varsigma }_{ijk}=& {\eta }_{\left(\varsigma \right)jk}+{\gamma }_{\left(\varsigma \right)jk}^{⊺}{\mathbf{x}}_{ijk}\hfill \end{array}$$

Where the first two equations refer to the structure of Model 2 and all three equations refer to the structure of Model 3. Note that the p ∗ 1 vector of effects γ_jk of EEG on each parameter could include the intercept term η_jk to create a (p + 1) ∗ 1 vector of effects ${\gamma }_{jk}^{\ast }$ (and the EEG vector x_ijk would include a value of 1 to be multiplied by the intercept term). We use this notation in Figure 4 for simplicity.

Because not all trials are believed to actually contain a decision-making process (i.e. the subject quickly presses a random button during a certain percentage of trials reflecting a “fast guess”), reaction times below a certain threshold were removed from analysis and cross-validation. Cutoff reaction times were found for each subject by using an exponential moving average of accuracy after sorting by reaction time (Vandekerckhove and Tuerlinckx, 2007). The rejected reaction times were all below 511 ms with a mean cutoff of 410 ms across subjects. This resulted in an average rejection rate of 1.4% of trials across subjects with a maximum of 6.3% of trials rejected for one subject and a minimum of 0.7% of trials rejected for 11 of the 17 subjects.

Each model was fit using JAGS with six Markov Chain Monte Carlo (MCMC) chains run in parallel (Tange, 2011) of 52,000 samples each with 2,000 burn-in samples and a thinning parameter of 10 resulting in 5,000 posterior samples in each chain. The posterior samples from each chain were combined to form one posterior sample of 30,000 samples for each parameter. All three models converged as judged by R̂ being less than 1.02 for all parameters in each model. R̂ is a statistic used to assess convergence of MCMC algorithms (Gelman and Rubin, 1992).

Posterior distributions were found for each free parameter in the three models. Credible intervals of the found posterior distributions were then calculated to summarize the findings of each model. EEG regressor effects were deemed to have weak evidence if the 95% credible interval between the 2.5^th and 97.5^th percentiles of the subject mean parameter μ_(γ)j was non-overlapping zero. effects were deemed to have strong evidence if the 99% credible interval between the 0.5^th and 99.5^th percentiles was non-overlapping zero.

2.4. Cross-validation

All trials from all subjects were used during initial exploration of the data. However once it was decided that the signal onset response was a candidate predictor of drift rate, cross-validation was performed using a training and test set of trials. Out-of-sample performance for both known and unknown subjects were found by randomly assigning two-thirds of the trials from each subject in a random sample of subjects (i.e. 13 of 17 subjects were chosen at random) as the training set and one-third of the trials from the 13/17 subjects and all trials from the remaining 4/17 subjects as the test set. After fitting the model with the training set, posterior predictive distributions of the accuracy-RT data were found for each subject. Posterior predictive distributions were calculated by drawing from the subject-level posteriors of the known subjects and by drawing from the condition-level posteriors of the unknown subjects. The posterior predictive distributions were then compared to the sample distribution of the test set.

In some recent papers, evaluation of models’ prediction ability has been left to the readers with the aid of posterior predictive coverage plots (e.g. see figures in Supplementary Materials). Here we formally evaluate the similarity of the posterior predictive distributions to the test samples via a “proportion of variance explained” calculation. Specifically, we calculated $R_{\mathrm{pred}}^2$ of subjects’ accuracy and correct reaction time 25th percentiles, medians, and 75th percentiles across subjects. $R_{\mathrm{pred}}^2$ is a measure of percentage variance in a statistic T (e.g. accuracy, correct-RT median, etc.) explained by in-sample or out-of-sample prediction. In this paper, $R_{\mathrm{pred}}^2$ is defined as the percentage of total between-subject variance of a statistic T explained by out-of-sample or in-sample prediction. It is a function of the mean squared error of prediction (MSEP) and the sample variance of the statistic T based on a sample size of J = 13 or J = 4 subjects for known and unknown subject calculations respectively. This measure also allows comparisons across studies with similar prediction goals. Mathematically, $R_{\mathrm{pred}}^2$ is defined as

$$R_{\mathrm{pred}}^2=1-\frac{{\sum }_{j=1}^J{(T_j-T_{\left(\mathrm{pred}\right)j})}^2∕(J-1)}{{\sum }_{j=1}^J{(T_j-\stackrel{‒}{T})}^2∕(J-1)}=1-\frac{{\mathrm{MSEP}}_T}{\widehat{\mathrm{Var}\left[T\right]}}$$ (2)

3. Results

The single-trial EEG measures “regressed” on diffusion model parameters were the peak positive and negative amplitudes and latencies (corresponding to P200 and N200 peaks respectively) in the 150 to 275 ms windows post noise-onset in the cue interval and post signal-onset in the response interval. However the magnitude and latency of the peak negative deflection (N200) in response to the noise stimulus and the magnitude and latency of the peak positive deflection (P200) in response to the signal stimulus were not informative (i.e. most condition-level effect posteriors of these measures overlapped zero significantly in models with all P200 and N200 measures included as regressors). For simplicity we only discuss results of models with P200 measures following the noise stimulus in the cue interval and N200 measures following the signal stimulus in the response interval. Example single trial amplitudes of these P200 and N200 peaks for Subject 12 are shown in Figure 5.

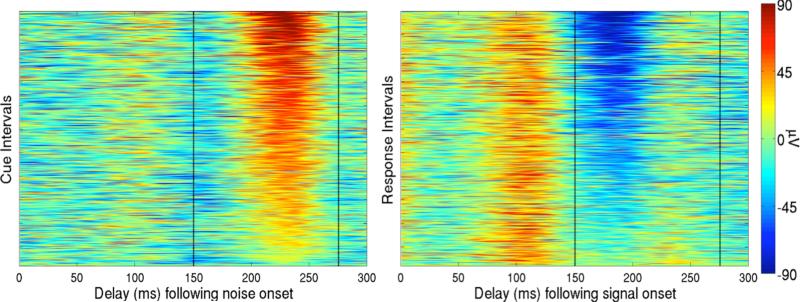
Figure 5.

Single-trial evoked responses of an example subject, Subject 12, to the visual noise during the cue interval (Left) and single-trial evoked responses to the visual signal during the response interval (Right). Single-trial P200 and N200 magnitudes were found by finding peak amplitudes in 150 to 275 ms time windows (as indicated by the vertical dashed lines) of the SVD-biased EEG data in both the cue and response intervals. The first 300 ms of the intervals are sorted by single-trial P200 magnitudes in the cue interval and single-trial N200 magnitudes in the response interval. Latencies of the single-trial P200 and N200 components correspond to known latencies of P2 and N1 ERP components.

Since no effects of explored measures were found on within-trial evidence accumulation variance in Model 3 (i.e. posterior distributions of γ_(ς)jk were centered near zero), the only EEG effects that will be discussed are those on evidence accumulation rate and non-decision time from a fit of Model 2. This paradigm also lead to significant improvement in correct-RT distribution prediction for those subjects whose behavior was missing. That is, we have shown that a new subject’s correct-RT distributions can be predicted when only their single-trial EEG is collected, given that other subjects’ EEG and behavior has been analyzed. A graphical example of the effects found with Model 2 in two representative trials are given in Figure 1.

3.1. Intercept terms of evidence accumulation rate and non-decision time

The intercept term of each variable gives the value of each variable not explained by a linear relationship to N200 and P200 amplitudes and latencies. That is, the intercept gives the value of each parameter that remains constant from trial to trial, with the between-trial variability of the parameter being influenced by the changing trial-to-trial EEG measures. Model 2's posterior medians of the condition level evidence accumulation rate intercepts μ_(ηδ)j and non-decision time intercepts μ_(ητ)j are reported. In low noise conditions, evidence accumulation rate intercepts were 1.46 evidence units per second (i.e. if there was no behavioral effect of EEG on each trial and no variance in the evidence accumulation process, it would take the average subject 343 ms to accumulate evidence since a decision is reached when α = 1 evidence unit is accumulated and subjects start the evidence accumulation process with .5 evidence units). In medium and high noise conditions, evidence accumulation rate intercepts were 1.30 and 0.86 evidence units per second respectively. Non-decision time intercepts were 340 ms in low noise conditions, 425 ms in medium noise conditions, and 440 ms in high noise conditions.

To understand the degree of influence of EEG on model parameters, approximate condition level evidence accumulation rates and non-decision times were calculated and then compared to the intercept of the respective parameter. Taking the mean peak positive and peak negative amplitudes and latencies across all subjects and trials in each noise condition and multiplying by the median posterior of the effects, it was found that evidence accumulate rate in low noise was 1.90 evidence units per second, 1.65 evidence units per second in medium noise, and 1.35 evidence units per second in high noise. It was also found that non-decision time was 393, 400, and 425 ms in the low, medium, and high noise conditions. The intercepts of non-decision time thus described approximately 86%, 94%, and 96% of the true condition means in low, medium, high noise conditions respectively. However, the intercepts of the drift rates only described approximately 77%, 79%, and 63% of the true condition means in low, medium, and high noise conditions respectively. While this gives the reader an idea of the strength of the influence of single-trial EEG measures on the parameters, better evaluations of the degree of effects are presented below.

3.2. Effects of attention on non-decision time in low-noise conditions

Strong evidence was found to suggest that in low noise conditions single-trial non-decision times τ_ijk are positively linearly related to delays in the EEG response to the visual signal as measured by the latency of the negative peak (N200) following stimulus onset. A probability greater than 99% of the condition-level effect being greater than zero in all subjects was found. This relationship to an EEG signature 150-275 ms post stimulus onset suggests an effect on preprocessing time rather than motor-response time. By exploring the posterior distribution of the mean effect across-participants μ_(γτ)j, it is inferred that non-decision time increases 12 ms (the posterior median) when there is a 40 ms increase in the latency of the single-trial negative peak (where 40 ms was the standard deviation across all trials and subjects) in the low noise condition, with a 99% credible interval of 3 to 21 ms. Figure 6 shows the per-subject effects of signal N200 latency on non-decision time in the low noise condition. No evidence was found to suggest that the signal N200 latency affected non-decision time in medium nor high noise conditions. 95% credible intervals for these increases in the subject mean non-decision time for 40 ms increased N200 delays were −9 to 4 ms and was −8 to 3 ms respectively. No evidence found to suggest that attentional delay to the noise, the noise P200 latency, affected non-decision time.

Weak evidence was found to suggest that magnitude of the response to the stimulus affects non-decision time in the low noise condition. The posterior median suggests that a 26.83 μV (the standard deviation) decrease in magnitude of the negative peak (i.e. moves the negative peak towards zero) leads to a 11 ms increase in non-decision time. The 95% credible interval of this effect of N200 signal magnitude on non-decision time was a 2 to 21 ms. No evidence was found to suggest that the magnitude in the medium and high noise conditions affected non-decision time.

3.3. Effects of attention on evidence accumulation

Evidence was found to suggest that per-trial response to the visual signal (measured by the negative peak, N200, amplitude) is positively correlated with per-trial evidence accumulation rates δ_ijk in each condition. In the low noise condition, μ_(γ(δ))j, which describes the across-subject mean of the effect of negative peak on drift rate, was found to have a 95% credible interval of .02 to .34 evidence units per second increase (where it takes α = 1 evidence unit to make a decision) and a posterior median of .17 evidence units per second increase for each magnitude increase (i.e. away from zero) of 26.83 μV , the standard deviation of the negative peak. Given the same magnitude increase, the posterior median of the effects in the medium and high noise conditions were .13 and .14 evidence units per second respectively with 95% credible intervals −.01 to .28 and 0 to .28 respectively.

Strong evidence was found to suggest that the magnitude of the positive peak of the response to the visual noise during the cue interval affected the future evidence accumulation rate in the medium noise and possibly high noise conditions. The median of the posterior distribution of the condition-level effect was .20 evidence units per second when there was a 27.67 μV increase, the standard deviation of the peak magnitude. A 99% credible interval of this effect was .04 to .32 evidence units per second. Figure 7 shows the effects of the noise P200 amplitudes on specific subjects’ single-trial drift rates in the medium noise condition. The probability of there being an effect of this P200 amplitude during the cue interval in the high noise condition was 94.6% (i.e. the amount of the posterior density of the condition-level effect above zero). The median of the posterior distribution of this effect was .09 evidence units per second with a 95% credible interval of −.02 to .22 evidence units per second when there is a 27.67 μV increase in a high noise trial.

3.4. Cross-validation

In-sample and out-of-sample posterior predictive coverage plots of correct-RT distributions for each condition and subject are provided in the Supplementary Materials. All three models perform well at predicting correct-RT distributions and overall accuracy of training data (i.e. in-sample prediction; see Table 3 and Discussion section). However by cross-validation we found that the addition of single-trial EEG measures of attentional onset improved out-of-sample prediction of accuracy and correct reaction time distributions of known subjects (i.e. those subjects who had 2/3 of their trials used in the training set). $R_{pred}^2$ indicates the percentage of variance explained by prediction in the given statistic across subjects. Table 1 contains $R_{pred}^2$ values for accuracy as well as summary statistics of correct-RT distributions of known subjects. Prediction was improved when using Model 3 for these subjects with at least 77.3% of variance in correct-RT medians being explained by out-of-sample prediction, but Model 2 performed almost as well in comparison to Model 1, the model without single-trial EEG inputs. Model 2 was able to predict at least 76.3% of the variance in correct-RT medians while Model 1 was able to predict at least 74.5% of the variance in correct-RT medians. In the low noise condition, Model 2 did not improve upon Model 1's explanation of variance in subject-level accuracy but better predicted accuracy in the other two conditions.

Table 3.

Percentage of variance across subjects explained by in-sample prediction ($R_{\mathrm{pred}}^2$) for summary statistics of known subjects' accuracy-RT distributions. All three models fit accuracy and correct-RT t₁ data very well, explaining over 92% of median correct-RT and over 90% of accuracy in each condition. However none of the models explain incorrect-RT t0 distributions well, a known problem for simple diffusion models that can be overcome by including variable drift rates directly in the likelihood function (Ratcliff, 1978; Ratcliff and McKoon, 2008).

Prediction of training data from known subjects
		Model 1 Comparison	Model 2 EEG-δ,τ	Model 3 EEG-δ,τ,ς
Low	25th t1 Percentile	96.5%	97.1%	97.8%
	t1 Median	96.6%	96.5%	97.3%
	75th t1 Percentile	91.4%	93.4%	94.5%
	Accuracy	95.1%	95.2%	97.3%
	t0 Median	–118.8%	–108.3%	–111.6%
Medium	25th t1 Percentile	86.0%	87.5%	88.6%
	t1 Median	95.9%	95.6%	96.3%
	75th t1 Percentile	84.7%	89.4%	90.1%
	Accuracy	90.7%	94.1%	95.3%
	t0 Median	–163.9%	–158.6%	–163.9%
High	25th t1 Percentile	85.4%	87.3%	86.7%
	t1 Median	93.1%	92.5%	92.9%
	75th t1 Percentile	79.1%	83.8%	84.0%
	Accuracy	95.9%	97.4%	95.9%
	t0 Median	–73.4%	–71.2%	–76.4%

Table 1.

Percentage of across-subject variance explained by out-of-sample prediction ($R_{\mathrm{pred}}^2$) for accuracy and summary statistics of correct-RT distributions of those subjects’ that were included in the training set. 13 of the subjects’ data were split into 2/3 training and 1/3 test sets. Posterior predictive distributions that predicted test set behavior were generated for 13 of the subjects by drawing from posterior distributions generated by the training set. In the Low, Medium, and High noise conditions, the 25^th, 50^th (the median), and 75^th percentiles and means were predicted reasonably well by the model without single-trial measures of EEG, Model 1. However including single-trial measures of EEG improved prediction of correct-RT distributions, especially in the Low noise condition, with Model 3 (which assumes evidence accumulation rate, non-decision time, and evidence accumulation variance vary with EEG per-trial) only slightly outperforming Model 2 (which assumes evidence accumulation rate and non-decision time vary with EEG per-trial).

Prediction of new data from known subjects
		Model 1 Comparison	Model 2 EEG-δ,τ	Model 3 EEG-δ,τ,ς
Low	25th t1 Percentile	81.6%	85.2%	85.6%
	t1 Median	74.5%	76.3%	77.3%
	75th t1 Percentile	60.2%	63.3%	63.8%
	Accuracy	24.5%	20.8%	27.7%
Medium	25th t1 Percentile	84.1%	85.1%	86.1%
	t1 Median	86.8%	87.6%	88.9%
	75th t1 Percentile	63.1%	68.2%	69.3%
	Accuracy	58.1%	63.5%	63.5%
High	25th t1 Percentile	73.0%	76.4%	76.6%
	t1 Median	77.4%	76.8%	77.8%
	75th t1 Percentile	71.0%	74.2%	74.2%
	Accuracy	46.3%	48.9%	51.3%

Larger gains in out-of-sample prediction were found for unknown subjects (i.e. those subjects who were not used in the training set). These improvements were particularly pronounced in the low noise condition. Model 2 outperformed Model 3, which outperformed Model 1 in turn, as shown in Table 2. From these results it is clear that Model 2 was the best model for out-of-sample prediction overall, especially for new subjects. In the low noise condition, Model 2 was able to explain 22.1% of between-subject variance in correct-RT 25^th percentiles in the low-noise condition while Model 1 was not able to predict any between-subject variance in this measure. While the included single-trial EEG measures in these type of models do not perform as well as new subject prediction when subject-average EEG measures of attention are included (Nunez et al., 2015), single-trial EEG does improve prediction. The improvements in $R_{\mathrm{pred}}^2$ across models suggest that it is possible that similar models with more single-trial measures of EEG could explain new subjects’ accuracy and correct-RT distributions.

Table 2.

Percentage of across-subject variance explained by out-of-sample prediction ($R_{\mathrm{pred}}^2$) for accuracy and summary statistics of new subjects' and correct-RT distributions. Posterior predictive distributions were generated for 4 new subjects by drawing from condition level posterior distributions. Most $R_{\mathrm{pred}}^2$ measures are negative because the amount of variance in prediction was greater than the variance of the measure across subjects; however the relative values from one model to the next are still informative about the improvement in prediction ability. The model without single-trial EEG measures, Model 1, does not predict new subjects' correct-RT distributions. Models with single-trial EEG measures of onset attention, Model 2 and Model 3, can predict some variance of the new subjects' 25^th percentiles, with Model 2 outperforming Model 3.

Prediction of new data from new subjects
		Model 1 Comparison	Model 2 EEG-δ,τ	Model 3 EEG-δ,τ,ς
Low	25th t1 Percentile	–9.8%	22.1%	17.9%
	t1 Median	–37.6%	–11.6%	–14.3%
	75th t1 Percentile	–67.3%	–46.7%	–47.6%
	Accuracy	–8.1%	–22.8%	–65.9%
Medium	25th t1 Percentile	–5.3%	8.4%	5.3%
	t1 Median	–30.7%	–22.5%	–25.7%
	75th t1 Percentile	–62.6%	–53.9%	–56.2%
	Accuracy	–13.1%	–35.5%	–67.7%
High	25th t1 Percentile	–1.7%	8.2%	7.7%
	t1 Median	–12.0%	–4.3%	–2.9%
	75th t1 Percentile	–37.6%	–25.5%	–23.7%
	Accuracy	–4.3%	–14.1%	–29.1%

3.5. P200 and N200 localizations

Both the subject-average P200 and N200 components were localized in time and space. All single-trial P200 and N200 amplitudes and latencies (i.e. single-trial peak positive and negative amplitudes 150 to 275 ms in the noise and response interval respectively) were averaged across trials for each subject. Localization in time and on the brain are based on these across-trial averages. The subject mean and standard deviation of the P200 latency during the cue interval was 220±12 ms while the mean and standard deviation the of N200 latency during the response interval was 217 ± 6 ms. Although these latencies differ slightly from traditional P2 and N1 findings (Luck et al., 2000), when viewing the event-related waveforms over all trials it is clear that the P2 and N1 are influenced by the single-trial measures. As an example, every single-trial evoked response of Subject 12 to the noise and signal are shown in Figure 5, sorted by peak P200 amplitude in the cue interval and sorted by peak N200 amplitude in the response interval. The P200 and N200 latencies of this subject correspond to traditional P2 and N1 components.

While EEG localization is an inexact process that is unsolvable without additional assumptions, the surface Laplacian has been shown to match closely to simulated cortical activity using forward models (i.e the mapping of cortical activity to scalp potentials) and have shown consistent results when used with real EEG data (Nunez and Srinivasan, 2006). Unlike 3D solutions, projections to the surface of the cortex (more accurately, the dura) are theoretically solvable, and have been used with success in past studies (see Nunez et al., 1994, for an example).

In this study we have found surface spline-Laplacians (Nunez and Pilgreen, 1991) on the realistic MNI average scalp (Deng et al., 2012) of the mean positive peak during the cue interval (the P200) and the mean negative peak during the response interval (the N200) by averaging over trials and subjects. The surface Laplacians were then projected onto one subject's cortical surface using Tikhonov (L2) regularization and a Finite Element (FE; Pommier and Renard, 2005) forward model to the MNI 151 average head, maintaining similar distributions of activity of the surface Laplacians on the cortical surface. The subject's brain was then labeled using the Destrieux cortical atlas (Fischl et al., 2004). Cortical topographic maps of both peaks are given in Figure 8. Because we expect the majority of the Laplacian to originate from superficial gyri (Nunez and Srinivasan, 2006), we have localized both the positive and negative peaks only to maximally active gyri. This localization suggested that both the P200 and N200 were in the following extrastriate and parietal cortical locations: right and left middle occipital gyri, right and left superior parietal gyri, right and left angular gyri, the left occipital inferior gyrus, the right occipital superior gyrus, and the left temporal superior gyrus. Although we should note that the exact localization must have some errors due to between-subject variance in cortex and head shape and between-subject variance in tissue properties.

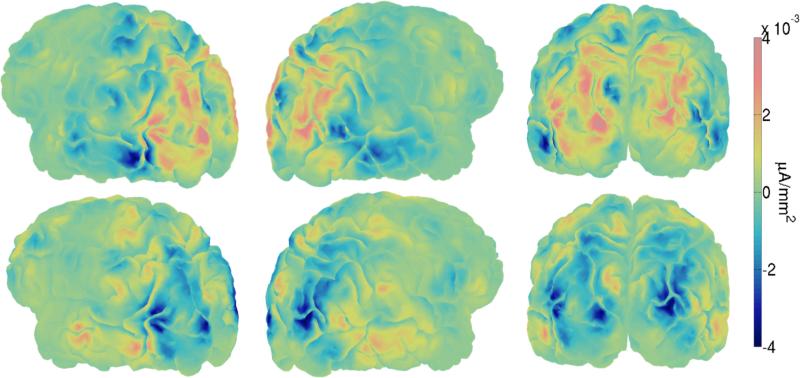
Figure 8.

Right and left sagittal and posterior views of localized single-trial P200 evoked potentials during during the cue interval (Top) and localized single-trial N200 evoked potentials during the response interval (Bottom) averaged across trials and subjects. The cortical maps were obtained by projecting MNI-scalp spline-Laplacians (Nunez and Pilgreen, 1991; Deng et al., 2012) onto a subject's anatomical fMRI image via Tikhonov (L2) regularization, maintaining similar distributions of activity of the surface Laplacians on the cortical surface. Blue and orange regions in microamperes per mm² correspond to cortical areas estimated to produce negative and positive potentials observed on the scalp respectively. These two particular projections of the Laplacians suggest that P200 and N200 activity occurs in extrastriate cortices and areas in the parietal lobe.

Brain regions found using this cortical-Laplacian method point to activity in early dorsal and ventral pathway regions associated with visual attention (Desimone and Duncan, 1995; Corbetta and Shulman, 2002; Buschman and Miller, 2007) and decision making (Mulder et al., 2014). Corroborating our findings, White et al. (2014) found that blood-oxygen-level dependent (BOLD) activity in the right temporal superior gyrus, right angular gyrus, and areas in the right lateral occipital cortex (e.g. the right middle occipital gyrus) correlated with non-decision time during a simple visual and auditory decision making task. It was hypothesized that this activity was due to motor preparation time instead of visual preprocessing time (White et al., 2014); however the time-scale of BOLD signals does not provide additional knowledge to separate visual preprocessing time from motor preparation time. Informed by EEG, BOLD signals associated with evidence accumulation rates have been previously localized to right and left superior temporal gyri and lateral occipital cortical areas, thought to correspond to early bottom-up and late top-down decision making processes respectively during a visual face/car discrimination task (Philiastides and Sajda, 2007). The right and left middle occipital gyri have also previously been shown to contribute to evidence accumulation rates during a random dot motion task (Turner et al., 2015).

4. Discussion

4.1. Attention influences perceptual decision making on each trial

The results of this study suggest that fluctuations in attention to a visual signal accounts for some of the trial-to-trial variability in the brain's speed of evidence accumulation on each trial in each condition. There is also evidence to suggest that increased response to the competing visual noise increases the brain's speed of evidence accumulation, but only in medium and high noise conditions. Although a simple explanation of this effect would be differences in trial-to-trial arousal, we note that the effect only occurs in medium-noise and high-noise conditions. We have previously found evidence that noise suppression during the cue interval predicts enhanced drift rates based on the subject-average SSVEP responses in these data (Nunez et al., 2015). Thus, our effect may reflect the attention the subject places on the cue, which determines whether to engage mechanisms of noise suppression, but we could not directly assess this possibility as new methods must be developed to measure SSVEPs on single trials. This would reflect a hypothesis based on the Perceptual Template Model that predicts that subjects will suppress attention to visual distractors during tasks of high visual noise (Lu and Dosher, 1998).

We assume that the effect of N200 latency on non-decision time during the response interval is on preprocessing time instead of motor response time. There was no a priori reason to believe that an attention effect that takes place 150-275 ms after stimulus onset would affect the speed of efferent signals to the muscle, given that the response times were at least 500 ms. These findings lead us to conclude that the effect of attention in response to the signal in low noise conditions is to reduce preprocessing delay time. This appears consistent with predictions of signal enhancement in low-noise conditions in the Perceptual Template Model. However, we note there is not a perfect equality between N200 latency and preprocessing time (the condition and subject-level coefficient posteriors are not centered on 1). And the identification of both preprocessing time and motor response time is not possible with a drift-diffusion model fit without additional assumptions or external inputs such as EEG.

Reaction time (RT) and choice behavior during visual decision making tasks are well characterized by models that assume a continuous stochastic accumulation of evidence. And many observations of increasing spike-rates of single neuron action potentials lend support to this stochastic theory of evidence accumulation on a neural level (Shadlen and Newsome, 1996, 2001). Recently some macroscopic recordings of the cortex have shown that increasing EEG potentials ramping up to P300 amplitudes are correlates of the stochastic accumulation of evidence (O'Connell et al., 2012; Philiastides et al., 2014; Twomey et al., 2015). It has been hypothesized that this EEG data reflects the evidence accumulation process itself (or a mixture of this process with other decision-making correlates) and not a correlated measure such as top-down attention. This hypothesis leads to the natural prediction that single-trial drift rates are explained by single-trial P300 slopes. However within a small region of the cortex, neurons will have diverse firing patterns during the decision making process, only some of which are observed to have increasing spiking-rate behavior indicative of stochastic evidence accumulation (Meister et al., 2013). The properties of volume conduction through the cortex, skull, and skin only allow for synchronous post-synaptic potentials to be observed at the scalp (Nunez and Srinivasan, 2006; Buzsaki, 2006). Therefore an increasing spike-rate as observed on the single-neuron level is not likely to be observed as an increasing waveform in EEG recorded from the scalp. We also would expect the evidence accumulation process to terminate before the response time since a portion of the response time must be dedicated to the motor response after the decision is made. This may not be the case for the ramping P300 waveform on single-trials even though it is predictive of model parameters (Philiastides et al., 2014). If the stochastic evidence accumulation process was truly reflected in the ramping of EEG, a testable prediction would be that the variance around the mean rate of the P300 ramp on each trial would be linearly related to the diffusion coefficient ς, in addition to single-trial P300 slopes being linearly related to the drift rate δ. There are many EEG measures thought to be related to attention such as event related potential (ERP) components, power in certain frequency bands, and steady-state visual evoked potential (SSVEP) responses. It is likely that EEG measures that share similar properties with stochastic evidence accumulation processes are in fact due to these correlates of attention or other forms of cortical processing that can influence the decision making process.

4.2. External predictors allow for trial level estimation of diffusion model parameters

The Wiener distribution (i.e. the diffusion model) used in this study does not incorporate trial-to-trial variability in drift rates within the probability density function as assumed by Ratcliff (1978). Instead we assume that each trial's drift rate is exactly equal to a linear function of EEG data and use an evidence accumulation likelihood function that does not assume drift rates vary trial-to-trial by any other means. Per-trial non-decision times and diffusion coefficients were also assumed to be exactly equal to linear functions of EEG data.

Per trial estimates of diffusion model parameters cannot be obtained without imposing constraints or including external inputs. In this study, we have shown that the single-trial P200 and N200 attention measures can be used to discover per trial estimates of all three free parameters, non-decision time, drift rate, and the diffusion coefficient. Non-decision time, the drift rate, and the evidence boundary could also be modeled as per trial estimates of external inputs, as would be useful in other speeded reaction time tasks where external per-trial physiological measurements are available. Other possible per-trial external inputs that could be used include: magnetoencephalographic (MEG) measures, functional magnetic resonance imaging (fMRI) measures, physiological measurements such as galvanic skin response (GSR), and near infrared spectroscopy (NIRS), where each modality may have multiple external inputs (e.g. multiple linear EEG regressors of single-trial parameters, as in this study). The more external inputs correlated with single-trial parameters included in the model, the better the single-trial estimate of the parameters will be. This will allow decision model researchers to better explore the efficacy of the diffusion model by comparing single-trial estimates of parameters.

4.3. Behavior prediction and BCI applications

We have observed that single-trial measures of EEG in a hierarchical Bayesian approach to decision-making modeling improves overall accuracy and correct-RT distribution prediction for subjects with observed behavior. This paradigm also lead to significant improvement in overall accuracy and correct-RT distribution prediction for those subjects whose behavior was missing. That is, we have shown that a new subject's accuracy and correct-RT distributions can be predicted when only their single-trial EEG is collected, given that other subjects’ EEG and behavior has been analyzed. If the goal of a future project is solely prediction (and no explanation of the cognitive or neural process is desired, as was in this paper), a whole host of single-trial EEG measures could be included in a hierarchical model of decision making, using perhaps a simpler model of decision making such as the linear ballistic accumulator model to ease analysis (e.g. Forstmann et al., 2008; Ho et al., 2009; van Maanen et al., 2011; Rodriguez et al., 2015) or a more complicated model to improve prediction. The set of single-trial measures could include: ERP-like components as we discussed in this paper, measures of evoked amplitudes in certain frequency bands, and measures of steady-state visual evoked potentials.

However, as observed in Table 3, we have not shown prediction of reaction times for when subjects committed errors because 1) few errors were committed by the subjects in the presented data and 2) the type of model we used has been shown to explain incorrect-RT distributions well only when intrinsic trial-to-trial variability in evidence accumulation rates (as opposed to extrinsic due to neural regressors, for which it has not been shown) is included in the likelihood function (Ratcliff, 1978; Ratcliff and McKoon, 2008). In future work we plan to compare the predictive ability of more complicated models containing both intrinsic trial-to-trial variability and extrinsic trial-to-trial variability in evidence accumulation rate due to external neural measures.

The prediction ability of the presented models for accuracy and correct-RT distributions may have implications for Brain-Computer Interface (BCI) frameworks, especially in paradigms which attempt to enhance a participant's visual attention to particular task to improve reaction time. To maximize prediction, every EEG attention measure should be included, and the predictors that offer the best out-of-sample prediction within initial K-fold validation sets should be included. After collection of behavior and EEG from a few participants and a hierarchical Bayesian analysis of the data, later participants’ single-trial preprocessing times or evidence accumulation rates could be predicted using only single-trial EEG measures. Conceivably this would allow for trial-by-trial intervention in order to enhance a participant's attention during the task, perhaps using neural feedback (e.g. via direct current stimulation or transcranial magnetic stimulation) during those trials in which a participant is predicted to be slow in their response because of a small evidence accumulation rate (e.g. when an N200 magnitude is small) or a slow preprocessing time (e.g. when an N200 latency is long). Although whether the participant could use such feedback in time to affect reaction time and accuracy remains to be tested.

4.4. Neurocognitive models

The term “neurocognitive” has been used to describe the recent trend of combining mathematical behavioral models and observations of brain behavior to explain and predict perceptual decision making (Palmeri et al., 2014). The usefulness of combining behavioral models and neural dynamics has been motivated on theoretical grounds. Behavioral models suggest links between subject behavior and cognition while laboratory observation and neuroimaging can suggest links between neural dynamics and cognition. The combination of these methods then provides a predictive chain of neural dynamics, cognition, and behavior. Another obvious benefit is the inference gain when predicting missing data. That is, we will be able to better predict behavior when brain activity is available. This is especially true when using hierarchical Bayesian models as they maintain uncertainty in estimates through different levels of the analysis (Vandekerckhove et al., 2011; Turner et al., 2013). While there are a variety of methods using cognitive models to find cognitive correlates in the brain dynamics (see Turner et al., 2016, for a review of these methods), some studies do not further constrain the cognitive models by informing those models with known neural links to specific cognitive processes. In this paper, and our previous study of individual differences (Nunez et al., 2015), we demonstrate another important use of neural data in cognitive models. Independent neural measures of cognitive processes, such as attention, can be used to better understand how cognition influences the mechanisms of behavior, furthering explanation and prediction of the cognitive process.

Highlights.

• Our goal is to elucidate the effect of attention on visual decision making.

• Models with linear relationships between diffusion model parameters and EEG were fit.

• Single-trial EEG attention measures explain evidence accumulation and preprocessing.

• Accuracy and correct reaction time distributions were predicted out-of-sample.