Endogenous circadian rhythm in an index of cardiac vulnerability independent of changes in behavior

Abstract

There exists a robust day/night pattern in the incidence of adverse cardiac events with a peak at ≈10 a.m. This peak traditionally has been attributed to day/night patterns in behaviors affecting cardiac function in vulnerable individuals. However, influences from the endogenous circadian pacemaker independent from behaviors may also affect cardiac control. Heartbeat dynamics under healthy conditions exhibit robust complex fluctuations characterized by self-similar temporal structures, which break down under pathologic conditions. We hypothesize that these dynamical features of the healthy human heartbeat have an endogenous circadian rhythm that brings the features closer to those observed under pathologic conditions at the endogenous circadian phase corresponding to ≈10 a.m. We investigate heartbeat dynamics in healthy subjects recorded throughout a 10-day protocol wherein the sleep/wake and behavior cycles are desynchronized from the endogenous circadian cycle, enabling assessment of circadian factors while controlling for behavior-related factors. We demonstrate that the scaling exponent characterizing temporal correlations in heartbeat dynamics does exhibit a significant circadian rhythm (with a sharp peak at the circadian phase corresponding to ≈10 a.m.), which is independent from scheduled behaviors and mean heart rate. Cardiac dynamics under pathologic conditions such as congestive heart failure also are associated with a larger value of the scaling exponent of the interbeat interval. Thus, the sharp peak in the scaling exponent at the circadian phase coinciding with the period of highest cardiac vulnerability observed in epidemiological studies suggests that endogenous circadian-mediated influences on cardiac control may be involved in the day/night pattern of adverse cardiac events in vulnerable individuals.

Adverse cardiac events are the leading cause of mortality in the United States (1). These events do not occur randomly during the day. Epidemiological studies demonstrate that myocardial infarction (2–6), stroke (7, 8), angina (9), ventricular arrhythmias (10), and sudden cardiac death (11, 12) have a 24-h day/night pattern with a primary occurrence peak around 10 a.m. This 24-h pattern of cardiac risk is widely assumed to be caused by day/night patterns in behaviors that affect cardiovascular variables such as autonomic balance, blood pressure, and platelet aggregability in vulnerable individuals. The suprachiasmatic nuclei of the anterior hypothalamus contain the principal endogenous circadian pacemaker, which is normally synchronized with the light/dark cycle and the sleep/wake cycle but also has independent effects on the sympathovagal balance of the autonomic nervous system (13, 14). These last effects raise the possibility that the circadian pacemaker contributes to the 24-h pattern of adverse cardiac events in vulnerable individuals.

Recent studies based on approaches derived from statistical physics have examined the extent of heartbeat fluctuations (the sum of the deviations in interbeat intervals after detrending) over a broad range of time scales (15–18). These studies revealed that heartbeat fluctuations in healthy subjects possess a self-similar temporal structure characterized by long-range power-law correlations over a range of time scales. This statistical feature changes with sleep/wake states (19) and under pathologic conditions such as congestive heart failure (20, 21). Moreover, the scaling exponent associated with these power-law correlations was shown to be one of the most sensitive markers for predicting mortality in a population-based study of heart failure subjects in the Framingham Heart Study (22). These findings suggest that the scaling exponent characterizing the temporal correlations in heartbeat fluctuations is a robust marker of cardiac dynamics that may be useful for the prediction of cardiac vulnerability. Such marked change in the temporal structure of cardiac dynamics may alter the timing of descending depolarization fronts in the myocardium, thus allowing for an occurrence of abnormal ventricular contractions triggered by preexisting lesions in the myocardium, the disruptive function of which would remain suppressed under a normal regime of heartbeat fluctuations.

Because of the robust day/night pattern of adverse cardiac events, we hypothesize that the dynamical features of human cardiac control exhibit an endogenous circadian rhythm, independent of activity. We also hypothesize that the exponent quantifying the scale-invariant temporal organization in heartbeat fluctuations changes with the circadian phase. Further, we specifically hypothesize that the scaling exponent will increase at the circadian phase corresponding to ≈10 a.m., the time of greatest cardiac vulnerability, thereby shifting this marker of cardiac dynamics closer to the values observed under pathologic conditions (20, 21). Because the sudden onset of adverse cardiovascular events occurs in ostensibly healthy asymptomatic people (23, 24), the study of healthy subjects can yield information concerning circadian or behavior-related mechanisms in cardiac vulnerability. To test these hypotheses, we analyze the heartbeat fluctuations of healthy subjects at different circadian phases in a protocol that accounts for changes in behavior to determine the independent endogenous circadian influences on normal cardiac control.

Data Collections and Methods

Subjects. We studied five healthy subjects (four males and one female), with a mean age of 25.8 years (range, 20–33 years). All subjects had no medical disorders as assessed by history, physical examination, overnight polysomnography, psychological examination, pulmonary function tests, a 12-lead ECG, and routine blood and urine chemistry. The study was approved by the relevant institutional human subjects internal review board. All subjects provided written informed consent before participation.

Forced Desynchrony Protocol. To distinguish the effect on the cardiac dynamics of the intrinsic circadian system while controlling for the daily behavior pattern, we collected physiologic data throughout a 10-day “forced desynchrony protocol” with subjects living in an individual suite (25–27). In this protocol, there were two initial baseline acclimatization days with 8-h sleep opportunities and 16 h of wakefulness. Subjects' sleep/wake behavior cycles were then adjusted to 28 h, with 9 h and 20 min of sleep opportunity and 18 h and 40 min of scheduled wakefulness. This 28-h recurring sleep/wake schedule was repeated for seven cycles (Fig. 1) in the absence of known zeitgebers, such as bright light, so that the body clock oscillated at its inherent rate. Light was kept at <10 lux, and the subjects had no external cues regarding the time of day. Room temperature was maintained at 23°C. Subjects repeated the same behavior schedule in all wake periods so that, statistically, the same behaviors, including the sleep/wake cycle, occurred evenly across all circadian phases by the end of the protocol. During the periods of wakefulness, activity was limited to walking around the suite, sitting, and resting. In addition, as part of a separate aim assessing circadian cardiopulmonary rhythmicity, noninvasive cardiopulmonary measurements were made every 2–4 h, including during two 30-min scheduled arousals from sleep during each sleep period.

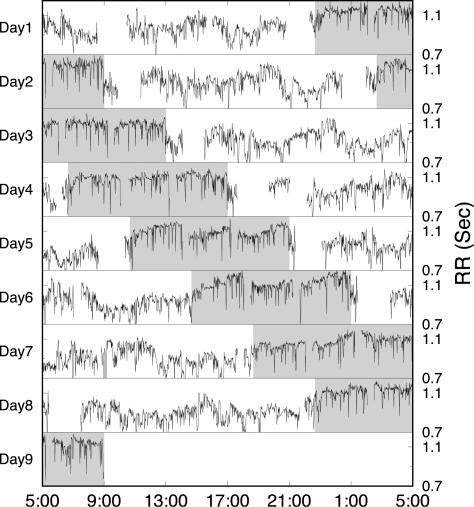
Fig. 1.

Heartbeat RR interval (the interval between two consecutive R waves in the normal sinus rhythm) time series during the forced desynchrony protocol in one individual. The sleep/wake cycle is adjusted to 28 h with a continuous wake period of 17 h and 40 min (marked by white background) followed by a period of 10 h and 20 min (marked by gray background) including 9 h and 20 min of sleep opportunity and two 30-min scheduled arousals from sleep. Gaps in the signal indicate missing data (e.g., when subjects were showering or during scheduled arousals from sleep). During each wake period, the same schedule is repeated so that, statistically, all behaviors are balanced across all circadian phases.

Measurements. To provide a marker of the endogenous circadian pacemaker, core body temperature (CBT) was recorded throughout the 10-day protocol by using a rectal temperature sensor (YSI 20463, Yellow Springs Instruments) with values stored to a computer once per minute.

For an assessment of the cardiac interbeat interval, a chest lead ECG was recorded on an ambulatory recording device (Vitaport, Temec Instruments, Kerkrade, The Netherlands) at 256 Hz over 196 h throughout the forced desynchrony protocol. Cardiac interbeat intervals were obtained from the ECG by using a QRS wave detector based on the Aristotle algorithm (28).

Estimation of Circadian Phases. CBT was used as the marker of the circadian phase (25). Each subject's phase and period of the CBT circadian rhythm was estimated by nonlinear least-squares regression (27), and a circadian phase was assigned to hourly averages of heartbeat data relative to the time of the minimum CBT (CBT minimum = 0° circadian phase corresponding to ≈5 a.m.).

Detrended Fluctuation Analysis (DFA). To estimate correlations in the heartbeat fluctuations, we used the detrended fluctuation analysis (29, 30). Compared with traditional correlation analyses such as autocorrelation, power-spectrum analysis, and Hurst analysis, the advantage of the DFA method is that it can accurately quantify the correlation property of signals masked by polynomial trends (31, 32, 41). The DFA method quantifies the detrended fluctuations F(n) of a signal at different time scales n. A power-law functional form F(n) ≈ n^α indicates the presence of self-similar organization in the fluctuations. The parameter α, called the scaling exponent, quantifies the correlation properties in the signal: if α = 0.5, there is no correlation and the signal is white noise; if α = 1.5, the signal is a random walk; if 0.5 < α < 1.5, there are positive correlations, where large heartbeat intervals are more likely to be followed by large intervals (and vice versa for small heartbeat intervals).

Analysis of Circadian Rhythmicity in Cardiac Dynamics. We separated all RR interval data into 1-h windows, and for each window, we calculated the values of the DFA scaling exponent α and the mean RR interval. We chose 1 h as the size of the window because the DFA method needs ≈3,000 data points for an accurate estimate of the scaling exponent α. For each 1-h data segment, we estimated the scaling exponent α over the same range of time scales, from 20 to 400 heartbeats. For each subject, we analyzed ≈124 h for wake periods and ≈62 h for sleep-opportunity periods throughout the forced desynchrony protocol (Fig. 1). After considering missing data caused by occasional interruptions during recording (e.g., when subjects were showering or during scheduled arousals from sleep) and removing the segments of noisy data, for each subject, we obtained ≈100 values for the DFA exponent α for wakeful periods and ≈60 DFA exponent values for sleep-opportunity periods. To each 1-h data point representing the DFA exponent value of interbeat intervals and mean RR intervals, we assigned a circadian phase (established from the analysis of CBT). Because sleep and wake states have different effects on cardiac dynamics (19), we analyzed wake and sleep-opportunity periods separately (Figs. 2 and 3).

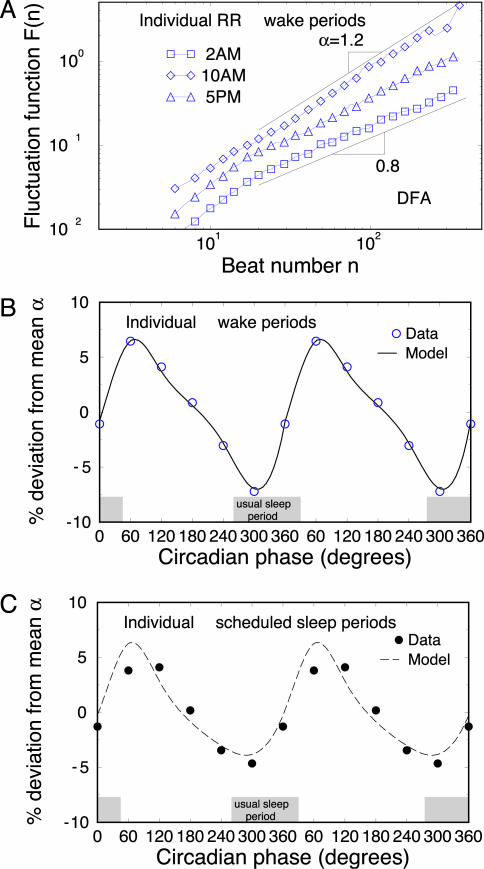
Fig. 2.

Circadian rhythms in the correlation property of heartbeat dynamics. (A) DFA results of 1-h RR intervals for an individual at three different times representing different circadian phases during wake periods. The scaling curves are vertically shifted for clarity. The power-law form of the fluctuation function F(n) ≈ n^α with α > 0.5 indicates presence of long-range correlations in the heartbeat signals. The value of α in each 1-h window is obtained by fitting F(n) in the range 20 < n < 400 beats. Significant circadian rhythms are observed in the deviation of the α value for individual data during both wake periods (B) and sleep-opportunity periods (C). The data are shown as symbols, and the cosinor model fits are shown as lines. The results of α in B and C are double-plotted to better visualize rhythmicity. The results are consistent for all five subjects during wake periods and sleep-opportunity periods. The individual's habitual sleep period when living outside the laboratory is indicated (gray shaded boxes).

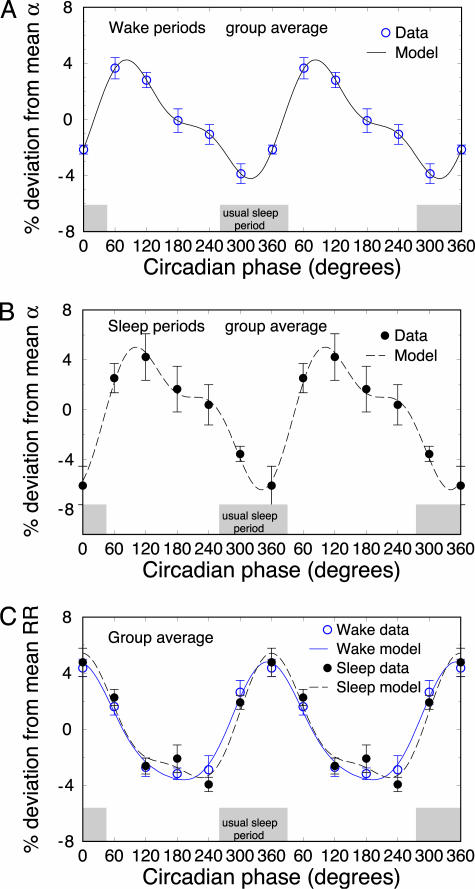
Fig. 3.

Circadian rhythms in the group average of the scaling exponent α for wake periods (A) and sleep-opportunity periods (B). Consistent and significant circadian rhythms are observed for wake periods (P = 0.01) and sleep-opportunity periods (P = 0.0003). Note the well pronounced peak at between 60° and 90° (9–11 a.m.). (C) The deviations of mean RR intervals also show significant circadian rhythms for both wake periods (P = 3.6 × 10^–10) and sleep-opportunity periods (P = 2.1 × 10^–9). However, this 24-h pattern of mean RR is extremely different from the pattern of the α value in A and B, showing a minimum value at between 180° and 240° (corresponding to a broad plateau in the heart rate at 5–9 p.m.) and a maximum at ≈0° (corresponding to the lowest rate at 5 a.m.). The results of are double-plotted to better visualize rhythmicity. The group average habitual sleep period when living outside the laboratory is indicated (gray shaded boxes).

Averaging the data according to the circadian phase yields effects caused by endogenous circadian rhythms independent of behavioral factors, because in the forced desynchrony protocol, each behavior is represented at each circadian phase. We assessed circadian rhythmicity for individuals' and group data by using cosinor analysis, which incorporates a circadian fundamental and a harmonic term (≈12 h cosine) (33). This analysis obtains a best-fit periodic function of the points (represented by the “model” curves in Figs. 2 and 3) and provides a probability (P value) that the rhythm is statistically significant (33). For group analyses, we expressed each individual's 1-h data points in normalized units (i.e., percentage difference from each subject's mean) and aligned with respect to CBT minimum before averaging for cosinor analysis. A graphical example of the cosinor analysis is shown for one individual in Fig. 2 and for the group in Fig. 3. For graphical purposes, data were divided into six circadian bins (60° or ≈4 h for each bin) and averaged within each bin (≈16 points for wake periods and ≈10 points for sleep-opportunity periods per bin per subject) (Fig. 2). Because we scheduled events corresponding to different behaviors within each 4-h period for each cycle in the forced desynchrony protocol and because these scheduled events repeat in every cycle at different circadian phases, introducing 4-h circadian bins eliminates variations in the 1-h α values due to (i) scheduled events with different levels of activity (34) and (ii) transitions between sleep stages during the sleep periods (35).

Results

In Fig. 2 A, we show the scaling behavior in heartbeat fluctuations for a single subject as assessed by the DFA method at different circadian phases (corresponding to 2 a.m., 10 a.m., and 5 p.m.). We observe a systematic change in the slope α of the scaling curve F(n), indicating that the self-similar/fractal structure of heartbeat fluctuations changes with the circadian phase. In Fig. 2B, we show the average deviation Δα of the scaling exponent α from its mean value for the same subject as in Fig. 2 A throughout all circadian phases during wake periods. We find a strong, statistically significant circadian rhythm with an amplitude of 11% of the average scaling exponent α, i.e., –5.7% < Δα < 5.6%. For this subject, we find that the minimum α value occurs at 330° (corresponding to 3 a.m.), whereas the maximum value of α occurs at 70° (corresponding to 9:40 a.m.). Further, we observe that a strong circadian rhythm is present not only during wake periods but also during the sleep-opportunity periods for the same subject (Fig. 2C).

We find that this circadian rhythm in the scaling exponent α is consistent for all five subjects. Moreover, we find a consistent and significant 24-h pattern in the group average α variation for both wake periods (P = 0.01, Fig. 3A) and the sleep-opportunity periods (P = 0.0003, Fig. 3B), with the average range of deviation being similar in both states (≈10%). We find that the maximum value of α occurs at between 60° and 90° during both awake and sleep-opportunity data sets. This period corresponds to ≈9–11 a.m., as hypothesized based on the time window of highest cardiac risk observed in epidemiological studies. We find that the minimum value of α occurs at between 300° and 360°. This period corresponds to ≈1–5 a.m., which is close to the center of the subjects' habitual sleep periods when living outside the laboratory but occurred during both wake and sleep-opportunity periods.

In addition, we find a consistent and significant circadian rhythm in the mean value of the RR intervals during both wake periods (P = 3.6 × 10^–10) and sleep-opportunity periods (P = 2.1 × 10^–9) (Fig. 3C) with a minimum at 180–240° (a broad plateau in the heart rate corresponding to 5–9 p.m.) and a maximum at ≈0° (lowest heart rate corresponding to ≈5 a.m.). We note that this 24-h pattern in the mean RR intervals (Fig. 3C) is different from the one we find for the heartbeat scaling exponent α (Fig. 3 A and B), which indicates separate circadian-mediated influences on these two statistical properties of cardiac dynamics.

Discussion

Our investigations demonstrate the presence of a strong circadian rhythm influence upon the dynamical and correlation properties of heartbeat fluctuations. Specifically, we find a pronounced peak in the heartbeat scaling exponent α at the circadian phase around 60–90°, corresponding to 9–11 a.m., a well known window of cardiac vulnerability. Because the scaling exponent α quantifies a robust scale-invariant/fractal structure in heartbeat fluctuations and has been shown to reflect underlying mechanisms of cardiac dynamic control (36, 37), our findings of a significant change in α at a specific circadian phase indicate a direct influence of the circadian pacemaker on cardiac dynamic control. Further, we find that the peak in α at 60–90° is not related to the circadian-mediated influence on the average heart rate, which displays a very different circadian rhythm with a broad plateau at between 180° and 240° (corresponding to 5–9 p.m.). Moreover, the circadian rhythm in the heartbeat scaling exponent α is not due to changes in behaviors, as all behaviors are balanced across the entire circadian cycle during the forced desynchrony protocol. It is interesting to note that the group average of the scaling exponent α exhibits a minimum during the habitual sleep period, regardless of whether or not the subjects were awake or asleep (Fig. 3 A and B). This finding supports previous reports of a decreased exponent α during sleep, compared with wakefulness (19), and during non-rapid eye movement sleep, compared with rapid eye movement sleep (35, 38, 39). Further, our observations suggest that the decrease in the exponent α during sleep observed in these previous studies may in part be caused by an endogenous circadian effect rather than by an effect of sleep alone. The decrease in the exponent α during the habitual sleep period observed in the present study is generally accompanied by an increase in the mean RR interval (decreased heart rate, Fig. 3C). These findings of a decrease in the exponent α and decreased heart rate during the usual sleep period are consistent with an increased parasympathetic cardiac tone. However, this is not a simple relationship across the entire circadian cycle, because the circadian peaks in α at 60–90° during both sleep and wakefulness are not accompanied by a peak in heart rate. This important dissociation between mean heart rate and the exponent α is notable because α provides a unique insight into cardiac dynamic regulation by quantifying scale-invariant structures in the nonequilibrium heartbeat fluctuations beyond the traditional concept of homeostatic equilibrium (40). Moreover, the information contained in the temporal structure of heartbeat fluctuations as measured by α appears to have considerable clinical relevance.

Previous studies have demonstrated that healthy heartbeat regulation is characterized by values of the scaling exponent α ≈ 1, whereas pathologic conditions such as congestive heart failure are characterized by significantly higher values of α (between 1.25 and 1.4). Because α = 1.5 corresponds to a process of integrated random fluctuations, values of α close to 1.5 as observed for some heart failure subjects indicate a relative loss of correlations associated with altered dynamics of cardiac control. Our findings of strong circadian rhythms leading to ≈10% amplitude variations around the average value of α for healthy young subjects indicates that the underlying mechanism of cardiac regulation is strongly influenced by the endogenous circadian pacemaker. It is possible that a similar circadian effect in vulnerable individuals (e.g., those with underlying cardiovascular disease such as cardiac arrhythmia, prior myocardial infarction and/or congestive heart failure) would contribute to the day/night pattern of adverse cardiac events previously observed in epidemiological studies, with a peak around the circadian phase corresponding to ≈10 a.m. This hypothesis is visualized schematically in Fig. 4, where a similarly strong circadian effect in subjects with heart disease may adversely alter their heartbeat dynamics, bringing the value of their exponent α even closer to the critical value of 1.5 at the circadian phase that corresponds with 9–11 a.m. We note that external behavioral factors such as exercise can further increase the exponent α (34), independent of the endogenous circadian influence on α that we describe here. Although the relative contribution of the independent behavioral and circadian effects is unknown, it is likely that both factors summate to produce the morning peak in adverse cardiac events. Whereas the exponent α has been shown to increase with disease (21) and to be a sensitive marker of survival (22), the mechanism by which impaired cardiac dynamic control can contribute to adverse cardiac events including sudden cardiac death remains to be elucidated.

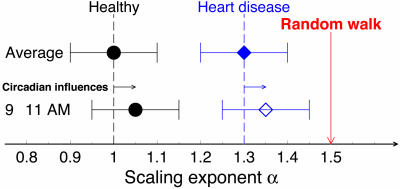
Fig. 4.

Illustration of circadian influences on long-range correlation properties of heartbeat fluctuations at the vulnerable circadian time between 9 a.m. and 11 a.m. Because of circadian influences in this specific time window, the long-range correlations for healthy subjects change toward the direction of a random walk, an integration of uncorrelated fluctuations that is associated with a random process without any underlying feedback control and characterized by α₀ = 1.5. The heartbeat correlation properties in cardiac diseases such as congestive heart failure are characterized by much higher values of the scaling exponent α ≈ 1.3 (16, 22). For these vulnerable subjects, it is plausible that identical circadian influences as observed in our healthy group could further shift the scaling index α (open diamond) toward the critical point α₀ = 1.5 corresponding to a random walk, potentially contributing to the peak in adverse cardiac events at 9–11 a.m.