Surface-enhanced Raman scattering on tunable plasmonic nanoparticle substrates

Abstract

Au and Ag nanoshells are investigated as substrates for surface-enhanced Raman scattering (SERS). We find that SERS enhancements on nanoshell films are dramatically different from those observed on colloidal aggregates, specifically that the Raman enhancement follows the plasmon resonance of the individual nanoparticles. Comparative finite difference time domain calculations of fields at the surface of smooth and roughened nanoshells reveal that surface roughness contributes only slightly to the total enhancement. SERS enhancements as large as 2.5 × 10¹⁰ on Ag nanoshell films for the nonresonant molecule p-mercaptoaniline are measured.

Since the initial discovery of surface-enhanced Raman scattering (SERS) (1–4), understanding how the local electromagnetic environment enhances the substrate-adsorbate complex's spectral response has been of central importance. It has become increasingly evident that plasmon resonances of the metallic substrate provide intense, local optical-frequency fields responsible for the electromagnetic contribution to SERS (5–7).

The lack of reliable techniques for controlling the properties of the local field at the metal surface has been a major experimental limitation in the quantification and understanding of SERS. A striking example of this is the series of experiments reporting enormous SERS enhancements of 10¹² to 10¹⁵ for dye molecules adsorbed on surfaces of aggregated Au and Ag colloid films (6, 8, 9). The SERS enhancements reported in these experiments have been attributed to localized plasmons, or “hot spots,” occurring randomly across this film that fortuitously provide the appropriate electromagnetic nanoenvironment for large SERS enhancements (10). More recent studies have shown that localized plasmons giving rise to very large field enhancements can be formed at the junctions between adjacent nanoparticles (11, 12). These plasmons can be described within the plasmon hybridization picture as dimer resonances (13–15). Likewise, self-similar geometries also provide a means for developing large field enhancements (10, 16).

Several experimentally realizable geometries, such as triangles (17), nanorings (18), and nanoshells (19), support well defined plasmon resonances whose frequencies can be controlled by judicious modification of the geometry of the nanoparticle. Each of these nanostructured geometries offers its own unique near-field properties: plasmon resonant frequency, spatial distribution of the near-field amplitude across the surface of the nanostructure, orientation dependence on polarization of the incident light wave, and spatial extent of the near field. The near-field properties of metallic nanoparticles can be calculated very precisely by a variety of methods, such as analytic Mie scattering theory for high-symmetry geometries, and numerical methods such as the discrete dipole approximation (DDA) (20) and the finite difference time domain (21) methods for nanoscale objects of reduced symmetry. Thus, we can approach a convergence between the electromagnetic fields determined theoretically and those achievable experimentally for an increasing range of nanoscale metallic geometries, ultimately leading to the development of precisely designed nano-optical components for SERS and other applications.

Independent control of the core and shell dimensions of nanoshells offers a valuable opportunity to systematically control the plasmon resonance frequency of a nanostructure. The plasmon resonant frequency of a nanoshell can be tuned from the visible region of the spectrum into the infrared (19, 22–25), giving rise to a host of useful applications (26–29). The plasmon resonances for Au and Ag nanoshells in this wavelength region are quite similar (22). The tunable plasmon frequency allows us to design substrates with plasmon resonances shifted far away from the electronic resonances of an adsorbate molecule, providing a strategy for separating the electromagnetic from the chemical effects in SERS. In addition, the spherical symmetry of the nanoshell provides us with a simple theoretical strategy for analyzing the near field at the nanoparticle surface. Previously reported solution-phase measurements of p-mercaptoaniline (pMA) on Ag nanoshells showed that the magnitude of the SERS enhancement for a saturated monolayer of nonresonant molecules bound to the nanoshell surface could be controlled by nanoparticle geometry with precise, quantitative agreement between theory and experiment (30). In a solution-phase geometry, however, significant reabsorption of the Stokes and anti-Stokes backscattered light by the resonant nanoshell absorbers limited the measured SERS enhancements to a maximum of ≈10⁶. Here we investigate Ag and Au nanoshells as SERS substrates, where the nanostructures are deposited as films onto an inert glass substrate. This simpler collection geometry yields much larger SERS enhancements relative to the solution phase, evaluated by direct experimental comparison with the unenhanced Raman signal of the adsorbate molecule (17). SERS measurements as a function of nanoparticle density indicate that the SERS response is due to the single nanoparticle resonance, even for the case when SERS is performed on dense multilayer nanoshell films. SERS enhancements on nanoshell films were also quantified as a function of nanoshell core and shell dimensions. For nanoshell dimensions resonant with the pump laser wavelength, a single particle response is obtained. Finite difference time domain simulations are used to investigate the effect of surface roughness on the SERS response by comparing the electromagnetic enhancement at the surface of a smooth vs. a roughened nanoshell. It was found that even for the case of a strongly roughened nanoshell, as long as the metal shell is continuous, the far-field plasmon response is retained, and the additional field enhancement at the surface of the nanoparticle contributes less than an order of magnitude to the overall SERS response. SERS enhancements as large as 10¹⁰ were observed when evaluated by direct comparison with unenhanced Raman spectra of the adsorbate.

Nanoshells can serve as a standalone SERS nanosensor of sufficient sensitivity or components of a film substrate that can be deposited on a variety of substrates by various methods (31). Such a near-infrared optimized SERS nanosensor is likely to be of utility in a variety of biological studies and biomedical applications, such as bioassays, intracellular spectroscopy (32), and molecular-level diagnosis of early-stage cancer (33).

Experimental Procedures

Poly(4-vinylpyridine) (PVP)/Au Nanoshell Films. Au nanoshells were fabricated as described in ref. 19. Au nanoshells were deposited onto PVP functionalized glass substrates (31). Glass substrates were first cleaned in a piranha cleaning solution (70% sulfuric acid/30% hydrogen peroxide), rinsed with Milli-Q water (Millipore), and submerged in a 1% solution of PVP (100 mg of PVP per 10 ml of ethanol) for 12 h. The substrates were then removed from the PVP solution, rinsed with ethanol, and submerged in an aqueous Au nanoshell suspension. The Au nanoshells (19) fabricated for these experiments had a silica core radius of 94 nm and a Au shell thickness of ≈9 nm, as determined by comparing UV-visible spectroscopy and Mie scattering theory, and independently verified by electron microscopy. The nanoshell deposition time was varied from 15 min to 24 h to obtain a variety of nanoshell particle densities in the films. To obtain the highest nanoshell densities, it was necessary to neutralize the nanoshell surface charge by the addition of 3 mg of sodium chloride 12 h into the deposition process. Finally, the PVP/nanoshell films were submerged in a 100 μM solution of pMA in ethanol for 3 h to ensure saturation of the available nanoshell surface.

Dense Nanoshell Films. Ag nanoshells were constructed by using 39-, 58-, 81-, and 94-nm radius silica cores, on which Ag shells ranging from 7 to 18 nm were deposited, as described in ref. 22. After fabrication, UV-visible spectroscopy measurements were correlated with Mie scattering theory for each nanoshell sample to verify core diameter and shell thickness (19, 22). These data showed that deviations in the shell thicknesses of ≈1 nm were present in all nanoshell samples. The Ag nanoshell films were fabricated by repeatedly evaporating 300-μl aliquots of ≈10⁸ particles per ml of nanoshell suspension onto a 7-mm² area of a glass microscope slide until complete surface coverage was achieved. pMA was deposited onto the nanoshell film by evaporating 10 μl of a 10 μM solution of pMA in ethanol.

Instrumentation. Absorption spectra were obtained by using a Cary 5000 UV-visible/near-infrared spectrophotometer in the range of 400 to 2,000 nm. Raman spectra were obtained with a Renishaw micro-Raman spectrophotometer by using a 782-nm excitation laser, a 2-μm-diameter spot size, and a 30-sec acquisition time. PVP/nanoshell films were sputter-coated with a thin (≈10 nm) layer of Au for analysis in a Phillips FEI XL-30 environmental scanning electron microscope. The scanning electron microscope analysis of these nanoshell films is presented first for clarity.

Results

SERS Dependence on Nanoshell Particle Density. In this series of experiments, we evaluated the intensity dependence of the SERS response for nanoshells with monolayer coverage of pMA, as a function of nanoparticle density. This evaluation was accomplished by preparing films of increasing nanoparticle density ranging from <3 Au nanoshells in the beam spot of our Raman microscope to dense multilayer films for SERS studies. Representative images of these films are shown in Fig. 1. Each Au nanoshell film was analyzed by using at least 20 scanning electron microscope images at ×2,000 magnification and 10 images at ×800 magnification. The film images were analyzed by counting the number of nanoshells in the entire image area, tabulating the number of isolated nanoshells, the number of aggregates, and the number of nanoshells in each of the aggregates. Nanoshells were considered to be in an aggregate only if they appeared to be in contact with another nanoshell. With some larger aggregates it was necessary to estimate the number of nanoshells present by dividing the area of the aggregate by the area of a single nanoshell. All nanoshell densities are tabulated as the number of nanoshells per 3.14 μm², consistent with the 2-μm diameter sampling area of our micro-Raman instrument. The individual and aggregate nanoshell densities for the series of films are tabulated in Table 1. The percentage of nanoshells in a cluster, or equivalently the percent probability that a nanoshell probed in this sample was part of an aggregate, was determined by dividing the number of nanoshells in a cluster by the total number of nanoshells in that sample. The percentage of aggregates was determined by normalizing the number of nanoshell aggregates by the total number of particles (the number of aggregates plus the number of free nanoshells). This is the percent probability that the laser spot is probing an aggregate during the Raman spectrum acquisition.

Fig. 1.

Representative environmental scanning electron microscope images of PVP/Au nanoshell films, characterized by the number of nanoshells per 2-μm spot (NS/spot). (a) 2.58 ± 0.32 NS/spot. (b) 16.66 ± 1.9 NS/spot. (c) Optical micrograph of a dense multilayer nanoshell film.

Table 1. Nanoshell density analysis of the PVP/Au nanoshell films.

Sample	Average number of nanoshells per spot	Nanoshells in clusters, %	Particles that are clusters, %
i	2.58 ± 0.32	29	14
ii	5.34 ± 0.53	25	12
iii	9.16 ± 0.51	21	14
iv	12.12 ± 1.7	47	39
v	16.66 ± 1.9	59	46
vi	15.75 ± 2.1	72	53
vii	32.15 ± 4.9	87	83

Complete coverage: 48.47

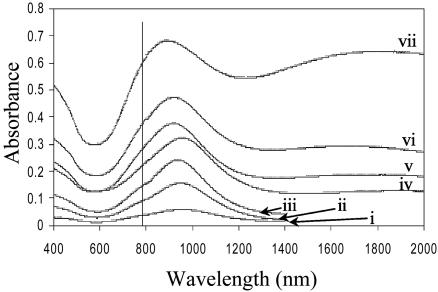
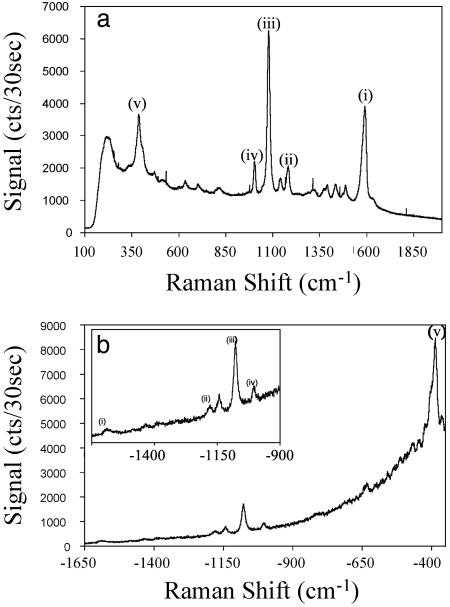
The UV-visible spectrum of nanoshell films as a function of nanoshell density is shown in Fig. 2. This spectrum consists of two important features: the isolated nanoshell plasmon resonance corresponds to the peak at ≈950 nm and the nanoshell aggregate resonance that becomes apparent at ≈1,800 nm as the nanoshell density increases. At the highest coverages, a significant fraction of the overall nanoshell film plasmon response has shifted into the infrared region of the spectrum. However, the curves in Fig. 2 are shown as measured, indicating that the plasmon response at the single nanoshell resonance nonetheless increases with an increasing number of nanoshells. To sample variability of the SERS spectrum across each PVP/nanoshell film, at least 30 Raman spectra were taken at random locations on each sample. A representative Stokes and anti-Stokes SERS spectrum of pMA on a nanoshell film is shown in Fig. 3. Each Raman spectrum was analyzed by subtracting the baseline from the peak magnitude at each specific Raman mode. This analysis was confined to the 390-, 1,077-, and 1,590-cm^–1 modes because they were the only observable modes at the lowest nanoshell densities used.

Fig. 2.

Absorption spectrum of the PVP/Au nanoshell films for each nanoshell density listed in Table 1. The pump laser wavelength of 782 nm is shown.

Fig. 3.

Stokes (a) and anti-Stokes (b) SERS spectrum of pMA on nanoshell film substrates. The 1,590-cm^–1 (i), 1,180-cm^–1 (ii), 1,077-cm^–1 (iii), 1,003-cm^–1 (iv), and 390-cm^–1 (v) ring vibrational modes of pMA are indicated.

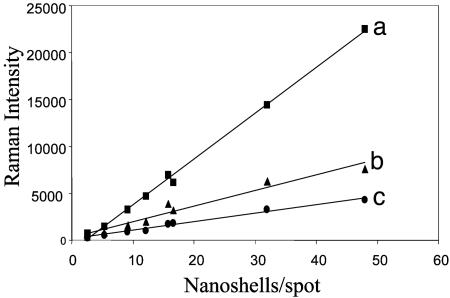
Magnitudes of these three Raman modes as a function of nanoshell density on each film are shown in Fig. 4. A linear response of the Raman mode intensities with nanoshell density is clearly observed, extending across the range of densities shown in Table 1 to a maximum density corresponding to the dense multilayer film shown in Fig. 1c. The linear dependence over this broad range indicates that the SERS response for nanoshells of these internal dimensions and at this pump laser wavelength is driven by the single nanoshell resonance response, not that of nanoshell dimers or aggregates. The maximum observed variation in the magnitudes of the Raman modes was ≈25%, obtained by sampling multiple spots across each sample. This error is just slightly larger than the statistical deviation in the number of nanoshells per spot shown in Table 1 (a maximum of ≈15%).

Fig. 4.

The 1,077-cm^–1 (a), 1,590-cm^–1 (b), and 390-cm^–1 (c) Raman modes as a function of Au nanoshell density on the substrate.

The SERS response of nanoshell films observed here is dramatically different from the Raman response of solid Au colloidal aggregate films as a function of nanoparticle density. Zhu et al. (34) recently performed a similar experiment with films composed of solid Au colloid and the same adsorbate molecule, at an excitation wavelength of 632 nm. For solid Au nanoparticles, this pump wavelength is resonant with the plasmon response of the “dimer” or aggregate plasmon and offresonance with respect to the single nanoparticle plasmon response. In these experiments, a drastically different behavior was observed: Only a minimal SERS response was reported until the solid colloid particle density exceeded a threshold corresponding to the onset of nanoparticle aggregates in the films, whereupon a dramatic supralinear increase in the Raman response was observed.

The Raman enhancement, G, is measured experimentally by direct comparison as (17, 34)

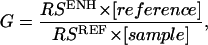[1]

where RS^ENH and RS^REF are the measured Raman magnitudes and [sample] and [reference] are the estimated number of molecules in the enhanced and reference samples, respectively. The number of molecules in the sample was estimated by using the average number of nanoshells per spot, the surface area of the nanoshell, and the packing density of pMA on the nanoshell surface (35). This analysis assumes that the entire nanoshell surface area contributes to the Raman response and is a conservative estimate, essentially a lower bound, of the Raman enhancement. The density of neat pMA (1.06 g/cm³) and the parameters of the optical beam are used to estimate the number of molecules in a nonenhanced sample as 3.14 × 10¹³ molecules (17). The enhancement is the weighted ratio of the measured Raman intensities of the enhanced signal vs. the nonenhanced signal. The observed Raman response is independent of nanoshell density, as would be expected if the response were attributable to the individual nanoshell plasmon response. The average Raman enhancements of the 1,077-, 1,590-, and 390-cm^–1 modes are 2.21 ± 0.42 × 10⁸, 1.04 ± 0.19 × 10⁸, and 5.72 ± 0.48 × 10⁷, respectively. This again reinforces our earlier conclusion that when the single nanoshell plasmon is resonant with the Raman pump laser, the individual nanoparticles give rise to the large Raman enhancements observed.

SERS Dependence on Nanoshell Dimensions. Ag nanoshell films were used to investigate the Raman response as a function of nanoshell core and shell dimensions. Dense nanoshell films were used exclusively in this series of measurements to ensure the same nanoshell densities per unit surface area and hence the same number of molecules probed in each measurement. This allows for the direct comparison of SERS enhancements from nanoshells of differing dimensions. The signal strengths of the 1,590-, 1,180-, 1,077-, 1,003-, and 390-cm^–1 ring modes (36) of pMA were monitored as a function of Ag shell thickness for four different silica core radii. These Raman modes are indicated in the spectrum shown in Fig. 3.

The calculation of the relative dependent Raman response due to the local electromagnetic field at a nanoshell surface follows the method of Kerker, Wang, and Chew (37). The field exciting the molecule is taken as the sum of the incident plane wave and the local electromagnetic field on the nanoshell surface as calculated by Mie scattering theory (38). The excited molecular layer on the nanoshell is treated as a layer of noninteracting dipoles all oriented perpendicular to the nanoshell surface with a molecular polarizability taken as unity and radiating at the Stokes shifted frequency. This models a monolayer coverage of Raman active molecules where the C_2v axes (36) of all molecules are perpendicular to the nanoshell surface. The Raman shifted electromagnetic field contribution is the sum of the electromagnetic field of the molecule's dipole and the nanoshell response at the Stokes shifted frequency ω_s:

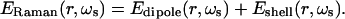[2]

The total electromagnetic contribution to the SERS process is generally considered to be proportional to the product of field contributions at the incident (ω_o) and shifted frequencies (39). Therefore, the measured Raman response should be proportional to |E_shell(ω_o)|²|E_Raman(ω_s)|². This SERS optimization factor, |E_shell(ω_o)|²|E_Raman(ω_s)|², is then calculated at each point on the nanoshell surface, assuming a monolayer of a molecule covering the surface of the nanoshell, and allowing for a coverage of 0.3 nm² per molecule (35). |E_shell(ω_o)|²|E_Raman(ω_s)|² is averaged over the surface of the nanoshell; we justify this because we are modeling the response of a complete layer of dipoles at the nanoshell surface. It should be emphasized that this is not a calculation of the overall Raman enhancement but rather a relative comparison of the electromagnetic response as a function of nanoshell geometry, under the same experimental conditions.

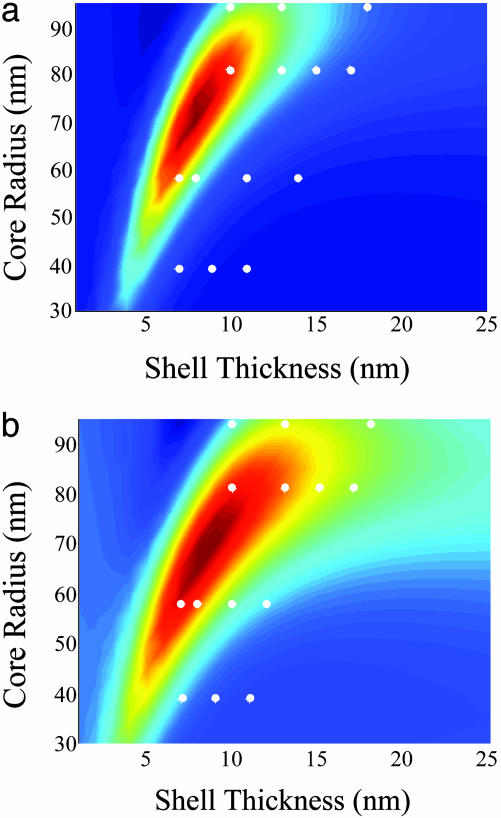
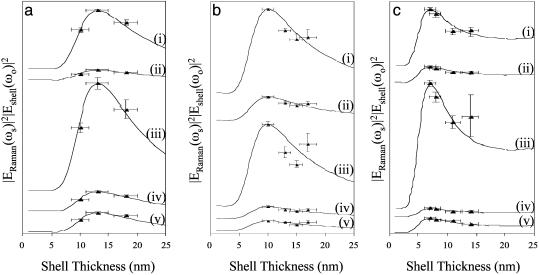
The calculated SERS optimization factor is shown as a function of core radius and shell thickness for the 1,590- and 390-cm^–1 Stokes modes in Fig. 5. This is the normalized Raman optimization factor for these two modes as a function of core radius and shell thickness for an excitation wavelength of 782 nm. The circles in Fig. 5 correspond to the specific Ag nanoshell dimensions fabricated in this series of experiments.

Fig. 5.

Calculated |E_shell(ω_o)|²|E_Raman(ω_s)|² of 1,590-cm^–1 (a) and 390-cm^–1 (b) modes as a function of silica core radius and silver shell thickness. The white dots indicate the fabricated nanoshell films.

The measured Raman spectra are compared to the electromagnetic theory in Fig. 6. For each mode, |E_shell(ω_o)|²|E_Raman(ω_s)|² is plotted for a specific core radius as a function of shell thickness. |E_shell(ω_o)|²|E_Raman(ω_s)|² is scaled and offset for comparison to measured values. The y-axis error bars arise from standard deviations between different nanoshell samples as well as different locations on the same sample. The x-axis error bars are the shell thickness deviations calculated from Mie scattering theory, assuming a Gaussian distribution in shell thickness. The excellent agreement of the measured and calculated SERS response of nanoshells in Fig. 6 a–c indicates that the SERS response follows the single-nanoshell electromagnetic response in this geometry when the individual nanoshells are tuned near the excitation and Stokes frequencies. Data were acquired in the case of the single-nanoshell plasmon resonance blue-shifted from the excitation wavelength. For these nanoshells, the excitation laser was tuned to the aggregate resonance wavelength, and the SERS response did not follow the single-nanoshell plasmon response. A rigorous analysis of this geometry is beyond the scope of this paper and will be the focus of future publications.

Fig. 6.

Comparison of the measured Raman modes to theoretical calculations extracted from the contour plots shown in Fig. 5. The normalized |E_shell(ω_o)|²|E_Raman(ω_s)|² of the 1,590-cm^–1 (i), 1,180-cm^–1 (ii), 1,077-cm^–1 (iii), 1,003-cm^–1 (iv), and 390-cm^–1 (v) Stokes modes are plotted for each fabricated core radius, where a is 94 nm, b is 81 nm, and c is 58 nm.

The Raman enhancement of these dense nanoshell films was determined experimentally following Eq. 1. The number of molecules in the enhanced sample was determined to be ≈1.05 × 10⁶ molecules. The Raman enhancements for the 1,077-, 1,180-, and 1,590-cm^–1 Stokes Raman modes as a function of core radius and shell thickness are shown in Table 2. These Raman enhancement values are consistent with the enhancement factors calculated in the nanoshell-density analysis.

Table 2. Raman enhancement as a function of silica core radius and Ag shell thickness.

Dimension, nm		Enhancement
Core	Shell	1,077 cm-1	1,180 cm-1	1,590 cm-1
94	10	1.3E+10	1.6E+09	2.0E+09
94	13	2.4E+10	1.8E+09	4.9E+09
94	18	1.8E+10	1.7E+09	3.1E+09
81	10	2.5E+10	4.3E+09	8.4E+09
81	13	1.1E+10	2.7E+09	2.4E+09
81	15	2.2E+09	4.2E+08	4.6E+09
81	17	1.6E+10	1.3E+09	5.0E+08
58	7	1.7E+10	2.7E+09	4.4E+09
58	8	1.3E+10	2.3E+09	3.7E+09
58	11	5.0E+09	9.9E+08	1.3E+09
58	14	1.3E+10	1.4E+09	2.6E+09
39	7	4.8E+09	6.9E+08	1.1E+09
39	9	1.6E+10	1.7E+09	2.1E+09
39	11	7.1E+09	1.1E+09	1.8E+09

Discussion

In none of our studies do we see an overwhelmingly large SERS response due to a nanoshell dimer plasmon resonance, as is characteristic of the plasmon response of colloidal aggregate films. There are several possible reasons for this observation. Our observations clearly indicate that tuning the individual nanoshell peak on resonance with the pump laser results in the enhancement following the individual nanoshell SERS response. However, from field calculations we do know that the predicted enhancement in the junction between two nanoparticles is much larger than the single-nanoshell near-field enhancement and that it also has a broader spectral response, so dimer plasmon resonances could be excited at the pump laser frequency used. The most likely explanation for the lack of a dimer plasmon contribution is that, in the dimer and small aggregates that are formed in these films, the junctions between particles are touching and too narrow to allow adsorbate molecules between the nanoparticles. Indeed, for nanoparticles as massive as nanoshells the interparticle forces are very strong; in all our films we have not yet observed nanoshell aggregates where the individual nanoparticles were less than a particle radius away but did not appear to be in direct contact.

It is also important to consider the effect of nanoscale roughness on the surface of the nanoshells and whether this surface roughness may be responsible for additional local field enhancements beyond the ideal case of the smooth spherical nanoshell described by Mie scattering theory (38).

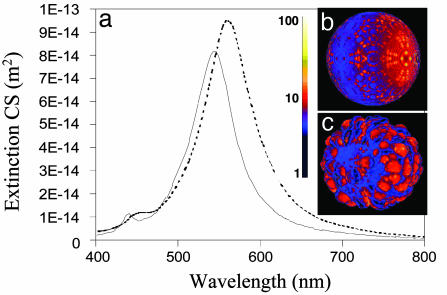
Finite difference time domain techniques (40) were used to examine the electromagnetic response in both the near and far field for a smooth vs. a roughened nanoshell (Fig. 7). For the topologies considered here, we find only a slight increase in local-field intensities relative to the smooth shell local field at the peak of each respective nanoparticle's plasmon resonance. The plasmon extinction spectrum is largely independent of roughness (although a small spectral peak shift does occur) provided the metallic shell is complete (Fig. 7a). We do note, however, that the near field just off the peak of the plasmon resonance falls off more sharply for a smooth nanoshell than for the roughened nanoshell topology considered here, perhaps leading to a slight increase of enhancement for the rougher nanostructure. When pinholes are introduced onto the nanoshell surface there is further local-field enhancement; however, the far-field plasmon response (i.e., the coupling between the near field at the nanoparticle surface and the input and output waves) is significantly reduced at the pump and Stokes wavelengths. Because the far-field plasmon response for all of the nanoshells used in these experiments corresponded well to that of a smooth nanoshell plasmon, and because of the systematic core-shell dependence observed in these experiments, we conclude that pinholes in the shell layer are not likely to be contributing significantly to the SERS enhancements measured in this series of experiments.

Fig. 7.

Finite-difference time-domain calculations of the far- and near-field plasmon response of a smooth and a rough but continuous nanoshell. (a) The extinction cross section of a smooth (solid line) and rough (dashed line) silver nanoshell with a 39-nm-radius core and a 9-nm-thick shell. The magnitudes of the electromagnetic field on the smooth nanoshell at the peak dipole resonance (545 nm) (b) and the rough nanoshell at the peak dipole resonance (562 nm) (c) are shown.

Conclusions

The geometrically tunable plasmon resonance and the large, reproducible SERS enhancements that can be optimized to a specific pump laser wavelength make nanoshell films ideal SERS substrates. The linear response in the magnitude of the SERS response observed in this series of experiments indicates that each individual nanoshell is contributing to the SERS enhancement independently, in contrast to Au colloid experiments that showed no enhancements unless Au colloid junctions were formed (34). The experiments described here have focused on the regime corresponding to individual nanoshell resonant enhancements and not the enhancement due to interparticle dimer plasmons. The observation of linear dependence of the SERS response implies that, in addition to the film geometry, nanoshells may be used as individual, standalone SERS nanosensors to probe various environments with submicrometer spatial resolution, such as that inside living cells. The strength of the SERS enhancements observed here also indicates that few-molecule sensitivity is achievable at individual nanoshell densities, an additional feature that may make nanoshells valuable as probes for intracellular spectroscopy. Tailoring the Raman enhancement specifically for near-SERS by using near-infrared pump laser wavelengths also essentially eliminates the generation of unwanted fluorescence, a significant problem in optical studies of biological and biomolecular systems. The high signal-to-noise ratio for nanoshell-resonant SERS in the nanoshell film geometry allows for direct measurements of the Stokes/anti-Stokes ratios in the Raman spectrum of adsorbate molecules, which will permit controlled, systematic studies of optical pumping effects in SERS, a topic of significant interest and controversy (6, 41).