A network perspective on the virus world

ABSTRACT

Viral evolution is characterized by high rates of horizontal gene transfer and fast sequence divergence. Furthermore, there are no universal genes shared by all viruses. As a result, distant relationships among viruses are better represented by a network than by a tree. Here we discuss 3 network representations of the virus world with decreasing levels of complexity, from a multilayer network that integrates sequence conservation and patterns of gene sharing to a classic genome similarity network. As new tools for network analysis are developed, we expect that novel insights into virus evolution will result from the study of more complex representations of the virus world.

Since The Origin of Species was published, the idea that all extant and past forms of life can be organized as a Tree of Life (TOL) has become quintessential to evolutionary biology. More than 150 years later, in the wake of the genomic revolution, the TOL remains a valid approximation, as long as horizontal gene transfer (HGT) among prokaryotes and viruses does not completely blur the tree-like pattern that arises from vertical descent with modification.¹ While HGT sets a fundamental limit to the TOL concept, high degrees of sequence divergence impose a technical limitation to the construction of deep phylogenetic trees. Because fast divergence and intense horizontal transfer are 2 main characteristics of viral evolution, the reconstruction of large-scale viral phylogenies poses a major technical and fundamental challenge to the interpretation of the virosphere as a tree. Furthermore, there are no universal genes shared by all or even most groups of viruses, which restricts phylogenetic analyses to discrete assemblages of more closely related viruses, thereby fragmenting and blurring the global understanding of the evolutionary relationships in the viral world. Instead, the evolutionary relationships among viruses can be more precisely represented as a network of gene sharing.²

Among many possible network representations,³ a highly informative description of the virus world is provided by a network with 2 layers (Fig. 1A). The gene layer consists of a sequence similarity network, with nodes representing viral genes and edges connecting pairs of homologous genes with a weight proportional to their sequence similarity. The second layer represents the viral genomes; nodes in the genome layer do not connect with each other, but rather to nodes from the gene layer: each genome node is connected to the genes that belong to that genome. A simpler representation of this 2-layer network can be obtained by aggregating the nodes from the gene layer into groups of homologous genes. Such groups appear in the gene layer as modules, i.e. sets of nodes that are much more densely connected with each other than with the rest of the network. Indeed, some popular methods to identify sets of orthologous or, more generally, homologous genes work by applying a module detection algorithm to a sequence similarity network.^4,5 Once genes are grouped into families of homologs, a bipartite network is obtained by connecting genome nodes and gene family nodes whenever a gene family is present in a genome (Fig. 1B). Compared with the 2-layer network, the bipartite network lacks the former's precise information on sequence similarity, which could be used to reconstruct single-gene phylogenies, but keeps the essential information on which gene families are shared by which genomes. A further simplification results from projecting the bipartite network into a genome similarity network (Fig. 1C). There are multiple ways to obtain a genome similarity network from a bipartite gene sharing network. The main step is defining a measure of similarity between genomes, such as the number of shared genes, the fraction of shared genes, or the probability that such number of shared genes occurs by chance. The network is then readily obtained by connecting pairs of genomes with edges, whose weights are proportional to the similarity between the genomes.

Figure 1.

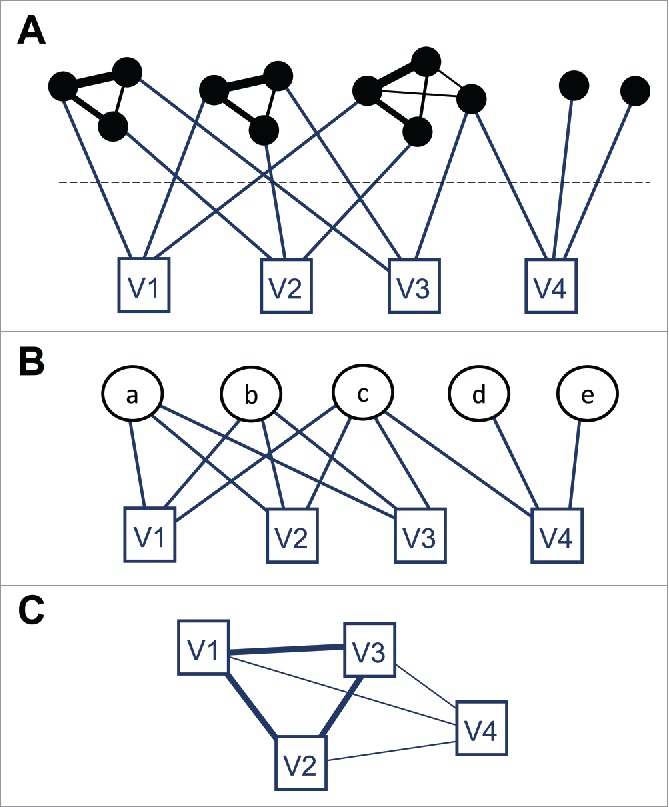
Three network representations of a toy virus world composed of 4 viral genomes (squares) and 12 genes (black circles) that belong to 5 gene families (white circles). (A) Two-layer network, with the gene layer on top and the genome layer at the bottom. Black edges of different thickness indicate the similarity between sequences in the gene layer. (B) Bipartite network, which results from clustering groups of homologous genes in the gene layer into gene family nodes. (C) Genome similarity network; the thickness of the links is proportional to the number of shared gene families.

Within the network framework, module detection algorithms^6,7 have become a useful tool to define classes of viruses. Multi-scale approaches based on information theory⁸ or repeated application of Newman's modularity⁹ allow the study of genome similarity networks at multiple taxonomic levels. Local algorithms, such as OSLOM,¹⁰ can detect overlapping modules (e.g. those resulting from mosaic genomes) and remove nodes whose module assignation is poorly supported statistically (e.g., single members of new taxa that occasionally share widespread genes with otherwise unrelated groups). Module detection in bipartite networks often involves Barber's modularity maximization¹¹ although relevant insights into the patterns of gene sharing and transmission can be obtained simply from the study of basic topological properties of the network.³ The inference of viral groups from genome similarity networks might not differ much from unsupervised machine learning techniques but the more realistic representation of the virus world as a bipartite network of gene sharing makes network-based approaches more powerful at dealing with decaying degrees of genomic similarity at long evolutionary distances, as well as with poorly sampled taxa.

Genome similarity networks are more compact and easier to analyze than their bipartite counterparts but have several limitations. First, they lack information on the kind of genes that make 2 genomes similar, making it difficult to discriminate between cases of shared host-related genes and shared ancestral genes. Moreover, some properties of the final network may depend on the particular measure used to evaluate genome similarity. Finally, the projection of bipartite networks can lead to structural artifacts, such as spurious scale-free degree distributions.¹²

Despite these limitations, genome similarity networks have been successfully applied to bacteriophages to reveal the internal structure of this group of viruses¹³ and to assign newly discovered phages to established families.¹⁴ More recently, a large collection of viruses with dsDNA genomes has been studied under the framework of bipartite networks.¹⁵ The analysis of the network showed that most dsDNA viruses belong to one of 2 major groups, each of which includes viruses from the 3 domains of life and is characterized by a distinct major capsid protein. Dissection of those groups leads to a hierarchy of subgroups which is consistent, despite some exceptions, with the established taxonomy of viruses. The hierarchical organization of the dsDNA virus world is founded on 3 classes of conserved genes: i) hallmark genes, such as capsid proteins, maturation proteases and packaging ATPases, that characterize and distinguish the 2 major viral groups, ii) connector genes, such as the baseplate proteins of myoviruses, that are shared by multiple subgroups within a group, and iii) signature genes that are highly specific to sets of related viruses (Fig. 2). Notably, most viruses that infect Archaea do not fall into the 2 major groups of dsDNA viruses and form a more fragmented network that is only weakly connected to the rest of the dsDNA virosphere, apparently reflecting the existence of stronger barriers to HGT among distinct groups of archaeal viruses and especially between viruses of archaea and bacteria.¹⁶ In general, the pattern of connections is poorly conserved in more than 80% of the gene families of the bipartite virus network, in accord with the major role of HGT in virus evolution.

Figure 2.

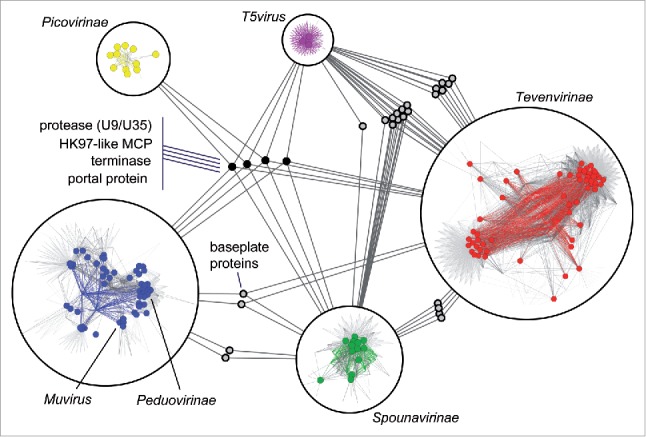
Hierarchical structure of a portion of the bipartite network for tailed bacteriophages (order Caudovirales). On the small scale, sets of related viruses and their associated gene families form densely connected modules. Within a module, genome nodes are represented as colored circles, whereas gene family nodes are denoted by the points where the edges (gray and colored lines) join. Colored edges connect the genomes of a module with the module's signature genes. On the large scale, modules connect with each other through shared connector genes, represented here as small gray circles. The 4 hallmark genes that are shared by most members of the order Caudovirales occupy a central position in the network (small black circles). This portion of the network corresponds to modules 9a, 9d, 12, 13, and 18 from ref. 15. MCP, major capsid protein.

As new tools for analysis of bipartite networks are developed, it soon will become possible to extend the network analyses to the entire virosphere and compare the findings from this approach with the patterns observed for viral hallmark genes.¹⁷ From a complementary perspective, multilayer networks, such as the 2-layer representation of the dsDNA virosphere described above, have recently become a focus of network science.¹⁸ Although technically challenging, a detailed analysis of the 2-layer network is a promising direction that will integrate sequence similarity and gene sharing in a unified framework. Eventually, additional layers accounting for host range, geographic location and environmental conditions would allow integration of information on genome evolution with ecological data, eventually resulting in a comprehensive picture of virus evolution.¹⁹

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.

Funding

This work was funded by US Department of Health and Human Services (Intramural funds).