ABSTRACT
Atherosclerosis enables to alter not only the microstructural but also the physical properties of the arterial walls by plaque forming. Few studies so far have been conducted to calculate the isotropic or anisotropic mechanical properties of the healthy and atherosclerotic human coronary arteries. To date there is a paucity of knowledge on the mechanical response of the arteries under different strain rates. Therefore, the objective of the concurrent research was to comprehend whether the alteration in the strain rates of the human atherosclerotic arteries in comparison with the healthy ones contribute to the biomechanical behaviors. To do this, healthy and atherosclerotic human coronary arteries were removed from 18 individuals during autopsy. Histological analyses by both an expert histopathologist and an imaged-based recognizer software were performed to figure out the average angle of collagen fibers in the healthy and atherosclerotic arterial walls. Thereafter, the samples were subjected to 3 diverse strain rates, i.e., 5, 20, and 50 mm/min, until the material failure occurs. The stress-strain diagrams of the arterial tissues were calculated in order to capture their linear elastic and nonlinear hyperelastic mechanical properties. In addition, Artificial Neural Networks (ANNs) was employed to predict the alteration of mean angle of collagen fibers during load bearing up to failure. The findings suggest that strain rate has a significant (p < 0.05) role in the linear elastic and nonlinear hyperelastic mechanical properties as well as the mean angle of collagen fibers of the atherosclerotic arteries, whereas no specific impact on the healthy ones. Furthermore, the mean angle of collagen fibers during the load bearing up to the failure at each strain rate was well predicted by the proposed ANNs code.
KEYWORDS: Artificial Neural Networks, atherosclerosis, collagen fiber, coronary artery, elastic modulus, mechanical properties, Mooney-Rivlin
Introduction
The main objective of solid mechanics in the cardiovascular systems is the examination of the mechano-biological performance of arteries not only in the healthy but also in the diseased condition, which may pave the way for better understanding their task according to their structure and mechanics, for example, a set of crucial information for medical actions and decision making on the diseases of the artery, design of vascular implants, including stents and grafts as well as for tissue engineering purposes.1 Formation of the atherosclerotic plaque and its rupture in more than 50% of cases are the main reason of death.2 Atherosclerosis alone stands as the first cause of unexpected death in middle age individuals in the United States.3 In the other words, 657,000 surgeries performed through the skin to access to the inner organs instead of open heart surgery in the United States in 2012.4 Atherosclerotic disease, therefore, is the most crucial pathology in the arterial system.5 The formation of atherosclerotic plaques in different arterial systems could trigger transient ischemic attacks and stroke.6 For example, atherosclerosis in the iliac arteries is the main root of peripheral artery disease.7
The internal structure of a soft biological tissue has a narrow relation with its macroscopic mechanical properties.8 Many experimental and continuum-based studies so far have been carried out to propose an especial model to shed light on this relation. It is obvious that a suitable material model, which established based on the microstructure of a soft biological tissue enables us to have a better outlook from the applied load and strain/deformation response of a tissue. Arterial wall is the most complicated soft biological tissue which its intricate microstructure has a strict correlation with its macrostructure mechanical properties. The mechanical properties of the arterial wall have been exhibited to be altered in different diseases, especially atherosclerosis. Once plaque progression begins in the arterial wall, the thickness of the innermost layer of the arterial wall, namely intima, begins to increase. The main structural components of atherosclerotic intima are collagen and elastin. Biomechanical behavior of atherosclerotic intima tissue largely depends on these components and its internal structure. Moreover, since coronary arteries are of dominant standing in the heart and circulation systems, restenosis after stenting is more general in the coronary arteries9,10 as well as the long-standing objectives of refining our knowledge on the mechanisms related to the coronary artery disease and improving stent designs, the current study focuses on the investigation of this arterial segment. To be able to understand the mechanisms involved in percutaneous transluminal coronary angioplasty actions as well as stent designs, it is of vital importance to have a deeper outlook about the mechanical properties of the healthy and atherosclerotic arterial walls of the coronary arteries in order to be able to establish a well-organized computational model.11
Elastin has a key asset in the elastic behavior of the arterial wall in respect to the variation of blood pressure over the cardiac cycle. Experimental studies reported the elastic modulus of 0.5–1.0 MPa for the arterial elastin.12,13 However, only a little amount of elastin is existed in the atherosclerotic intima tissue, and elastin is mainly located in the medial layer (media) of the artery. Therefore, elastin can be taken into account as a minor contributor to the mechanical response of the atherosclerotic intima tissue.
Collagen fibers also divided into different types, however, only some of them can be found in the atherosclerotic intima tissue, such as I, III, IV, and V.14 Stiffness of individual collagen fibers was estimated as 400 MPa to 1 GPa,12 but no distinction was made between different collagen types.15 Due to the high stiffness of collagen, it is expected that the amount and organization of collagen in the arterial wall have a substantial influence on its overall mechanical behavior.16
So far few studies have been carried out to quantify the mechanical properties of the healthy and atherosclerotic human coronary arteries, and the data of these characteristics under different strain rates are limited. In addition, our understandings about the orientation of collagen fibers in the arterial wall during the load bearing up to the failure are limited. To date, both in vitro17,18 and in vivo19,20 studies have been carried out to capture the mechanical behavior of healthy and atherosclerotic arteries. Recently, Karimi et al.21 performed an experimental study to take the axial mechanical properties of the healthy and atherosclerotic human coronary arteries into account. Their results revealed that the atherosclerotic arteries are significantly (p < 0.05) stiffer than that of healthy ones. However, the nonlinear mechanical behavior of the arterial wall as well as the role of collagen fibers in their study have not been considered yet. The nonlinear mechanical behavior of the healthy and atherosclerotic arterial wall, then, added to their study using different hyperelastic material models.22,23 Holzapfel et al.24 proposed a constitutive framework, namely Holzapfel-Ogden-Gasser, for arterial wall according to the description of its passive mechanical properties. Their model was enabled to consider the role of collagen fibers family in the media and adventitia layers in a cylindrical shape structure. In addition, very recently an anisotropic constitutive equation was proposed which enables to explicitly consider the role of collagen fibers in the mechanical behavior of the arterial wall.25 However, the variation in the pattern of collagen fibers during load bearing at different strain rates in their study have not been studied. Yang et al. proposed a model that contacting different functions, such as electrical, mechanical, and chemical ones, of smooth muscle cells.26 Zulliger et al. also added a pseudo-strain energy function to the previous equation to describe the mechanical properties of arterial wall by taking the role of collagen, elastin, and smooth muscle into account.27 Regardless of the findings of these studies, the variations of arterial mechanical properties under different strain rates for the healthy and atherosclerotic arteries remain unclear. The variation of mean collagen fibers' angle during load bearing, moreover, has not been determined.
Arterial wall generally is a 3-layer structure, including the intima, the media, and the adventitia. It has been reported that in the media, collagen fibers are positioned in 2 helically distributed families. In the other words, they seem to be orientated in a very close position to the circumferential direction. However, in the outer (adventitia) and the intima layers, position of the collagen fibers is almost exclusively dispersed.28 Fiber-reinforced models up to now could nearly define the mechanical behavior of the arterial walls in which the collagen fibers presumed to be located in an isotropic ground matrix.29 A complicate mechanical behavior of the arterial wall, however, proposed an introduction of statistical distribution functions with the intention of finding a more realistic and precise approach to capture the curliness of the collagen fibers in the arterial wall.30,31
It is obvious that the average angle of collagen fibers in the arterial wall subjected to a dramatic alteration according to the applied load, nevertheless, the proposed models so far could not be able to have a prediction about the orientation of collagen fibers during load bearing. This study executed a grouping of experimental and numerical analyses to determine the effect of strain rates on the mechanical properties of the healthy and atherosclerotic human coronary arteries thru both the uniaxial and histological data. In addition, it was aimed to benefit from Artificial Neural Networks (ANNs) model to predict the variation of mean angle of collagen fibers during load bearing in the uniaxial tensile test machine at different strain rates.
Results
A typical arterial wall along with the experimental setup is displayed in Fig. 1. Eighteen healthy and atherosclerotic human coronary arteries were removed from the cadavers within 5 hours' postmortem and used for experimental mechanical measurement. The experimental setup was consisted of a group of 3 CCD cameras which helped us to lively measure the strain/displacement of the samples during load bearing up to the failure point. Before the mechanical measurement begins, the mean angle of collagen fibers was experimentally measured using both the customized optical microscope and an image based recognizer software to make sure a precise calculation. The histological analyses revealed that the mean angle of collagen fibers at the initial stage before load application are insignificantly different in a way that the average angle of collagen fibers in the healthy and atherosclerotic arterial walls was 37.491 ± 3.843 and 43.121 ± 4.098, respectively. Thereafter, the samples were located on the testing machine and subjected to 3 diverse strain rates, including 5, 20, and 50 mm/min. The stress-strain diagrams of the coronary tissues at the strain rate of (a) 5, (b) 20, and (c) 50 mm/min were calculated and presented in Fig. 2. The elastic modulus and maximum stress of the healthy and atherosclerotic coronary arteries were then calculated from the experimental stress-strain diagrams and plotted in Figs. 3 and 4, respectively. Young's modulus or elastic modulus is defined as a mechanical property of linear elastic solid material which accounts as the force applied to the sample in respect to the resultant stretch of that material. The term maximum stress is also defined as the highest amount of stress that a tissue can bear during its load bearing. The linear elastic analysis revealed that strain rate has no significant effect on the mechanical properties of the healthy arterial wall since at almost all 3 strain rates the same mechanical coefficients were observed. However, this effect is substantial for the atherosclerotic coronary arteries as the highest elastic modulus (13.10 MPa) and maximum stress (7.81 MPa) were seen for the atherosclerotic arteries at the strain rate of 50 mm/min. Interestingly, regardless of the state of arteries, the mechanical properties of the arteries up to a strain rate of 20 mm/min have not been significantly altered. The healthy coronary arteries, in addition, displayed the same mechanical behavior regardless of strain rate. In addition, the amount of elastic modulus found for the tissue at the strain rate of 20 mm/min was low enough (0.55 ± 0.06 MPa) to lead to such small standard deviation value. That is, the quantity of the elastic modulus, the dimensions of the arterial walls, and the other conditions of the test were close enough to provide such small value for us. However, by increasing the amount of strain rate, the amount of variation was increased accordingly which triggered such considerable standard deviation at the strain rate of 50 mm/min for the atherosclerotic artery with the elastic modulus of 13.10 ± 0.64 MPa. The reason might be related to the scattering and nature of the connective tissues which have different dimensions usually according to the case conditions. Nonlinear mechanical behavior of the coronary arteries was also numerically investigated using Mooney-Rivlin constitutive equation. The material coefficients of the model were calculated based on the mean curve of the experimental data using nonlinear optimization method-trust region algorithm32,33 and listed in Table 1.
Figure 1.
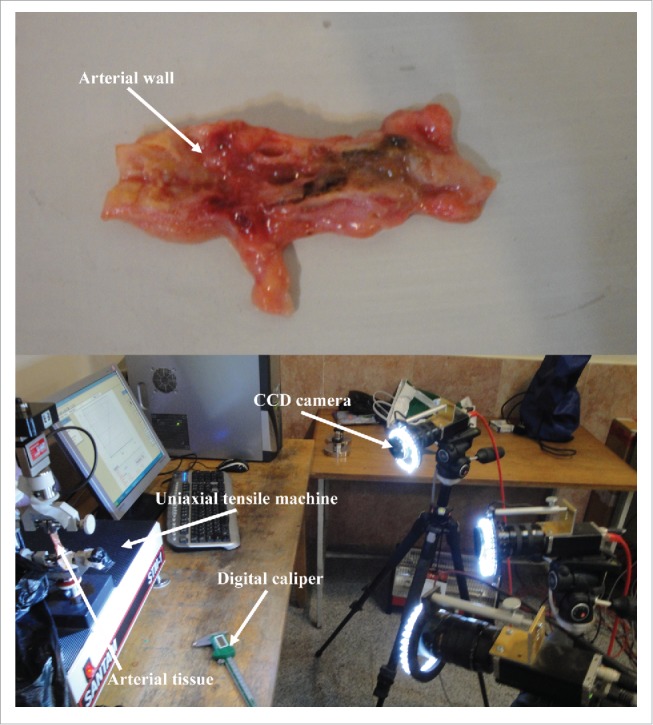
A typical coronary artery wall was mounted on the uniaxial tensile test machine and force is applied until failure occurred. A digital caliper was used to measure the average width and length of the tissue samples. During the test, a group of 3 CCD cameras were used to quantify the displacement/strain of the samples using DIC method.
Figure 2.
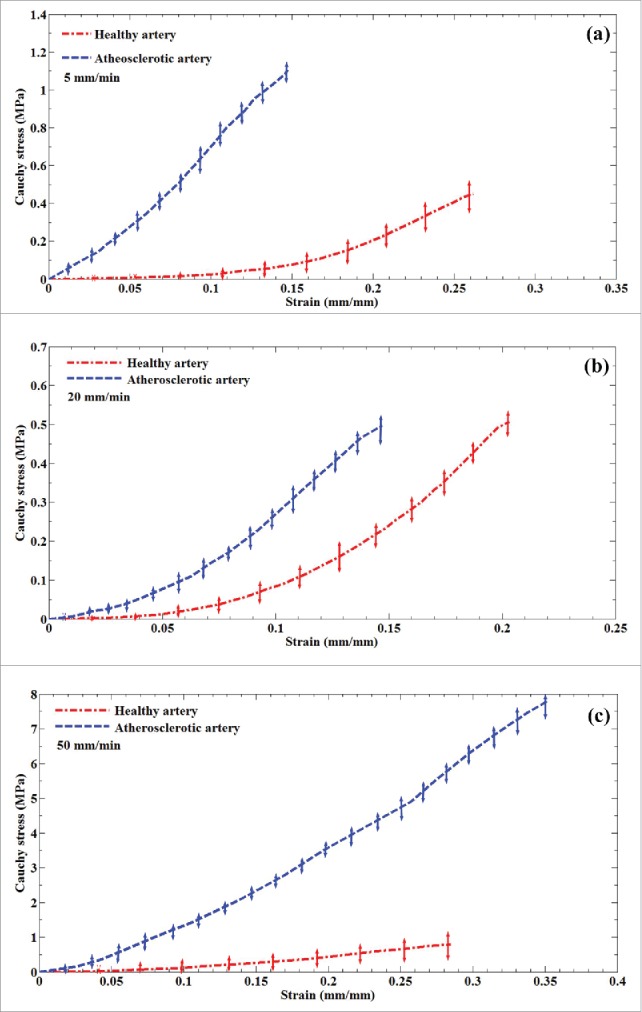
The mean stress-strain diagrams of the healthy and atherosclerotic human coronary arteries. Tests have been carried out at 3 different strain rates, including (a) 5, (b) 20, and (c) 50 mm/min. It helps us to investigate the role of strain rate on the mechanical behavior of arteries.
Figure 3.
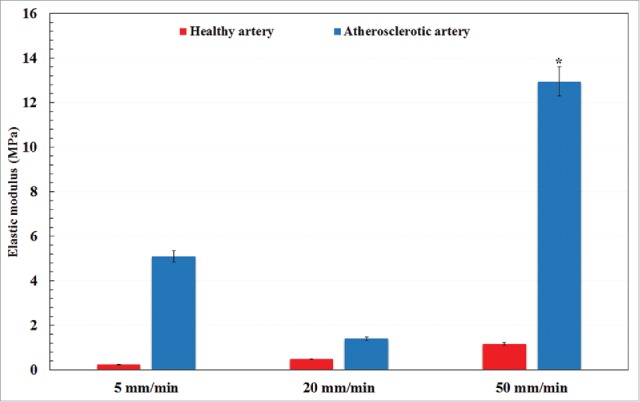
A comparative histogram representation of the elastic modulus of healthy and atherosclerotic human coronary arteries under different strain rates. *p < 0.05 compared with atherosclerotic artery at 5 mm/min.
Figure 4.
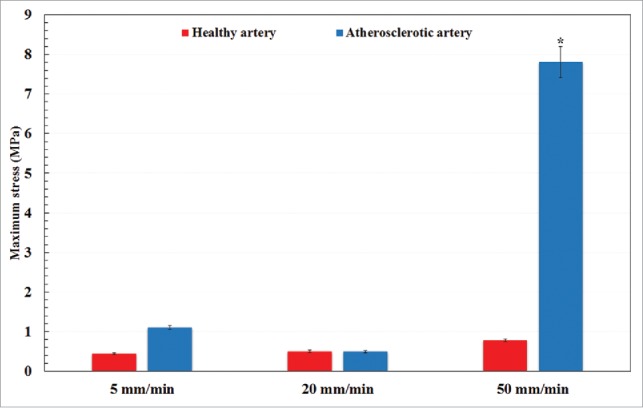
A comparative histogram representation of the maximum stress of healthy and atherosclerotic human coronary arteries under different strain rates. *p < 0.05 compared with atherosclerotic artery at 5 mm/min.
Table 1.
The identified hyperelastic material coefficients of the healthy and atherosclerotic human coronary arteries under different strain rates.
| Material type (strain rate) | C10 (MPa) | C01 | C02 | C20 | C11 |
|---|---|---|---|---|---|
| Healthy artery (5 mm/min) | 2.101 | −2.091 | −92.125 | −58.245 | 145.826 |
| Atherosclerotic artery (5 mm/min) | 0.666 | 0.087 | −15.778 | −80.191 | 107.893 |
| Healthy artery (20 mm/min) | −0.067 | 0.064 | 12.383 | 3.728 | −13.176 |
| Atherosclerotic artery (20 mm/min) | 4.286 | −4.196 | −685.670 | −564.653 | 1243.348 |
| Healthy artery (50 mm/min) | 4.997 | −4.989 | −69.483 | −41.456 | 105.463 |
| Atherosclerotic artery (50 mm/min) | 35.598 | −35.333 | −270.832 | −133.138 | 367.679 |
In order to anticipate the alteration of the collagen fibers' angle during load bearing in the testing machine, it was decided to employ the Artificial Neural Networks (ANNs) method. The mean angle of collagen fibers based on the strain rate, stress, and strain data were, therefore, predicted using ANNs code. The results were reported as a grid function as well as collagen fibers' gradient, and shown in Fig. 5 for (a and b) the healthy and (c, d) the atherosclerotic coronary arteries. In these figures, grid function stands as the outcome of the ANNs code regarding the variation of collagens' angle at each stress or strain value. Gradient, in addition, is a generalization of the usual concept of derivative of a function in one dimension to a function in several dimensions. In here, as theta at the same time is the function of stress and strain, gradient is defined as the derivation of its function in each direction. Thereafter, its values are plotted in this figure to compare the behavior of the collagen fibers among the healthy and atherosclerotic arterial tissues under different strain rates. The gradient function has 2 important character, including the angle and magnitude. The angle stands as the tendency of the function whether to the x or y axis which in here refers to the stress or strain. That is, if a function has an angle up to the y axis it has a higher tendency or dependency to the y axis and vice versa. The magnitude of the gradient will determine how fast the function rises in that direction. For instance, if a gradient function has a higher length and an angle with the tendency to the y axis, we can say that this function has a fast rising to the y axis component and vice versa. The reason why we employed the gradient function for the results is that it enables us not only have a better understanding about the variation of collagen fibers' angle at each value of stress and strain but also to inform us the dependency of the fibers' angle to the stress or strain at each point by showing the angle for the gradient function at each point. The grid function plot (Fig. 5a) as well as the gradient function plot (Fig. 5b) results for the healthy arterial walls explicitly indicated that the variation of the strain rate has no significant role on the collagen fibers' angle in the elastic region of the stress-strain curves since they almost keep their active reaction against the applied load regardless of the strain rate. In addition, analysis on the gradient of the collagen fibers showed that although at the initial region of the stress and strain values there are some small variation in the length and angle of the gradients, at the higher strain-lower stress regions there is no variation not only in the length but also in the angle of gradients at the strain rates of the 5 and 20 mm/min. The difference between the elastic modulus observed in Fig. 3 is the cause of the length and angle differences of Fig. 5b. However, at the higher strain-higher stress regions only the collagen fibers at the strain rates of 50 mm/min still try to become parallel to the load direction which implies that even at the higher strain and stress values collagen fibers can bear load and keep their activeness as indicated in Fig. 5b. To sum up, at higher strain/stress values the collagen fibers at the strain rates of 5 and 20 mm/min reach to their highest angle (90°) and this is why no gradient is visible for them. In contrast, at the strain rate of 50 mm/min the collagen fibers in the arterial wall are still changing and this is why a gradient is visible for them. The results depicted that almost before the strain value of 15% the collagen fibers at the strain rates of 5 and 20 mm/min reach to their highest angle while at the strain rate of 50 mm/min the angle of fibers are still increasing. This issue is well represented in the analysis conducted for the angle of collagen fibers since at a higher strain rate, they are still bearing more load and tend to show a stiffer behavior compared to the healthy ones. This might be one of the most important reasons that why the atherosclerotic arterial walls are significantly stiffer than that of the healthy ones at the strain rate of 50 mm/min. In addition, at higher stress and strain values the atherosclerotic arteries still show some quantities of stress and strain which imply that the stiffness of these arteries compared to the healthy ones. In Fig. 5c and d the grid functions and gradient of collagen fibers at their whole stress-strain boundaries are plotted respectively to shed light on the comparative analysis with the other 2 strain rates, the same boundary was magnified. In order to have a better outlook about the role of the strain rate on the length and angle variation of the gradient function at each strain rate, a separate figure of each strain rate is presented in Fig. 6. The error (E) of ANNs were 0.0009841 and 0.0045 for the healthy and atherosclerotic arteries which certify the accuracy of the modeling results. The results on the response of the collagen fibers to the amount of stress and strain were quite in agreement as the values of elastic modulus were reported for the healthy and atherosclerotic arterial walls. That is, at the lower strain values, the healthy and atherosclerotic arterial walls regardless of the strain rates, showed suitable activeness for the collagen fibers. However, by considering the role of strain rate into the mechanical response of the collagen fibers, it was found that higher strain values the atherosclerotic collagen fibers almost lose their performance against the applied load and become invisible. In contrast, the healthy ones at all 3 strain rates come into action and can bear mechanical load up to the failure point.
Figure 5.
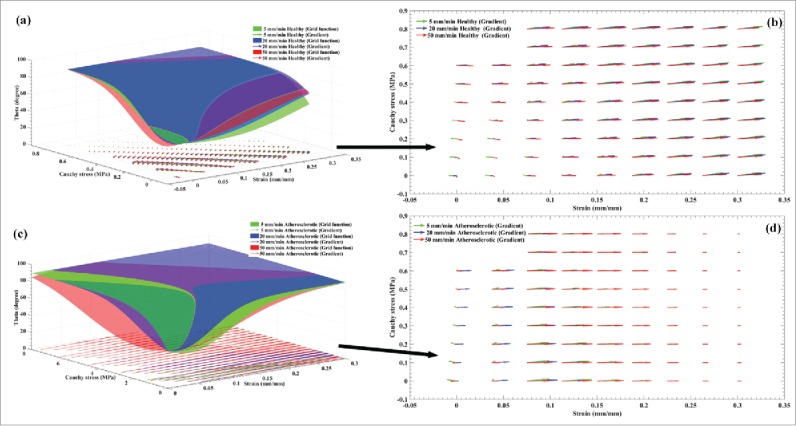
Representation of (A) the ANNs grid function and the gradient of the collagen fibers during the application loading for the healthy coronary arteries at the strain rates of 5, 20, and 50 mm/min. In order to clearly show the distribution of the gradient of the collagen fibers for the healthy arteries at 3 different strain rates, (B) their distributions are magnified and presented. Similarly, (C) the ANNs grid function and the gradient of the collagen fibers during the application loading for the atherosclerotic coronary arteries at the strain rates of 5, 20, and 50 mm/min. In order to clearly show the distribution of the gradient of the collagen fibers for the atherosclerotic arteries at 3 different strain rates, (D) their distributions are presented.
Figure 6.
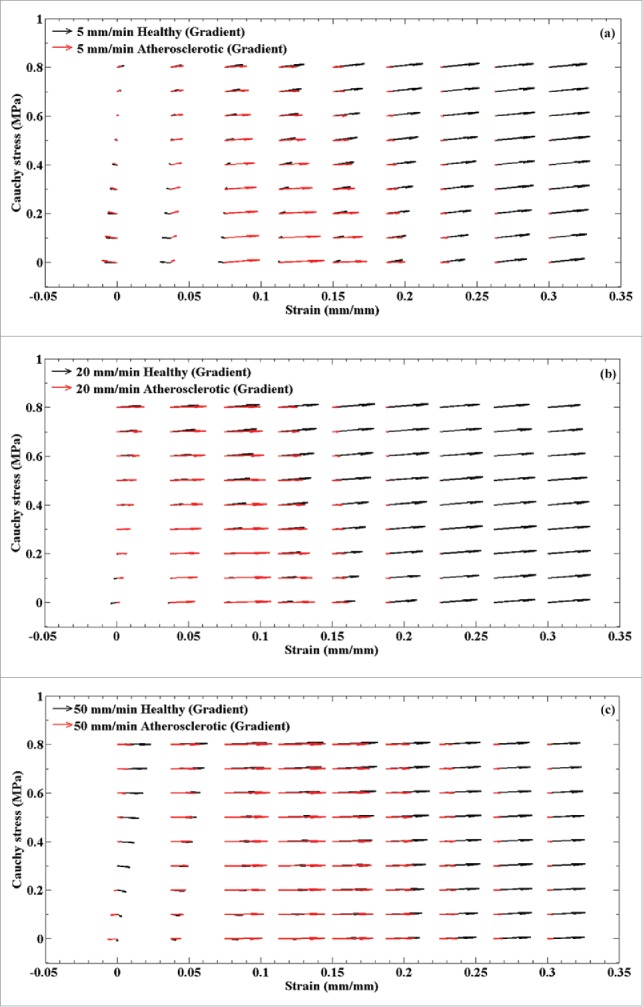
A comparative gradient demonstration for the healthy and atherosclerotic coronary arteries under various strain rates, i.e., (A) 5, (B) 20, and (C) 50 mm/min.
Discussion
The mechanical properties of the arterial wall have a key asset in its performance as a vessel in the human body. However, there are some specific diseases that can alter the mechanical properties of the arterial wall. Atherosclerosis is a special form of coronary artery disease that can change not only the microstructure properties but also the physical properties of the coronary arterial wall. It is reported that the atherosclerotic artery loses its collagen content and becomes stiffer than healthy arteries. In addition, it is well stated that collagen is responsible for the large strain/deformation of the arterial wall and, obviously, has almost entirely the main role in the arterial wall mechanics. This study benefitted from a combination of uniaxial tensile test data as well as histostructural data to compare the mechanical properties of the healthy and atherosclerotic human coronary arteries. To the best of the authors' knowledge, this is the first study that measure the mechanical properties of the healthy and atherosclerotic human coronary arteries under different strain rates. In addition, this study also proposed a new ANNs-3 layers' code based on bi-polar sigmoid function to anticipate the average angle of collagen fibers in the arterial wall during load bearing up to failure.
The lack of mechanical data on the healthy and atherosclerotic coronary arteries and, especially, on their wall stiffness/strength hinders the application of numerical models and simulations to arterial problems, and stops physicians from understanding the response of coronary arteries to the different interventions in advance.34 In this study, the reported non-linear behavior can be attributed to the collagen fibers.35 For low strain values, collagen is mainly present in a wavy pattern and the fibers do not contribute to the loading capacity.36 Upon increasing strain, collagen fibers align and stretch. Since the collagen fibers are generally stiff, they lead to the non-linear increase in stiffness. These effects are observed for collagen in healthy arteries. Healthy arteries are found to be relatively deformable with nonlinear behavior37 under various stress-strain behavior at different zones of the stress-strain curves.38 The stiffness response of the arterial wall is believed to be related to the anisotropically distributed wavy collagen fibrils embedded in the matrix of arterial wall39,40 which strengthen the anisotropic mechanical behavior of the arteries. The mechanical response of the arterial wall under different strain rates revealed that healthy arteries keep their mechano-physiological conditions under different loading condition, however, the atherosclerotic arteries loss its condition under higher strain rates.
Regarding the variation of mean collagen fiber angle during the load bearing, the results revealed that these angles in the atherosclerotic arteries were more alert than that in the healthy ones. The collagen fibers in the healthy arterial walls tend to be independent on the strain rates and, consequently, the pattern of alteration for them is slow (Fig. 5a and b). In contrast, the collagen fibers in the atherosclerotic artery illustrated a strong dependency on the strain rates in a way that at the strain rate of 50 mm/min the highest elastic modulus and stress were observed. The numerical prediction by ANNs was confirmed this process especially at the highest stress and strain values. These results suggest that our model was enabled to predict the variation of collagen angles at various strain rates comprehensively. In the other words, at the lower strain values as well as the strain rates (5 and 20 mm/min), the collagen fibers in the atherosclerotic arterial walls can tolerate load and come to effect, however, at higher strain values as well as strain rates the collagen fibers almost reach to their highest degree parallel to the applied load and, as a result, they are only sensitive to strain values. This indicated by gradient analysis as well, since at a higher strain values the angle of the gradients are almost zero parallel to the horizontal axis of the diagram. A comparative analysis on the collagen fibers of the healthy and atherosclerotic coronary arteries at different strain rates revealed that healthy collagen fibers have an active reaction to the applied load regardless of the strain rates due to the length of the gradient function as presented in Fig. 6. That is, they can bear load not only at a lower stress/strain value (elastic region) but also at a higher stress/strain value (nonlinear region). Controversy, the behavior of the collagen fibers in the atherosclerotic arterial wall implies that they might not be active enough under various loading conditions and they may fail to bear enough load comparing to the healthy ones at a higher stress/strain value. On the other hand, the variation of the angle of the gradient for the healthy arterial walls indicates its dependency to both the stress and strain but more to stress. A comparative representation of the gradient functions of the healthy and atherosclerotic arterial walls regardless of the strain rates are also illustrated in Fig. 7. This figure was plotted as a mean value of all values reported in Fig. 6 to provide a deeper view on the variation of the length (amount of stress and strain) and angle (dependency to the stress or strain) of the collagen fibers at each point of the stress-strain diagrams. However, the atherosclerotic arterial walls almost entirely lose their dependency to the stress values (Fig. 7). With these considerations in mind we can come up with this idea that the healthy arteries can keep their logical/natural mechanical response at various strain rates since their gradients are active not only at the lowest amount but also at the highest amount of stress and strain values. They also can show reaction to both the stress and strain. However, in the atherosclerotic arteries, due to the stiffness, which induced by plaque formation, the collagen fibers lose their natural behavior and cannot show their logical/natural behavior not only at the lowest but also at the highest amount of stress and strain values and, as a result, become dependent to the strain only. This will lead to a stiff behavior of the arterial wall under different strain rates, especially at the strain rate of 50 mm/min. In a nutshell, the results suggest that the atherosclerotic artery are more vulnerable to strain rather than stress and this is why a heavy sport is not recommended for them since it will induce a high amount of strain to the arterial wall due to the blood pressure. There is a need to find a correlation among the growth, remodeling, and disease with that of the stress and strain of the tissue in various environment. This is why a constitutive model is enabled to address the mechanical behavior of the tissue in detail is required. In addition, the dimensions of stent struts have a profound influence on the stress concentration of the inner layer of the arterial wall and in the medical consequences after stenting;41,42 stent struts might invoke intimal laceration and endothelial cell denudation,43,44 which is a local effect. Hence, not only in this specific case but also in general medical needs, the knowledge of the mechanical properties of the arterial wall and its response to the mechanical load is imperative.
Figure 7.
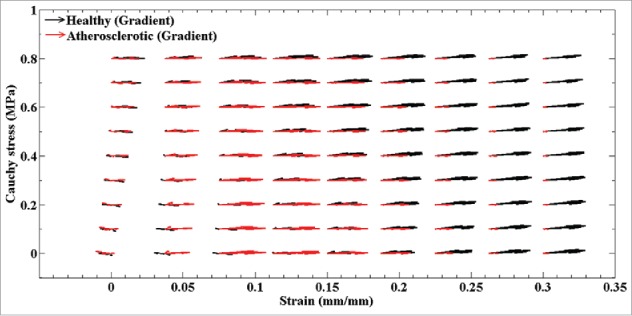
A comparative gradient demonstration for the healthy and atherosclerotic coronary arteries regardless of the amount of the strain rates.
The physical properties of the arterial wall would be substantial for anticipation of the plaque rupture45,46 and it is obvious that such information would pave the way to reach to a more accurate condition for this prediction. In addition, these raw data would provide a wide range of testing condition for the clinicians to assess the functionality of the innovative drugs for plaque vulnerability investigations.45,46 In this study, coronary artery was considered as a single layer isotropic structure. By considering that, the effects of collagen fibers in other directions would not be taken into account and, as a result, there will be no directional definition for the arterial wall. Although this may consider as a limitation of this study, the findings of this study could well compare and predict the mechanical behavior and angle of collagen fibers during load bearing up to failure. In addition, it should be noted that the results are still promising and further research are do required. However, the proposed ANNs function enables to well predict the mean angles of collagen fibers in the arterial wall. The functions by which the cardiovascular system helps the biologic organism are mechanical. It is implicit, therefore, it is crucial to comprehend and to calculate the mechanical properties of the cardiovascular system before its biologic functions can be understood and measured. One of the major components of the cardiovascular system is its arterial network, the mechanical properties of which determine the propagation of energy from the heart to the periphery. The relationships of blood flow and blood pressure, of intravascular pressure and vessel volume, of pulse wave velocity and blood pressure for sure depend on the mechanical properties of the blood vessel walls and this is why there is a need to know the mechanical properties of the arterial wall.
Conclusions
The mechanical properties of the coronary arteries may vary under different strain rates. However, so far the biomechanical properties of the healthy and atherosclerotic human coronary arteries, including linear elastic and nonlinear hyperelastic, under different strain rates have not been well determined. Therefore, in this study a combination of uniaxial and histological data was employed to calculate the mechanical properties of healthy and atherosclerotic human coronary arteries at 3 different strain rates, i.e., 5, 20, and 50 mm/min. Elastin is believed to be responsible of the small strain/deformation while collagen fibers are in charge of large strain/deformations of the arterial wall. ANNs code was, hence, used to predict the alteration of mean angle of collagen fibers during load bearing up to failure. The results demonstrated the significant role of strain rates on the mechanical and structural properties of the atherosclerotic arteries, such as elastic modulus, maximum stress, hyperelastic coefficients, and collagen fiber orientations. However, no significant alteration, in terms of mechanical properties, has been observed for the healthy arteries at different strain rates. The highest elastic modulus and maximum stress were observed for the atherosclerotic arteries at the strain rate of 50 mm/min. Though, the lowest one were belonged to the atherosclerotic arteries at the strain rate of 20 mm/min. Furthermore, our ANNs code well predicted the mean collagen fiber angles from its initial condition up to breakage. These findings suggest that in order to get more precise mechanical conception about the arterial mechanics, the effect of strain rate in atherosclerotic arteries must be taken into account.
Materials and methods
Experimental testing
The processes of sample preparation,47,48 in vitro surgical,49 and tensile tests50,51 have comprehensively been reported in our previous studies. Fleetingly, the coronary arteries were gathered during the autopsy of 18 male individuals within 5 hours' post-mortem. Nine out of 18 samples were healthy and the rest was atherosclerosis. Therefore, only 2 groups of the healthy and atherosclerotic ones were employed in the current study. Three different strain rates, i.e., 5, 20, and 50 mm/min, were used that in each of which 3 healthy and 3 atherosclerotic arteries from dissimilar cadavers were tested. Each artery was cut along the axial direction. The same region among all the tissue samples were cut to minimize any possible differences regarding the locations in the tissue samples. However, since it was not plausible to apply different strain rates on one tissue sample due to the dimension of the samples, therefore, different tissues were employed in this case, yet the testing samples were harvested from the same locations of all of them. The dimensions of the arterial walls, including outer diameter, initial wall thickness, and length of the coronary artery segments were accurately measured. Initial wall thickness was measured in at least 10 points of the arterial wall and the mean of that was used in the further stress-strain measurements. The arterial thicknesses of the healthy and atherosclerotic walls were 2.01 ± 0.11 and 2.22 ± 0.15 mm, respectively. Each sample was divided into 2 parts for the following histological and mechanical analyses to be able to consider the natural behavior of the collagen fibers in the mechanical behavior of the arterial wall. In order to minimize tissue degradation, the coronary artery samples after removal from the human body were put in solution of 0.90% w/v of NaCl at 4–5°C to lessen tissue degradation due to post-mortem issues. Right before the mechanical measurements, the coronary artery samples were taken out from the physiological saline and mounted on the testing machine. Some pretests have been carry out to assess the preconditioning condition of the arterial walls. These tests revealed that the importance of preconditioning can be realized after 10 cycles. Thus, 10 cyclic preconditioning according to the primary results were applied to the samples via a small displacement before the experimental analysis starts. Defining a start point for soft tissues is difficult as they usually contain even small amount of residual stress, therefore, a suitable pre-load according to the experimental measurements was applied to the arterial walls.52,53 Tensile force with the strain rates of 5, 20, and 50 mm/min was next then put on each specimen up to the failure of the arterial walls and the gained stress-strain diagram was employed for additional investigates. All material removal was carried out under the authorization of donors and under the ethical rules of Legal Medicine Organization according to the 2008 Declaration of Helsinki.
Digital Image Correlation (DIC) technique
The Digital Image Correlation (DIC) technique was employed to quantify the displacement/strain of the arterial walls under axial loading. DIC is an optical and contactless method enables to determine the difference of DIC points on the tissues by comparing the surface of images in the deformed (after applying load in the tissue) and undeformed (reference/initial state of the tissue) conditions. This process is fulfilling by defining a grid on a reference image (which is taken at the first condition of the tissue), thereafter, a group of subset is defined about each node of this grid (the grid is located on the monitor and the nodes were imaginary defined on that). Image processing approach would also be used to identify the most alike subset in the deformed condition according to few statistical techniques.54 The DIC method was carried out using a group of 3 Charged Coupled Device (CCD) high speed video camera (Sony Xc-75, Tokyo, Japan). In order to define the DIC points, black color dots were irregularly distributed on each sample.55 The video cameras enable to capture 280 frame/second with the resolution of 2048×1088 pixels which provide very accurate data for further processing. The Simi Motion® 2D/3D (Simi Reality Motion Systems GmbH, Max-Planck-Straße, Unterschleißheim, Germany) video camera software was also helped us to lively measure the deformation of each marker in respect to the other one. DIC software could track the markers according to the following equations:
| (1) |
| (2) |
| (3) |
As u and v are standing as the displacements of the each DIC points at (rC, sC), and uL and vL are the displacements of a random point (rL, sL) nearby each pixel. L1 and L2 based on the intensity of each DIC pixels in the undeformed/reference and the deformed images. The Eq. 1 will resolve at diverse values and locations of the deformed condition. To get an accurate outcome, the normalized correlation equation a following can be employed.
| (4) |
The uppermost quantity of the overhead equation is at 1.
Histology analysis
The histology analysis has been performed same as that of our previous study.25,56 The strip samples were fixed using 4% buffered formaldehyde solution (pH 7:4) and prepared for histological analyses before the test starts. Arterial tissues were kept in a way to maintain their in-plane geometries and then cut at 3 μm in layer positioning followed by light staining. The mid-section of the arterial tissue was almost used for the histological analyses. Therefore, the strips are now ready to be seen under microscope in a way that x1 and x2 represent the circumferential and the axial directions of the arterial wall, respectively. To achieve more precise results, both a skilled histopathologist and numerical technique (a written code which enables to identify each collagen fiber along with its angle in an image via image recognizing software) were used on 41 collagen fibers per specimen and the mean in-plane angle of collagen fibers for each histological image were accurately determined.25
Collagen fiber orientation in the arterial wall
Arterial wall is consisted of 3 layers, namely intima, media, and adventitia. The intima is the deepest layer of the artery. The alignment of the collagen fibers in the intima is not even through the thickness of the layer and randomly dispersed.57 The media is located between the intima and adventitia layers of the artery wall and it consisted of a bunch of elastin and collagens in a 3-dimensional network.58 The collagens in this layer are almost circumferentially oriented.59 The adventitia is the farthest layer that contains of 2 helically organized families of fibers which they dispersed in a way that their angle largely deviated from their mean orientations.60,61 It is known that the collagen fibers have a key asset in the mechanical strength of the arterial wall. In the unstressed tissue the collagen fibers are randomly distributed which brings about the adventitia displays low stiffness compared to the media in the stress-free condition. Nevertheless, a higher amount of load would lead to alignment of the collagen fibers and, as a result, the adventitia becomes stiffer to bear overstretch and rupture. In the other words, the collagen fibers initially in the arterial wall are randomly distributed, however, at a larger strain/deformation the angle of collagen fibers is going to be aligned with loading direction. In the current research, since we were unable to determine the mean angle of collagen fibers in each layer of the arterial wall, the arterial wall was considered as a one-layer structure. Therefore, the histology image that was employed for the imaging analysis was an image of an inner side of the arterial wall as a whole. Although this may consider as a limitation of this work, it is the authors' belief that this study is promising and further research is required.
Constitutive equation
The elastic modulus is the ratio of alteration in the stress values in respect to the strain and, therefore, stands for the strength of a material. The elastic modulus of the tissue is defined as the slope of the stress-strain curve in the elastic deformation region. In here, the elastic deformation of the tissues was considered as the 30% of the strain failure. Mooney-Rivlin hyperelastic constitutive model was employed to define the mechanical response of arterial wall. The isotropic hyperelastic material function W is a scalar function of the right Cauchy-Green deformation tensor, C.62,63 Since the arterial wall is considered to behave like an incompressible and isotropic material,23 the Mooney-Rivlin model can be proposed as following:
| (5) |
where J = det(F) called Jacobian and stands as the determinant of deformation gradient. In a normalized deformation gradient , and are the first and second invariants of the Cauchy-Green strain tensor: . Cij are the material coefficients that will be determined using the nonlinear least square fit-trust region algorithm optimization technique. The λ1, λ2, and λ3 introduced as the principal stretches and then the strain invariants are expressed as following:
| (6) |
| (7) |
| (8) |
Since the arterial wall is presumed to behave like an incompressible material, the third deviatory strain invariant equals to 1 ().64
Artificial Neural Networks
In this study, Artificial Neural Networks (ANNs)-Multi Step Ahead Prediction algorithm was used to predict the mean orientation of collagen fibers in the healthy and atherosclerotic human coronary arteries during load bearing.65 The stress, strain, initial collagen fiber angles (from histology analysis), ultimate collagen fiber angles, and strain rate of each sample were known. The stress and strain as well as the strain rate of the samples were implemented into the ANNs code from the uniaxial experimental data. Initial angle of the collagen fibers was also experimentally measured and implemented into the code. It is known that arterial collagen fibers are responsible of load bearing in large strain/deformation. Moreover, it is expected that the mean angle of collagen fibers reaches to almost 90° in the maximum stress condition. These considerations were contemplated and implemented into the 3-layer ANNs code as displayed in equation 9.
.

(9)
The first-layer (first down layer) is related to the inputs of the model, such as strain rate, strain, and stress. The second-layer is consisted of Bi-Polar Sigmoid Function which trained with different inputs to be able to map the inputs to the outputs of the code. The last or third-layer is consisted of mean angle of collagen fibers during load bearing.
The relation of each neuron through its network with other neurons in the first and second layers are defined as following:
| (10) |
In addition, Bi-Polar Sigmoid Function in these 2 layers is expressed as following:
| (11) |
The relation of each neuron through its network with other neurons in the second and third layers are defined as following:
| (12) |
In addition, Bi-Polar Sigmoid Function in these layers is stated as following:
| (13) |
The proposed neural network code enables to provide a grid function that can predict the angle of collagen fibers during load bearing up to failure.
Statistical analysis
ANOVA was used at first to identify the variation of results and if statistical differences were found student's t-test was employed to compare the data between 2 different groups via SPSS software version 16.0 (SPSS Inc., Chicago, IL, United States). Data are reported as mean ± std at a significance level of p < 0.05.
Ethical issues
The use of experimental on the human body was approved by the committee of the Legal Medicine Organization (LMO) with the letter ID of 65987/253. This study was also entirely adhered to the declaration of the Helsinki in 2008.
Disclosure of potential conflicts of interest
No potential conflicts of interest were disclosed.
Acknowledgments
This study, including the numerical and experimental sections, was carried out in the Tissue Engineering and Biological Systems Research Laboratory of Iran University of Science and Technology under the supervision of Professor Mahdi Navidbakhsh. We thank Professor Susumu Kudo and Professor Toshihiro Sera for their great help and time to read the manuscript and give us their comments to write the manuscript.
References
- [1].Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol 2005; 289(5):H2048-H58; PMID:16006541; http://dx.doi.org/ 10.1152/ajpheart.00934.2004 [DOI] [PubMed] [Google Scholar]
- [2].Virmani R, Kolodgie FD, Burke AP, Farb A, Schwartz SM. Lessons from sudden coronary death a comprehensive morphological classification scheme for atherosclerotic lesions. Arterioscler Thromb Vasc Biol 2000; 20(5):1262-75; PMID:10807742; http://dx.doi.org/ 10.1161/01.ATV.20.5.1262 [DOI] [PubMed] [Google Scholar]
- [3].Tabas I. Apoptosis and plaque destabilization in atherosclerosis: the role of macrophage apoptosis induced by cholesterol. Cell Death Differ 2004; 11:S12-S6; PMID:15143347; http://dx.doi.org/ 10.1038/sj.cdd.4401444 [DOI] [PubMed] [Google Scholar]
- [4].Go AS, Mozaffarian D, Roger VL, Benjamin EJ, Berry JD, Borden WB, Bravata DM, Dai S, Ford ES, Fox CS, et al.. Heart disease and stroke statistics–2013 update: a report from the American Heart Association. Circulation 2013; 127(1):e6; PMID:23239837; http://dx.doi.org/ 10.1161/CIR.0b013e31828124ad [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Falk E, Shah PK, Fuster V. Coronary plaque disruption. Circulation 1995; 92(3):657-71; PMID:7634481; http://dx.doi.org/ 10.1161/01.CIR.92.3.657 [DOI] [PubMed] [Google Scholar]
- [6].Harrison M, Marshall J. Angiographic appearance of carotid bifurcation in pateints with completed stroke, transient ischaemic attacks, and cerebral tumour. Br Med J 1976; 1(6003):205-7; PMID:1247779; http://dx.doi.org/ 10.1136/bmj.1.6003.205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Criqui MH, Coughlin SS, Fronek A. Noninvasively diagnosed peripheral arterial disease as a predictor of mortality: Results from a prospective study. Circulation 1985; 72(4):768-73; PMID:4028377; http://dx.doi.org/ 10.1161/01.CIR.72.4.768 [DOI] [PubMed] [Google Scholar]
- [8].Schaar JA, Regar E, Mastik F, McFadden EP, Saia F, Disco C, de Korte CL, de Feyter PJ, van der Steen AF, Serruys PW. Incidence of high-strain patterns in human coronary arteries assessment with three-dimensional intravascular palpography and correlation with clinical presentation. Circulation 2004; 109(22):2716-9; PMID:15159286; http://dx.doi.org/ 10.1161/01.CIR.0000131887.65955.3B [DOI] [PubMed] [Google Scholar]
- [9].Hausleiter J, Sebastian M, Li A, Abbey CK, Honda H, Makkar R, Whiting JS, Eigler N. A porcine coronary stent modelof increased neointima formation in the left anterior descending coronary artery. Zeitschrift für Kardiologie 2002; 91(8):614-9; PMID:12426824; http://dx.doi.org/ 10.1007/s00392-002-0822-2 [DOI] [PubMed] [Google Scholar]
- [10].Kastrati A, Schömig A, Elezi S, Schühlen H, Dirschinger J, Hadamitzky M, Wehinger A, Hausleiter J, Walter H, Neumann FJ. Predictive factors of restenosis after coronary stent placement. J Am Coll Cardiol 1997; 30(6):1428-36; PMID:9362398; http://dx.doi.org/ 10.1016/S0735-1097(97)00334-3 [DOI] [PubMed] [Google Scholar]
- [11].Rahmani S, Alagheband M, Karimi A, Alizadeh M, Navidbakhsh M. Wall stress in media layer of stented three-layered aortic aneurysm at different intraluminal thrombus locations with pulsatile heart cycle. J Med Eng Tech 2015; 39(4):239-45; http://dx.doi.org/ 10.3109/03091902.2015.1040173 [DOI] [PubMed] [Google Scholar]
- [12].Fung Y-C. Biomechanics. 1990. New York, NY: Springer. http://dx.doi.org/ 10.1007/978-1-4419-6856-2 [DOI] [Google Scholar]
- [13].Lillie M, Gosline J. Mechanical properties of elastin along the thoracic aorta in the pig. J Biomech 2007; 40(10):2214-21; PMID:17174959; http://dx.doi.org/ 10.1016/j.jbiomech.2006.10.025 [DOI] [PubMed] [Google Scholar]
- [14].Rekhter MD. Collagen synthesis in atherosclerosis: too much and not enough. Cardiovasc Res 1999; 41(2):376-84; PMID:10341837; http://dx.doi.org/ 10.1016/S0008-6363(98)00321-6 [DOI] [PubMed] [Google Scholar]
- [15].Brüel A, Ørtoft G, Oxlund H. Inhibition of cross-links in collagen is associated with reduced stiffness of the aorta in young rats. Atherosclerosis 1998; 140(1):135-45; PMID:9733224; http://dx.doi.org/ 10.1016/S0021-9150(98)00130-0 [DOI] [PubMed] [Google Scholar]
- [16].Sawabe M. Vascular aging: from molecular mechanism to clinical significance. Geriatrics Gerontology Int 2010; 10(s1):S213-S20; http://dx.doi.org/ 10.1111/j.1447-0594.2010.00603.x [DOI] [PubMed] [Google Scholar]
- [17].Beattie D, Xu C, Vito R, Glagov S, Whang M. Mechanical analysis of heterogeneous, atherosclerotic human aorta. J Biomech Eng 1998; 120(5):602-7; PMID:10412437; http://dx.doi.org/ 10.1115/1.2834750 [DOI] [PubMed] [Google Scholar]
- [18].Baldewsing RA, Danilouchkine MG, Mastik F, Schaar JA, Serruys PW, van der Steen AF. An inverse method for imaging the local elasticity of atherosclerotic coronary plaques. IEEE Trans Inf Technol Biomed 2008; 12(3):277-89; PMID:18693495; http://dx.doi.org/ 10.1109/TITB.2007.907980 [DOI] [PubMed] [Google Scholar]
- [19].van Popele NM, Grobbee DE, Bots ML, Asmar R, Topouchian J, Reneman RS, Hoeks AP, van der Kuip DA, Hofman A, Witteman JC. Association between arterial stiffness and atherosclerosis The Rotterdam Study. Stroke 2001; 32(2):454-60; PMID:11157182; http://dx.doi.org/ 10.1161/01.STR.32.2.454 [DOI] [PubMed] [Google Scholar]
- [20].Wykretowicz A, Gerstenberger P, Guzik P, Milewska A, Krauze T, Adamska K, Rutkowska A, Wysocki H. Arterial stiffness in relation to subclinical atherosclerosis. Eur J Clin Invest 2009; 39(1):11-6; PMID:19087126; http://dx.doi.org/ 10.1111/j.1365-2362.2008.02057.x [DOI] [PubMed] [Google Scholar]
- [21].Karimi A, Navidbakhsh M, Shojaei A, Faghihi S. Measurement of the uniaxial mechanical properties of healthy and atherosclerotic human coronary arteries. Mater Sci Eng C 2013; 33(5):2550-4; http://dx.doi.org/ 10.1016/j.msec.2013.02.016 [DOI] [PubMed] [Google Scholar]
- [22].Karimi A, Navidbakhsh M, Faghihi S, Shojaei A, Hassani K. A finite element investigation on plaque vulnerability in realistic healthy and atherosclerotic human coronary arteries. Proc Inst Mech Eng H 2013; 227(2):148-61; PMID:23513986; http://dx.doi.org/ 10.1177/0954411912461239 [DOI] [PubMed] [Google Scholar]
- [23].Karimi A, Navidbakhsh M, Shojaei A, Hassani K, Faghihi S. Study of plaque vulnerability in coronary artery using Mooney–Rivlin model: a combination of finite element and experimental method. Biomed Eng Appl Basis Commun 2014; 26(01):153-60; http://dx.doi.org/ 10.4015/S1016237214500136 [DOI] [Google Scholar]
- [24].Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elas Phys Sci Solids 2000; 61(1-3):1-48; http://dx.doi.org/ 10.1016/S0022-3697(99)00252-8 [DOI] [Google Scholar]
- [25].Karimi A, Navidbakhsh M, Shojaei A. A combination of histological analyses and uniaxial tensile tests to determine the material coefficients of the healthy and atherosclerotic human coronary arteries. Tissue Cell 2015. April; 47(2):152-8; http://dx.doi.org/ 10.1016/j.tice.2015.01.004 [DOI] [PubMed] [Google Scholar]
- [26].Yang J, Clark JW, Bryan RM, Robertson C. The myogenic response in isolated rat cerebrovascular arteries: smooth muscle cell model. Med Eng Phys 2003; 25(8):691-709; PMID:12900184; http://dx.doi.org/ 10.1016/S1350-4533(03)00100-0 [DOI] [PubMed] [Google Scholar]
- [27].Zeiher AM, Goebel H, Schächinger V, Ihling C. Tissue endothelin-1 immunoreactivity in the active coronary atherosclerotic plaque a clue to the mechanism of increased vasoreactivity of the culprit lesion in unstable angina. Circulation 1995; 91(4):941-7; PMID:7850978; http://dx.doi.org/ 10.1161/01.CIR.91.4.941 [DOI] [PubMed] [Google Scholar]
- [28].Holzapfel GA. Nonlinear solid mechanics: a continuum approach for engineering science. Meccanica 2002; 37(4):489-90; http://dx.doi.org/ 10.1023/A:1020843529530 [DOI] [Google Scholar]
- [29].Lanir Y. Constitutive equations for fibrous connective tissues. J Biomech 1983; 16(1):1-12; PMID:6833305; http://dx.doi.org/ 10.1016/0021-9290(83)90041-6 [DOI] [PubMed] [Google Scholar]
- [30].Wuyts F, Vanhuyse V, Langewouters G, Decraemer W, Raman E, Buyle S. Elastic properties of human aortas in relation to age and atherosclerosis: a structural model. Phys Med Biol 1995; 40(10):1577; PMID:8532741; http://dx.doi.org/ 10.1088/0031-9155/40/10/002 [DOI] [PubMed] [Google Scholar]
- [31].Zulliger MA, Fridez P, Hayashi K, Stergiopulos N. A strain energy function for arteries accounting for wall composition and structure. J Biomech 2004; 37(7):989-1000; PMID:15165869; http://dx.doi.org/ 10.1016/j.jbiomech.2003.11.026 [DOI] [PubMed] [Google Scholar]
- [32].Byrd RH, Gilbert JC, Nocedal J. A trust region method based on interior point techniques for nonlinear programming. Math Program 2000; 89(1):149-85; http://dx.doi.org/ 10.1007/PL00011391 [DOI] [Google Scholar]
- [33].Nie P-Y, Ma C-F. A trust region filter method for general non-linear programming. Appl Maths Computat 2006; 172(2):1000-17; http://dx.doi.org/ 10.1016/j.amc.2005.03.004 [DOI] [Google Scholar]
- [34].Claes E, Atienza JM, Guinea GV, Rojo FJ, Bernal JM, Revuelta JM, Elices M. Mechanical properties of human coronary arteries. Engineering in Medicine and Biology Society (EMBC), 2010 Annual International Conference of the IEEE; 2010: IEEE; 2010. p.3792-5. [DOI] [PubMed] [Google Scholar]
- [35].Mulvihill J, Cunnane E, McHugh S, Kavanagh E, Walsh S, Walsh M. Mechanical, biological and structural characterization of in vitro ruptured human carotid plaque tissue. Acta Biomater 2013; 9(11):9027-35; PMID:23871944; http://dx.doi.org/ 10.1016/j.actbio.2013.07.012 [DOI] [PubMed] [Google Scholar]
- [36].Mulvihill JJ, Walsh MT. On the mechanical behaviour of carotid artery plaques: the influence of curve-fitting experimental data on numerical model results. Biomech Model Mechanobiol 2013; 12(5):975-85; PMID:23192833; http://dx.doi.org/ 10.1007/s10237-012-0457-9 [DOI] [PubMed] [Google Scholar]
- [37].Roy CS. The elastic properties of the arterial wall. J Physiol 1881; 3(2):125-59; PMID:16991309; http://dx.doi.org/ 10.1113/jphysiol.1881.sp000088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Abé H, Hayashi K, Sato M. Data book on mechanical properties of living cells, tissues, and organs. Springer; 1996. [Google Scholar]
- [39].Roach M, Song S. Variations in strength of the porcine aorta as a function of location. Clin Invest Med 1994; 17(4):308-18; PMID:7982294 [PubMed] [Google Scholar]
- [40].Samila ZJ, Carter SA. The effect of age on the unfolding of elastin lamellae and collagen fibers with stretch in human carotid arteries. Can J Physiol Pharm 1981; 59(10):1050-7; http://dx.doi.org/ 10.1139/y81-160 [DOI] [PubMed] [Google Scholar]
- [41].Holzapfel GA, Stadler M, Gasser TC. Changes in the mechanical environment of stenotic arteries during interaction with stents: computational assessment of parametric stent designs. J Biomech Eng 2005; 127(1):166-80; PMID:15868799; http://dx.doi.org/ 10.1115/1.1835362 [DOI] [PubMed] [Google Scholar]
- [42].Kastrati A, Mehilli J, Dirschinger J, Dotzer F, Schühlen H, Neumann FJ, Fleckenstein M, Pfafferott C, Seyfarth M, Schömig A. Intracoronary stenting and angiographic results strut thickness effect on restenosis outcome (ISAR-STEREO) trial. Circulation 2001; 103(23):2816-21; PMID:11401938; http://dx.doi.org/ 10.1161/01.CIR.103.23.2816 [DOI] [PubMed] [Google Scholar]
- [43].König A, Schiele TM, Rieber J, Theisen K, Mudra H, Klauss V. Influence of stent design and deployment technique on neointima formation and vascular remodeling. Zeitschrift für Kardiologie 2002; 91(3):98-102; PMID:12641022 [DOI] [PubMed] [Google Scholar]
- [44].Rogers C, Tseng DY, Squire JC, Edelman ER. Balloon-artery interactions during stent placement a finite element analysis approach to pressure, compliance, and stent design as contributors to vascular injury. Cir Res 1999; 84(4):378-83; http://dx.doi.org/ 10.1161/01.RES.84.4.378 [DOI] [PubMed] [Google Scholar]
- [45].Finet G, Ohayon J, Rioufol G. Biomechanical interaction between cap thickness, lipid core composition and blood pressure in vulnerable coronary plaque: impact on stability or instability. Coron Artery Dis 2004; 15(1):13-20; PMID:15201616; http://dx.doi.org/ 10.1097/00019501-200402000-00003 [DOI] [PubMed] [Google Scholar]
- [46].Cheng GC, Loree HM, Kamm RD, Fishbein MC, Lee RT. Distribution of circumferential stress in ruptured and stable atherosclerotic lesions. A structural analysis with histopathological correlation. Circulation 1993; 87(4):1179-87; PMID:8462145; http://dx.doi.org/ 10.1161/01.CIR.87.4.1179 [DOI] [PubMed] [Google Scholar]
- [47].Karimi A, Navidbakhsh M, Razaghi R, Haghpanahi M. A computational fluid-structure interaction model for plaque vulnerability assessment in atherosclerotic human coronary arteries. J Appl Phys 2014; 115(14):144702-10; http://dx.doi.org/ 10.1063/1.4870945 [DOI] [Google Scholar]
- [48].Karimi A, Razaghi R, Shojaei A, Navidbakhsh M. An experimental-nonlinear finite element study of a balloon expandable stent inside a realistic stenotic human coronary artery to investigate plaque and arterial wall injury. Biomed Tech (Berl) 2015. December 1; 60(6):593-602. [DOI] [PubMed] [Google Scholar]
- [49].Karimi A, Navidbakhsh M, Razaghi R. A finite element study of balloon expandable stent for plaque and arterial wall vulnerability assessment. J Appl Phys 2014; 116(4):044701-10; http://dx.doi.org/ 10.1063/1.4891019 [DOI] [Google Scholar]
- [50].Karimi A, Navidbakhsh M, Razaghi R. Plaque and arterial vulnerability investigation in a three-layer atherosclerotic human coronary artery using computational fluid-structure interaction method. J Appl Phys 2014; 116(6):064701-10; http://dx.doi.org/ 10.1063/1.4893368 [DOI] [Google Scholar]
- [51].Karimi A, Faturechi R, Navidbakhsh M, Hashemi SA. A nonlinear hyperelastic behavior to identify the mechanical properties of rat skin under uniaxial loading. J Mech Med Biol 2014; 14(05):1450075-89; http://dx.doi.org/ 10.1142/S0219519414500754 [DOI] [Google Scholar]
- [52].Karimi A, Navidbakhsh M, Alizadeh M, Shojaei A. A comparative study on the mechanical properties of the umbilical vein and umbilical artery under uniaxial loading. Artery Res 2014; 8(2):51-6; http://dx.doi.org/ 10.1016/j.artres.2014.02.001 [DOI] [Google Scholar]
- [53].Karimi A, Navidbakhsh M. A comparative study on the uniaxial mechanical properties of the umbilical vein and umbilical artery using different stress–strain definitions. Australas Phys Eng Sci Med 2014. December; 37(4):645-54; http://dx.doi.org/ 10.1007/s13246-014-0294-5 [DOI] [PubMed] [Google Scholar]
- [54].Nguyen TL, Hall SA, Vacher P, Viggiani G. Fracture mechanisms in soft rock: identification and quantification of evolving displacement discontinuities by extended digital image correlation. Tectonophysics 2011; 503(1):117-28; http://dx.doi.org/ 10.1016/j.tecto.2010.09.024 [DOI] [Google Scholar]
- [55].Karimi A, Kudo S, Navidbakhsh M, Razaghi R. A combination of experimental and numerical analyses to measure the compressive mechanical properties of tennis ball. Biomed Eng Appl Basis Commun 2015; 27(4):1550039-46; http://dx.doi.org/ 10.4015/S1016237215500398 [DOI] [Google Scholar]
- [56].Karimi A, Rahmati SM, Navidbakhsh M. Mechanical characterization of the rat and mice skin tissues using histostructural and uniaxial data. Bioengineered 2015; 6(3):153-60; PMID:25837446; http://dx.doi.org/ 10.1080/21655979.2015.1036202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface 2006. February 22; 3(6):15-35; http://dx.doi.org/ 10.1098/rsif.2005.0073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Clark J, Glagov S. Structural integration of the arterial wall. I. Relationships and attachments of medial smooth muscle cells in normally distended and hyperdistended aortas. Lab Invest 1979; 40(5):587-602; PMID:571497 [PubMed] [Google Scholar]
- [59].Staubesand J. Anatomie der Blutgefäße. I. Funktionelle Morphologie der Arterien, Venen und arterio-venösen Anastomosen. Angiology 1959; 23-82. [Google Scholar]
- [60].Canham PB, Finlay HM, Dixon JG, Boughner DR, Chen A. Measurements from light and polarised light microscopy of human coronary arteries fixed at distending pressure. Cardiovasc Res 1989; 23(11):973-82; PMID:2611805; http://dx.doi.org/ 10.1093/cvr/23.11.973 [DOI] [PubMed] [Google Scholar]
- [61].Finlay H, McCullough L, Canham P. Three-dimensional collagen organization of human brain arteries at different transmural pressures. J Vasc Res 1995; 32(5):301-12; PMID:7578798 [DOI] [PubMed] [Google Scholar]
- [62].Bhatti MA. Advanced topics in finite element analysis of structures. New York: John Wiley & Sons, Inc; 2006. [Google Scholar]
- [63].Sasson A, Patchornik S, Eliasy R, Robinson D, Haj-Ali R. Hyperelastic mechanical behavior of chitosan hydrogels for nucleus pulposus replacement—Experimental testing and constitutive modeling. J Mech Behav Biomed Mater 2012. April; 8:143-53; http://dx.doi.org/ 10.1016/j.jmbbm.2011.12.008 [DOI] [PubMed] [Google Scholar]
- [64].Karimi A, Navidbakhsh M, Haghi AM. An experimental study on the structural and mechanical properties of polyvinyl alcohol sponge using different stress-strain definitions. Adv Polym Tech 2014; 33(S1); http://dx.doi.org/ 10.1002/adv.21441 [DOI] [Google Scholar]
- [65].Itchhaporia D, Snow PB, Almassy RJ, Oetgen WJ. Artificial neural networks: current status in cardiovascular medicine. J Am Coll Cardiol 1996. August; 28(2):515-21; http://dx.doi.org/ 10.1016/0735-1097(96)00174-X [DOI] [PubMed] [Google Scholar]