Protein Folding and Structure Prediction from the Ground Up II: AAWSEM for α/β Proteins

Abstract

The atomistic associative memory, water mediated, structure and energy model (AAWSEM) is an efficient coarse-grained force field with transferable tertiary interactions that incorporates local in sequence energetic biases using structural information derived from all-atom simulations of long segments of the protein. For α helical proteins, the accuracy of structure prediction using AAWSEM has been established previously. In this article, we examine the capability of AAWSEM to predict the structure of α/β proteins. We also elaborate on an iterative approach that uses the structures from a first round of AAWSEM simulation as fragment memories. This iterative scheme improves the quality of the structure prediction and makes the free energy profile more funneled toward native configurations. We explore the use of clustering analyses as a way of evaluating the confidence in various structure prediction models. Clustering using a local relative order parameter (mutual Q) of the predicted structural ensemble turns out to be optimal. The tightest cluster according to mutual Q generally has the most correctly folded structure. Since there is no bioinformatic input, AAWSEM amounts to an ab initio protein structure prediction method that combines the efficiency of coarse-grained simulations with the local structural accuracy that can be achieved from all-atom simulations.

Graphical Abstract

Introduction

Determining the structure of proteins has advanced through an extensive collaboration between theorists and experimentalists. Experimental efforts now routinely resolve protein structures with high resolution, enlarging the Protein Data Bank (PDB) by thousands each year.¹ Nevertheless, an overwhelming number of biologically interesting systems remain untouched due to experimental limitations and the vastness of sequence space. To address these systems, computational efforts must be largely relied upon to predict protein structures.

Over the past few decades, structure prediction methods using either a top-down (Homology modeling) or a ground-up viewpoint (ab initio methods including coarse-grained models and explicit atomistic simulations) approaches have been developed. Among these, homology modeling has the most power, achieving its accuracy by employing the evolutionary database.² The evolutionary approach doesn’t always work well because of the still somewhat spotty coverage of structures. Atomistic simulations in principle avoid this bioinformatic limitation. In fact, detailed atomistic simulations with a well-optimized force field have already been shown capable of folding many small to medium size protein from the ground up.³ As protein size increases, however, an exhaustive search of conformational space with these force fields becomes prohibitively expensive computationally. The evolutionary conservation of structures, the basis of homology modeling, is the result of the funneled nature of evolved protein energy landscapes and this gives hope for being able to sample even large systems efficiently.^4–7 Energy landscape theory quantifies the funneled nature of a landscape, and has led to the development of an optimized family of coarse-grained force fields that can be used to sample the configurations of even a large protein efficiently.^4,7–11

Energy landscape analysis suggests that local signals (interactions along the backbone involving residues close in sequence) contribute a large fraction of the specificity of folding.¹² Studying fragments of a protein thus provides a shortcut to predicting the structure of the protein in its entirety. The associative memory Hamiltonian (AMH) incorporated such local signals using information from the PDB database of solved structures. Using this bioinformatic input along with a coarse-grained force field optimized by energy landscape theory, AMH is efficient in structure prediction and protein docking.^4,8 When the sequence of the target has closely related homologs of known structures, AMH amounts to an efficient homology modeling tool but it can also be used when no homologues are available and only local patches of sequence can be found in the structural database. We have shown an augmented version of AMH with water-mediated interactions, known as the associative memory, water mediated, structure and energy model (AWSEM), can go further than homology modeling and allows moderate resolution structure predictions even without there being any homologues whose structures are known.^9,10,13 The AWSEM force field has been used to predict structures of both globular and membrane proteins,^11,14 and to study protein-protein association¹⁵ and the early phases of protein aggregation.¹⁶ The AWSEM force field employs structural information about protein fragments, which we call memories. In its standard use, the memories that are chosen are bioinformatically derived from the PDB by local sequence similarity (rather than global homology).¹² Again the database can be spotty in its coverage even at the local in sequence level. To overcome this limitation, we have explored how to incorporate fragment memories that are selected from atomistic simulations rather than from solved crystal structures. We call the resulting force field the atomistic associative memory, water mediated, structure and energy model (AAWSEM).¹⁷ AAWSEM combines the efficiency of coarse-grained simulations on the full protein level with the local structural accuracy from all-atom simulations of shorter protein segments. Owing to the smaller size of the segments, simulating them atomistically is much easier than simulating the protein as a whole. We have already shown that AAWSEM can predict the structures of six α-helical proteins without any bioinformatic input.¹⁷

Of course, coarse-grained force fields based on fragment information can only be as good as their input. Some atomistic force fields have been criticized for their improper local bias.¹⁸ In addition, while the forces stabilizing helices and stabilizing the turns in a helical protein are local, this locality of interaction is far less clear for proteins with β strands that unavoidably involve the pairing of more distant parts of the sequence in sheets. The previous AAWSEM calculation used as input atomistic calibration on segments containing roughly 20 to 30 amino acids. This should be long enough to capture many elements of simple β strand architectures but perhaps not all.

Thus in this paper we turn our attention to α/β proteins and examine ways around both the questions of improper local bias in the atomistic simulations and the nonlocality of structure in β strands. For the former issue we explore the use of the CHARMM36 force field¹⁹ which has been tuned to avoid too strong a bias to α helices. To address the nonlocality issue we employ an iterative scheme that uses the first round of predictions from AAWSEM to account for nonlocal effects on local fragment structure.

Here we develop an advanced version of AAWSEM model using the CHARMM36 force field for fragment input¹⁹ and explore a scheme of iteration: The predicted structures with lowest potential energy from a first round of predictions are used by a second round of prediction as improved fragment memories, a strategy previously used by us.²⁰ We examine the prediction power of AAWSEM in this form for five α/β proteins (1UBQ, TOP7, T089, T120 and T251). Even in the laboratory, the folding of α/β proteins can be a challenge, due to the high cooperativity of hydrogen bonding and the possible thermodynamic traps coming from energetically similar but structurally different β-strand topologies.²¹ Among the five proteins, the folding mechanisms of 1UBQ^22,23 and TOP7²⁴ have been extensively studied by us previously. The examples of T089, T120 and T251 were also studied by us in a previous paper using AWSEM with bioinformatic but non-homologous input, i.e., in a de novo structure predition mode.¹⁰ We find that the iterative prediction with AAWSEM improves the quality of the results from the initial round of AAWSEM. The correctly predicted structures are also found in a very tight cluster after one performs hierarchical clustering of the predicted structures using their relative Q as the measure of structural similarity. This clustering demonstrates the well funneled nature of the AAWSEM force field for α/β proteins.

Methods

Detailed protocol of AAWSEM

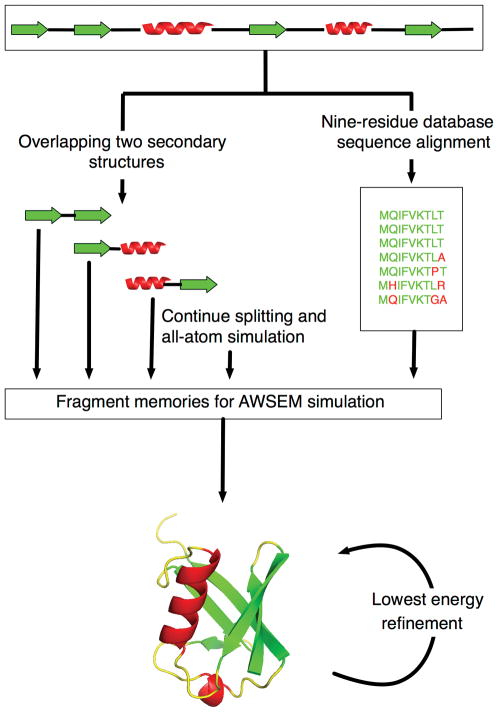
The protocol of AAWSEM has been detailed earlier by us in Chen et al.¹⁷ In this paper (Fig. 1), we use a different atomistic force field and we improve the performance by carrying out an iterative scheme. This scheme employs a second round of prediction that is guided by the fragment memories generated from the first prediction run. These fragments are extracted from those snapshots of the first round that have the lowest potential energy in the original AAWSEM force field. We study the five α/β proteins shown in Fig. 2.

Figure 1.

Protocol for structural prediction using database AWSEM (right side of figure) and AAWSEM (left side). The secondary structure of T089 is used as an illustration, and different secondary structures are color labeled. An iterative scheme, which is to use the predicted structure with lowest potential energy for a second round of AAWSEM prediction, is indicated in the bottom.

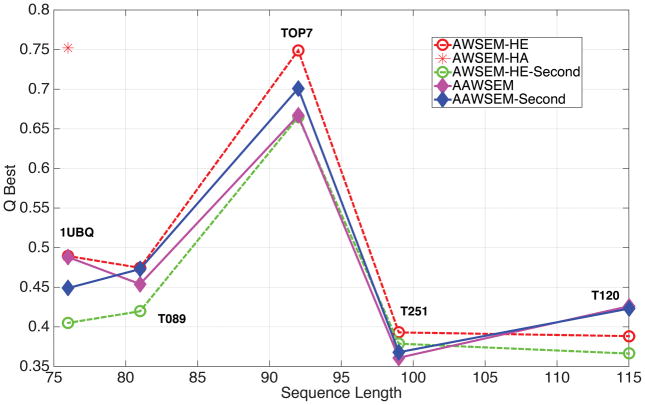
Figure 2.

A summary of the prediction results for 5 α/β Proteins. Only the predictions with highest Q value are reported here. From left to right are: Ubiquitin (PDB ID: 1UBQ), T089 (PDB ID: 1E4F), TOP7 (PDB ID: 1QYS), T251 (PDB ID: 1XG8) and T120 (PDB ID: 1FU1). Q is used as an evaluation metrics. The maximum Q values in each prediction runs were plotted against the sequence length of each of the five proteins. The red star represents a structure prediction for 1UBQ using AWSEM that allowed for the presence of homologues. Simulations using homologues only are typically of higher quality still.

The AAWSEM Force Field

AAWSEM is a version of the AWSEM force field most of whose details are those described in Davtyan et al, which should be consulted for further detailed information.^11,17 We briefly summarize the common features here. AAWSEM is a predictive coarse-grained protein folding force field that employs 3 sites per amino acid whose parameters have been optimized based on the energy landscape theory. The AAWSEM hamiltonian consists of a backbone term V_backbone, a many body burial term V_burial, a contact term V_contact and a hydrogen bonding term V_HB. The hydrogen bonding term, V_HB, is associated with the secondary structural weight. In AAWSEM this term encodes one bias for the α-helix conformation and another bias term for predicting β-strand hydrogen bond formation. The strengths for these two terms are based on the secondary structural prediction using Jpred.²⁵

$$V_{\text{total}}=V_{\text{backbone}}+V_{\text{contact}}+V_{\text{burial}}+V_{\text{HB}}+V_{\text{FM}}$$ (1)

Apart from these biases, V_FM, a fragment based associative memory term, in the form

$$V_{FM}=-{\lambda }_{FM}\sum \sum \mathit{exp}\left[-{(r_{ij}-r_{ij}^m)}^2/2{\delta }_{ij}^2)\right],$$ (2)

guides local interactions during protein folding. r_ij defines the distance between C_α atoms in a certain configuration, while $r_{ij}^m$ defines the distance in the memory structures and ${\delta }_{\text{ij}}^2={\mid \mathrm{i}-\mathrm{j}\mid }^{0.15}$ defines a width dependent on sequence separation. In our simulation, the memory structures referenced by V_FM come from two different sources. In the “bioinformatic mode”, an exhaustive search of structures with locally similar sequence from the PDB is used in the simulation. In the implementation with the AAWSEM force field, the fragments are obtained from a detailed explicit solvent simulation of protein segments.

In the atomistic input simulation, the full sequence is first segmented in a overlapping fashion according to the knowledge-based secondary structure prediction using Jpred. The atomistic simulations of these segments are initialized in random structures. The Continuous Simulated Tempering (CST) method,^26,27 an enhanced sampling technique, is used to obtain a thermodynamic ensemble for each segment. The temperature range implemented in CST is between 290K and 350K. After that, a “single linkage” algorithm is used to cluster structures obtained at low temperature (T < 330K). λ_FM is a scaling weight assigned to each fragment memory that is determined by the size of each cluster from atomistic simulations.

Details for the All-Atom input simulations

The atomistic simulations were performed with the CHARMM36 force field using 0.15 M NaCl ions and the TIP3P model for water in a dodecahedral box containing approximately 20000 to 40000 water molecules depending on the initially chosen structure of the polypeptide segment. In our previous paper on AAWSEM studying six α-helical proteins, we used CHARMM27.²⁸ The latter atomistic force field has a stronger helical bias than CHARMM36, but that did not seem to influence the prediction power for helical proteins. For α/β proteins, the better balanced CHARMM36 should be a better choice (A comparison for TOP7 using these two force fields shows the prediction using CHARMM36 is better, details in Supporting Information Fig. S7). Each protein segment was simulated for 300ns with the GROMACS software package.²⁹

Order Parameters for Structure Analysis and Umbrella Sampling

To survey energy landscapes quantitatively, one can use order parameters to classify structures. The structural similarity between two different protein configurations can be quantified globally by Q^αβ (mutual Q).

$$Q^{\alpha \beta }=\frac{2}{(N-2)(N-3)}\sum _{j>i+2}\mathit{exp}\left[-{(r_{ij}^{\alpha }-r_{ij}^{\beta })}^2/2{\delta }_{ij}^2)\right]$$ (3)

where N is the total number of residues. To evaluate the quality of predictions in comparison with a known (or postulated) native structure, this metric can be used with a reference structure considered to be native. We write this quality measure simply as Q in that case.

To characterize free energy landscapes, we use umbrella sampling employing a harmonic potential in Q to restrain constant temperature molecular dynamics simulations within windows based on reference values:

$$V_{Q-\mathit{bias}}=\frac{1}{2}{k}_{Q-\mathit{bias}}{(Q-Q_0)}^2$$ (4)

with k_Q–bias =200 kcal/mol. The reference values for Q₀ are chosen to be equally spaced from 0 to 0.98 with a step size 0.02. The data from different windows are combined using the weighted histogram analysis method (WHAM) to construct full free-energy profiles.

Simulation Details using AAWSEM

All prediction simulations using AAWSEM were performed using the software of the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).³⁰ All the umbrella sampling simulations were carried out for 10 million steps at 350K. All the annealing simulations were started with extended conformations and simulated for 10 million steps starting from 600K cooling to 300K.

Hierarchical Clustering Analysis of Predicted Structures

A hierarchical algorithm in MATLAB, with “centroid” linkage, is used to cluster the predicted structures from AAWSEM simulations. We obtain clusters using several specific order parameters (mutual Q, RMSD and score of CE-alignment) to build the linkage matrix. Specific clusters are recognized with a cutoff. The central structure of any cluster is calculated for further visualization. The mean value of the mutual-Q inside the cluster is used as the metric to describe the tightness of this cluster. The mean value of the mutual-Q however is not the only metric that can be employed.

Visualization of Structural Ensembles

In order to describe an ensemble of predicted structures, we superimpose all the predicted structures in the ensemble and represent them as a shadow. The central structure of the cluster is highlighted in color and shown as opaque.³¹ All structures are aligned together using CE alignment to show the structural variance of the predicted ensemble.

Results

Prediction Results for Five α/β Proteins

The prediction results are summarized in Fig. 2. The results indicate the prediction power of AAWSEM using five typical proteins all having composite α/β structures. The maximum predicted Q values with reference to its native structure of each protein are presented for predictions employing both the homolog-excluded model using bioinformatically chosen fragment input (AWSEM-HE) and the AAWSEM model. By excluding homologues, the AWSEM-HE result can still essentially be viewed as an ab initio prediction, although not a “bottom-up” one. Generally speaking, the best predictions with the database having homologues excluded shows a slightly better performance than the strictly bottom up predictions obtained purely from the AAWSEM approach for our test cases in the first round. 1UBQ and T120 have comparable best predictions for both schemes.

Iterative optimization schemes have been adopted successfully in other protein structure refinement and structure prediction protocols.^32,33 We explore here an iterative method that uses the predictions from the previous round as the fragment memories for a final round of predictions. Since the water-mediated non-local interactions have been optimized in both AWSEM and AAWSEM, iterative refinement of the fragments locally might be expected to improve the predictions. AAWSEM with iteration indeed successfully improves the prediction results for most cases (except for 1UBQ, which will be discussed later). Iteration, however, typically did not improve the predictions from the AWSEM-HE model.

The failure of iterative prediction for AWSEM-HE to improve quality suggests that iterations, not surprisingly, can sometimes amplify input errors as much as correct them. Without bioinformatic input that generally helps, AAWSEM nevertheless does give a good average quality for fragment memories from atomistic simulations, and the optimized water-mediated interactions consistently improves those predictions. Taken together, AAWSEM, which gets its fragment memories from all-atom simulations sampled according to a thermodynamic distribution, seems to be a better candidate for employing iteration, at least for α/β proteins.

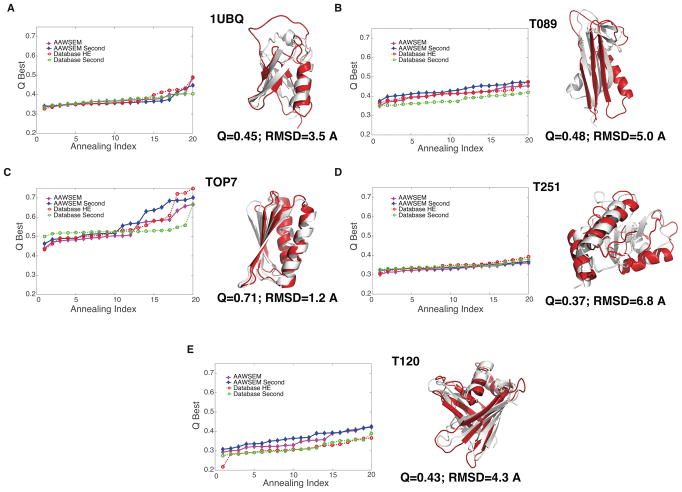
Figure 3 shows the annealing profiles for 20 runs for each protein. This plot shows the relatively good quality of AAWSEM and AWSEM-HE results. Except for 1UBQ, the general trend of the prediction for the second round (blue) of AAWSEM is to be better than it was for the first round (magenta). In two cases (T089 and T120) iterative AAWSEM does better than first round AWSEM-HE.

Figure 3.

Prediction quality for each of the 5 α/β Proteins. Left: A total of 20 simulated annealing runs were completed for each protein with different prediction algorithms: Purple filled diamonds indicate the first round with AAWSEM; blue filled diamonds for the second round with AAWSEM; red empty squares for the first round with HE-database; green empty squares for the second round with HE-database;. In each case, the Q values of different runs are arranged in the order of ascending quality. Right: The alignment of the best predicted structures from AAWSEM with their native counterparts. The predicted structures are shown in red and the native structures are shown in white.

Structural alignments between the best predicted structures and the crystallized native structures are shown to the right side of the annealing profiles in Fig. 3. The results indicate a generally good tertiary structure alignment, especially in the prediction of TOP7 and T120, where secondary structures also align perfectly. In the case of 1UBQ, although the overall structural topology is correct and the secondary structures align perfectly, the major shift arises from a random loop region (residue 45 to 65) that connects the α-helix and β-sheet. We note that although fully atomistic simulations of ubiquitin show the crystal structure to be stable, so far, fully atomistic simulations have not been successful in folding ubiquitin starting from an extended state,³⁴ unlike what we see AAWSEM can do. We note that even in perfectly funneled model simulations ubiquitin’s assembly mechanism is not purely progressive but involves backtracking, i.e., one part of the protein must partially unfold before the whole molecule can complete its folding.³⁵ This feature of the mechanism undoubtedly makes the results sensitive to the annealing schedule²² which monotonically encourages native structure formation.

Clustering Analysis for Predicted Structures of Five α/β Proteins

Simulations always lead to a multiplicity of predictions. How can one choose the best structures out of an ensemble? Using the potential energy of the simulation or using some relatively complete scoring function as a metric often proves useful.³³ Unfortunately, scoring metrics fluctuate a lot (proteins with incorrect symmetries sometimes share similar potential energies: the mirror image structures of TOP7 that contain nearly all the contacts of the true native structure differ only by about several kJ/mol in potential energy from fully correct structures with the AAWSEM force field).

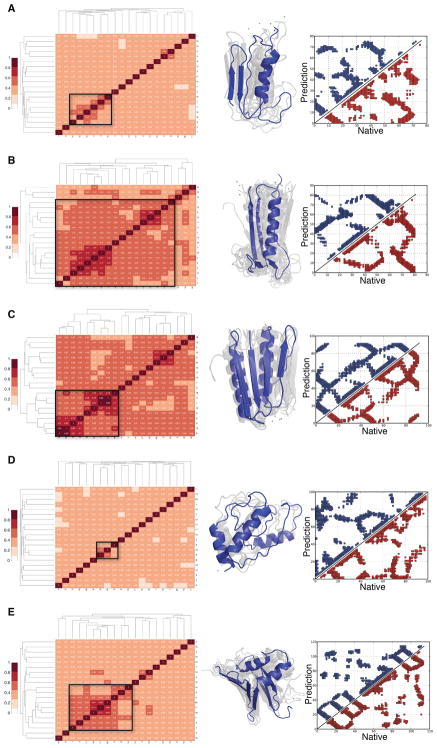
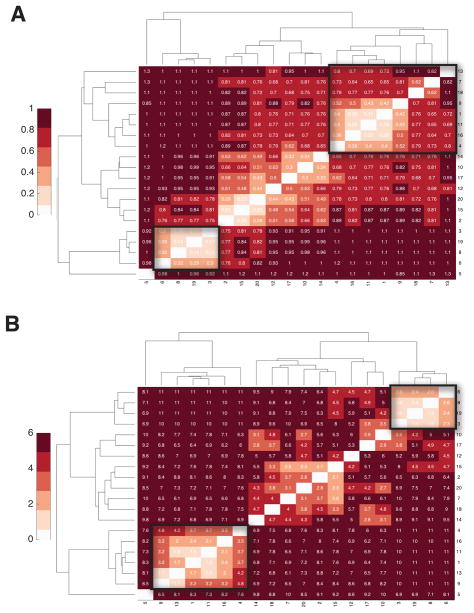
We suggest here using hierarchical clustering to pick apart the ensemble of predictions. We find the best clustering uses Q^αβ as the metric. As shown in Fig 4, the tightest cluster based on Q^αβ (labeled with a black square) usually corresponds to the most native-like structures, while the smaller and more diffuse clusters usually represent more misfolded structures. The shadow of the best structural clusters shows small variances for the five α/β Proteins (the misfolded ensembles with large variances are not shown). The central structures (colored blue in each shadow) identified from the folded cluster have very similar contact maps to those of the actual native structures.

Figure 4.

Clustering Analysis for Predicted Structures using relative Q as the metric. From top to bottom are (A) 1UBQ, (B) T089, (C) TOP7, (D) T251 and (E) T120. 20 predicted structures were hierarchically clustered and shown in a heatmap on the left. The tightest cluster is identified in a black square on the heatmap, and structures from this cluster are shown in the middle. On the right are the contact maps for the central structure of the tightest cluster (shown in blue) and the native structure (shown in red).

A tight cluster having many native-like configurations signals the funneled nature of protein folding landscapes for 1UBQ, T089, TOP7 and T120. In T251, the structures turn out to be barely correlated after hierarchical clustering (Fig. 4D). In other words, the landscape appears to be glassy with many quite different structures having similar free energies. T251 turns out to be easily trapped in a glassy state in structure prediction using either the database fragment memories or the atomistic fragment memories in the AAWSEM force field (Fig. 3D). This broad rugged landscape suggests to us that this protein of unknown function may be involved in allosteric changes. In the SI one can compare the frustration pattern of the AAWSEM predicted structure and the reported crystal structure of T251, which shows more frustration (Fig S9A and B). Previous work on structure refinement of T251 using fully atomistic force fields also showed that the crystal structure of T251 is rather difficult to model and refine.³⁶ Indeed that work showed the crystal structure was in part unstable under the atomistic force field. We also find that results with the AAWSEM force field. We find that attempting structure prediction with even the native structure as memory is not able to fold the structure properly(Fig S9C and D). In our experience, this is very unusual and we must entertain the idea that either there are potential defects in the crystal structure of T251 or that our models miss an essential cofactor or partner for folding.

In contrast to the cluster analysis using Q^αβ, Cluster analyses of the predicted ensemble (TOP7) using two other common metrics, RMSD and CE-score, show considerable scatter rather than yielding a single-tight cluster as happens with the Q^αβ metric(Fig 5, Fig S2, Fig S3, Fig S4, Fig S5, and Fig S6). The differences in behavior found using the three order parameters suggests Q to be the best choice of order parameter for clustering.³⁷

Figure 5.

Comparing clustering analysis of a structural ensemble (TOP7) using different local metrics. (A): Clustering analysis using RMSD as the metric. The nearly correctly folded structures scatter over multiple clusters (inside the black squares). (B): Clustering analysis using the score from CE alignment as the measure. The nearly correctly folded structures again scatter over multiple clusters (inside the black squares).

Discussion

Iteration of AAWSEM Improves the Funneling of the Landscape

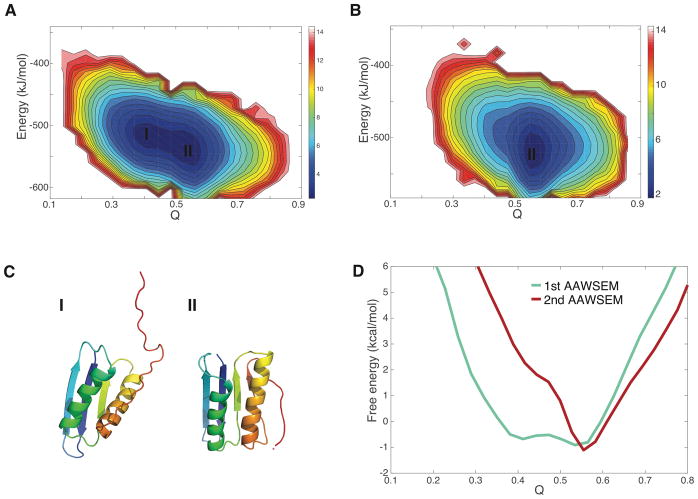
While implementing the structure prediction protocol documents the useful side of iterating AAWSEM, to understand the performance of iterative AAWSEM, it is interesting to compare the free energy profiles of TOP7 from the first iteration with the profiles for the initial round. The second round dynamics is guided by the fragment interactions from the first round structures that have the lowest potential energy. The free energy profile generated using the total potential energy along with Q as order parameters shows there are two basins in the first round(Fig. 6 A). The first basin (lower Q values ~ 0.4) represents partially folded structures of TOP7, while the second (Q ~ 0.6) contains nearly completely-folded structures (Fig. 6A). Similar free energy profiles for TOP7 using the bioinformatically guided AWSEM-HE model can be found in Truong et al.²⁴ The low-Q basin also corresponds to a possible kinetic trap during the folding process of TOP7. The native structure of TOP7 is thermodynamically favorable, but reaching it is somewhat kinetically unfavorable.³⁸

Figure 6.

Free energy landscapes of TOP7. (A) Free energy landscape of TOP7 using the AAWSEM potential energy and Q as the order parameters. The plot shows two thermodynamically stable basins. (B) Free energy landscape of TOP7 using Iterative-AAWSEM with potential energy and Q as the order parameters. The plot contains only one of the basins from the first round. (C) Representative structures from the two basins. (D) Free energy profiles for different models with Q as the order parameter are shown.

The free energy profile based on the iterative AAWSEM landscape no longer contains the first lower Q basin that was comprised of partially folded structures(Fig. 6B and C). The landscape is more funneled towards the native state, after iteration.

Possible mirror-image structures in the predicted structures of TOP7

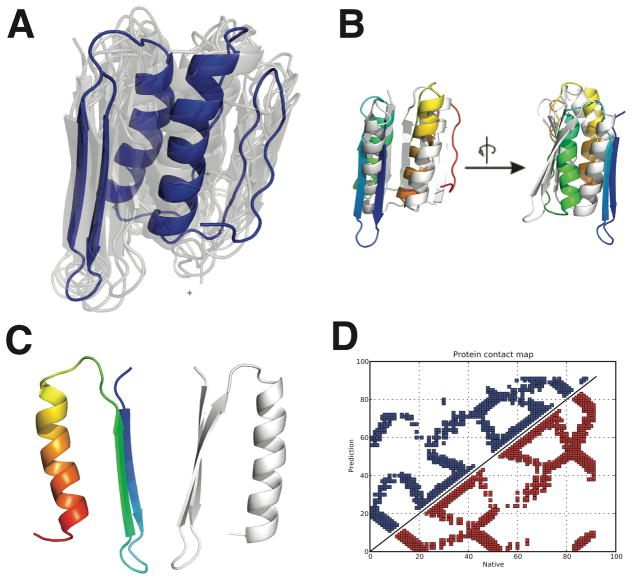
Clustering with the mutual Q metric reveals two structural ensembles for TOP7 (Fig. 4C). The clusters were determined with a threshold of 0.6 (structures with mutual Q larger than 0.6 were considered to be in the same cluster). The tightest cluster, which includes the structure with the largest mean mutual Q value, corresponds to the correctly folded ensemble (as detailed above), but the other cluster represents a misfolded ensemble populated with “mirror-image” structures (Fig. 7A and B). The predicted “mirror-image” structures of TOP7 share similar contacts with the native but have an overall inverted symmetry, while still keeping the usual chirality of α helices (Fig 7 C and D).³⁹ As a computationally designed protein lacking an evolutionary history, while the native structure of TOP7 has been validated to be thermodynamically favorable, it has turned out to be kinetically difficult to access.³⁸ In the laboratory the folding landscape of TOP7 is rugged with multiple non-native conformational traps.³⁸ It is possible that the predicted mirror-image structures formed by AAWSEM are contributing to the kinetic traps in the laboratory. Atomistic simulations often encounter such mirror-image structures.^40–42

Figure 7.

Predicted mirror-image structures for TOP7. (A): The structural ensemble of the non-native cluster found from structure prediction. (B): Alignment of the picked central structure of the ensemble (colored from blue to red) and the native structure (colored white) in two different views related by 90° rotation. (C): The mirror-image domain of the misfolded structure is compared with its native counterpart. (D): Comparison of the contact maps of the mirror-image (blue) and the native (red) structure.

Frustration analysis of T120 and T089 and their natural complexes suggests there can be internal domain swapping in monomer mis-prediction

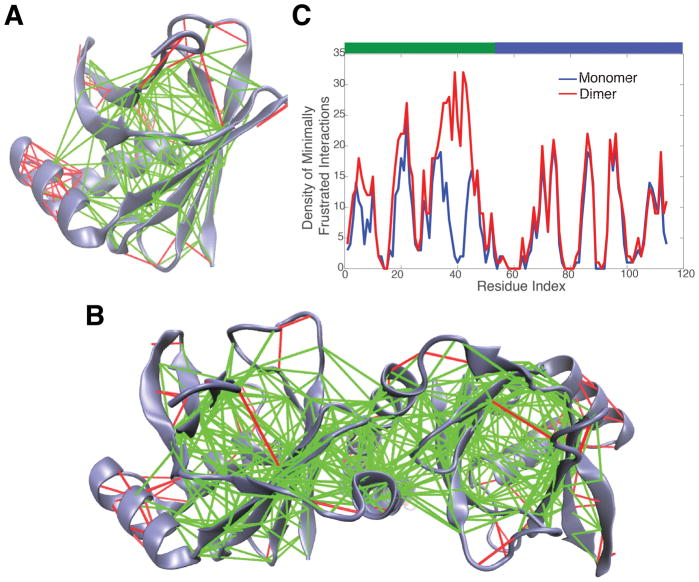
T120 is an N-terminal domain of human XRCC4DNA repair protein (PDB ID: 1FU1, also a CASP4 target). It is a single domain of a much larger complex. The native structure of this protein is composed of two sandwich-like β-sheets with two helices linking together (Fig. 8 A). The unstable β-sheet in our prediction corresponds to the binding interface between the N-terminal and C-terminal domain in the larger protein complex. In order to quantify the stability of this region, we carried out frustration analysis of T120 by itself and in the complex using the Frustratometer.⁴³ Although both the isolated and in-complex T120 show mostly minimally frustrated patterns on the 4-strand β-sheet (Fig. 8A and B), the protein has a higher density of minimally frustrated contacts in the complex (Fig. 8 C). This suggests these additional contacts with the C-terminal of protein complex stabilize the 4-strand β-sheet of T120. These interfacial contacts cannot be made when the monomer is folded by itself without its partner. The monomer essentially undergoes an internal domain swap, employing strong interfacial interactions inappropriately to stabilize the monomer, a pattern we have previously seen for oligomeric membrane proteins.⁴⁴

Figure 8.

Frustration analysis of T120 folding. The frustratograms show calculated configurational frustration of T120 (A) and its complex 1FU1 (B). Minimally frustrated contacts are shown in green and highly frustrated contacts are shown in red. (C): Comparison of the density of minimally frustrated contacts in T120 (Blue) and 1FU1 (Red) on each residue. The green bar above represents the 4-strand β-sheet that interacts with the additional parts in T120 complex.

A similar pattern was also found in T089, a single domain from the protein complex 1E4F. In the T089 native structure, a long three-strand β-sheet is wrapped around the α-helix, and interacts with the rest of 1E4F. Frustration analysis shows that the binding-interface has a higher density of minimally frustrated contacts in the structure of the complex than it has in the T089 monomer alone (Fig S1). Frustration analysis then suggests it might be easier to predict more accurately its structure by simulating the entire multimolecular complex, rather than its parts individually. Just as in experimental structure determinations, computational predictions will benefit from paying attention to the context provided by a protein chain’s partners in vivo.

Conclusion

In conclusion, we have explored the AAWSEM force field using the CHARMM36 force field and including an iterative scheme. The present study of five α/β proteins documents the prediction capabilities of both AAWSEM and the iterative AAWSEM algorithm. Iterative AAWSEM displays improved structure prediction capabilities. Iteration increases the funneling of the landscape towards the native structure. Clustering analyses with mutual Q as the order parameter effectively identify the structural clusters that have the most native-like configurations. AAWSEM and iterative AAWSEM appear to be useful in predicting protein structure from the ground up without any bioinformatic input.