A new general method for simultaneous fitting of temperature and concentration dependence of reaction rates yields kinetic and thermodynamic parameters for HIV reverse transcriptase specificity

Abstract

Recent studies have demonstrated the dominant role of induced fit in enzyme specificity of HIV reverse transcriptase and many other enzymes. However, relevant thermodynamic parameters are lacking, and equilibrium thermodynamic methods are of no avail because the key parameters can only be determined by kinetic measurement. By modifying KinTek Explorer software, we present a new general method for globally fitting data collected over a range of substrate concentrations and temperatures and apply it to HIV reverse transcriptase. Fluorescence stopped-flow methods were used to record the kinetics of enzyme conformational changes that monitor nucleotide binding and incorporation. The nucleotide concentration dependence was measured at temperatures ranging from 5 to 37 °C, and the raw data were fit globally to derive a single set of rate constants at 37 °C and a set of activation enthalpy terms to account for the kinetics at all other temperatures. This comprehensive analysis afforded thermodynamic parameters for nucleotide binding (K_d, ΔG, ΔH, and ΔS at 37 °C) and kinetic parameters for enzyme conformational changes and chemistry (rate constants and activation enthalpy). Comparisons between wild-type enzyme and a mutant resistant to nucleoside analogs used to treat HIV infections reveal that the ground state binding is weaker and the activation enthalpy for the conformational change step is significantly larger for the mutant. Further studies to explore the structural underpinnings of the observed thermodynamics and kinetics of the conformational change step may help to design better analogs to treat HIV infections and other diseases. Our new method is generally applicable to enzyme and chemical kinetics.

Introduction

HIV RT is responsible for the replication of viral RNA, and accordingly inhibitors of HIV RT are the cornerstone of combination therapy to combat HIV infections, including both nucleoside analogs and non-nucleoside inhibitors (1–3). Nucleoside analogs serve as substrates for the polymerase reaction, but they lack a 3′-OH on the ribose mimic, and consequently they block further polymerization after incorporation. Thus, the mechanistic basis for enzyme specificity is fundamental to understanding the effectiveness of nucleoside analogs and evolution of resistance. In prior work (4), we showed that following the weak nucleotide binding to an open state of the enzyme, RT rapidly closes to align residues to afford catalysis according to the minimal pathway,

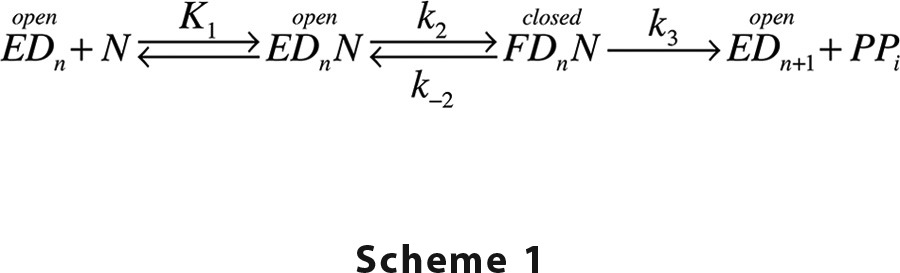where ED_n represents an open enzyme-DNA complex with DNA n residues in length, N represents the nucleoside triphosphate, and FD_nN represents the closed, nucleotide-bound state of the enzyme. Because PP_i release is fast following incorporation of a correct base with a DNA template, we have simplified the model by eliminating steps after the rate-limiting chemistry step (k₃).

DNA polymerases such as HIV RT represent an ideal model for studying enzyme specificity because fidelity is physiologically important, and the alternate substrates are known. Moreover, one can easily perform single-turnover experiments by mixing an ED complex with one nucleotide to initiate a single reaction cycle. Because the next base would be a mismatch, the enzyme undergoes only a single enzyme cycle to bind nucleotide, close, perform catalysis, and then open. Using a fluorescently modified HIV RT, the time course of a single turnover has been monitored by stopped-flow methods to record changes in enzyme structure involving closing after nucleotide binding and reopening after chemistry (4). Thus, the nucleotide concentration dependence of the fluorescence transient allows resolution of all rate constants shown in Scheme 1 except k₋₂, which is measured separately (4). However, because the rate constant for reopening of the FD_nN complex (k₋₂) is small relative to the forward rate of chemistry (k₃), enzyme specificity is solely determined by the binding affinity of the nucleotide in the open state of the enzyme (K₁) and the rate at which the enzyme closes; that is, k_cat/K_m = K₁k₂, whereas k_cat = k₃. The value of k₋₂ is not important as long as it is significantly less than k₃. Although this model has caused significant controversy and misunderstanding (5), it is supported by direct kinetic measurements (4) and MD simulations (6, 7) and provides a rationale to explain the effectiveness of certain nucleoside analogs and the evolution of resistance (4, 8). Moreover, induced fit may afford a general mechanism to increase enzyme specificity by enhancing the discrimination between desired and alternative substrates (9–11). However, thermodynamic parameters for these critical substrate binding and conformational change steps are lacking. In prior work (4), the rate constant for the nucleotide-induced conformational change (k₂) at 37 °C was derived by extrapolation of measurements as a function of temperature on an Arrhenius plot. Here we present the simultaneous, global fitting of the temperature and concentration dependence of the substrate-induced conformational change steps to derive thermodynamic parameters governing specificity.

Results and discussion

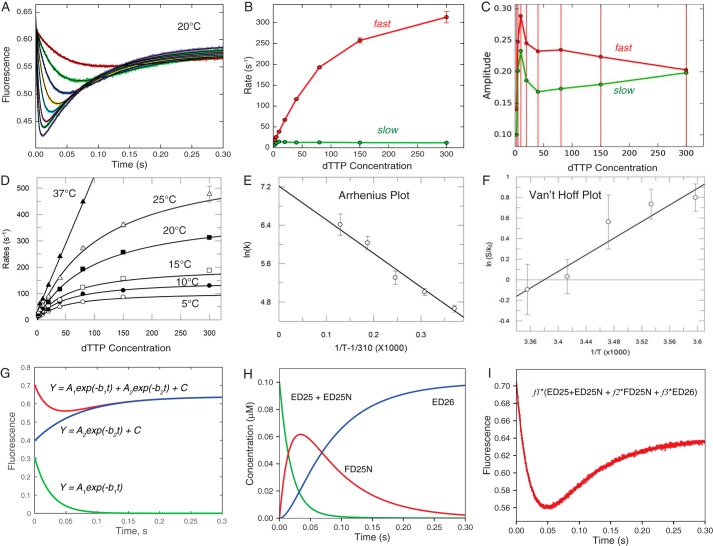
First we show conventional analysis of stopped-flow transients to measure the kinetics of nucleotide binding and incorporation by HIV RT and the temperature dependence to extrapolate parameters to 37 °C. At each temperature, individual transients are fit to a double exponential function (Equation 1) as illustrated in Fig. 1A with data collected at 20 °C.

$$Y=A_1·e^{-b_1·t}+A_2·e^{-b_2·t}+C$$ (Eq. 1)

Figure 1.

Conventional fitting of temperature dependence of dTTP binding and incorporation by MDCC-labeled WT_HIVRT. We examined the nucleotide concentration dependence of fluorescence signals arising from changes in the structure of the enzyme-DNA complex from open to closed (high to low fluorescence) as described previously (4) and summarized under “Experimental procedures.” The experiments were performed at 5, 10, 15, 20, 25, and 37 °C. The raw data are shown in Fig. 2. A, transients at 20 °C were fit to a double exponential function (Equation 1) by nonlinear regression; the thin black line shows the fitted curve. B, concentration (μm) dependence of the rates of the fast and slow phases derived from fitting data in A with error bars showing the standard errors. C, concentration (μm) dependence of the absolute amplitudes of the fast and slow phases; note the amplitude of the fast phase is positive, and that for the slow phase is negative according to Equation 1, but here we plot the absolute value of the amplitudes. Error bars show the standard errors. D, the concentration dependence of the fast decrease of fluorescence (corresponding to conformational closing) was fit to hyperbolic function (Equation 2) to obtain the maximum rate of the conformational change (k₂) and the K_d for ground state binding at each temperature. E, the temperature dependence of k₂ was analyzed by Arrhenius plot to estimate a maximum rate for k₂ of 1360 ± 300 s⁻¹ at 37 °C, as well as the activation enthalpy of 58 ± 6 kJ/mol. Note here that the x axis is 1/T − 1/310, so that extrapolation to zero gives the rate at 37 °C. Extrapolation to 1/T = 0 leads to huge errors. F, analysis of the temperature dependence of the equilibrium constant for nucleotide binding (S/K_d), where [S] = 100 μm (physiological concentration) on a Van't Hoff plot to give an extrapolated K_d = 186 μm at 37 °C and ΔH = −33.6 kJ/mol. G, fitting of the data at 20 °C at 10 μm dTTP to a double exponential function is shown along with the separate terms for the fast and slow phases according to Equation 1 (A₁ = 0.308, b₁ = 40.5, A₂ = 0.242; b₂ = 14.2, C = 0.639); amplitudes are in fluorescence units, and rates are in s⁻¹. H, time dependence of individual species (20 °C and 10 μm dTTP) contributes to the observed fluorescence change derived during global fitting. I, the observed signal at 20 °C at 10 μm dTTP was fit using three scaling factors, here represented by f1, f2, and f3 for each of the three fluorescence states (f1 = 7.05, f2 = 0.684, and f3 = 0.908) from the time dependence of individual species.

The concentration dependence of the rates and amplitudes of the fast and slow phases are shown in Fig. 1 (B and C), respectively. Note the large errors on the estimates of the amplitudes that impact the estimates of the rates as discussed below. The nucleotide concentration dependence of the rate of the fast phase is shown in Fig. 1D, fit to a hyperbola (Equation 2) to define K₁ and k₂.

$$\text{Rate}=\frac{K_1{k}_2\left[\text{S}\right]}{K_1\left[\text{S}\right]+1}$$ (Eq. 2)

This analysis was repeated at each temperature. However, at 37 °C the rates of the fast phase at the highest concentrations are too fast to determine either the maximum rate (k₂) or ground state binding affinity (K₁) using this method. In Fig. 1E we use an Arrhenius plot to analyze the temperature dependence of k₂ to extrapolate to k₂ = 1360 ± 300 s⁻¹ at 37 °C and yield an activation enthalpy of 58 ± 6 kJ/mol for the conformational change step. In Fig. 1F a Van't Hoff plot of the temperature dependence of the ground state equilibrium constant revealed 1/K₁ = K_d = 186 ± 38 μm at 37 °C and ΔH₁ = −33.6 ± 6 kJ/mol, summarized in Table 1. Note that the temperature dependences of K₁, k₂, and k₃ (not shown) were linear (log scale versus 1/T), so we did not need to consider including a change in heat capacity in our analysis.

Table 1.

Kinetic and thermodynamic parameters

Constants in the first six rows were obtained directly from data fitting; the remaining constants were calculated from the measured parameters. The parameters are shown with standard errors derived in globally fitting the data by nonlinear regression. As described under “Results,” we calculated ΔG₁′ = −RT ln(K₁[S]) at 37 °C and at a physiological standard state with [S] = 100 μm, which was then used to compute −TΔS₁′.

Parameter	Wild-type conventional	Wild-type global fit	TAMs global fit
1/K1 (μm)	186 ± 38	283 ± 6	1460 ± 30
k2 (s−1)	1360 ± 300	1720 ± 32	4420 ± 85
k3 (s−1)	32 ± 2	37.2 ± 0.2	66 ± 0.1
ΔH1 (kJ/mol)	−33 ± 6	−34 ± 0.2	−35 ± 0.6
ΔH‡2 (kJ/mol)	58 ± 6	58 ± 0.5	73 ± 0.5
ΔH‡3(kJ/mol)	44 ± 6.4	44.3 ± 0.2	44 ± 0.1
K1k2 (μm−1s−1)	7.3 ± 2	6.1 ± 0.2	3.3 ± 0.1
ΔG1′ (kJ/mol)	1.6 ± 0.4	2.7 ± 0.07	6.8 ± 0.05
−TΔS1′ (kJ/mol)	34 ± 10.6	36.7 ± 1.2	41.8 ± 0.8

Although this is the currently accepted method for data analysis, there are several limitations. First, some of the data must be excluded from the analysis either because the rate is too fast to measure at higher concentrations and temperatures or the two exponentials are not well resolved at the lower concentrations. Moreover, fitting curves to multiexponential functions is error-prone because it disregards important relationships between rates and amplitudes. Fig. 1C shows that the amplitudes of both phases derived by fitting the data to Equation 1 increase and then decrease. However, it is apparent from inspection of the primary data in Fig. 1A that the amplitudes of both the fast and slow phases increase monotonically as a function of dTTP concentration to a maximum signal change of ∼0.2. The observed increase in the amplitudes (Fig. 1C) above 0.2 is a function of fitting to a double exponential function, as illustrated in Fig. 1G, showing that the observed signal is treated as the sum of two exponential functions with opposing amplitudes but comparable rates. Although the exponential function affords a mathematically valid solution to the rate equations to mimic the data, the amplitudes are not physically meaningful under all circumstances. When the two rates are comparable, the fitting routines often return functions with very large opposing amplitudes, so the observed reaction is represented as a small difference between large numbers, and errors in amplitudes propagate to errors in rates, tending to overestimate both rates and both amplitudes. This effect has been shown to produce overestimates of rate constants when two phases cannot be resolved (12). Consequently, unless two rates differ by approximately a factor of 3 or more, resolution of the two phases by conventional fitting can be problematic. Marginal data either are eliminated from subsequent analysis or introduce errors. For example, data at 37 °C are excluded from conventional analysis of the temperature dependence, even though the slope of the concentration dependence accurately defines the most important kinetic parameter, K₁k₂ = k_cat/K_m (Fig. 1D) at 37 °C. Finally, it is important to recognize that when fitting the data using equations, the large number of independent parameters needed to fit the data contributes to increased uncertainty. For example, in fitting eight traces at each of the six temperatures to a double exponential function (Fig. 1), a total of 240 independent parameters are derived to extract only six kinetic and thermodynamic parameters (Table 1).

Here we overcome these limitations by globally fitting an entire data set including the concentration dependence of the reactions at temperatures ranging from 5 to 37 °C. Fitting based on numerical integration of the rate equations is preferred because both rates and amplitudes are derived based directly on the model. The simulation leads to a prediction of the time course of individual species as shown in Fig. 1H. Fitting the signal then requires application of fluorescence (or absorbance) coefficients to estimate the contribution of each species to the final signal as shown in Fig. 1I. Here, as in fitting to a double exponential function, three amplitude terms are required to fit the data. However, when fitting the data by simulation, these three scaling factors are global terms that apply to the full data set over the range of substrate concentrations. By fitting all of the data simultaneously, the global scaling factors are derived without ambiguity, and they are physically meaningful by defining the change in fluorescence for each state. Federova has performed thermodynamic analysis of rate constants derived at different temperatures by simulation-based data fitting followed by conventional Van't Hoff analysis (28). Here we combine these approaches to derive kinetic and thermodynamic parameters in one step.

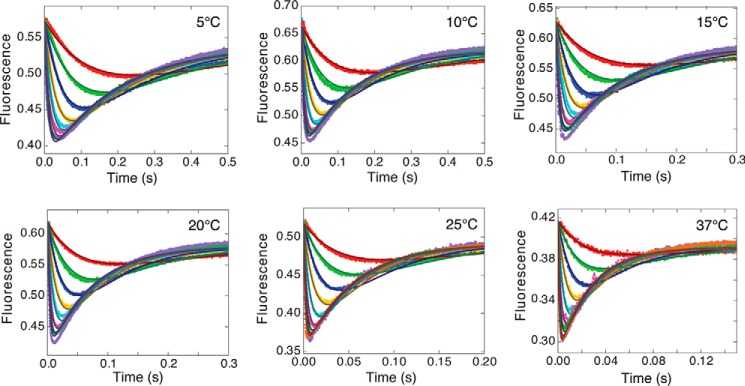
To globally fit data collected over a range of temperatures, KinTek Explorer (13, 14) data fitting software was modified to accommodate an exponential dependence for each rate constant. Fig. 2 shows single-turnover kinetic studies performed by mixing the ED_n complex with dTTP and monitoring the signal from fluorescently labeled HIV RT (4) at each temperature. The full data set was fit simultaneously to derive a single set of rate constants at a reference temperature (37 °C in this case) and a set of activation enthalpies for each rate constant to fit the data at all temperatures simultaneously. The smooth lines illustrate the global fit to the data (Fig. 2).

Figure 2.

Temperature and concentration dependence of nucleotide binding and incorporation by wild-type HIV RT. Each panel shows the concentration-dependent transients of the fluorescence signal recorded after mixing the ED complex with various concentrations of dTTP (2.5, 5, 10, 20, 40, 80, 150, and 300 μm) at the temperatures shown; at 25 and 37 °C, an additional trace at 600 μm dTTP is also included. The measurements were made using MDCC-labeled HIV RT as described under “Experimental procedures.” The smooth curves represent the global fit of all data based upon the parameters summarized in Table 1.

The time course was modeled using numerical integration of the rate equations (Scheme 1) to derive a single set of rate constants. The observable signal was defined as the sum of the contributions of each species to the total fluorescence with scaling factors for each species,

$$Y=f_1*\left(E{D}_{\text{n}}+E{D}_{\text{n}}N+f_2*F{D}_{\text{n}}N+f_3*E{D}_{\text{n}+1}\right)$$ (Eq. 3)

where f₁ scales the fluorescence signal to concentration, whereas f₂ and f₃ define the change in fluorescence in forming FD_nN and ED_n+1, respectively, relative to ED_n and ED_nN. Different fluorescence scaling factors were used for data at each temperature, but the relative change in fluorescence in forming the closed complex was nearly constant (f₂ = 0.62 ± 0.04); that is, the enzyme closing results in a 38% reduction in fluorescence. Only 24 parameters were needed to fit the full data set (Fig. 2) including three scaling factors at each of the six temperatures and the six global kinetic and thermodynamic parameters shown in Table 1. These values are comparable to those obtained by conventional data fitting, but the errors were significantly smaller with the global data fitting. The larger standard errors associated with conventional fitting result from the propagation of errors from the individual measurements, which have greater uncertainty because of the systematic and random errors outlined above.

The specificity constant for HIV RT is defined by the product of the equilibrium constant for ground state dTTP binding (K₁) and the rate of the conformational change from the open to the closed state (k₂), k_cat/K_m = K₁k₂ (4). Thus, the specificity for cognate nucleotide incorporation is defined by states that are difficult to study directly. That is, it is difficult to know what governs the rate of such a large enzyme conformational change, and ground state binding cannot be measured by equilibrium methods because binding leads to rapid enzyme closure. For these reasons, equilibrium thermodynamic measurements fail to provide the most important information in this system. Analysis of the temperature and substrate concentration dependence provides critical kinetic and thermodynamic parameters underlying specificity based on measurements made during binding and incorporation of a normal substrate, without resorting to the use of analogs or mutants that prevent chemical reaction to allow measurements at equilibrium.

For wild-type enzyme, dTTP binds to the open enzyme state with a K_d = 283 μm, which is slightly unfavorable at the physiological concentration of ∼100 μm dTTP and 37 °C. In Table 1 we report the free energy for a reference state based on the estimated physiological concentration of dTTP rather than the 1 m standard state,

$$\Delta G\prime =-RT\ln \left(K_1\left[\text{S}\right]\right)$$ (Eq. 4)

where the product K₁[S] = [S]/K_d,1 is a dimensionless number that defines the thermodynamic driving force for binding at the physiological concentration of substrate [S].

Substrate binding is exothermic, which is offset by a large negative entropy change as the protein becomes more ordered. It is tempting to interpret these changes in terms of ionic interactions between charged residues (notably between the nucleotide and Lys-65 and Arg-72) and the ordering of protein structure, but these interpretations must be tempered by the knowledge that the net energy difference is dominated by the role of water. The conformational change step is a function of changes in structure throughout the protein, as revealed by our MD simulations (6, 7).

The conformational change occurs at a rate of 1720 s⁻¹ at 37 °C, which is too fast to measure by stopped-flow methods. Nonetheless, data at 37 °C are included in the global fitting because the amplitude of the fast transient still provides information to help define the rate of closing, and the concentration dependence of the rate at lower substrate concentrations accurately defines K₁k₂, which in this case defines the specificity constant. By globally fitting the full data set, we also obtain an accurate estimate of k₂ at 37 °C and the activation enthalpy governing the conformational change. In addition, because enzyme reopening is limited by the rate of the chemical reaction at the active site, the rate of chemistry (k₃) and its activation enthalpy are also well defined by monitoring the fluorescence signal (4).

It should be noted that the use of fluorescence methods allows experiments to be performed at low enzyme concentrations (100 nm), which allows more accurate measurement of submicromolar K_d values. This overcomes the significant errors in isothermal titration calorimetry measurements, for example, that require 200-fold higher enzyme concentrations yielding erroneous K_d values because the binding is too tight to measure accurately (15). Based upon measurement of k₋₂, we estimate the net K_d for nucleotide binding to be 6–100 nm (4, 16) at equilibrium. However, the rates of catalysis and subsequent product release are much faster than enzyme reopening with bound substrate (k₋₂), so the two-step binding reaction does not come to equilibrium during turnover (4). This understanding emphasizes the importance of kinetic measurements to define thermodynamic parameters governing enzyme specificity. After all, specificity is a kinetic phenomenon quantified by k_cat/K_m.

We also report in Table 1 the results obtained with mutant of HIV RT resistant to thymidine analogs (TAMs mutants, shown in Fig. 3) (2, 3, 17–21). The results show a significantly weaker ground state binding of dTTP (K₁) but a faster rate of the conformational change (k₂) and chemistry (k₃); accordingly, the specificity constant (K₁k₂) is reduced only 2-fold. Interestingly, the enthalpy change in ground state binding (ΔH₁) and the activation enthalpy for the conformational change (ΔH^‡₂) are both increased with the TAMs mutant, but the activation enthalpy for the chemistry step (ΔH^‡₃) is unchanged. Thus, although the mutations alter the binding of dTTP in the ground state and affect the dynamics of the conformational change step, they apparently only modestly affect the alignment and reactivity of catalytic residues in the closed state. It is noteworthy that both the rate and the activation enthalpy for the conformational change step are larger for the TAMs mutant than for the wild-type enzyme.

Figure 3.

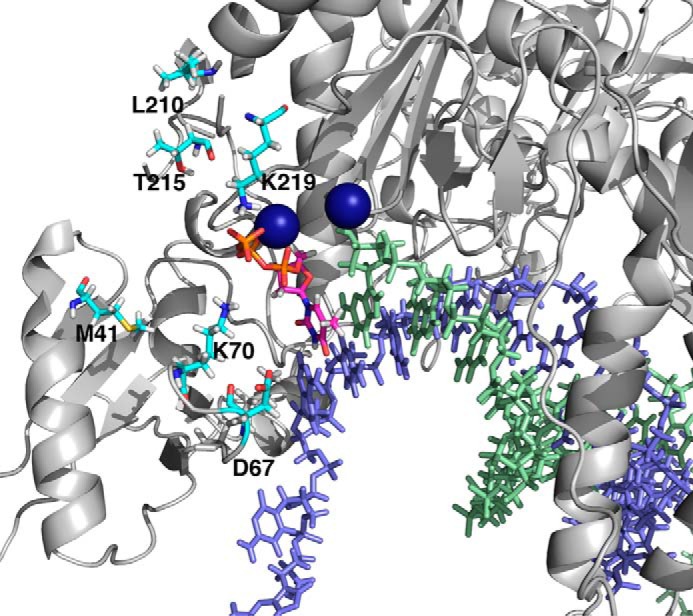
Locations of TAMs mutations. The positions for the TAMs mutations (M41L, D67N, K70R, L210W, T215Y, and K219E) are illustrated in cyan. The template strand is in light blue, the primer strand is in light green, and the incoming nucleotide in is magenta. Two Mg²⁺ ions are shown as dark blue spheres.

One might be tempted to compute the Gibbs free energy of activation and entropy of activation terms using the Eyring equation (22).

$$k=\frac{k_{\text{B}}T}{h}·e^{-\Delta G^{‡}/RT}$$ (Eq. 5)

However, this equation applies to gas phase kinetics, having a reference point for the expected rate at zero activation energy based on the vibration frequency of a single bond, defined by k_BT/h. This is not applicable to such a complex system involving protein dynamics described here. Rather one would apply a modified form of the Eyring equation,

$$k=A·e^{-\Delta G^{‡}/RT}$$ (Eq. 6)

where the value of A could be derived by analysis of the temperature dependence of MD simulations. We have conducted MD simulations to provide molecular details and predict the rate constant for the conformational change at 37 °C (6, 7). Repeating this calculation at multiple temperatures could provide estimates of the Gibbs free energy of activation and the entropy of activation.

It is possible to compare mutant and wild-type enzyme parameters to compute relative changes in entropy of activation based on a comparison between measured rates and enthalpies of activation. The rate of the conformational change step (k₂) is faster for the TAMs mutant than for WT enzyme, but the activation enthalpy is greater for the mutant. Taking the ratio of the rates for WT versus mutant (m) allows elimination of the unknown pre-exponential factor for transition state theory to yield the following.

$$T\Delta S_{\text{WT}}^{\P }-T\Delta S_{\text{m}}^{\P }=\text{RT}·\ln \left(k_{\text{WT}}/k_{\text{m}}\right)+\Delta H_{\text{WT}}^{\P }-\Delta H_{\text{m}}^{\P }$$ (Eq. 7)

From the numbers given in Table 1, we calculate that TΔS_WT^‡ − TΔS_m^‡ = −17 kJ/mol. Thus, for the mutant, either the ground state is more ordered or the transition state for the conformational change is more disordered. Because ΔH^‡ and ΔS^‡ for the conformational change step are both increased in the TAMs mutants relative to WT, it is reasonable to suppose that the mutations stabilize and order the ground state structure (ED_nN) to favor the incorporation of dTTP reported here. Mutations M41L, K70R, and D67N are all in the fingers domain that undergoes the largest changes in structure (Fig. 3). These changes in structure and thermodynamics for dTTP favor the binding and incorporation of dTTP relative to AZT-triphosphate (AZTTP),² affording modest resistance. The rate of the conformational change step is 2-fold slower for AZT compared with dTTP for the TAMs mutant (8).

Understanding AZT resistance has been a challenge because the net change in k_cat/K_m for mutant versus wild-type comparing dTTP versus AZT-triphosphate yields only a 2-fold change in discrimination (8, 23).³ Analysis of the rates of incorporation of dTTP versus AZT-triphosphate for mutant versus wild-type enzyme has revealed the underlying basis for the minimal discrimination. Although TAMs mutants decrease the rate constant for incorporation, this has an additional effect of allowing the conformational change to come to equilibrium, leading to a lower K_m value, compensating for the slower rate. Thus, the change in k_cat/K_m is much less than the change in k_cat (8). Interestingly, the results shown here reveal substantial changes in the kinetics and thermodynamics for dTTP binding and incorporation, which highlight of the structural changes caused by the TAMs mutations affecting dTTP binding. Fig. 4 shows the free energy profiles for dTTP versus AZTTP for WT and the TAMs mutant. For WT enzyme, AZTTP is a better substrate than dTTP because of the tighter ground state binding (K₁) and faster conformational change step (k₂). For the TAMs mutant, the conformational change step is faster for dTTP than AZTTP. However, now the chemistry step (k₃) is slow enough that the conformational change step comes to equilibrium and k_cat/K_m = ∼K₁k₃/(1 + K₂). Thus, the net resistance AZTTP is only 2-fold in comparing k_cat/K_m for AZTTP versus dTTP for WT versus mutant as a result of changes in the kinetic parameters for all three steps (8).

Figure 4.

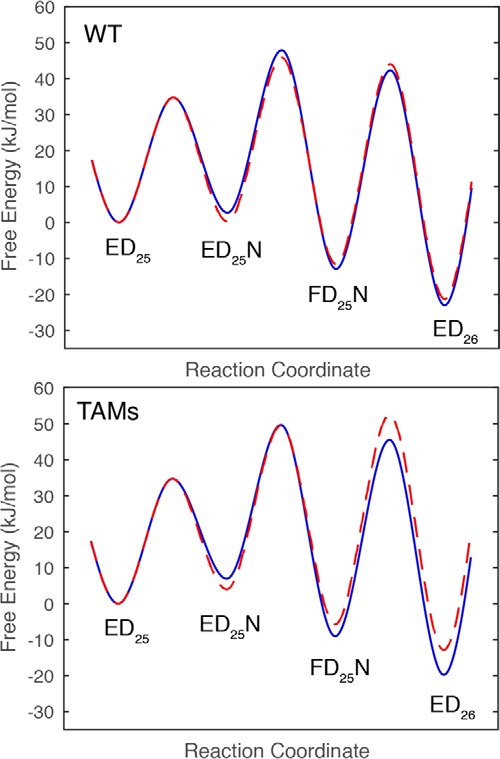
Free energy profiles for WT and TAMs with dTTP and AZT. The free energy profiles were constructed based upon the data in this report and (8). The free energies of activation were calculated from the Eyring equation, ΔG^‡ = −RT ln(k/(α·k_BT//h)), where α is a transmission coefficient set at 0.01 to better illustrate the free energy differences. The free energy profiles for dTTP are shown in blue, and those for AZT-triphosphate are red dashed lines.

The minimal resistance toward incorporation of AZT has led to the proposal that resistance is largely due to an ATP-dependent excision reaction to remove the chain terminating AZT and the suggestion that the multiple mutations in the TAMs group assist in the binding of ATP (17, 25, 26). Our recent analysis has shown that AZT resistance is a function of changes to all of the kinetic properties of the enzyme and cannot be explained solely on the basis of ATP-dependent excision so that discrimination during incorporation makes an important contribution to net resistance and cannot be neglected.³

To fit the temperature dependence globally, KinTek Explorer (13, 14) software was modified to include an exponential term for each rate constant. This modification has also allowed the global fitting of the rates of protein folding and unfolding as a function of denaturant concentration (27) in a more convenient form than described previously (24). It can also be used to examine voltage-dependent and pressure-dependent rate constants.

Our new methods can also be used to rigorously interpret temperature-jump (T-jump) experiments, performed by allowing the system to equilibrate at one temperature, then rapidly jumping to a new temperature and monitoring the rate of re-equilibration. In the present case, the simulation software can be used to predict the results of a T-jump experiment by setting k₃ = 0 (to model the use of dideoxy-terminated DNA to block chemistry and allow equilibrium binding) and then setting the enthalpy for the conformational change to a value comparable with that seen for nucleotide binding (ΔH₂ = −30 kJ/mol). Simulation of a T-jump from 5 to 37 °C (beyond the range allowed experimentally) predicts a fluorescence change of only 0.17% at a rate of 145 s⁻¹, which the simulations show is a function of the re-equilibration of nucleotide binding, with little contribution of the conformational change per se. Because the equilibrium constant for the conformational change step is so large, a rapid jump from one temperature to another will not provide a measureable signal. Thus, simultaneous analysis of temperature and concentration dependence provides more information than afforded by T-jump experiments typically used to estimate the rates of reactions that are too fast to measure by stopped-flow methods. Analysis of the concentration dependence as a function of temperature provides data to resolve the contribution of individual reactions to the observed signal. Our current method reveals limitations and eliminates the need for T-jump experiments to estimate the rates of reactions that are too fast to measure by stopped-flow methods at one temperature.

In summary, our analysis demonstrates the utility of globally fitting transient kinetic data collected over a range of substrate concentrations and temperatures to derive kinetic and thermodynamic parameters governing enzyme specificity. Nucleotide binding is exothermic but is marginally stable relative to the physiological substrate concentrations, but substrate binding triggers an enzyme conformational change, which is the major determinant of specificity. The new tools outlined here provide a rapid method for the analysis of multiple mutants with various nucleotide analogs and cognate nucleotides to more fully establish the kinetic and thermodynamic basis for nucleotide specificity and resistance, which can be complemented by MD simulations to provide insights into the molecular basis for the observed effects. The method of analysis presented here should be broadly applicable to a large range of chemical and enzymatic reactions.

Experimental procedures

Expression and purification of unlabeled and MDCC-labeled HIV reverse transcriptase

Unlabeled HIV RT protein was expressed and purified following methods previously described (4, 8). Briefly, the two subunits of RT were individually expressed in T7 Express Competent Escherichia coli (New England Biolabs), mixed in a 1:1 ratio, and purified by tandem Q-Sepharose and Bio-Rex 70 columns followed by a single-stranded DNA affinity column. The MDCC-labeled protein was expressed and purified following the same procedure except that an additional chromatographic step with Bio-Rex 70 column was performed to remove excess MDCC after the labeling reaction. The enzymes were assayed by pre-steady-state burst experiments to determine the active site concentrations, divided into aliquots, rapidly frozen, and stored at −80 °C. Thymidine analog resistance mutations, TAMs (M41L, D67N, K70R, L210W, T215Y, and K219E) were introduced into the plasmid expressing RT, and the protein was purified and characterized in the same manner at WT.

DNA for kinetic studies

Semirandom DNA primers and templates (Table 2) were ordered from Integrated DNA Technologies and purified by gel extraction. Annealing of primers and templates was carried out by mixing the two oligonucleotides at a 1:1.2 molar ratio (excess template) and incubating at 95 °C for 5 min, followed by slow cooling to room temperature.

Table 2.

DNA substrates for kinetic assays

Here are the sequences of the d25/d45 primers/templates used in these studies. The bold, underlined letter A shows the templating base.

Primer/template	Sequence
d25	5′-GCCTCGCAGCCGTCCAACCAACTCA-3′
d45	3′-CGGAGCGTCGGCAGGTTGGTTGAGTAGCAGCTAGGTTACGGCAGG-5′

Magnesium ion concentrations

All experiments were performed in a buffer containing 50 mm Tris, pH 7.5, 100 mm KCl, and 0.1 mm EDTA at 37 °C. During preincubation to form the E-DNA complex, 0.1 mm EDTA was included, and then 10 mm MgCl₂ was added with nucleotides to start the reaction.

Stopped-flow kinetic assays

Stopped-flow assays were performed using a KinTek AutoSF-120x (Austin, TX) to measure the kinetics of enzyme conformational changes and the rates of dTTP binding and incorporation using MDCC-labeled HIV RT as described previously (4). Various concentrations of dTTP were rapidly mixed with a preformed enzyme-DNA/RNA complex (100 nm MDCC-labeled WT_HIVRT and 150 nm d25/d45), and the reactions were monitored by stopped-flow fluorescence methods. Similar experiments were performed at lower temperatures (5, 10, 15, 20, and 25 °C), and the data were fit globally to estimate the rate of fingers closure at 37 °C, which was too fast to measure directly. Fluorescence was observed by excitation of MDCC at 425 nm and monitoring emission with a 475-nm band-pass filter with a 50-nm bandwidth.

Conventional data fitting

The data in Fig. 2 were fit at each temperature to a double exponential function (Equation 1) by nonlinear regression using functions built into KinTek Explorer software. Observed concentration dependence of the rate of the fast phase was then fit to Equation 2 by nonlinear regression using GraFit.

Global data fitting

The data in Fig. 2 were fit globally based on numerical integration of rate equations using KinTek Explorer software version 6.0 (14), which includes the capability to fit temperature-dependent rate constants. For fitting fluorescence transients, extinction coefficients for each species were included as variables in the data fitting as described previously (4). Confidence contour analysis (13) was used to investigate whether the parameters were well constrained by the data. In the current studies, the parameters were well constrained, and the upper and lower limits derived from the confidence contour analysis were sufficiently symmetrical, so we only reported the standard errors derived by nonlinear regression.

Author contributions

A. L. and J. L. Z. performed the experiments and assisted with the data fitting and writing of the paper. K. A. J. conceived of the study and worked with A. L. and J. L. Z. in the data fitting and writing of the paper.