Using cognitive training studies to unravel the mechanisms by which the approximate number system supports symbolic math ability

Abstract

A picture is emerging that preverbal nonsymbolic numerical representations derived from the approximate number system (ANS) play an important role in mathematical development and sustained mathematical thinking. Functional imaging studies are revealing developmental trends in how the brain represents number. We propose that combining behavioral and neuroimaging techniques with cognitive training approaches will help identify the fundamental relationship between the ANS and symbolic mathematics. Understanding this relationship should ultimately benefit educators by providing ways to harness the ANS and hopefully improve math readiness in young children.

Introduction

The human mathematical mind is unique in its ability to accomplish feats such as calculating the trajectory of a rocket to mars, proving the Pythagorean Theorem, or counting the precise number of butterflies in a picture book. Mathematical ability is complex and multifaceted and relies on many component skills including but not limited to working-memory [1], executive function [2], and language [3]. The approximate number system (ANS) may serve as another critical foundation for mathematics [4,5]. The ANS supports our ability to roughly estimate the number of objects in a set (e.g. nonsymbolic quantity representation) without relying on verbal counting [5]. Here, we review both behavioral and neuroimaging data that examine the relationship between the ANS and symbolic mathematical abilities and argue that primitive numerical abilities scaffold symbolic math representations. We propose that the tools of cognitive neuroscience and educational psychology may together uncover the mechanisms by which this scaffolding takes place.

A foundational building block for mathematics: the approximate number system

The ANS is present in a wide variety of animal species [5]; it emerges early in human development [6], and it continues to function throughout adulthood [7]. ANS representations are much like representations of other fundamental perceptual continua such as brightness or size in that they follow Weber’s law whereby reaction time and error rates decrease as the ratio or distance between to-be-compared quantities increases [8]. Although nonhuman animal and human infant numerical abilities are limited to imprecise enumeration supported by the ANS, adult educated humans are capable of representing exact symbolic numbers (e.g. ‘16′ or ‘sixteen’), and this forms the basis of mathematical operations. There is debate over the nature of the initial preverbal representations that ground children’s first number words. One proposal is that the ANS scaffolds the acquisition of exact symbolic numerals and subsequent math skills over development and remains tied to symbolic math faculties into adulthood [4]. However, alternative hypotheses suggest that ANS representations are only mapped onto number words later in development and are not involved in symbol grounding [9].

The association between the ANS and math achievement

A key source of evidence that the ANS scaffolds symbolic math is that ANS acuity and symbolic math achievement are correlated across the life span [e.g. 7,10–12]. Individuals with greater precision in discriminating between approximate numerical magnitudes tend to have higher scores on standardized measures of math achievement (see [13] for a meta-analysis). In fact, the association between ANS and symbolic math may be strongest in preschool aged children [14,15^•,16]. ANS acuity measured before children enter formal school predicts later math abilities [17,18] suggesting that strengthening the ANS might improve children’s readiness to learn math upon school entry. ANS acuity is also lower in children with dyscalculia (severe math difficulties) [19,20], see also [21]. Although these findings suggest a relationship between ANS and symbolic math, recent meta-analyses have shown this relationship to be relatively weak [13,15^•,22] and a substantial number of studies have failed to find this correlation [e.g. 23–26]. There are a number of possible explanations for these conflicting results such as diverse dependent measures in both nonsymbolic comparison tasks and standardized tests of math achievement, poor reliability for measures of ANS acuity [27,28, but see 29], true age-dependent differences in the relationship between ANS and math, or the involvement of perceptual processes and inhibitory control related to nonsymbolic discrimination [25,26,30,31] (see [32–35] for detailed reviews of the correlational research). A recent study that failed to find a behavioral correlation between ANS acuity and math performance nevertheless found that individual differences in the size of the neural ratio effect in the bilateral IPS during nonsymbolic comparison correlated with standardized scores of math achievement [36^••]. This finding suggests that the relationship between ANS and math may be better revealed by neuroimaging than behavioral indices.

Causal relationship between the ANS and math achievement

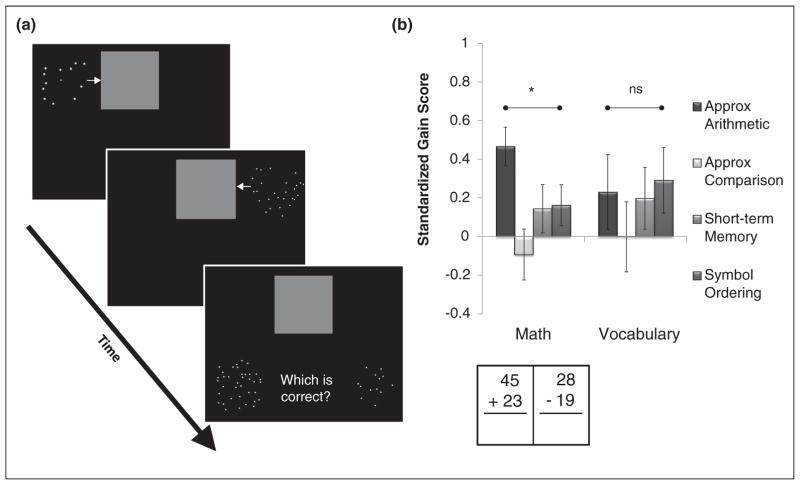
Cognitive training studies provide an avenue to move beyond correlations and address the potential causal relationship between ANS acuity and symbolic math ability. Park and Brannon (2013) first demonstrated that computerized approximate arithmetic training enhanced symbolic arithmetic skills. In their study, adults were trained to approximately add and subtract sets of dots over the course of 10 days (e.g. 30 + 16 dots is 46 dots or 60 dots — see Figure 1a). Following this approximate arithmetic training, participants showed specific improvements in performing complex symbolic arithmetic problems, whereas no improvements were observed for a group of participants in a no-contact control condition or a fact training condition [37]. In a follow-up study, Park and Brannon replicated these results and further demonstrated that training approximate arithmetic resulted in greater gains in symbolic arithmetic skills in comparison to training visuo-spatial short-term memory, approximate number comparison, and symbolic ordering [38^••] (see Figure 1b). The fact that participants in the symbol ordering and numerical comparison conditions did not show improvements on symbolic addition and subtraction argues against the idea that the effect was driven by expectations that number related exercises would improve performance [39] see also [40^••]. Together these findings suggest that the manipulation of approximate quantities required by arithmetic is driving the transfer effect. One study in young children suggests that training approximate arithmetic may be effective early in development [41^••]. Although more studies are necessary to explore the efficacy of training approximate arithmetic in pre-school aged children and children with mathematical difficulties using pre and post-test designs, if successful this approach could have important educational implications. Given that approximate arithmetic games do not require recognition of Arabic numerals or mastery of the verbal counting system this type of training has the potential to improve math readiness in preschool children at risk for math difficulties.

Figure 1.

(a) During an addition trial of the approximate arithmetic training task, an array of dots moves behind a screen followed by a subsequent an array of dots. Participants are then asked to select the dot array that matches the sum. On other trials participants had to make a greater-or-less-than comparison between the sum and a single array. (b) The approximate arithmetic training was shown to improve performance on complex addition and subtraction compared to a vocabulary task to a greater extent than approximate number comparison, short-term memory, and symbolic ordering training. A portion of the data replotted from [38].

The relationship between the ANS and symbolic number in the brain

Dehaene proposed that the construction of the uniquely human mathematical mind through culture and education is made possible by co-opting brain systems that evolved to represent nonsymbolic quantity [42,43]. This hypothesis rests partly on the finding from functional magnetic resonance imaging (fMRI) studies that the bilateral intra-parietal sulcus (IPS) is a key neural substrate of both nonsymbolic and symbolic quantity processing [42,44–47]. For example, when adults compare the numerical magnitude of Arabic numerals, activity within the bilateral IPS is modulated by distance [47] consistent with behavioral ratio effects. Similar distance related changes in activity have been found in the bilateral IPS when participants are presented with a deviant stimulus that differs in numerosity following adaptation to a steady stream of nonsymbolic quantities (arrays of dots) [45]. These findings have been taken as indirect evidence that there is a common neural code within the bilateral IPS for representing symbolic and nonsymbolic quantities (but see [48] for an alternative view).

There is also evidence that the left IPS becomes specialized for symbolic number. Symbolic and nonsymbolic quantities activate overlapping parietal regions partially lateralized to the right IPS [49,50]. By contrast, there is greater association of the left parietal cortex for exact symbolic compared to approximate nonsymbolic tasks [44,50]. Specifically, using cross format fMRI adaptation, Piazza and colleagues found evidence that the left IPS contained sharper neural tuning curves for symbolic numerals compared to the right IPS. Consistent with these findings, Holloway et al. (2010) found that the right IPS was activated for both symbolic and nonsymbolic number comparison, but found specific activity in the left angular gyrus for symbolic comparison.

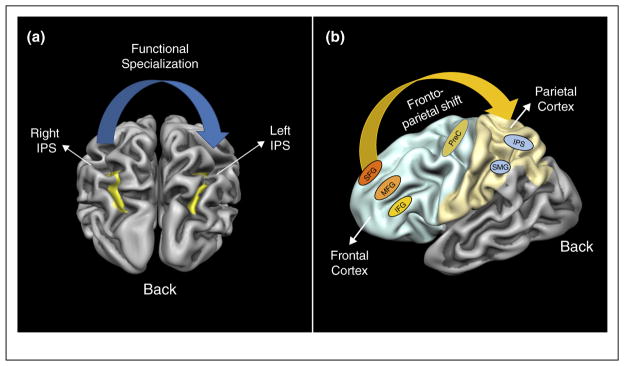
Developmental studies are uniquely suited to investigate the emergence of symbolic representations. Indeed, the neural signatures of the ANS are evident in the right IPS in infants [51^•,52] and young children [53]. Number representation becomes more lateralized to left IPS over the course of development and may be driven by acquisition of the symbolic number system [54] (see Figure 2a). In direct support of this idea, Emerson and Cantlon found that activation in the right IPS during a dot to numeral matching task was stable in children between four and nine years of age across two fMRI sessions; however, numeral matching acuity was positively correlated with longitudinal increases in left IPS activity [55^••]. Comparably, Vogel and colleagues (2015) found age related changes in ratio dependent neural recovery following adaptation to symbolic numerals in the left IPS; however, activity in the right IPS was invariant across all ages (age 6–14 years) [56^••]. Furthermore, children with a stronger neural ratio effect in the left IPS during symbolic number processing exhibited higher arithmetic scores [57^•].

Figure 2.

An illustration of the developmental changes in brain activity for numerical and arithmetic tasks. (a) A cartoon depiction of the developmental specialization of the left IPS. (b) Fronto-parietal shift over the course of development. IPS: intraparietal sulcus, SFG: superior frontal gyrus, MFG: middle frontal gyrus, IFG: inferior frontal gyrus, PreC: precentral gyrus, SMG: supramarginal gyrus.

Another proposed developmental trend in the neural bases of numerical representation is a fronto-parietal developmental shift. When children and adults perform nonsymbolic and symbolic number comparison, neural distance effects are found in both the IPS and the prefrontal cortex. Adults, however, show larger neural distance effects in the IPS in comparison to children [58–60]. Relatedly, Rivera and colleagues (2005) found age was positively correlated with activity in the left parietal cortex, such as the left supramarginal gyrus, left IPS, as well as the left lateral occipital temporal cortex during addition and subtraction. By contrast, young children exhibited greater activity in the prefrontal cortex including bilateral superior and middle frontal gyri, left inferior frontal gyrus, and the left hippocampus [61] (see Figure 2b).

Thus, the emerging picture is that the right IPS processes nonsymbolic magnitudes at birth and remains stable over development supporting the acquisition of symbolic representations in the left IPS. Changes in the left IPS reflect experience-dependent refinement of symbolic representations as a consequence of increasing fluency with numbers [55^••,56^••]. As symbolic numbers are introduced they activate the IPS with preferentially encoding in the left hemisphere (see Figure 2a). The fronto-parietal shift may thus reflect the fact that children initially recruit prefrontal areas associated with working memory and attention resources when attempting to solve arithmetic problems and learn symbolic numerals. Subsequently, as they develop stronger more automatic associations between symbols and the quantities they represent, activation shifts to the left IPS [54]. Under this scenario, the prefrontal cortex might play a key role in learning semantic associations, but the associations themselves are instantiated in IPS. After the associations are fully automatized the IPS is recruited by both symbolic and nonsymbolic number and prefrontal activity decreases (see Figure 2b) [62].

Overlapping neural activity for symbolic and nonsymbolic numerical processing tasks has been taken as evidence that the ANS scaffolds symbolic mathematical development [44,63]. However, neural overlap between symbolic and approximate numerical representations does not necessitate that the two are causally related [64]. In fact, recent studies using multi-voxel pattern analyses in adults have in some cases uncovered dissimilar patterns of activity in the bilateral IPS for approximate and symbolic number processing [65,66^•]. These results show that despite overlapping activation in the IPS for symbolic and approximate numerical processing, the underlying representational structure is highly format dependent. Thus, an alternative possibility is that distinct symbolic representations in the IPS (left IPS) are constructed independent of the ANS [9,54,67]. It will be important to conduct similar fMRI studies with young children because one possibility is that numerical representations are format independent early in development and diverge with numerical experience into adulthood.

Future directions: using training studies to uncover how the human mathematical mind develops

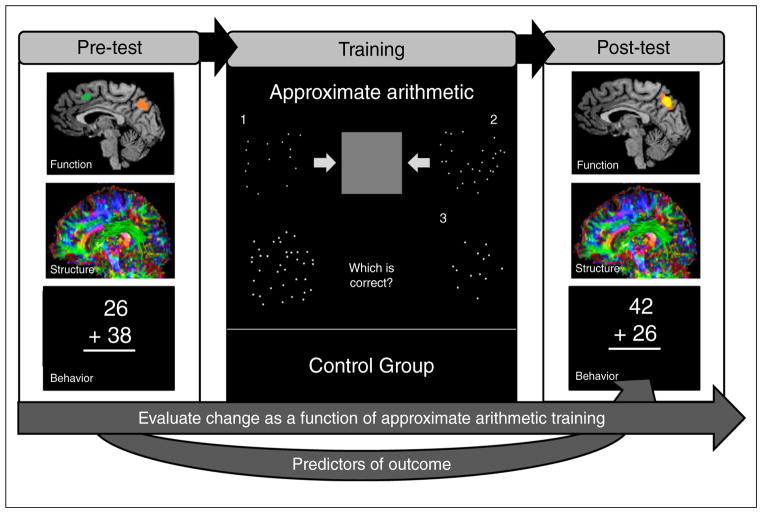
As discussed above, longitudinal studies using fMRI and other non-invasive neuroimaging tools are revealing developmental trends in brain development that coincide with changes in numerical cognition. However, it is difficult to know which brain changes are related to math development and which are related to other concurrent cognitive development. We propose that brain imaging before and after cognitive training is a promising tool that can help differentiate the specific developmental brain changes that underlie a child’s acquisition of the symbolic number system and map the emergence of the mathematical mind. FMRI training studies as cartooned in Figure 3, should provide fundamental insights into the relationship between the approximate arithmetic and symbolic math, which can be used as a model to evaluate behavioral and neural changes as a function of different types of ANS training programs.

Figure 3.

A schematic illustration of a neuroimaging pre-test and post-test training design. Neural analytical tools can be used to identify both functional and structural neuro-markers, as well as behavioral performance can be used to either predict individual differences in training gains and/or uncover the relationship between approximate arithmetic and symbolic math. The schematic of the approximate arithmetic represents one trial, however, in the true task, the dot arrays are not displayed simultaneously as depicted.

Indeed, pre-test and post-test functional neuroimaging studies have already begun to uncover important neural changes associated with math interventions in participants with dyscalculia [68^•,69], math anxiety [70^•], and Turner syndrome (a genetic condition associated with deficits in math skills) [71^•]. For example, Iuculano and colleagues found that children with DD exhibited aberrant widespread neural activity in prefrontal cortex, the bilateral IPS, regions in the ventral temporal-occipital cortex, and right hippocampus when performing an addition verification task in comparison to typically developing controls. Following an eight week one-on-one tutoring program that focused on building procedural and conceptual knowledge of basic arithmetic, children with DD showed normalization of brain activity. Specifically, regions that showed atypical activation before receiving tutoring, no longer differentiated children with DD and typically developing children at post-test. Furthermore, training induced functional plasticity, characterized by individual change in neural activity between pre and post-test scans, predicted gains in arithmetic performance following tutoring with greater sensitivity than behavioral measures. These results reveal that a network of brain regions associated with visuo-spatial processing, attention, working memory and basic numerical processes were remediated by the one-on-one tutoring program [68]. Furthermore, children with Turner Syndrome, who received general number sense and executive function training showed significantly increased activity in the parietal cortex and decreased activity in regions located in the prefrontal cortex, hippocampus, and amygdala during complex arithmetic problems following training [71^•]. These preliminary findings reveal neural changes in the fronto-parietal network associated with improvements for complex arithmetic and suggest that the fronto-parietal shift may be a significant indicator of math fluency and remediation efficacy; however, the specificity of these findings needs to be further examined with relevant control groups.

Cognitive training studies, such as those conducted by Park and Brannon [37,38^••], lay the foundation for exploring multiple neural mechanistic hypotheses for the relationship between approximate arithmetic training and symbolic mathematics. First, approximate arithmetic training may increase the association between symbolic representations of numbers and the quantities they represent. If approximate arithmetic training indeed increases the precision of the ANS, and processing symbolic numerals involves accessing their corresponding ANS representations, then increasing ANS precision may facilitate symbolic numeral processing. One potential brain corollary of this change might be increased lateralization of symbolic representations to the left IPS similar to the changes observed over development [55^••,56^••], or increased functional connectivity between right and left IPS. Alternatively, approximate arithmetic may benefit symbolic arithmetic due to the shared cognitive operations of addition and subtraction rather than any associated increase in ANS precision. If this is the case we might expect changes in a broader network of prefrontal and parietal areas as a function of approximate arithmetic training (see Box 1 for open empirical questions for future research). Relatedly, some research has suggested that the relationship between ANS acuity and symbolic math is driven by inhibitory control mechanisms necessary to suppress information from visual perceptual cues to make discriminative judgments based on quantity [25,26,31]. For example, a recent training study with low income preschool children has shown that ANS acuity training using nonsymbolic comparison reduces the effect of irrelevant visual perceptual cues on performance during comparison tasks at post-test [72]. Thus, one possibility is that approximate arithmetic training improves inhibitory control comparable to nonsymbolic discrimination training and thus may result in changes in neural networks in prefrontal cortex associated with executive function. Another brain area that may play a special role in arithmetic is the hippocampus, where decreasing activation correlates with improving arithmetic skills [61,73]. Increases in functional connectivity between the hippocampus and bilateral dorsolateral prefrontal cortex and the left IPS has been found to be associated with longitudinal improvements in fact retrieval fluency [73]. One intriguing possibility is that approximate arithmetic affects hippocampal activity by improving the conceptual understanding of basic arithmetic that might facilitate automatic coding of arithmetic facts. Neuroimaging tools in combination with pre-test and post-test behavioral training designs in both adults and children should yield answers to these exciting questions, and provide an important bridge between neuroscience, cognitive science, and education. However, there are many open empirical questions pertaining to the role of the ANS (or approximate arithmetic) in developing symbolic numerical representations and subsequent math skills (see Box 1) that warrant further investigation before this work can be directly translated to the classroom. Furthermore, by combining different analytical tools to study how individual differences in sensitivity to training are linked with brain changes we may ultimately come to a better understanding of how to tailor interventions to students.

Box 1. Open empirical questions.

• Does training approximate numerical abilities have enduring effects on symbolic math performance? Are the effects dose-dependent?

• At what age or mathematical skill level would approximate arithmetic training provide the greatest benefit for mathematical improvement? Can approximate arithmetic training be useful to increase math readiness in preschool children?

• What cognitive and neural mechanistic processes subserve positive transfer effects to symbolic arithmetic skills? Can studying how the brain changes as a function of training provide insight into the mechanism of transfer?

• Does approximate arithmetic training induce structural or functional changes in the bilateral IPS?

Conclusions

There remain many unanswered questions about the precise nature of the relationship between the ANS and symbolic mathematical abilities. Behavioral training studies provide strong support for the proposal that the uniquely human mathematical mind builds upon the evolutionarily ancient ANS. Developmental cognitive neuroscience is uncovering trends in brain development associated with the emergence of the uniquely human mathematical abilities. By combining functional brain imaging methods with cognitive training designs, we will be able to identify the neural networks that change as children become symbolic processors. Ultimately, we hope this endeavor will uncover the true nature of the relationship between the ANS and symbolic math and allow the development and design of interactive and engaging training tools for improving math skills in both typically and atypically developing children at home or in the classroom.