Modeling Sex Differences in Pharmacokinetics, Pharmacodynamics, and Disease Progression Effects of Naproxen in Rats with Collagen-Induced Arthritis

Abstract

Naproxen (NPX) is a frequently used nonsteroidal anti-inflammatory drug for rheumatoid arthritis (RA). Lack of quantitative information about the drug exposure–response relationship has resulted in empirical dosage regimens for use of NPX in RA. Few studies to date have included sex as a factor, although RA predominates in women. A pharmacokinetic, pharmacodynamic, and disease progression model described the anti-inflammatory effects of NPX in collagen-induced arthritic (CIA) male and female rats. Three groups of rats were included for each sex: healthy animals, CIA controls, and CIA rats given a single 50-mg/kg dose of NPX intraperitoneally. Paw volumes of healthy rats indicated natural growth, and disease status was measured by paw edema. An innovative minimal physiologically based pharmacokinetic (mPBPK) model incorporating nonlinear albumin binding of NPX in both plasma and interstitial fluid (ISF) was applied. Arthritic rats exhibited lower plasma and ISF albumin concentrations and reduced clearances of unbound drug to explain pharmacokinetic profiles. The unbound ISF NPX concentrations predicted by the mPBPK model were used as the driving force for pharmacological effects of NPX. A logistic growth function accounting for natural paw growth and an indirect response model for paw edema and drug effects (inhibition of k_in) was applied. Female rats showed a higher incidence of CIA, earlier disease onset, and more severe symptoms. NPX had stronger effects in males, owing to higher unbound ISF NPX concentrations and lower IC₅₀ values. The model described the pharmacokinetics, unbound NPX in ISF, time course of anti-inflammatory effects, and sex differences in CIA rats.

Introduction

Rheumatoid arthritis (RA), a chronic systemic inflammatory autoimmune disease, affects nearly 1% of adults worldwide and significantly reduces health-related quality of life. The pathogenesis of RA involves a complex interplay between both environmental and genetic factors, leading to the infiltration of immune cells and increased production of various proinflammatory mediators such as cytokines and prostaglandins (PG) in joints (McInnes and Schett, 2011). In particular, PG play an important role in the generation of typical inflammatory responses such as pain, fever, redness, and swelling through local vasodilation and amplification of cytokine signaling (Funk, 2001; Ricciotti and FitzGerald, 2011; Aoki and Narumiya, 2012). Therefore, PG signaling has been a major therapeutic target of RA.

Naproxen (NPX), a traditional nonsteroidal anti-inflammatory drug (NSAID), has been extensively used in the long-term treatment of RA and other joint diseases because of its rapid relief of inflammatory symptoms and well tolerated adverse effects (Watson et al., 2002). Similar to other NSAIDs, NPX exerts its anti-inflammatory effects mainly through the inhibition of cyclooxygenase (COX) activity and directly blocks the formation of PG at sites of inflammation, thereby suppressing the inflammatory responses (Vane, 1971; Crofford, 2013). However, dosing regimens for NPX in treating RA have been empirical due to the lack of convincing information on the relationship between drug exposure and clinical response. The NPX concentration–response relationship in RA was explored (Dunagan et al., 1988; Day et al., 1995), but only a trend was obtained and the pharmacokinetics (PK) and pharmacodynamics (PD) of NPX were not quantitatively analyzed. Recent studies (Huntjens et al., 2006, 2010) assessed the correlation between in vitro and in vivo exposure-effect relationships of NPX as well as the impact of chronic inflammation on the PK/PD of NPX. However, the nonlinear PK behavior of NPX was not considered. Other studies merely described the nonlinear exposures of NPX in acute inflammation (Josa et al., 2001; Krekels et al., 2011). The clinical efficacy of NPX appeared to be better correlated with its unbound concentrations in synovial fluid (SF), as synovium is the proposed site of action in RA (Jalava et al., 1977; Netter et al., 1989; Bertin et al., 1994; Day et al., 1995). In spite of this literature, there are limited quantitative insights into the PK/PD relationships of NPX in chronic inflammatory conditions such as RA. Similar to other autoimmune diseases, RA predominates in women (Jawaheer et al., 2006; van Vollenhoven, 2009). However, very few preclinical studies to date include sex as a factor in PK/PD. Most studies were carried out in males, with little information available on potential sex differences in drug action in RA.

The collagen-induced arthritic (CIA) rat model is the most frequently used animal model for RA and mimics many disease characteristics of human RA (Stuart et al., 1982; Holmdahl et al., 2001). The impact of sex and RA on the PK of NPX was assessed using this animal model, in which concentration-dependent binding was incorporated into a two-compartment model (2CM) to account for the nonlinearity and disease effects of NPX PK (Li et al., 2017). However, there are advantages to be gained by use of an extended minimal physiologically based pharmacokinetic (mPBPK) model for describing the PK of NPX, particularly for describing unbound NPX in interstitial fluid (ISF) and SF, adjacent to the site of action.

This study has two purposes. One is to assess and validate a proposed mPBPK model for quantitating the PK of unbound NPX in normal and CIA male and female rats and provide the biophase concentrations. The second is to develop a PK/PD disease (DIS) model for evaluation of the time course of disease progression and anti-inflammatory effects of NPX in male and female CIA rats.

Materials and Methods

Animals.

Male and female Lewis rats (aged 5–8 weeks) were purchased from Harlan (Indianapolis, IN), weighing approximately 110–160 g for females and 170–220 g for males, and were age matched for each sex group at the time of PK/PD studies. Care of animals, induction of arthritis, measurements of paw edema, and other experimental details are presented in our companion article (Li et al., 2017).

Drug.

The sodium salt of NPX, (S)-6-Methoxy-α-methyl-2-naphthaleneacetic acid sodium salt (N51601) was obtained from Sigma-Aldrich Inc. (St. Louis, MO). The NPX working stocks were freshly prepared as a sodium NPX solution in phosphate-buffered saline (pH 8) and were filtered through 0.22-μm filters before use. The drug was administered intraperitoneally in a volume of 1 ml/kg.

Experimental Design.

Hind paw swelling was used as the indicator for edema. Two cross-sectional areas of the paw were measured by digital calipers (VWR Scientific, Rochester, NY) as previously described (Earp et al., 2008).

Pilot studies showed that peak edema without drug treatment was observed on day 16 for females and day 21 for males. Rats with a paw volume increase of at least 50% in one or both hind paws were considered to be arthritic after evaluation on day 15 for females and day 20 for males. Eight female and eight male CIA rats were selected and randomly divided into two subgroups per sex: vehicle control groups (n = 4) that received only phosphate-buffered saline intraperitoneally, or treatment groups (n = 4) that received 50 mg/kg NPX intraperitoneally. Control or treatment groups received injections on day 16 for females and day 21 for males. The hind paws of four healthy females and four healthy males were measured through the entire study to obtain the natural paw growth. Paw edema and body weights were monitored before disease induction (day 0) and post-induction on days 3, 7, 9, 10, 11, 13, 14, and 15 for both sex groups and also on days 17, 18, 19, and 20 for CIA males. Starting from the dosing day, paw edema was measured before dosing and at 1, 2, 4, 6, 8, 12, 24, and 36 hours after dosing and on postdose days 3, 4, 5, 6, 7, 8, 9, and 10.

Serial blood samples were collected from the saphenous vein at 15, 30, and 45 minutes and 1, 2, 4, 6, 9, 12, and 24 hours postdose and were processed and analyzed for NPX by liquid chromatography–tandem mass spectrometry as described by Li et al. (2017).

PK Model.

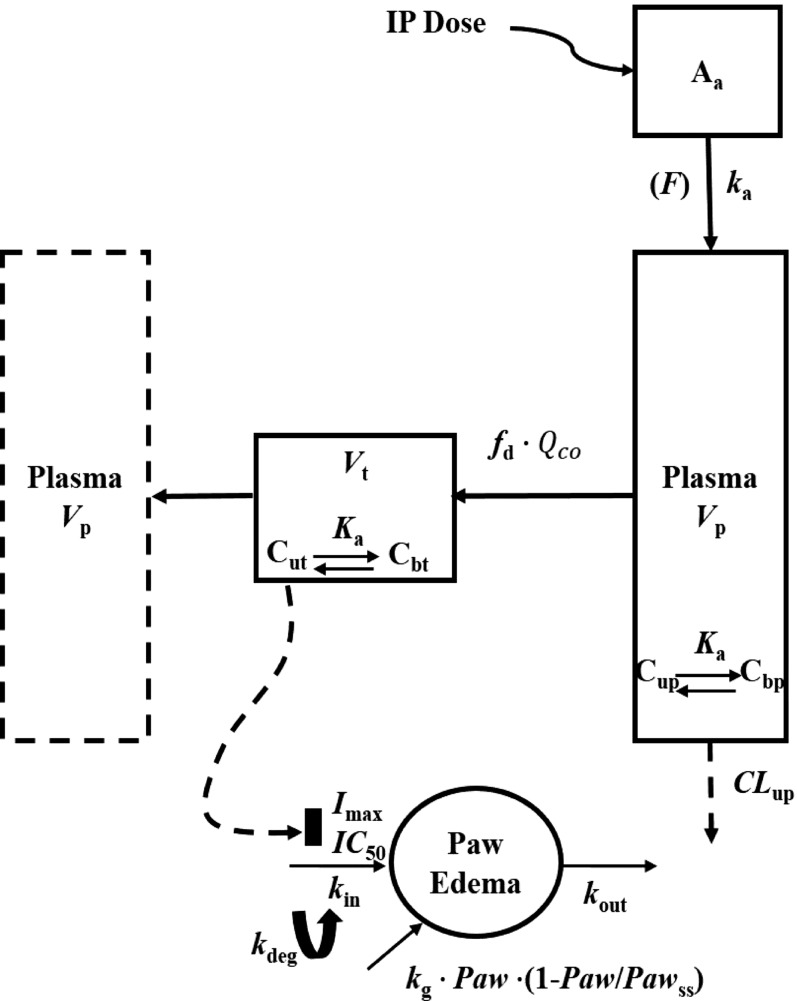
The extended mPBPK model with plasma and one tissue compartment is shown in Fig. 1. The differential equations for the PK are as follows:

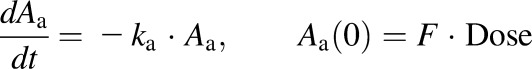(1)

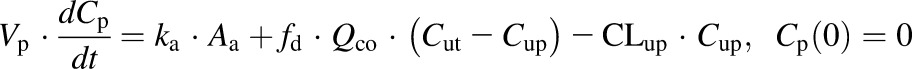(2)

(3)

where A_a indicates the amount of NPX at the absorption site, k_a is the first-order absorption rate constant, C_p and C_t are total NPX concentrations in V_p (plasma volume) and V_t (ISF volume), Q_co is cardiac output plasma flow, f_d is the fraction of Q_co that perfuses V_t, CL_up is clearance of unbound NPX from plasma, C_up and C_ut are the unbound NPX concentrations in plasma and ISF, and F is the bioavailability of the intraperitoneal dose calculated to be about 0.9 from literature intravenous data in rats (Lauroba et al., 1986). The physiologic restrictions of relevant parameters are as follows:

Fig. 1.

Scheme of the mPBPK/PD/DIS model for PK and effects of NPX on paw edema in CIA rats. Parameters are defined in the text and in Tables 1 and 2.

f_d ≤ 1 and V_p + V_t = extracellular fluid volume (extracellular fluid = 206.29 ml/kg) (Shah and Betts, 2012)

To account for the nonlinearity of NPX PK, the model incorporated nonlinear protein binding in both plasma and ISF. The unbound concentrations in both plasma and ISF were calculated from measurements of total NPX, albumin concentrations, and binding parameters obtained using ultrafiltration as described in our companion article (Li et al., 2017):

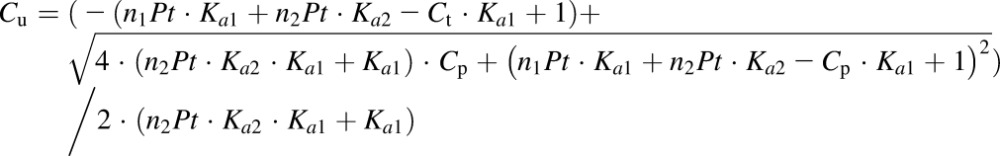(4)

where C_u and C_t are the unbound and total drug concentrations in plasma or ISF, Ka₁ and Ka₂ are the association constants for the first and second class of binding sites, n₁ and n₂ are the numbers of first and second class of binding sites, and Pt is albumin concentration in plasma or ISF.

Several PK modeling assumptions were made. First, the distribution and elimination processes operate only on free drug. Second, penetration of NPX into cells is expected to be minimal (Poulin, 2015); thus, the distribution of NPX is restricted to plasma and ISF. Third, the concentration-dependent binding of NPX is limited to albumin in both plasma and ISF. Fourth, the binding affinity of NPX to albumin is the same in both plasma and ISF in all animals. Fifth, the ratio of ISF-to-plasma albumin concentration is 0.5 for healthy rats and 0.9 for CIA rats (Li et al., 2017). The unbound NPX concentrations in ISF were calculated using the final PK model parameters and were used as the driving force for PD effects in CIA rats.

This model was confirmed as relevant by comparing observed PK data for NPX in plasma and ISF from a study in which plastic sponges were implanted subcutaneously into each animal to absorb the inflammatory exudate and NPX concentrations in the exudate were measured as the ISF concentrations. These data were digitized from the literature (Doherty et al., 1977; Huntjens et al., 2006) and compared with the model-predicted concentration-time profiles. In addition, data for total and unbound naproxen concentrations in plasma and SF from human subjects (Day et al., 1999) were compared.

PD and Disease Progression Model.

Three different models were tested and compared for fitting the disease progression profiles for paw edema with and without NPX treatment. The first model was a transduction-based feedback model that consisted of a series of transit compartments accounting for both the production and natural remission of paw edema (Liu et al., 2011). The second was an indirect response model containing zero-order natural growth combined with a feedback on the production of paw edema (Lon et al., 2013). The third model applied a logistic growth function to describe the natural growth of the paw instead of a zero-order growth parameter. The final model equations and initial conditions are as follows:

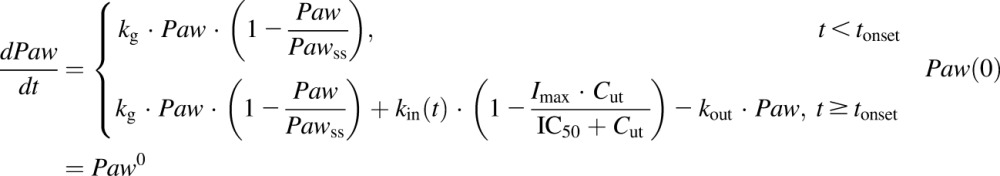(5)

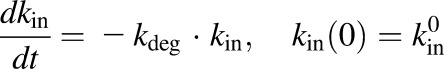(6)

where Paw is the sum of ankle and paw areas of a rat hind foot, Paw⁰ is the paw size on day 0, Paw_ss is the normal paw size at steady state, k_g is the natural growth rate constant of the paw in healthy rats, t_onset is the time delay observed before disease onset, is a function of time and represents the production of paw edema after disease onset, is the production rate constant of paw edema at t_onset, and k_deg is a linear decline in k_in accounting for the natural remission of arthritis. Drug-related parameters I_max and IC₅₀ are the maximum inhibition effect of NPX on paw edema and NPX concentration at 50% of maximum inhibition, respectively.

Model Fitting and Data Analysis.

Model fittings were performed by nonlinear regression using the maximum likelihood algorithm in ADAPT 5 (University of Southern California, Los Angeles, CA) (D’Argenio et al., 2009). The model code is provided in the Supplemental Material. All PK data from Li et al. (2017) and PD data from this study were naive-pooled before analysis. The PK profiles were first fitted and the estimated PK parameters were fixed and used in the PK/PD model. The variance model used was as follows:

(7)

where V_i represents the variance of the i^th data point, Y_i is the i^th model-predicted plasma concentration, and σ₁ and σ₂ are variance model parameters that were estimated together with other system parameters during model fitting. Model selection was based on the goodness-of-fit criteria which included the Akaike information criterion, visual inspection of the fitted profiles, and coefficients of variation (CV%) of the parameter estimates. Statistical analysis of paw measurements were performed by the t test using SPSS software (version 22; IBM SPSS Statistics, Chicago, IL), and P < 0.05 was considered statistically significant.

Results

Pharmacokinetics.

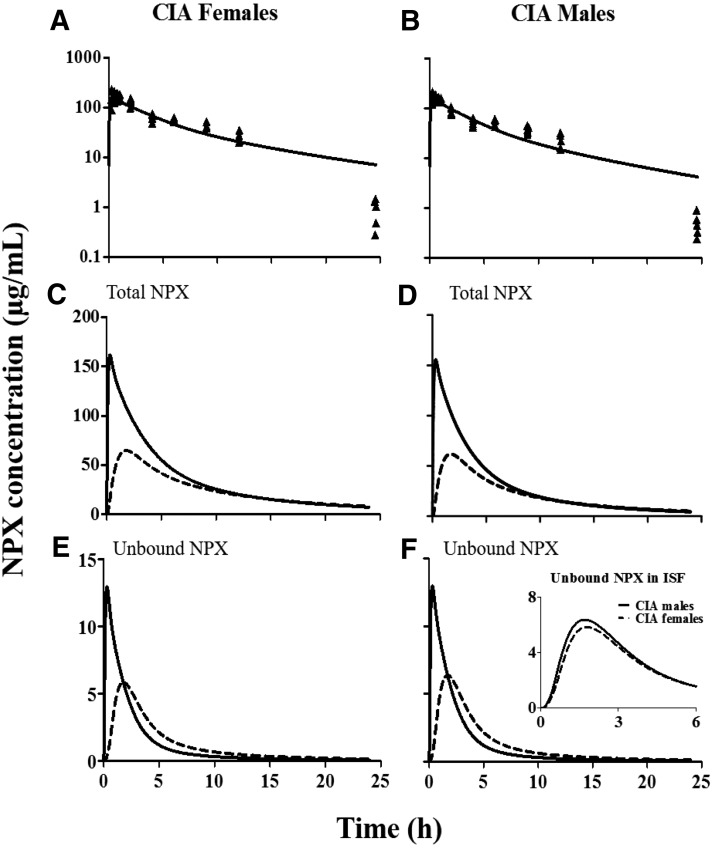
The final PK/PD model is displayed in Fig. 1. The mPBPK model features utilization of a physiologic structure along with parameters (V_p, V_ISF, and Q_co) applicable to rats, obtained from the literature (Shah and Betts, 2012), and fixed in the model fitting. Concentration-dependent protein binding in both plasma and ISF based on our measurements was incorporated into the basic mPBPK model to account for the nonlinearity of NPX PK. All PK data from our previous study (Li et al., 2017) were modeled simultaneously with different albumin concentrations and unbound clearance terms assigned to arthritic versus healthy rats (see the model code for PK estimation in the Supplemental Material). The PK profiles of total NPX after giving 50-mg/kg intraperitoneal doses to female and male arthritic rats as well as the model fittings are shown in Fig. 2, A and B. The PK parameter estimates are listed in Table 1. As can be seen from these results, this model described the PK data well with reasonable CV% values for the estimated parameters. The absorption of NPX from the intraperitoneal injection site was rapid (k_a of approximately 1 h⁻¹). Arthritic rats showed lower unbound plasma clearance of NPX (1438 ml/h per kg) compared with healthy rats (1968 ml/h per kg), which is in accordance with findings in humans (van den Ouweland et al., 1987). The estimated tissue distribution rate of NPX was much lower (f_d = 0.15) than the cardiac plasma flow (when f_d = 1), which is in line with the permeability-limited distribution of NPX, as it is a highly ionized drug.

Fig. 2.

Model fittings of NPX plasma concentration versus time profiles (A and B) and fitted total and unbound NPX concentrations in plasma (solid lines) and ISF (dashed lines) (C–F) in female (left) and male (right) arthritic rats that received 50-mg/kg intraperitoneal doses of NPX. Symbols are total plasma concentration measurements and curves depict model fittings or predictions. The inset figure is the comparison of unbound ISF NPX concentrations in CIA females (dashed line) and males (solid line).

TABLE 1.

Pharmacokinetic parameter estimates for NPX in healthy and CIA rats after intraperitoneal administration

Parameter	Definition	Estimate	CV%
ka (l/h)	Absorption rate constant	0.98	8.3
fd	Fraction of cardiac plasma flow	0.15	12.9
CLArthritic (ml/h per kg)	Unbound plasma clearance in arthritic rats	1438	3.2
CLHealthy (ml/h per kg)	Unbound plasma clearance in healthy rats	1968	5.3
Vp (ml/kg)	Plasma volume	32.36a	Fixed
Vt (ml/kg)	ISF volume	173.93a	Fixed
Qco (ml/h per kg)	Cardiac plasma flow	7650a	Fixed

^aPhysiologic parameter values obtained from Shah and Betts (2012).

Figure 2, C to F, illustrates the model-predicted total and unbound NPX concentrations in both plasma and ISF in male and female CIA rats after 50-mg/kg intraperitoneal dosing (see the model code for PK simulation 1 in the Supplemental Material). The peak concentrations of total and unbound NPX in plasma are greater than those in ISF. The distribution of NPX into and out of tissues is relatively slow, resulting in more sustained tissue concentrations compared with the PK profiles in plasma. As shown in the inset in Fig. 2F, unbound ISF NPX concentrations are slightly higher in males than in females, which are accounted for in the model fittings by the lower albumin concentrations in male ISF.

Model simulations using the PK parameters listed in Table 1 overlaid with literature-reported NPX concentration-time profiles in plasma and presumed ISF from rats are displayed in Fig. 3 (see the model code for PK simulations 2 and 3 in the Supplemental Material). The model predictions agree well with these independent experimental PK data, with close predictions of NPX concentrations for a range of doses in these two studies. Furthermore, direct measurements of total and unbound plasma and SF concentrations of naproxen in subjects given single doses (Bertin et al., 1994) and multiple oral doses (Day et al., 1999) exhibit profiles closely resembling those shown in Fig. 2, with total and unbound SF concentrations being much lower than plasma concentrations with a similar later peak and longer persistence than in plasma.

Fig. 3.

Predicted (solid curves) and literature-reported (symbols) total NPX concentrations in plasma (closed circles) and ISF (open circles) versus time after oral administration of 10 mg/kg NPX to female rats (from Doherty et al., 1977) and bolus intraperitoneal injection of 2.5, 10, and 25 mg/kg NPX to male rats (from Huntjens et al., 2006).

PD and Disease Progression.

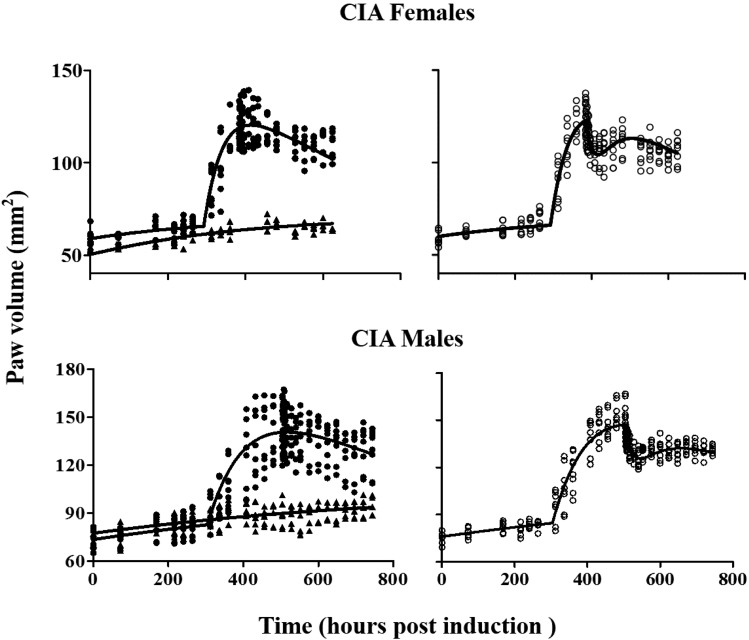
Natural growth of paws in healthy rats, disease progression of paws in control and NPX-treated CIA rats, and the model fittings are shown in Fig. 4. After collagen induction, a typical pattern of paw edema progression without treatment features a delayed disease onset, a rapid rise to peak disease status, and a later slow remission phase. There was no significant difference (P > 0.05) in paw volume of CIA rats among all groups before drug or placebo dosing (day 16 for females and day 21 for males). A significant reduction in paw edema (P < 0.05) was observed in both female and male arthritic rats 1 day after a single dose of NPX compared with control CIA rats.

Fig. 4.

Disease progression of paw edema in female (upper) and male (lower) arthritic rats (n = 4) after no drug (closed circles) and 50 mg/kg NPX (open circles). Time courses of paw volumes in male and female healthy rats (n = 3) are shown (closed triangles). Lines are model fittings of all data jointly yielding parameters listed in Table 2.

With model-predicted unbound NPX concentrations in ISF (Fig. 2) used as the driving force for the PD effects, the model was able to simultaneously characterize the paw volume-time profiles of all groups very well (see the model code for PD estimation in the Supplemental Material). The final PD/DIS parameter estimates are summarized in Table 2. All parameters were well estimated with acceptable CV% values. A logistic function was applied to describe the natural growth of the paw before disease onset (days 0–11 for females and days 0–13 for males). The gradual increase in paw sizes in both healthy and CIA rats was well captured and the natural growth rate constant (k_g) was estimated to be 0.003 h⁻¹ for females and 0.002 h⁻¹ for males.

TABLE 2.

Pharmacodynamic parameter estimates for unbound ISF effects of NPX in healthy and CIA rats

Parameter	Definition	Estimate (CV%)
		Females	Males
tonset (h)	Time of disease onset	289 (1.07)	308 (0.5)
kout (l h)	Loss of edema rate constant	0.013 (41.3)	0.007 (20.6)
kdeg (l/h)	Loss of production rate constant	0.001 (29.0)	0.001 (16.6)
kg (l/h)	Natural growth rate constant	0.003 (33.8)	0.002 (41.8)
Imax	Maximum inhibition on production of paw edema	0.75 (40.1)	1.0 (Fixed)
IC50 (µg/ml)	Unbound NPX concentration at 50% maximum inhibition	0.221 (56.4)	0.136 (45.9)
Pawss (mm2)	Paw size at steady state	70.2 (4.6)	102.2 (7.9)
kin0,c (mm2/h)	Disease production rate constant at tonset for control group	2.21 (24.6)	1.36 (12.0)
Paw0,c (mm2)	Paw size on day 0 for control group	58.92 (1.6)	73.49 (1.8)
kin0,t (mm2/h)	Disease production rate constant at tonset for treatment group	2.31 (23.3)	1.44 (11.6)
Paw0,t (mm2)	Paw size on day 0 for treatment group	59.99 (1.6)	76.02 (1.6)
Paw0,ng (mm2)	Paw size on day 0 for natural growth group	50.38 (2.9)	77.43 (1.8)

Sex differences were seen in paw edema disease progression in CIA rats. Disease onset was earlier and its incidence was higher in female compared with male CIA Lewis rats. This is in agreement with RA findings in humans (van Vollenhoven, 2009). The estimated t_onset value for female arthritic rats (289 hours) was smaller than that for males (308 hours), which is close to the male values reported previously (Earp et al., 2009; Lon et al., 2011, 2013). The induction rate of arthritis was higher in females (80%) than in males (60%), and the maximum paw size increase was approximately 2-fold for females and 1.7-fold for males compared with healthy controls. The disease production rate constant at t_onset (k_in0) was about 2.2 mm²/h for females and 1.4 mm²/h for males, which is consistent with the clinical evidence that females have greater immune reactivity (Cutolo et al., 2004b). The loss of production rate constant k_deg was estimated to be 0.001 h⁻¹ for both sex groups. The loss of edema rate constant (k_out) was estimated to be 0.007 h⁻¹ for males, comparable to our previous value (0.005 h⁻¹) (Lon et al., 2011), whereas the k_out for females was estimated to be 0.013 h⁻¹.

The anti-inflammatory effects of NPX in CIA rats also exhibited sex differences. The maximum effect of NPX on paw edema (I_max) was 0.75 for females and 1.0 for males. Preliminary fittings allowing the I_max for male rats to vary yielded an estimate that was larger than 1. I_max is the maximum fractional extent of inhibition with an upper limit of 1 and thus was set as 1 in our final model fittings. The IC₅₀ of NPX was larger in females (0.221 µg/ml) compared with that in males (0.136 µg/ml). These results indicate that the single doses of NPX have moderate but significant anti-inflammatory effects on paw edema in both sex groups and with slightly more potency in males, which occurs in concert with the higher unbound NPX concentrations in ISF of male arthritic rats (Fig. 2).

Discussion

PK of NPX.

In our previous study, the nonlinear PK of a range of doses of NPX was explored with comparisons based on sex and the presence of RA, in which a 2CM incorporating nonlinear binding was applied (Li et al., 2017). This model was an extension of a published 2CM that included only linear protein binding, and it functioned reasonably well for addressing major PK issues such as sex and RA. However, there is limited physiologic relevance in such models. The PK parameters depend only on the quality of the PK data and have ambiguous biologic features regarding tissue distribution. Drug concentrations outside of plasma, especially when protein binding is nonlinear, cannot be reasonably predicted using a 2CM in which the peripheral volume is an apparent parameter with unclear physiologic relevance. Nevertheless, compartmental models are extensively used in PK and reasonably capture measured plasma concentrations (Huntjens et al., 2006). The mPBPK model has physiologic and anatomic properties, with drug specificity added in consideration of nonlinear protein binding and expectations that ionized weak acids such as NSAIDs distribute primarily in plasma and ISF (Cao and Jusko, 2012). With various assumptions made, the model allows calculation of NPX concentrations in ISF. These were verified by assessment of directly measured PK profiles observed in ISF and SF in the literature. Both the 2CM and mPBPK models allowed a global analysis of all PK data over a range of doses simultaneously, showed that differing albumin concentrations accounted for most of the sex and disease differences, and that RA produced a lower clearance of unbound NPX.

Like all NSAIDs, NPX is a weak acid (pK_a = 4.15), which is highly ionized (fraction ionized > 0.99) at physiologic pH. Owing to the pH differences between extracellular fluid (pH 7.4) and cell water (pH 7.0), NPX is probably localized mainly in the extracellular space with negligible cell water distribution (Poulin, 2015). The reported small volume of distribution (about 0.14 l/kg) supports this (Day et al., 1995). Therefore, ISF was assigned as the tissue space for NPX. Again, as with most NSAIDs, NPX shows extensive and strong binding to plasma proteins at therapeutic concentrations (>99%), with binding predominantly to albumin (Mortensen et al., 1979). Somewhat less binding was found in ISF and tissues due to lower protein concentrations (Wanwimolruk et al., 1983; Day et al., 1995). It was demonstrated previously that nonlinear protein binding of NPX also occurs in SF in addition to plasma (Day et al., 1995). Thus, concentration-dependent binding of NPX to albumin in both plasma and ISF were components of the mPBPK model.

In a basic mPBPK model, the partition coefficient (K_p) is a constant that must be estimated when total drug concentrations are used with linear binding. Since K_p reflects the ratio of unbound plasma (f_up) to unbound tissue (f_ut) binding, there is no K_p in the current PK model because such binding was already accounted for. According to the traditional view, K_p = f_up/f_ut; here, K_p is not a constant but changes with time and total drug concentrations.

The estimated f_d value for NPX was much smaller than 1 (Table 1), indicating that the distribution rate of unbound NPX into tissues was much lower than cardiac output plasma flow and thus was mainly controlled by permeability. The comparable parameter in a 2CM is distribution clearance, viz CL_D = f_d × Q_co.

The clearance of NPX depends primarily on hepatic metabolism through CYP2C9 and CYP1A2 (Miners et al., 1996). Thus, a lower unbound clearance (CL_up) could be expected in arthritic rats, since inflammation is associated with reduced cytochrome P450 activity due to the proinflammatory mediators (Slaviero et al., 2003; Renton, 2005). Both the nonlinear 2CM and the present mPBPK model yielded similar values and conclusions regarding the effect of sex and CIA on clearance of unbound NPX.

CIA Model of Arthritis.

Sex differences occur in many autoimmune diseases such as RA, with a higher prevalence (sex ratio of 3:1), earlier onset, and more severe disease course in women (Linos et al., 1980; Sokka et al., 2009; van Vollenhoven, 2009). Female sex is also a risk factor for a worse outcome with the same treatments (Symmons, 2002). The reasons for such differences are not well understood, but it is likely that genetic factors and hormones play a role. Female estrogens may be involved in RA onset, whereas androgens might play a suppressive role in disease development (Van Vollenhoven and McGuire, 1994; Cutolo et al., 2004a,b). In addition, muscle strength among men is generally better, which might allow for more successful compensation for functional losses (van Vollenhoven, 2009). All of these factors are possible contributors to the sex differences in RA.

The utility of various rat models of arthritis was compared previously (Earp et al., 2009), and the CIA rat model mirrors many aspects of human RA in a relatively short experimental timeframe, such as immune cell infiltration, synovial cell proliferation, and bone destruction. Chronic doses of oral NPX were shown to have good efficacy in female CIA rats (Takeshita et al., 1997). In this study, the effects of single intraperitoneal doses of NPX were investigated. Paw swelling (edema) in CIA rats, as one of the most important features of RA, was used as the endpoint of interest. The disease progression of CIA rats in our study exhibited similar sex difference characteristics as human RA. Actual paw volumes were fitted in this study, which was preferable to use of relative paw ratios (Earp et al., 2009), because of the size differences between male and female rats.

PD of NPX.

The current PD model consists of a logistic growth function and an indirect response model. The logistic growth function allowed an upper limit of paw growth to be anticipated, so that the natural growth in healthy rats and the slight initial increase in paw edema in arthritic rats could be characterized realistically. The paw size increase in CIA rats was attributed to both natural paw growth and paw swelling. The parameters k_g and Paw_ss were obtained through joint fitting of the paw data from all groups with the logistic growth function. The turnover of paw edema in CIA rats was described by the indirect response model composed of a zero-order production process (k_in) and a first-order dissipation process (k_out). The production of paw swelling was triggered by a series of immune responses resulting from infiltration of immune cells to inflamed tissues and synthesis of proinflammatory mediators upon recognition of type II porcine collagen as an exogenous stimulus. On the other hand, anti-inflammatory cytokines such as interleukin-4 and interleukin-10 serve as a counterbalance to the activity of proinflammatory cytokines resulting in the later reduction of paw edema (k_out). A time-dependent change in either generation or loss processes in chronic degenerative diseases such as RA could result in natural disease remission (Post et al., 2005). Therefore, a linear function k_deg was introduced to negatively regulate the disease production k_in. Different initial estimates of k_in and Paw were assigned to each group considering their intrinsic variation to allow for flexibility in fitting. The inhibition of k_in characterized the effects of NPX, which is mechanistically in line with the pharmacology of NPX. NSAIDs suppress the enzymatic activity of COX and directly inhibit the formation of PG that determine inflammatory responses. Therefore, when NPX was added, the drug inhibition parameters (I_max and IC₅₀) would cause a decrease in k_in producing the observed reduction in paw volumes (Fig. 4). Our study demonstrated that a single dose of NPX exerts moderate but significant anti-inflammatory effects on reducing paw edema in both female and male arthritic rats. Males showed better responses, as partly attributable to their higher unbound ISF NPX concentrations (Fig. 2) and as reflected by their I_max and IC₅₀ values (Table 2). This is in accordance with findings of NPX effects in humans (Symmons, 2002).

In conclusion, with incorporation of nonlinear binding in both plasma and ISF, the mPBPK model worked well in handling the effects of reduced albumin concentrations, sex, and disease on distribution and disposition of NPX and also confirmed plasma and tissue (ISF, SF) concentrations of NPX in other published studies in rats and humans. The PK/PD relationship of NPX could be established more realistically by using ISF unbound concentrations, mimicking the biophase, as the driving force of its PD effects. The mPBPK/PD/DIS model captured the paw volume versus time profiles in both healthy and CIA rats with or without treatment and further revealed sex differences in natural disease progression and effects of NPX. Future studies might assess a wider range and chronic doses of NPX and seek more physiologic and disease-related biomarkers (e.g., the expression of COX and PG) in paw tissues to allow for the development of more mechanistic insights and advanced PK/PD/DIS models. This study can serve as a basis for better quantitative assessment of both the PK as well as the PD properties of other NSAIDs and aid in designing drug combination studies with other antirheumatic drugs to assess possible synergies and improve rational dosing regimens in RA treatment.

Abbreviations

2CM

two-compartment model

CIA

collagen-induced arthritic

COX

cyclooxygenase

CV

coefficient of variation

DIS

disease progression

ISF

interstitial fluid

mPBPK

minimal physiologically based pharmacokinetic

NPX

naproxen

NSAID

nonsteroidal anti-inflammatory drug

N51601

(S)-6-Methoxy-α-methyl-2-naphthaleneacetic acid sodium salt

PD

pharmacokinetics

PG

prostaglandin

PK

pharmacodynamics

RA

rheumatoid arthritis

SF

synovial fluid

Authorship Contributions

Participated in research design: Li, DuBois, Almon, Jusko.

Conducted experiments: Li, DuBois.

Performed data analysis: Li, Jusko.

Wrote or contributed to the writing of the manuscript: Li, DuBois, Almon, Jusko.