Recurrence Quantification Analysis of Sentence-Level Speech Kinematics

Abstract

Purpose

Current approaches to assessing sentence-level speech variability rely on measures that quantify variability across utterances and use normalization procedures that alter raw trajectory data. The current work tests the feasibility of a less restrictive nonlinear approach—recurrence quantification analysis (RQA)—via a procedural example and subsequent analysis of kinematic data.

Method

To test the feasibility of RQA, lip aperture (i.e., the Euclidean distance between lip-tracking sensors) was recorded for 21 typically developing adult speakers during production of a simple utterance. The utterance was produced in isolation and in carrier structures differing just in length or in length and complexity. Four RQA indices were calculated: percent recurrence (%REC), percent determinism (%DET), stability (MAXLINE), and stationarity (TREND).

Results

Percent determinism (%DET) decreased only for the most linguistically complex sentence; MAXLINE decreased as a function of linguistic complexity but increased for the longer-only sentence; TREND decreased as a function of both length and linguistic complexity.

Conclusions

This research note demonstrates the feasibility of using RQA as a tool to compare speech variability across speakers and groups. RQA offers promise as a technique to assess effects of potential stressors (e.g., linguistic or cognitive factors) on the speech production system.

Variability is an inherent property of speech motor systems because articulators rarely reproduce the same trajectory pattern(s) during repetitions of the same sentence, even when that sentence is produced in the same context and by the same speaker. Variability has been operationally defined as the inconsistency (or variance) of a quantity over repeated measurements, whether within or across bouts of behavior. In speech research, the measurements in question might be of any speech-related signal (e.g., kinematic, acoustic) that changes over time. A common approach to quantifying sentence-level kinematic variability has been the spatiotemporal index (STI; Smith, Goffman, Zelaznik, Ying, & McGillem, 1995), which is a linear index of variability that is normalized by time and amplitude.

In practical terms, the STI provides a value that indicates how much each signal from a set of repeated signals deviates from the mean of that set of signals. The STI is useful because it allows investigators to examine connected speech (e.g., phrases, sentences), and it provides a metric that can be used to examine the effect of system stressors (e.g., linguistic complexity, social–cognitive or emotional demands) on speech motor control. In controlled speech tasks, typically developing children exhibit greater variability (higher STI values) than adults (Maner, Smith, & Grayson, 2000; Schötz, Frid, & Löfqvist, 2013; Smith & Zelaznik, 2004), children who stutter exhibit greater STI than typically developing peers (Smith, Goffman, Sasisekaran, & Weber-Fox, 2012), and speakers who stutter exhibit greater STI than controls when linguistic complexity increases (Cai et al., 2011; Jackson, Tiede, & Whalen, 2013; Kleinow & Smith, 2000).

Despite the benefits associated with using a composite approach such as the STI (e.g., relative ease of use, single outcome measure or single dependent variable), there are potential limitations to its use in speech motor control. By definition, STI is a global measure of the quantity of variability across a set of utterances (Smith et al., 1995); it does not assess the evolution of speech movements within utterances. The STI implies that stable speech systems produce repetitions of utterances (in the same context) consistently or with the same or similar kinematic profiles. The more similar these profiles are, the closer to zero STI becomes. From this perspective, stability is inferred from the speaker's ability to converge onto an underlying movement template (e.g., for lip aperture over time), and deviation from this presumed template is interpreted as noise and a reflection of uncontrollability in the speech motor system (see Smith et al., 1995). However, there are many reasons for which a speaker would alter the kinematic profile of his or her speech, not all of which necessarily make that speaker less stable. For example, sentences produced with different stress or prosody may affect STI values (Maner et al., 2000). This does not imply that the speaker's speech motor system is less stable, but rather that he or she is choosing to use a different strategy across productions. Dromey, Boyce, and Channell (2014) highlighted the fact that asking speakers to deliberately change their speech rate (which Smith and colleagues did) alters their approach to speech production. This voluntary adjustment to speech motor control could also feasibly affect STI values.

Furthermore, because start and end points of utterances for STI calculation require alignment, the time course of the original trajectories is distorted through normalization procedures (as pointed out by Lucero, 2005; Lucero, Munhall, Gracco, & Ramsay, 1997; Ward & Arnfield, 2001). Defending their STI approach, Smith, Johnson, McGillem, and Goffman (2000) argued that for their purpose of measuring the effects of contextual variables on speech, linear normalization procedures were sufficient because their questions did not require the identification of speech landmarks (though, they did in fact specify start and end points at peak velocity points). Still, Jackson, Tiede, Beal, and Whalen (2016) found significant correlations between STI and sentence duration—sentences with longer duration were associated with higher STI values, and those with shorter duration were associated with lower STI. Taken together, results from Lucero (2005), Ward and Arnfield (2001), and Jackson et al. (2016) suggest that utterance duration may significantly influence STI values.

Speech motor control research will benefit from novel methods that go beyond the quantification of the amount of variability across utterances to characterize the nature of variability within utterances. Assessing the nature of variability provides information about features such as the stability, determinism, and complexity of speech production that often cannot be assessed by quantifying simply how much variability occurs. Assessing variability within utterances preserves the timing dimension critical to speech production, because normalization procedures are not required. The approach we test here for quantifying the nature of variability within utterances is recurrence quantification analysis (RQA).

Recurrence Quantification Analysis

RQA (Marwan, Carmen Romano, Thiel, & Kurths, 2007; Webber & Marwan, 2015; Webber & Zbilut, 1994, 2005) is a nonlinear approach to assessing patterns in time-series data. It essentially identifies the degree to which a measured time series repeats itself, and the nature of those repetitions, whether they reflect deterministic or predictable dynamics or are incidental due to random fluctuation. RQA has been applied to a broad range of measurements in physiology, cognitive science, social sciences, and physical sciences (Marwan, Riley, Giuliani, & Webber, 2014; Webber & Marwan, 2015). RQA can be used to analyze very short time series and makes no assumptions about the underlying distribution of the data or whether the data arise from a linear or nonlinear process.

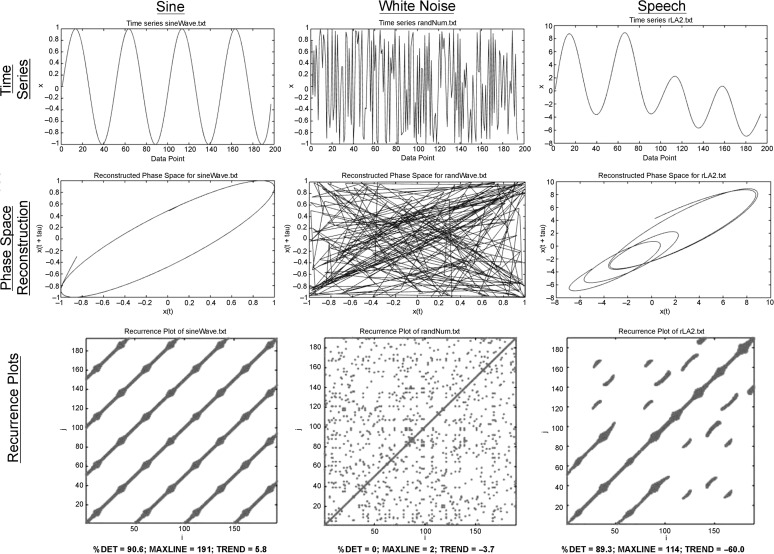
RQA as typically implemented utilizes a phase space reconstruction method that is based on Takens' (1981) theorem. That theorem states that it is possible to identify important features of a system's dynamics on the basis of a one-dimensional time series/trajectory (such as lip aperture over time) by utilizing time-delayed copies of the measured time series as stand-in dimensions for unobserved system variables. Plotting the measured time series and time-delayed copies creates a higher-dimensional, reconstructed phase space—a visualization of how the trajectory evolves when embedded in this reconstructed space. Phase space reconstruction removes potential distortions that result from projecting a (potentially) high-dimensional system onto the single dimension of the measurement variable, and it has been mathematically proven to preserve certain invariants of the system's dynamics even if they are not known a priori. Thus, phase space reconstruction plausibly sidesteps the challenge of not knowing the nature (and number) of underlying variables of a system, as long as one variable of that system is known. The top and middle rows in Figure 1 represent time series and corresponding reconstructed phase space plots, respectively, for a sine wave, noise, and a speech signal, respectively. The speech signal represents one trial/utterance from the data set; the sine wave and noise signals were generated using basic functions in MATLAB.

Figure 1.

RQA for three time series: Sine (left), white noise (center), and speech (right; from data set). Top row: Raw time series, with sample on the x-axis and amplitude on the y-axis. The speech signal reflects lip aperture during the utterance Buy Bobby a puppy. Middle row: Phase space reconstructions, with amplitude for original signal on the x-axis and time-delayed signal on the y-axis. Parameters: EMBED = 4; DELAY = 2; radius = 15%; line length = 5. Bottom row: Recurrence plots for each signal; original trajectory is reflected on the x-axis and time-delayed trajectory is reflected on the y-axis. Corresponding percent determinism (%DET), longest repeated string of data points in the time series (MAXLINE), and measure of stationarity (TREND) indexes are provided at the bottom.

RQA coupled with phase space reconstruction has great potential in speech research because even though investigators are able to measure articulatory motion, the identification and measurement of other variables that shape speech production (including, potentially, variables related to higher-order processes such as language, cognition, or emotion) are far more difficult tasks. The next section provides an example, including parameter selection, phase space reconstruction, and subsequent recurrence plot (RP) generation for one trial from the data set. Quantifications founded on the RPs, which yield the RQA indices, are addressed in the section after that.

Applying RQA to Speech Production: An Example

This research note is intended to provide an introduction to RQA, with the aim of showing researchers and clinicians how RQA can be used to assess speech data. The reader is referred to Webber and Zbilut (2005) for a more comprehensive presentation of the concepts described here. The reader is also directed to additional resources throughout this section.

A typical preliminary step in RQA is specifying the phase space reconstruction parameters DELAY and EMBED. DELAY refers to the number of samples used to create the time-delayed trajectories, such that 1 + DELAY becomes the first point of the second dimension, 1 + 2*DELAY becomes the first point of the third dimension, and so on. A DELAY value should be chosen that minimizes the amount of mutual information for a given time series so that new (rather than redundant) information about the system is gained by adding each new dimension (Fraser & Swinney, 1986). A DELAY of 8 was initially indicated as appropriate for the trajectories examined here because a DELAY of greater than 8 did not add new information to the phase space plot. However, because the target signals were relatively short (i.e., approximately 200–250 samples), using this high of a delay value yielded artifacts (e.g., zeroes, 100% values) in the RQA indices (e.g., percent recurrence, percent determinism; these indices are discussed in detail later herein). Thus, to avoid potential floor and ceiling effects in those indices, lower DELAY values were probed such that the RQA functions generated good spreads in percent recurrence (i.e., approximately 3%–6%) and percent determinism (i.e., approximately 80%–99%). These values were obtained with DELAY set at 4. Heuristics have been established for selecting all RQA parameters. As just illustrated, adjustment of these values is licensed so long as there is valid reason (e.g., 0 or 100% values or overly high recurrence rates). Generally speaking, RQA is fairly robust with regard to variation in these parameters (Webber & Zbilut, 2005), particularly the embedding parameters (Iwanski & Bradley, 1998).

EMBED (or embedding) refers to the number of dimensions to be used to reconstruct the phase space. Selection of EMBED can be guided by the false nearest neighbors methodology (Abarbanel & Kennel, 1993), in which EMBED is increased by integer increments until the distortions caused by projection—identified as “false neighbors” (data points that appear close in phase space until addition of a new dimension pulls them apart)—are removed. An EMBED of 4 was initially determined, because most false neighbors were removed at approximately 4 dimensions. However, once again, the brief nature of the data series required selection of a lower parameter value than was ideal. Good spreads in percent recurrence (i.e., approximately 3%–6%) and percent determinism (i.e., approximately 75%–90%) were obtained with an EMBED of 2.

After DELAY and EMBED are established, distance and recurrence matrices are constructed. The following example (adapted from Webber, 2004) is based on the first five samples of one utterance from one speaker. Given the time series (TS)

$$\mathit{TS}\mathit{=}\left[\mathit{1.28}\mathit{,}\mathit{1.97}\mathit{,}\mathit{2.66}\mathit{,}\mathit{3.33}\mathit{,}\mathit{3.98}\mathit{,}\mathit{4.60}\mathit{,}\mathit{5.19}\mathit{,}\mathit{7.73}\mathit{,}\mathit{6.23}\mathit{.}\mathit{\dots }\mathit{\dots }\mathit{\dots }\text{.}\right]$$

and implementing the DELAY of 4 and EMBED of 2 (and using only the first five data points), the following time-delayed trajectories are constructed:

$$\begin{array}{l}V\mathit{1}\mathit{=}\left[\mathit{1.28}\mathit{,}\mathit{3.98}\right]\hfill \\ V\mathit{2}\mathit{=}\left[\mathit{1.97}\mathit{,}\mathit{4.60}\right]\hfill \\ V\mathit{3}\mathit{=}\left[\mathit{2.66}\mathit{,}\mathit{5.19}\right]\hfill \\ V\mathit{4}\mathit{=}\left[\mathit{3.33}\mathit{,}\mathit{7.73}\right]\hfill \\ V\mathit{5}\mathit{=}\left[\mathit{3.98}\mathit{,}\mathit{6.23}\right]\hfill \\ \dots \dots \dots \dots \dots \dots \dots \text{.}\hfill \end{array}$$

Euclidean distances between these time-delayed trajectories are then calculated. For example, the Euclidean distance between V2 and V4 is calculated as

$$V\mathit{4}\mathit{:}V\mathit{2}\mathit{=}\mathit{SQRT}\left({\left(\mathit{1.97}\mathit{‐}\mathit{3.33}\right)}^{\mathit{2}}\mathit{+}{\left(\mathit{4.60}\mathit{‐}\mathit{7.73}\right)}^{\mathit{2}}\right)\mathit{=}\mathit{3.41}$$

The distance matrix is constructed by finding the distances for each cell in the 5 × 2 matrix:

$$\begin{array}{l}\left[\mathit{1},\mathit{5}\right]\mathit{=}\mathit{3.51}\mathit{;}\left[\mathit{2},\mathit{5}\right]\mathit{=}\mathit{2.59}\mathit{;}\left[\mathit{3},\mathit{5}\right]\mathit{=}\mathit{1.68}\mathit{;}\left[\mathit{4},\mathit{5}\right]\mathit{=}\mathit{1.63}\mathit{;}\left[\mathit{5},\mathit{5}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{4}\right]\mathit{=}\mathit{4.27}\mathit{;}\left[\mathit{2},\mathit{4}\right]\mathit{=}\mathit{3.41}\mathit{;}\left[\mathit{3},\mathit{4}\right]\mathit{=}\mathit{2.63}\mathit{;}\left[\mathit{4},\mathit{4}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{3}\right]\mathit{=}\mathit{1.84}\mathit{;}\left[\mathit{2},\mathit{3}\right]\mathit{=}\mathit{0.91}\mathit{;}\left[\mathit{3},\mathit{3}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{2}\right]\mathit{=}\mathit{0.93}\mathit{;}\left[\mathit{2},\mathit{2}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{1}\right]\mathit{=}\mathit{0.00}\hfill \end{array}$$

Note that only the upper triangle of the matrix is shown. This is because the lower triangle mirrors the upper triangle (i.e., yields the same values). This is the case for all RQA measures that are based on a single time series. In addition, the center diagonal, or line of identity (LOI), is represented by “0” values because these cells represent a comparison of the trajectory with itself.

An additional parameter setting is the rescaling option, which is used to shrink the magnitude of the distance matrix. This can be achieved by dividing each element of the distance matrix by either the mean or maximum distance of the matrix. Here, values are rescaled on the basis of the mean distance (i.e., 2.34).

$$\begin{array}{l}\left[\mathit{1},\mathit{5}\right]\mathit{=}\mathit{1.50}\mathit{;}\left[\mathit{2},\mathit{5}\right]\mathit{=}\mathit{1.11}\mathit{;}\left[\mathit{3},\mathit{5}\right]\mathit{=}\mathit{0.72}\mathit{;}\left[\mathit{4},\mathit{5}\right]\mathit{=}\mathit{0.70}\mathit{;}\left[\mathit{5},\mathit{5}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{4}\right]\mathit{=}\mathit{1.82}\mathit{;}\left[\mathit{2},\mathit{4}\right]\mathit{=}\mathit{1.46}\mathit{;}\left[\mathit{3},\mathit{4}\right]\mathit{=}\mathit{1.12}\mathit{;}\left[\mathit{4},\mathit{4}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{3}\right]\mathit{=}\mathit{0.78}\mathit{;}\left[\mathit{2},\mathit{3}\right]\mathit{=}\mathit{0.39}\mathit{;}\left[\mathit{3},\mathit{3}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{2}\right]\mathit{=}\mathit{0.40}\mathit{;}\left[\mathit{2},\mathit{2}\right]\mathit{=}\mathit{0.00}\hfill \\ \left[\mathit{1},\mathit{1}\right]\mathit{=}\mathit{0.00}\hfill \end{array}$$

The next step is to create the recurrence matrix, which involves identifying when the system recurs or revisits a prior state. This is done by comparing distances between all possible pairs of data points in the reconstructed phase space and comparing those distances to a threshold value. This threshold value, or RADIUS, determines the points in the distance matrix that are sufficiently close to be registered as recurrent, so that the recurrence matrix—and ultimately the RP—can be constructed. RADIUS effectively allows for recurrence to occur without an exact match in data values. Thus, a state is represented by an acceptable range of data points, such that neighbors in phase space theoretically represent the same state. RADIUS is selected such that it falls within a range for which there is a linear scaling relation in a plot of percent recurrence as a function of RADIUS, and percent recurrence values are kept relatively low (e.g., 1%–5%; Shockley, 2014). A RADIUS of 18% of overall mean distance is used here to construct the following recurrence matrix for this particular sample time series. Note that 15% was more appropriate and was used for the full data set because each trial consisted of approximately 200–250 samples (compared with five samples in this example).

$$\begin{array}{l}\left[\mathit{1},\mathit{5}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{2},\mathit{5}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{3},\mathit{5}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{4},\mathit{5}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{5},\mathit{5}\right]\mathit{=}\mathit{1}\hfill \\ \left[\mathit{1},\mathit{4}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{2},\mathit{4}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{3},\mathit{4}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{4},\mathit{4}\right]\mathit{=}\mathit{1}\hfill \\ \left[\mathit{1},\mathit{3}\right]\mathit{=}\mathit{0}\mathit{;}\left[\mathit{2},\mathit{3}\right]\mathit{=}\mathit{1}\mathit{;}\left[\mathit{3},\mathit{3}\right]\mathit{=}\mathit{1}\hfill \\ \left[\mathit{1},\mathit{2}\right]\mathit{=}\mathit{1}\mathit{;}\left[\mathit{2},\mathit{2}\right]\mathit{=}\mathit{1}\hfill \\ \left[\mathit{1},\mathit{1}\right]\mathit{=}\mathit{1}\hfill \end{array}$$

Plotting the recurrence matrix yields an RP. An RP represents the points in phase space at which the states of the system recur (i.e., are neighborly), on the basis of the selected parameters (Eckmann, Kamphorst, & Ruelle, 1987). A value of “1” in the recurrence matrix is represented by a dot in the RP (vs. empty or “0” locations). The bottom row of Figure 1 presents RPs for the sine wave, noise, and speech signal examples.

Quantification of the RP

RPs provide a qualitative (and visual) assessment of a time series. RQA systematically quantifies patterns within the RP or recurrence matrix using series of algorithms that have been developed for this purpose. This research note focuses on four RQA indices: percent recurrence (%REC), percent determinism (%DET), MAXLINE, and TREND. (Note that other RQA indices are available, and some of these may also be useful in characterizing speech signals.)

%REC quantifies the percentage of points out of all possible points from the distance matrix that fall within the established recurrence threshold (i.e., RADIUS). It thus represents the percentage of recurrent points out of all possible points in the RP.

%DET quantifies the percentage of recurrent points that fall along diagonal lines of at least LINE length (here, 5 points), not including points along the LOI (Webber & Zbilut, 1994). In previous work that examined physiological data (e.g., postural sway, cardiac signals), the LINE parameter was set to 2; this low threshold ensured that patterning was evident in the data (because the number of diagonal lines is the basis of several RQA indexes). However, because the target trajectory in the present work (i.e., lip aperture for Buy Bobby a puppy) yielded sine-wave–like times series, LINE was set to 5 so that the RQA variables did not reach ceiling values (as recommended by Shockley, personal communication, June, 2014). In effect, %DET is a measure of predictability, or the patterned structure of recurrence of the system under study. %DET helps to differentiate data that may appear complex or irregular yet that possess predictable structure from truly random or stochastic processes (for relevant discussion, see van Lieshout & Namasivayam, 2010). %DET is calculated as the percentage of points in diagonal lines out of all possible recurrent points.

MAXLINE captures the longest repeated string of data points in the time series; this is indicative of stability because more stable system dynamics are less likely to be interrupted by a perturbation. MAXLINE is thus a measure of stability of the time series. High MAXLINE values reflect high stability; smaller (shorter) MAXLINE values represent signals that are more chaotic. MAXLINE is the longest diagonal line (excluding the LOI) in the RP.

TREND is a measure of stationarity of a time series, or how the mean state of the time series evolves throughout a given trial. Many linear methods assume a constant level, or mean, throughout a time series (as well as stationary variance through the time series). Thus, the system's mean state is relatively static during production of the signal under study. RQA does not make this assumption. Rather, complex systems may have mean states that are theoretically moving (Riley, Balasubramaniam, & Turvey, 1999). TREND measures this drift or change in level over time. TREND values near zero indicate that the recurrent points of a time series are consistent as the time series evolves (i.e., reflecting greater homogeneity). TREND values deviating from zero indicate less consistency in the degree of recurrence as the time series evolves (more heterogeneity; Webber & Zbilut, 2005). TREND for physiological data tends to be negatively signed, because it represents the “paling” or lessening of recurrence away from the LOI (Riley et al., 1999). TREND is calculated as the slope of the regression line for %REC as a function of distance from the LOI (Riley et al., 1999).

RQA values are provided for the sine wave, white noise, and speech signals at the bottom of Figure 1. Note that the sine wave demonstrates relatively high %DET, whereas noise exhibits zero %DET (because this time series is random). Due to the sine-like, predictable nature of the speech trajectory (for Buy Bobby a puppy), the speech signal exhibits relatively high %DET (only slightly lower than that for the sine wave), indicating that this utterance is similar in determinism to the sine wave. MAXLINE indicates that stability is highest for the sine wave, lower for speech, and virtually nonexistent for noise. Thus, the sine wave is only slightly more deterministic than speech, but speech is markedly less stable than the sine wave. Noise exhibits virtually no stability. Both the sine wave and noise exhibit low TREND values (near zero). This is because as time passes (i.e., traveling orthogonally from the LOI towards the bottom-right corner [or top-left corner]), the patterns of recurrence for the sine wave and noise are similar. Thus, for the sine wave, there are dense diagonal lines parallel to the LOI throughout the time series; for noise, there are scattered dots throughout the time series (but the “pattern of scatter” is similar to that of the sine wave). For speech, however, TREND is relatively high, because as time passes, patterns of recurrence are not as similar. Therefore, some lines are short, and others are longer, whereas some are denser, and others are not as dense. A truly nonstationary process (e.g., a sine wave superimposed on a linear trend) would show even higher TREND values.

The above example and Figure 1 demonstrate that RQA can be used to assess variability in speech production data. In the only study ¹ to implement RQA including phase space reconstruction in speech, van Lieshout and Namasivayam (2010) examined the deterministic structure of time series of the relative phasing between tongue body and bilabial closing gestures. They found that faster productions exhibited less deterministic structure in the relative phase patterns. They also demonstrated the feasibility and potential benefits of using RQA to examine speech data, but their small study examined the production of short, nonsense syllables rather than full sentences, and it examined intergestural coordination rather than leveraging the power of Takens' (1981) theorem to unravel the dynamics of gestural articulation on the basis of a single measured kinematic variable. The current work applied RQA, in addition to the STI technique, to the movement trajectories of one gesture (i.e., lip aperture) for a relatively large data set (21 speakers) during production of a simple sentence both produced in isolation and embedded in more linguistically complex structures. Adding linguistic complexity highlighted the benefits of using RQA to examine the influence of increasing demands on the speech motor system.

Methodology

Research Protocol

This research protocol was approved by the Institutional Review Board of the Graduate Center of the City University of New York. The data set presented constitutes the control group from the first author's dissertation project, which examined variability in adult speakers who do and do not stutter. Those results are presented in full in Jackson et al. (2016).

Participants

Participants included 21 adult speakers (7 female, 14 male; ages M = 25.3 years, SD = 2.5 years). All speakers reported English as their primary language, and all speakers reported learning English before age 6 years. Multilingual speakers were not excluded, as it was determined that the benefits of including them for this proof-of-concept study (e.g., larger sample, more heterogeneous group) outweighed any potential confounding factors (e.g., decreased language and/or speech ability due to less exposure to English). No participants reported a positive history of speech–language, neurological, or psychological impairment. All participants passed a pure-tone hearing screening at 500, 1,000, 2,000, and 4,000 Hz at 20 dB hearing level.

Stimuli

Stimuli were adapted from Kleinow and Smith (2000). The target phrase, Buy Bobby a puppy, was produced in isolation (Base), as well as embedded in one “longer-only” sentence, and two longer and more linguistically complex sentences. The longer-only sentence (L1; Four one three two five Buy Bobby a puppy ten eight nine eleven) was intended to lengthen the sentence with minimal linguistic complexity and also reduce the probability of speech alteration due to rote counting effects (thus the numbers were shuffled). The two sentences with longer and more linguistically complex structures followed perspective embedment guidelines, reflecting mental states of actors, so that each state added an additional level of perspective (Whalen, Zunshine, & Holquist, 2012; Zunshine, 2006). Using reading time as a proxy for complexity, Whalen et al. (2012) found that greater levels of embedding were indeed more complex. These stimuli were: He wants Karen to tell John to buy Bobby a puppy at my store (P1; level 1 perspective embedment), and You want Samantha to buy Bobby a puppy now if he wants one (P2; level 2 perspective embedment). Participants produced the utterance “Buy Bobby a puppy” 20 times in each sentence (i.e., Base, L1, P1, P2, in randomized order) for a total of 80 tokens per speaker. Participants were instructed to speak “normally”; as intended, speakers were not overly fast, slow, loud, or quiet.

Experimental Protocol

Participants were seated approximately 2 m from an Optotrak Certus 3020 (Northern Digital, Waterloo, Ontario), a commercially available camera system that uses infrared emitting diodes (IREDs) to track movement in three dimensions. The current study focused on lip aperture (i.e., the distance between the upper and lower lip IREDs), so head-movement correction procedures were not necessary. Two IREDs were placed at the sagittal midline of the vermillion border of the upper and lower lips of each participant. An Audio-Technica MicroSet directional microphone with an AT8539 Power Module on a boom stand was placed ~20 cm in front of the participant's mouth for audio recording. The Optotrak Data Acquisition Unit (ODAU) recorded coregistered audio.

Stimuli were presented on a 20-in. (50-cm) monitor (Dell ST2320L full high-definition light-emitting diode widescreen) using Presentation software (Neurobehavioral Systems, Berkeley, CA). The monitor was placed approximately 30–40 cm directly next to the Optotrak, which minimized potential interference between the screen and Optotrak. Each sentence appeared on the monitor for 5 s and was preceded by 1 s of silence and a blank screen. Before data collection, participants were instructed to test the range of IRED detectability by moving their heads to the left and right; they were provided with verbal feedback when this movement caused the IREDS to go out of range. IREDS positions were recorded using First Principles (Northern Digital), the proprietary software for Optotrak data collection. Participants were instructed to attempt to remain stationary during the experiment, though minimal movement was permitted as long as IRED view was not obstructed (see following regarding trials that were discarded due to IRED obstruction).

Data Collection

Two types of data were collected: kinematic and acoustic. Kinematic signals were sampled at 250 Hz and subsequently low-pass filtered with a third-order Butterworth filter with a 10-Hz cutoff frequency. Acoustic signals were digitized at 16.5 kHz and low-pass hardware filtered at 7.5 kHz. Lip aperture was calculated as the by-sample Euclidean distance between the upper and lower lip IREDs. To register start and end points in kinematic trajectories, audio files were first manually labeled to mark the target utterance (i.e., Buy Bobby a puppy), ensuring that the marking for the beginning of the utterance preceded Buy, and the marking for the end of the utterance followed puppy. Because acoustic and kinematic files were aligned, it was possible to transpose markings from the audio to kinematic files.

To extract the registered target utterance from kinematic trajectories, a three-point central differencing method was used to first determine lip aperture velocity. The beginning of the utterance was subsequently registered at the peak velocity of the first opening movement (i.e., release of /b/ in Buy); the end of the utterance was registered at peak velocity of the last opening movement (i.e., the release of the second /p/ in puppy; as in Smith et al., 1995). Custom procedures in MATLAB were implemented for trajectory registration.

Dependent Variables

Three RQA indices, %DET, MAXLINE, and TREND, were calculated as specified in the “Quantification of the Recurrence Plot” section (%REC was only used for establishing parameters). The following phase space reconstruction and RQA parameters were used: DELAY = 4; EMBED = 2; RADIUS = 15%; rescaling = mean distance; LINE = 5, as described above. ² STI was determined by summing the 50 standard deviations calculated at 2% intervals across the overlaid time- and amplitude-normalized waveforms (following Smith et al., 1995). Utterance duration was calculated as the time between the lip aperture peak velocity point immediately following the release of /b/ in Buy and the peak velocity point immediately following the second /p/ in puppy.

Results

Disfluent trials were excluded from analysis. Disfluencies were determined perceptually by the first author, a licensed speech–language pathologist, and confirmed by a second speech–language pathologist. Disfluencies included repetitions, hesitations, pauses, and irregular prosodic patterns. In addition, a pilot study was conducted to identify harder-to-observe (or more subtle) disfluencies. That study determined that hesitations and/or pauses were the most common source of disfluency in the data set, and that pauses/hesitations exceeding 6% of the total duration of the utterance represented an appropriate threshold for fluency/disfluency discrimination (i.e., pauses/hesitations longer than 6% were considered disfluent). In total, 2.14% (36/1,680) of the utterances were marked as disfluent. In addition, local shape-preserving interpolation was used to correct for missing data points due to technical failure or IRED obstruction. Trials for which there were more than 25 consecutive data points missing (in the target utterance) were also excluded from analysis; these included 1.31% (or 22/1,680) of total trials.

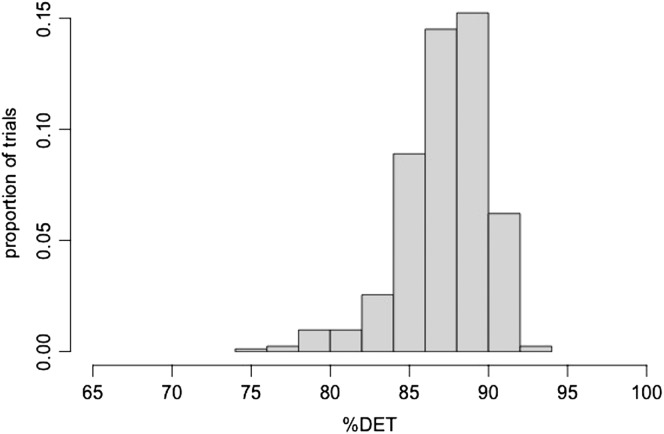
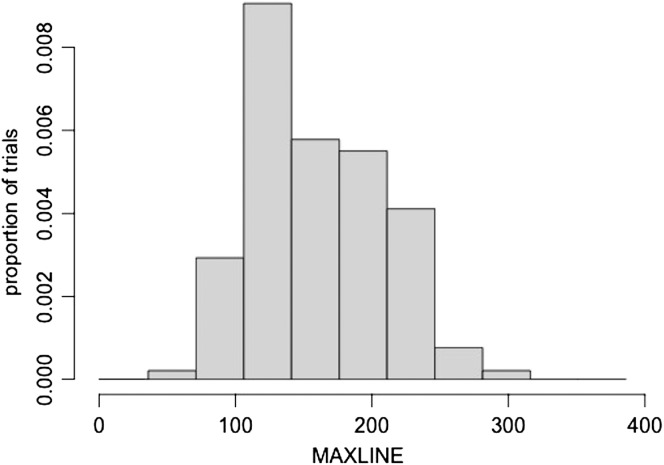
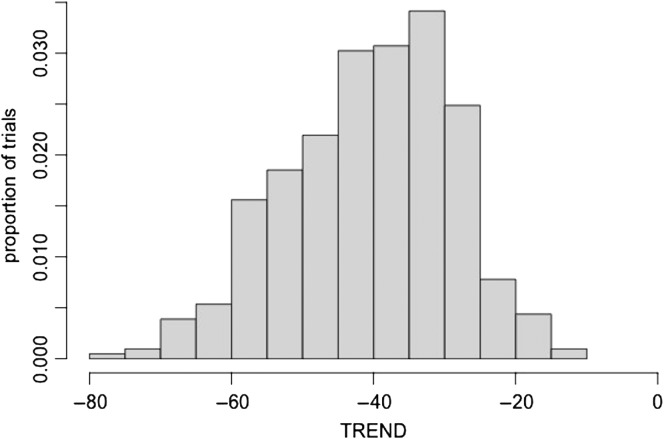
%DET, MAXLINE, and TREND were calculated for each remaining trial from each participant. Figures 2 –4 present histograms of %DET, MAXLINE, and TREND, respectively, for Base (the target utterance produced in isolation). As is evident from the figures, the three indices yielded close-to-normal (Gaussian-like) distributions (%DET exhibited a negative skew). To demonstrate the utility of using RQA to examine system stressors on speech production (here, linguistic complexity), linear mixed models were constructed using the lme4 package (Bates, Maechler, Bolker, & Walker, 2014, p. 4) in R (R Core Team, 2014). The lmerTest function (Kuznetsova, Brockhoff, & Christensen, 2014) was also used to provide Satterthwaite p-value approximations for reader convenience. Linear mixed models are regression methods that permit the examination of (multiple) fixed and random variables concurrently (Baayen, 2008). The model-building approach described by Baayen was followed, and models were fit using the restricted maximum likelihood technique.

Figure 2.

Histogram for percent determinism (%DET), only for Base sentence.

Figure 3.

Histogram for the longest repeated string of data points in the time series (MAXLINE), only for Base sentence.

Figure 4.

Histogram for the measure of stationarity (TREND), only for Base sentence.

The statistical models for %DET, MAXLINE, TREND, and duration (the dependent variables [DV]) included sentence and trial as fixed factors, and participant as a random factor: lmer(DV ~ sentence + c.(trial) + [1|participant]). Trial was included as a fixed factor to account for possible practice effects, which are often found in speech production research. Here, “c” indicates that trial numbers were centered in order to avoid spurious correlations in the model, and this was achieved by subtracting the overall mean from each data point without scaling (Baayen, 2008). Participant was included as a random factor to account for variation due to repeated measures and individual differences not otherwise accounted for by the model. The linear mixed model used for STI was similar, except it did not include trial as a fixed factor.

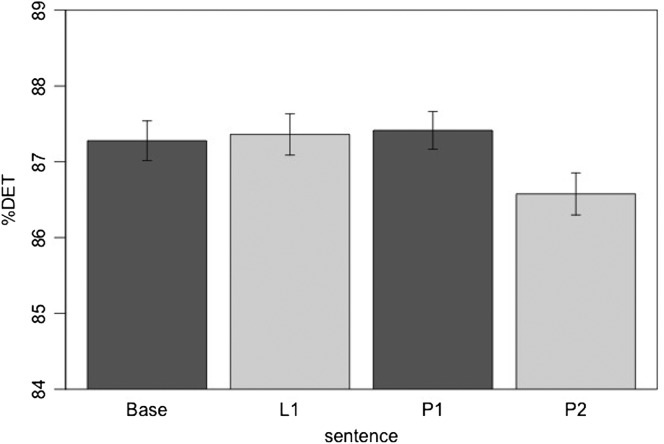
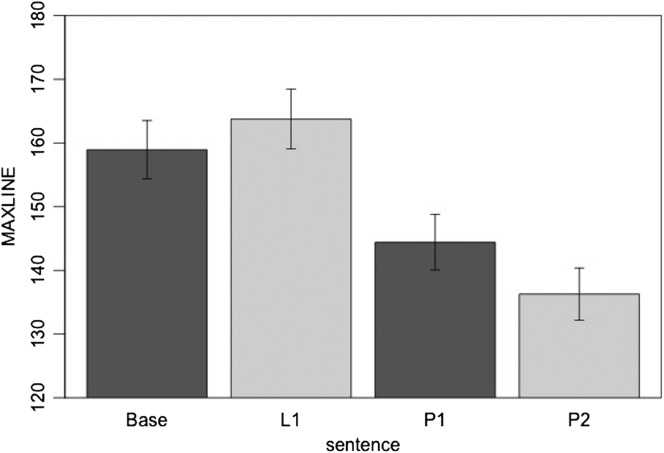
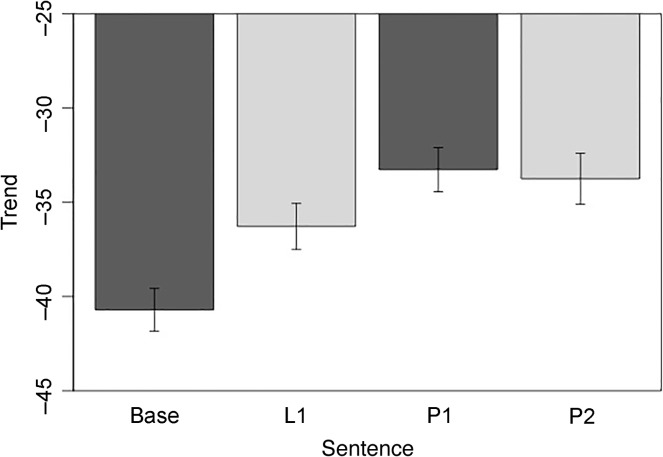
Compared with the Base condition, P2 showed lower %DET (t = −4.11, p < .001); L1 and P1 did not differ from Base (see Figure 5). Thus, the utterance embedded in the most complex structure (on the basis of perspective embedment guidelines) exhibited the least deterministic structure. Compared with Base, P1 (t = −6.47, p < .001) and P2 (t = −10.21, p < .001) yielded lower MAXLINE, indicating that stability decreased as a function of linguistic complexity. In contrast, the longer-only sentence contributed to increased stability (t = 2.33, p < .02) (see Figure 6). Regarding TREND, significant differences were found between Base and L1 (t = 6.33, p < .001), P1 (t = 10.44, p < .001), and P2 (t = 9.62, p < .001; see Figure 7). This means that the least complex utterance (i.e., Base) was produced with the least stationarity. Post-hoc tests with Bonferroni correction at α/3 = .017 demonstrated that both P1 and P2 yielded more stationarity than L1 (t = 4.06, p < .001; t = 3.25, p < .01, respectively), indicating that length and linguistic complexity increased stationarity more than just length alone.

Figure 5.

Percent determinism (%DET) for each sentence. Error bars show SE of the mean.

Figure 6.

Longest repeated string of data points in the time series (MAXLINE) for each sentence. Error bars show SE of the mean.

Figure 7.

Measure of stationarity (TREND) for each sentence. Error bars show SE of the mean.

Significant differences were not found for STI, indicating that normalized, across-trial variability was not affected by linguistic complexity in this study. Both P1 (t = −6.69, p < .001) and P2 (t = −13.33, p < .001) yielded shorter utterance durations (for the target phrase alone), indicating that embedding an utterance in a linguistically complex sentence contributed to increased speech rate for that utterance.

Discussion

The purpose of this study was to determine the feasibility and usefulness of applying RQA to examine sentence-level kinematic variability in speech production. Three RQA indices were calculated: %DET, MAXLINE, and TREND (though, as noted, other RQA indices are available and may prove useful in speech research). These indices measured determinism, stability, and stationarity, respectively, for each time series (i.e., trial) in the study. Given the specified parameters, all indices returned values that spanned suitable ranges for speech. %DET yielded values between approximately 75% and 95%, indicating the presence of deterministic structuring of lip aperture variation (i.e., predictability). Because RQA indices are strongly dependent on parameter settings, their values cannot be taken as calibrated absolutes—thus it would be inaccurate to claim that the lip aperture variations were 75%–95% deterministic (and thus 5%–25% random noise). However, examining the ways in which these values change in different contexts (or also in disordered populations) may help to better characterize the nature of speech variability in typical and atypical speakers. For example, it was found that in typical speech production, the most linguistically complex stimuli yielded lower determinism than did less complex stimuli. Thus, deterministic structure decreased with linguistic complexity; simpler sentence productions were more regular and predictable than the most complex sentences, which exhibited a greater degree of random variation. This finding appears to contrast with results from Kleinow and Smith (2000), as well as current STI results, which showed that linguistic complexity did not yield higher STI (more variability) in typically developing adult speakers. It appears that %DET captures a different aspect of linguistic-driven speech variability, perhaps a more subtle aspect that is tied to the way in which a signal varies rather than the extent to which it varies, and noticeable only when evaluated within an utterance. It will be interesting to examine pathological speakers in this regard, as it has been shown, for example, that stroke and Parkinson's disease contribute to more deterministic structure of postural sway (Ghomashchi, Esteki, Nasrabadi, Sprott, & Bahrpeyma, 2011; Schmit et al., 2006, respectively).

MAXLINE results indicated that introducing linguistic complexity via the carrier sentence reduced stability, a finding that corroborates %DET results. However, the longer-only sentence had the opposite effect, resulting in higher MAXLINE values, demonstrating that embedding the target sentence in a longer sentence increased stability. One possible explanation is that the speakers entrained to the “rhythm” of counting before and/or after the target utterance (Four one three two five Buy Bobby a puppy ten eight nine eleven), despite efforts to minimize this effect (i.e., shuffling the numbers). This potential rhythm would not be present, or it would be present to a much lesser degree, in linguistically meaningful speech, or speech without counting. Of course, this explanation requires further testing, for example, using metronomic and other counting tasks.

TREND results indicated that stationarity increased for the longer-only sentence, and then again for the longer and more complex sentences. Therefore, the mean state of the speech system fluctuated to a greater degree during the least linguistically complex utterances. This finding may on the surface appear to conflict with both the %DET and MAXLINE results, which indicated that linguistic complexity contributed to reduced determinism and stability. A possible explanation is that the overall position of lip aperture is less constrained during production of simpler linguistic structures, thus allowing more room for articulators to drift, and conversely more constrained when the target utterance is embedded in more complex structures. Although lip aperture kinematics showed more constraint in varying about a given lip aperture value during more complex productions, the %DET and MAXLINE results indicate that the variations about that mean value were less deterministically structured and less stable. This may be an indication that speech motor systems exhibit less flexibility during linguistically complex speech because of increased stationarity occurring simultaneously with decreased determinism and stability.

The fact that linguistic complexity contributed to shorter utterance duration for the target phrase, but not to decreased STI, may on the surface appear to conflict with the argument that duration influences STI. Furthermore, a significant correlation was not found here between duration and STI. However, examining 41 speakers (the 21 speakers analyzed here, and 20 speakers who stutter), Jackson et al. (2016) found a significant correlation between STI and duration. This was due to the within-group STI variance for the stuttering group (i.e., some speakers who stutter exhibited high STI, whereas others exhibited low STI; also reported by Kleinow & Smith, 2000) and was not characteristic of the control group. Thus, duration appears to be a confounding factor if STI values fluctuate within the data set (as it does for speakers who stutter, for example). It is important to note that Kleinow and Smith did not report durational changes reflective of increased syntactic complexity, which conflicts with the findings here. However, speakers in the study by Kleinow and Smith repeated the sentences after the sentences were auditorily presented to them. It is possible that the participants knowingly or unknowingly entrained to the rate of these model utterances/cues. In Jackson et al. (2016), participants were free to use a rate that was preferable to them—they were not given instructions or a model; they were just asked to read from the monitor.

Last, it should be emphasized that RQA and STI measure different attributes of variability (i.e., structure of variability and amount of variability, respectively). Indeed, “different measures of variability can depict conflicting stories, and it is important not to rely on a single method and to seek expertise in using and interpreting such variables” (van Lieshout & Namasivayam, 2010, p. 210). However, the selection of approach is dependent upon the research question. Still, a benefit of RQA is that it provides a broader and more comprehensive view of the nature of variability. For example, a linear approach assumes that when comparing trial to trial variability, trajectories should be the same—and that anything deviating from the mean trajectory represents noise in the system. Thus, if one word is prolonged in a particular trial, it will affect the variability of all the words due to the normalization of time. From this perspective, an inverse relationship exists between variability and stability. From a nonlinear, dynamic perspective, variance is not simply noise, but rather it reflects both deterministic and stochastic (random) processes (Riley & Turvey, 2002). RQA provides a technique to parse these different components and to quantify not just how much a signal varies but the manner in which the signal varies. The RQA indices used here—%DET, MAXLINE, and TREND—characterized speech production in terms of determinism, stability, and stationarity, and captured linguistically driven differences in speech motor control that would not have been realized using across-trial, linear measures (i.e., STI).

Considerations

There are three issues that should be considered. First, STI was criticized earlier herein for the assumption that effector movements associated with a repeated utterance exhibited by a stable system should converge on the same trajectory “template.” Indeed, many approaches to measuring variability will by definition carry this same assumption (e.g., variability measures that quantify variation about the mean tacitly treat the mean trajectory as a template). A significant strength of many time-series analysis methods is that they do not carry this assumption, and they are more concerned with how the trajectory evolves over time. However, many time-series analyses, including nonlinear ones, assume cyclicity (or oscillations, however complex) in the data. RQA does not explicitly assume that is the case, but the time-delayed/embedding procedure is more straightforwardly implemented when that is the case, and several of the RQA indices lack clear interpretations when the data are more highly stochastic. The assumption that articulator trajectories during speech exhibit cyclicity may not always hold, but in the current study, it seemed reasonable because the target utterance (Buy Bobby a puppy) was chosen explicitly because its lip aperture trajectory exhibits a “sine-like” pattern.

Second, RQA requires the a priori selection of parameters, and the selection process can be complicated. Although relative comparisons of RQA indices are typically robust in the face of variation in those parameters, the exact values obtained for the RQA indices are dependent upon these parameters. Whereas there are established heuristics for parameter selection that were used as a starting point for the current analysis, it was also ultimately necessary to determine an appropriate set of parameters that yielded meaningful output given the nature of the data at hand. In the present study, time-series length constrained parameter values. Further work with RQA of speech will help delimit the ranges of values that provide interpretable results.

Third, approaches rooted in nonlinear dynamics are often criticized for reducing dimensionality of the system under study. For example, it is possible that there are more than two interacting variables (i.e., the number of embedding dimensions used here) in speech. In general, it is often unknown how many variables constitute a complex system. RQA when implemented in combination with phase space reconstruction potentially sidesteps this issue by quantifying trajectories as they orbit a higher-dimensional reconstructed phase space that is related to the system's “true” phase space by smooth, differentiable transforms that preserve important quantitative characteristics about the system's dynamics. Indeed, the current results demonstrate how RQA can differentiate between conditions, even if the number of dimensions/variables of the system is ultimately unknown.

Conclusion

Overall, this work demonstrates that RQA, a technique that is relatively easy to implement given the appropriate tools, can complement existing methods for measuring speech variability by assessing the nature of variability within utterances without the use of normalization procedures, which alter the raw kinematic trajectories. RQA can be used as a tool to examine how certain variables (e.g., linguistic, social–cognitive) affect the speech motor system, and it may increase ecological validity in speech research in that repeated utterances/signals are not required. RQA may also be a promising tool to examine speech production throughout development and in pathological systems.

Funding Statement

This research was supported by National Institutes of Health Grant DC-002717 to Haskins Laboratories and National Science Foundation Grant 1513770 (awarded to Eric S. Jackson).