Improving treatment strategies for patients with metastatic castrate resistant prostate cancer through personalized computational modeling

Abstract

Metastatic castrate resistant prostate cancer (mCRPC) is responsible for the majority of prostate cancer deaths with the median survival after diagnosis being 2 years. The metastatic lesions often arise in the skeleton, and current treatment options are primarily palliative. Using guidelines set forth by the National Comprehensive Cancer Network (NCCN), the medical oncologist has a number of choices available to treat the metastases. However, the sequence of those treatments is largely dependent on the patient history, treatment response and preferences. We posit that the utilization of personalized computational models and treatment optimization algorithms based on patient specific parameters could significantly enhance the oncologist’s ability to choose an optimized sequence of available therapies to maximize overall survival. In this perspective, we used an integrated team approach involving clinicians, researchers, and mathematicians, to generate an example of how computational models and genetic algorithms can be utilized to predict the response of heterogeneous mCRPCs in bone to varying sequences of standard and targeted therapies. The refinement and evolution of these powerful models will be critical for extending the overall survival of men diagnosed with mCRPC.

INTRODUCTION

Nearly 30,000 men are projected to die from prostate cancer in 2014 in the USA alone [1]. The majority of these men will succumb to mCRPC. These metastases typically arise in the skeleton where they induce extensive bone destruction and formation that in turn greatly impact the patient’s quality of life and overall survival. Upon diagnosis, the medical oncologist will administer second line treatment options based on a dialog with the patient and NCCN guidelines.

The NCCN guidelines for prostate cancer treatment were generated from the collective experiences of the world’s foremost genitourinary oncology experts and are a gold standard in regards to how patients with mCRPC should be treated [2]. For example, if a patient with advanced disease is diagnosed with symptomatic mCRPC, the oncologist will continue to ablate serum levels of testosterone and administer an anti-bone resorptive such as bisphosphonates or anti-receptor activator of nuclear KB ligand (RANKL) based therapies. The choice of hormonal and chemotherapies that can be utilized include, but are not limited to, abiraterone, enzalutamide, docetaxel, mitoxantrone and, cabazitaxel. In addition, we are at the beginning of a period that will potentially see multiple therapies on-line that specifically target molecules commonly overexpressed or aberrantly activated in mCRPC such as c-Met, AKT and JAK/STAT [3–6]. How to pick which therapies and the combination/sequence in which to apply them will become ever more challenging as small differences in efficacy may result in a big impact on individual patient survival. Further complicating the treatment and decision-making process is the inter-patient heterogeneous nature of mCRPCs [7], so there is a necessity for rapidly predicting a specific patient’s response to administered therapies.

To generate new tools and approaches that could address this challenge in the clinical setting, a recent workshop was held at the H. Lee Moffitt Cancer Center and Research Institute [8]. This workshop was comprised of genitourinary surgeons, oncologists, biologists, pathologists, epidemiologists and mathematical modelers. The group focused on using available parameters and knowledge about mCRPC to capture the basic elements of tumor-bone interaction and the impact of both standard-of-care and new targeted therapies on the disease. The results of this integrated model demonstrate the power of the approach and suggest that enhancing the sophistication could significantly improve the overall survival for men diagnosed with mCRPC.

BACKGROUND

Mathematical and computational models are powerful tools that can be directly applied in the clinical setting for treatment guidance. These models can either use quantifiable outcomes and work backwards (top-down approach) toward inferences about mechanism or start from assumptions on mechanisms and calibrate parameters so that the outcomes emerge (bottom-up approach) [9]. Top-down models can help utilize existing data when very little is known about the biology of the disease. Statistical models such as nomograms are regularly used by clinicians to predict the probability of prostate cancer survival based on age, Gleason score, Karnofsky performance status, PSA, alkaline phosphatase and albumin levels [10]. Also the Linear Quadratic Model of radiation response is an established mathematical model that allows the radiation oncologist to design treatment schedules based on empirical radiation damage and repair rates [11]. Additionally, mathematical models have been used to optimize the scheduling of radiation therapy of GBM patients [12], and to predict whether leukemia patients can cease treatment and remain cancer-free [13]. For prostate cancer, the application of cell death rate analysis functions and PSA thresholds has also facilitated predictions of castration resistance emergence during intermittent androgen deprivation [14]. These models generally work by “fitting” their assumptions to existing clinical data in a top-down approach, but we will conversely use a bottom-up methodology utilizing known parameters to predict how cancers will behave over time. This type of model can incorporate the established biology of heterogeneous clones in prostate cancer and predict how each of those clonal populations respond to therapies and, interact with the surrounding microenvironment [15, 16]. We posit that this approach can not only yield novel insights about the biology of the disease but also help design new therapeutic approaches that can help delay or even overcome the emergence of resistance to known treatments.

Designing a mCRPC-Bone Microenvironment Interactome

Producing a useful mechanistic mathematical model of the treatment of heterogeneous metastatic disease requires the collective expertise of physicians, biologists and mathematicians. The mathematical model must be as simple as possible without losing significant complexity, be parameterized carefully with robust clinical and biological data and be easily implemented to provide rapid and reliable outputs that can help guide the medical oncologist in regards to treatment strategy. The model’s output relies upon the accuracy of its assumptions, so making false assumptions or neglecting significant elements can lessen the validity of a model’s results. By calibrating a model to fit within reasonable parameter ranges, one can determine how sensitive the results are to different parameters. However, the model itself can be used to test different assumptions.

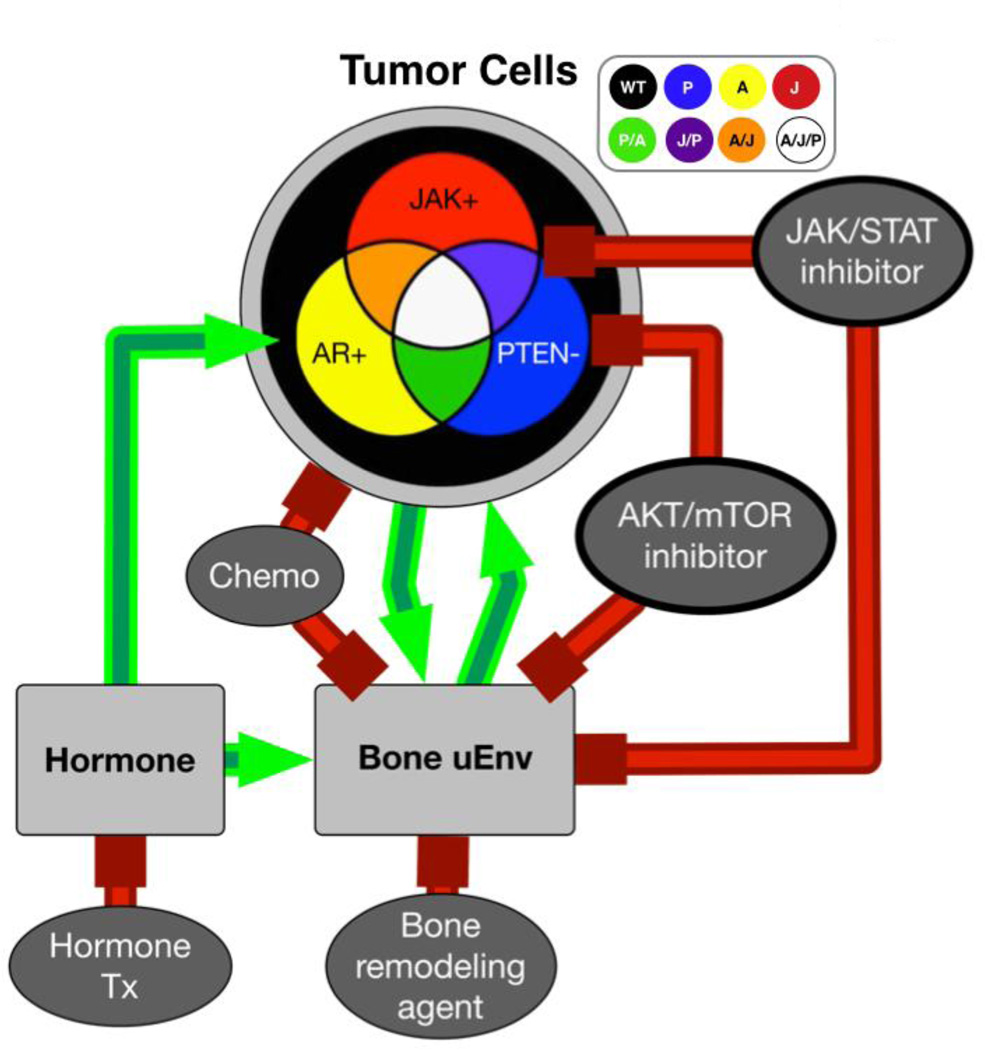
In this case, we consider a heterogeneous mCRPC. This heterogeneity translates into different clonal populations with varying genetic mutation content that in turn can lead to multiple phenotypes. These phenotypes could then plausibly have different growth rates, treatment susceptibility and interactions with the surrounding bone microenvironment (Fig 1A). mCRPCs can promote bone remodeling and formation that in turn generates a positive feedback loop known as the “vicious cycle” [17]. Elevated hormone levels can subsequently perpetuate this cycle. To capture patient-specific cancer heterogeneity, we modeled a cancer cell population that could have any combination of three common druggable mutations/alterations in signaling pathway activity. These included the androgen receptor (AR), Phosphatase and TENsin homolog (PTEN) and, Janus Kinase/Signal Transducers and Activators of Transcription (JAK/STAT) pathways. AR and JAK/STAT activity drives proliferation while loss of PTEN enhances AKT mediated cancer cell survival and proliferation. In the model, each cell may possess alterations in any of these molecules/pathways so that the in silico mCRPCs are potentially comprised of up to 8 permutations of cancer cell types, assumed to be present at observation and not acquired during further progression. These mutations can affect the proliferation rates and responses of the clones to targeted therapies (Fig. 1). Importantly, any number of mutations can be included in computational model but for the purposes of this example, we limited the number to three.

Figure 1.

Interactome demonstrating the interactions between mCRPCs that are comprised of multiple subtypes of cancer cell populations with the surrounding bone microenvironment and the response of each compartment to applied treatments. For this in silico example, mCRPC cell populations are either mutated individually for AR, JAK or PTEN, a mix of two mutations or, all three. mCRPC cells not harboring these mutations are illustrated as wild type (WT) population. The surrounding bone microenvironment is also considered wild type for each of the mutations being examined. Green arrows represent positive effects while red indicate negative or blocking actions.

From this interactome we estimated the baseline initial conditions (hormone levels, rate of bone remodeling and the heterogeneity of the mCRPC) and parameterized the interaction rates between them, which are represented as green stimulatory arrows or red inhibitory lines. The aim of the mathematical model example presented here is not to completely capture all the elements that characterize the heterogeneity of mCRPC and the surrounding microenvironment but only those that involve the therapeutic options that can be applied in the clinic. Importantly, more mutations/cell types and their effects can be added to or subtracted from the model foundation for further refinement. However, a novel aspect of this mathematical model is the consideration of the impact of applied treatments on the bone microenvironment and indirectly on the behavior of the cancer cells.

We examined the parallel effects of 5 therapies on this system to include in the interactome: hormone deprivation therapy (Hx), chemotherapy (Cx), a bone resorption inhibitor (Rx), an AKT inhibitor (Px) and a JAK/STAT inhibitor (Jx). Based on the literature these treatments can affect the tumor and the tumor microenvironment in different ways. For example, Hx treatment inhibits AR activity and in turn prevents tumor growth. Cx treatment can impact the survival of all cell types in the bone microenvironment. Rx treatment has an indirect affect on tumor growth by preventing bone turnover while the Px and Jx treatments are likely to only target cancer cells expressing those specific molecules in the tumor-bone microenvironment (Fig. 1). Once the interactome was established, we generated a system of first order linear ordinary differential equations (ODEs) to define these interactions in a way that would represent the number of each cell type, the hormone level, the amount of bone remodeling over time and the impact of treatment.

Designing and Parameterizing the mCRPC Computational Model

Mathematical modeling represents a way to integrate diverse clinical and biological data. Here we define a system of ODEs that integrates the changes in the tumor and the bone microenvironment over time with the application of specific treatments.

$${\dot{T}}_i=T_i(\underset{\text{proliferation}}{\underbrace{\alpha }}+\underset{\text{bone stimulation}}{\underbrace{\beta B}}+\underset{\text{JAK/STAT pathway}}{\underbrace{{\gamma }_J{m}_{J,i}(1-J_X{\tau }_J)}}+\underset{\text{AKT pathway}}{\underbrace{{\gamma }_P{m}_{P,i}(1-P_X{\tau }_P)}}+\underset{\text{androgen stimulation}}{\underbrace{{\gamma }_A{m}_{A,i}H}}-\underset{\text{chemotherapy}}{\underbrace{C_X{\tau }_C}})$$ (1)

$$\dot{B}=B(\underset{\text{tumor stimulation}}{\underbrace{\sigma \sum _{i=1}^8{T}_i}}+\underset{\text{androgen stimulation}}{\underbrace{\eta H}}-\underset{\text{chemotherapy}}{\underbrace{C_X{\nu }_C}}-\underset{\text{AKT inhibition}}{\underbrace{P_X{\nu }_P}}-\underset{\text{JAK/STAT stimulation}}{\underbrace{J_X{\nu }_J}}-\underset{\text{Rank ligand}}{\underbrace{R_X{\nu }_R}})$$ (2)

Equation 1 defines the tumor as the sum of the multiple tumor phenotypes (T_i, where i represents each phenotype combination with a mutation status (m_A,i, m_J,i, and m_P,i = [0,1] = [off, on] for AR, JAK/STAT and PTEN, respectively) that will grow and respond differentially to applied treatments (C_x, H_x, R_x, J_x, P_x = [0,1] = [off, on]) over time. Hormone therapy (H_x) is represented by reducing the hormone level (H) by 80% from baseline levels. Equation 2 describes how the bone microenvironment (B) is impacted by tumor cells, hormone stimulation, and treatments over time. These two equations are coupled so that the bone microenvironment influences the growth of the mCRPCs while the mCRPCs can impact the behavior of the bone microenvironment.

In order to solve the model equations, we utilized values obtained from the literature, information from clinicians in regards to how treatments are applied to patients and, in cases where the information available was abstract or missing, we used practical estimates and assumptions (Table 1). When no published data is available, empirical clinical and biological data can be generated to integrate into the model. For our example, we assumed that the initial mCRPC size was 1×10⁶ cells (minimum size detectable with current imaging technology) with a baseline-volume doubling rate 18 days [18, 19]. We then estimated the total number of cells in the bone marrow to be on average 7×10¹¹ cells and made the assumption that the patient would succumb to the disease when the cancer cells reached this number [20]. The rate of bone-stimulated tumor growth was estimated to be three times that of the tumor growth alone [21]. Based on pre-clinical and clinical information we also estimated the impact of the chosen therapies on cancer cell growth rates and on bone behavior [22–30]. Some of these values were derived from in vitro observations and were normalized to correlate with those obtained from in vivo studies. We next integrated estimates for all of the parameters in the ODEs except for the composition of the tumor, which is specific to the patient. Finally, with the mathematical model parameterized, treatment optimization can be achieved via genetic algorithms [31].

TABLE 1.

Parameters used to power computational model.

Parameter	Definition	Value	Reference
mJ,i, mP,i, mA,i	mutational status of cell type i	[off, on] = [0, 1]	-
Cx, Hx, Rx, Jx, Px	drug status	[off, on] = [0, 1]	-
α	proliferation rate	2.6 × 10−3 d−1	[18]
β	bone-to-tumor stimulation	2.6 × 10−9 d−1	[21]
σ	tumor-to-bone stimulation	2.6 × 10−9 d−1	[39]
γA	AR tumor stimulation	3.1 × 10−3 d−1/(ng/mL)	[18]
η	hormone-to-bone stimulation	2.5 × 10−3 d−1/(ng/mL)	b
H0	baseline hormone level (Hx off)	3.5 ng/mL	a, [40]
H1	hormone deprivation level (Hx on)	0.7 ng/mL	a, [40]
γP	PTEN tumor stimulation	4.3 × 10−4 d−1	b
γJ	JAK/STAT tumor stimulation	9.7 × 10−4 d−1	b
τC	Cx tumor inhibition	2.4 × 10−3 d−1	[41]
γ P*(1- τP)	Px tumor inhibition	2.1 × 10−2 d−1	b, [25]
γ J*(1- τJ)	Jx tumor inhibition	1.8 × 10−2 d−1	b, [23]
νR	Rx bone inhibition	3.1 × 10−1 d−1	[21,24]
νJ	Jx bone inhibition	1.0 × 10−3 d−1	[28]
νC	Cx bone inhibition	1.0 × 10−3 d−1	b
νP	Px bone inhibition	3.4 × 10−4 d−1	[27]
-	time step	1 d	-
-	treatment time	12 weeks	a
-	initial number of cells	106	[14]
-	initial bone density	0.13	a
-	bone marrow capacity	7×1011 cells	[15]

^aindicates information derived from clinicians while

^bis assumed data for which no empirical information exists at this time.

Finding Optimal Treatments with a Genetic Algorithm

Genetic algorithms (GAs) are optimization techniques whose design mimics Darwinian-type evolution. In a GA, a population of potential solutions to a problem is created, and through an iterative process, the solutions that better match or optimize the problem are selected, transformed and combined so that new, potentially better, solutions can be found. If properly designed, it is possible to ‘evolve’ the initial population of solutions so that after a number of iterations, an optimized solution in the population satisfies the constraints set by the designer [32].

To this end, we designed a GA that optimizes treatment options for a specific mCRPC patient. Each treatment option is characterized by a sequence of 12-week treatments. Although not a feature at the moment, it is clear that GAs can optimize not only the order of the treatments but also the duration of each. In its current implementation, each individual solution is a vector that identifies which of the 5 treatments is to be used at each 12-week interval. In order to evaluate the fitness of a given individual, i.e. sequence of treatments, we use a fitness function. This fitness function evaluates how a given sequence of treatments, encoded into a GA individual, maximizes the time until the number of cells fills the capacity of the bone marrow. After this evaluation, the GA produces a new generation of individuals in which optimal treatment sequences are retained while those that performed poorly during the evaluation are discarded. As the number of potential solutions considered at any given time is constant, the space left by poorer performers is replaced with new individuals generated from better responding patients. After each iteration, there is some alteration (changing a treatment in the sequence) to allow for variation. This process quickly produces individuals with more optimal treatment strategies that may improve with each generation.

RESULTS

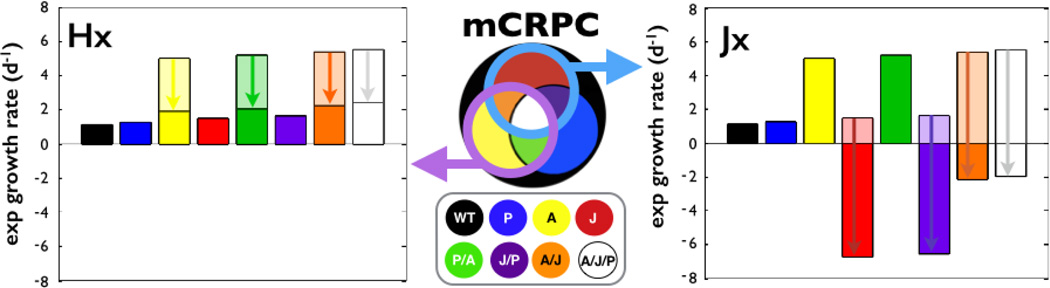
A key advantage of the approach is the ability to examine the effect of individual therapies on the growth of each mCRPC and also the ability to compare the efficacy of those therapies. For example, comparing Hx to Jx treatment in different monoclonal populations (only a single subtype of cells exist in tumor population) reveals that Hx impacts mCRPCs with the fastest growing clones while Jx, as expected, selectively eliminates those cancer cells dependent on JAK/STAT activity (Fig. 2). Overall, Hx affects those mCRPCs with cells that harbor AR mutations while Jx affects those with JAK/STAT mutations. Therefore, each treatment can target four different cancer cell populations but importantly to different net effects due to the influence of how the combination of stimulatory and inhibitory interactions under that treatment affect each tumor subtype.

Figure 2.

The response of monoclonal mCRPCs to continuous hormonal (Hx) or JAK/STAT (Jx) treatment. In this in silico example, both therapies impact cancer cells with a particular mutation and therefore, have the potential to impact the growth of 4 clones. The arrows illustrate the decreases in the growth rate compared to untreated. Clones with AR mutations (left panel) have the fastest growth rates under no treatment, but with hormone deprivation therapy, the growth rate is reduced. JAK/STAT inhibitor (right panel) not only reduces growth, but selectively eliminates cells with that mutation.

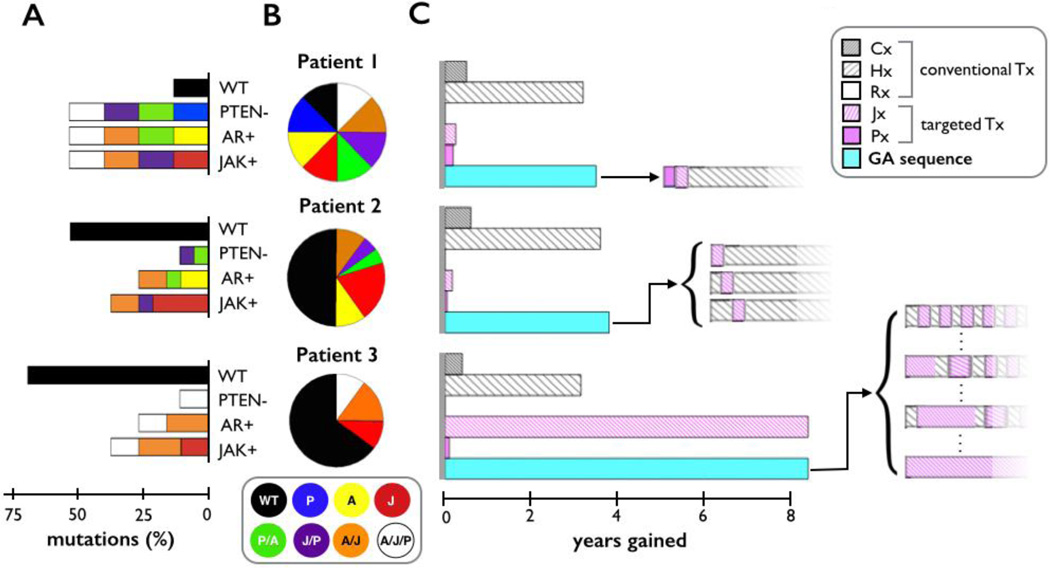
The more likely clinical scenario however, is that the mCRPC will be heterogeneous in nature and the choice of treatment will depend on the specific mix of cell subtypes identified in the patient biopsy. In the clinic, the initial degree of heterogeneity would be inferred from the patient’s biopsy and depend on the mutations of interest. To initiate the model, we assumed a potential worst-case scenario, where there’s a maximum degree of heterogeneity so that all cell subtypes are equally represented (Fig. 3A & 3B, Patient 1). The application of individual continuous treatments to this population revealed Hx to be the most efficacious with an increase in overall survival from the untreated case of 3.2 years (Fig. 3C, Patient 1). The targeted therapies (Px and Jx) enhanced overall survival by only 2.8 and 2.0 months, respectively. Cx performed slightly better by extending overall survival by 5.4 months. Interestingly, the model predicted that, although the inhibition of RANKL (Rx) reduced bone formation, it had little effect on overall survival, an observation consistent with clinical findings [33].

Figure 3.

The effect of continuous treatment or GA-derived treatment sequences on interpatient mCRPC heterogeneity. Three mCRPCs patients with varying degrees of mutational composition (bars) and cell subtype (pie charts) were generated (A). Patient 1 has an equal representation of all cell subtypes while Patients 2 and 3 have the same percentages of mutations but different distributions of cancer cell subtypes. The three in silico patients were then administered various treatments (B). Each Patient’s mCRPC response to continuous treatment (conventional and targeted) and GA optimized (blue bar) was assessed in terms of overall survival (years gained). GA braced bracket illustrates each therapy sequence and duration.

The efficacy of the applied therapies is critically dependent on the percent composition of mutations, but is also dependent on the distribution of cancer cell subtypes in the mCRPC models. Therefore, we next compared how the subtype distribution of the in silico heterogeneous mCRPCs affects outcomes. Patient 1 is initiated with an equal number of cancer cell subtypes. In this patient, each mutation is present in 50% of the cell population. The mCRPCs in Patients 2 and 3 have 35.1% JAK/STAT mutations, 25.1% AR mutations, and 10.25% PTEN mutations (Fig. 3A), but the actual cell subtype distribution of these mCRPCs is different (Fig. 3B). Results with single treatments illustrate that Hx efficiently treats Patient 2, which has a higher degree of heterogeneity and similar effects were noted in Patient 3 (Fig. 3C). In contrast, all of the mutated cells in Patient 3 had the JAK/STAT mutation and application of Jx treatment was substantially more efficacious than the Hx therapy (by 5.2 years).

Finding an optimal single continuous treatment for a specific tumor provides a good first approximation to how treat a patient, but we can also employ the GA to find an optimal sequence, in which several treatments can be utilized in an order that maximizes overall survival. In each case, the GA finds at least one sequence that is either equal to or better than the single treatment optimum. For Patient 1, applying Jx first then Px before continuous Hx resulted in a gain of 2.9 months over Hx alone. For Patient 2, applying one round of Jx within the initial 3 rounds of treatment extended life by 2 months. For Patient 3, continuous treatment of Jx was the optimal treatment, but we also found that up to 50% of the treatments could be switched with Hx in any order with no change in the outcome.

These preliminary applications of computational modeling identify that Hx is the most efficacious treatment strategy for mCRPCs in general and agrees with clinical findings using androgen deprivation therapies [34]. However, the model also identifies that there may be more optimal personalized treatment schedules for different mCPRC compositions. Applying our optimization algorithm to the patient with most heterogeneous tumor resulted in an optimized treatment schedule that is essentially the standard of care. But, in patients where there same mutations exist but there is a different distribution of cell subtypes, GA optimizations illustrate that the standard of care works best in one (Patient 2) and a targeted therapy works best in the other (Patient 3).

DISCUSSION

Herein, we have described examples of how combining hypothetical personalized genetic data from a patient with an evolutionary algorithm and a minimal mathematical model can be used to optimize a therapeutic strategy in patients with mCRPC. Iterating through a GA identifies treatment sequences that can reduce tumor burden and extend overall survival for a given patient. Unlike other novel models using top-down approaches to fine-tune equations that reflect clinical observations, the computational model here takes a bottom-up approach in parameterizing equations with known values to predict potential outcomes, outcomes that can be validated with retrospective or prospective in vivo studies. The results with this approach not only match the standard of care treatment using conventional therapies, but critically, allow for the incorporation of targeted therapies such as JAK/STAT, AR and PTEN. This method could provide a platform where other pathways, tumor phenotypes, and microenvironmental influences could be investigated.

The relatively simple model described herein predicts that hormone ablation (Hx) is the best option for extending overall survival for most tumors since it directly inhibits the growth of cells that are dependent on AR signaling and these cells have the fastest growth rate. This observation resonates with the results of extensive clinical trials using androgen deprivation strategies and comes to the same conclusion with a relatively straightforward computational model. Interestingly, chemotherapies were observed to only incrementally extend overall survival regardless of applying the therapy before or after hormonal therapy. The model also includes the potential impact of applied therapies on the bone microenvironment. Androgens have been shown to regulate bone formation, and therefore the potential impact of hormonal therapy on the process can be determined. This model is also a first approximation and the framework set up lends itself to refinement. For example, as we learn more about immunotherapies and immune cell interactions in the mCRPC bone-microenvironment, we can easily include immune components such as T-cells since clinical therapies (dendritic based sipuleucel-T for example) are being utilized for the treatment of mCRPC [35]. Further, we have defined the bone microenvironment as a single output (either bone is formed or not) and this could be further refined to take into account the impact of therapies specifically on osteoclast, osteoblasts and their precursors as we have previously shown [36]. An obvious additional test of the model could be in evaluating combinations of therapies to extend the overall survival of the patients, especially those with highly heterogeneous tumors.

A key revelation using this type of modeling approach was that the response of the mCRPCs was critically dependent on the extent of intra-tumor heterogeneity. The results identified logically that the more heterogeneous the cancer the less effective the targeted treatments would be in extending overall survival. The model also shows that it is not the total percentage of mutations within the tumor but the percentage of subtypes harboring those mutations that is an important factor in treatment efficacy and overall survival.

Incorporating GAs for the treatment of mCRPCs can also assist the medical oncologist in defining the optimal treatment strategy to apply to newly diagnosed patients. Each run of the GA is personalized for a specific tumor. In our example, we considered three mutations and illustrated the various ways these mutations can be dispersed across the cancer cells that comprise the mCRPC. Clearly, more mutations can be integrated into the model and the GA. The GA may also provide a way to bridge the gap between the measured patient-specific data and the actual subpopulation cell numbers required by the mathematical model. To provide dynamic real-time predictions at point-of-care using biopsy testing for these mutations and avoid bias, we can find an average by using many different versions of the patient that recapitulate the identified mutations of interest with various distributions of subpopulations. Each version of the patient can be evaluated for fitness of the individual treatment sequence and correlated with the average survival time. Further, the GA evolves a population of optimal treatment strategies. For example, in the case of Patient 3 (Fig. 3), the GA found many strategies that optimized patient survival to the same degree. This provides flexibility in strategy in case an alternative is needed due to treatment resistance or patient/physician preference. In Patients 1 and 2, the GA improved overall survival by several months compared to standard of care treatment findings that underscore the potential value of such models in the clinical setting. In this context, recent clinical evidence has identified how altering the sequence of standard of care therapies can improve overall survival by up to 12 months [37].

Clearly, understanding the heterogeneity profile of the mCRPCs will be important in parameterizing these models so they can ultimately be of use to the medical oncologist as they consider an optimal treatment strategy for the patient. To validate the model outputs, retrospective biopsies from patients with mCRPC combined with treatment and outcome information can be utilized. The number of cells in each subpopulation can be counted and the heterogeneity profile determined via automated quantitative analysis (AQUA). These parameters can then be entered into the model along with the actual patient’s treatment schedule to correlate patient outcome with model output. There are, of course, a number of caveats to the model presented herein. For example, the application of AKT inhibitors (Px) has been shown to abrogate androgen signaling and therefore, AKT inhibitors could directly impact androgen signaling in other clones that do not have PTEN mutations [38]. These indirect effects could be integrated into the interactome of future iterations of the model. It also is possible that the obtained biopsy does not capture the wide degree of mutational variability potentially present in the mCRPC and therefore, the initial data entered into the model may not provide an optimal treatment sequence. However, information obtained from the biopsy should still provide sufficient information so that the model and GA can provide a superior treatment strategy than standard of care alone. Another caveat is that it is likely that a patient with a visually detectable mCRPC could have occult metastases in other areas, raising the possibility that a computationally optimized treatment based on the heterogeneity of a single biopsy could have differential effects on other metastases. However, a recent report has identified that there is intrapatient similarity in regards to mCRPC kinase signaling pathways suggesting that multiple or occult metastases could respond in the same manner to applied therapies [7]. By retrospective validation and subsequent alteration of the biological parameters, in addition to prospectively “shadowing” clinical trials in patients diagnosed with mCRPC, we allow for the refinement of the method and its implementation as a valuable medical oncology tool in the clinic.

CONCLUSIONS

The treatment strategies pursued by the medical oncologist for the treatment of mCRPC are often based on NCCN guidelines, the patient’s medical history and their preferences. However, there is currently a paucity of information available as to how altering the sequence of treatments or adding targeted therapies will impact an individual’s mCRPC response. This is a challenge that is further exacerbated by the heterogeneity comprising each patient’s cancer. Herein, we have provided an example of how relatively simple computational models can be used in a predictive capacity to determine patient outcome in response to treatments. By viewing the disease in a more heterogeneous and interactive manner, we can have a better understanding of mCRPC and the effects of the available treatments on a specific tumor composition. Further refinement of parameters should yield powerful models that can assist the medical oncologist in the decision-making process. Such models will be especially important for predicting the impact of targeted therapies and the delivery of precision medicine for the treatment and cure of mCRPC patients.

ABBREVIATIONS

ADT

Androgen deprivation therapy

AR

Androgen receptor

GA

Genetic algorithm

JAK/STAT

Janus kinase /Signal transducers and activators of transcription

mCRPC

Metastatic castrate resistant prostate cancer

NCCN

National comprehensive cancer network

ODE

Ordinary differential equation

PSA

Prostate serum antigen

PTEN

Phosphatase and tensin homolog

RANKL

Receptor activator of nuclear kappa B ligand