Plant “electrome” can be pushed toward a self-organized critical state by external cues: Evidences from a study with soybean seedlings subject to different environmental conditions

ABSTRACT

In the present study, we have investigated how the low-voltage electrical signals of soybean seedlings change their temporal dynamic under different environmental conditions (cold, low light, and low osmotic potential). We have used electrophytografic technique (EPG) with sub-dermal electrodes inserted in 15-days-old seedlings located between root and shoot, accounting for a significant part of the individual seedlings. Herein, to work on a specific framework to settle this type of the study, we are adopting the term “electrome” as a reference to the totality of electrical activity measured. Taking into account the non-linear dynamic of the plants electrophysiology, we have hypothesized that the stimuli, as applied in a constant way, could push the system to a critical state, exhibiting spikes without a characteristic size, indicating self-organized criticality (SOC). The results from the power spectral density analysis (PSD), showed that the interval of the large majority of the β exponents were between 1.5 and 3, indicating that the time series, regardless environmental conditions, showed long-range temporal correlation (long memory for β≠0 and β≠2). The analyses from the histograms of the runs showed different patterns of distributions concerning the experimental conditions. However, the runs exhibiting typical spikes, mostly under low light and osmotic stress, showed power law distribution with exponent μ ≅ 2, which is an indicative for SOC. Overall, our results have confirmed that the temporal dynamic of the electrical signaling shows a complex non-linear behavior with long-range persistence. Moreover, the hypothesis that plant electrome can exhibit a self-organized critical state evoked by environmental cues, dissipating energy by bursts of electrical spikes without a characteristic size, was reinforced. Finally, new perspectives for research and additional hypothesis were presented.

Introduction

To face the constant challenges imposed by the changing environment, plants evolved a sophisticated system of perception, involving the capacity to sense many stimuli by specific sensors, processing information, and to respond by alterations in different scales of organization (molecular, physiologic and morphological). Insofar plants are modular organisms, the question about the integration of signals from the different parts of their body (from roots to shoots), have major relevance to the stability maintenance of the whole organization of plants under potentially stressful situations. Therefore, plants show an informational system constituted by a complex network of signal transduction from cell-cell to long distance communication, enabling integration of their body parts (modules), providing the ability to adjust their phenotype to different environmental conditions.^1-3

Among a plenty of signals with different natures,⁴ electrical signals are able to inform distant cells about local stimuli, triggering proper physiologic responses to a multitude of environmental cues.,^5,6 Studies linking electrical signaling with physiologic responses to environmental changes are often based on the analysis of action potentials (APs) or variation potentials (VPs), taking into account mostly parameters as frequency, amplitude, distance of propagation and time frame.^5,7,8,9 However, quite often mixed electrical potential waves are recorded, for instance, as result of overlapping APs and VPs (among other voltage variations), creating a complex web of systemic information in which several electrical signals may be layered on top of each other in time and space,¹⁰ which makes hard accessing a proper signal analysis.¹¹ Recently, Saraiva et al.¹² have demonstrated that electrical signals in plants, measured as time series of low voltage variations in whole tissues, can exhibit high complex dynamic patterns (actually, chaotic behavior instead purely white noise). Moreover, the complexity of the electrical signals showed dependence of the environmental stimulation (osmotic stress), exhibiting burst of electrical spikes following a power law (i.e. spikes without a characteristic size).

The complexity of electrical signals in organisms, emerging from a plethora of different processes in time and space, has been named as “electrome.”¹³ Electrome, a novel term created in analogy with genome, proteome, transcriptome and so on, can be used to describe the totality of the ionic currents in different scales of organization in biologic systems. It is a collective and versatile term to designate the electric dimension of living entities that is based on gradients of ions, which generate energy potentials. Thus, we can refer to cell electrome, tissue electrome, organ electrome, and organism electrome. Such term includes the ionic currents associated with APs, VPs and other ionic currents that propagate through cytoskeleton, into the same temporal scale. Together, the system formed by plasma membrane with the ionic channels and pumps, anchored by cytoplasm cytoskeleton, which is linked with the nucleus actin skeleton and DNA molecules associated with it, forms a complex “membrane-cytoskeleton-DNA.” This complex system transports, integrates and processes electrical and molecular signals that can stores information and engenders a genetic and cognitive memory that operate together.¹³

In plants, based on empirical studies,¹⁴ Debono¹⁵ have correlated electrophytografic activity (EPG) as resultant of an integration of intracellular APs derivate from synchronized “protoneural networks,” diffusing information at the whole plant level. EPGs are extracellular spontaneous surface potential variations, as well as evoked bursts of spikes recorded at the level of leaves or roots. Synchronized electrical activity of cells in plant tissues have been hypothesized by Masi et al.¹⁶ when electrical spikes were measured by microelectrode technique in root apex. The likely physiologic role of these EPGs is to contribute to the integrative properties of plants, allowing long-distance integration of signals. Accordingly, low voltage potential variations recorded at the level of group of polarized cells or tissues could participate to the fine regulation of physiologic functions of plants.¹⁵

In the present study, we have investigated how the low-voltage electrical signals of soybean seedlings change their temporal dynamic under different constant environmental conditions. Herein, to work on a specific framework to settle this type of the study, we are adopting the term “electrome”¹³ as a reference to the non-local electrophysiology measurements. Accordingly, in this study we have used EPG technique with sub-dermal electrodes inserted in 15-days-old seedlings,¹² supposedly representing the electrome of the whole plants insofar the measurements were performed in tissues (from epidermis to vascular vessels) located between root and shoot, accounting for a significant part of each individual seedling. Moreover, taking into account the non-linear dynamic of the plants electrophysiology, we have hypothesized that the stimuli, as applied uniformly producing a constant tension in the plants, could push the system to a critical state, exhibiting spikes without a characteristic size.

Originally, the concept of self-organized criticality (SOC) was presented as an attempt to explain the 1/f^β noise in nature, specially, the pink noise (β = 1).^17,18 In general terms, SOC is a ubiquitous phenomenon in nature regardless on the details of the physical system under study. For instance, earthquakes, sandpiles, droplet formation, dynamic of populations, and biologic evolution itself are systems that, under certain circumstances, can reach a self-organized critical state.^18,19 Systems that potentially can reach a self-organized critical state are constituted by multiple components interacting locally with their neighbors (for example, groups of cells connected by plasmodesmata) and, when subjected to a constant external perturbation, show responses without a characteristic length of scale. In the critical state, if we build an histogram of some physical variable x, we will observe the probability density function (pdf) will follow a power law $f\left(\left|x\right|\right)\sim {\left|x\right|}^{-\mu }, 1<\mu <3$, asymptotically when $\left|x\right|\to \infty$.²⁰ Recent studies with EEG in human brains have showed evidences of SOC,^21,22 as well as in plant electrophysiology.¹² We have suggested that SOC behavior could have the role to improve the efficiency of dissipation of disturbances, avoiding a catastrophic collapse of the whole system.

Results

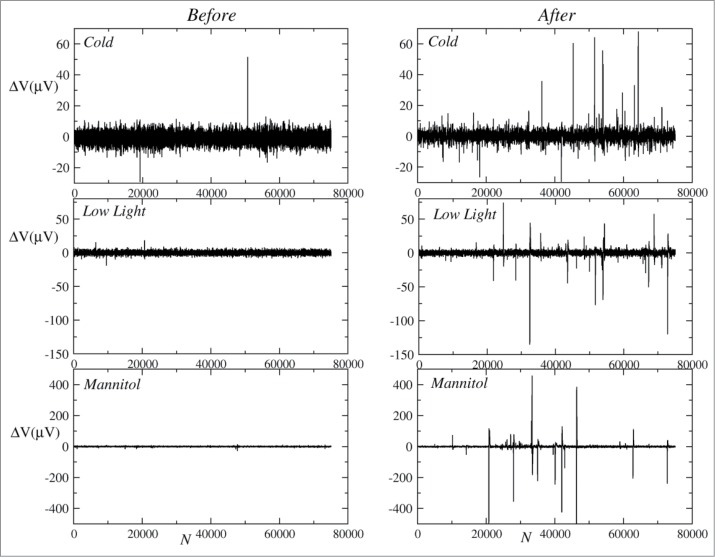
A naked-eye inspection of the original runs (Fig. 1) showed qualitative differences between the electrical signals before and after the environmental stimuli. While the baseline of all signals was, in module, 9.6 ± 1.2 μV, after stimuli, spikes up to 500 μV were observed, mainly in the treatments with low light and osmotic stress. The maximum magnitude of the spikes was limited by the standard voltage cutoff (500 μV) of the measurement protocol used herein, which was compatible to the results of spikes observed in the studies of Masi et al.¹⁶

Figure 1.

Representative original data of the ΔV (low voltage variation) time series before and after environment stimuli of the 3 treatments (cold, low light, osmotic stress by mannitol). To allow easier visual comparison before and after stimuli, the scale of y axes were adjusted to each treatment. N is the length of time series in arbitrary units. Sampling rate was f = 125 Hz thus, to convert x axes to seconds, divide N by f.

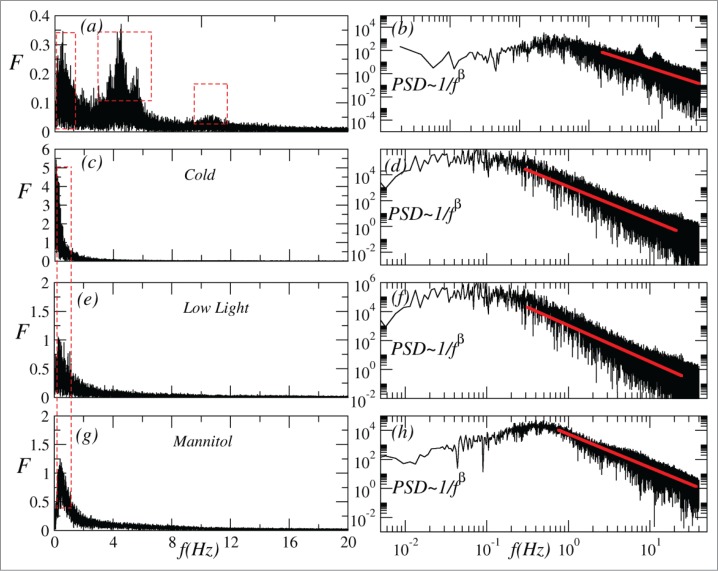
The spectral analysis by FFT (Fig. 2a, c, e and g) showed a remarkable difference between the runs before and after stimuli. Before the treatments (Fig. 2a) it was observed fundamental frequencies around 0.9 ± 0.6 Hz, a range of mean frequencies of 4.8 ± 0.9 Hz, and higher frequencies around 10.2 ± 0.9 Hz with lower amplitudes. However, after the 3 environmental treatments, only the fundamental frequencies remained (Fig. 2c, e and g).

Figure 2.

Representative spectrum analysis performed by fast Fourier transform (FFT) of time series recorded before (a) and after environmental stimuli (c) cold, (e) low light, (g) mannitol; and power spectrum density function (PSD) of time series before (b) and after environmental stimuli (d) cold, (f) low light, (h) mannitol. The doted red lines in the graphs a, c, e and g highlights the main frequencies observed in each treatment (fundamental frequencies between 0.5 and 1.5 Hz and, only in the runs before stimuli, medium frequencies around 4 Hz, and higher frequencies around 9 Hz). In the graphs b, d, f and h the β exponents were (n = 20): under cold conditions β = 2.85 ± 0.69, under low light β = 1.96 ± 0.30, and β = 2.58 ± 0.34 under osmotic stress; before stimuli β = 1.51 ± 0.21.

The β exponents calculated from power spectrum density function (PSD ∼1/f^β) indicated a range of colored noises (Fig. 2 b, d, f and h). The electrical signals recorded in the plants under controlled conditions (before stimuli) showed an average β = 1.51 ± 0.21, a typical reddened noise. However, the runs under the different environmental conditions can be described as brown (β = 2) to black noise (β = 3). Under cold conditions, β = 2.85 ± 0.69 (Fig. 2d), while under low light β = 1.96 ± 0.30 (Fig. 2f), and β = 2.58 ± 0.34 under osmotic stress (Fig. 2h). In the lowest frequencies, as expected for all PSDs analyzed, β values approach to white noise (β = 0), likely from instrumental origin. A paired t-Test showed that β values before stimuli were lower (P < 0.0001) than β values for the all treatments. Low light treatment exhibited the lowest (P < 0.001) β values among the 3 stimuli. There was no significant difference (P = 0.17) in β values between cold and osmotic stress treatments.

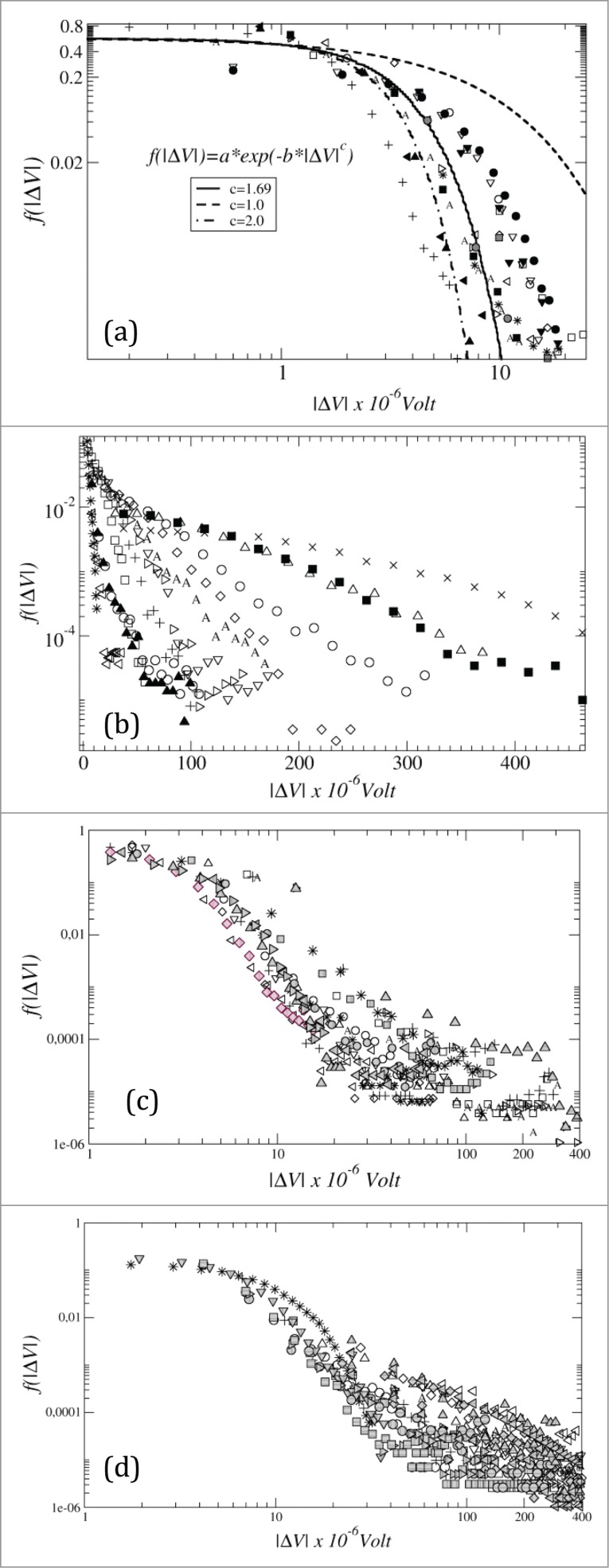
The log-log plots of the tail of the probability density function (pdf, $f\left(\left|\Delta v\right|\right)$) indicated different distributions for each plant condition (Fig. 3). The histogram of the runs before stimuli (Fig. 3a) showed distributions varying between a typical exponential (c = 1) and a Gaussian (c = 2) distribution, with exponent c = 1.69 ± 0.18. Overall, there is no a unique type of distribution fiting throughout the runs in the different conditions tested. However, no run showed a typical Gaussian distribution, as it was expected since the runs showed a long-range time correlation (Fig. 2). Nevertheless, it was possible to observe differences in the density of spikes among the treatments, with a high density of spikes in the runs scored under osmotic stress and a low density of spikes under cold conditions (Fig. 3).

Figure 3.

Probability density functions ((pdf, $\text{f}\left(\left|\Delta \text{v}\right|\right)$) of the tail of the of the runs (a) before stimulus (log-log), (b) cold (log-linear), (c) low light (log-log), osmotic stress (log-log). In (a) the dashed line represents the modeled exponential distribution (c = 1), the continuous line is the fit of the distribution $\left(\left|\Delta v\right|\right)=a*exp\left(-b*{\left|\Delta v\right|}^c\right)$, with c = 1.69 ± 0.18, and the dot-dashed line is the modeled Gaussian distribution (c = 2). Plots b, c and d have non-defined distribution.

Furthermore, analyzing closer the runs exhibiting typical spikes (ΔV values between 100 and 500 μV) we have observed that under low temperature the runs showed exponential distribution (straight line in the log-linear plot, r² ≅ 0.99) (Fig. 4a). On the other hand, the runs recorded under low light and osmotic stress showed typical power law distributions with μ = 2.5 ± 0.6 (Fig. 4b) and μ = 2.1 ± 0.3 (Fig. 4c), respectively.

Figure 4.

Histograms (probability density functions $f\left(\left|\Delta v\right|\right)\sim {\left|\Delta v\right|}^{-\mu }$) of the absolute values of the electrical signals |ΔV| plotted with the whole scored time series (N ≈300,000). Plot (a), cold treatment, showing typical cases of exponential distribution (straight line in the log-linear plot, r² ≅ 0.99); plots (b) low light treatment, and (c) osmotic stress by mannitol were plotted as log-log, showing typical power law distributions with the slopes μ = 2.5 ± 0.6 (b) and μ = 2.1 ± 0.3 (c).

Discussion

As previously suggested^12,15 the dynamic of global electrical signals in plants, emerging from the integration of local (cell-to-cell) electrical activity, is not a pure stochastic noise (white noise), and can be related to the physiologic state of the plants under different environmental conditions.

A variety of natural phenomena are well described by 1/f^β-type noises, with β ranging from 0 (white noise) to > 2 (reddened noise).,^19,23,24 In our study, the interval of the β exponents values (often from 1.5 up to 3) of the PSD functions (Fig. 2) indicated that the time series, regardless environmental conditions, showed long-range temporal correlation (long memory for β≠0 and β≠2).²⁵ This implies that the current value of the biologic signal (e.g. the variation of low voltage, as herein) co-varies not only with its most recent value but also with its long-term history (persistence) in a scale-invariant manner.²⁶ Insofar electrical signals in plants have been related to physiologic responses to environmental stimuli,^5,6 it is reasonable to hypothesize that the persistence in the electrical dynamics could affects the spread of the signaling in plant's responses to stimuli. Accordingly, our results of β exponents showed that (Fig. 2), under environmental perturbation, there was a trend for darker noises. According to Cuddington and Yodzis²³ darker noises (β > 2) are related with higher persistence, which could support for the electrical long distance signaling at whole plant level. The long-range time correlation indicates that the low-voltage signals of the plants are not a random noise, likely carrying meaning information for the whole plant organization.

Such as other non-linear complex phenomena, the dynamic of the electrome shall be considered as an emergent property, that is, a collective property of the system, which is non-reductive to the underlying mechanisms engendering single electrical events in the plasma membranes. Accordingly, De Loof¹³ holds that there are not 2 identical electromes. Each cell has its own electrome that is different from any other cells, even considering 2 cells derived from mitosis. This is reasonable insofar the daughter cells has different distribution of quantities and types of ionic channels and pumps, as well as different cytoskeleton structure. Thus, the dynamic that emerges from integration of electrical signals of each cell in a tissue must exhibits a high level of complexity. On the other hand, as observed herein, eventual bursts of spikes emerge as an outcome of self-organized collective behavior among groups of cells.,^15,16

To try elucidating the possible roles of the temporal dynamic of electrical signaling in the plant-environment relationship, our study brings evidence that plants can be pushed to a self-organized critical state under some specific situations. The power law distribution of the spikes in the log-log histogram (pdf), only in plants subjected to environmental stimuli supports this hypothesis. According to Bak et al.¹⁷ SOC systems are barely stable and, then, perturbations can cause a cascade of energy dissipation on all length scales, following a power law distribution (scale invariance), allowing efficient dissipation of disturbances throughout the system. Power law distributions, specifically when 1< μ < 3 (as in our results of plants under low light and osmotic stress), can be signatures of SOC states.^17,18,19

Recent studies with EEG in human brains have also showed evidences of SOC.^21,22 However, SOC has been associated to a normal brain functioning and disturbances, such as epileptic seizures attacks, deviate neuronal activity from a power-law distribution.²² Thus, while SOC seems to be the normal state for brain functioning, our results have suggested that the critical state in plants can be induced under stressful environmental conditions. Yet, it is not clear what is the meaning of SOC for biologic systems stability. By one hand, critical states can be associated to optimal information processing and computational capabilities (brain specialties)²² and, on the other hand, in the critical state, systems can dissipate energy (tensions) efficiently,¹⁷ which is a very important capacity for plants under stressful situations. Accordingly, the spectral analysis (Fig. 2) showed that, after environmental stimuli, the higher frequencies have disappeared, which could be an indicative of lower energy cost of the system, as a consequence of the energy dissipation efficiency. Under stressful conditions, saving energy is an efficient strategy for surviving. This was more evident especially under osmotic stress, since under lower temperatures the activity of the spikes was constrained insofar cold reduces the activity of the ion pumps, lowering electrical activity in the membranes.¹⁵

These findings, by one hand, brings new insights about the possible role of the electrical signaling in the coordination of fine tuning metabolic adjustments, as well as an important factor to dissipate excessive energy under stressful situations. However, by the other hand, precisely because the high complexity involved in the electrome dynamic, the understanding about the “mechanisms” that cause such complexity, as well as, the likely “mechanisms” by which electrical signaling affect the metabolic regulation may be unlikely to be completely uncovered. Despite of the well understood knowledge on the cellular mechanisms engendering electrical phenomena underlying APs and VPs,^7,8 a comprehensive understanding of the realm of the electrical phenomena in higher scales (from tissues to whole organism) can be far more difficult.¹³

Concluding remarks and perspectives

Our study supports the hypothesis that plant electrome can exhibit a self-organized critical state evoked by environmental cues, dissipating energy by bursts of electrical spikes without a characteristic size (scale invariance). Moreover, we have confirmed that the temporal dynamic of the electrical signaling shows a complex non-linear behavior with long-range correlation (memory).¹²

At least hypothetically for now, the persistence of the electrical signals observed in our study could support the hypothesis of a plant electrical memory, as claimed by Volkov et al.²⁷ in a study proposing a mechanism of short-term electrical memory in the Venus flytrap. Actually, memory has been considered an essential attribute allowing plants to face environmental stresses and to improve their learning responses in the future (such as acclimation or priming responses). Until now, different molecular mechanisms have been envisaged as the basis of plant memory, such as calcium waves, different epigenetic modifications of DNA and histones, and regulation of timing via biologic clocks.^28,29 Recently, it have been speculated that ionic currents self generated by cells could be one of the basis of cognitive memory from bacteria to human brain, including plants.¹³

Moreover, de Arcangelis and Herrmann³⁰ have proposed that learning can be a phenomenon occurring in a self-organized critical state. The proposed model was able to reproduce quantitatively the experimentally observed critical state of brains and, at the same time, learns and remembers logical rules. Additionally, insofar brain dynamics is influenced by neuroanatomical connectivity,²¹ learning was dependent of the plastic adaptation of the synaptic strengths in the neuronal network, affecting the appearance of critical states.³⁰ Insofar our results showed evidence of SOC behavior in electrical signaling in plants at the organism level, the likely relationship between SOC and learning it is an insightful “food for thought” for future discussion of plant learning modeling.¹

Finally, toward future investigation, we propose to study, based on non-linear time series analysis, the ubiquity of the complex behavior of electrical signaling in the plant responses to environment, testing for different species and different environmental cues. Maybe, a possible strategy could be by stimulating the plants with their own patterns of electrical signal and cross-testing between each other, comparing with expected physiologic responses (for instance, stomatal responses, metabolic changes and so on). Additionally, we have hypothesized a posteriori that the individual electrical signatures could be representative of the physiologic state of the plants that, by means of sophisticate techniques of patterns recognition, could provide a method to diagnose specific physiologic conditions of each individual, some similar to the electrical brain signatures in humans.³¹

Material and methods

Plant model and initial growth conditions

In this study, soybean [Glycine max (L) Merrill] cv. Intact Bt/RR was used as plant model. Seedlings were obtained from seeds germinated in 180 mL pots with vermiculite as substrate. The pots were kept in maximum capacity of water retention during both germination and early seedling development under controlled conditions in a growth chamber (Phytotron EL-101, Eletrolab, Brazil): day/night temperature of 28/22°C, respectively, 14h of photoperiod with 500 μmol photons m⁻² s⁻¹, and air humid around 60%. The plants were irrigated daily with ½ strength Hoagland nutrient solution, preventing, at same time, both starvation and salinization. The amount of irrigation was determined after weighing the pots with its maximum water retention and verifying the daily evaporation loss.¹²

Treatments

To accomplish the objective to test for SOC hypothesis, 15 days-old seedlings (after germination) were subjected to 3 treatments constituted of constant potential stress factors (osmotic, low light and cold). To observe spike-like responses with no characteristic size, it is essential that the disturbances be imposed as homogeneous as possible, creating a constant tension in the system, without driving the likely differences on magnitude of responses. Thus, we can ensure that the different sizes of the spikes are not evoked by stimuli with different intensities, being an outcome from the self-organization of the system.

The first experiment, with osmotic stress, was performed to try reproducing the findings in,¹² which have showed the first evidence of SOC in plant electrophysiology. Therefore, the seedlings were osmotically stimulated with a mannitol solution with water potential of −2.0 MPa, applied directly on the substrate of the pots, taking care to avoid any mechanical contact with the plants. The second experiment was performed with a low light treatment, reducing the light intensity in the growth chamber to 50 μmol photons m⁻² s⁻¹ during the measurements. The third experiment was performed reducing the temperature in the growth chamber to 15°C during measurements.

All the 3 experiments were performed with 20 replicates (plants) each.

Data acquisition

The bioelectric time series were recorded using a device of electronic acquisition with 4 channels (model MP36, Biopac Systems, US) with high input impedance. The sampling rate used was 125 Hz with 2 filters, one high-pass (0.5 Hz cutoff frequency) and a low-pass (1.5 kHz cutoff frequency). The signals were amplified with a gain of 20,000 x, allowing high resolution to capture the voltage variations ($\left|\text{Δ}v\right|\approx 500\mu V$ cutoff voltage) before and after stimuli, to perform suitable and reliable time series analyses.

With the objective to acclimate the seedlings to the conditions of data acquisition, one day before each experimental session sub-dermal needle electrodes (model EL452, Biopac Systems, US) were inserted into the region between the stem and the roots, below the first pair of simple leaves. Acclimation to the electrodes is required because their insertion induces action potentials and local fluctuations in potential variation, which is stabilized in a few hours with the disappearance of the evoked electrical variations.³² Each pair of electrodes (positive/negative) was inserted into the stem at a fixed distance (1 cm from each other) and 2–3 mm in depth, ensuring contact with the conducting vessels of the plants. The parts of the electrodes outside the plants were isolated from each other by a block of polystyrene. All bioelectric measurements were taken inside a Faraday cage properly grounded to prevent electric noise from the laboratory environment. A third electrode was attached to the structure of the Faraday cage to obtain adequate electrical grounding. In each experimental session, data were collected from 4 plants simultaneously, using a total of 20 plants in each treatment.

Data gathering was performed continuously during 1h before and 1h after application of the each specific environmental stimuli in the same plant for each replicate.

Time series analyses

In this study, we analyzed the time series ΔV = {Δv₁, Δv₂,…,Δv_N}, where Δv_i is the potential difference between the electrodes inserted in the plants, as described above. The series analyzed correspond to samplings with the total length N ∼75,000 points, corresponding to 600 s (using 125Hz) of the data measured before and after stimuli.

Therefore, first, a spectrum analysis was performed by fast Fourier transform (FFT) to decompose the series allowing observing dominant frequencies throughout the spectrum 125/2 Hz. Second, the power spectral density (PSD) was calculated, it describe how the power of the waves are distributed over frequency (ΔV² Hz⁻¹), to evaluate the exponent β when$PSD\sim 1/f^{\beta }, with$ β typically ranging from −1 to 3. For some values of the spectral exponent β indicates the noise color: white noise (β = 0), red (or pink noise) noise (β = 1), brown noise (β = 2) and black noise (β = 3).^23,24 Typically, a white noise contains an equal mix of all frequencies. Colored noises have a preponderance of frequencies of a given range. If a time series is dominated by long-range cycles, the noise is called reddened.²³

Additionally, a histogram (pdf) of the absolute value of the magnitudes of the spikes |ΔV| was plotted with the whole scored time series (∼1 h of sampling, N ≈300,000), and in some cases we have found a power law $f\left(\left|\Delta v\right|\right)\sim {\left|\Delta v\right|}^{-\mu }.$ The exponent μ can be obtained by slope the straight lines on scale log-log. According to Lévy flight model, when 1 < μ < 3 the random variable has infinite variance,^33,34 meaning that the data show scale invariance. Herein, in the cases when 1 < μ < 3 was observed in the runs recorded under stimulation, we have considered as an indicative for SOC behavior.

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.