Abstract.
Near infrared (NIR) light has been widely used for measuring changes in hemoglobin concentration in the human brain (functional NIR spectroscopy, fNIRS). fNIRS is based on the differential measurement and estimation of absorption perturbations, which, in turn, are based on correctly estimating the absolute parameters of light propagation. To do so, it is essential to accurately characterize the baseline optical properties of tissue (absorption and reduced scattering coefficients). However, because of the diffusive properties of the medium, separate determination of absorption and scattering across the head is challenging. The effective attenuation coefficient (EAC), which is proportional to the geometric mean of absorption and reduced scattering coefficients, can be estimated in a simpler fashion by multidistance light decay measurements. EAC mapping could be of interest for the scientific community because of its absolute information content, and because light propagation is governed by the EAC for source–detector distances exceeding 1 cm, which sense depths extending beyond the scalp and skull layers. Here, we report an EAC mapping procedure that can be applied to standard fNIRS recordings, yielding topographic maps with 2- to 3-cm resolution. Application to human data indicates the importance of venous sinuses in determining regional EAC variations, a factor often overlooked.
Keywords: baseline optical properties of tissue, effective attenuation coefficient (EAC or μeff), functional near infrared spectroscopy, diffuse optical tomography, brain imaging
1. Introduction
The most common application of near-infrared (NIR) light for studying the human brain is functional near-infrared spectroscopy (fNIRS). fNIRS is based on measuring changes in the optical properties of brain tissue in the NIR range (650 to 950 nm) to estimate fluctuations in the concentration of oxy- and deoxyhemoglobin associated with neural activity. This method is based on the differential absorption of NIR light of different wavelengths by these chromophores.1–6 fNIRS may be employed using a channel-based approach, relying on the modified Beer–Lambert equation, or by using diffuse optical tomography (DOT).7–11 In both cases, knowledge of optical baseline properties is fundamental to the accuracy of the fNIRS procedures.
Currently, in almost all cases, investigators assume that the basic optical properties of the tissue are constant across subjects and can therefore be estimated based on measurements conducted in previous, ad-hoc studies. In fact, much work has been done to quantify the reduced scattering and absorption coefficients of intact, living tissue, including the head and its tissue layers both in vivo and ex vivo.12 This work relies on specialized time-domain (TD)13,14 and frequency-domain (FD)15–17 recording systems. TD systems use very short pulses of light and rely on the distribution of photons’ arrival time to estimate the optical properties of the underlying tissue. However, these instruments are very expensive and are, therefore, limited to only a few source–detector pairs, severely limiting the “field of view” of the recording. FD systems use light modulated at radiofrequencies () and employ the frequency-domain multidistance (FDMD) method to estimate absolute absorption and reduced scattering coefficients.18–20
Although modern FD systems are capable of recording from many channels, the FDMD method is difficult to apply to large sampling areas, such as the whole human head, because this method requires calibrating the intensity and phase values obtained across multiple channels. This can be very laborious when many sources and detectors are used. In addition, large FD instruments are not very common. Thus, most of the relevant papers have reported data from only one or two small areas (typically on the forehead), and there has been no publication reporting a systematic measurement of variations of absolute optical parameters across the head. This paucity of data is particularly important because different types of tissues may vary in their optical properties and are distributed differently across the brain and across individuals.
Whereas TD or FD systems are required to compute the separate absorption and reduced scattering coefficients of tissue, far from the medium’s boundaries ( from the surface of the head), the effective attenuation coefficient (EAC or ) is sufficient for determining light attenuation in the diffusion regime19 and, therefore, provides an important part of the information about the optical properties of tissue required for practical applications. Moreover, measurement of the EAC at multiple wavelengths may provide further important information about the tissue status.
Here, we introduce a new procedure for estimating EAC based on a multichannel, multidistance approach. This procedure is a modified version of the FDMD method, similarly relying on the drop in light intensity as a function of source–detector distance (multidistance approach). However, critically, since this procedure only measures EAC (and not the reduced scattering and absorption coefficients separately) it does not require phase (or time-of-flight) information and, using averaging and linear decomposition analysis, it can avoid calibration procedures. Here we show that, by applying this method to local subsets of a relatively large number of channels (20 or more), we can derive low-resolution topographic maps of EAC across the head. Importantly, this approach can be based on the same data and subjects collected for fNIRS studies and can also be used with the more affordable continuous-wave (CW) instruments, which only record changes in intensity and are commonly available in the fNIRS research field. The major limitations of this approach are that (a) the information retrieved lacks depth characterization and (b) the EAC estimates have limited spatial resolution (2 to 3 cm).
Our procedure relies on an equation [Eq. (1)] that links light decay, as a function of distance from a source, with the EAC.21 This equation was derived for a semi-infinite, homogeneous medium. The human head is of course neither semi-infinite nor homogeneous. Although the FDMD procedure has been applied successfully to the human head when sampling small volumes,16 tissue inhomogeneity may lead to errors in the computation of EAC for large areas (see Ref. 22 for similar problems when using FD methods to estimate the absorption and reduced scattering coefficients of tissue). Therefore, here we will assess how departures from homogeneity influence EAC estimation. We will also consider the problems generated by departures of the head’s geometry from that of a semi-infinite medium, by considering them as problems of “local curvature.”
When the multidistance method is used on multisource, multidetector data recorded in vivo, some issues need to be considered. One important problem is that the range of light intensities can vary widely across different source–detector distances (by a factor of up to , if the range of distances is on the order of 40 to 50 mm). This range is greater than the dynamic range of the apparatus used for the measurement (photo multiplier tubes, or avalanche photo diodes, APDs, coupled with A/D converters), which is typically on the order of , leading to either ceiling or floor effects in the data. To address this issue, we typically combine data from detectors with different amplification factors. This procedure, however, introduces the problem of how to combine intensity measurements obtained from different detectors. This problem can be overcome by indirectly estimating the intensity of the light reaching the detectors from another feature of the data—the quantum/shot-noise inherent to recorded data, caused by random variations in the arrival time of photons at the detector.23 With high internal gain detectors such as PMTs or APDs, if a reasonable number of photons are detected, quantum/shot-noise is the major source of variance in intensity data at high frequencies (). At lower frequencies, variance over time is also determined by other factors, such as physiological phenomena (e.g., arterial pulsation, respiration, or movement artifacts). The relationship between quantum/shot noise and the number of photons detected is known and can be expressed by a simple equation [see Eq. (3) in Sec. 2]. If detector gain remains constant across multiple detectors, this procedure is still valid.
When very low numbers of photons reach the detectors, the thermal noise of the electronics within the detector system becomes the main source of variance in the data. However, channels with low signal levels can be easily identified and excluded from the EAC computation because the slope of the log noise by distance function becomes flat. We thus decided to use the signal-to-noise ratio (i.e., the coefficient of variation) of the intensity data to estimate the amount of light detected. This procedure allows for an expansion of the range of source–detector distances employed up to .
A second issue that arises with recorded data is the variability of the light injected and detected due to differences in source and detector efficiency and optode-scalp coupling variability (henceforth we refer to this problem as optode-to-scalp coupling, O-S coupling). In previous applications, limited to measuring the optical properties of only one small area of the head, variability in O-S coupling could be typically controlled for by using only one detector and multiple calibrated sources.20 In our approach, which aims at mapping these properties across the head, we need a different approach. Specifically, we dampen the effect of O-S coupling variability on EAC estimation by increasing the number of sources and detectors used for each EAC computation. In fact, if the number of independent optodes is sufficiently high, the coupling efficiency can be considered a source of Gaussian random noise (an assumption tested in this paper based on in vivo recordings) and the influence of O-S coupling can be reduced. Averaging and postprocessing correction procedures based on estimating the variance in the log intensity due to O-S coupling can also be used to further reduce this problem. When performing regression analyses, at a fixed level of noise, the greater the range of the independent variable, the smaller the error. For this reason, we employed optical montages with a wide range of source–detector distances (20 to 60 mm).
Once obtained, EAC measures can be used to determine accurate optical values to describe light diffusion across the head (forward models)24 and potentially for other applications. Current approaches to the generation of forward models employ anatomical information from T1-weighted (T1w), and sometimes T2-weighted (T2w), magnetic resonance images (MRI) to segment the head into four or five compartments [skin, bone, cerebrospinal fluid (CSF), gray matter, and white matter], each of which is assigned different optical properties, which in turn are estimated based on previously published values.25 This approach generates a nonhomogeneous model of the baseline optical properties of the brain. The major limitation of this approach is that the anatomical model is applied without verifying that it accounts for the actual variations in optical properties that occur across the head. For instance, the lipid content (and therefore the scattering properties) of the skin layer may vary significantly as a function of age and gender. Even more importantly, this model ignores components, such as the vascular bed and large venous sinuses, which are not visible in typical structural MR images but can potentially have a great influence on the optical properties of the human head because of their high absorption. Actual measurement of the EAC properties of tissue may help address these issues. For example, a particular model can be validated at a low level of resolution by comparing simulated estimations of EAC with EAC estimated from in vivo data and with the same optode layout. Note that, because of the low resolution of the procedure and the heterogeneity of the head, the validation would be effective at a coarse level of resolution. However, gross inaccuracies in the model utilized could be easily identified by this procedure.
2. Methods
The current paper reports a series of studies, based on simulation and real data processing, designed to introduce and test the accuracy of the EAC mapping procedures we developed. An application of the algorithm is also presented.
First, we describe the problem of EAC estimation and mapping using simulated recordings. This section includes
-
1.
Computation of EAC estimates in a semi-infinite geometry in a homogeneous medium.
-
2.
Quantification of the error introduced on the estimated EAC when considering nonflat geometries.
-
3.
Demonstration that local variations in EAC can be accurately retrieved spatially using a regional approach.
Second, we describe how this approach can be applied to real data recorded both in phantoms and in vivo. Specifically, this section includes
-
1.
Demonstration that accurate EAC estimations can be obtained for real high-density data using a shot-noise approach, regression procedures, and O-S coupling estimates. This was accomplished using both finite element model (FEM) simulations and data recorded in a phantom with known optical properties.
-
2.
Application of the EAC mapping procedure to data recorded with a high-density optical montage covering most of the scalp of five young adults and testing of the procedure’s reliability.
Third, we use this procedure to test whether current head models accurately predict the distribution of optical parameters observed in human heads. Specifically, we are interested in determining whether major variations in EAC across the head may be due to the presence of large veins in intracranial areas (venous sinuses). The influence of veins is not considered by current models of the optical properties of the head, which include only other types of tissue (i.e., skin, skull, CSF, gray and white matter), probably due to the expense and inconvenience of obtaining MR venograms and arteriograms.
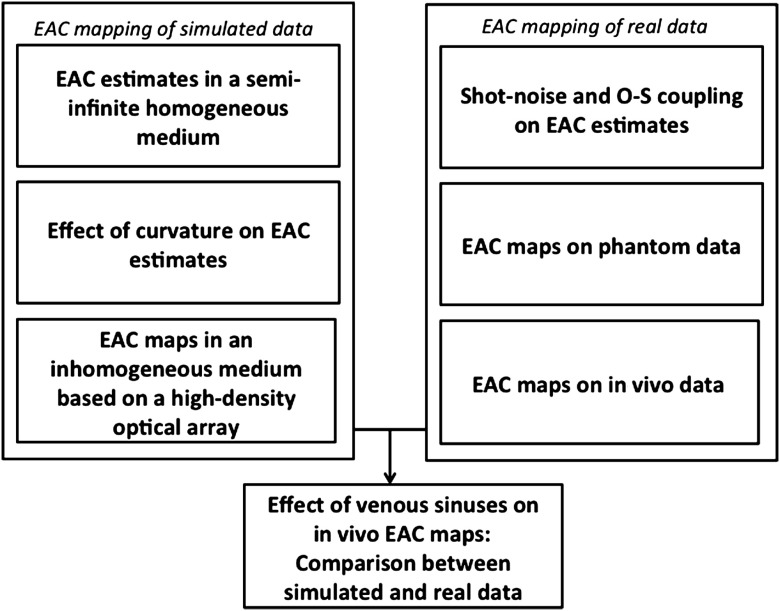
For our analyses, we used three types of data: simulated data based on various types of analytical and FEM models varying in their level of realism (e.g., semi-infinite slab models, nonuniform models, and realistic-head models derived from MR images), phantom data obtained from physical models with optical properties intended to mimic the human head, and data recorded from human subjects. The choice of the type of data used for each analysis, including the number and arrangement of sources and detectors (montage), was dictated by the question asked. A flowchart summarizing the paper’s structure is shown in Fig. 1.
Fig. 1.
Flowchart of the paper’s structure. EAC, effective attenuation coefficient; O-S, optode-scalp coupling.
2.1. EAC Computation
EAC estimation relies on the known exponential decay in optical fluence rate as a function of distance from the illumination point on the tissue surface. The slope (i.e., the exponential factor linking optical fluence to source–detector distance) of this decay function is determined by the optical properties of the tissue (and, more precisely, by a combination of the absorption and reduced scattering coefficients of the tissue, EAC), as well as by its geometric properties and boundary conditions. Specifically, for a semi-infinite, homogeneous medium with zero boundary conditions, the CW reflectance recorded at a distance from a source is linked to the EAC through the following equation (derived from Ref. 21):
| (1) |
where is a factor that depends on but does not depend on distance and is affected by source power and detector efficiency, and is the EAC defined as in Ref. 21
| (2) |
where and are the absorption and reduced scattering coefficients, respectively. Note that, in diffusive media where , the EAC can be considered proportional to the geometric mean of absorption and reduced scattering coefficients. Equation (1) is valid when ( in vivo), making the left-hand side of the equation linear with . With these simplifying assumptions, it is possible to retrieve information about the EAC of the tissue investigated using a multidistance approach by regressing the log of the light intensity (multiplied for the term) as a function of source–detector distance [Note that a similar approach, based on a point source (a laser source) but a wide view detector (a CCD camera) is employed by a technique called “spatially resolved diffuse reflectometry” (SRDR).26–31 However, because of the large dynamic range required by the exponential decay of light as a function of distance in a turbid medium, SRDR is limited to study the light attenuation within the first 10 to 15 mm from the source where the light intensity decay is not linear, rendering the separate quantification of reduced scattering and absorption possible for very superficial structures. Differently from SRDR, here we used the standard approach employed by diffuse optical methods, in which separate “single point” detectors are employed for the measurement of the radial dependence of light attenuation around a source. The advantage of this approach is that it allows us to employ different dynamic ranges for different detectors, thus greatly expanding the total dynamic range of the measurement. As a consequence, we can study a large range of source–detector distances (from 20 to 60 mm). Further, rather than focusing on short radial distances, we examined longer source–detector distances (greater than 20 mm), which are more sensitive to optical properties of deep structures. Using a 20- to 60-mm interoptode distance range, the log of light decay can be considered linear, thus greatly simplifying the problem of accurately estimating its slope.]
2.2. Light Modeling
NIR light propagation in biological tissue is well approximated by the diffusion equation.32 In order to test our assumptions and to run comparisons between simulations and real results, we used both analytical solutions33 and FEM approaches applied to the diffusion equation. 34
For FEM simulations, high-resolution meshes (maximum tetrahedral ) were generated using the MATLAB® function iso2mesh35 for homogeneous slab geometry, homogeneous spherical geometry, and heterogeneous head geometry. The heterogeneous head geometries were based on segmented T1w MR images. Segmentation of subjects’ heads into skull and scalp, CSF, white matter and gray matter [an example can be seen in Fig. 11(b)] was performed using statistical parametric mapping functions applied to T1w images.36 Baseline optical properties (, , and refraction index ) of the tissues at the relevant wavelength were taken from previous papers.30,37 A combination of T1w and T2w segmentation is required to differentiate skull and scalp. Here, for practical purposes, and given the similarities of the optical properties of skull and scalp, we only used T1w images and attributed the skull’s values to both structures. Optical properties vary considerably more among skull, CSF, and brain. The optical values at the wavelength of interest (830 nm) were set to the following values: scalp and skull: , ; CSF: , ; gray matter: , ; white matter: , . The refraction index was set at for all compartments, simulations, and mediums considered. In order to improve the heterogeneous model, veins were added to the T1w segmented structures in some simulations. Veins were identified using thresholded, high-pass filtered MRI venograms (Gaussian filter, full-width half-maximum: 15 mm, threshold: 15% of maximum value). These venograms were then aligned to the T1w image and, when included in the model, the optical properties of the veins were set to , (obtained from Ref. 38). When included in the model, the vein compartment substituted some of the CSF layer.
Fig. 11.
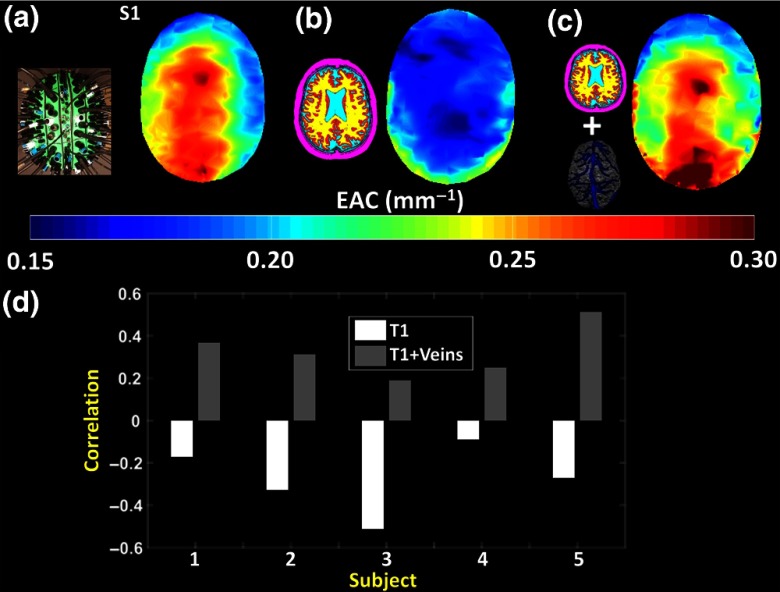
(a) Recording helmet seen from the top (inset); EAC map (top view) obtained from one participant (S1); (b) MR T1w segmentation of the same subject (inset; purple: scalp and skull; turquoise: CSF; red: gray matter; yellow: white matter); simulated EAC map (top view) based on a standard four-layer model of optical tissue properties, derived from the segmented T1w image of the same subject; (c) MR T1w segmentation combined with the MR-derived venogram of the same subject, superimposed over a gray matter rendering (inset); Simulated EAC map (top view) in which the veins have been added to the four-layer model. (d) Spatial correlations between recorded and simulated EAC maps for each subject. Positive and statistically significant () correlations were obtained for each subject when veins were added to the model. Negative correlations were instead obtained when only the T1w-segmented structures were considered.
The FEM software NIRFAST39 was used to model the light propagation through the investigated medium, both for homogeneous finite geometries and heterogeneous heads. NIRFAST was used to compute the boundary data for a given optode distribution when simulations were employed.
2.3. EAC Values
EAC values, defined in Eq. (1), were computed using a more general and accurate solution of the diffusion equation33 as a function of optical parameters when a simple semi-infinite geometry is employed (considering source–detector distances from 20 up to 60 mm). The linear assumption was tested by performing regression analyses on simulated data based on a set of different baseline optical properties covering most of the range commonly observed in human head tissues.
EAC is computed based on interoptode Euclidean distances, but its estimated value can also be affected by surface geometry. To test the effect of a curved surface, EAC was estimated using FEM. A spherical medium was generated with constant optical properties (, ) and different curvatures (simulated by sphere radiuses ranging from 50 to 150 mm). The bulk absorption and reduced scattering coefficients were chosen to represent commonly accepted average values of optical properties of the head in the NIR range.38 The range of sphere radiuses was chosen to approximate adult human head curvatures. Different light intensities were computed by moving a source relative to a fixed detector on the sphere surface. The linear assumption was tested by computing regression analyses for simulations based on a set of surface curvatures covering the range likely to be observed in normal adult human heads.
2.4. Construction of Topographic EAC Maps from Two-Dimensional Optode Array
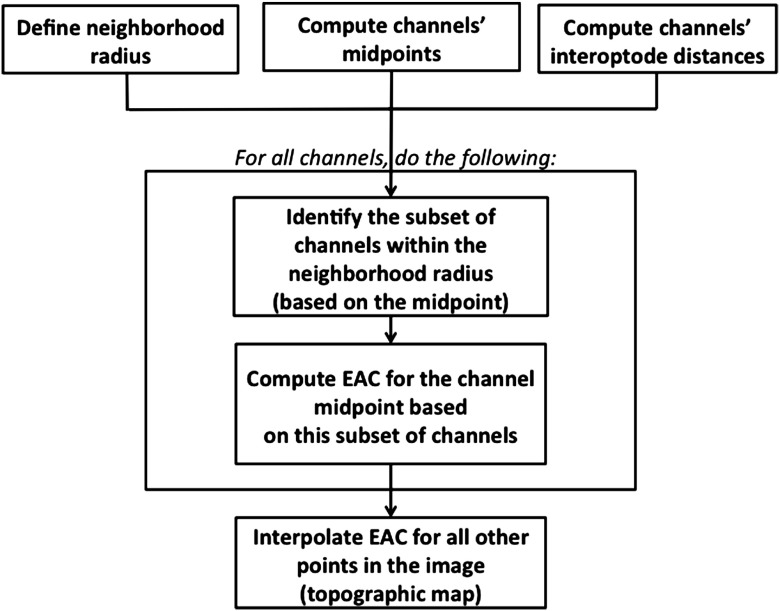
In order to quantify local variations in EAC using a topographic two-dimensional (2-D) approach, we developed an algorithm that computed EAC for each channel (source–detector pair) using subsets of channels in close proximity (neighbors) to the channel being estimated. A flowchart of the procedure is reported in Fig. 2; a more formal description of the algorithm is as follows:
Fig. 2.
Flowchart of the procedures used for EAC mapping.
-
1.
Locate the ’th channel center (the midpoint) for the channel composed by the ’th source at position and the ’th detector at position as: , where is the set of all the channels considered in the measurement.
-
2.
Estimate interoptode distance for the ’th channel composed by the ’th source at position and the ’th detector at position as: .
-
3.
Define a neighborhood radius .
-
4.
Define a subset of channels for the ’th channel such that the ’th channel where , .
-
5.
Compute at location for the channel using Eq. (1) and the subset of channels .
-
6.
Obtain topographic images by cubic spline interpolation of the values among all channels’ centers .
The number of channels considered for each EAC estimate can be adjusted by modifying the neighborhood radius , thereby affecting (in opposite direction) the accuracy of EAC estimation and the resolution of the topographic image. The effect of varying was investigated in some of the analyses.
The performance of this image reconstruction process was tested using simulated FEM data. Simulations were based on a homogeneous slab medium (, , ) with a cylindrical inhomogeneity (10 mm diameter parallel to the investigation surface, up to 40 mm depth, ) at the center of the cube face. One face of the cube was covered by a square grid of optodes [alternating source and detector fibers with a 15-mm minimum interfiber distance, see Fig. 3(c)]. Only channels with source–detector distances and were used for the analysis. The accuracy and resolution capabilities of the algorithm were estimated using different neighborhood radiuses.
Fig. 3.
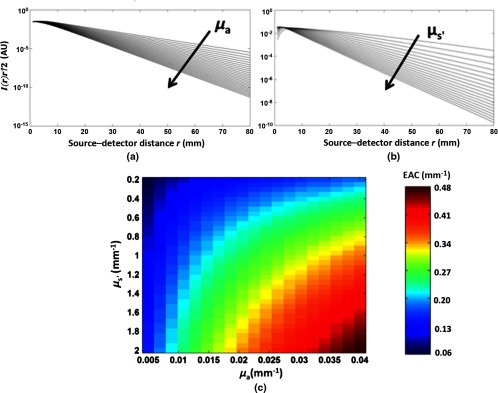
(a) Analytic solutions for light reflectance [multiplied by the term, left-hand side of Eq. (1)] as a function of source–detector distance for a semi-infinite homogeneous medium (semilogarithmic plot). Different curves represent different absorption coefficients of the medium (from to , in steps of , arrow depicting ascending values). The reduced scattering coefficient was fixed at . (b) Analytic solutions for light reflectance [multiplied by the term, left-hand side of Eq. (1)] as a function of source–detector distance for a semi-infinite homogeneous medium (semilogarithmic plot). Different curves represent different reduced scattering coefficients of the medium (from to , in steps of , arrow depicting ascending values). The absorption coefficient was fixed at . (c) EAC estimates obtained using a multidistance regression approach using interoptode distances between 20 and 60 mm. The EAC estimates are reported as a function of the absorption and reduced scattering coefficients (from to and from to ).
2.5. EAC Estimation in Recorded Data
2.5.1. Intensity estimation in recorded data
In order to enable comparisons between intensity values obtained from detectors with different amplifications, we used indirect measures of light intensity obtained from estimates of signal-to-shot noise ratios. This procedure is accurate when physiological variability is small with respect to shot noise. This is true for frequencies above 10 Hz, where even the higher frequency components of the heartbeat signal are negligible. We therefore estimated the light intensities from the computed signal-to-shot noise ratio as23
| (3) |
where is the amount of light detected, var is the variance operator, is the electrical signal recorded by the photodetector above 10 Hz, is the average electrical signal, and SNR is the signal-to-noise ratio of the recorded signal.
Note that when a CW system is used, is the relative change of the continuous component of the light recorded. However, this approach is general and can be applied to other measured quantities when more complex instruments are employed. For example, when an FD system is used, the SNR can be estimated at a particular modulation frequency as power or phase variability. In fact, although different signals can have slightly different sensitivities to physiological noise, when shot noise is dominant () the results are practically identical (if no sources of ambient noise are present).
This procedure can be applied when detected light intensity is above a minimum level. When light intensity is very low (i.e., low SNR), other sources of noise (such as thermal noise) become stronger than shot noise, invalidating Eq. (3). However, the SNR as a function of interoptode distance becomes flat when thermal noise becomes dominant. This property was used to identify the maximum useful interoptode distance in the real data.
2.5.2. Effects of O-S coupling on EAC estimation
Another important issue when dealing with recorded data is that different optodes generally have different coupling and efficiency levels. Generally, this problem requires using only one detector and many, phantom calibrated, sources. This procedure is difficult to apply to real data as the O-S coupling obtained in phantoms may not be easily replicated when placing the optodes on an actual human head. However, if combinations of multiple sources and multiple detectors are used simultaneously for each EAC computation, the effects of variations in O-S coupling on EAC estimation can be drastically dampened.
Mathematically, this problem can be conceived as the estimation of the standard error of the slope in a univariate regression analysis. In this case, the standard error of the slope can be expressed as
| (4) |
where is the number of samples, is the ’th residual of the regression analysis, is the ’th independent variable, and is the average value of the independent variable. Note that, in this particular case is the estimate of the standard error of the EAC, is the number of channels used for each EAC computation, and and are the ’th interoptode distance and the average interoptode distance, respectively. This equation is valid if the distribution is Gaussian. We investigated the standard error of the slope as a function of the intensity of the residuals and number of independent samples (number of channels in our case) by fixing the interoptode distance range between 20 and 60 mm (i.e., the ranges we used for in vivo measurements).
A further statistical correction to O-S coupling can be introduced. Specifically, the effect of O-S coupling should be equivalent for all those channels that share the same source or the same detector, independently of source–detector distance. In Eq. (1), this effect is equivalent to changing the value of (intercept). In other words, the effect of O-S coupling can be modeled as the effect of a covariate and can be removed using a covariance analysis. A critical requirement, however, is that O-S coupling can be accurately estimated from the data.
This problem can be expressed by considering the intercept factor in Eq. (1) as the algebraic sum of three factors:
| (5) |
where reflects local scattering and absorption together with the average O-S coupling while and reflect the O-S coupling variability for a particular channel.
To dampen the effects of and , we assume that is constant across all channels used to compute a local value of EAC (i.e., we assume the tissue to be locally homogeneous over the area identified by the selected neighborhood radius) and that the averages of all and values are equal to 0. We can therefore estimate by entering all channels (irrespective of their source and detector) in the regression procedure using
| (6) |
where is the estimated light intensity, is the interoptode distance, is the average log light intensity (multiplied by the term), is the average interoptode distance, Cov is the covariance operator, and Var is the variance operator, considering in the simple regression procedure, where is a channel and is the set of all the good channels used in the measurement.
The values of and for each source and detector are estimated by computing separate regressions including only the channels having that particular source (in the case of ) or that particular detector (in the case of ), using Eq. (7) (for ) and Eq. (8) () written as follows:
| (7) |
where is the estimated amount of light, is the interoptode distance, is the average log light intensity (multiplied by the term), and is the average interoptode distance considering where is the set of all the good channels using a specific source .
| (8) |
where is the estimated amount of light, is the interoptode distance, is the average log light intensity (multiplied by the term), and is the average interoptode distance considering where is the set of all the good channels using a specific detector .
Once these values are computed, we can subtract the effect of and from the intensity value obtained for each channel, and effectively covary out O-S coupling from the regression. This procedure results in a reduction of the error of the EAC (slope) estimate. Note that this procedure is effective when each source or detector is used in a large number of channels (the intercept estimation needs to be accurate).
Note that this approach implies computing a single value of and for each source and detector, even if the channels used for their computation extend over an area that may be bigger than that used to estimate EAC values. Thus, local variation in over this area may, in principle, introduce error in the estimation of and . However, we found this type of local variability in to be quite small compared to the variability in and found in vivo. For this reason, this procedure is likely to reduce the error in the estimation of EAC.
We ran a simulation to demonstrate the impact of including different numbers of channels in the regression analysis involved in EAC estimation, as well as the effect of statistical correction on the regression intercept. In this simulation, O-S coupling was modeled as a random effect on log light intensity (Gaussian distribution with a and , chosen to mimic realistic in vivo conditions). Note that the Gaussian assumption of O-S coupling was tested in this paper and strengthened by an outlier removal procedure. This simulation was based on an alternating grid of 16 sources and 16 detectors (256 channels and 15 mm minimum interoptode distance) positioned on the surface of a homogeneous semi-infinite medium. Baseline optical properties were set to: absorption , reduced scattering coefficient . EAC values were computed by using random subsets of the original channels, varying in number between 5 and 200. This channel randomization procedure was repeated 100 times, to assess the variability of the EAC estimates. EAC values were also computed before and after O-S coupling correction.
2.5.3. Optical and MRI data recording
Optical data were acquired from phantoms and five human subjects with a multichannel FD commercial NIR spectrometer (ISS Imagent™, Champaign, Illinois) equipped with 128 laser diodes (64 emitting light at 690 nm and 64 at 830 nm) and 24 photomultiplier tubes (PMTs). Time multiplexing was employed, so that each detector picked up light from 16 different sources at different times within a multiplexing cycle. The sampling rate was set to 39.0625 Hz. Light was sent to the scalp (or optical phantom) using optic fibers (0.4 mm core) and from the scalp (or optical phantom) back to the detectors using fiber bundles (3 mm diameter). Although we used an FD system for recording, because the purpose of this paper is to introduce a method that could be applied to data acquired with a CW system, only DC light intensity data were used for this paper (although closely matching data were obtained when phase variance was used to estimate shot noise).
Structural MRIs were recorded from each subject on a Siemens 3T TRIO scanner using a three-dimensional (3-D) magnetization prepared rapid gradient echo protocol [, , , (sagittal), , , ]. Venograms were also acquired for each subject with the same scanner [, , (sagittal), , , ].
2.5.4. Phantom studies: procedures
A phantom study was set up to assess the stability and accuracy of the EAC estimation methods under the experimental conditions. Because of the known similarity between the scattering properties of milk and human brain tissue in the NIR spectral range, homogenized skim milk was used as the bulk substance in the phantom experiment, with India ink added to it to mimic the tissue’s absorption properties.40 The milk was placed in a black 4-l tank and was kept at a constant temperature using ice. A square array of alternating optodes [minimum source–detector ; covered area , see Fig. 8(a)] was arranged on the surface of the milk. Baseline absorption values were measured using an FDMD method.16 The estimated absorption and reduced scattering values of the milk medium over a 2-min recording were and at a wavelength of 830 nm. A solid rectangular silicone phantom (50-mm thick, 40-mm wide, 100-mm long with , and at 830 nm wavelength) was embedded at the center of the medium surface.
Fig. 8.
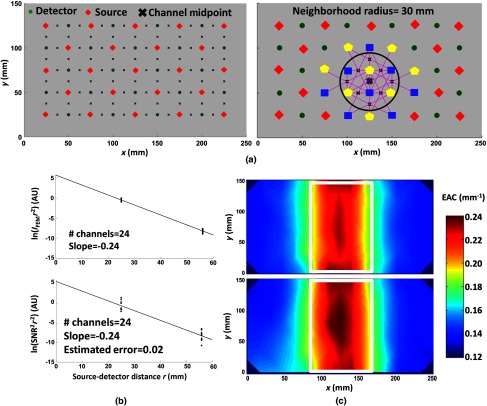
(a) Left image: Optode montage used for the simulated and real phantom data, together with the channel centers (midpoints). Right image: Optode montage with sources (yellow), detectors (blue), channels (represented as magenta lines), and the centers of each channel, reported as black x’s, involved in the computation of the EAC at the position indicated by the thick gray X, using a neighboring radius of 30 mm. (b) Top image: Logarithm of the intensity (multiplied by the term), computed using FEM simulations, as a function of interoptode distance, for the channels involved in the computation of EAC at the gray X point [Fig. 8(a), right image]. Bottom image: Logarithm of the (multiplied for the term), for real data at the same location. Although increased noise was found for in vivo data, the EAC estimates at the location of interest were identical (). The estimated standard error for the real measurement was [based on Eq. (4)]. (c) Top image: EAC maps obtained using light intensity in FEM simulated data. Bottom image: Topographic map of EAC obtained using the signal-to-shot noise ratio of recorded data. The white rectangle represents the original inhomogeneity position and shape (50 mm thick, 40 mm wide, and 100 mm long). Both images were obtained using a neighborhood sphere radius of 30 mm (average number of channels for each , ).
The data used to estimate phantom EAC were acquired for 30 s. Light intensity at each detector was estimated from the continuous wave component (DC intensity) of the recorded signal [high-pass filtered, 10 Hz, as defined in Eq. (3)].
2.5.5. Human study: participants and procedures
Five young adults (age range 18 to 30, average age 25 years, 3 women) signed informed consent documents and participated in an experiment whose procedures were approved by the University of Illinois Institutional Review Board. They performed a resting-state paradigm31 in which they were instructed to look at a cross-hair on a monitor and to try not to think of anything in particular. Two 6-min blocks were recorded using four separate optical recording montages. A total of 384 channels (192 at 830 nm and 192 at 690 nm) were acquired for each montage, with source–detector distances varying between 15 and 80 mm for a total of 1536 channels covering most of the scalp surface.
Fiducial markers were placed on each participant’s left and right preauricular points and on the nasion (Na). Fiducials, optodes, and other scalp locations were digitized with a Polhemus FastTrak 3-D digitizer (Colchester, Vermont; accuracy: 0.8 mm) using a recording stylus and three head-mounted receivers, which allowed for small movements of the head in between measurements. Optode locations and structural MRI data were coregistered using fiducials and a surface-fitting Levenberg and Marquardt algorithm.41,42 See Fig. 10(b) for source and detector locations in a representative subject, rendered onto their T1w image. Preprocessing involved movement correction,43 high-pass filtering (10 Hz), SNR computation [Eq. (3)], maximum distance identification, and optode efficiency correction [Eqs. (5)–(8)].
Fig. 10.
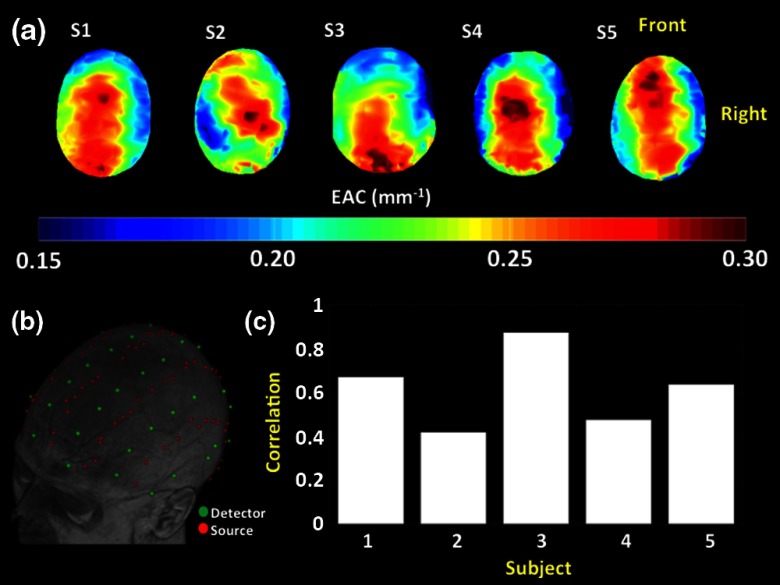
(a) Topographic EAC maps obtained from five adult subjects (18 to 30 years), with a neighborhood radius of 30 mm. The results were obtained using 830-nm light. (b) Example of the optode montage used for optical recording, overlaid over a subject’s structural MRI. (c) Image correlations between each subject’s EAC map and the average map of the other four subjects.
Topographic EAC maps (axial views) were obtained for each of the five subjects. To evaluate the reliability of the measurements, the optodes used for estimating EAC were split randomly into two groups and two EAC images were generated for each subject. The average difference and image correlation between the two images were estimated for each subject. This random split of the optodes was only used to estimate reliability. Note that, although the optodes used were different for the two images, a random sampling of a large, high density, number of optodes, created two equally spread optode montages covering all the scalp with a reasonable density. This aspect, together with the low resolution of the procedure, allowed us to test the reliability using this procedure. For all other analyses presented in this paper, all “good” channels (i.e., those yielding sufficient light) were used to maximize the SNR. To evaluate the consistency of these maps across subjects, image correlations were computed between each subject’s maps and the map obtained by averaging the four remaining subjects. The EAC measurements computed from the recorded data using the multidistance approach presented here were then compared to the simulated EAC estimates, derived from standard FEM models based on T1w image tissue segmentation. They were also compared with a similar model in which veins, derived from MRI venograms, were added.
3. Results
3.1. EAC Values
A simulation was run to determine that Eq. (1) is valid across a wide range of optical parameters as applied to a homogeneous semi-infinite medium and to estimate the possible EAC values found in vivo.
Figures 3(a) and 3(b) report the analytic solutions for light reflectance [multiplied by the term, left-hand side of Eq. (1)] as a function of distance between sources and detectors located on the medium surface. Figure 3(a) reports results obtained with a fixed reduced scattering parameter () and variable absorption coefficients (from to , with increments). Figure 3(b) reports results obtained with a fixed absorption parameter () and variable reduced scattering coefficients (from to , with increments).
Figure 3(c) reports the EAC estimates obtained by regressing the log light reflectance (multiplied by the term) as a function of interoptode distance, based on interoptode distance values between 20 and 60 mm. A minimum distance of 20 mm was chosen in order to make the assumption hold for all the optical properties considered. The EAC estimates are reported as a function of the absorption and reduced scattering coefficients (from to and from to ). EAC values can vary in vivo between the values of 0.05 and . The maximum error of the estimated EAC based on Eqs. (1) and (2) across the optical values considered was with an intercept standard deviation of 0.2. In order to test the linearity of the log light intensity as a function of distance, correlations were also computed between interoptode distances (20 to 60 mm) and the diffuse optical reflectance (adjusted for the term) for all the combinations of optical parameters considered. The average absolute correlation obtained was 0.999 (). The lowest absolute correlation obtained was 0.997. These results strongly support the linearity of the relationship between source–detector distance and the log of the intensity of the light reaching the detector [corrected by the term, Eq. (1)]. These data also support the claim that Eq. (1) is valid for semi-infinite, homogeneous media across the source–detector, absorption, and reduced scattering values typically found in diffuse optical imaging applications.
Note that, although the head structure is optically not homogeneous, it has been extensively proven using the FDMD method that the linearity assumption holds locally when in vivo head measurements are performed, both in infants and adults.16,44,45
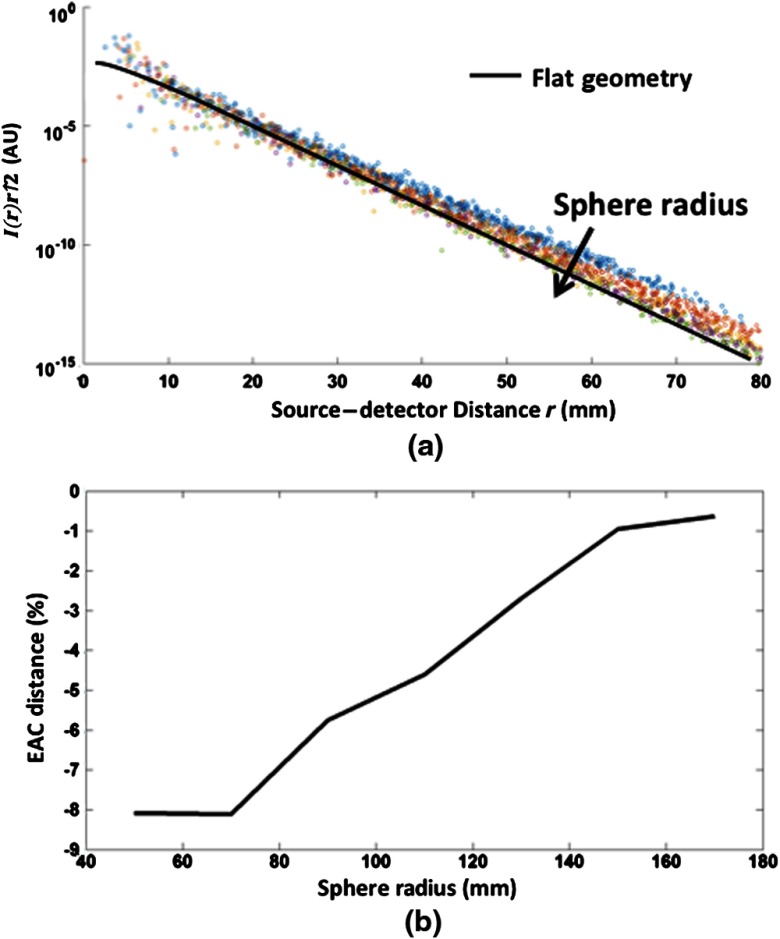
A second simulation was performed in order to estimate the effect of a curved, finite space (such as the head) on EAC estimates. Figure 4(a) reports the reflectance (multiplied by the term) derived from FEM simulations as a function of Euclidean interoptode distance in a spherical geometry ( and ). Different colors represent reflectance values obtained with different sphere radiuses (from to , with 20 mm increments). The continuous line depicts the reflectance obtained in a flat geometry. Figure 4(b) reports the percent distance in EAC estimates (compared to flat-surface estimates) as a function of the sphere radius. Smaller radiuses (high curvature) decrease the estimated EAC up to a few percentage points. The average absolute correlation obtained between the reflectance [corrected term, Eq. (1)] and the Euclidean interoptode distance across all sphere radiuses was 0.9965 (). The weakest absolute correlation obtained was 0.9955. No clear effect of sphere radius on the linearity of the problem was found (within FEM noise level).
Fig. 4.
(a) Simulated reflectance [multiplied by the term, left-hand side of Eq. (1)] as a function of interoptode distance obtained using FEM in a spherical geometry (, , semilogarithmic plot). Different colors represent different sphere radiuses (from to , in steps of 20 mm, arrow depicting ascending sphere radius). The continuous line depicts the reflectance obtained with a flat geometry. (b) Percent distance in EAC estimates as a function of sphere radius.
These data indicate that the presence of a curved surface produces a small but systematic bias in the EAC estimates obtained from Eqs. (1) and (2), with a tendency to underestimate EAC for regions of higher curvature (smaller radius). This effect, however, is less than 10%, even for the spheres with the highest curvature. Note that the radius of an adult human head is of the order of 80 to 90 mm whereas that of a newborn is of the order of 45 to 50 mm. An in-depth evaluation of curvature effects as a function of the population considered (from neonates to adults) can be found in Ref. 46.
3.2. Topographic Two-Dimensional Image Reconstruction
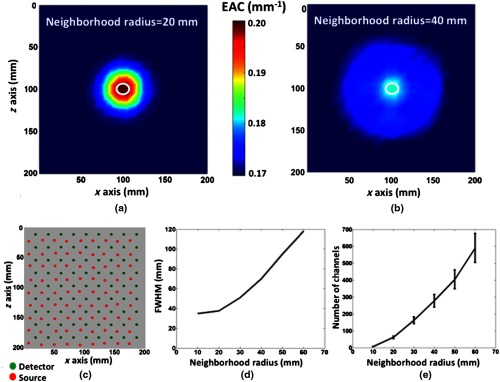
Figure 5(a) reports the topographic image of EAC obtained with a neighborhood radius of 20 mm, based on simulated data. Figure 5(b) reports the same image with a neighborhood radius of 40 mm. The white circles represent the original inhomogeneity position projected onto the medium’s surface. The procedure used to derive these topographic images was able to correctly retrieve the position of the inhomogeneity, with a resolution dependent on the neighborhood sphere radius. Note that the spatial localization power was tested in these images. Consider that this particular simulation was affected by the partial volume effect, because of the small inhomogeneity used and the low resolution of the procedure. This is evident when comparing the two images obtained with different neighborhood radiuses [Fig. 5(b) presents a less intense reconstructed inhomogeneity when compared to Fig. 5(a)]. A bigger inhomogeneity is needed to test the accuracy in reconstructed EAC values (refer to Fig. 8 presented later in this paper). Figure 5(d) reports the full width half maximum (FWHM) resolution estimate of the image reconstruction procedure as a function of the neighborhood radius: the resolution of the image is positively correlated with the neighborhood radius. Figure 5(e) reports the average number of channels and related standard deviation that were involved in the computation of EAC as a function of neighborhood radius. Note that the standard deviation bars are nonzero because of the finite geometry employed. In a semi-infinite medium with an infinite, regularly spaced optode montage on the surface, there would be no variability in the number of channels for each EAC computation at a given neighborhood radius. This number is positively correlated with (the square of) the neighborhood radius (when a fixed optode density is considered), and it is an important parameter to take into account when applying the algorithm to recorded data. For recorded data applications, including more channels for each EAC computation leads to better EAC estimates (as it will be discussed later, see Fig. 7), generally losing spatial resolution because of the increased neighborhood radius. Another way of increasing the number of channels considered in each EAC computation is to increase the optode’s density, which will increase precision without sacrificing spatial resolution. Consider that for this simulation, the optode density chosen was particularly high, and as such it can be considered a best-case scenario. Note, finally, that the closest source–detector pairs (15 mm distance) were not used for EAC computation.
Fig. 5.
(a and b) Topographic images of EAC obtained with simulated FEM data on a cubic medium (, 15 mm minimum interoptode distance grid, , , with a cylindrical 10-mm-diameter absorption inhomogeneity, , up to 40 mm depth). (a) Topographic image obtained with a neighborhood radius of 20 mm. The white circle indicates the actual position and shape of the inhomogeneity. (b) Topographic image obtained with a neighborhood radius of 40 mm. The white circle indicates the actual position and shape of the inhomogeneity. (c) Optode array used for the simulations (15 mm minimum interoptode distance grid). (d) FWHM of the image reconstruction procedure as a function of the neighborhood radius. (e) Average number of channels, and related standard deviation, involved in the computation of each channel’s EAC as a function of the neighborhood radius.
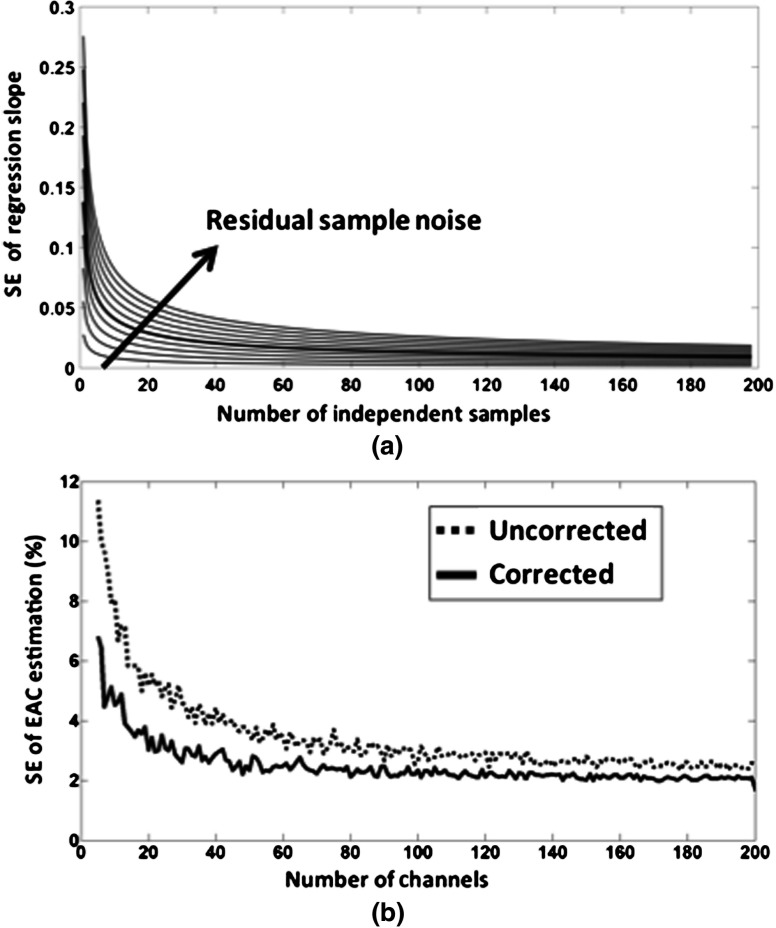
Fig. 7.
(a) Standard error of the slope as a function of the number of independent sampled used with varying residual sample noise [Eq. (4)]. Since the standard error in Eq. (4) depends also on the independent variable values (interoptode distances in this particular case), a homogeneous distribution of distances between 20 and 60 mm was used for this analysis. The thicker line represents a residual sample noise of , which is similar to the level of noise found in vivo. (b) EAC error (%) as a function of the number of channels averaged in the process, separately for data uncorrected and corrected for optode effects.
3.3. Estimating EAC from Recorded Data
Two main assumptions are considered when computing EAC from recorded data. First, the SNR of the recorded data is mainly influenced by quantum/shot noise and can provide a good estimate of light intensity in the absence of quantitative measures of intensity. Second, the noise introduced by O-S coupling can be diminished by considering a sufficient number of channels for each EAC computation and by statistical correction procedures.
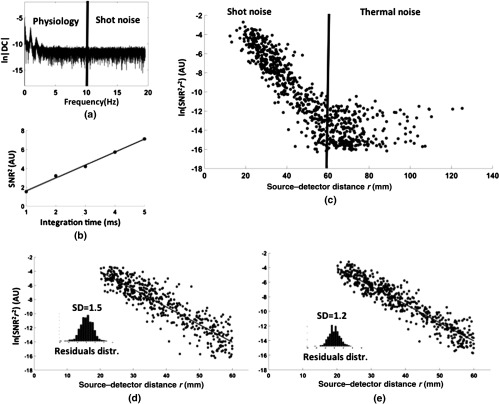
Figure 6(a) reports a typical spectrum of the logarithm of the SNR for signals recorded in vivo. The spectrum can be divided into two regions. In the first region (lower frequency ranges, below 10 Hz), spectrum peaks can be related to physiological fluctuations of the signal (such as hemodynamics, respiration, Mayer waves, and pulse waves). Above 10 Hz, the spectrum is practically flat, and its power is mainly related to quantum/shot noise if a sufficient number of photons are detected. In fact, Fig. 6(b) reports the (computed above 10 Hz) for a particular channel during an in vivo measurement where the integration time of the detector was manipulated (between 1 and 5 ms). At a constant source power, the integration time increases the number of photons detected, and the high linearity of the versus integration time (, ) supports the assumption of shot noise prevalence in the frequency band considered [Eq. (3)].
Fig. 6.
(a) A typical spectrum of the logarithm of the SNR for signals recorded in vivo. The spectrum is practically flat above 10 Hz, and its power is mainly related to quantum/shot noise. (b) (computed above 10 Hz) for a particular channel during an in vivo measurement, as a function of the integration time of the detector. (c) Logarithm of the SNR (multiplied by the term) for each channel as a function of interoptode distance, obtained from a set of data recorded in vivo. The vertical line shows the maximum distance used in the computation. (d) Logarithm of the SNR (multiplied by the term) as a function of interoptode distance obtained from good channels (below 60 mm interoptode distance). Note that the SNR values do not lay on a straight line for both tissue inhomogeneities and O-S coupling. The inset histogram reports the relative frequency of the residuals of a linear interpolation considering all the good channels. (e) Logarithm of the SNR (multiplied by the term) as a function of interoptode distance obtained from good channels (below 60 mm interoptode distance) after O-S coupling correction.
Figure 6(c) reports the logarithm of the SNR (multiplied by the term) for each channel as a function of interoptode distance, obtained from a set of data recorded from one subject. The vertical line shows the maximum distance used in our computation. The maximum distance separates the scatterplot into two regions. In the left region, the SNR decreases linearly with distance (with variability due to the heterogeneity of the human head and O-S coupling). In the right region, the SNR plateaus because light intensity is very low and the shot noise is small compared to other sources of noise. Equation (3) is assumed to be valid for channels with distances below the maximum distance chosen. Therefore, only these channels are included in the computation of EAC. An outlier identification procedure further identified channels with very low levels of light and removed them from the computation algorithm. Specifically, after the identification of the maximum usable interoptode distance, the data were linearly interpolated and the residuals were examined. Channels that had a residual value greater than five times the SD of the residual distribution were excluded from further computations. Figure 6(d) reports the logarithm of the SNR as a function of interoptode distance obtained from good channels (below 60 mm interoptode distance). Note that the SNR values do not lie on a straight line due to both tissue inhomogeneities and O-S coupling. However, the data provide good homoscedasticity, further supporting the implemented statistical procedure for noise dampening. Assuming O-S coupling as the only source of noise, we estimated the O-S coupling for the five in vivo measurements that presented similar results as the ones reported in Fig. 6(d). O-S coupling was estimated from the residual of a linear interpolation of the data [as shown in Fig. 6(d)] and their Gaussian properties were tested with a Kolmogorov–Smirnov test (average noise , all ). This procedure can be considered to represent a “worst case scenario” since it yields overestimation of both intensity and departure from normality of O-S coupling.
Figure 6(e) reports the logarithm of the SNR as a function of interoptode distance obtained after O-S coupling correction. As expected, a reduction in the variance of the data is present in this figure. Figure 7(a) reports the standard error of the slope as a function of the number of independent samples used with varying residual sample noise [Eq. (4)]. Since the standard error in Eq. (4) depends also on the independent variable values (interoptode distances in this particular case), we considered a homogeneous distribution of distances between 20 and 60 mm in this analysis. The thicker line in the graph represents a residual sample noise of , which is similar to the level of noise found in vivo.
Note that the standard error of the slope represents the error of the implemented EAC mapping. This error needs to be compared to the EAC values generally measured in vivo (the actual slope of the regression), and it is generally at least an order of magnitude smaller when a sufficient number of independent samples (channels) are employed. However, the measurements are not completely independent (each optode can be involved in multiple channels), and a further optode efficiency correction procedure can be introduced [Eqs. (5)–(8)]. To quantify the effects of channel numerosity and of the correction procedure for suppressing the effect of O-S coupling on the accuracy of EAC computation, we ran a simulation where Gaussian noise was added to the log intensity data of each source and detector. Figure 7(b) shows the EAC error as a function of the number of channels averaged in the process, separately for uncorrected and corrected data. As the figure shows, the EAC estimate error was reduced to 2% to 3% when a large number ( or more) of neighboring channels and the correction algorithm were employed in the EAC computation. As stated before, in order for the O-S coupling correction procedure to work, it is important that the parameter [Eq. (5)] does not change as a function of tissue optical properties. We determined that, for a homogeneous medium, the parameter across a wide range of optical properties had a . Note that this variability is lower than that of the O-S coupling introduced in the simulations (which we estimated from in vivo data, ). Thus, the correction procedure should improve the EAC estimation reliability at a given number of channels when a flat homogeneous medium is investigated.
Both different medium geometries and tissue inhomogeneities can affect the variability of the parameter . This aspect is difficult to address for in vivo head studies since the actual properties of the different head tissues are not exactly known. However, as a first step we simulated light intensity signals and estimated the intercept parameter on heterogeneous head models using the optode montages used in vivo [Fig. 10(b)], segmentations of the T1w images of the five subjects that underwent the in vivo experiment, and a priori optical parameters. For these particular simulations, the parameter was found to have . Note that this variability is still lower than the level of variability found in vivo.
For practical purposes, the use of multiple channels for each EAC computation (with a good combination of sources and detectors) is mandatory in order to suppress O-S coupling variability and to obtain a reliable EAC estimate. The O-S coupling correction can be applied to further improve the reliability of the EAC estimate when the intercept factor can be accurately estimated for each optode and the optical parameter changes over space are assumed to be within reasonable ranges.
We then investigated the validity of using the data SNR (to estimate light intensity), multiple combinations of sources and detectors (using a regression approach), and O-S coupling corrections to estimate EAC in phantom data. Specifically, we compared the EAC maps computed from data recorded from the surface of a milk tank containing a known inhomogeneity to maps obtained from FEM simulated data (keeping the montage, medium and inhomogeneity constant for the two approaches). Figure 8(a) (left image) reports the optode montage employed in the simulated and real phantom data, together with the channel centers used to compute EAC maps. Figure 8(a) (right image) reports the optode montage employed, highlighting the sources (reported in yellow), the detectors (reported in blue), the channels (represented as magenta lines), and the center of the channels (reported as small black x’s) involved in the computation of the EAC in the position marked by the large gray “X,” using a neighborhood radius of 30 mm. Twenty-four channels were employed in the computation of the EAC in that particular point. Figure 8(b), top graph, reports the log of the intensity (multiplied by the term), computed using FEM simulations, as a function of interoptode distance for the channels involved in the computation of EAC in the black point [Fig. 8(a), right image]. Figure 8(b), bottom graph, reports the log of the (multiplied for the term), for real data in the same location. Although the real data showed an increased level of noise, the EAC estimates for the real and simulated data in the location of interest were identical (). The estimated standard error for the real measurement was [based on Eq. (4)].
Figure 8(c) (top) reports a topographic map of EAC obtained using light intensity in FEM simulated data, whereas Fig. 8(c) (bottom) presents the topographic map of EAC obtained using the signal-to-shot noise ratio of recorded data. The white rectangle represents the shape and position of the inhomogeneity. Both images were obtained using a neighborhood sphere radius of 30 mm. The similarities are clear both qualitatively and quantitatively. The spatial correlation between the two images, computed across all voxels, was (). Note that this analysis also demonstrated the ability of the procedure to correctly quantify the EAC across space (milk: and , ; phantom: and , , at 830 nm wavelength).
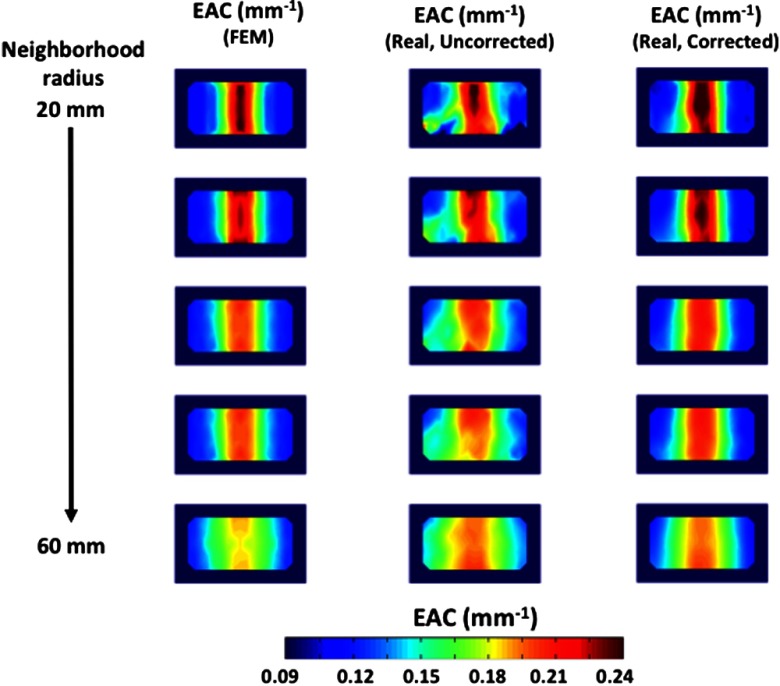
Figure 9 explores the different image reconstruction capabilities of the procedure as a function of the neighborhood radius employed (from 20 to 60 mm, 10 mm steps from top to bottom), and the type of data (from left to right, FEM simulated, real data uncorrected for the optode effect, and real data corrected for the optode effect). Clear similarities can be noted between the simulated FEM data and the real data (particularly for the corrected ones), even for the smaller neighborhood radiuses. The location and intensity of the optical inhomogeneity are correctly identified using real data. Moreover, a partial volume effect can be noted when the neighborhood radius increases.
Fig. 9.
Different images reconstructed using the developed EAC estimation procedure. From top to bottom images differed for the neighborhood radiuses employed (from 20 to 60 mm, in 10 mm steps). From left to right columns indicate different data types (FEM simulated data, real data, and real data corrected for optode effects, respectively).
3.4. Full-Head EAC Maps from Human Subjects
Figure 10(a) reports topographic EAC images (based on 830 nm light) projected to the axial surface of structural MRI images of five subjects. Very similar images were obtained using 690 nm light (average image correlation , ) with an average small increase in EAC values (5% compared to the 830 nm). These images were obtained using an optode array covering most of the scalp surface [Fig. 10(b)] and a neighborhood radius of 30 mm (average number of channels for each EAC computation: , ). Reliability tests were performed on each subject by generating the EAC images twice, employing half of the optodes available for each image computation (with optodes randomly chosen, and no optode shared between the two images). Although the split-half data showed decreased SNR (because of a decreased number of optodes), the root mean square error between the two images across the five subjects was 3%, . For each subject we also computed the correlation between the EAC values for each of the two images (the correlation was computed across voxels). The average value of this correlation across subjects was , . Note that this correlation was based on images computed using different optodes. Nevertheless the intrinsic low resolution of the images and the high number of channels employed allowed for this procedure to provide a lower-bound estimator of the reliability of the EAC mapping method. There are clear similarities in the patterns of EAC across participants. In particular, dorsal and occipital regions appear to have higher EAC values compared to lateral frontal and temporal regions. Intersubject consistency analyses were performed on the images by correlating each subject’s image with the average of the other four subjects (a single correlation was measured for each subject using all the available voxels). The rationale of this procedure was to show spatial similarities between EAC maps. The correlations ranged from 0.4 to 0.85 (all ) and are reported in Fig. 10(c). The images were coregistered based on their center. Due to small differences in the shapes of the topographic EAC maps, only pixels where EAC was computed for all the images could be used for the spatial correlation analyses. No warping procedure was applied. In fact, on average, only 6% of the pixels (3% SD) were removed from each image during this procedure. Given the relatively low spatial resolution of the method, we would not expect major changes in the spatial correlations if a warping procedure were applied.
We hypothesized that the major changes in EAC across the head might be due to the presence of large veins in superficial intracranial areas (venous sinuses). Figures 11(a)–11(c) show EAC maps (projected to the axial surface) based on (a) measurements recorded from a participant; (b) simulated measurements based on segmentation of the same subject’s T1w image; and (c) simulated measurements where veins (obtained from a segmented venogram from the same subject) were added to the T1w segmentation. Figure 11(d) shows the spatial correlation of the two simulated results with the actual measurements for each of the five subjects. Positive and statistically significant () spatial correlations were obtained for each subject when veins were added to the model, whereas negative spatial correlations were obtained when only skull/scalp, CSF, and white and gray matter were considered. Thus, considering only the tissue layers available with a standard T1w image results in largely inaccurate estimates (based on a spatial correlation metric) of local variations in EAC across the head in our dataset. This problem is greatly ameliorated by the inclusion of the vein compartment in the forward model.
4. Discussion
Accurate characterization of fNIRS imaging data requires some knowledge of the optical properties of the imaged tissue. The EAC (which is a combination of the absorption and reduced scattering coefficients) could be a useful tool for understanding how light propagates through the head, as EAC is the main parameter affecting light propagation in deep structures (for depths exceeding few mm). Here we reported on a procedure that estimates the EAC of tissues directly at a low level of resolution, in the same subjects who participated in a high-density fNIRS study. This procedure can produce 2-D maps of EAC and does not require additional measurements beyond the data that are recorded for a standard fNIRS study. With this procedure, EAC is derived from the slope of a regression function linking the log of light intensity to the interoptode distance. This means that EAC can be computed using CW systems, which are more common than FD or TD systems, although the computation still requires a high-density recording array. In this paper, we present a series of simulations and phantom studies indicating that this procedure yields accurate results (with an error significantly lower than 10%), provided that several issues are accounted and corrected for.
First, the linearity assumption (critical for regression) is only accurate for interoptode distances , as it requires a diffusion regime and negligible boundary effects. This should not constitute a problem for human studies, where longer distances are typically used in order to image the brain’s cortical surface. Second, the medium’s optical properties are not the only determinants of the amount of light reaching the detector: geometric properties of the medium, and in particular the surface curvature, are also relevant. This effect is typically limited (less than 10%), but it can also be corrected if the curvature is known.
When applying the EAC estimation to recorded (rather than simulated) data, we also had to solve two additional problems. First, we needed to deal with the problem of estimating the intensity of the light reaching the detectors when detectors vary in their amplification factor. We show here that this problem can be addressed by estimating light intensity from the shot noise existing in the data. Shot noise itself is estimated from the variability of high frequency () intensity data (or from the variability of phase data available for FD instrumentation). Phantom data showed that this procedure is effective, allowing for light intensity estimation across a wide range of interoptode distances. Second, we had to suppress O-S coupling effects, which generate noise in the estimation process. Two statistical approaches were used for dealing with this problem and dampening its effect. The first involved increasing the number of optodes (both sources and detectors) employed in each EAC computation; the second involved considering the O-S coupling as a random covariate and, therefore, subtracting it from the intercept of the regression function used to compute EAC. Simulated and phantom studies indicate that these approaches can reduce the EAC estimation error to a few percentage points (Figs. 5–7).
Based on this strategy, we developed procedures for 2-D (topographic) EAC mapping. These procedures are based on computing the EAC for each channel based on a set of neighborhood channels. To determine the validity of this approach, we ran both simulated and phantom studies. They show that the procedure is accurate in estimating EAC and in localizing inhomogeneities, although spatial resolution is limited to a few cm (this resolution depends on the radius used to define the neighborhood over which the regression is computed).
Finally, we applied the 2-D EAC mapping procedure to optical data recorded from five participants using a high-density, extended optical montage, made up of 1536 channels. The intrasubject and intersubject consistency of these maps was evaluated and found to be high. These EAC maps, however, clearly differed from those predicted on the basis of a four-layer model derived from segmented MR images (including skin-skull, CSF, gray matter, and white matter compartments31), even at the low level of resolution afforded by the procedure. The main difference was a high EAC level observed in dorsal and occipital regions, which was not predicted by the standard four-compartment model. We hypothesized this difference to be due to the presence of large veins in these regions, which are not included in the standard model. We therefore added veins (derived from MR venograms obtained in the same participants) to the model, and obtained much improved fits of the model to the data. We take this finding to indicate that the standard model of baseline optical properties was inaccurate because it failed to account for the major role that large cerebral veins (and in particular the venous sinuses on the surface of the brain) exert on the diffusion of photons. Moreover, the procedure, although providing spatial distributions of EAC not predicted by standard models of head optical properties, produced EAC values across the head that are compatible with absorption and reduced scattering coefficients typically found in vivo.38
Using our approach, EAC maps can be derived directly from each subject in the study. In fact, the data used for EAC estimation can be obtained during standard fNIRS recording, since they are based on shot noise estimation. This may be used to account for individual variability in brain and vascular anatomy. It also eliminates the problem that unforeseen EAC phenomena may be present in a particular individual (e.g., those due to arterial-venous malformations).
The main requirements for obtaining EAC estimates are that a high-density optode array and a high-sampling rate be used in the recording (based on the Nyquist theorem a sampling frequency above 20 Hz is needed). As the procedure is based on a multidistance logic,18–20 the optical montage needs to contain a mix of channels with different interoptode distances (preferably between 20 and 60 mm). Even with such a montage, the spatial resolution of the procedure is limited because it requires combining data from multiple channels. For instance, in our data set, based on a very large montage (768 channels per wavelength), the spatial resolution is still a few cm.
Although further research is needed, it is clear that EAC is a critical determinant of the differential sensitivity of diffuse optical measurement to phenomena occurring at various locations within the brain. In fact, with zero-boundary conditions and source detector distances above , light sensitivity can be approximated as depending only on the EAC. Therefore, improved knowledge about EAC in the human head may greatly improve estimates of light sensitivity patterns and DOT image reconstruction. Here, we introduced a procedure that allows us to derive such estimates from CW high-density diffuse optical imaging recordings without the need of additional apparatus and recording sessions.
In addition, the procedure described here can provide absolute measures of EAC that can be used for functional purposes. For instance, by computing EAC for light sources of different wavelengths, it is possible to generate an EAC spectrum—and in fact a low-resolution map of it. These maps could be used for different purposes, by making some additional assumptions. For instance, if the scattering coefficient is assumed, the procedure could be used to generate absolute maps of absorption, such as those needed to compute tissue oxygenation. Although in this study the procedure was employed on healthy subjects, EAC maps could be sensitive to pathological brain conditions (e.g., superficial hemorrhages, strokes, etc.). Further, if a specific spectral dependence of the reduced scattering coefficients could be assumed, the spectral dependence of the differential pathlength factor could be assessed. This may reduce possible crosstalk when estimating oxy- and deoxyhemoglobin fluctuations with fNIRS.
Limitations of the proposed approach include: (a) the fact that it is based on an equation derived from a homogeneous model that it is applied to subregions of the head, thus volume averaging of the estimate of the EAC in each subregion is likely to occur; and (b) the relatively low resolution, combined with the limited penetration of optical data (30 mm at most),30 which limits the depth resolution capabilities of the approach.
5. Conclusion
We have developed a procedure to generate EAC topographic maps of the human head using an extended, high-density optical recording array that, among other applications, could be used for testing and improving forward models for fNIRS studies. An important feature of our approach is that it can provide absolute estimates of a combination of optical properties for each participant and across the entire head (albeit of EAC, and not separately of absorption and reduced scattering coefficients) on the basis of continuous wave data. The procedure relies on the estimation of light decay as a function of source–detector distance and it does not require independent calibration data. This opens the possibility of using instruments providing these types of data for recording not only differential effects (as in most fNIRS work) but also baseline, absolute effects. EAC maps with a resolution of 2 to 3 cm can be obtained. Application of the procedure to human recordings indicates the importance of venous sinuses in determining regional EAC variations, a factor typically overlooked in the current literature. Moreover, the technology could be particularly useful for empirically comparing different subject populations and for clinical applications. Note that in the work presented here we have focused on data obtained at a single wavelength. However, EAC can be measured separately at different wavelengths, thus providing EAC spectra.
Acknowledgments
This work was supported by grants NIMH 5R56MH097973 (Drs. G. Gratton and M. Fabiani, PIs) and NCRR grant S10-RR029294 (Dr. G. Gratton PI).
Biographies
Antonio M. Chiarelli is a research associate in the Cognitive Neuroimaging Lab at the Beckman Institute at University of Illinois. He received his BS degree in physics engineering and MS degree in optics and photonics from the Polytechnic in Milan, Italy, in 2006 and 2009, respectively. In 2013 he received his PhD in neuroimaging technologies from University of G. D’Annunzio in Chieti-Pescara, Italy. His research interests focus on functional optical brain imaging methods (including hardware, analytic developments, and applications).
Edward L. Maclin received his PhD from New York University in 1983. He is a research assistant professor at the Beckman Institute, University of Illinois. Following his postdoctoral fellowship at Mount Sinai Hospital/CUNY he directed the Electrophysiology Laboratory in the Department of Biological Psychiatry at the New York State Psychiatric Institute/Columbia University. From 1989 to 1997, he was technical director of the Center for Magnetoencephalography at the Albuquerque Veterans Medical Center. He joined the Cognitive Neuroimaging Laboratory in 1997.
Kathy A. Low received her PhD from the University of Missouri in 1997. She has extensive experience in multimodal imaging, including diffuse optical imaging, electrophysiology, and structural and functional MRI techniques. For the past 15 years, she has served as a senior research scientist in the Cognitive Neuroimaging Lab, coordinating and implementing many large-scale multimodal imaging studies involving participants from infants to old age.
Sergio Fantini is professor of biomedical engineering and principal investigator of the Diffuse Optical Imaging of Tissue Laboratory (DOIT Lab) at Tufts University. The research in the DOIT Lab aims to develop noninvasive applications of diffuse optics to assess cerebral perfusion, detect breast cancer, and quantify skeletal muscle oxygenation. His research resulted in 11 patents and about 200 scientific publications. He coauthored with Professor Irving Bigio in Boston University a textbook on quantitative biomedical optics.
Monica Fabiani is a professor of psychology and neuroscience at the University of Illinois and a faculty member at the Beckman Institute. She received her PhD in biological psychology from the University of Illinois in 1990. She cochaired the Biological Intelligence Group at the Beckman Institute from 2005 to 2010 and was the president of the Society for Psychophysiological Research from 2007 to 2008. She is the editor of the Journal Psychophysiology and a fellow of the Association for Psychological Science.
Gabriele Gratton received his MD degree from the University of Rome in 1980 and his PhD from the University of Illinois in 1991. He is a professor of psychology and neuroscience at the University of Illinois. He received the Provost Outstanding Junior Faculty Research Award from the University of Missouri and the Early Career Award from the Society for Psychophysiological Research (SPR). He is a fellow of the Association for Psychological Science and was the president of SPR in 2010.
Disclosures
None of the authors has financial interests in any of the companies manufacturing the equipment mentioned in this paper or other conflicts of interest.
References
- 1.Boas G., “Noninvasive imaging of the brain,” Opt. Photonics News 15(1), 52–55 (2004). 10.1364/OPN.15.1.000052 [DOI] [Google Scholar]
- 2.Ferrari M., Mottola L., Quaresima V., “Principles, techniques, and limitations of near infrared spectroscopy,” Can. J. Appl. Physiol. 29(4), 463–487 (2004). 10.1139/h04-031 [DOI] [PubMed] [Google Scholar]
- 3.Gibson A., et al. , “Recent advances in diffuse optical imaging,” Phys. Med. Biol. 50(4), R1 (2005). 10.1088/0031-9155/50/4/R01 [DOI] [PubMed] [Google Scholar]
- 4.Hoshi Y., Tamura M., “Dynamic multichannel near-infrared optical imaging of human brain activity,” J. Appl. Physiol. 75(4), 1842–1846 (1993). [DOI] [PubMed] [Google Scholar]
- 5.Villringer A., et al. , “Near infrared spectroscopy (NIRS): a new tool to study hemodynamic changes during activation of brain function in human adults,” Neurosci. Lett. 154(1), 101–104 (1993). 10.1016/0304-3940(93)90181-J [DOI] [PubMed] [Google Scholar]
- 6.Villringer A., Chance B., “Non-invasive optical spectroscopy and imaging of human brain function,” Trends Neurosci. 20(10), 435–442 (1997). 10.1016/S0166-2236(97)01132-6 [DOI] [PubMed] [Google Scholar]
- 7.Boas D. A., Dale A. M., Franceschini M. A., “Diffuse optical imaging of brain activation: approaches to optimizing image sensitivity, resolution, and accuracy,” Neuroimage 23, S275–S288 (2004). 10.1016/j.neuroimage.2004.07.011 [DOI] [PubMed] [Google Scholar]
- 8.Eggebrecht A. T., et al. , “A quantitative spatial comparison of high-density diffuse optical tomography and fMRI cortical mapping,” Neuroimage 61(4), 1120–1128 (2012). 10.1016/j.neuroimage.2012.01.124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.White B. R., Culver J. P., “Phase-encoded retinotopy as an evaluation of diffuse optical neuroimaging,” Neuroimage 49(1), 568–577 (2010). 10.1016/j.neuroimage.2009.07.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zeff B. W., et al. , “Retinotopic mapping of adult human visual cortex with high-density diffuse optical tomography,” Proc. Natl. Acad. Sci. U. S. A. 104(29), 12169–12174 (2007). 10.1073/pnas.0611266104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhan Y., et al. , “Image quality analysis of high-density diffuse optical tomography incorporating a subject-specific head model,” Front. Neuroenerg. 4, 6 (2012). 10.3389/fnene.2012.00006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bigio I. J., Fantini S., Quantitative Biomedical Optics: Theory, Methods, and Applications, Cambridge University Press, Cambridge, United Kingdom: (2016). [Google Scholar]
- 13.Dalla Mora A. D., et al. , “Towards next-generation time-domain diffuse optics for extreme depth penetration and sensitivity,” Biomed. Opt. Express 6(5), 1749–1760 (2015). 10.1364/BOE.6.001749 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liebert A., et al. , “Time-resolved multidistance near-infrared spectroscopy of the adult head: intracerebral and extracerebral absorption changes from moments of distribution of times of flight of photons,” Appl. Opt. 43(15), 3037–3047 (2004). 10.1364/AO.43.003037 [DOI] [PubMed] [Google Scholar]
- 15.Chance B., et al. , “Phase modulation system for dual wavelength difference spectroscopy of hemoglobin deoxygenation in tissues,” Proc. SPIE 1204, 11 (1990). 10.1117/12.17711 [DOI] [Google Scholar]
- 16.Choi J., et al. , “Noninvasive determination of the optical properties of adult brain: near-infrared spectroscopy approach,” J. Biomed. Opt. 9(1), 221–229 (2004). 10.1117/1.1628242 [DOI] [PubMed] [Google Scholar]
- 17.Delpy D. T., et al. , “Estimation of optical pathlength through tissue from direct time of flight measurement,” Phys. Med. Biol. 33(12), 1433–1442 (1988). 10.1088/0031-9155/33/12/008 [DOI] [PubMed] [Google Scholar]
- 18.Fantini S., et al. , “Quantitative determination of the absorption spectra of chromophores in strongly scattering media: a light-emitting-diode based technique,” Appl. Opt. 33(22), 5204–5213 (1994). 10.1364/AO.33.005204 [DOI] [PubMed] [Google Scholar]
- 19.Fishkin J. B., Gratton E., “Propagation of photon-density waves in strongly scattering media containing an absorbing semi-infinite plane bounded by a straight edge,” J. Opt. Soc. Am. A 10(1), 127–140 (1993). 10.1364/JOSAA.10.000127 [DOI] [PubMed] [Google Scholar]
- 20.Franceschini M. A., et al. , “Optical study of the skeletal muscle during exercise with a second-generation frequency-domain tissue oximeter,” Proc. SPIE 2979, 807 (1997). 10.1117/12.280229 [DOI] [Google Scholar]
- 21.Hueber D. M., et al. , “New optical probe designs for absolute (self-calibrating) NIR tissue hemoglobin measurements,” Proc. SPIE 3597, 618 (1999). 10.1117/12.356784 [DOI] [Google Scholar]
- 22.Dehaes M., et al. , “Assessment of the frequency-domain multi-distance method to evaluate the brain optical properties: Monte Carlo simulations from neonate to adult,” Biomed. Opt. Express 2(3), 552–567 (2011). 10.1364/BOE.2.000552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Horowitz P., Hill W., The Art of Electronics, Cambridge University Press, Cambridge, United Kingdom: (1989). [Google Scholar]
- 24.Chiarelli A. M., et al. , “Combining energy and Laplacian regularization to accurately retrieve the depth of brain activity of diffuse optical tomographic data,” J. Biomed. Opt. 21(3), 036008 (2016). 10.1117/1.JBO.21.3.036008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eggebrecht A. T., et al. , “Mapping distributed brain function and networks with diffuse optical tomography,” Nat. Photonics 8(6), 448–454 (2014). 10.1038/nphoton.2014.107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Andree S., et al. , “Spatially resolved reflectance used to deduce absorption and reduced scattering coefficients,” Proc. SPIE 7368, 73680I (2009). 10.1117/12.831601 [DOI] [Google Scholar]
- 27.Bevilacqua F. P., et al. , “Superficial tissue optical property determination using spatially resolved measurements close to the source: comparison with frequency-domain photon migration measurements,” Proc. SPIE 3597, 540 (1999). 10.1117/12.356857 [DOI] [Google Scholar]
- 28.Kienle A., et al. , “Spatially resolved absolute diffuse reflectance measurements for noninvasive determination of the optical scattering and absorption coefficients of biological tissue,” Appl. Opt. 35(13), 2304–2314 (1996). 10.1364/AO.35.002304 [DOI] [PubMed] [Google Scholar]
- 29.Hjalmarsson P., Thennadil S. N., “Spatially resolved in vivo measurement system for estimating the optical properties of tissue in the wavelength range 1000–1700 nm,” Proc. SPIE 6628, 662805 (2007). 10.1117/12.728183 [DOI] [Google Scholar]
- 30.Quin J., Lu R., “Measurement of the optical properties of fruits and vegetables using spatially resolved hyperspectral diffuse reflectance imaging technique,” Postharvest Biol. Technol. 49(3), 355–365 (2008). 10.1016/j.postharvbio.2008.03.010 [DOI] [Google Scholar]
- 31.Xia J. J., et al. , “Characterizing beef muscles with optical scattering and absorption coefficients in VIS-NIR region,” Meat Sci. 75(1), 78–83 (2007). 10.1016/j.meatsci.2006.07.002 [DOI] [PubMed] [Google Scholar]
- 32.Ishimaru A., “Diffusion of light in turbid material,” Appl. Opt. 28(12), 2210–2215 (1989). 10.1364/AO.28.002210 [DOI] [PubMed] [Google Scholar]
- 33.Farrell T. J., Patterson M. S., Wilson B., “A diffusion theory model of spatially resolved, steady‐state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo,” Med. Phys. 19(4), 879–888 (1992). 10.1118/1.596777 [DOI] [PubMed] [Google Scholar]
- 34.Paulsen K. D., Jiang H., “Spatially varying optical property reconstruction using a finite element diffusion equation approximation,” Med. Phys. 22(6), 691–701 (1995). 10.1118/1.597488 [DOI] [PubMed] [Google Scholar]
- 35.Fang Q., Boas D. A., “Tetrahedral mesh generation from volumetric binary and grayscale images,” in IEEE Int. Symp. on Biomedical Imaging: from Nano to Macro (ISBI ‘09), pp. 1142–1145, IEEE; (2009). 10.1109/ISBI.2009.5193259 [DOI] [Google Scholar]
- 36.Penny W. D., et al. , Statistical Parametric Mapping: The Analysis of Functional Brain Images, Academic Press, Cambridge, Massachusetts: (2011). [Google Scholar]
- 37.Tian F., Liu H, “Depth-compensated diffuse optical tomography enhanced by general linear model analysis and an anatomical atlas of human head,” Neuroimage 85, 166–180 (2014). 10.1016/j.neuroimage.2013.07.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 39.Dehghani H., et al. , “Near infrared optical tomography using NIRFAST: algorithm for numerical model and image reconstruction,” Commun. Num. Methods Eng. 25(6), 711–732 (2009). 10.1002/cnm.v25:6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Waterworth M. D., et al. , “Optical transmission properties of homogenized milk used as a phantom material in visible wavelength imaging,” Australas. Phys. Eng. Sci. Med. 18(1), 39–44 (1995). [PubMed] [Google Scholar]
- 41.Chiarelli A. M., et al. , “Comparison of procedures for co-registering scalp-recording locations to anatomical magnetic resonance images,” J. Biomed. Opt. 20(1), 016009 (2015). 10.1117/1.JBO.20.1.016009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Whalen C., et al. , “Validation of a method for coregistering scalp recording locations with 3D structural MR images,” Hum. Brain Mapp. 29(11), 1288–1301 (2008). 10.1002/hbm.v29:11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chiarelli A. M., et al. , “A kurtosis-based wavelet algorithm for motion artifact correction of fNIRS data,” NeuroImage 112, 128–137 (2015). 10.1016/j.neuroimage.2015.02.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Franceschini M. A., et al. , “Assessment of infant brain development with frequency-domain near-infrared spectroscopy,” Pediatr. Res. 61, 546–551 (2007). 10.1203/pdr.0b013e318045be99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.De Blasi R. A., et al. , “Cerebral and muscle oxygen saturation measurement by frequency-domain near-infra-red spectrometer,” Med. Biol. Eng. Comput. 33(2), 228–230 (1995). 10.1007/BF02523048 [DOI] [PubMed] [Google Scholar]
- 46.Dehaes M., et al. , “Assessment of the frequency-domain multi-distance method to evaluate the brain optical properties: Monte Carlo simulations from neonate to adult,” Biomed. Opt. Express 2(11), 552–567 (2011). 10.1364/BOE.2.000552 [DOI] [PMC free article] [PubMed] [Google Scholar]