Fast sampling with Gaussian scale-mixture priors in high-dimensional regression

Summary

We propose an efficient way to sample from a class of structured multivariate Gaussian distributions. The proposed algorithm only requires matrix multiplications and linear system solutions. Its computational complexity grows linearly with the dimension, unlike existing algorithms that rely on Cholesky factorizations with cubic complexity. The algorithm is broadly applicable in settings where Gaussian scale mixture priors are used on high-dimensional parameters. Its effectiveness is illustrated through a high-dimensional regression problem with a horseshoe prior on the regression coefficients. Other potential applications are outlined.

1. Introduction

Continuous shrinkage priors have recently received significant attention as a mechanism to induce approximate sparsity in high-dimensional parameters, and can mostly be expressed as global-local scale mixtures of Gaussian distributions (Polson & Scott, 2010; Bhattacharya et al., 2015). These global-local priors (Polson & Scott, 2010) aim to shrink noise coefficients while retaining any signal, thereby providing an approximation to the operating characteristics of discrete mixture priors (George & McCulloch, 1997; Scott & Berger, 2010), which allow a subset of the parameters to be exactly zero.

A major attraction of global-local priors has been computational efficiency and simplicity. Posterior inference poses a stiff challenge for discrete mixture priors in moderate to high-dimensional settings, but the scale-mixture representation of global-local priors allows parameters to be updated in blocks via a fairly automatic Gibbs sampler in a wide variety of problems. These include regression (Caron & Doucet, 2008; Armagan et al., 2013), variable selection (Hahn & Carvalho, 2015), wavelet denoising (Polson & Scott, 2010), factor models and covariance estimation (Bhattacharya & Dunson, 2011; Pati et al., 2014), and time series (Durante et al., 2014). Rapid mixing and convergence of the resulting Gibbs sampler for specific classes of priors has been recently established in the high-dimensional regression context by Khare & Hobert (2013) and Pal & Khare (2014). Moreover, recent results suggest that a subclass of global-local priors can achieve the same minimax rates of posterior concentration as the discrete mixture priors in high-dimensional estimation problems (Bhattacharya et al., 2015; van der Pas et al., 2014; Pati et al., 2014).

In this article, we focus on computational aspects of global-local priors in the high-dimensional linear regression setting

$$y=X\beta +\epsilon ,\epsilon ~\mathrm{N}(0,{\sigma }^2{\mathrm{I}}_n),$$ (1)

where X ∈ ℜ^n×p is a n × p matrix of covariates with the number of variables p potentially much larger than the sample size n. A global-local prior on β assumes that

$${\beta }_j\mid {\lambda }_j,\tau ,\sigma ~\mathrm{N}(0,{\lambda }_j^2{\tau }^2{\sigma }^2)(j=1,\dots ,p),$$ (2)

$${\lambda }_j~f(j=1,\dots ,p),$$ (3)

$$\tau ~g,\sigma ~h,$$ (4)

where f, g and h are densities supported on (0, ∞). The λ_js are usually referred to as local scale parameters while τ is a global scale parameter. Different choices of f and g lead to different classes of priors. For instance, a half-Cauchy distribution for f and g leads to the horseshoe prior of Carvalho et al. (2010). In the p ≫ n setting where most entries of β are assumed to be zero or close to zero, the choices of f and g play a key role in controlling the effective sparsity and concentration of the prior and posterior distributions (Polson & Scott, 2010; Pati et al., 2014).

Exploiting the scale-mixture representation (2), it is straightforward in principle to formulate a Gibbs sampler: the conditional posterior of β given λ = (λ₁, …, λ_p)^T, τ and σ is given by

$$\beta \mid y,\lambda ,\tau ,\sigma ~\mathrm{N}(A^{-1}{X}^{\mathrm{T}}y,{\sigma }^2{A}^{-1}),A=(X^{\mathrm{T}}X+{\mathrm{\Lambda }}_{\ast }^{-1}),{\mathrm{\Lambda }}_{\ast }={\tau }^2\text{diag}({\lambda }_1^2,\dots ,{\lambda }_p^2).$$ (5)

Further, the p local scale parameters λ_j have conditionally independent posteriors and hence λ = (λ₁, …, λ_p)^T can be updated in a block by slice sampling (Polson et al., 2014) if conditional posteriors are unavailable in closed form. However, unless care is exercised, sampling from (5) can be expensive for large values of p. Existing algorithms (Rue, 2001) to sample from (5) face a bottleneck for large p to perform a Cholesky decomposition of A at each iteration. One cannot resort to precomputing the Cholesky factors since the matrix Λ^* in (5) changes at each iteration. In this article, we present an exact sampling algorithm for Gaussian distributions (5) which relies on data augmentation. We show that the computational complexity of the algorithm scales linearly in p.

2. The algorithm

Suppose we aim to sample from N_p(μ, Σ), with

$$\mathrm{\sum }={({\mathrm{\Phi }}^{\mathrm{T}}\mathrm{\Phi }+D^{-1})}^{-1},\mu =\mathrm{\sum }{\mathrm{\Phi }}^{\mathrm{T}}\alpha ,$$ (6)

where D ∈ ℜ^p×p is symmetric positive definite, Φ ∈ ℜ^n×p, and α ∈ ℜ^n×1; (5) is a special case of (6) with Φ = X/σ, D = σ²Λ_* and α = y/σ. A similar sampling problem arises in all the applications mentioned in §1, and the proposed approach can be used in such settings. In the sequel, we do not require D to be diagonal, but we assume that D⁻¹ is easy to calculate and that it is straightforward to sample from N(0, D). This is the case, for example, if D corresponds to the covariance matrix of an AR(q) process or a Gaussian Markov random field.

Letting Q = Σ⁻¹ = (Φ^TΦ + D⁻¹) denote the precision, or inverse covariance, matrix and b = Φ^Tα, we can write μ = Q⁻¹b. Rue (2001) proposed an efficient algorithm to sample from a N(Q⁻¹b, Q⁻¹) distribution that avoids explicitly calculating the inverse of Q, which is computationally expensive and numerically unstable. Instead, the algorithm in §3.1.2 of Rue (2001) performs a Cholesky decomposition of Q and uses the Cholesky factor to solve a series of linear systems to arrive at a sample from the desired Gaussian distribution. The original motivation was to efficiently sample from Gaussian Markov random fields where Q has a banded structure, so the Cholesky factor and the subsequent linear system solvers can be computed efficiently. Since Q = (Φ^TΦ + D⁻¹) does not have any special structure in the present setting, the Cholesky factorization has complexity O(p³) (Golub & van Loan, 1996, Chapter 4.2.3), and becomes prohibitive for large p. We present an alternative exact mechanism to sample from a Gaussian distribution with parameters as in (6) below:

Algorithm 1

1. Sample u ~ N(0, D) and δ ~ N(0, I_n) independently.

2. Set v = Φu + δ.

3. Solve (ΦDΦ^T + I_n)w = (α − v) to obtain w.

4. Set θ = u + DΦ^Tw.

Proposition 1

Suppose θ is obtained by following Algorithm 1. Then, θ ~ N(μ, Σ), where μ and Σ are as in (6).

Proof

By the Sherman–Morrison–Woodbury identity (Hager, 1989) and some algebra, μ = DΦ^T(ΦDΦ^T + I_n)⁻¹α. By construction, v ~ N(0, ΦDΦ^T + I_n). Combining steps (iii) and (iv) of Algorithm 1, we have θ = u + DΦ^T(ΦDΦ^T + I_n)⁻¹(α − v). Hence θ has a normal distribution with mean DΦ^T(ΦDΦ^T + I_n)⁻¹α = μ. Since cov(u, v) = DΦ^T, we obtain cov(θ) = D − DΦ^T(ΦDΦ^T + I_n)⁻¹ΦD = Σ, again by the Sherman–Morrison–Woodbury identity. This completes the proof; a constructive proof is given in the Appendix.

While Algorithm 1 is valid for all n and p, the computational gains are biggest when p ≫ n and N(0, D) is easily sampled. Indeed, the primary motivation is to use data augmentation to cheaply sample ζ = (v^T, u^T)^T ∈ ℜ^n+p and obtain a desired sample from (6) via linear transformations and marginalization. When D is diagonal, as in the case of global-local priors (2), the complexity of the proposed algorithm is O(n²p); the proof uses standard results about complexity of matrix multiplications and linear system solutions; see §1.3 & 3.2 of Golub & van Loan (1996). For non-sparse D, calculating DΦ^T has a worst-case complexity of O(np²), which is the dominating term in the complexity calculations. In comparison to the O(p³) complexity of the competing algorithm in Rue (2001), Algorithm 1 therefore offers huge gains when p ≫ n. For example, to run 6000 iterations of a Gibbs sampler for the horseshoe prior (Carvalho et al., 2010) with sample size n = 100 in MATLAB on a INTEL(E5-2690) 2.9 GHz machine with 64 GB DDR3 memory, Algorithm 1 takes roughly the same time as Rue (2001) when p = 500 but offers a speed-up factor of over 250 when p = 5000. MATLAB code for the above comparison and subsequent simulations is available at https://github.com/antik015/Fast-Sampling-of-Gaussian-Posteriors.git.

The first line of the proof implies that Algorithm 1 outputs μ if one sets u = 0, δ = 0 in step (i). The proof also indicates that the log-density of (6) can be efficiently calculated at any x ∈ ℜ^p. Indeed, since Σ⁻¹ is readily available, x^TΣ⁻¹x and x^TΣ⁻¹μ are cheaply calculated and log |Σ⁻¹| can be calculated in O(n³) steps using the identity |I_r + AB| = |I_s + BA| for A ∈ ℜ^r×s, B ∈ ℜ^s×r. Finally, from the proof, μ^TΣ⁻¹μ = α^TΦΣ⁻¹Φ^Tα = α^TΦ{D − DΦ^T(ΦDΦ^T + I_n)⁻¹ΦD}Φ^Tα = α^T{(ΦDΦ^T + I_n)⁻¹ΦDΦ^T}α, which can be calculated in O(n³) operations.

3. Frequentist operating characteristics in high dimensions

The proposed algorithm provides an opportunity to compare the frequentist operating characteristics of shrinkage priors in high-dimensional regression problems. We compare various aspects of the horseshoe prior (Carvalho et al., 2010) to frequentist procedures and obtain highly promising results. We expect similar results for the Dirichlet–Laplace (Bhattacharya et al., 2015), normal-gamma (Griffin & Brown, 2010) and generalized double-Pareto (Armagan et al., 2013) priors, which we hope to report elsewhere.

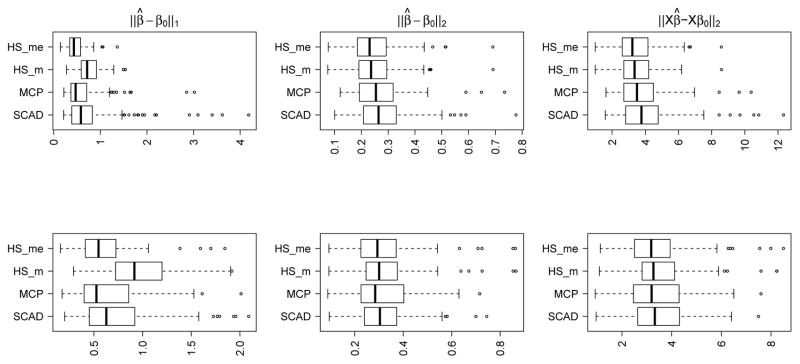
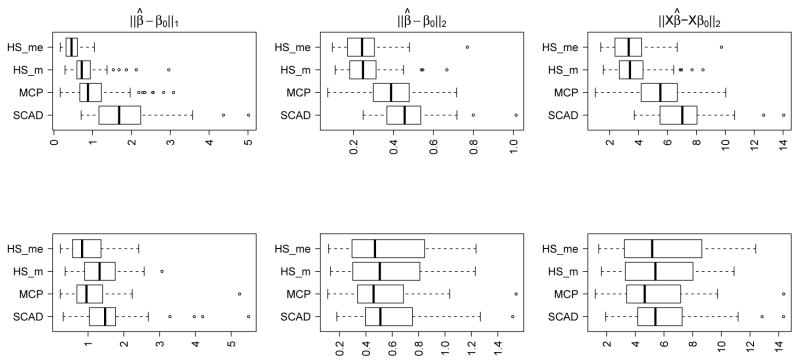
We first report comparisons with smoothly clipped absolute deviation (Fan & Li, 2001) and minimax concave penalty (Zhang, 2010) methods. We considered model (1) with n = 200, p = 5000 and σ = 1.5. Letting x_i denote the ith row of X, the x_is were independently generated from N_p(0, Σ), with (i) Σ = I_p and (ii) Σ_jj = 1, Σ_jj′ = 0.5 (j ≠ j′ = 1, …, p), compound symmetry. The true β₀ had 5 non-zero entries in all cases, with the non-zero entries having magnitude (a) {1.5, 1.75, 2, 2.25, 2.5} and (b) {0.75, 1, 1.25, 1.5, 1.75}, multiplied by a random sign. For each case, we considered 100 simulation replicates. The frequentist penalization approaches were implemented using the R package ncvreg via 10-fold cross-validation. For the horseshoe prior, we considered the posterior mean and the point-wise posterior median as point estimates. Figures 1 and 2 report boxplots for ℓ₁, ||β̂ − β₀||₁, ℓ₂, ||β̂ − β₀||₂, and prediction, ||Xβ̂ − Xβ₀||₂, errors across the 100 replicates for the two signal strengths. The horseshoe prior is highly competitive across all simulation settings, in particular when the signal strength is weaker. An interesting observation is the somewhat superior performance of the pointwise median even under an ℓ₂ loss; a similar fact has been observed about point mass mixture priors (Castillo & van der Vaart, 2012) in high dimensions. We repeated the simulation with p = 2500 with similar conclusions. Overall, out of the 24 settings, the horseshoe prior had the best average performance over the simulation replicates in 22 cases.

Fig. 1.

Boxplots of ℓ₁, ℓ₂ and prediction error across 100 simulation replicates. HSme and HSm respectively denote posterior point wise median and mean for the horeshoe prior. True β₀ is 5-sparse with nonzero entries ±{1.5, 1.75, 2, 2.25, 2.5}. Top row: Σ = I_p (independent). Bottom row: Σ_jj = 1, Σ_jj′ = 0.5, j ≠ j′ (compound symmetry).

Fig. 2.

Same setting as in Fig 1. True β₀ is 5-sparse with non-zero entries ±{0.75, 1, 1.25, 1.5, 1.75}.

While there is now a huge literature on penalized point estimation, uncertainty characterization in p > n settings has received attention only recently (Zhang & Zhang, 2014; van de Geer et al., 2014; Javanmard & Montanari, 2014). Although Bayesian procedures provide an automatic characterization of uncertainty, the resulting credible intervals may not possess the correct frequentist coverage in nonparametric/high-dimensional problems (Szabó et al., 2015). This led us to investigate the frequentist coverage of shrinkage priors in p > n settings; it is trivial to obtain element-wise credible intervals for the β_js from the posterior samples. We compared the horseshoe prior with van de Geer et al. (2014) and Javanmard & Montanari (2014), which can be used to obtain asymptotically optimal elementwise confidence intervals for the β_js. We considered a similar simulation scenario as before. We let p ∈ {500, 1000}, and considered a Toeplitz structure, Σ_jj′ = 0.9^|j−j′|, for the covariate design (van de Geer et al., 2014) in addition to the independent and compound symmetry cases stated already. The first two rows of Table 1 report the average coverage percentages and 100×lengths of confidence intervals over 100 simulation replicates, averaged over the 5 signal variables. The last two rows report the same averaged over the (p − 5) noise variables.

Table 1.

Frequentist coverages (%) and 100×lengths of pointwise 95% intervals. Average coverages and lengths are reported after averaging across all signal variables (rows 1 and 2) and noise variables (rows 3 and 4). Subscripts denote standard errors (%) for coverages. LASSO and SS respectively stand for the methods in van de Geer et al. (2014) and Javanmard & Montanari (2014). The intervals for the horseshoe (HS) are the symmetric posterior credible intervals.

p	500									1000
Design	Independent			Comp Symm			Toeplitz			Independent			Comp Symm			Toeplitz
	HS	LASSO	SS	HS	LASSO	SS	HS	LASSO	SS	HS	LASSO	SS	HS	LASSO	SS	HS	LASSO	SS
Signal Coverage	931.0	7512.0	823.7	950.9	734.0	804.0	944.0	807.0	795.6	942.0	7812.0	855.1	941.0	772.0	827.4	951.0	763.0	808.3
Signal Length	42	46	41	85	71	75	86	79	74	39	41	42	82	76	77	105	96	95
Noise Coverage	1000.0	990.8	991.0	1000.0	981.0	990.8	981	981.0	990.6	990.0	991.0	980.9	1000.0	991.0	990.1	1000.0	991.0	990.2
Noise Length	2	43	40	4	69	73	5	78	73	0.6	042	41	0.7	76	77	0.3	98	93

Table 1 shows that the horseshoe prior gives superior performance. An attractive adaptive property of shrinkage priors emerges, where the lengths of the intervals automatically adapt between the signal and noise variables, maintaining the nominal coverage. The frequentist procedures seem to yield approximately equal sized intervals for the signals and noise variables. The default choice of the tuning parameter λ ≍(log p/n)^1/2 suggested in van de Geer et al. (2014) seemed to provide substantially poorer coverage for the signal variables at the cost of improved coverage for the noise, and substantial tuning was required to arrive at the coverage probabilities reported. The default approach of Javanmard & Montanari (2014) produced better coverages for the signals compared to van de Geer et al. (2014). The horseshoe and other shrinkage priors are free of tuning parameters. The same procedure used for estimation automatically provides valid frequentist uncertainty characterization.

4. Discussion

Our numerical results warrant additional numerical and theoretical investigations into properties of shrinkage priors in high dimensions. The proposed algorithm can be used for essentially all the shrinkage priors in the literature and should prove useful in an exhaustive comparison of existing priors. Its scope extends well beyond linear regression. For example, extensions to logistic and probit regression are immediate using standard data augmentation tricks (Albert & Chib, 1993; Holmes & Held, 2006). Multivariate regression problems where one has a matrix of regression coefficients can be handled by block updating of the vectorized coefficient matrix; even if p < n, the number of regression coefficients may be large if the dimension of the response if moderate. Shrinkage priors have been used as a prior of factor loadings in Bhattacharya & Dunson (2011), who update the p > n rows of the factor loadings independently, exploiting the assumption of independence in the idiyosyncratic components, but their algorithm does not extend to approximate factor models, where the idiyosyncratic errors are dependent. The proposed algorithm can be adapted to such situations by block updates of the vectorized loadings. Finally, we envision applications in high-dimensional additive models where each of a large number of functions is expanded in a basis, and the basis coefficients are updated in a block.

Appendix

We provide a constructive proof of Proposition 1 as suggested by a reviewer. Without loss of generality let D = I_p since if z ~ N(ΣΦ^Tα, Σ) then D^1/2z ~ N(μ̃, Σ̃) where Σ̃ = (Φ̃^TΦ̃ + I_p)⁻¹ and μ̃= Σ̃Φ̃^Tα with Φ̃ = ΦD^−1/2. Now using the Sherman–Morrison–Woodbury matrix identity we can write

$${({\mathrm{\Phi }}^{\mathrm{T}}\mathrm{\Phi }+{\mathrm{I}}_{\mathrm{p}})}^{-1}={\mathrm{I}}_{\mathrm{p}}-{\mathrm{\Phi }}^{\mathrm{T}}{(\mathrm{\Phi }{\mathrm{\Phi }}^{\mathrm{T}}+{\mathrm{I}}_n)}^{-1}\mathrm{\Phi }={\{{\mathrm{I}}_{\mathrm{p}}-{\mathrm{\Phi }}^{\mathrm{T}}{(\mathrm{\Phi }{\mathrm{\Phi }}^{\mathrm{T}}+{\mathrm{I}}_n)}^{-1}\mathrm{\Phi }\}}^2+{\mathrm{\Phi }}^{\mathrm{T}}{(\mathrm{\Phi }{\mathrm{\Phi }}^{\mathrm{T}}+{\mathrm{I}}_n)}^{-2}\mathrm{\Phi }.$$

Then, if u ~ N(0, I_p) and δ ~ N(0, I_n) are independent and we set

$$\theta =\{{\mathrm{I}}_{\mathrm{p}}-{\mathrm{\Phi }}^{\mathrm{T}}{(\mathrm{\Phi }{\mathrm{\Phi }}^{\mathrm{T}}+{\mathrm{I}}_n)}^{-1}\mathrm{\Phi }\}u+{\mathrm{\Phi }}^{\mathrm{T}}{(\mathrm{\Phi }{\mathrm{\Phi }}^{\mathrm{T}}+{\mathrm{I}}_n)}^{-1}\delta +{\mathrm{\Phi }}^{\mathrm{T}}\alpha -{\mathrm{\Phi }}^{\mathrm{T}}{(\mathrm{\Phi }{\mathrm{\Phi }}^{\mathrm{T}}+{\mathrm{I}}_n)}^{-1}\mathrm{\Phi }{\mathrm{\Phi }}^{\mathrm{T}}\alpha ,$$

then θ has the desired distribution (6). Algorithm 1 follows from some straightforward algebra.