Auto-calibrated Wave-CAIPI Reconstruction; Joint Optimization of K-space Trajectory and Parallel Imaging Reconstruction

Abstract

Purpose

Fast MRI acquisitions often rely on efficient traversal of k-space and hardware limitations or other physical effects can cause the k-space trajectory to deviate from a theoretical path in a manner dependent on the image prescription and readout parameters. Additional measurements or generalized calibrations are typically needed to characterize the discrepancies. We propose an auto-calibrated technique to determine these discrepancies.

Methods

A joint optimization is used to estimate the trajectory simultaneously with the parallel imaging reconstruction, without the need for additional measurements. Model reduction is introduced to make this optimization computationally efficient and ensure final image quality.

Results

We demonstrate our approach for the Wave-CAIPI fast acquisition method that utilizes a cork screw k-space path to efficiently encode k-space and spread the voxel aliasing. Model reduction allows for the 3D trajectory to be automatically calculated in fewer than 30s on standard vendor hardware. The method achieves equivalent accuracy to full gradient calibration scans.

Conclusions

The proposed method allows for high quality Wave-CAIPI reconstruction across wide ranges of protocol parameters, such as FOV location/orientation, bandwidth, TE, resolution, and sinusoidal amplitude/frequency. Our framework should allow for the auto-calibration of gradient trajectories from many other fast MRI techniques in clinically relevant time.

Introduction

Fast MRI techniques play a central role in both clinical and research settings due to the potential benefits in shortened scan time, increased temporal sampling/resolution, and reduced distortion. Many of these acquisitions rely on efficient encoding of k-space through the use of continuously slewed gradient fields. Limitations in gradient hardware and other physical effects, such as eddy currents, can cause the trajectory to deviate from the theoretical path. Detailed calibration of the applied trajectory is critical for the accurate reconstruction of images from the accelerated data. In addition, these calibrations can change over time and are dependent on the imaging parameters. For example, EPI(1) is the widely adopted fast Cartesian acquisition scheme that changes phase encoding directionality during the continuous acquisition of multiple readout lines. In most situations, there will be a misalignment between even-odd phase encoding lines that will result in significant ghosting within the reconstructed image. This has necessitated the acquisition of additional navigators to correct for the imperfections in gradient performance.

For more sophisticated trajectories, e.g. Spiral(2), Bunched Phase Encode(3), Wave-CAIPI(4), entire calibration scans(5) can be required to properly characterize and correct for gradient errors. This is critical as even small errors in the trajectory can cause substantial blurring or ghosting artifacts(6). Although these calibration scans are not specific to a patient, they are dependent on the protocol parameters and patient orientation prescription. This severely limits the practical utility of such methods as these acquisition settings change regularly (especially FOV orientation), and the calibration scan would need to be re-acquired per patient. There has also been work examining the use of probes to calculate the MR field and dynamics(7). Limitations in existing methods has led to several attempts to fully model the gradient behavior using system theory(8–10). However, these methods require extensive setup to build a transfer function based upon the system theory approximation and the n will need to be re-tuned after regular scanner maintenance. There has also been recent work toward estimating the image along with non-Cartesian gradient trajectory errors(6) or coil sensitivity maps(11) self-consistently, i.e. iterating between updating either the image or trajectory/parallel imaging parameters. However, the self-consistent optimization strategy utilized in these works deviates from more established optimization approaches for solving non-linear least squares problems. This can limit the applicability/performance of such methods to specific acquisition scenarios. Finally, there has been recent work on self-calibrating radial acquisitions based upon GRAPPA operator gridding (12).

In this work, we introduce a joint optimization approach to find the best gradient model parameters that describe the corrupted trajectory along with the corresponding image to be reconstructed from the under-sampled k-space data acquired through parallel imaging. The optimization considers the quality of both the trajectory parameter estimates and the image simultaneously to ensure robust reconstruction for either Cartesian or non-Cartesian fast MRI acquisitions. Model reduction on both types of variables facilitates the direct application of joint optimization to this large non-convex estimation problem. We illustrate our approach for the Wave-CAIPI acquisition strategy where sinusoidal gradients are superimposed on conventional Cartesian readouts to create a cork-screw trajectory. This widely spreads the voxel aliasing and improves the parallel imaging performance(4,13). For clinically relevant susceptibility weighted imaging (SWI), the joint optimization allows for the accurate estimation of gradient trajectory errors without additional calibration data and requires less than 30s of additional computation time on standard vendor's hardware. The accuracy of our auto-calibrated technique outperforms lengthy calibration scans and enables protocol parameters to be flexibly changed as part of routine use in clinical settings.

Theory

There is a rich history of algorithms for solving non-linear least squares problems in applied mathematics, statistics, and economics. There are many well established techniques such as trust-region, Levenberg-Marquardt, and Nelder-Mead Simplex(14–16) which are formulated in an attempt to robustly arrive at local minimum. These methods jointly (simultaneously) consider all optimization variables and employ different schemes to progress the variables toward a better solution. However, the methods can be computationally prohibitive and may have convergence issues when the number of variables grows large. We will illustrate how model reduction facilitates the joint optimization of the gradient trajectory and imaging parameters. We will then introduce a simplified fast greedy search method that enables the accurate estimation of the parameters.

Joint Optimization

SENSE(17) parallel imaging minimizes ${\sum }_{i=1}^N{\Vert F{C}_{i}x-k_i\Vert }_2$, where F is a Fourier operator that describes the trajectory, C_i is a parallel receive sensitivity, and k_i is the observed k-space data, and x is the image. In the case of trajectory errors F can be replaced with F(g), where the mapping to k-space is now a function of gradient parameters g. In our joint estimation framework, the objective is to minimize ${\sum }_{i=1}^N{\Vert F\left(g\right)C_{i}x-k_i\Vert }_2$ across both x and g (18,19). The parameterization of the encoding operator F(g) is dependent on the sequence of interest and the gradient errors, see (6) for examples related to typical non-Cartesian trajectories. Note that the optimization variables {x, g} can number in the millions, restricting direct use of established optimization techniques. In this work, we will address the large number of optimization variables through model reduction and demonstrate our joint optimization technique for Wave-CAIPI applied to the standard Cartesian 3D GRE acquisition(4). It is important to note that degeneracy in the solution space can occur if a trajectory operator can commute until it is combined with the image. However, this is not the case for the Wave-CAIPI model or many other standard fast MRI applications.

3D GRE Wave-CAIPI

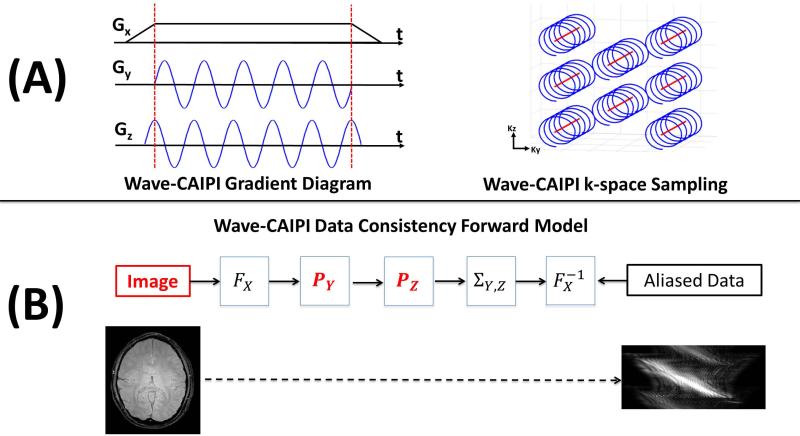
Figure 1(A) illustrates the combination of the linear gradient along the readout G_x, and the sinusoidal gradients played along the phase encode G_y and 3D partition direction G_z. By combining these gradients with a staggered CAIPIRINHA(20) sampling scheme, we arrive at the k-space coverage shown in Figure 1(A). As shown in (4), the encoding created by the sinusoidal gradients G_y and G_z can be captured through a separable point spread function (PSF). Figure 1(B) shows the relationship between the image, the PSF, and the accelerated image space data that has been acquired. In hybrid space (F_x) each k_x line of data at a given (y,z) position gets a unique phase modulation, linearly proportional to their spatial position, which are contained in P_y and P_z respectively. That is, assuming a matrix size [N_x,N_y,N_z], P_y will be of size [N_x,N_y] and P_z is of size [N_x,N_z]. After the wave aliased data has been collapsed, based upon the CAIPIRINHA sampling scheme, it is then returned to image space $\left(F_x^{-1}\right)$ and matched against the acquired accelerated data. An example of the Wave-CAIPI aliasing pattern is shown in the bottom of Figure 1(B).

Figure 1.

Illustration of gradients and k-space coverage for the Wave-CAIPI method are shown in (A). The linear readout direction gradient X is combined with sinusoidal gradients in Y and Z. CAIPIRINHA staggered Cartesian sampling is used for efficient encoding of k-sapce. The forward model used for Wave-CAIPI reconstruction is shown in (B). Both the image and the separable PSF terms P_Y and P_z are considered variables in the joint optimization approach. The aliasing effect based upon the Wave-CAIPI encoding scheme is shown below.

Model Reduction

As mentioned above, there will N_x(N_y + N_z) parameters associated with the PSF and N_xN_yN_z imaging voxels that need to be jointly optimized. Based upon clinically desirable resolutions, slice coverage, and the larger readout oversampling factors used to effectively capture the Wave-CAIPI encoding(4) this can correspond to millions of unknowns. However, we will demonstrate that the number of variables that need to be considered for the estimation of gradient imperfections can be reduced by orders of magnitude while still matching the accuracy of a lengthy calibration scan approach.

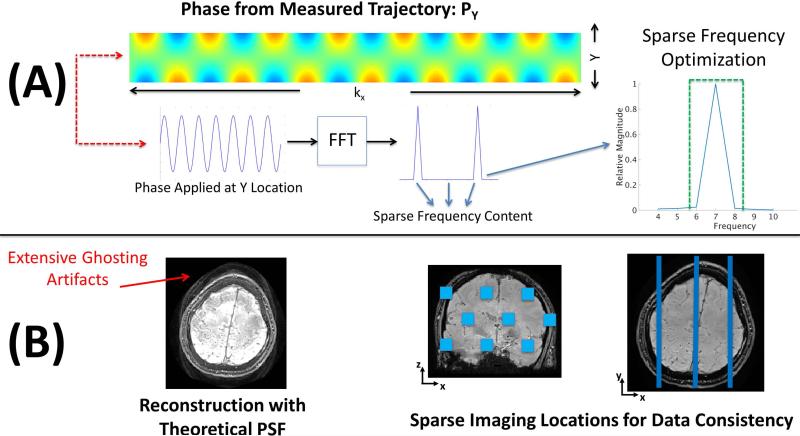
Figure 2(A) shows a typical measured P_y for an acquisition at 2mm isotropic resolution, assuming 7 wave cycles at a bandwidth of 100Hz/pixel. The unwrapped phase map is of size [N_x,N_y] = [768, 84] and was generated by acquiring two fully sampled data sets R = R_y × R_z = 1 × 1 = 1, one with no wave gradients and another with just the Y sinusoidal gradient applied. The PSF is then calculated by taking the ratio from the hybrid space (F_x) of the two data sets. As shown in (4) the PSF can be denoised by regressing the measured PSF against a variety of terms, e.g. a linear trend based upon FOV orientation. If the gradients were operating perfectly the phase applied to any Y location would correspond to a perfect sine wave with energy only at a single frequency. However, as we can see from Figure 2(A) there is broadening that occurs at both the fundamental frequency and DC. Using a limited frequency band we can capture almost all of the energy and accurately describe this function. This corresponds to a very small number of complex values that will need to be optimized. This reduces the number of PSF variables that need to be considered by two orders of magnitude. Alternatively, the frequency content that needs to be optimized can be automatically determined by computing an initial RMSE gradient vector. The RMSE gradient vector is calculated by examining the change in RMSE based upon a small perturbation for each possible variable. A reduced parameter set can be found by examining the relative impact of each variable toward reducing the error.

Figure 2.

(A) shows an example of a measured PSF calculated using fully sampled calibration scans. The phase is computed by taking the hybrid space ratio of an acquisition with no wave gradients and one with the Y wave gradient employed. The measured PSF only requires a sparse number of frequencies to be represented accurately. (B) shows an example of ghosting artifacts in the presence of trajectory errors. Here, the theoretical PSF is used to reconstruct the image. Distribution of SENSE test locations are shown on the right. As the ghosting artifacts appear globally, only a small number of parallel imaging test locations are required to guide the optimization.

Figure 2(B) shows the substantial ghosting artifacts that can arise when reconstructing in the presence of trajectory errors. As can be seen these ghosting artifacts are present in nearly every region of the image. By limiting our joint optimization to a small representative set of voxels, we can ensure these artifacts have been mitigated globally while ameliorating the computational challenges associated with joint optimization. Similar to the original CAIPIRINHA method(20), Wave-CAIPI reconstruction benefits from the attribute that the complete reconstruction can be divided into small decoupled reconstruction problems, each of which can be solved rapidly. Specifically, if we assume acceleration factors R_y and R_z then each Wave-CAIPI sub-problem would be across N_xR_yR_z voxels. Based upon the CAIPIRINHA factor this corresponds to aliased voxels from highly distributed readouts across the (y,z) dimensions. Figure 2(B) shows a typical arrangement of highly separated test locations that sparsely cover the imaging volume. In practice, less than 10 sub-problems are required to successfully guide the joint optimization. This small number of sub-problems is sufficient to clearly differentiate the data consistency benefits of reconstruction using a high quality gradient trajectory estimate when compared to reconstruction in the presence of trajectory errors. In cases where higher frequency modeling terms are required to describe the trajectory, the number of sub-problems required to arrive at an accurate solution is likely to increase.

It is important to note that other acquisition schemes may not correspond to fully decoupled reconstruction problems. However, encoding matrices for many fast MRI acquisition techniques have locality properties, i.e. much larger interactions between neighboring voxels. Therefore, the reconstruction across any small region of interest (assuming all other voxels are fixed at the best current estimate) will only be accurate in the interior of the region and less accurate as you move toward the boundary (21). By reconstructing different overlapping regions of interest (21) as the joint optimization progresses, accurate voxel estimates can be propagated throughout the entire image. The algorithm will converge when there is no change in trajectory variables and the image (the boundary of any region of interest reconstruction will then be correct).

Fast Greedy Search

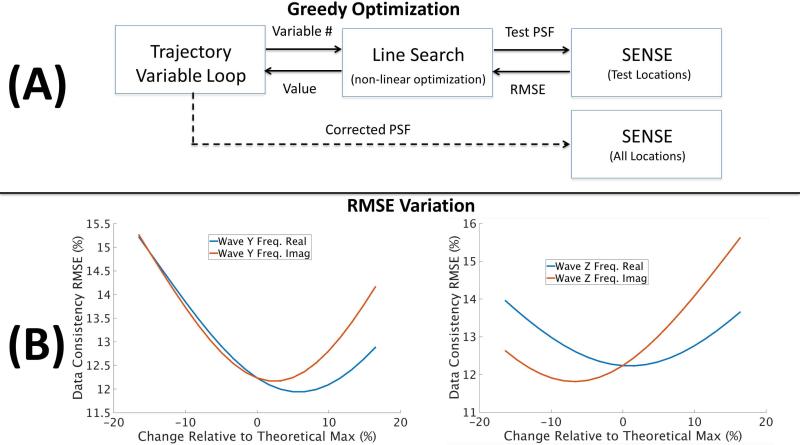
We introduce a fast greedy search algorithm that can be used to effectively solve the joint optimization across the reduced parameter set, see Figure 3(A) for a flow diagram of the approach. In this procedure we optimize the trajectory variables sequentially in order of importance, see description of RMSE gradient vector above. For each variable (real and imaginary parts optimized separately) a line search is performed (golden section search (22)) to improve the data consistency objective. That is, we identify a closed error region around each of the frequency components being optimized and use the quality of the objective to narrow in on a local minimum. The value of the objective function corresponds to calculating the data consistency RMSE associated with the solution of the SENSE problem, which is solved only across the test locations (see Figure 2(B)). For a given trajectory estimate, the solution of the SENSE problem corresponds to the optimal voxel values that can be coupled together with the trajectory variables within the joint optimization. By solving the SENSE problem as we update the trajectory parameters, we ensure only RMSE optimal voxel information is used to guide the joint optimization.

Figure 3.

(A) the joint optimization can be efficiently solved through the use of a fast greedy search. A line search is performed for each of the variables used to describe the gradient trajectory. The objective function corresponds to the data consistency RMSE based upon the SENSE solution, across the small number of test locations. Multiple passes are performed until the method converges to a local minimum. (B) the sensitivity of RMSE to changes in the trajectory variables is illustrated. Here, the percentage change is shown relative to the theoretical gradient amplitude (see Figure 2). Smooth variation in the objective along with clear local minima can be observed.

Figure 3(B) shows the smooth variation in data consistency RMSE as the frequency content is manipulated; both real and imaginary values are shown for the Y and Z gradients. The amount of change is shown relative to the peak theoretical amplitude for the trajectory, see Figure 2(A). This relative measure allows for simple heuristics to be used to bound the search space, e.g. 20% max error. This search process is then repeated for the neighboring frequencies included in the narrow frequency band along with the DC term. Multiple optimization passes through the gradient trajectory variables are performed until only small RMSE improvements are observed and the local minimum for PSF has been obtained. Finally, the optimized PSF can be used for the complete SENSE reconstruction across the full volume.

Methods

In order to demonstrate both the accuracy and computational efficiency of our approach, in vivo data were acquired from a healthy volunteer subject to institutionally approved protocol consent. Data were collected from the subject at two scanners, with different gradient hardware, in attempt to further validate the robustness of the approach. The experiments on the 3T Siemens Skyra scanner were performed with the standard Siemens 32ch array coil and for the 3T Siemens Prisma-Fit scanner the data were acquired with the Siemens 64ch head-neck array coil, without the use of the 12ch neck elements.

Our method was tested for two multi-echo 3D GRE Wave-CAIPI imaging protocols, assuming an acceleration factor R = R_y × R_z = 3 × 3. The first was constructed to closely match protocols used in clinical settings (based on SWI protocols distributed by the manufacturer) and the other to match research literature focusing on Quantitative Susceptibility Mapping (QSM) (4). For both protocols, data were collected from two echoes where the mean echo time corresponds to the desired TE. The following sequence parameters were used for the 1min 18s clinical protocol: resolution 0.76×0.76×1.5mm³, FOV 240×210×144mm³, phase resolution=69%, TR=41ms, TE=13.7, 30.1ms, flip angle=15°, bandwidth=100Hz/pixel, Wave parameters: 31 cycles with max gradient slew=160mT/m/ms and max amplitude=24mT/m. The 1min 51s research protocol has imaging parameters: resolution 1.0×1.0×1.0mm³, FOV 256×192×120mm³, phase resolution=100%, TR=42ms, TE=15.0, 32.0ms, flip angle=15°, bandwidth=100Hz/pixel, Wave parameters: 27 cycles with max gradient slew=180mT/m/ms and max amplitude=35mT/m. In each case, a FLASH reference scan (under 2s) acquired the center 30×30 region of k-space to be used for the estimation of ESPIRiT(23) sensitivity maps. The multi-echo Wave-CAIPI sequence was designed to be flow compensated, through the insertion of additional bipolar gradients, and the reconstructed multi-echo data were combined through root-sum-of-square for the magnitude and TE weighted combination of the unwrapped echo phases. The joint optimization and Wave-CAIPI reconstruction were embedded into the Siemens ICE framework, allowing for auto-calibrated online SWI reconstruction. The computational performance was measured using standard Siemens Skyra and Prisma reconstruction hardware. In order to investigate the accuracy of the joint optimization, we have included functionality that allows for the retrospective reconstruction of the data with either the theoretical PSF or measured PSF. Following the procedure described in (4) the measured PSF is found by acquiring 3 fully sampled calibration scans, i.e. no wave, wave gradient Y, wave gradient Z.

Results

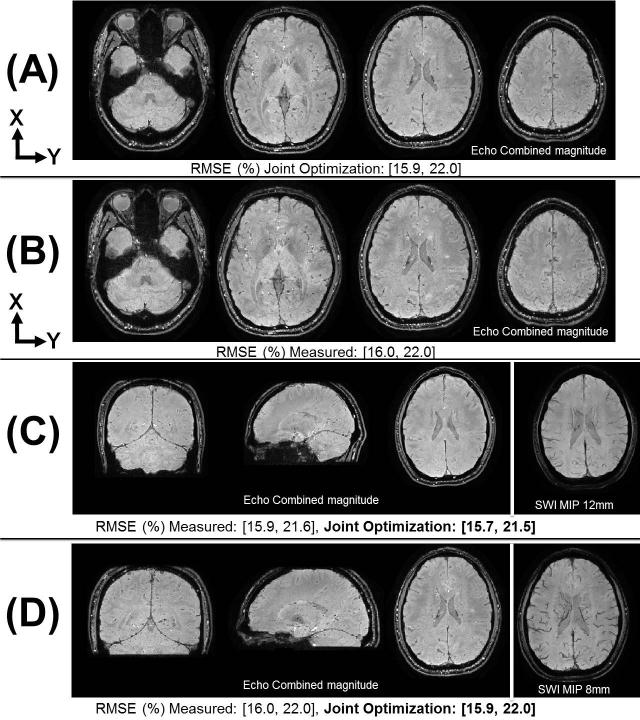
Figure 4(A,B) shows a reconstruction comparison, from the Skyra scanner, when using the jointly optimized PSF and the measured PSF from fully sampled calibration data respectively. Echo combined 1mm isotropic magnitude images are shown for several partitions and the data consistency RMSE (of individual TE volumes) is reported below each set of images. Figure 4(C,D) shows reconstruction results, from the Skyra scanner, using the jointly optimized PSF for the 0.76×0.76×1.5mm³ and 1mm isotropic protocols respectively. Here, the 3D echo combined magnitude images along with an 8 partition averaged SWI image are provided. The data consistency RMSE is also compared against the measured calibration approach. As can be seen in Figure 4 the joint optimization performed at least as well as the measured PSF in all cases, with a max RMSE difference within 2% and similar image quality.

Figure 4.

Reconstruction comparison of measured PSF and auto-calibrated joint optimization approaches for R_y × R_z = 3 × 3 Wave-CAIPI multi-echo 3D-GRE data. (A,B) shows data acquired at 1.0×1.0×1.0mm³ resolution with FOV 256×192×120mm³. The echo combined TE=23.5ms magnitude images are shown for several partitions. The data consistency RMSE (of individual TE volumes) is reported below the respective images. (C,D) shows auto-calibrated joint optimization results for two protocols; echo combined TE=21.9 and TE=23.5ms magnitude images are shown respectively along with the SWI images averaged across 8 partitions. (C) contains images acquired at 0.76×0.76×1.5mm³ resolution with FOV 240×210×144mm³ (D) contains images acquired at 1.0×1.0×1.0mm³ resolution with FOV 256×192×120mm³.

Table 1 shows a comparison of the frequency content for the jointly optimized PSF when compared to the theoretical gradient waveform. Both protocols were acquired on the two scanners and the FOV was rotated in an attempt to maximize brain coverage. It can be clearly seen that the amplitude of the wave deviates several percent from the theoretical value, which can correspond to over a 30% increase in data consistency RMSE. In addition, the asymmetry between the Y and Z directional Primsa gradient coils is evident with the 4× larger deviations in estimated amplitudes when compared to the Skyra scanner. The per echo data consistency RMSE is shown below the PSF values in Table 1. Both scanners showed a consistent 1-2% variation in RMSE between the two protocols. This variation can be attributed to the differences in resolution, slice coverage, and SNR associated with the acquired TE for each protocol.

Table 1.

Estimated PSF frequency content from the joint optimization across two scanners and two protocols. The estimated values are compared against the theoretical for both the Y and Z gradient waveforms. The resolution and per echo data consistency RMSE are reported below the PSF values.

	Frequency	Theoretical PSF		Skyra Scanner		Prisma Scanner
		Real	Imag	Real	Imag	Real	Imag
Y Gradient	0	0.000	0.000	−0.038	0.000	0.000	0.000
	26	0.000	0.000	0.000	−0.005	0.000	−0.003
	27	0.000	0.834	0.003	0.837	0.004	0.829
	28	0.000	0.000	0.000	0.003	0.000	0.002
Z Gradient	0	1.668	0.000	1.680	0.000	1.668	0.000
	26	0.000	0.000	−0.007	−0.002	−0.003	0.000
	27	0.000	0.834	0.051	0.832	−0.012	0.849
	28	0.000	0.000	0.005	0.000	0.002	−0.002
Resolution: 1.0×1.0×1.0mm3				RMSE (%): [17, 24]		RMSE (%): [13, 18]

	Frequency	Theoretical PSF		Skyra Scanner		Prisma Scanner
		Real	Imag	Real	Imag	Real	Imag
Y Gradient	0	0.000	0.000	0.038	0.000	0.000	0.000
	30	0.000	0.000	0.000	−0.002	0.000	0.000
	31	0.000	0.567	0.003	0.546	−0.001	0.565
	32	0.000	0.000	0.000	0.002	0.000	0.000
Z Gradient	0	1.130	0.000	1.170	0.000	1.170	0.000
	30	0.000	0.000	−0.002	0.000	−0.002	0.000
	31	0.000	0.567	0.014	0.544	−0.026	0.576
	32	0.000	0.000	0.000	0.000	0.002	0.000
Resolution: 0.76×0.76×1.5mm3				RMSE (%): [16, 22]		RMSE (%): [12, 16]

Finally, the joint optimization converged within 30s for all protocols and scanners/coils used. The total post scan reconstruction time was less than 2min for the 32ch array coil data on the Skyra scanner and under 4min 30s using the 64ch array coil (52 elements enabled) on the Prisma scanner. In all cases, the vendor's global singular value based channel compression was enabled.

Discussion and Conclusions

In this work we propose a joint optimization strategy that can be used to determine gradient trajectories for auto-calibrated image reconstruction. The technique is applicable to both Cartesian and non-Cartesian fast MRI acquisition techniques. The reduction of optimization variables is a key element that allows for a non-alternating joint reconstruction of the unknowns. We demonstrate a reduction, several orders of magnitude, in both the gradient trajectory modeling parameters as well as the parallel imaging voxels for Wave-CAIPI. This reduced model allows for direct application of established optimization techniques for solving the non-linear least squares problem. As can be seen in previous works (6), gradient trajectories for many commonly used fast acquisitions can be compactly represented. Thus, the consideration of the reduced modeling for gradient trajectories will serve as a starting point to develop new encoding techniques.

We have demonstrated online reconstruction with our joint optimization approach for clinically relevant 3D GRE Wave-CAIPI data. The joint optimization was able to be computed in fewer than 30s, even when utilizing the larger 64ch array coil (52 elements enabled). The computational cost for the optimization can be further improved with the use of GPU resources that are available on many scanner platforms. The computational cost can be further improved with the use of a priori information about the system hardware. This information can be incorporated into the optimization as an initial guess for the trajectory parameters. In addition to the computational efficiency of our approach, we have also demonstrated comparable accuracy to full calibration based methods. Additional qualitative evaluation of the joint optimization approach has been performed through testing across wide ranges of protocol parameters, such as FOV location/orientation, bandwidth, TE, resolution, and sinusoidal amplitude/frequency. The results shown in this work are for a single subject across 2 different scanners (from the same manufacturer). Further quantification of the accuracy of the method should be performed across manufacturers and additional subjects.

Finally, we consider extending our joint optimization approach to estimate many other encoding effects that can be represented compactly. For example, B₀ and B₁ field maps(18,19) as well as parameters related to subject motion(24). When these additional modeling terms are included, the encoding will likely become fully coupled. However, the locality of interactions in typical encoding situations should allow for efficient model reduction through the use of sliding regions of interest (domain decomposition (21)).