Ramped-amplitude NOVEL

Abstract

We present a pulsed dynamic nuclear polarization (DNP) study using a ramped-amplitude nuclear orientation via electron spin locking (RA-NOVEL) sequence that utilizes a fast arbitrary waveform generator (AWG) to modulate the microwave pulses together with samples doped with narrow-line radicals such as 1,3-bisdiphenylene-2-phenylallyl (BDPA), sulfonated-BDPA (SA-BDPA), and trityl-OX063. Similar to ramped-amplitude cross polarization in solid-state nuclear magnetic resonance, RA-NOVEL improves the DNP efficiency by a factor of up to 1.6 compared to constant-amplitude NOVEL (CA-NOVEL) but requires a longer mixing time. For example, at τ_mix = 8 μs, the DNP efficiency reaches a plateau at a ramp amplitude of ∼20 MHz for both SA-BDPA and trityl-OX063, regardless of the ramp profile (linear vs. tangent). At shorter mixing times (τ_mix = 0.8 μs), we found that the tangent ramp is superior to its linear counterpart and in both cases there exists an optimum ramp size and therefore ramp rate. Our results suggest that RA-NOVEL should be used instead of CA-NOVEL as long as the electronic spin lattice relaxation T_1e is sufficiently long and/or the duty cycle of the microwave amplifier is not exceeded. To the best of our knowledge, this is the first example of a time domain DNP experiment that utilizes modulated microwave pulses. Our results also suggest that a precise modulation of the microwave pulses can play an important role in optimizing the efficiency of pulsed DNP experiments and an AWG is an elegant instrumental solution for this purpose.

INTRODUCTION

Dynamic nuclear polarization (DNP) is widely accepted as a powerful technique for improving the sensitivity of nuclear magnetic resonance (NMR) signals,¹ but instrumental considerations to date have dictated that only continuous wave (CW) microwave irradiation can be utilized in the experiments.^2–8 These CW experiments, namely, the cross effect and solid effect, enhance signal intensities by one to two orders of magnitude and enable otherwise impossible experiments,^9–16 but they nevertheless exhibit an inverse dependence on the B₀ field.^3,8,17–21 Furthermore, to adjust the relaxation times so that the experiments function with optimal efficiency, it is often necessary to perform them at cryogenic temperatures and/or high microwave power.^22–29 As a consequence, these requirements limit the applicability of DNP in NMR. There are ongoing efforts that address these limitations, for example, by utilizing the Overhauser effect in insulating solids that scales linearly with the Zeeman field, B₀, and requires much less microwave power.^30,31 However, a more general approach to address the inverse field dependence is pulsed or time domain DNP. Specifically, what is needed is a repertoire of pulse sequences that allow an efficient transfer of polarization from electrons to nuclei regardless of B₀. Although pulsed DNP often requires intense peak microwave power, the average power is low due to the low duty cycle. Thus, in combination with rapid polarization transfers, pulsed DNP is potentially the method of choice for experiments at ambient temperature.

The development of time domain DNP dates from the late 1980s and was stimulated by the need for methods to prepare polarized targets for neutron diffraction experiments using short lifetime photo-excited triplet states.^32,33 Pulse sequences including nuclear orientation via electron spin locking (NOVEL) and the integrated solid effect (ISE) were introduced and employed for these applications.^34–37 In contrast, contemporary applications in magic angle spinning (MAS) NMR rely heavily on CW DNP, in particular the cross effect using biradical polarizing agents.^38–41 It is worth noting that attempts to apply pulsed DNP were initiated about the same time as the first gyrotron based MAS DNP/NMR experiments, a technique that has been widely used over the last decade.⁴² The slow progress of pulsed DNP is the result of a paucity of pulse microwave amplifiers operating at high output powers (kW) and high frequencies (above 100 GHz). Nevertheless, the potential of time domain experiments has stimulated the development of new DNP sequences such as DNP in the nuclear rotating frame (NRF), the dressed state solid effect (DSSE), polarization of nuclear spin enhanced by ENDOR (PONSEE), and a sequence based on optimum control theory.^43–46 Furthermore, recent advances in microwave amplifier technology establish pulsed DNP as a promising technique on the horizon.^47,48

Among these sequences listed above, NOVEL, a rotating frame-lab frame analogue of Hartmann-Hahn cross polarization (CP), can potentially play the same role for DNP as does CP in solid state NMR.^49,50 CP belongs to a family of “sudden” experiments in which the density operator nutates around the Hamiltonian, giving rise to the transfer of polarization. In powder samples, the interference of different dipolar coupling strengths leads to 50% polarization transfer efficiency at quasi-equilibrium (long contact time). Even though ramped amplitude (RA)-CP appears to be very similar to CP, it differs fundamentally in that it is an “adiabatic” process whereby the Hamiltonian changes slowly allowing the density operator to follow, and the polarization transfer occurs virtually at the center of the ramp. This happens approximately simultaneously for all orientations and distances, thereby suppressing transient oscillations and generating 100% polarization transfer efficiency that is a factor of ∼2 larger than that obtained with constant amplitude (CA)-CP.^51–53

Recently, we demonstrated high DNP efficiency using the NOVEL pulse sequence under the sample conditions used in DNP/NMR experiments.^54,55 Inspired by the advantage of RA-CP (vide supra), we report herein the performance of the ramped amplitude (RA)-NOVEL sequence utilizing the newly available arbitrary waveform generator (AWG) function on an X-band EPR spectrometer. The AWG allows precise and convenient manipulations of microwave pulses and was used to ramp the amplitude of the spin locking pulse. With this innovation we obtained a factor of up to 1.6 larger DNP enhancement. The improvement appears to be versatile with respect to the polarizing agent as well as the shape of the ramp (linear vs. tangent) as long as the ramp is sufficiently long.

BACKGROUND

In this section, we provide a brief theoretical description relevant to the experiments that follow. The description is in part similar to that presented previously,⁵⁴ the extension being the discussion of linear RA-NOVEL. With the microwave applied on resonant with the EPR transition, the Hamiltonian in the microwave rotating frame can be written as

$$H={\omega }_{1S}{S}_x-{\omega }_{0I}{I}_z+\left(A{I}_z+B{I}_x\right)S_z,$$

where the first term originates from the microwave spinlock field, the second term corresponds to the Zeeman interaction of proton, and A and B are the isotropic and anisotropic hyperfine coupling, respectively. In the tilted frame defined such that

$$S_x\to S_z,S_y\to S_y,S_z\to -S_x,$$

the Hamiltonian is transformed to

$$H={\omega }_{1S}{S}_z-{\omega }_{0I}{I}_z-\left(A{I}_z+B{I}_x\right)S_x.$$

Using perturbation theory, we separate the Hamiltonian into the unperturbed H₀ and the perturbation H₁ which are given as follows:

$$H_0={\omega }_{1S}{S}_z-{\omega }_{0I}{I}_z,$$

$$H_1=-A{I}_z{S}_x-B{I}_x{S}_x.$$

At the NOVEL condition $\left({\omega }_{1S}={\omega }_{0I}\right)$, the contribution from the A term of H₁ is proportional to $\frac{A}{2{\omega }_{0I}}$. Even in the case of 1,3-bisdiphenylene-2-phenylallyl (BDPA) or sulfonated-BDPA (SA-BDPA) radicals $\left(A\sim 5\text{MHz}\right)$, and at low field $\left({\omega }_{0I}\approx 15\text{MHz}\right)$, the ratio is small (1/6). Moreover, our RA-NOVEL experimental data (vide infra) for SA-BDPA and trityl-OX063, which have negligible isotropic coupling, reveal a strong similarity. Thus, to simplify the subsequent treatment of the Hamiltonian, we assume that the isotropic hyperfine coupling term can be neglected, an assumption that will be more relevant at higher B₀ fields. Under these circumstances, H₁ is truncated to

$$H_1\approx -B{I}_x{S}_x.$$

The Hamiltonian becomes block diagonal

$$H=H_0+H_1\approx {\omega }_{1S}{S}_z-{\omega }_{0I}{I}_z-B{I}_x{S}_x=H_{ZQ}\oplus H_{DQ},$$

where ZQ and DQ correspond to zero quantum and double quantum, respectively. At the NOVEL condition $\left({\omega }_{1S}={\omega }_{0I}\right)$, the matrix form of the Hamiltonian in each subspace is given as

$$H_{ZQ}=\frac{1}{2}\left(\begin{array}{cc}\hfill -\left({\omega }_{1S}+{\omega }_{0I}\right)\hfill & \hfill \frac{B}{2}\hfill \\ \hfill \frac{B}{2}\hfill & \hfill \left({\omega }_{1S}+{\omega }_{0I}\right)\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill -{\omega }_{0I}\hfill & \hfill \frac{B}{4}\hfill \\ \hfill \frac{B}{4}\hfill & \hfill {\omega }_{0I}\hfill \end{array}\right),$$

$$H_{DQ}=\frac{1}{2}\left(\begin{array}{cc}\hfill -\left({\omega }_{1S}-{\omega }_{0I}\right)\hfill & \hfill \frac{B}{2}\hfill \\ \hfill \frac{B}{2}\hfill & \hfill \left({\omega }_{1S}-{\omega }_{0I}\right)\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \frac{B}{4}\hfill \\ \hfill \frac{B}{4}\hfill & \hfill 0\hfill \end{array}\right).$$

While the perturbation effect in the ZQ subspace can be ignored ($B\mathrm{/}2{\omega }_{0I}$ is small), its contribution in the DQ subspace drives the polarization transfer at a rate that depends on the strength of the anisotropic interaction. In a powder sample, interference of different distances and orientations leads to 50% efficiency at quasi-equilibrium (long mixing time).

In the case of a linear ramp centered at ${\omega }_{1S}={\omega }_{0I}$, we assume that the mixing time ${\tau }_{mix}$ is long compared to the period of the microwave frequency, in which case the matrix form of H_DQ is

$$H_{DQ}(t)=\left(\begin{array}{cc}\hfill -\frac{1}{2}{\dot{\omega }}_{1S}t\hfill & \hfill \frac{B}{4}\hfill \\ \hfill \frac{B}{4}\hfill & \hfill \frac{1}{2}{\dot{\omega }}_{1S}t\hfill \end{array}\right),$$

where ${\dot{\omega }}_{1s}$ is the ramp rate and $-\frac{{\tau }_{mix}}{2}\le t\le \frac{{\tau }_{mix}}{2}$. Thus we arrive at the situation discussed with Landau-Zener theory.⁵⁶ If the ramp in the microwave amplitude is adiabatic satisfying the condition

$$\frac{B^2}{16{\dot{\omega }}_{1S}}\gg 1$$

for all possible values of B, then the polarization transfer occurs at the center of the ramp for all orientations and distances. This leads to 100% efficiency which is a factor of 2 improvement compared to CA-NOVEL. The adiabatic condition also suggests that a stronger coupling enables a faster ramp rate.

EXPERIMENTAL

EPR and pulsed DNP/NMR experiments were performed on a Bruker ElexSys E580 X-band EPR spectrometer using an EN 4118X-MD4 ENDOR probe. The probe consists of a dielectric resonator wrapped with a saddle coil for RF excitation. In normal operation, the coil is untuned to permit ENDOR experiments spanning a broad range of RF frequencies. However, for our DNP/NMR experiments, the RF coil was locally tuned to the desired ¹H frequency (∼15 MHz) by a module of tuning and matching capacitors to improve the RF excitation efficiency and detection sensitivity. An iSpin-NMR spectrometer purchased from Spincore Technologies, Inc. (Gainesville, FL, US) was used for the RF excitation and detection of the NMR signals. The ¹H NMR signals were acquired via a solid echo sequence with 8-step phase cycling. The signals were processed using a home-written MATLAB program.⁵⁷

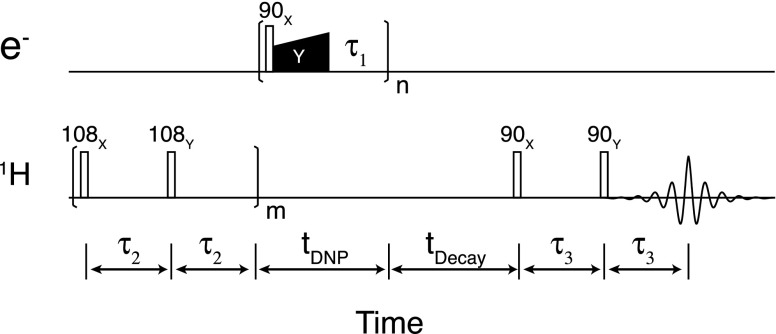
The microwave bridge of the EPR spectrometer is equipped with a SpinJet AWG commercially available from Bruker BioSpin. The desired waveform is achieved by sideband suppression mixing of the main carrier frequency with the waveform generated by the SpinJet. The AWG has 8 output channels each of which has 192 kSa of memory, 14 bits of amplitude resolution, and 0.625 ns time resolution corresponding to a bandwidth of ±400 MHz about the carrier. The SpinJet AWG allows the amplitude modulation (amplitude ramp) during the locking pulse (microwave pulse Y in Fig. 1). In this paper, the locking pulse is used interchangeably with the mixing time or contact time.

FIG. 1.

Ramped-amplitude NOVEL pulsed DNP sequence. The pulse sequence is identical to the constant-amplitude NOVEL sequence except for the amplitude modulation of the microwave locking pulse (Y pulse). The amplitude is ramped from ${\omega }_{1S}-\left(\mathrm{\Delta }{\omega }_{1S}/2\right)$ to ${\omega }_{1S}+\left(\mathrm{\Delta }{\omega }_{1S}/2\right)$, corresponding to the ramp size of $\mathrm{\Delta }{\omega }_{1S}$, with linear or tangent shape profiles.

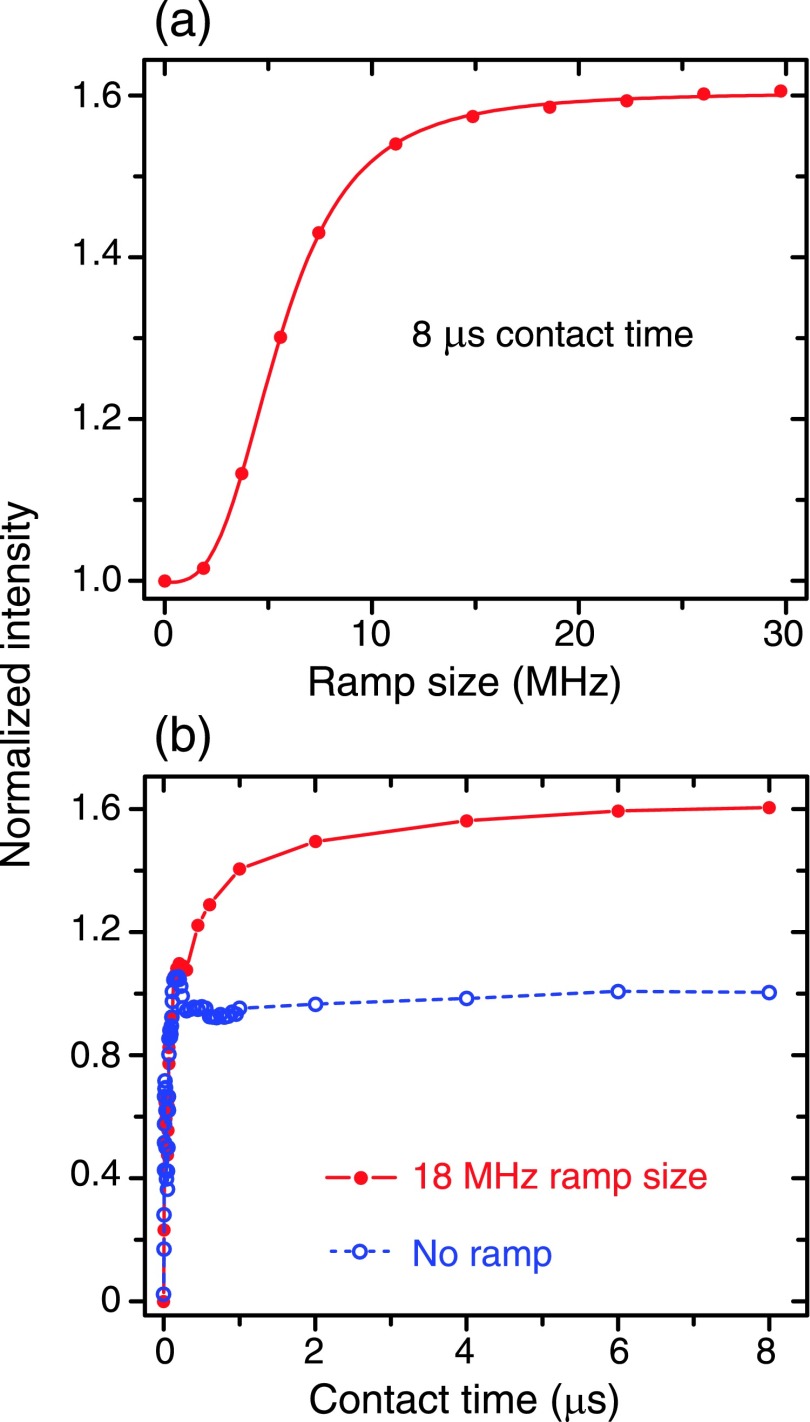
Samples for the experimental data shown in Figures 2 and 3 consisted of 40 mM SA-BDPA dissolved in glycerol-d₈/D₂O/H₂O (60/30/10 volume ratio) at 80 K. The data in Figure 4 were obtained from polystyrene doped with 2% BDPA at 300 K.

FIG. 2.

Performance of the RA-NOVEL sequence on a sample containing 40 mM SA-BDPA in glycerol-d8/D₂O/H₂O (60/30/10 volume ratio) at 80 K. (a) Optimization of the ramp size. The length of the locking pulse was fixed at 8 μs, whereas the ramp size was varied from 0 to ∼30 MHz. The resulting DNP-enhanced NMR signals were normalized to that obtained with the CA-NOVEL sequence (a ramp size of 0 MHz). The intensity reaches a plateau at ∼18 MHz of ramp size (ramp from 6 MHz to 24 MHz). (b) Contact time dependent curves for CA-NOVEL (no ramp) and RA- NOVEL with 18 MHz ramp size. In comparison, RA-NOVEL builds up more slowly (3 μs compared to 150 ns) and reaches higher efficiency in a quasi-equilibrium state (long mixing time). The DNP efficiency is improved by a factor of 1.6 using RA-NOVEL.

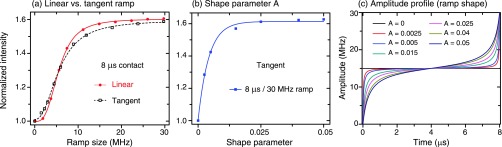
FIG. 3.

Comparison between different ramp profiles at 8 μs contact time and 30 MHz ramp size. (a) Negligible difference between linear and tangent ramps at 8 μs contact time. (b) Performance of difference tangent ramp schemes characterized by a single shape parameter A. The corresponding amplitude profiles are given in (c). The data were taken on the same samples and temperatures described in Fig. 2.

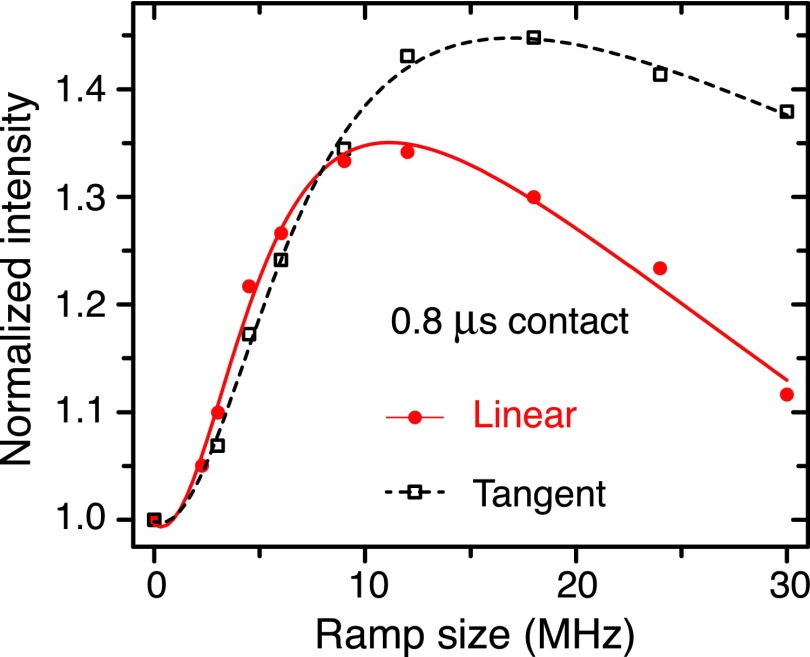
FIG. 4.

Linear vs. tangent ramps at short contact time (0.8 μs). The difference becomes apparent at a large ramp size. In this case, tangent ramp appears to be more efficient. In both cases, the optimum ramp rate is indicative of the adiabaticity of the ramped-NOVEL sequence. Experiments were performed at room temperature on a sample of polystyrene doped with 2% BDPA.

RESULTS

We implemented the pulse sequence shown in Figure 1, which is identical to the NOVEL sequence except for the amplitude modulation of the microwave locking pulse (the Y pulse). The optimization of all the experimental parameters was accomplished using the procedure described in our previous study.⁵⁴ For the pre-saturation on ¹H, we used a chain of 16 pulses (m = 8) with the inter-pulse delay of ${\tau }_2=5$ ms. For NMR signal detection, the solid echo sequence was used with ${\tau }_3=20$ μs. The recovery delay for the electron $\left({\tau }_1\right)$ was typically 10 ms and 1.5 ms for SA-BDPA and trityl-OX063, respectively, at 80 K. The microwave pulses were repeated n times for the ¹H polarization to buildup. For a full buildup, we used $n=3T_b/{\tau }_1$ in which $T_b$ is the buildup time constant of ¹H. Typically, n can be as large as ∼10,000. Additionally, the size, rate, and shape of the ramp required optimization. Figure 2(a) illustrates the effect of the ramp size on the DNP efficiency while the mixing time was fixed at 8 μs on a sample containing 40 mM SA-BDPA. The DNP-enhanced NMR signals were normalized to those obtained with the CA-NOVEL sequence (ramp size = 0 MHz). The intensity increases with the ramp size and plateaus at ∼18 MHz, which corresponds to a ramp from 6 MHz to 24 MHz. We obtained an enhancement of ∼85 with CA-NOVEL, consistent with our previous study, and ∼135 with RA-NOVEL which corresponds to a factor of up to 1.6 improvement. The improvement in the DNP enhancement is further confirmed in Figure 2(b) wherein we incremented the mixing time up to 8 μs with and without the amplitude ramp. In comparison to CA-NOVEL, the polarization in the RA-NOVEL builds more slowly but results in higher efficiency.

We investigated the performance of a tangential ramp at τ_mix = 8 μs (Figure 3). As revealed in Figure 3(a), we found negligible differences between linear and tangent ramps, with both saturating at a ∼20 MHz ramp size with 1.6 improvement. In Figures 3(b) and 3(c), we varied the ramp shape, characterized by a single shape parameter A, with the following ramp profile:

$${\omega }_{1S}(t)={\omega }_{0I}-A\cdot \tan \left\{\arctan \left[\frac{{\omega }_{0I}}{A}\left(1-2\frac{t}{{\tau }_{mix}}\right)\right]\right\}.$$

A = 0 corresponds to the constant-NOVEL sequence (no ramp). For A > 0 we obtain different tangent profiles having an initial slope decreasing with increasing A (Figure 3(c)), but the ramp size is fixed to $2{\omega }_{0I}$ (∼30 MHz).

In Figure 4, we compare the performance of linear and tangent ramps at a short mixing time of 0.8 μs as opposed to 8 μs on a sample of polystyrene doped with 2% BDPA. These data were acquired at room temperature (300 K). We found that there exists an optimum ramp size and thus ramp rate, which is indicative of the adiabaticity of the pulse sequence.

DISCUSSION

The improvement (ramped-amplitude vs. constant-amplitude) obtained with RA-NOVEL is similar to that achieved experimentally with RA-CP. A detailed study by Metz et al. in CP MAS NMR experiments showed an improvement factor of up to 1.6 and the possibility of extending this effect to a 1.8 enhancement with a sufficiently long mixing time.⁵¹ In our experiments, the longest mixing times allowed by the traveling-wave tube (TWT) were ∼10 μs, and larger improvements might be possible with extended microwave pulses. The theoretical limit (a factor of 2 improvement) was only observed with RA-CP in a model system of diluted spin pairs such as ¹H–¹³C in a sample of 2–¹³C–²H₃-alanine diluted in perdeuterated alanine.⁵⁸ Our results approach the theoretical value, and optimization of the sample conditions may lead to further improvement.

In practice, when applied on multi-spin systems, the improved performance of RA-CP is often attributed to the compensation for the chemical shift anisotropy (CSA) by a broader excitation bandwidth and for the Hartmann-Hahn mismatch due to the inhomogeneity of radio frequency irradiations. Our experiments were performed at low field at which the g-anisotropy, the electronic analog of the CSA, is negligible. If the broader bandwidth were responsible, one would expect the efficiency to monotonically increase with the size of the ramp. However, as seen in Figure 4, this was not the case. At short mixing time (τ_mix = 0.8 μs), we observed an optimum ramp size above which the efficiency decreases. Furthermore, the inhomogeneity of the Larmor frequency is negligible and the microwave field strength ${\omega }_{1S}$ measured by nutation experiments (data not shown) shows ∼10% inhomogeneity (∼1.5 MHz at the NOVEL condition) which is one order of magnitude smaller than the optimum ramp size, thus the mismatch is less of an issue in NOVEL than it is in CP. Therefore, it is likely that the improvement in the DNP enhancement of RA-NOVEL is due to the adiabatic properties of the pulse sequence. This also explains the difference between linear and tangent ramps. At long mixing times, the difference is negligible because the sweep rate is slow regardless of the modulation scheme. At short mixing times, the difference is apparent and the superior performance of a tangent ramp compared to its linear counterpart is also well-known for RA-CP.⁵²

It is worth noting that RA-NOVEL requires a longer mixing time. In particular, the mixing time employed in a CA-NOVEL is ∼10² ns as compared to the μs (∼10³ ns) time for RA-NOVEL. This has a practical implication on the design of pulsed DNP experiments. Given the same experimental conditions, a ramped-amplitude experiment would impose a higher duty cycle on the microwave amplifier. Furthermore, the repetition time is on the order of the electronic relaxation time, and when T_1e is short, RA-NOVEL might exceed the duty cycle limit of the microwave amplifier. For example, in our previous study we obtained a high enhancement at room temperature on a BDPA/PS sample when running the microwave amplifier near its designed 1% duty cycle.⁵⁴ Making the contact time ∼10 times longer is not possible in such cases. However, as long as the duty cycle permits, RA-NOVEL always provided larger enhancements compared to CA-NOVEL.

Furthermore, the long mixing time in RA-NOVEL makes it more suitable for radicals with long electronic relaxation T_1e’s such as BDPA or SA-BDPA, the latter being a water-soluble derivative of BDPA. SA-BDPA has a long T_1e ∼ 50 ms at 1 mM concentration in a frozen solution at 80 K and 5 T.⁵⁹ Our experiment utilized a concentrated sample of 40 mM, with T_1e of ∼10 ms. At the longest contact time (∼10 μs) allowed by the TWT, the duty cycle is 0.1%, which is still significantly below the 1% limit for the TWT. We note that RA-NOVEL might not be the method of choice for DNP using photo-excited triplet states wherein the short lifetime (μs or less) of the triplet states is not compatible with long mixing times.

Another prominent feature of BDPA-type radicals is the strong hyperfine coupling, which can be as large as 5.3 MHz.^54,60,61 The trityl-OX063 radical, on the other hand, was designed to remove all the ¹H’s that couple to the unpaired electron to facilitate solution Overhauser effect DNP mediated by electron-nuclear dipolar coupling.^62–64 Our experimental data on both SA-BDPA and trityl-OX063 radicals show consistent results. Specifically, both require a ramp size of ∼20 MHz and contact time of ∼3 μs. Furthermore, the improvement factors are also similar: 1.6 for SA-BDPA and 1.45 for trityl-OX063 (enhancement of 175 for CA-NOVEL and 250 for RA-NOVEL on sample containing 40 mM radical, data not shown). This suggests that the improvement of RA-NOVEL is generic, regardless of the radicals used. At higher fields where the difference in g anisotropy becomes significant, the difference between the two types of radicals might be more pronounced.

Finally, we emphasize the benefit of modulating the microwave amplitude to improve the DNP enhancement. Various groups have demonstrated this in the context of CW DNP.^65–70 Our results show that it is also important to modulate the microwave power in pulsed DNP experiments. To this end, an AWG is an elegant solution to conveniently manipulate the properties of the microwave pulses in a precise manner. In particular, using an AWG allows control of the amplitude, frequency, and phase of the microwave pulses. In a forthcoming paper, we will discuss another pulsed DNP sequence based on the modulation of the frequency rather than the amplitude of the microwave pulses. Our study parallels the trend in recent years of integrating an AWG into EPR spectrometers.⁷¹ The implementation of this approach has been performed at both low and high frequencies.^69,71 With the availability of fast (a few GSa/s) and cost-effective AWG, we anticipate that AWG will evolve into a standard component for the next generation of DNP/NMR instrumentation.

CONCLUSIONS

In summary, by modulating the amplitude of the microwave pulses using an arbitrary waveform generator (AWG), we have demonstrated that ramped-amplitude NOVEL gives rise to a significant improvement in the DNP enhancement when compared to constant amplitude-NOVEL. In particular, RA-NOVEL lengthens the contact time by about an order of magnitude and improves the DNP efficiency by a factor of up to 1.6 which is 80% of the theoretical value. The fact that it requires longer mixing times suggests that RA-NOVEL should be used instead of constant-NOVEL as long as T_1e is long and/or the duty cycle of the microwave amplifier is not exceeded. Thus, at the moment RA-NOVEL is suitable for narrow-line radicals with long T_1e’s such as BDPA and its derivative SA-BDPA. Our study emphasizes the importance of the ability to modulate the microwave pulses in order to optimize the DNP efficiency.