Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Nov 3;121(15):3364–3375. doi: 10.1021/acs.jpcb.6b08445

Convergence and Sampling in Determining Free Energy Landscapes for Membrane Protein Association

Jan Domański †,‡, George Hedger †, Robert B Best ‡, Phillip J Stansfeld †, Mark S P Sansom †,*
PMCID: PMC5402295  PMID: 27807980

Abstract

graphic file with name jp-2016-084453_0008.jpg

Potential of mean force (PMF) calculations are used to characterize the free energy landscape of protein–lipid and protein–protein association within membranes. Coarse-grained simulations allow binding free energies to be determined with reasonable statistical error. This accuracy relies on defining a good collective variable to describe the binding and unbinding transitions, and upon criteria for assessing the convergence of the simulation toward representative equilibrium sampling. As examples, we calculate protein–lipid binding PMFs for ANT/cardiolipin and Kir2.2/PIP2, using umbrella sampling on a distance coordinate. These highlight the importance of replica exchange between windows for convergence. The use of two independent sets of simulations, initiated from bound and unbound states, provide strong evidence for simulation convergence. For a model protein–protein interaction within a membrane, center-of-mass distance is shown to be a poor collective variable for describing transmembrane helix–helix dimerization. Instead, we employ an alternative intermolecular distance matrix RMS (DRMS) coordinate to obtain converged PMFs for the association of the glycophorin transmembrane domain. While the coarse-grained force field gives a reasonable Kd for dimerization, the majority of the bound population is revealed to be in a near-native conformation. Thus, the combination of a refined reaction coordinate with improved sampling reveals previously unnoticed complexities of the dimerization free energy landscape. We propose the use of replica-exchange umbrella sampling starting from different initial conditions as a robust approach for calculation of the binding energies in membrane simulations.

1. Introduction

Biological membranes are a complex mixture of multiple species of lipids and proteins, the interactions of which play a key role in cell function. The balance of interactions between different components within the membrane also determines its longer range (nano to microscale) structure. Of particular interest are the intramembrane interactions of proteins with lipids1 and adjacent proteins, the latter playing key roles in membrane protein folding2 and function.3 Molecular simulations have the potential to provide a detailed and quantitative understanding of protein and lipid interactions in membranes. In particular, simulations permit the computation of free energy landscapes or potentials of mean force (PMF) of interactions between the different membrane components (e.g., refs (4) and (5)). By enabling binding free energies to be computed, PMFs can also provide mechanistic insights into biologically relevant intermolecular interactions, which in turn can be compared to available experimental measurements. However, determining free energies for molecules embedded in lipid membranes is particularly challenging. For example, the lateral diffusion coefficient of common lipids in lipid bilayers is two to 3 orders of magnitude smaller than that of water.6 Therefore, sampling methods based on molecular dynamics will be impeded by the resulting slow diffusion of any molecule embedded in the membrane, a situation which is exacerbated in complex and crowded membrane environments.7

To calculate the binding free energy surface between two species, a sufficiently representative sample of the relevant configurations of the system have to be visited such that the relative weights of different free energy basins can to be established. Determining such a sample, and when it is sufficient (or “converged”), form the central task of any method for computing free energies. While incompletely converged simulations may provide insights into the location of stable states on a free energy surface, it is still possible that the relative free energies of different states on that surface may even be qualitatively incorrect. These challenges are starting to be recognized in simulations of membrane-systems.8 Therefore, for quantitative interpretation, and for comparison with experiment, it is essential to obtain converged and therefore reproducible results.

Enhanced sampling methods have been widely used to address the sampling challenge in membrane simulations. Here we focus in particular on those based on a reaction coordinate, or collective variable (CV), which include, e.g., umbrella sampling,9 metadynamics,10 and adaptive bias force.11 Replica exchange (RE) umbrella sampling (US) is particularly advantageous due to straightforward setup and faster convergence (relative to standard umbrella sampling) due to exchanges between replicas.12 This sampling method has been applied to calculate protein–lipid and protein–protein binding free energies in both all-atom (AA) and coarse-grained (CG) simulations.13−15 Umbrella sampling requires a collective variable (CV) that defines the binding/unbinding transition of the interaction. The most commonly used CV is a center-of-mass distance between two species (protein–lipid or protein–protein) within the membrane, which is used to define the umbrella windows. The initial configurations of the simulation windows are generally selected by translation along this reaction coordinate. Discarding an initial fraction of a simulation sufficient to allow for equilibration, a reweighting can be performed, using tools such as WHAM16,17 or, equivalently, MBAR,18 recovering the unbiased potential of mean force after subtracting the effect of the umbrella potentials. It is often assumed that if this PMF fails to change with increased simulation time, then the PMF calculation is converged. Of course, this is a necessary but insufficient test when calculating PMFs for complex membrane systems, as we will illustrate.

Here we present three examples of typical membrane PMF calculations, two for protein–lipid (one simple, one more complex) and one for protein–protein interactions within a lipid bilayer (Figure 1). We use the coarse-grained (CG) Martini force field which has been employed in a number of such studies recently (recently reviewed in ref (19)). Our examples are the mitochondrial transport protein ANT binding to cardiolipin (CL),20 the potassium channel Kir 2.2 binding to phosphatidyl inositol 4,5-bisphosphate (PIP2),21 and dimerization of the transmembrane (TM) helix of glycophorin A (GpA),22 the latter being the prototypical system for studying protein–protein interactions within a membrane. We study the dimerization of GpA and its mutants, using a new collective variable, based on the intermolecular contact matrix in the GpA dimer, to obtain a well-converged PMF. We provide strong evidence of convergence in both cases: starting the simulations with all replicas in a bound or all in an unbound initial configuration has no effect on the result. The importance of exchanges between windows is also highlighted, with absence of exchanges resulting in slower convergence. We compare our simulation results with experimental data, allowing us to explore limitations of the current CG force field.

Figure 1.

Figure 1

Open in a new tab

(A) Possible choices for initialization of umbrella sampling simulations: “default” (cyan) corresponds to replicas starting close to the bias center for each window; “bound” (blue) corresponds to all the replicas close to one end of the collective variable (CV) range; and “unbound” (red) corresponds to all replicas close to the other end of the CV range. (B) The three simulation systems explored in this article: ANT, the adenine nucleotide transporter (in blue) interacting with a cardiolipin (CL; red) molecules; Kir2.2, an inward rectifier potassium channel (gray) with a subunit (blue) interacting with a PIP2 (red) molecule; and GpA, the glycophorin TM transmembrane (TM) helix dimer, with the two TM helices (i.e., monomers) in red and blue. In each case the lipid bilayer is indicated by its phosphate particles (in green) with the remainder of the lipid molecules and the water on either side of the bilayer are omitted for clarity. For each system bound and unbound system snapshots are shown, in the upper and lower panel, respectively.

2. Methods

Molecular Simulation Methods

Molecular dynamics was performed in GROMACS (version 4.6.7; www.gromacs.org),23 using a time step of 20 fs. Semi-isotropic Berendsen pressure coupling24 was used for equilibration with coupling constant of 12 ps and Parrinello–Rahman25 coupling with coupling constant of 12 ps for production simulations with a reference pressure of 1 bar in both XY and Z directions. Similarly, a Berendsen thermostat was used for equilibration with coupling constant of 1 ps and a stochastic velocity rescaling temperature control26 for production with characteristic time of 1 ps, keeping the temperature constant around 310 K. A cutoff of 1.2 nm was used for Lennard-Jones (LJ) interactions, with the potential switched off smoothly between 0.9 and 1.2 nm. Coulombic interactions were calculated using the Particle Mesh Ewald (PME) method,27 with a grid spacing of 0.12 nm and a real-space cutoff of 1.2 nm. These settings were consistently used in the ANT/CL, KIK/PIP2, and glycophorin simulations.

Force Field

The CG Martini force field was used for the simulations: for ANT/CL and GpA, version 2.1 of Martini was used28−30 with a 4-tail bead POPC model. For Kir2.2/PIP2 version 2.2 was used31 with the older 5-tail bead POPC model.32 PIP2 lipid parameters taken from ref (33) and cardiolipin parameters were obtained from ref (34).

Umbrella Sampling

The PLUMED2 package35,36 (2.2-hrex, compiled from https://github.com/GiovanniBussi/plumed2/tree/v2.2-hrex) was used to patch GROMACS 4.6.7 and define the collective variables and perform the biasing.

Replica exchanges are evaluated using the Boltzmann criterion.

graphic file with name jp-2016-084453_m001.jpg
graphic file with name jp-2016-084453_m002.jpg

where the probability of exchange between two replica windows 1 and 2 with umbrella potentials U1 and U2 is dependent on the difference Δ between the energies of the protein configurations X1 and X2 (those in windows 1 and 2 before exchange) in these potentials before and after the trial exchange (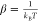Inline graphic, where kB is Boltzmann’s constant and T is the absolute temperature). Exchanges are determined according to a Metropolis criterion, always being accepted if e–Δ ≥ 1 and if e–Δ < 1 being accepted if a random number r drawn from a uniform distribution on [0,1) is less than e–Δ.

In this work, we have applied the final umbrella potentials to each window. In some cases, this may generate large forces due to the system being out of equilibrium. This can readily be overcome by including an appropriate initialization protocol (e.g., equilibrating the umbrella closest to the initial condition first, then using this to equilibrate the next umbrella and so on). If the landscape is rougher (as in an all atom simulation), it will be harder to converge the two initial conditions, although “slow growth” methods, e.g., ref (37), may be helpful in the situation. Even if convergence is not achieved, the comparison will expose this fact, which otherwise would be overlooked.

Analysis and Visualization

MDAnalysis38 was used to automate plumed input generation and GromacsWrapper39 was used for topology file manipulation. VMD40 was used to produce the molecular renderings.

ANT/Cardiolipin

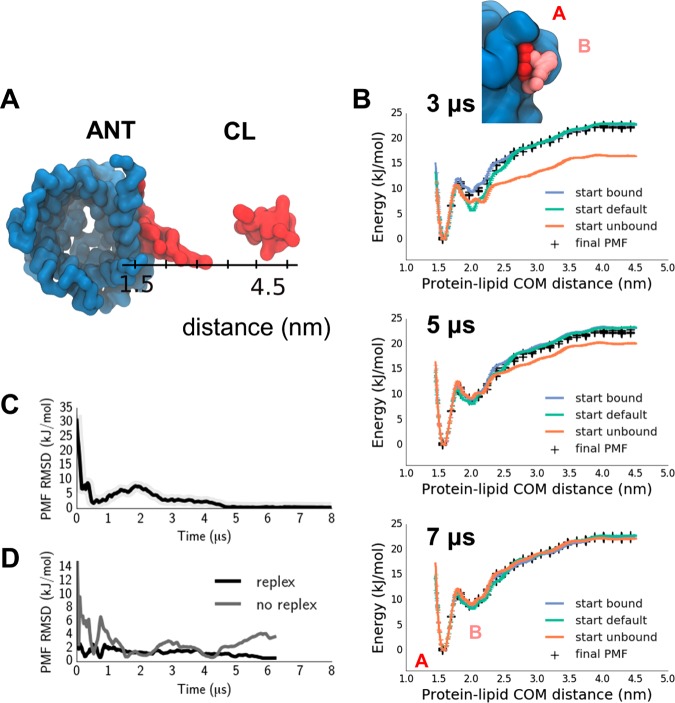
The system was setup as described in ref (20) with a simple POPC bilayer assembled around the position restrained protein (with force constant of 1000 kJ/mol/nm2). The final system contained 279 POPC molecules, a single cardiolipin molecule in the upper leaflet, and over 4200 coarse-grained water particles. Randomly selected water particles were converted into sodium and chloride ions to neutralize the system and mimic the experimentally used buffer. Initial configurations for the umbrella sampling windows were generated via a steered MD (SMD) molecular dynamics simulation. A collective variable (CV) was defined to permit sampling along a path orthogonal to the binding site surface (Figure 2A). This CV corresponded to the distance between the CG glycerol particle (GL0) of cardiolipin and the backbone bead of the Proline in the conserved Px[D/E]xx[K/R] motif, found on the odd-numbered TM helices and present in all members of this protein family (Figure 2A). We have chosen to sample along this linear coordinate because it is most relevant to binding to the known native binding sites, whereas using a radial coordinate would also average over non-native binding. In addition, a linear coordinate greatly facilitates sampling. To prevent the protein from rotating within the bilayer, the 3 Proline backbone particles of the three equivalent sites on ANT were position restrained (400 kJ/mol/nm2 on the X and Y dimensions). To keep the CL lipid molecule from diffusing away from the line coordinate, an additional harmonic restraint is defined with a force constant of 1000 kJ/mol/nm2, keeping the Y-component of the CV close to a fixed value. Umbrella sampling was set up with 32 windows, spaced linearly between 1.6 and 4.5 nm on the cardolipin headgroup–protein center-of-mass distance, with a force constant of 1000 kJ/mol/nm2. Exchanges were attempted every 10000 steps.

Figure 2.

Figure 2

Open in a new tab

Cardiolipin binding to ANT, providing an example of calculating a PMF for a lipid interacting with a specific binding site on an integral membrane protein. (A) Representative structures of the closest (protein lipid COM distance =1.5 nm) and furthest (4.5 nm) replicas in the cardiolipin-ANT binding simulations. (B) PMFs starting from 3 different initial configurations (default in cyan, unbound in orange, bound in blue; black crosses indicate the final PMF for comparison; see Figure 1 for definitions), computed after 3, 5, and 7 μs of the simulation (within each case the first half of the simulation discarded as equilibration). Thus, the final PMF contains data pooled from 2 replica exchange simulations, corresponding to the starting bound and unbound initial conditions. (C) Root mean square difference between the two PMFs started from “all bound” and “all unbound” configurations as a function of time. (D) PMF RMSD to the final PMF of simulations started from the default initial condition and either allowing for replica exchange (labeled replex) or without exchanges (labeled no replex).

Kir2.2

For computational efficiency, the wild-type Kir structure PDB 3SPI(21) was truncated in PyMol,41 removing residues before Asp-61 and after Thr-191, preserving Arg-186, which coordinates the 5′ phosphate in this structure. This residue was then mutated to Ala in the mutant system. The martinize script was used to obtain a coarse-grained topology in each case and an elastic network was generated to stabilized the protein structure in simulation.

The protein was inserted into a POPC bilayer, solvated, and equilibrated using the MemProtMD pipeline.42 Position restraints with a force constant of 1000 kJ/mol/nm2 were used in equilibration to keep the protein from moving. The short-tail PIP2 molecules from the 3SPI crystal structure were used as the starting conformation for the bound conformation of PIP2. Sodium and chloride ions were added to 0.15 M to mimic the buffer generally used experimentally. The final system contained over 12 000 particles with 4 PIP2 lipids, 360 POPC lipids, and over 6000 water particles.

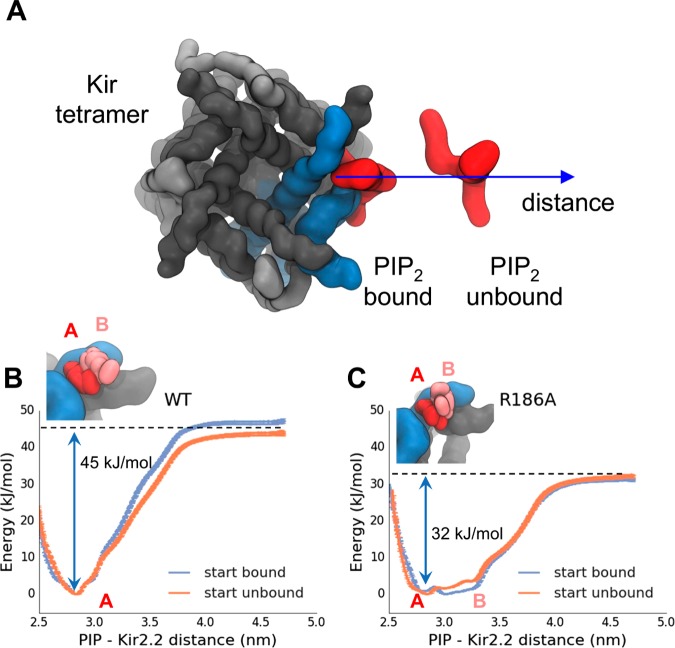
The collective variable was chosen to be the distance between the PIP2 headgroup and the center of mass of the nearest Kir2.2 chain. Sixteen umbrella sampling windows were setup, with the CV linearly spaced between 2.6 and 4.5 nm with a force constant of 500 kJ/mol/nm2 (Figure 3A). Exchanges between replicas were attempted every 10 000 steps. The initial structure for all windows of the “start bound” simulation was 3SPI. After 50 ns of umbrella sampling, a frame from the last window was used to initialize all windows of the “start unbound” simulation. The distance is roughly parallel to the X-axis of the simulation box and so an additional bias is applied to prevent the lipid from diffusing in Y, with a force constant of 100 kJ/mol/nm2. To prevent the Kir from rotating in the bilayer, a position restraint was applied to the backbone particles of the protein, with a force constant of 100 kJ/mol/nm2 on X- and Y-coordinates.

Figure 3.

Figure 3

Open in a new tab

PIP2 binding to Kir2.2, providing an example of a PMF for a charged lipid interacting with a specific binding site on an integral membrane protein. (A) Representative structures of the PIP2 bound (PIP–Kir2.2 distance 2.7 nm) and PIP2 unbound (3.4 nm) replicas in the PIP2–Kir2.2 binding simulations. (B,C) PMFs along a CV defined by the PIP2 headgroup distance to the Kir monomer center of mass. PMFs are shown starting from two initial configurations: with lipid bound in all replicas (blue) or unbound (orange) PMFs are shown for (B) the wild-type protein and (C) a mutant protein (R186A) with reduced PIP2-binding affinity mutant.

Instead of using an initial steered MD simulation to generate the unbound configurations (as was done for the ANT simulations) we relied on a short umbrella sampling run starting from bound with the umbrella centered far away from the protein. While this resulted in large initial forces, these quickly taper off as the lipid moves closer to the target window distance. Because the coarse-grained energy landscape is relatively smooth this has no adverse effect.

GpA

The solution NMR structure of GpA in a detergent micelle (PDB id 1AFO(22)) was used as a starting structure for the simulation. The protein was inserted into a POPC bilayer using g_membed.43 The system contained 125 POPC lipids and over 1400 coarse-grained water particles.

Umbrella sampling simulations were setup with 16 windows, spaced linearly between DRMS = 0 and 2.5 nm relative to the native, with a force constant of 100 kJ/mol/nm2. Exchanges were attempted every 1000 steps.

All the windows of start bound simulations were initialized from the 1AFO structure. After 50 ns, frames from each window were used to initialize the “start default” simulation, and the last window frame was used to initialize the “start unbound” simulation. This is similar to what was done in Kir2.2 simulations, as described in the previous section.

Definition of DRMS

Distance root-mean-square displacement DRMS between two configurations XA and XB is defined below.

graphic file with name jp-2016-084453_m004.jpg

where d(xia,xj) is the distance between the coordinates xi and xj of atoms i and j in configuration XA and the sum runs over all atom pairs (i,j) in a specified contact list. Because all-to-all distances have to be considered this becomes computationally expensive with increasing number of particles. Therefore, pairs of atoms are only included in the contact list if those atoms are within some cut off distance in the “native” bound state. Here we use a lower and upper cut offs of 0.1 and 0.6 nm, respectively. We then further restrict the atoms used in the calculating of the collective variable by taking only pairs involving one atom from each molecule (for glycophorin this becomes interhelical DRMS). Only the transmembrane region between Glu-72 and Ile-95 was used to calculate the interhelical DRMS (both backbone and side-chain beads were included).

Calculation of the Dimerization Kd from the Potential of Mean Force

The dissociation constant (Kd) for the GpA dimer can be defined as

graphic file with name jp-2016-084453_m005.jpg 1

where [A] is monomer concentration (per lipid area) when the system is in monomers and [AA] is the dimer concentration when the helices are dimerized and y is the fraction of time it is bound. Eq 1 can be derived by requiring either (i) that the time- or ensemble-averaged chemical potential of the monomer state and dimer state should be equal at equilibrium (and neglecting pressure contributions to free energy) or (ii) that the time-averaged forward and reverse fluxes for dimerization should be equal at equilibrium. Since in this case, 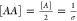Inline graphic, where σ is the lipid area (defined as the circle whose radius (L) is the mean helix–helix distance in the last window of the umbrella sampling simulation),

graphic file with name jp-2016-084453_m007.jpg 2

A reference concentration of 1 molecule per nm2 is used. The standard free energy of dissociation is then ΔG0 = −RTln Kd. An analogous expression was derived by De Jong et al.44 (see also45) for heterodimers.

To determine the fraction bound (y), one has to integrate the PMF using some suitable dividing surface.

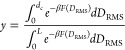graphic file with name jp-2016-084453_m008.jpg

where β = 1/(kBT), kB is Boltzmann’s constant, and T is the absolute temperature. dc is the dividing value of DRMS separating bound and unbound state, chosen as 2.0 nm, and where the free energy value starts decreasing toward bound; the value of y is not highly sensitive to this choice.

3. Results and Discussion

Protein–Lipid Interactions: A Biologically Relevant Lipid

Protein–lipid interactions play a key role in membrane protein stability and function1 and so it is important to be able to characterize the strength of such interactions via PMF calculations. A well-defined interaction between a lipid molecule and a protein is provided by that between cardiolipin (CL) and ANT (Figure 1B). The ADP/ATP carrier (AAC1/ANT) is located in the inner membrane of the mitochondria. It possesses a 3-fold pseudosymmetric structure with 3 CL binding sites which have previously been characterized structurally.46,47 From a sampling perspective, this is an interesting system because CL is an anionic 4-tailed lipid, and thus might be anticipated to be more challenging to sample in terms of its interactions with a membrane protein than a neutral 2-tailed lipid.

A collective variable (CV) was defined to permit sampling along a path orthogonal to the binding site surface (Figure 2A; see Methods Section for details). Two independent sets of simulations were performed, with the CL molecule either initially bound (d = 1.7 nm) to site 1 on ANT, or unbound (d = 4.5 nm). The bound configuration was the most representative structure of an ANT/CL complex from a long equilibrium, unbiased MD simulation in which the cardiolipin spontaneously bound to the site, which corresponds closely to the crystallographically observed configuration of CL at this site.20 An additional independent simulation was prepared in which the CL molecules were initially positioned with uniform spacing along the umbrella coordinate (see Figure 1A for a schematic representation of these three initial starting conditions). The unbound configurations were generated using accelerated MD, starting from the bound configuration, and applying a force pushing the CL out and away from its binding site.

The umbrella sampling simulation was unbiased using WHAM,16,17 yielding a PMF with 2 distinct minima, at d = 1.5 nm and d = 2.0 nm, with well-depths of 20 and 10 kJ/mol, respectively (Figure 2B). The PMFs are well-converged, within 1 kJ/mol of each other after 7 μs. The progress of convergence can be monitored via calculating the root-mean-square difference between a PMF derived from simulations started with all replicas bound and a PMF starting from all unbound. This PMF RMSD becomes <1 kJ/mol after 5 μs (Figure 2C, upper plot). Up to this difference, the PMF is thus insensitive to the initial conditions. An overlap of distance histograms from the different umbrella windows is shown in SI Figure 1A. Multiple binding and unbinding transitions are observed in the continuous trajectories obtained by following the replicas through exchanges (SI Figure 1B). Convergence is aided by allowing for exchange between replicas, which is attempted every 10000 steps and accepted via an analogous criterion to that for temperature replica exchange.12 In the absence of such exchanges, the PMF RMSD remains ∼2 kT even after 7 μs, with no sign of convergence (Figure 2C, lower plot).

The two minima (A and B in Figure 2B) correspond to configurations of ANT with bound or partially bound CL, respectively. Representative frames show the headgroup particles of CL bound tightly into the ANT in minimum A, while in minimum B the phospholipid headgroup is about 0.5 nm further away from the binding pocket surface. While minimum A is considerably deeper than B, it can only be accessed by crossing a ∼ 5 kJ/mol barrier. Assessing the relative depth of these two minima would be very difficult using standard unbiased MD simulation, and presents a sampling challenge to the replica exchange umbrella sampling approach.

We are therefore confident that, from the umbrella sampling with replica exchange, we have a well converged PMF for the interaction of a lipid with a membrane protein. We note that the duration of our simulations (5–7 μs) is longer than often used for determining PMFs in a membrane environment (e.g., 1 μs5). While we find that the well-depth for the deeper minimum is within 2.5–5 kJ/mol of the final value, had the simulation been run for 1 μs, the rest of the PMF may not be well converged. We also note that a commonly used criterion, the PMF well-depth not changing over time is a necessary but not sufficient to demonstrate that a simulation is converged. This is especially the case in membrane protein/lipid simulations where “memory effects” of the initial conditions are likely to play a key role in determining convergence. Furthermore, it appears that the simulations started from the “bound” state converge much more quickly to the final PMF than those started from “unbound”. This is most likely related to the chosen coordinate not uniquely defining the bound state: thus, applying a force to separate the protein and lipid is effective in producing representative unbound states (since distance is sufficient to define fully unbound states). However, pulling the molecules together can create non-native states at the desired intermolecular separation which evolve more slowly to the correctly bound state as the bias force is not pushing non-native bound states toward the native-like bound or partially bound states. Note that this faster convergence starting from bound would only be expected if the most stable bound state (in the context of the force field) was used to initialize the runs.

Protein–Lipid Interactions: A More Complex Case, Kir/PIP2

PIP2 is a key lipid molecule involved in regulation and/or recognition in many membrane processes,48 including the activity of ion channels.49 It has a somewhat more complex polyanionic headgroup than CL. Here we explore the PMF of PIP2 interactions with the TM domain of the Kir2.2 potassium channel. Both structural and functional experimental data are available for this interaction,49 as well as simulation studies which demonstrate that extended equilibrium CG simulations will permit PIP2 to find its experimentally observed binding site (Figure 1B), in which the anionic headgroup binds to basic residues on the protein surface close to bilayer/water interface.33,50 A number of binding site mutants exists, with reduced apparent affinity for PIP2.51,52 Thus, this system provides both a further opportunity to explore convergence of protein/lipid PMFs, and to explore the sensitivity of such (CG) PMFs to mutations in key lipid-binding side chains.

As detailed above, the CV was defined as a distance between the PIP2 headgroup and the center of mass of the Kir2.2 subunit containing the binding site (Figure 3A). For wild-type (WT) Kir2.2, the potential of mean force shows a single minimum, 45 kJ/mol deep, with the PIP2 bound at the native site observed in the crystal structure (Figure 3B). Comparison of the bound/unbound profiles demonstrates convergence of the PMF to within an RMSD of 2.5–5 kJ/mol after 4–5 μs umbrella sampling with replica exchange. The depth of the energy minimum, corresponding to interaction of PIP2 with a binding site containing 6 basic side chains, is comparable to that of PIP2 interacting with a juxtamembrane binding site of the EGFR (−42 kJ/mol), a (less structured) binding site which contains 5 basic side chains.5

The Kir2.2 mutant R186A (which has a reduced apparent affinity for PIP2) has one fewer arginine in the PIP2 binding site, but still can be crystallized with a short-chain PIP2 molecule bound.21 The PMF shows a rather broad well, with depth of about 32 kJ/mol (Figure 3C). Representative structures reveal that partially unbound and fully bound configurations of the PIP2 headgroup at the mutant binding site have about the same free energy of interaction (Figure 3C, inset), which is ca. 70% of that of PIP2 bound to the WT channel. Thus, the PMF suggests that the effect of the R186A mutation may be more complex than simply a reduction in affinity of the site for PIP2. To better understand the role of electrostatics in the Kir2.2–PIP2 interaction, we repeated the calculation with a PIP2 molecule in which the phosphate particle charges had been neutralized (SI Figure 2). This reduces the well-depth by about 2-fold, but interestingly the energy minimum remains at about the same position on the CV.

Protein–Protein Interactions in a Membrane

Protein–protein interactions, and in particular interactions between TM helices within a bilayer, play key roles in folding,53 stability,54 and function3 of membrane proteins. Thus, it is of considerable interest to understand the free energy landscapes of membrane protein–protein interactions. It is also anticipated to be more challenging both in terms of selection of a suitable CV and of establishing convergence than is the case for even protein/lipid interactions in a membrane.

One of the best studied examples of protein–protein interactions in a membrane, both experimentally22,55−62 and computationally4,45,63−68 is that of dimerization of the glycophorin (GpA) TM domain (Figure 1B). Both NMR22 and more recent crystallographic62 data reveal the GpA TM domain to form a parallel TM helix dimer with an interhelix crossing angle of ca. −20° and a helix/helix interface containing a key glycine-rich sequence motif. Both the wild-type structure and dimerization-disrupting mutants have been characterized via a range of biochemical methods55−60 and also in silico, the latter both at the coarse-grained4,66,67 and all-atom45,68 resolution. It is therefore an ideal system to probe protein–protein interactions within a membrane.

A “good” CV describing TM helix dimerization in a membrane should allow the dimer to be separated, and also allow us to readily distinguish native from near-native dimer configurations. We defined a set of intermolecular (i.e., between the TM helix monomers) native distances in the GpA TM dimer structure. Using those distances as a reference we then define a distance root-mean-square displacement (DRSM) relative to the native TM dimer configuration. As previously (see above) three independent sets of simulations were run: one starting with all windows in the bound configuration; one starting with all the windows in unbound configuration; and one with the windows spaced at uniform intervals along the CV. The initial “bound” structure was a CG model derived directly from the PDB 1AFO solution NMR structure of GpA in a detergent micelle.22

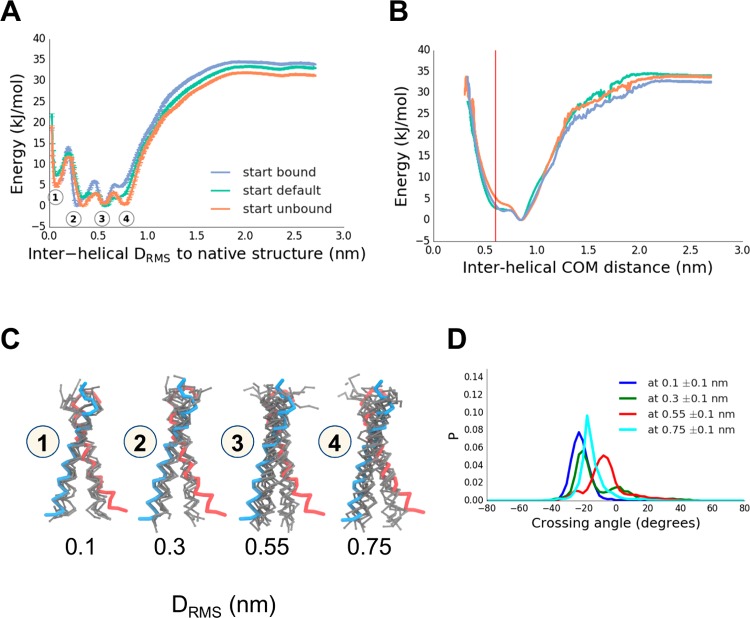
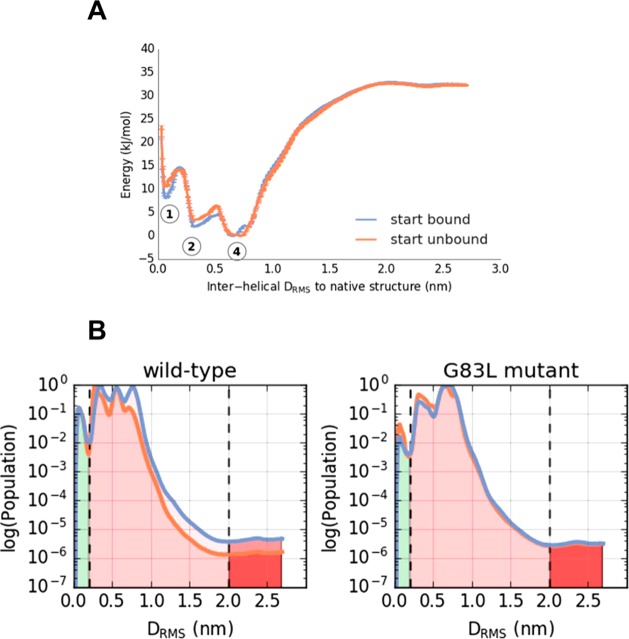
The PMF thus obtained (Figure 4A) could be shown to be independent of the initial configuration and converges around 6 μs (as judged from the PMF RMSD plot; SI Figure 3) to within 2.5 kJ/mol between the simulations. The dimerization landscape has 4 minima, with a well-depth of about 35 kJ/mol relative to the unbound state. Notably, the native minimum (labeled 1 in Figure 4A) is not the lowest free energy configuration, but rather a near-native minimum (labeled 2 in Figure 4A) is more stable. Projecting the PMF from sampling along the DRMS CV onto the helix–helix center of mass distance (D), we find that a non-native dimerized state, with a helix–helix separation of 0.9 nm (versus 0.6 nm for the native) is the free energy minimum (Figure 4B). Minima 1 and 2 correspond to native and near-native configurations (characterized by helix–helix crossing angles of −25° and −20° compared to −23° and −20° in the 1AFO NMR structure and the 5EH4 crystal structure, respectively). Minima 3 and 4 represent non-native configurations, with the helices more closely parallel to one other (Figure 4C), and crossing angles of −15° and −5°, respectively. The simulations are well converged, with multiple dimerization and dissociation events (SI Figure 3).

Figure 4.

Figure 4

Open in a new tab

Dimerization of the TM helix of glycophorin A (GpA), providing an example of a protein–protein interaction within a membrane. (A) GpA dimerization showing a PMF along a reaction coordinate (CV) defined by the intermolecular DRMS to the native dimer structure (PDB id 1AFO). Three initial conditions used, which had either all replicas in the native configuration (“bound”, blue), all replicas initially dissociated (“unbound”, orange), or replicas linearly spaced apart (“default”, cyan). Observed 4 energy minima are labeled 1–4, corresponding to DRMS values of about 0.1, 0.3, 0.55, and 0.75 nm, respectively. (B) Reweighted PMF along a CV corresponding to the interhelical distance (the native structure distance is in red at ∼0.6 nm). (C) Representative structures (in gray; wireframe backbone) from each of the four minima labeled in the PMF in (A). The two subunits of the experimental (PDB id 1AFO) are shown in blue and in red. (D) Crossing angle distributions for the structures seen in PMF minima labeled in (A), with crossing angle defined as a torsion angle between flanking backbone atoms of residues number 78–88.

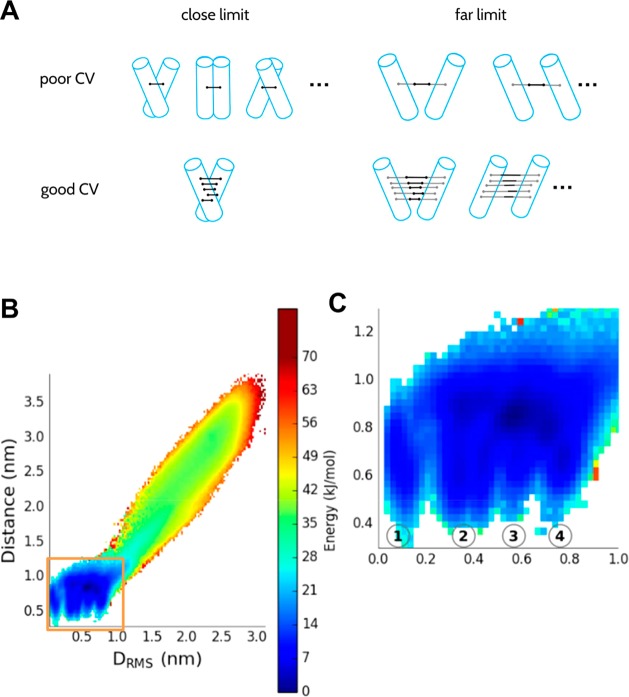
This finding was somewhat unexpected. Previous CG PMFs for GpA dimerization, whether by umbrella sampling MD4 or by a Monte Carlo approach67 were calculated along helix–helix distance. While the DRMS and D behave similarly at large (>1.5 nm, Figure 5B, SI Figure 4) separations, at short distances D is unable to discriminate between closely related native and non-native dimer configurations. Thus, D is a relatively poor collective variable since these native, near native, and non-native states are clearly separated by a free energy barrier when projected onto DRMS (Figure 4A). Projecting our PMF onto a 2D surface defined by the DRMS and D plane confirms that D collapses together a number of states which are separated by DRMS (Figure 5B). A key question is whether the observed non-native states are in fact experimentally relevant, or simply due to the limited resolution that can be achieved with the coarse-grained model. While the existing experimental structures all favor a very tightly defined native structure,62 that does not rule out the possibility that there may be an appreciable population of other states at equilibrium (although it seems unlikely). A second method of validating the results is compared with dissociation constants determined from recent steric trap methods, which allow an estimate of the dimer stability in a lipid bilayer.60 In order to compute Kd from the PMF, we need to define what is meant by the bound state. If we provisionally define all configurations in which the TM helices are separated by a distance of less than 2.3 nm (corresponds to DRMS of ∼2.0 nm) (since the steric trap method would not distinguish native from non-native states if the helices have a native separation), we obtain a Kd of 1.1 × 10–6 molecules per nm2, compared with the experimental estimate of 1.3 × 10–9 molecules nm2,60 an acceptable difference considering the simplicity of the simulation model, which lacks detailed specific interactions, such as hydrogen bonds. The PMF also shows that the non-native bound states constitute the vast majority of the bound population, which might suggest that they are in fact relevant.

Figure 5.

Figure 5

Open in a new tab

(A) Schematic/cartoon of D vs DRMS as “poor” and “good” CVs. While at far separation both CVs describe the system similarly, at close separation, D collapses the phase space and can correspond to a number of very different configurations, while DRMS is able to distinguish native from near-native helix–helix packing arrangements. (B) 2D PMF along D and DRMS, obtained by reweighing the original 1D umbrella sampling simulation along DRMS. Inset (C; magnified) shows the minima 1–4 which have different DRMS values and essentially the same D.

As an alternative, more stringent, experimental test of our free energy landscape, we therefore consider the effects of mutations. The tight packing of GpA TM helices is mediated via a conserved GXXXG motif.69 Mutations that introduce a bulky side-chain residue in place of one of the Gly residues are known to disrupt dimerization.63 Thus, both G83L and G83I prevent dimerization.55,57,58,60 We have simulated the G83L mutant dimer to obtain PMFs as before starting either from bound or unbound configurations; because isoleucine and leucine are represented in an almost identical way in the Martini force field, the results for G83I are expected to be very similar.

The Kd computed from these PMFs is indistinguishable from that of wild-type, strongly suggesting that the populated binding modes are not representative of the experimental distribution. We can obtain further insight from the detailed differences between the PMFs. The G83L PMF shows that in fact the most native-like minimum (minimum number 1 in Figure 4) is destabilized, albeit by 5 ± 2.5 kJ/mol relative to the WT PMF (Figure 6A), compared with 19 kJ/mol in experiment.60 The quantitative discrepancy may be due to the coarse-grained nature of the model. In addition, the range of experimental constructs (based largely on a chimeric protein formed by fusion of the GpA TM domain with staphylococcal nuclease) and environments (detergent micelles vs in vitro lipid bilayers vs bacterial cell membranes) makes quantitative comparisons difficult. Nonetheless, the reproduction of a destabilizing effect is consistent with experiment and intuition, based on the published structures.22,62 There is also a similar destabilization of the native-like states with lower DRMS to the experimental structure. On the other hand, there is virtually no change in free energy for the minimum between 0.7 and 0.8 nm. This is because residue 83 has a smaller role in the binding interface in this case. Because this minimum (number 4 for the mutant, in which the helix crossing angles are bimodally distributed with peaks at −20 and 20 degrees (SI Figure 5), is the most stable bound species in the mutant, this allows the Kd to remain essentially unchanged in the G83L mutant simulations. Overall these results suggest that, at the least, the population of stable non-native dimer states is too large in the simulation, particularly for those with largest DRMS from native.

Figure 6.

Figure 6

Open in a new tab

Effects of a “disruptive” mutation on the dimerization of the TM helix of GpA. (A) PMF for dimerization of a mutant (G83L) of GpA (compare with the wild type PMF in Figure 4A). The three energy minima labeled correspond to the structures in Figure 4C. Two initial conditions were used, which had either all replicas in the native configuration (“bound”, blue), or all replicas initially dissociated (“unbound”, orange). (B) Comparison of the population distributions derived from the wild-type and G83L GpA PMFs. From these one may estimate a ΔΔG of 0 or 4 kJ/mol (with unbound state defined at 2.0 nm or 0.2 DRMS respectively) for destabilization of the native dimer by the G83L mutation.

We also explored the robustness of the GpA TM helix dimer PMF to variations in the CG model applied. Thus, the results discussed above used the Martini 2.1 force field; recalculation using the more recent version, Martini 2.2,31 does not seem to change the PMF appreciably (SI Figure 6). We also explored whether the use of PME vs shifted electrostatics within Martini, and the effect of different restraints on secondary structure (dihedral vs elastic network). The resultant PMFs (SI Figure 7) suggest that the results are relatively robust to the restraints, and that the use of PME leads to some relative stabilization of the native dimer structure. Thus, we are confident we have achieved a well sampled and converged PMF within the limitations of the Martini force field.

4. Conclusions

In summary, we show how PMF calculations for membrane systems, for both protein–lipid and protein–protein interactions, benefit from stronger tests of convergence than is sometimes the case. Exchanges between umbrella sampling windows speed-up convergence and independent initial conditions provide an easily interpretable condition for convergence. Additionally, care must be taken in selection of suitable CV. For certain systems, such as lipid–protein interactions, a simple center of mass distance appears sufficient to achieve good sampling. However, for protein–protein interactions in a membrane, we implemented a different collective variable, namely an intermolecular distance matrix RMSD.

We have illustrated our case with an example of the interaction of an integral membrane protein with cardiolipin, a topic of general importance as the energetics of such interactions have been explored by CG MD for a number of proteins from mitochondrial membranes, e.g., refs (70), (71), (20), and (72). We have extended this analysis to a well-characterized interaction of PIP2 with an inward rectifier potassium channel. This is also of broad relevance given recent evidence for a role on PIP2 interactions in regulating a number of ion channel proteins.49 In particular, we show that with replica exchange and CG simulations of >5 μs, one can obtain demonstrably converged protein/single lipid PMFs, thus allowing exploration of the effects of binding site mutations and/or changes in lipid species on the strength of lipid/protein interactions. These calculations use the Martini CG force field: it will be of interest in the future to attempt such free energy calculations with an all-atom force field. We anticipate that in this case establishing convergence will be more demanding, as the free energy landscape will likely be more rugged.

Using our DRMS collective variable, we find that ΔG for GpA dissociation in Martini 2.1 is in agreement with experiment (values ranging from −24 kJ/mol73 to −51 kJ/mol60). For the native state the well-depth observed is −28 kJ/mol, which compares well with other PMF-based estimates of −30 kJ/mol67 and −40 kJ/mol4 from CG simulations, and of −44 kJ/mol45 and −60 kJ/mol68 from all-atom simulations. However, while the CG force field can qualitatively reproduce the effect of a dimer-disrupting mutation on the native bound conformation, it does not appreciably alter the dimer stability. The small effect of the mutation on stability is due to the large population of non-native bound states that are not much affected by the mutation. That the CG force field is not quantitatively successful in capturing the effects of such mutations is perhaps not surprising given the role of interactions which are not explicitly present in the CG energy function, e.g., Cα-H···O H-bonds, in stabilizing the GpA native helix dimer62,74 over non-native bound states. The use of the DRMS reveals a more complex energy landscape than was previously seen for GpA dimerization, such that a near-native dimer is the most stable configuration. Comparable complexities of an apparently simple free energy landscape for TM helix interactions have recently been seen for CG metadynamics studies of dimerization of the EGFR TM domain.75

A clear future extension of this study, especially in terms of TM helix–helix interactions, will be to obtain demonstrably converged PMFs from all-atom simulations. Two all-atom PMFs of GpA TM helix dimerization are available45,68 but would merit revisiting in the context of the greater complexity of the (CG) free energy landscape revealed via the use of the DRMS as a CV. This will doubtless prove challenging due to much larger number of degrees of freedom in all-atom simulations and the high viscosity of the lipid bilayer.

Acknowledgments

J.D. was supported under the Wellcome Trust and National Institutes of Health Four-year PhD Studentship program (grant number WT100946AIA). R.B. and J.D. were supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health. This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov). Research in M.S.P.S.’s group is supported by the Wellcome Trust and the BBSRC. G.H. was supported by an MRC studentship. The authors thank Giovanni Bussi and Carlo Camilloni for their help in setting up and modifying the PLUMED2 code. Our thanks to our colleagues for their helpful comments on this work.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.6b08445.

  • Additional figures and analysis, and links to downloadable setup files and code (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp6b08445_si_001.pdf (1.6MB, pdf)

References

  1. Hedger G.; Sansom M. S. P. Lipid interaction sites on channels, transporters and receptors: recent insights from molecular dynamics simulations. Biochim. Biophys. Acta, Biomembr. 2016, 1858, 2390–2400. 10.1016/j.bbamem.2016.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Popot J. L.; Engelman D. M. Helical membrane protein folding, stability, and evolution. Annu. Rev. Biochem. 2000, 69, 881–922. 10.1146/annurev.biochem.69.1.881. [DOI] [PubMed] [Google Scholar]
  3. Endres N. F.; Das R.; Smith A. W.; Arkhipov A.; Kovacs E.; Huang Y. J.; Pelton J. G.; Shan Y. B.; Shaw D. E.; Wemmer D. E.; et al. Conformational coupling across the plasma membrane in activation of the EGF receptor. Cell 2013, 152, 543–556. 10.1016/j.cell.2012.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Sengupta D.; Marrink S. J. Lipid-mediated interactions tune the association of glycophorin A helix and its disruptive mutants in membranes. Phys. Chem. Chem. Phys. 2010, 12, 12987–12996. 10.1039/c0cp00101e. [DOI] [PubMed] [Google Scholar]
  5. Hedger G.; Koldsø H.; Sansom M. S. P.; Shorthouse D. Free energy landscape of lipid interactions with regulatory binding sites on the transmembrane domain of the EGF receptor. J. Phys. Chem. B 2016, 120, 8154–8163. 10.1021/acs.jpcb.6b01387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Filippov A.; Orädd G.; Lindblom G. The effect of cholesterol on the lateral diffusion of phospholipids in oriented bilayers. Biophys. J. 2003, 84, 3079–3086. 10.1016/S0006-3495(03)70033-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Javanainen M.; Hammaren H.; Monticelli L.; Jeon J.-H.; Miettinen M. S.; Martinez-Seara H.; Metzler R.; Vattulainen I. Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes. Faraday Discuss. 2013, 161, 397–417. 10.1039/C2FD20085F. [DOI] [PubMed] [Google Scholar]
  8. Neale C.; Pomès R. Sampling errors in free energy simulations of small molecules in lipid bilayers. Biochim. Biophys. Acta, Biomembr. 2016, 1858, 2539–2548. 10.1016/j.bbamem.2016.03.006. [DOI] [PubMed] [Google Scholar]
  9. Torrie G. M.; Valleau J. P. Monte-Carlo free-energy estimates using non-Boltzmann sampling - application to subcritical Lennard-Jones fluid. Chem. Phys. Lett. 1974, 28, 578–581. 10.1016/0009-2614(74)80109-0. [DOI] [Google Scholar]
  10. Leone V.; Marinelli F.; Carloni P.; Parrinello M. Targeting biomolecular flexibility with metadynamics. Curr. Opin. Struct. Biol. 2010, 20, 148–154. 10.1016/j.sbi.2010.01.011. [DOI] [PubMed] [Google Scholar]
  11. Comer J.; Gumbart J. C.; Henin J.; Lelievre T.; Pohorille A.; Chipot C. The adaptive biasing force method: everything you always wanted to know but were afraid To ask. J. Phys. Chem. B 2015, 119, 1129–1151. 10.1021/jp506633n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Sugita Y.; Kitao A.; Okamoto Y. Multidimensional replica-exchange method for free-energy calculations. J. Chem. Phys. 2000, 113, 6042–6041. 10.1063/1.1308516. [DOI] [Google Scholar]
  13. Cote S.; Binette V.; Salnikov E. S.; Bechinger B.; Mousseau N. Probing the Huntingtin 1–17 membrane anchor on a phospholipid bilayer by using all-atom simulations. Biophys. J. 2015, 108, 1187–1198. 10.1016/j.bpj.2015.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Park S.; Kim T.; Im W. Transmembrane helix assembly by window exchange umbrella sampling. Phys. Rev. Lett. 2012, 108, 108102. 10.1103/PhysRevLett.108.108102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Park S.; Im W. Two dimensional window exchange umbrella sampling for transmembrane helix assembly. J. Chem. Theory Comput. 2013, 9, 13–17. 10.1021/ct3008556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Souaille M.; Roux B. Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations. Comput. Phys. Commun. 2001, 135, 40–57. 10.1016/S0010-4655(00)00215-0. [DOI] [Google Scholar]
  17. Hub J. S.; de Groot B. L.; van der Spoel D. g_wham A free weighted histogram analysis implementation Including robust error and autocorrelation estimates. J. Chem. Theory Comput. 2010, 6, 3713–3720. 10.1021/ct100494z. [DOI] [Google Scholar]
  18. Shirts M. R.; Chodera J. D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Marrink S. J.; Tieleman D. P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. 10.1039/c3cs60093a. [DOI] [PubMed] [Google Scholar]
  20. Hedger G.; Rouse S. L.; Domański J.; Chavent H.; Koldsø H.; Sansom M. S. P.. Lipid loving ANTs: molecular simulations of cardiolipin interactions and the organization of the adenine nucleotide translocase in model mitochondrial membranes. Biochemistry 2016. 10.1021/acs.biochem.6b00751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hansen S. B.; Tao X.; Mackinnon R. Structural basis of PIP2 activation of the classical inward rectifier K+ channel Kir2.2. Nature 2011, 477, 495–498. 10.1038/nature10370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. MacKenzie K. R.; Prestegard J. H.; Engelman D. M. A transmembrane helix dimer: structure and implications. Science 1997, 276, 131–133. 10.1126/science.276.5309.131. [DOI] [PubMed] [Google Scholar]
  23. Pronk S.; Pall S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  25. Parrinello M.; Rahman A. Polymorphic transitions in single-crystals - a new molecular-dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  26. Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  27. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  28. Monticelli L.; Kandasamy S. K.; Periole X.; Larson R. G.; Tieleman D. P.; Marrink S. J. The MARTINI coarse grained force field: extension to proteins. J. Chem. Theory Comput. 2008, 4, 819–834. 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
  29. Marrink S. J.; Risselada J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
  30. Marrink S. J.; de Vries A. H.; Mark A. E. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B 2004, 108, 750–760. 10.1021/jp036508g. [DOI] [Google Scholar]
  31. de Jong D. H.; Singh G.; Bennett W. F. D.; Arnarez C.; Wassenaar T. A.; Schafer L. V.; Periole X.; Tieleman D. P.; Marrink S. J. Improved parameters for the Martini coarse-grained protein force field. J. Chem. Theory Comput. 2013, 9, 687–697. 10.1021/ct300646g. [DOI] [PubMed] [Google Scholar]
  32. Wassenaar T. A.; Ingolfsson H. I.; Boeckmann R. A.; Tieleman D. P.; Marrink S. J. Computational lipidomics with Insane: a versatile tool for generating custom membranes for molecular simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. 10.1021/acs.jctc.5b00209. [DOI] [PubMed] [Google Scholar]
  33. Stansfeld P. J.; Hopkinson R. J.; Ashcroft F. M.; Sansom M. S. P. The PIP2 binding site in Kir channels: definition by multi-scale biomolecular simulations. Biochemistry 2009, 48, 10926–10933. 10.1021/bi9013193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Dahlberg M.; Maliniak A. Mechanical properties of coarse-grained bilayers Formed by cardiolipin and zwitterionic lipids. J. Chem. Theory Comput. 2010, 6, 1638–1649. 10.1021/ct900654e. [DOI] [PubMed] [Google Scholar]
  35. Tribello G. A.; Bonomi M.; Branduardi D.; Camilloni C.; Bussi G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. 10.1016/j.cpc.2013.09.018. [DOI] [Google Scholar]
  36. Bussi G. Hamiltonian replica exchange in GROMACS: a flexible implementation. Mol. Phys. 2014, 112, 379–384. 10.1080/00268976.2013.824126. [DOI] [Google Scholar]
  37. Jefferys E.; Sands Z. A.; Shi J. Y.; Sansom M. S. P.; Fowler P. W. Alchembed: a computational method for incorporating multiple proteins into complex lipid geometries. J. Chem. Theory Comput. 2015, 11, 2743–2754. 10.1021/ct501111d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Michaud-Agrawal N.; Denning E. J.; Woolf T. B.; Beckstein O. MDAnalysis: a toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011, 32, 2319–2327. 10.1002/jcc.21787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Beckstein O.; Domański J.; Somogyi A.. GromacsWrapper: v0.3.3. http://doi.org/10.5281/zenodo.17901 (accessed November 1, 2016).
  40. Humphrey W.; Dalke A.; Schulten K. VMD - Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  41. PyMOL Molecular Graphics System, version 1.8; Schrodinger, LLC, 2016. [Google Scholar]
  42. Stansfeld P. J.; Goose J. E.; Caffrey M.; Carpenter E. P.; Parker J. L.; Newstead N.; Sansom M. S. P. MemProtMD: automated insertion of membrane protein structures into explicit lipid membranes. Structure 2015, 23, 1350–1361. 10.1016/j.str.2015.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wolf M. G.; Hoefling M.; Aponte-Santamaría C.; Grubmüller H.; Groenhof G. g_membed: Efficient insertion of a membrane protein into an equilibrated lipid bilayer with minimal perturbation. J. Comput. Chem. 2010, 31, 2169–2174. 10.1002/jcc.21507. [DOI] [PubMed] [Google Scholar]
  44. De Jong D. H.; Schafer L. V.; De Vries A. H.; Marrink S. J.; Berendsen H. J. C.; Grubmuller H. Determining equilibrium constants for dimerization reactions from molecular dynamics simulations. J. Comput. Chem. 2011, 32, 1919–1928. 10.1002/jcc.21776. [DOI] [PubMed] [Google Scholar]
  45. Hénin J.; Pohorille A.; Chipot C. Insights into the recognition and association of transmembrane a-helices. The free energy of a-helix dimerization in glycophorin A. J. Am. Chem. Soc. 2005, 127, 8478–8484. 10.1021/ja050581y. [DOI] [PubMed] [Google Scholar]
  46. Pebay-Peyroula E.; Dahout-Gonzalez C.; Kahn R.; Trezeguet V.; Lauquin G. J.; Brandolin G. Structure of mitochondrial ADP/ATP carrier in complex with carboxyatractyloside. Nature 2003, 426, 39–44. 10.1038/nature02056. [DOI] [PubMed] [Google Scholar]
  47. Nury H.; Dahout-Gonzalez C.; Trezeguet V.; Lauquin C. J. M.; Brandolin G.; Pebay-Peyroula E. Structural basis for lipid-mediated interactions between mitochondrial ADP/ATP carrier monomers. FEBS Lett. 2005, 579, 6031–6036. 10.1016/j.febslet.2005.09.061. [DOI] [PubMed] [Google Scholar]
  48. McLaughlin S.; Wang J.; Gambhir A.; Murray D. PIP2 and proteins: interactions, organization, and information flow. Annu. Rev. Biophys. Biomol. Struct. 2002, 31, 151–175. 10.1146/annurev.biophys.31.082901.134259. [DOI] [PubMed] [Google Scholar]
  49. Hansen S. B. Lipid agonism: The PIP2 paradigm of ligand-gated ion channels. Biochim. Biophys. Acta, Mol. Cell Biol. Lipids 2015, 1851, 620–628. 10.1016/j.bbalip.2015.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Schmidt M. R.; Stansfeld P. J.; Tucker S. J.; Sansom M. S. P. Simulation-based prediction of phosphatidylinositol 4,5-bisphosphate binding to an ion channel. Biochemistry 2013, 52, 279–281. 10.1021/bi301350s. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Lopes C. M. B.; Zhang H. L.; Rohacs T.; Jin T. H.; Yang J.; Logothetis D. E. Alterations in conserved Kir channel-PIP2 interactions underlie channelopathies. Neuron 2002, 34, 933–944. 10.1016/S0896-6273(02)00725-0. [DOI] [PubMed] [Google Scholar]
  52. Logothetis D. E.; Zhang H. L.; He C.; Yan X. X.; Mirshahi T. Activation of inwardly rectifying K+ channels by distinct PtdIns(4,5)P-2 interactions. Nat. Cell Biol. 1999, 1, 183–188. 10.1038/11103. [DOI] [PubMed] [Google Scholar]
  53. Popot J. L.; Engelman D. M. Membrane protein folding and oligomerization: the two-state model. Biochemistry 1990, 29, 4031–4037. 10.1021/bi00469a001. [DOI] [PubMed] [Google Scholar]
  54. Faham S.; Yang D.; Bare E.; Yohannan S.; Whitelegge J. P.; Bowie J. U. Side-chain contributions to membrane protein structure and stability. J. Mol. Biol. 2004, 335, 297–305. 10.1016/j.jmb.2003.10.041. [DOI] [PubMed] [Google Scholar]
  55. Lemmon M. A.; Flanagan J. M.; Treutlein H. R.; Zhang J.; Engelman D. M. Sequence specificity in the dimerisation of transmembrane a-helices. Biochemistry 1992, 31, 12719–12725. 10.1021/bi00166a002. [DOI] [PubMed] [Google Scholar]
  56. Fleming K. G.; Ackerman A. L.; Engelman D. M. The effect of point mutations on the free energy of transmembrane alpha-helix dimerization. J. Mol. Biol. 1997, 272, 266–275. 10.1006/jmbi.1997.1236. [DOI] [PubMed] [Google Scholar]
  57. Fleming K. G.; Engelman D. M. Specificity in transmembrane helix-helix interactions can define a hierarchy of stability for sequence variants. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 14340–14344. 10.1073/pnas.251367498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Duong M. T.; Jaszewski T. M.; Fleming K. G.; MacKenzie K. R. Changes in apparent free energy of helix-helix dimerization in a biological membrane due to point mutations. J. Mol. Biol. 2007, 371, 422–434. 10.1016/j.jmb.2007.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Anbazhagan V.; Schneider D. The membrane environment modulates self-association of the human GpA TM domain-Implications for membrane protein folding and transmembrane signaling. Biochim. Biophys. Acta, Biomembr. 2010, 1798, 1899–1907. 10.1016/j.bbamem.2010.06.027. [DOI] [PubMed] [Google Scholar]
  60. Hong H.; Blois T. M.; Cao Z.; Bowie J. U. Method to measure strong protein-protein interactions in lipid bilayers using a steric trap. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 19802–19807. 10.1073/pnas.1010348107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Sarabipour S.; Hristova K. Glycophorin A transmembrane domain dimerization in plasma membrane vesicles derived from CHO, HEK 293T, and A431 cells. Biochim. Biophys. Acta, Biomembr. 2013, 1828, 1829–1833. 10.1016/j.bbamem.2013.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Trenker R.; Call M. E.; Call M. J. Crystal structure of the glycophorin A transmembrane dimer in lipidic cubic phase. J. Am. Chem. Soc. 2015, 137, 15676–15679. 10.1021/jacs.5b11354. [DOI] [PubMed] [Google Scholar]
  63. Treutlein H. R.; Lemmon M. A.; Engelman D. M.; Brunger A. T. The glycophorin A transmembrane domain dimer: Sequence specific propensity for a right handed supercoil of helices. Biochemistry 1992, 31, 12726–12733. 10.1021/bi00166a003. [DOI] [PubMed] [Google Scholar]
  64. Woolf T. B.; Petrache H. I.; Grossfield A.; MacKenzie K.; Engelman D. Molecular dynamics simulations of the transmembrane domain of glycophorin A: Implications for pair formation. Biophys. J. 1999, 76, A19–A19. [Google Scholar]
  65. Cuthbertson J. M.; Bond P. J.; Sansom M. S. P. Transmembrane helix-helix interactions: comparative simulations of the glycophorin A dimer. Biochemistry 2006, 45, 14298–14310. 10.1021/bi0610911. [DOI] [PubMed] [Google Scholar]
  66. Psachoulia E.; Bond P. J.; Fowler P. W.; Sansom M. S. P. Helix-helix interactions in membrane proteins: coarse grained simulations of glycophorin helix dimerization. Biochemistry 2008, 47, 10503–105012. 10.1021/bi800678t. [DOI] [PubMed] [Google Scholar]
  67. Janosi L.; Prakash A.; Doxastakis M. Lipid-modulated sequence-specific association of glycophorin A in membranes. Biophys. J. 2010, 99, 284–292. 10.1016/j.bpj.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Kuznetsov A. S.; Polyansky A. A.; Fleck M.; Volynsky P. E.; Efremov R. G. Adaptable lipid matrix promotes protein-protein association in membranes. J. Chem. Theory Comput. 2015, 11, 4415–4426. 10.1021/acs.jctc.5b00206. [DOI] [PubMed] [Google Scholar]
  69. Lemmon M. A.; Treutlein H. R.; Adams P. D.; Brunger A. T.; Engelman D. M. A dimerisation motif for transmembrane a helices. Nat. Struct. Biol. 1994, 1, 157–163. 10.1038/nsb0394-157. [DOI] [PubMed] [Google Scholar]
  70. Arnarez C.; Mazat J.-P.; Elezgaray J.; Marrink S.-J.; Periole X. Evidence for cardiolipin binding sites on the membrane-exposed surface of the cytochrome bc1. J. Am. Chem. Soc. 2013, 135, 3112–3120. 10.1021/ja310577u. [DOI] [PubMed] [Google Scholar]
  71. Arnarez C.; Marrink S. J.; Periole X. Identification of cardiolipin binding sites on cytochrome c oxidase at the entrance of proton channels. Sci. Rep. 2013, 3, 1263. 10.1038/srep01263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Duncan A. L.; Robinson A. J.; Walker J. E. Cardiolipin binds selectively but transiently to conserved lysine residues in the rotor of metazoan ATP synthases. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 8687. 10.1073/pnas.1608396113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Fleming K. G.; Ren C. C.; Doura A. K.; Eisley M. E.; Kobus F. J.; Stanley A. M. Thermodynamics of glycophorin A transmembrane helix dimerization in C14 betaine micelles. Biophys. Chem. 2004, 108, 43–49. 10.1016/j.bpc.2003.10.008. [DOI] [PubMed] [Google Scholar]
  74. Senes A.; Ubarretxena-Belandia I.; Engelman D. M. The Ca ---H···O hydrogen bond: a determinant of stability and specificity in transmembrane helix interactions. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 9056–9061. 10.1073/pnas.161280798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Lelimousin M.; Limongelli V.; Sansom M. S. P. Conformational changes in the epidermal growth factor receptor: role of the transmembrane domain investigated by coarse-grained metadynamics free energy landscape calculations. J. Am. Chem. Soc. 2016, 138, 10611–10622. 10.1021/jacs.6b05602. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp6b08445_si_001.pdf (1.6MB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES