Comparative architectures of mammalian and chicken genomes reveal highly variable rates of genomic rearrangements across different lineages

Abstract

Molecular evolution studies are usually based on the analysis of individual genes and thus reflect only small-range variations in genomic sequences. A complementary approach is to study the evolutionary history of rearrangements in entire genomes based on the analysis of gene orders. The progress in whole genome sequencing provides an unprecedented level of detailed sequence data to infer genome rearrangements through comparative approaches. The comparative analysis of recently sequenced rodent genomes with the human genome revealed evidence for a larger number of rearrangements than previously thought and led to the reconstruction of the putative genomic architecture of the murid rodent ancestor, while the architecture of the ancestral mammalian genome and the rate of rearrangements in the human lineage remained unknown. Sequencing the chicken genome provides an opportunity to reconstruct the architecture of the ancestral mammalian genome by using chicken as an outgroup. Our analysis reveals a very low rate of rearrangements and, in particular, interchromosomal rearrangements in chicken, in the early mammalian ancestor, or in both. The suggested number of interchromosomal rearrangements between the mammalian ancestor and chicken, during an estimated 500 million years of evolution, only slightly exceeds the number of interchromosomal rearrangements that happened in the mouse lineage, over the course of about 87 million years.

Whole genome sequencing provides an unprecedented level of detailed sequence data for comparative studying of genome organizations beyond the level of individual genes, and highlighting rearrangements shaping our genomes. The analysis revealed evidence for a larger number of rearrangements than previously thought, and shed some light on previously unknown features of eukaryotic evolution (Lander et al. 2001). The comparative analysis of recently sequenced rodent genomes and the human genome allowed reconstruction of the putative genomic architecture of the murid rodent ancestor (Bourque et al. 2004), while the architecture of the ancestral mammalian genome and the rate of rearrangements in the human lineage remained unknown.

Genome rearrangement studies start with identification of corresponding orthologous regions in different genomes. The definition of orthologous regions has been gradually shifting from requirements of DNA-level alignment, corresponding to strict conservation of gene order and orientation and applicable to genomes as close as human and mouse (Lander et al. 2001; Waterston et al. 2002), to a more fuzzy definition accommodating small-range rearrangements to capture intuitively the same gene neighborhood in more diverged genomes (Zdobnov et al. 2002; Kent et al. 2003; Pevzner and Tesler 2003). Once the orthologous regions, termed synteny blocks, are defined, we can explore the space of possible shufflings of the blocks to find a most parsimonious scenario of rearrangements that explains the current organization of the genomes.

Rearrangement analyses were initially restricted to unichromosomal genomes (Palmer and Herbon 1988; Sankoff et al. 1992; Bafna and Pevzner 1995; Blanchette et al. 1999; Cosner et al. 2000). But the advent of large-scale sequencing and comparative mapping projects (O'Brien et al. 1999; Murphy et al. 2000; Lander et al. 2001; Waterston et al. 2002; Gibbs et al. 2004) has encouraged the development of methods to also analyze rearrangements in multichromosomal genomes (Hannenhalli and Pevzner 1995; Bourque and Pevzner 2002; Tesler 2002a).

In the current study, we considered two different types of evidence to establish orthologous genomic regions, referred to in the manuscript as synteny blocks. One stems from DNA-DNA alignments, referred as sequence-based data, and the other from protein-protein alignments, referred to as gene-based data. We then applied GRIMM-Synteny (Pevzner and Tesler 2003) to determine the synteny blocks. These synteny blocks were used as input to the GRIMM (Tesler 2002a,b) and MGR (Bourque and Pevzner 2002) algorithms to reconstruct the likely rearrangement evolutionary scenarios, considering inversions, translocations, fusions, and fissions. In the process, MGR also estimates the number of rearrangement events on the evolutionary tree and suggests the reconstructed genomes of a murid rodent ancestor, referred later as RA, and a boreoeutherian ancestor (Murphy et al. 2001) of human, mouse, and rat; the latter is a good approximation to the mammalian ancestor, and therefore we refer to it as MA.

Results

The analysis of rearrangements in human, mouse, rat, and chicken was done on two distinct data sets. The first data set consisted of gene-based data while the second was obtained directly from sequence-based data; see Methods for further details, and Figure 1 for an illustration. As expected, the results highlight advantages and disadvantages of the two types of inputs, but overall the high level of similarity between the solutions confirms the robustness of the method.

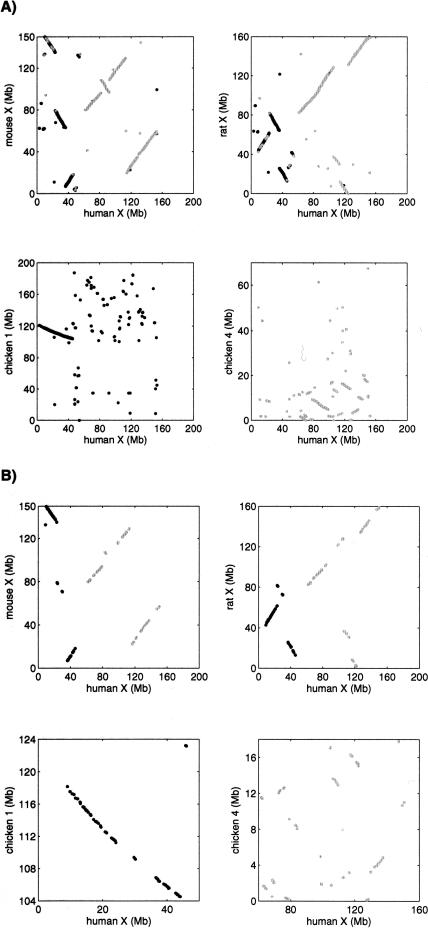
Figure 1.

(A) Dot-plots of anchors based on UCSC alignments for the mammalian X-chromosome versus chicken Chromosomes 1 and 4. The data are very noisy. Many spurious hits are visible on the plots, and there are additional spurious hits between the mammalian X-chromosome and the other chicken chromosomes (data not shown). These spurious hits were filtered out by GRIMM-Synteny because they did not congeal into a block of sufficiently large size. (B) Dot-plots of genes on the mammalian X-chromosome versus chicken Chromosomes 1 and 4. The data are more sparse but much cleaner than the alignment-based data. There were no spurious hits between the mammalian X-chromosome and the other chicken chromosomes.

Gene-based data

To generate synteny blocks using genes as anchors, we started from a set of 6447 four-way orthologous genes, pre-filtered for evidence of conserved pairwise synteny using SyntQL (Zdobnov et al. 2002; E. Zdobnov, unpubl.); see the Methods section. We imposed a minimum of at least three genes per synteny block and allowed for various levels of tolerance for microrearrangements; see the Methods section for a description. The results are shown in Table 1 (see also Supplemental material). The solutions obtained in the various runs are very consistent both in terms of the number of rearrangements on the edges of the recovered scenario (see Table 2) and of the observed chromosomal associations in the putative ancestors (see Table 3). In the rest of this section, we present a detailed description of the results on run gene7, which allows for genes to be merged into the same block when there are up to two intervening genes per species. In this run, there are 586 synteny blocks, comprising a total of 6140 genes. Since some of the three-way human-mouse-rat synteny blocks described in Gibbs et al. (2004) and Bourque et al. (2004) have less than three genes, these blocks did not make it into our set of four-way synteny blocks. Furthermore, since not every mammalian gene has an ortholog in chicken, some of the previously defined human-mouse-rat synteny blocks “lost” some of their genes and were deleted in the four-way comparison by falling below the three genes per block requirement. Finally, some of the previously identified three-way blocks were fragmented onto multiple chicken chromosomes or rearranged in chicken, thus splitting them into multiple four-way blocks. As a result, our 586 four-way synteny blocks correspond to only 299 three-way synteny blocks after projecting to human, mouse, and rat genomes. The average size of the four-way synteny blocks is 3.2 Mb in human, 2.9 Mb in rat, 2.8 Mb in mouse, and only 1.2 Mb in chicken.

Table 1.

Four-way human-mouse-rat-chicken synteny blocks based on orthologous genes

	Human	Mouse	Rat	Chicken
Chromosomes included	1–22, X	1–19, X	1–20, X	1–24, 26–28, 32 W, Z
Total length (Mb)	3020	2577	2720	940
Run gene4
No. of blocks	627	627	627	627
Mean synteny block length (kb)	2865	2515	2644	1075
Max synteny block length (kb)	49,242	45,201	48,457	22,013
Total synteny block length (kb)	1,796,071	1,576,879	1,657,662	673,793
Total synteny block length (% of genome)	59.48%	61.18%	60.95%	71.67%
No. of breakpoint regions	604	607	606	596
Mean breakpoint region length (kb)	1727	1436	1613	410
Max breakpoint region length (kb)	45,875	25,984	30,583	5725
Total breakpoint region length (kb)	1,043,037	871,671	977,759	244,635
Total breakpoint region length (% of genome)	34.54%	33.82%	35.95%	26.02%
No. of genes per block	3–120, mean 9.7
Run gene7
No. of blocks	586	586	586	586
Mean synteny block length (kb)	3205	2794	2945	1196
Max synteny block length (kb)	49,242	45,201	48,457	22,013
Total synteny block length (kb)	1,877,940	1,637,099	1,725,810	700,581
Total synteny block length (% of genome)	62.19%	63.52%	63.45%	74.52%
No. of breakpoint regions	563	566	565	555
Mean breakpoint region length (kb)	1731	1436	1635	394
Max breakpoint region length (kb)	30,387	18,196	30,583	5725
Total breakpoint region length (kb)	974,336	812,924	923,608	218,520
Total breakpoint region length (% of genome)	32.26%	31.54%	33.96%	23.24%
No. of genes per block	3–120, mean 10.5
Run gene10
No. of blocks	567	567	567	567
Mean synteny block length (kb)	3358	2930	3089	1253
Max snyteny block length (kb)	49,242	45,201	48,457	22,013
Total synteny block length (kb)	1,903,906	1,661,039	1,751,281	710,366
Total synteny block length (% of genome)	63.05%	64.45%	64.39%	75.56%
No. of breakpoint regions	544	547	546	536
Mean breakpoint region length (kb)	1745	1442	1646	390
Max breakpoint region length (kb)	30,387	18,196	30,583	5725
Total breakpoint region length (kb)	949,037	788,984	898,578	208,834
Total breakpoint region length (% of genome)	31.43%	30.61%	33.04%	22.21%
No. of genes per block	3–120, mean 10.9
Run gene20
No. of blocks	518	518	518	518
Mean synteny block length (kb)	3787	3327	3495	1413
Max synteny block length (kb)	49,242	45,201	48,457	22,013
Total synteny block length (kb)	1,961,447	1,723,141	1,810,421	731,745
Total synteny block length (% of genome)	64.95%	66.86%	66.56%	77.83%
No. of breakpoint regions	495	498	497	487
Mean breakpoint region length (kb)	1801	1460	1689	392
Max breakpoint region length (kb)	30,387	18,196	30,583	5725
Total breakpoint region length (kb)	891,495	726,883	839,439	191,143
Total breakpoint region length (% of genome)	29.52%	28.20%	30.86%	20.33%
No. of genes per block	3–120, mean 12.0

Several sets of four-way synteny blocks were formed from orthologous genes by allowing for various levels of rearrangements of the genes within the blocks. Runs gene4 through gene20 allow an increasing span of rearrangements, as explained in the text under “GRIMM-Synteny parameters.” Statistics are shown on the sizes of the blocks and the breakpoint regions between them (excluding chromosome ends).

Table 2.

Number of rearrangements on derived evolutionary trees

	All rearrangements							Interchromosomal
	Gene-base (geneX)				Sequence-based			Gene-based (geneX)				Sequence-based
Run	4	7	10	20	100K	200K	300K	4	7	10	20	100K	200K	300K
MA–chicken	4.2	5.3	4.4	4.7	3.9	3.7	4.9	2.5	3.4	2.7	3.4	2.3	2.1	3.7
RA–mouse	0.4	0.5	0.5	0.5	0.5	0.5	0.7	0.6	0.8	0.7	0.8	0.5	0.5	0.7
RA–rat	0.5	0.6	0.5	0.6	0.5	0.5	0.5	0.4	0.5	0.5	0.6	0.4	0.3	0.5
MA–RA	1.4	1.7	1.4	1.4	1.5	1.5	2.1	2.1	2.4	2.0	1.9	1.6	1.6	2.3
MA–human	1	1	1	1	1	1	1	1	1	1	1	1	1	1

The total number of rearrangements and the total number of interchromosomal rearrangements on the edges of the evolutionary tree between the human, mouse, rat, and chicken genomes (see top of Fig. 2) are shown for both gene-based and sequence-based data at various thresholds. MA is the mammalian ancestor and RA is the rodent ancestor. The numbers are normalized using the MA–human edge to simplify comparison.

Table 3.

Chromosome associations and syntenies of the reconstructed mammalian ancestor

	Gene-based				Sequence-based
Run	gene4	gene7	gene10	gene20	100K	200K	300K
Human chromosome associations in MA
3/21	+	+	+	+	+	+	+
4/8	+	+	+	+	+	+	+
12/22a	+	+	+	+	+	+	+
12/22b	+	+	+	+	+	+	+
7/16	–	–	–	–	–	–	–
14/15	+	–	–	+	–	+	–
16/19	+	–	–	–	+	+	–
Human chromosomes syntenies in MA
8	–	–	–	+	–	–	–
9	–	–	–	–	–	+	–
13	+	+	+	+	+	+	+
14	+	+	+	+	+	+	+
15	–	–	–	–	–	–	+
16	–	–	+	+	–	–	–
17	+	+	–	–	–	–	–
18	–	–	–	+	–	–	–
19	–	–	+	–	–	–	–
20	+	+	+	+	+	+	+
21	+	+	+	+	+	+	+
X	+	+	+	+	+	+	+
Chicken chromosome syntenies in MA
7	–	–	–	–	+	–	–
10	–	–	–	–	–	+	+
12	–	+	–	–	–	–	–
13	–	–	–	–	–	+	+
15	–	+	–	+	–	–	–
16	+	+	+	+	N/A	N/A	N/A
17	+	+	–	–	+	+	–
18	+	+	+	+	–	–	+
20	+	+	+	+	+	+	+
21	+	+	+	+	+	+	+
22	–	–	–	–	–	–	+
23	+	+	+	+	+	+	+
24	+	+	+	+	+	+	+
27	+	+	+	+	+	+	+
28	–	–	+	–	–	–	–
32	–	–	–	–	+	+	+
W	–	–	–	–	–	–	–

Using these 586 four-way blocks, GRIMM reveals evidence of at least 441 pairwise rearrangements (of the order and orientation of the whole blocks) between chicken and human, 511 between chicken and mouse, and 506 between chicken and rat. Using the same blocks suggests at least 219 rearrangements between human and mouse, 220 between human and rat, and 75 between mouse and rat. The fact that these last three numbers are ∼25% smaller than the ones described in Bourque et al. (2004) (they were, respectively, 293, 299 are 100) is largely explained by the ∼25% reduction in the number of blocks due to the inclusion of a fourth genome and to the use of genes instead of similarity anchors.

Running MGR on the 586 synteny blocks generates a rearrangement scenario, and two putative ancestors shown in Figure 2. MGR uses heuristics to attempt to minimize the number of rearrangements on the tree, but does not guarantee the result is a most parsimonious solution. On the recovered tree, there are 73 rearrangements between human and MA and 389 between chicken and MA. There are also 38 rearrangements between mouse and RA and 41 between rat and RA. Finally, there are 122 rearrangements between MA and RA. These numbers are lower bounds based on the assumption that the tree is correct; it is possible that nature used a less efficient sequence of steps or operations besides those considered.6 These numbers, normalized using the MA-human edge, are displayed in Table 2.

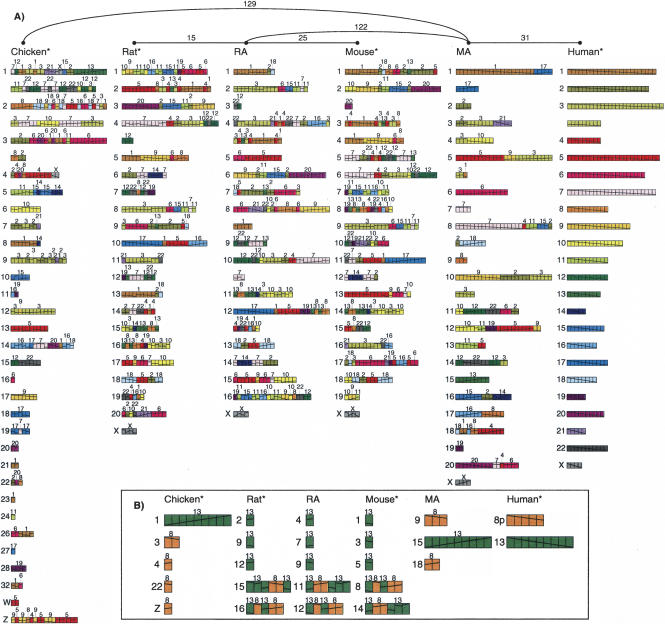
Figure 2.

Ancestral murid rodent ancestor (RA), ancestral mammalian ancestor (MA), and evolutionary tree recovered by MGR using the human, mouse, rat, and chicken genomes. Each genome is represented as an arrangement of 586 synteny blocks computed by GRIMM-Synteny on gene-based data in run gene7. Each synteny block is drawn as one unit, regardless of its length in nucleotides. Chromosomes with too many blocks are split into multiple lines. Each human chromosome is assigned a unique color, and a diagonal line is drawn through the whole chromosome. In other genomes, this diagonal line indicates the relative order and orientation of the rearranged blocks. Black triangles below ancestral chromosomes indicate weak adjacencies. The unrooted phylogram at the top of the figure shows the topology of the evolutionary tree; the last common ancestor of human, mouse, rat, and chicken would be somewhere on the edge between Chicken and MA. The minimum number of rearrangements required to convert between two genomes is shown on each edge of that tree.

The rearrangement scenario corresponding to Figure 2 confirms a high ratio of intrachromosomal versus interchromosomal rearrangements on the chicken edge. This was computed by attempting to maximize the number of inversions on the MA-chicken edge while staying within the constraint of 389 steps; however, it is only an approximation, because (1) there could be an alternative sequence of 389 steps with a higher ratio, and (2) intrachromosomal rearrangements could have been mimicked by interchromosomal rearrangements. This ratio varies: 2.8 on the MA-chicken edge, 1.7 on the RA-rat edge, 1.4 on MA-human edge, 0.7 on the RA-mouse edge, and 0.7 on the MA-RA edge.7 The number of interchromosomal rearrangements on the path from human to chicken (132) is only slightly higher than the number of interchromosomal rearrangements on the path from human to mouse and rat (124 and 116). It implies an extremely slow rate of interchromosomal rearrangements along the chicken edge in the evolutionary tree: 0.19 rearrangements per million years on the MA-chicken edge as compared to 0.34 on the MA-human edge and 1.1 on the MA-mouse edge.8

Figure 2 also reveals a large number of inversions that scramble the genomic make-up of individual chromosomes. For example, chicken Chromosome 19 (GGA19) is “built” from synteny blocks residing on only two human chromosomes (HSA7 and HSA17) that form a complex shuffle represented by eight different unicolored segments (four from HSA7, alternating with four from HSA17, and those in turn contain intrachromosomal rearrangements). These segments likely arose from a translocation of HSA7 and HSA17, creating a chromosome that was further shuffled by inversions on the evolutionary path between human and chicken. To sort out some of the intrachromosomal (inversions) from the interchromosomal (translocations/fusions/fissions) rearrangements and in an attempt to “reverse” history, we perform a maximal number of initial inversions in the four starting genomes,9 thus making every chromosome less shuffled than it appears in Figure 2. By performing all these initial inversions, we reduce the number of four-way blocks from 586 down to 311 new “pre-ancestral” synteny blocks. We call these four modified genomes “pre-ancestors.”10 Figure 3 illustrates the proposed organization of these pre-ancestors and of the two ancestors (RA and MA) using this smaller number of segments.

Figure 3.

(A) Four pre-ancestors (marked with ^*), obtained after carrying out a maximal number of initial inversions, and two putative ancestors (murid rodent ancestor, RA, and mammalian ancestor, MA) for gene-based data in run gene7. Each genome is represented by an arrangement of 311 new synteny blocks obtained after carrying out the initial inversions and condensing the 586 initial four-way blocks. (B) Arrangement of the set of 14 blocks from HSA8p and HSA13, which are contiguous in the pre-ancestors of all species but are found on four different chromosomes in chicken, mouse, and rat. The two putative ancestral arrangements of these blocks, as recovered by MGR, are also shown.

Because the pairwise distances between the initial genomes are substantial, it is possible to find alternative ancestors also minimizing the total number of rearrangement events on the evolutionary tree. By exploring some of these alternative ancestors (see Methods), we can partition all the adjacencies of the recovered ancestor into “strong” and “weak” adjacencies depending on whether they are present or not present in all of the observed alternative ancestors.11 In run gene7, we find 524 strong adjacencies and 83 weak adjacencies12 (see Fig. 2). Many of the previously postulated chromosome associations of the placental ancestor correspond to strong adjacencies in MA. These associations are 3/21, 4/8, 12/22a, and 12/22b (Murphy et al. 2003; Stanyon et al. 2003). Other ancestral chromosome associations missing from MA (e.g., 7/16, 14/15, and 16/19) are currently only associated to other chromosomes by weak associations, meaning that in this analysis they were left as unresolved. The synteny of six human chromosomes (13, 14, 17, 20, 21, X) and of 10 chicken chromosomes (12, 15-18, 20, 21, 23, 24, 27) is preserved in MA. In stark contrast, the rodent Chromosome X is the only rodent chromosome whose synteny is preserved in MA. This is consistent with the affirmation that interchromosomal rearrangements have been very frequent in rodents. Results about chromosomal associations and syntenies are summarized in Table 3.

The reconstruction of the murid rodent ancestor, RA, is also coherent with the reconstruction of the same ancestor in Bourque et al. (2004). The human chromosome associations 3/21, 4/8, and 12/22 are once again recovered in RA. The association 16/19 is missing from the current reconstruction, but blocks from these two human chromosomes are found on the same chromosome in RA (although they are not adjacent). The analysis of alternative ancestors reveals 576 strong adjacencies and only 26 weak adjacencies in RA (see Fig. 2).

Some large regions of mammalian genomes are extremely well conserved across many species. The X-chromosome is one such example where the limited amount of exchange of genetic material with the other chromosomes (see Fig. 1) allows a detailed analysis of its rearrangement history. In the most parsimonious rearrangement scenario of the 17 synteny blocks on the X-chromosome of human-mouse-rat and of the homologous blocks on chicken Chromosomes 1 and 4, there are 20 rearrangements in total. There are no rearrangements between human and MA (i.e., human order is ancestral), 14 rearrangements (13 inversions and one fusion) between chicken and MA, two inversions between MA and RA, one inversion between mouse and RA, and three inversions between rat and RA. Moreover, the scenario recovered is optimal and MA and RA are unique. For that optimal score, the number of steps on each edge is unique, but the specific order is not.

The set of blocks on the human X-chromosome is an example of a set of blocks that is not interrupted by any foreign block (a block outside that set) in any of the four genomes (although blocks can reside on multiple chromosomes in each genome). We call this a set of contiguous blocks. Large sets of contiguous blocks are interesting because they can be analyzed for rearrangements independently from the rest of the genome. HSA8p and HSA13 is an example of a well-conserved region, but, unfortunately, it does not form a set of contiguous block in run gene7 because the blocks from HSA8p are interrupted on GGA3 by blocks from HSA2 and on GGA4 by blocks from HSA4 (see Fig. 2). Blocks from HSA8p on GGA3-4 were probably interspersed with other blocks by a series of more recent inversions. Fortunately, we can undo these inversions by using the pre-ancestors (see Fig. 3A) where HSA8p and HSA13 do form a set of contiguous blocks. This specific region is shown in Figure 3B. The rearrangement scenario highlights how some chromosomes are well preserved in chicken but shuffled in rodent, whereas others are well conserved in rodent but more shuffled in chicken.

Sequence-based data

We also generated similarity blocks using four-way unique alignments as anchors. We include three runs, called 100K, 200K, and 300K (see Table 4 and Supplemental material). In run 300K, two anchors are put into the same block if they are within 300 kb of each other in all genomes, and then resulting blocks smaller than 300 kb are deleted. The other runs are analogous. See the Methods section for more details. Running MGR on each set of fourway blocks generated at 100K, 200K, and 300K (see Fig. 4) produces rearrangement scenarios and putative ancestors whose features are summarized in Tables 2 and 3.

Table 4.

Four-way human-mouse-rat-chicken synteny blocks based on sequence alignments

	Human	Mouse	Rat	Chicken
Chromosomes included	1–22, X	1–19, X	1–20, X	1–24, 26–28, 32, W, Z
Total length (Mb)	3020	2577	2720	940
Run 100K
No. of blocks	583	583	583	583
Mean synteny block length (kb)	2713	2436	2566	1083
Max synteny block length (kb)	44,708	38,350	41,531	16,085
Total synteny block length (kb)	1,581,616	1,420,395	1,495,964	631,341
Total synteny block length (% of genome)	52.37%	55.11%	55.00%	67.15%
No. of breakpoint regions	560	563	562	553
Mean breakpoint region length (kb)	2254	1815	2065	509
Max breakpoint region length (kb)	40,507	19,233	33,229	5247
Total breakpoint region length (kb)	1,262,211	1,021,678	1,160,670	281,338
Total breakpoint region length (% of genome)	41.80%	39.64%	42.67%	29.92%
No. of anchors per block	5–2915, mean 234.2
Run 200K
No. of blocks	474	474	474	474
Mean synteny block length (kb)	3556	3191	3365	1409
Max synteny block length (kb)	44,292	38,350	41,501	16,085
Total synteny block length (kb)	1,685,370	1,512,364	1,595,170	667,927
Total synteny block length (% of genome)	55.81%	58.68%	58.65%	71.04%
No. of breakpoint regions	451	454	453	444
Mean breakpoint region length (kb)	2534	2034	2316	550
Max breakpoint region length (kb)	46,565	14,435	32,219	7563
Total breakpoint region length (kb)	1,142,700	923,594	1,049,169	244,138
Total breakpoint region length (% of genome)	37.84%	35.84%	38.57%	25.97%
No. of anchors per block	11–3213, mean 319.6
Run 300K
No. of blocks	430	430	430	430
Mean synteny block length (kb)	4049	3620	3814	1596
Max synteny block length (kb)	45,607	38,350	42,466	16,085
Total synteny block length (kb)	1,740,889	1,556,569	1,639,876	686,262
Total synteny block length (% of genome)	57.65%	60.40%	60.29%	72.99%
No. of breakpoint regions	407	410	409	400
Mean breakpoint region length (kb)	2662	2136	2451	562
Max breakpoint region length (kb)	44,269	15,587	32,219	10,187
Total breakpoint region length (kb)	1,083,594	875,902	1,002,423	224,812
Total breakpoint region length (% of genome)	35.88%	33.99%	36.85%	23.91%
No. of anchors per block	16–3410, mean 370.6

Several sets of four-way synteny blocks were formed from sequence alignments at different resolutions. “100K” blocks must be at least 100 kb in each species and allow for anchors to be displaced up to 100 kb in a certain metric, as explained in the text under “GRIMM-Synteny parameters.” Statistics are shown on the sizes of the blocks and the breakpoint regions between them (excluding chromosome ends).

Figure 4.

Ancestral murid rodent ancestor (RA), ancestral mammalian ancestor (MA), and evolutionary tree recovered by MGR using the human, mouse, rat, and chicken genomes. Each genome is represented as an arrangement of 430 synteny blocks computed by GRIMM-Synteny on sequence-based data in run 300K.

We find that there are about four to five times as many total rearrangements between chicken and MA as between human and MA. Between the rodents and MA, there are about twice as many. For interchromosomal rearrangements, there are about three times as many between chicken and MA as there are between human and MA, and there are also three times as many between each rodent and MA as between human and MA.

Some of the putative ancestral human chromosome associations were observed in all runs (3/21, 4/8, 12/22a, and 12/22b), while others were only recovered in some of the runs (14/15, 16/19) or not recovered at all (7/16). Some human chromosome syntenies were systematically preserved in MA (13, 14, 20, 21, and X) and similarly, some chicken chromosome syntenies were found in MA for all runs (20, 21, 23, 24, and 27). Many of the discrepancies observed in Table 3 can be explained by differences in the coverage of gene-based data versus sequence-based data. For instance, two chicken chromosome syntenies (22, 32) are only observed in sequence-based data mainly because they are covered by fewer blocks (1 block each in run 300K) (see Fig. 4) in those data sets. Chicken Chromosome 16 is an even more drastic example: in gene-based data a single short block represents it, whereas in sequence-based data, it is not represented at all.

Microrearrangement scenarios

The analysis of rearrangements in mammalian genomes is complicated by microrearrangements (small-scale rearrangements within synteny blocks). The GRIMM-Synteny algorithm preserves information about microrearrangements in each block it forms, allowing us to run MGR independently on the genes or anchors within each synteny block. This generated a microrearrangement scenario, including a microevolutionary tree, for each of these synteny blocks. See Figure 5 for an example. We looked at the usefulness of using microrearrangements as evolutionary characters for phylogenetic tree reconstructions. A microevolutionary tree is said to be a “perfect match” if its topology agrees with the known topology for human-mouse-rat-chicken (as depicted at the top of Fig. 2).13 If it does not agree with the known topology, it is said to be a mismatch. A recovered topology can only agree or disagree with the known topology if the internal edge of the recovered tree has at least one rearrangement. Otherwise, the recovered topology is said to be inconclusive. The results are summarized in Table 5. The trees recovered are very accurate: for both gene-based and sequence-based data, the proportion of mismatches is very low. For gene-based data, a large proportion of synteny blocks (∼65%) do not have any microrearrangements, which leads to inconclusive topologies. In contrast, with sequence-based data, this proportion is relatively small (∼25%) and leads to a higher fraction of perfect matches (∼25%). As expected, the total number of microrearrangements is much higher for sequence-based data than for gene-based data. This is explained in part by the fact that many of the microrearrangements in sequence-based synteny blocks lay outside exons.

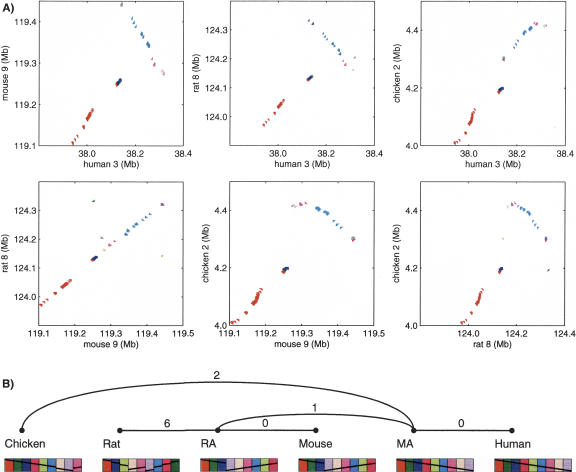
Figure 5.

(A) Dot-plots of similarity anchors in a four-way synteny block with microrearrangements. The block was computed by GRIMM-Synteny on sequence-based data in run 300K. The block length is 380 kb in human, 340 kb in mouse, 364 kb in rat, and 419 kb in chicken. The anchors divide into nine groups, indicated by different colors; these groups have a different order and orientation in each genome. Within each group, the anchors have the same relative order in all genomes (or an overall flip of the whole group), but their absolute spacing is not preserved. (B) Microrearrangement history for the same block as generated by MGR. The nine colored blocks correspond to the nine groups of anchors in the dot-plots. The minimum number of inversions required to convert between synteny blocks in two genomes is shown on each edge of the tree.

Table 5.

Microrearrangements scenarios on applying MGR independently to genes/anchors within synteny blocks

	Gene-based				Sequence-based
Run	gene4	gene7	gene10	gene20	100K	200K	300K
Blocks	627	586	567	518	583	474	430
Conserved blocks	0.758	0.660	0.628	0.577	0.425	0.259	0.193
Perfect match	0.016	0.026	0.026	0.037	0.177	0.251	0.298
Mismatch	0.002	0.007	0.009	0.010	0.003	0.006	0.016
Inconclusive	0.982	0.967	0.965	0.953	0.820	0.743	0.686
Microrearrangements	272	383	437	543	1408	1941	2329
Microrearrangements (force topology)	273	387	442	548	1410	1944	2336

“Blocks” indicates the number of synteny blocks in each run. “Conserved blocks” stands for the fraction of synteny blocks in which gene/anchor order is preserved in human-mouse-rat-chicken. “Perfect match” is the fraction of recovered topologies that agrees with the known topology for these four genomes (this requires the internal edge to have at least one rearrangement). “Mismatch” is the fraction of recovered topologies that do not agree with the known topology. “Inconclusive” is the fraction of recovered topologies with a zero-length internal edge, which cannot be used to verify any topology. “Microrearrangements” indicates the total number of rearrangements within these synteny blocks. “Microrearrangements (force topology)” is similar, but the scenario is computed with the constraint that it must obey the correct topology.

We separately ran MGR within the same synteny blocks while imposing the known topology for human-mouse-rat-chicken; this only leads to a slight increase in the total number of microrearrangements (see Table 5).

In Table 6, we compute the proportion of the microrearrangements over the different edges of the tree. The results show that most of the microrearrangements (∼60%) occurred on the chicken to MA edge but that a large portion (∼20%) occurred on the rat to MA edge. If we take into account the divergence time, this suggests either an accelerated rate of microrearrangements in rat or a higher rate of errors in the rat assembly. Figure 5 shows a block in which a large inversion occurred on the evolutionary path leading to rodents but in which an additional six inversions are required to explain the arrangement of anchors in rat.

Table 6.

Estimated proportion of microrearrangements on each edge of the tree

	Gene-based				Sequence-based
Run	gene4	gene7	gene10	gene20	100K	200K	300K
MA–chicken	0.60	0.60	0.63	0.64	0.65	0.61	0.58
RA–mouse	0.03	0.03	0.03	0.04	0.10	0.08	0.09
RA–rat	0.23	0.22	0.20	0.17	0.14	0.18	0.20
MA–RA	0.04	0.05	0.06	0.05	0.09	0.09	0.09
MA–human	0.09	0.10	0.10	0.10	0.03	0.3	0.03

Scenarios were obtained by applying MGR independently to genes/anchors within synteny blocks and imposing the proper topology shown at the top of Figure 2. Columns do not always add up to 1 because of rounding.

Discussion

Choosing a set of orthologous genes rather than the “similarity anchors” as in Gibbs et al. (2004) has some benefits. Since the chicken genome is rather distant from mammalian genomes, using similarity anchors (at lower similarity thresholds, due to the distance) leads to many spurious hits (Fig. 1), which are difficult to unambiguously assemble into synteny blocks. Moreover, highly diverged genes may not generate any four-way anchors (based on exact nucleotide l-mer matches) but still can be reliably detected with amino acid scoring matrices.

Using GRIMM-Synteny on “similarity anchors” also has advantages. For instance, it allows avoiding the identification of orthologous versus paralogous copies of genes. It is also less affected by high-copy-number gene families (such as kinases or GPCRs). Moreover, it retains information in regions outside of exons. This extra information can be useful for the analysis of microrearrangements, but it can also be an asset in the reconstruction of the ancestral genomes by keeping stronger footprints of past events.

Although the two initial data sets are different, the properties of the evolutionary tree and of the reconstructed ancestors obtained at various thresholds are largely consistent. We observed a high ratio of inversions over all types of rearrangements in chicken but, overall, a relatively slow rate of rearrangements in this lineage. The large number of inversions in chicken can also be confirmed by the analysis microrearrangements within the synteny blocks. Finally, we also observed an accelerated rate of interchromosomal rearrangements in rodents.

Future developments could include more systematic ways of comparing synteny blocks generated using different programs, different sets of parameters, different types of input (e.g., gene vs. sequence data) but also different sets of initial genomes. Similarly, new metrics could also be developed to compare the ancestral reconstructions not only at the level of chromosome associations, chromosome syntenies, and rates of rearrangements but also at the level of actual synteny blocks and suggested adjacencies. Such metrics would need to account for the multiplicity of alternative solutions.

Methods

We compared these assemblies: Human (NCBI build 34, July 2003; UCSC hg16); Mouse (NCBI build 30, Feb. 2003; UCSC mm3); Rat (Baylor HGSC v. 3.1, June 2003; UCSC rn3); and Chicken (WUSTL Feb.2004, UCSC galGal2).

Gene-based comparisons used a set of 6447 four-way orthologous genes obtained by intersection of less strictly defined pairwise synteny maps, requiring at least two neighboring orthologous genes but allowing for up to four intervening genes, computed with SyntQL (Zdobnov et al. 2002; E. Zdobnov, unpubl.) on all best reciprocal BLASTP matches (Altschul et al. 1997) in cross-genome comparison. SyntQL relies on an optimized relational database engine to retrieve all minimal synteny blocks defined by a number of constraints (e.g., two pairs of orthologous genes between two genomes located closely on these genomes) formulated in an SQL query that are then merged into longer synteny blocks over shared orthologous pairs.

Sequence-based comparisons used alignments computed by Angie Hinrichs in the UCSC consortium using BLASTZ, MULTIZ, and other tools (Kent et al. 2003; Schwartz et al. 2003; Blanchette et al. 2004). Initially these contained 343,645 four-way alignments (and many more partial alignments, which we did not use); however, many of these four-way alignments have conflicting coordinates. We filtered out regions with duplications identified by Evan Eichler (in prep.) and other duplications we observed on dot-plots, and then applied the GRIMM-Anchors algorithm (Bourque et al. 2004) to reduce it to 208,032 four-way anchors.

GRIMM-Synteny parameters

We added more parameters to the GRIMM-Synteny algorithm, described for sequence-based data in Pevzner and Tesler (2003) and for unsigned gene-based data in Murphy et al. (2003). In the present study, for sequence-based data, we start with a set of anchors (four-way unique alignments in this case) described by their chromosome, start and end in nucleotides, and orientation. The distance between two points (x₁, x₂, x₃, x₄) and (y₁, y₂, y₃, y₄; measured in nucleotides) in the same four-way chromosome window is the Manhattan distance |x₁ - y₁| +... + |x₄ - y₄|. The distance between two anchors is the distance between their closest terminals (there are two choices of terminal for each anchor, determined by the signs of the alignments). In the original GRIMM-Synteny, two anchors were joined together when the distance was less than a specified threshold. We now use a per species distance: the closest terminals are determined based on the total distance, and then the anchors are joined if in all species, the gap |x_i - y_i| is (strictly) below the per species gap threshold G_i. The “300K” data set in the text of this paper uses G_i = 300,000 for all species. The “100K” and “200K” data sets in the tables use G_i = 100,000 and G_i = 200,000, respectively.

In the original GRIMM-Synteny, we then discarded blocks whose span was below a minimum size in human. In this study, we set minimums in all species. In the present study, we discarded blocks whose span was (strictly) below a minimum size C_i in any species; in the sequence-based runs 100K, 200K, and 300K, we chose to set C_i = G_i. Occasionally, the blocks that make it past this filter will have conflicting coordinates in one species (the coordinate interval of block A is a subinterval of block B in one species), in which case we split the blocks up to resolve this.

We then merged together blocks that form a strip of consecutive blocks in the exact same order (allowing an overall flip) and chromosome window in all genomes, without interruption by other blocks. This step is appropriate for analyzing rearrangements, but may not be appropriate for other purposes.

Our “signed” gene-based data was analyzed with the same procedure but with a “gene” metric instead of a “nucleotide” metric; all genes in the data set are assigned an identical size. Specifically, the j-th consecutive gene in a chromosome is assigned span 2j through 2j + 1, and the orientation of the gene determines which coordinate is the “start” and which is the “end.” Our “gene7” data set used throughout this paper uses the procedure described above with G_i = 7 for all species. Two genes A and B are joined together if there are up to two intervening genes between them in every species, with certain constraints on flipping A and B: at two intervening genes, the relative orientations of A and B must be the same in all species or one of them can be flipped, and with less than two intervening genes, either or both can be flipped. Next, we discarded blocks supported by less than three genes, and finally, we merged together strips of blocks as before. The gene4, gene10, and gene20 data sets similarly used 4, 10, or 20 in place of 7. G_i = 4 (respectively, 10 or 20) has the effect of allowing 1 (respectively, 4 or 9) intervening gene, but A and B must remain in the same relative orientation in all species, or up to 0 (respectively, 3 or 8) intervening genes, but A and B may be flipped arbitrarily.

In contrast, the data set in Murphy et al. (2003) was “unsigned” gene-based data, because some data were obtained from RH maps and therefore signs were not available. All genes were given equal size 1, the j-th gene on a chromosome was assigned the single point coordinate j, and had just one end instead of two.

Search for alternative ancestors

Starting from the ancestral reconstruction MA obtained with MGR and the three adjacent genomes on the evolutionary tree (human, chicken, and RA), we generated a list of rearrangements in MA that did not increase the sum of the distances to those adjacent genomes. An alternative ancestor (at distance 1 from MA) is associated to each of these rearrangements. We repeated the process starting from these new alternative ancestors by using both a breadth-first-search and a depth-first-search approach. We kept the first 6000 alternative ancestors (3000 from each approach). We used a similar method to look for alternative reconstructions of RA.

Specifically, in run gene7, we found a list of 83 rearrangements in MA that did not increase the overall tree score. Using a breadth-first-search approach, we looked at all 83 corresponding alternative ancestors (at distance 1 from MA). We generated a new list of rearrangements that did not increase the overall tree score for each of these alternative ancestors. Since most of the rearrangements from the initial list of 83 are commutative, the number of alternative ancestors at distance 2 from MA is ∼(83 × 82)/2 = 3403. In practice, it could even be larger because some of these rearrangements “unlock” new rearrangements that do not increase the overall score either. For the purpose of the current analysis, we stopped once we had a total of 3000 distinct alternative ancestors (83 at distance 1 from MA and 2917 at distance 2).

We also used a depth-first-search approach to look for different alternative ancestors of MA. Starting only from the first alternative ancestor identified at distance 1 from MA, we found 80 alternative ancestors at distance 2. Starting from the first of these alternative ancestors, we found 80 new alternative ancestors but at distance 3 from MA. We repeated the process iteratively. When the first ancestor at distance x did not suggest any ancestor at distance x + 1, we moved down to another ancestor at distance x. When we ran out of ancestors at distance x, we stepped back to the list of ancestors at distance x - 1. In practice, we stopped once we reached a total of 3000 distinct ancestors found at various distances from MA. In run gene7, the distance between MA and the alternative ancestors found with the depth-first-search approach ranged from 1 to 38 rearrangements.