Abstract
Many biomolecules undergo conformational changes associated with allostery or ligand binding. Observing these changes in computer simulations is difficult if their timescales are long. These calculations can be accelerated by observing the transition on an auxiliary free energy surface with a simpler Hamiltonian and connecting this free energy surface to the target free energy surface with free energy calculations. Here we show that the free energy legs of the cycle can be replaced with energy representation (ER) density functional approximations. We compute: 1) The conformational free energy changes for alanine dipeptide transitioning from the right-handed free energy basin to the left-handed basin and 2) the free energy difference between the open and closed conformations of β-cyclodextrin, a “host” molecule that serves as a model for molecular recognition in host-guest binding. β-cyclodextrin contains 147 atoms compared to 22 atoms for alanine dipeptide, making β-cyclodextrin a large molecule for which to compute solvation free energies by free energy perturbation or integration methods and the largest system for which the ER method has been compared to exact free energy methods. The ER method replaced the 28 simulations to compute each coupling free energy with 2 endpoint simulations, reducing the computational time for the alanine dipeptide calculation by about 70% and for the β-cyclodextrin by > 95%. The method works even when the distribution of conformations on the auxiliary free energy surface differs substantially from that on the target free energy surface, although some degree of overlap between the two surfaces is required.
Keywords: energy representation, molecular dynamics simulations, distribution function, conformational changes, solvation free energy
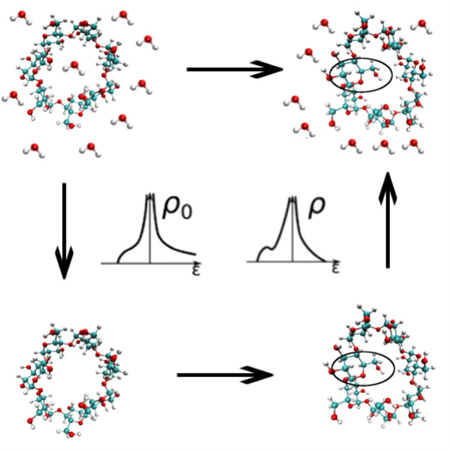
Graphical abstract
The free energy differences associated with conformational changes are difficult to compute in explicit solvent. Instead, these free energy differences can be computed on an auxiliary free energy surface and the desired free energy difference obtained by adding the free energies of transferring the end states from the auxiliary surface to the target surface. Here we show that computing these transfer free energies with the energy representation method substantially reduces the cost of these calculations.
INTRODUCTION
Many proteins undergo large-scale conformational changes during folding or to perform different functions, and many biomolecular targets of interest in drug discovery undergo large conformational changes upon binding to ligands. Estimating the free energies of folding, allostery, and binding therefore requires the evaluation of free energy differences associated with conformational changes1–3. In principle, these free energy differences could be computed by running molecular dynamics simulations of the systems, waiting for them to spontaneously undergo the conformational transitions, and measuring the relative probabilities of the conformational states. However, if the free energy barriers between the conformational states of interest are large, then the system will remain kinetically trapped in one of the states during the timescales accessible to molecular dynamics, making such direct calculations become computationally too costly or unfeasible. For example, in a previous paper, using the solvated alanine dipeptide free energy surface as an example, we ran molecular dynamics simulations and found that it would require approximately 4 µs of simulation time to obtain converged estimates of the free energy difference between the right- and left-handed regions of the Ramachandran plot4. Such long simulations are expensive, even for small systems, and for many conformational changes of larger biomolecules the required timescales could be many orders of magnitude larger.
Many different techniques have been developed to get around this problem (eg. replica-exchange molecular dynamics5,6, metadynamics7, accelerated molecular dynamics8, adaptive umbrella sampling9, transition path sampling10, milestoning11, and Markov state models12–15). Alternatively, the simulations can be run with various implicit solvent models16–21, which by averaging over the coordinates of the solvent greatly reduce the degrees of freedom of the system. However, because implicit solvent models perform this averaging in an approximate way, the accuracies of their predictions can be difficult to evaluate18,22–26.
In a recent paper we proposed a new implicit/explicit thermodynamic cycle that takes advantage of the speed of implicit solvent simulations but is designed to give the same answer as exhaustive sampling in explicit solvent. If a conformational transition of interest occurs faster in implicit solvent or vacuum or the simulation is simply faster in an implicit solvent model because of the many fewer degrees of freedom in the system, then we can estimate the desired free energy change on this auxiliary (implicit solvent or vacuum) free energy surface and obtain the free energy difference on our target (explicit solvent) free energy surface by connecting the two free energy surfaces with focused free energy calculations4. In that case, computing conformational free energy changes in vacuum and/or implicit solvent and connecting those free energy surfaces to the explicit solvent free energy surface reduced the necessary computational time to obtain the free energy changes by >90%.
In the present study we show that the free energies connecting the target and auxiliary free energy surfaces with free energy calculations can be replaced by the results of free energy functional/endpoint energy representation (ER)27–31 calculations that use data from the endpoints of the free energy calculations to estimate these connecting free energy differences. We show that doing so reduces by ~70% the cost of obtaining the conformational free energy changes for alanine dipeptide and by more than 95% the computational cost of obtaining conformational free energy estimates for β-cyclodextrin, a flexible “host” molecule used to investigate molecular recognition32–38. β-cyclodextrin contains 147 atoms, as compared to the 22 atoms in alanine dipeptide, making these calculations a stringent test of the proposed method. Indeed, the number of atoms in β-cyclodextrin is much larger than the numbers of atoms in most molecules for which solvation free energies have been computed with free energy methods. We also show that while these methods do require some overlap between the conformational distributions on the auxiliary and target free energy surfaces, these distributions can be quite different. For β-cyclodextrin, for example, the system had two free energy minima in explicit solvent but only one minimum in vacuum.
METHODOLOGY
Connecting free energy surfaces
In principle, the free energy difference (ΔG1,A→B) between two states A and B on a target (1) free energy surface can be computed from a molecular dynamics trajectory by
| (1) |
where k is Boltzmann’s constant, T is the temperature, and and are the probabilities that the system is in state A and B, respectively. However, if the two states are separated by a large free energy barrier, then molecular dynamics simulations started in either state A or state B can remain kinetically trapped in that state, making computing and difficult.
In a previous paper we showed that computing ΔG1,A→B by computing the free energy difference (ΔG0,A→B) between states A and B on an auxiliary free energy (0) surface and connecting the two free energy surfaces with free energy calculations can be much more efficient4. We therefore proposed the following equation:
| (2) |
where and are the probabilities that the system falls in a small region (a1) of state A in the auxiliary and target free energy surfaces, respectively, and are the probabilities that the system falls in a small region (b1) of state B in the auxiliary and target free energy surfaces, respectively, and ΔG0→1,a1 and ΔG0→1,b1 are the free energies required to move a system restrained to a1 and b1, respectively, from the auxiliary to the target free energy surface.
In this equation, the terms and reflect the local curvature of the target and auxiliary free energy surfaces. They are not sensitive to changes in the free energy difference between the A and B basins on the target and auxiliary free energy surfaces. They are the differences between the free energies required to restrain a system in basin A or B to a1 or b1 on the target free energy surface and those on the auxiliary surface.
Endpoint method: Energy representation approximate functional
In Equations 1 and 2, state 1 refers to the solution system of interest, and a natural choice of state 0 is the isolated solute in vacuum and the pure solvent uncoupled to the solute. In this case, ΔG0→1,a1 and ΔG0→1,b1 of Equation 2 correspond to the solvation free energies of the solute restrained to a1 and b1, respectively. Computing solvation free energies with molecular dynamics methods, such as free energy perturbation (FEP) and thermodynamic integration (TI), is computationally expensive and usually requires the introduction of fictitious intermediate states connecting the state where the solvent and solute are uncoupled (the initial state) to the state where they are fully coupled (the final state).
To reduce the computation time for the solvation free energy, in this work we also resort to the ER method27–31. Within the framework represented by Equation 2, a fast scheme for obtaining ΔG0→1,a1 and ΔG0→1,b1 that explicitly accounts for the intramolecular flexibility within the a1 and b1 regions is required. The ER method meets this requirement. It is a theory of distribution functions in solution and was formulated by adopting the solute-solvent pair interaction energy for the coordinate of the distribution functions. Among a variety of approximate free-energy methods39–50, the ER method is unique in its high accuracy, efficiency, and range of applicability30,31,51–53. In ER, the simulations are performed only at the initial and final states (endpoints) of the solute insertion process, and a set of energy distribution functions obtained from the endpoint simulations provides the solvation free energy through an approximate functional. The intramolecular flexibility does not require special treatment, furthermore, and is handled as a natural part of the MD data analysis. It has also been observed for small molecules that the error due to the use of the approximate functional is not larger than the error due to the force field. We employ ER for ΔG0→1,a1 and ΔG0→1,b1 of Equation 2.
The solvation free energy Δμ is the free-energy change for turning on the solute-solvent interaction. In the ER method, the value of the solute-solvent interaction υ of interest is adopted as the coordinate ε for the solute-solvent distribution and the instantaneous distribution ρ̂e is defined as
| (3) |
where ψ is the configuration of the solute molecule, xi is the configuration of the ith solvent molecule, the sum is taken over all the solvent molecules, and a superscript e is attached to emphasize that a function is represented over the energy coordinate. Let ρe(ε) and be the statistical averages of ρ̂e(ε) in the solution system of interest (state 1 of Equation 2) and in pure solvent with the solute uncoupled (state 0), respectively. Δμ can be then be expressed exactly as
| (4) |
where Ωe(ε) represents the contribution due to the change in the solvent-solvent correlation upon introduction of the solute. In the present study we use an approximate Ωe(ε) obtained by adopting hypernetted-chain(HNC)–type and Percus-Yevick(PY)–type expressions. See Appendix and previous papers for the explicit form of Ωe(ε) and methodological details28,30,31.
In Equation 2, regions a1 and b1 should not be made too “small” because when a1 or b1 is small, the probabilities appearing in the second and fourth terms are small, which may lead to statistical errors in those terms. On the other hand, the sizes of the regions should not be too “large”, either. In this case, computing ΔG0→1,a1 and ΔG0→1,b1 would require sampling a wide range of solute configurations, requiring long simulation times. This tradeoff exists even when the ER endpoint scheme is employed. The method requires simulations at state 1 (solution of interest) and state 0 (solute at isolation in vacuum) and is advantageous when the solute configuration space to be sampled is not too wide. As mentioned above, the solute can be flexible when the free energy is computed with the ER method. Still, the computation is faster when the solute flexibility is restricted, and as a result the endpoint method is well suited for use in Equation 2 as a substitute for more standard free energy methods, such as TI.
Alanine dipeptide
In a previous paper4 we showed that using vacuum and implicit solvent models as auxiliary energy surfaces could accelerate the computation of various free energy differences for alanine dipeptide in different free energy basins. In the present paper we compare the results from those calculations to those we obtain by computing ΔG0→1,a1 and ΔG0→1,b1 with the ER method. This method requires three MD simulations. One is of the solution system of interest, and corresponds to the fully coupled state (for both the electrostatic and van der Waals interactions) of the TI calculation in our previous paper4. The parameters and settings for this MD were identical to those in TI4, and the MD trajectory was sampled every 100 fs to obtain the energy distribution function. The second MD is of pure water. The MD procedures were also unchanged from those in TI4, except that the simulation length was shortened to 20 ps with a sampling interval of 100 fs. In the third simulation, an MD simulation was carried out for an isolated solute in vacuum. The electrostatic potential was then handled by its bare form of 1/r, and the MD length was 20 ns with 100 fs for the sampling interval. The other options, including the restraints on the solute, were the same as those for the solution, and the correction due to the periodic boundary condition was implemented by the self-energy scheme54,55. The solute configurations in vacuum were inserted into pure water as test particles at random positions and orientations to determine the distribution functions corresponding to the density of states of solute-solvent pair interactions and the solvent-solvent pair correlations. The test-particle insertion was carried out 1000 times per pure-water configuration sampled, leading to the generation of 2 × 105 solute-solvent configurations in total.
As noted above, the MD of pure water was as short as 20 ps. This is possible because the insertions at random positions and orientations average out the structural inhomogeneity of the pure-solvent system, which might be transiently present on a ps time scale. The spatial inhomogeneity is exploited to reduce the computation time, and in this sense, the averaging over time is replaced by the averaging over space. It should be further noted that the solute sampled from its MD at isolation in vacuum is inserted into pure solvent to take the ensemble averages at state 0 of Equation 2 and Equations 7 and 8 in the Appendix. This means that at state 0, the effect of solute-solvent interaction is not yet turned on for the solute structure. The difference in the solute structure between the solution and vacuum arises through introduction of the solute-solvent interaction and is reflected in the solvation free energy computed through Equation 4.
For the alanine dipeptide, all values except the endpoint calculations were taken from our previous paper4. In those calculations the system was constrained to 3° × 3° patches of Ramachandran space with harmonic restraints on the backbone dihedral angles with restraint constants set to maintain the system in the desired ranges of dihedral angles.
β-Cyclodextrin
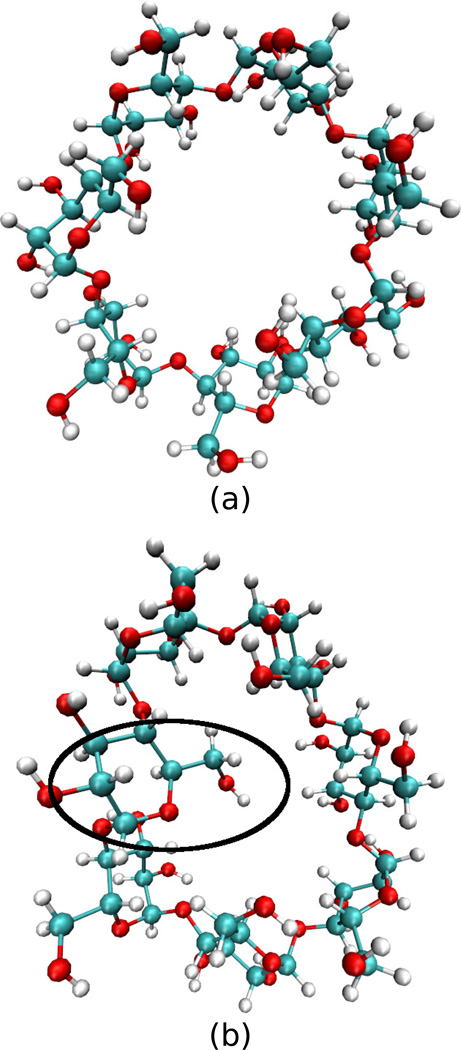
The flexible host β-cyclodextrin adopts two interconverting configurations in water, an open configuration where the planes of the sugar rings are nearly perpendicular to the plane of the molecule and a closed configuration where one of the sugar rings rotates so that its plane is closer to the plane of the molecule, with its COH2 arm entering the interior of the β-cyclodextrin ring (Figure 1).
Figure 1.
Illustrations of the (a) open and (b) closed configurations of β-cyclodextrin. The black oval highlights the sugar whose COH2 group has rotated into the plane of the β-cyclodextrin.
To track this transition, we defined a collective variable (Θ) as follows:
For each sugar ring we defined an angle (θi) as follows:
- For each ring we defined the plane of the cyclodextrin molecule to be the plane defined by three points:
- The center of mass of the 7 glycosidic oxygens.
- The carbon connecting the sugar ring to the next sugar ring.
- The carbon connecting the sugar ring to the previous sugar ring.
- We defined the plane of the sugar ring to be the plane defined by three points:
- The carbon connecting the sugar ring to the next sugar ring.
- The carbon connecting the sugar ring to the previous sugar ring.
- The carbon on the COH2 arm of the sugar ring.
We then defined θi to be the torsion angle between these two planes. If the COH2 arm was rotated directly out of the cyclodextrin molecule but in the plane of the cyclodextrin, we defined θi to be −π rad, and if it was rotated into the cyclodextrin molecule and in the plane of the cyclodextrin we defined θi to be 0 rad.
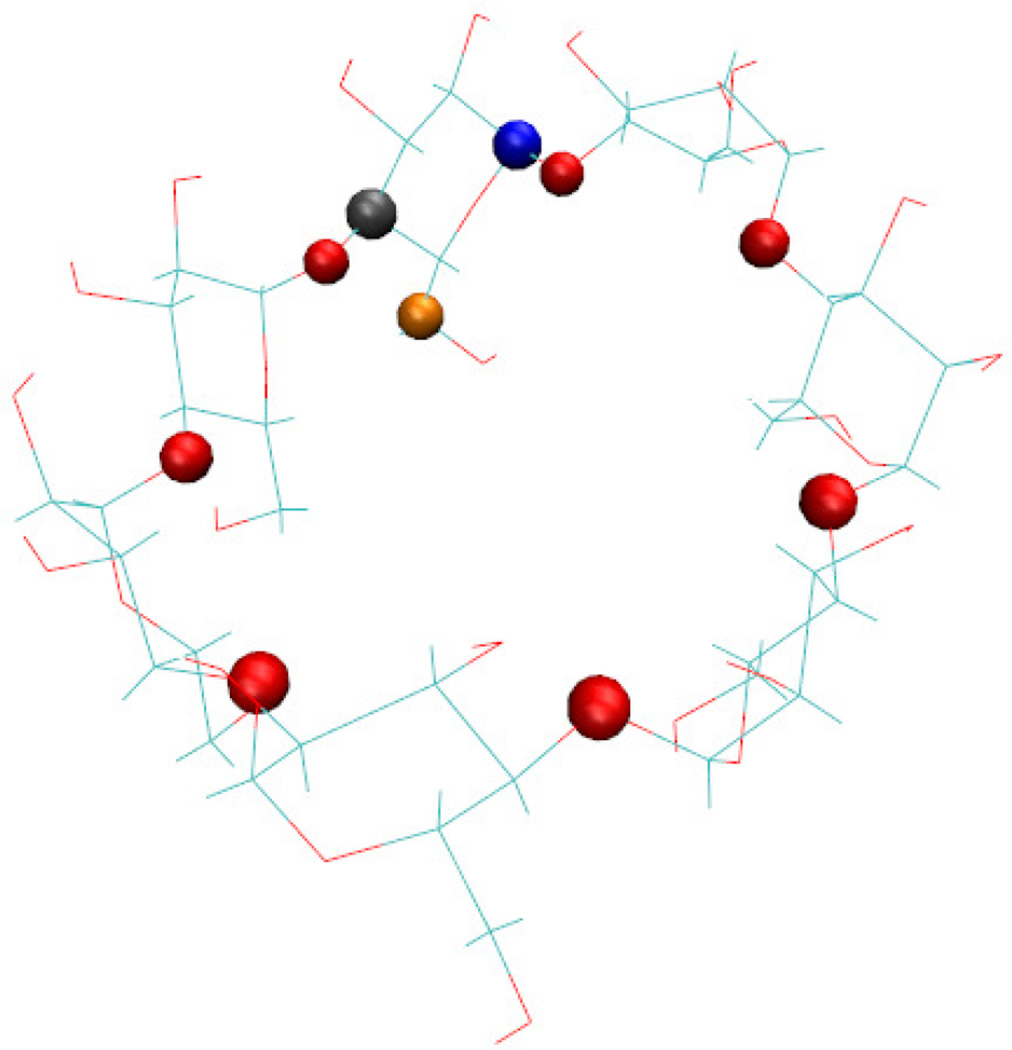
We then defined Θ to be the greatest of the θi. It is therefore the angle between the plane of the cyclodextrin and the plane of the sugar that is most rotated into the cyclodextrin ring. The atoms used in this definition are illustrated in Figure 2.
Figure 2.
A figure showing the atom types used in the definition of Θ. The red spheres are the 7 glycosidic oxygens that connect the sugars of the cyclodextrin ring, the blue sphere is the carbon joining the first ring to the previous ring, the gray sphere is the carbon joining the first ring to the next ring, and the orange atom is the carbon on the arm of the first ring.
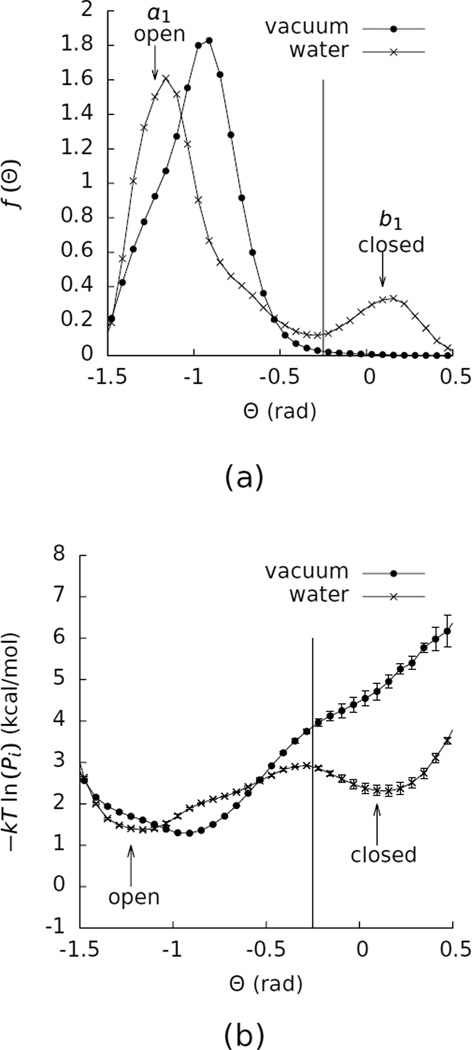
Figure 3 shows a histogram of Θ in water. This histogram has two peaks, one at about Θ = −1.25 rad, corresponding to the open state, and one at about Θ = 0 rad, corresponding to the closed state. We divided the full range of Θ into the 100 bins shown in Figure 3. We defined the boundary between these two states to be Θ = −0.25 rad, and we defined a1 to correspond to the bin with −1.25663 rad < Θ <−1.19381 rad and b1 to correspond to the bin with 0.0628318 rad < Θ < 0.125664 rad.
Figure 3.
(a) Histograms of the probability density (f (Θ)) of Θ for β-cyclodextrin in vacuum and water. The vertical line marks the division between the open and closed states at Θ = −0.25. The arrows labeled “open” and “closed” identify the bins used for connecting the two free energy surfaces. (b) Potentials of mean force in Θ for β-cyclodextrin in vacuum and water. These curves were computed by calculating −kT ln (Pi) for each Θ bin i, where k is Boltzmann’s constant, T is the temperature, and Pi is the probability that the system is in bin i. The error bars on this curve represent the differences between the value of −kT ln (Pi) obtained from the full simulations and from the first halves of the simulations. The vacuum data were taken from a 500 ns simulation, and the water data were taken from a 200 ns simulation.
Molecular dynamics details
For β-cyclodextrin we simulated the unrestrained system in water for 200 ns and in vacuum for 500 ns. From these simulations all quantities in Equations 1 and 2 except ΔG0→1,a1 and ΔG0→1,b1 were computed. The estimate of ΔG0,A→B was obtained from this simulation following Equation 1. The parameters for β-cyclodextrin were taken from the OPLS 2005 force field56, and the TIP3P parameters57 were used for the water. These simulations were run with the Groningen Machine for Chemical Simulations (GROMACS) version 4.5.458,59. The vacuum simulation was run for 2.5 × 108 steps with a time step of 2 fs and GROMACS’s leap-frog integrator60. The lengths of the bonds connecting hydrogen atoms to other atoms were constrained with the default LINCS algorithm61. Electrostatic and Lennard-Jones interactions were cut off at 10 Å, and the temperature was maintained at 300 K with the Berendsen thermostat62. Periodic boundary conditions were not used for this simulation. The simulation in water used the same options except that periodic boundary conditions were used with smooth particle-mesh Ewald electrostatics63. A constant pressure of 1 atm was maintained with the Berendsen barostat62, and for the production simulation the temperature was maintained at 300 K with GROMACS’s stochastic dynamics integrator64. For the simulation in water 1451 water molecules were added to the system, and it was minimized with 50000 steps of the steepest descent algorithm. The system was then run at constant volume for 50000 steps with GROMACS’s leap-frog integrator60 and a constant temperature of 300 K maintained with the Berendsen thermostat62, followed by an additional 50000 steps at constant pressure with GROMACS’s leap-frog integrator60 and a constant temperature of 300 K maintained with the Berendsen thermostat62. Finally, the system was run for 1 × 108 steps with a constant temperature maintained at 300 K with GROMACS’s stochastic dynamics integrator64.
For β-cyclodextrin ΔG0→1,a1 and ΔG0→1,b1 were computed with TI in GROMACS version 5.1.058,59 patched with PLUMED version 2.2.165. Starting structures of β-cyclodextrin in bins a1 and b1 were taken from the simulation run in water, and for the structure in a1 and b1 3397 and 3459 water molecules, respectively, were added. These systems were then each minimized for 50000 steps with the steepest descent algorithm and the same molecular dynamics options as for the simulation in water.
Next, for the system in a1 Θ was restrained by
imposing an upper harmonic wall on one of the θi at −1.19381 with a force constant of 1000 kJ/mol/rad2,
imposing a lower harmonic wall on this θi at −1.25663 with a force constant of 1000 kJ/mol/rad2, and
imposing an upper harmonic wall on all other θi at −1.25663 with a force constant of 1000 kJ/mol/rad2,
and for the system in b1 Θ was restrained by
imposing an upper harmonic wall on one of the θi at 0.125664 with a force constant of 100000 kJ/mol/rad2,
imposing a lower harmonic wall on this θi at 0.0628318 with a force constant of 100000 kJ/mol/rad2,
imposing an upper harmonic wall on all other θi at 0.05 with a force constant of 50 kJ/mol/rad2, and
imposing a lower harmonic wall on all other θi at −2.8 with a force constant of 1000 kJ/mol/rad2.
Setting the values of these restraint constants involved a tradeoff between two different concerns: 1) If they are too weak the system will not remain in the desired region of phase space, but 2) if they are too strong the system will experience energy drift from hitting the harmonic walls. The values used here were selected because they produced stable simulations with only small numbers of configurations falling outside the desired regions of phase space. Restraining β-cyclodextrin to b1 required more complicated restraints than restraining it to a1, probably because the system is less stable in the closed (b1) than open (a1) configuration. Also, note that these restraints are not simple at-bottomed restraints on Θ. We should therefore expect some differences between the value of ΔG1,A→B computed with Equation 1 and that computed with Equation 2 with these definitions of ΔG0→1,a1 and ΔG0→1,b1. However, this difference was too small to be observed in this study, as can be seen from the Results.
After imposing restraints, 11 4-ns (2 × 106 steps) simulations were run for each system where the electrostatic interactions between the solute and solvent were reduced by a factor of λ (λ = 0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9, and 1.0). In each of these simulations the derivative (dU/dλ) of the potential energy of the system with respect to λ was computed every 0.2 ps (100 steps). The averages (〈dU/dλ〉i) of these quantities in each simulation i were then combined to compute the free energy (ΔGel) of turning on the electrostatic interaction between the solute and solvent by TI66,67:
| (5) |
Once the electrostatic interactions had been turned off, the Lennard-Jones interactions between the solute and solvent were slowly switched off using GROMACS’s soft-core method68 with α = 0.5, a soft-core power of 1, and σ = 0.3. Lambda-space was divided into 17 windows (λ = 0,0.1,0.2,0.3,0.4,0.5,0.55,0.6,0.65,0.7,0.75,0.8,0.85,0.9,0.94,0.985, and 1), and 4 ns simulations were run in each window. The free energy of turning on the Lennard-Jones interactions was then computed using the same method as in Equation 5 and combined with ΔGel to obtain ΔG0→1,a1 and ΔG0→1,b1 (Table 2). During these simulations the intramolecular nonbonded interactions of the solute were maintained, so the reference state was the same as that used in the ER calculations.
Table 2.
Data to calculate the free energy difference (ΔG1,A→B) between the closed and open states of β-cyclodextrin in water by connecting the free energy surface in vacuum to that in water with both free energy calculations and endpoint methods. The times required to compute ΔG0,A→B, , and were significantly smaller than the times required to compute ΔG1,A→B, ΔG0→1,a1, and ΔG0→1,b1, as can be seen by observing the small sizes of the error bars on the first set of quantities. The time required to compute ΔG1,A→B was therefore dominated by the calculations of ΔG0→1,a1 and ΔG0→1,b1. The values for ΔG0,A→B, , and are common between TI and the endpoint method. The computation time for each of ΔG0→1,a1 and ΔG0→1,b1 in the endpoint method corresponds to that for a single λ for TI.
| Equation 1 |
Equation 2 TI |
Equation 2 free energy functional/end point methods |
||
|---|---|---|---|---|
| ΔG1,A→B | 1.0±0.1 | 1.0±0.8 | 1.2±0.2 | |
| ΔG0,A→B | 3.12874 ±0.00007 | |||
| −0.393±0.002 | ||||
| ΔG0→1,a1 | −56.4±0.3 | −46.6±0.1 | ||
| −0.35±0.01 | ||||
| ΔG0→1,b1 | −58.5±0.5 | −48.5±0.1 | ||
| Simulation time (ns) | ~200 | ~200 | ~8 |
The simulations used to obtain ΔG0→1,a1 and ΔG0→1,b1 were run with the same options as for the unrestrained simulation in water except that the lengths of bonds connecting hydrogen atoms to other atoms were constrained with SHAKE69 rather than LINCS61.
The solvation free energies were also computed by the ER method. The computational schemes were parallel to those described in the Alanine dipeptide subsection of the Methodology section. The only differences are that the MD of pure water was done over 200 ps and that 2 × 106 solute-solvent configurations in total were prepared by test-particle insertions. As is so for alanine dipeptide noted in “Alanine dipeptide” subsection, in addition, the ER calculations for β-cyclodextrin were done with exactly the same potential functions and restraints as the TI calculations.
RESULTS
Alanine dipeptide
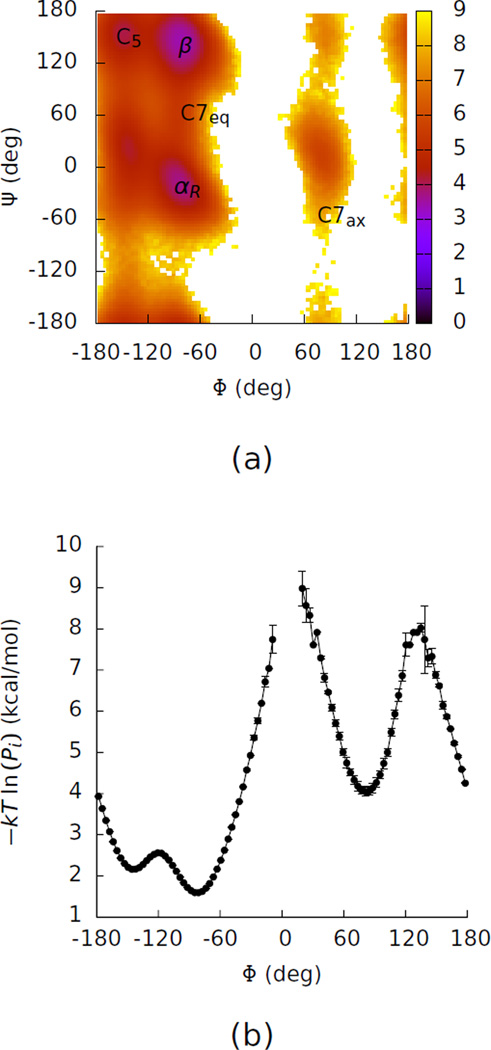
Previously we computed the free energy differences between right-handed and left-handed helical basins by computing the free energies in vacuum and generalized-Born solvent and connecting these calculations to the calculations in explicit solvent with free energy calculations4. Figure 4 shows a Ramachandran plot for alanine dipeptide in explicit solvent taken from our previous paper. These calculations were much more efficient than computing the free energies directly by determining the populations of the two basins in explicit solvent, which requires barrier crossing, where the first passage time in explicit solvent was ~100 ns.
Figure 4.
(a) A two-dimensional potential of mean force in Φ and Ψ for alanine dipeptide in water. This map was computed by calculating −kT ln (Pi) for each bin i, where k is Boltzmann’s constant, T is the temperature, and Pi is the probability that the system is in bin i. The map is in units of kcal/mol. The labels identify the basins in Table 1. (b) A one-dimensional potential of mean force in Φ for alanine dipeptide. The gap in the curve shows bins where no samples were obtained. The error bars on this curve represent the differences between the value of −kT ln (Pi) obtained from the full simulation and from the first half of the simulation.
Here we show that using the free energy functional/endpoint methods described above lead to further substantial improvements in the efficiency of these calculations (Table 1). The calculation of the coupling free energies, ΔG0→1,a1 and ΔG0→1,b1 cost about 25 ns each with TI. Replacing these two calculations with free energy functional/endpoint calculations can nearly eliminate the time required for this portion of the calculation, reducing the time required for the total calculation by about 70%.
Table 1.
A comparison of the data obtained with endpoint methods to those obtained with free energy methods for alanine dipeptide. The values in the 3rd and 4th columns were taken from our previous paper4. The simulation times are approximately the time that would be required to achieve the listed accuracy and are taken from our previous paper. For the calculations using thermodynamic integration (TI) and Equation 2, about 50 ns was used to compute ΔG0→1,a1 and ΔG0→1,b1, and about 20 ns was used to compute the curvature terms, and . The computation time for each of ΔG0→1,a1 and ΔG0→1,b1 in the endpoint method corresponds to that for a single λ for TI. The results for the endpoint method are rounded to multiples to 0.1, and the errors are not shown when they are rounded to 0. All energies are in kcal/mol.
| Equation 1 |
Equation 2 TI |
Equation 2 free energy functional/end point methods |
||
|---|---|---|---|---|
| ΔG1,αR→C7ax | 4.0±0.2 | 4.1±0.2 | 4.3±0.2 | |
| αR | ΔG0→1,a1 | −14.4±0.01 | −12.8 | |
| ΔG0→1,b1 | −9.4±0.02 | −7.6±0.1 | ||
| ΔG1,β→C7ax | 4.8±0.2 | 4.8±0.2 | 5.4±0.2 | |
| β | ΔG0→1,a1 | −12.2±0.3 | −11.0±0.1 | |
| ΔG0→1,b1 | −9.4±0.02 | −7.6±0.1 | ||
| ΔG1,C5→C7ax | 4.0±0.2 | 3.9±0.2 | 4.6±0.1 | |
| C5 | ΔG0→1,a1 | −10.9±0.3 | −9.8 | |
| ΔG0→1,b1 | −9.4±0.02 | −7.6±0.1 | ||
| ΔG1,C7eq→C7ax | 3.2±0.2 | 3.2±0.2 | 3.4±0.1 | |
| C7eq | ΔG0→1,a1 | −9.2±0.3 | −7.6±0.1 | |
| ΔG0→1,b1 | −9.4±0.02 | −7.6±0.1 | ||
| Simulation time (ns) | ~4000 | ~70 | ~22 | |
With the endpoint calculation with ER, an approximate functional is used for obtaining G0→1,a1 and ΔG0→1,b1. In previous work, benchmark computations were conducted for amino-acid analog solutes in water, and the deviations between the ER and exact results were found to be less than 1 kcal/mol51–53. The ER functional is expected to deteriorate in its performance when the solute size is larger. According to a study of size effects for hard-sphere solutes70, ER estimates of the solvation free energies of larger solutes are less favorable than the exact values, and these differences increase with solute size. These observations are in agreement with the data in Table 1. The values of G0→1,a1 and ΔG0→1,b1 given by the ER method are within about 2 kcal/mol of those given by TI, but these differences in the solvation free energies partially cancel, leading to the differences between the conformational free energy differences given by the ER method and those given by TI being less than 1 kcal/mol. These observations show that the ER method provides a fast alternative to obtain accurate estimates of free-energy differences between basins in combination with Equation 2.
β-cyclodextrin
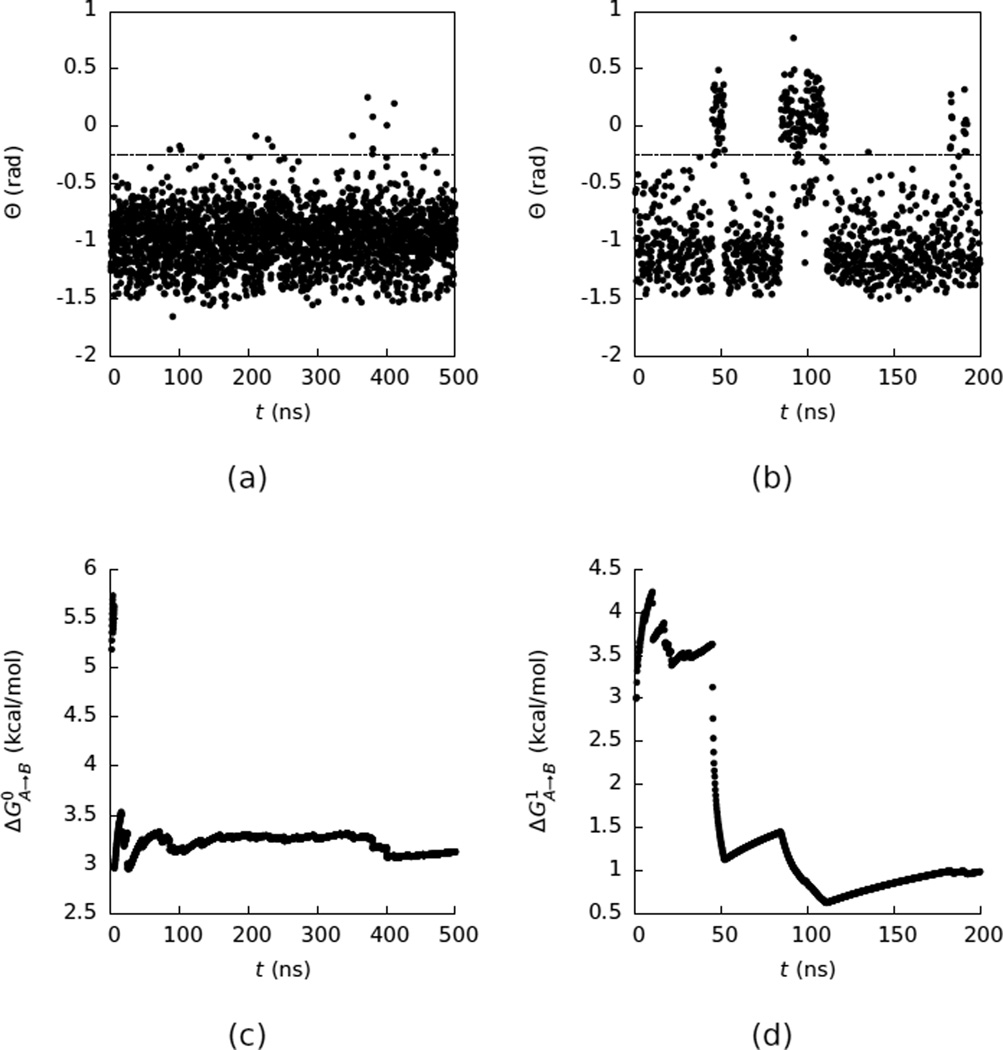
For β-cyclodextrin we were interested in computing ΔG1,A→B, the free energy difference between the open and closed states. In principle, ΔG1,A→B can be computed by simulating the system in explicit water and using Equation 1. However, the time between transitions for this system is rather long (~60 ns), making direct estimates of ΔG1,A→B converge slowly (Figure 5). From a 200 ns simulation of the system in explicit water we obtained ΔG1,A→B = 0.99 ± 0.14 kcal/mol.
Figure 5.
(a) A time series of Θ as a function of time (t) for β-cyclodextrin in vacuum. The dashed line at Θ = −0.25 marks the division between the open and closed states. Only every 2500’th frame from the simulation is plotted. (b) The same as (a) but in water. Only every 1000’th frame from the simulation is plotted. (c) A convergence plot of the free energy (ΔG0,A→B) difference between the closed and open states in vacuum computed with Equation 1 using only the data collected up to simulation time (t) as a function of t. (d) The same as (c) but in water.
In contrast, in vacuum β-cyclodextrin only has one free energy minimum (Figure 3) and does not have a slow switching between the open and closed states (Figure 5). This observation suggests that computing ΔG1,A→B by connecting the vacuum and explicit water free energy surfaces with Equation 2 can be useful. The results of such a calculation are summarized in Table 2. As described in the Methodology section, the calculations connecting the vacuum free energy surface to the explicit solvent free energy surface with free energy calculations used approximately the same amount of simulation time as the unrestrained simulation in explicit solvent. We can therefore compare the efficiencies of these calculations by comparing the approximate errors in the two estimates. For this system computing ΔG1,A→B by connecting the free energy surfaces was less efficient than simply calculating this free energy from an unrestrained simulation in water. This observation contrasts with what was found previously for alanine dipeptide, where computing the free energy difference between the αr and C7ax states by connecting implicit and vacuum free energy surfaces to the explicit water free energy surface was much more efficient than by analyzing the unrestrained trajectory in explicit water. Computing free energy differences by connecting free energy surfaces becomes more efficient when the switching time between the states is longer.
Using the ER method to compute ΔG0→1,a1 and ΔG0→1,b1 in Equation 2 reduced the computational time required to compute ΔG1,A→B by more than 95% (Table 2); this corresponds to more than a 25-fold speedup given the smaller errors with ER than with TI. The differences between the solvation free energies given by the ER method and those given by TI are ~10 kcal/mol and are larger than those observed for alanine dipeptide. Although the ER method has been employed for computing the solvation free energies of proteins with a few hundred residues in explicit solvent71–77, its predictions have only been compared to exact values for small molecules51–53. The values reported here for β-cyclodextrin constitute one of the largest TI calculations reported to date and may offer targets for further improvement of the ER functional. However, the difference between ΔG0→1,a1 and ΔG0→1,b1 given by the ER method is in good agreement with that given by TI. We therefore conclude that using the ER method and Equation 2 to compute conformational free energy differences is a promising approach to employ as the system size increases, one which can be further developed.
CONCLUSIONS
In a previous study4 we showed that computing conformational free energy changes for alanine dipeptide could be accelerated by performing the calculations on auxiliary free energy surfaces in vacuum or implicit solvent and connecting those free energy surfaces to our target explicit solvent free energy surface. In the present paper we show that these calculations can be greatly accelerated by computing the free energies linking the auxiliary and target free energy surfaces in solution with free energy functional/endpoint methods. For β-cyclodextrin doing so reduces the cost of the calculation by more than 95%. The energy cycle is an attractive method to which to apply energy functional/endpoint methods, which approximate the solvation free energy of a molecule from simulations run at the endpoints of the transformation, because endpoint methods converge faster when the conformational degrees of freedom of the solute are restrained, and to perform the energy cycle we restrain the system to small patches in phase space in each basin. As mentioned above, in the method as presented there is a tradeoff between the desire to make the patches smaller to make the calculations of the linking free energies easier and the desire to make them larger to make the computation of the probabilities easier.
Additionally, we found that the thermodynamic cycle can be used even when the conformational distribution on the auxiliary free energy surface differs substantially from the distribution on the target free energy surface, as is the case for β-cyclodextrin for which the explicit solvent free energy surface contains two minima, whereas the vacuum surface contains only one. The conformational distributions on the two free energy surfaces do have to overlap in the collective variables of interest, but this overlap does not have to be large, as it was not here.
Acknowledgments
This research was supported in part by a grant from the NIH (GM30580), a NSF major research instrumentation grant (CNS-09-58854), and a NIH equipment grant (OD020095). We thank Bin Zhang and Di Cui for their help with this work. The work is further supported by the Grants-in-Aid for Scientific Research (Nos. 15K13550 and 26240045) from the Japan Society for the Promotion of Science and by the Elements Strategy Initiative for Catalysts and Batteries and the Post-K Supercomputing Project from the Ministry of Education, Culture, Sports, Science, and Technology, and the computations were conducted partly through the HPCI System Research Project (Project IDs:hp160013, hp160019, and hp160214).
APPENDIX
In this appendix, we show the explicit form of the free-energy functional in the energy-representation (ER) method28,30,31. The target quantity of the method is the solvation free energy Δμ. It is computed with Equation 4, and the inputs for the computation are the three distribution functions ρe, , and constructed from the instantaneous distribution (histogram) ρ̂e defined by Equation 3. To be more specific, ρe(ε) is obtained in the solution system of interest (state 1 of Equation 2) through
| (6) |
where 〈⋯〉 denotes the ensemble average at state 1, and and are calculated in pure solvent with the solute uncoupled (state 0) through
| (7) |
| (8) |
where 〈⋯〉0 means the ensemble average at state 0 and is taken by test-particle insertions of the solute into pure solvent. When the pure solvent is homogeneous, is equal to the (number) density of bulk solvent multiplied by the density of states for the solute-solvent pair potential. The solvent-solvent correlation at two-body level in pure solvent is further expressed by over the coordinates introduced by the solute that is inserted as a test particle.
From the three distribution (correlation) functions given above, we also define two functions through
| (9) |
| (10) |
where ωe is the solvent-mediated part of the solute-solvent potential of mean force in the energy representation27–31. It vanishes when the solvent-solvent correlation is absent. is also the solvent-mediated part of the response function of the solute-solvent distribution to the solute-solvent interaction in pure solvent. Using ωe and , Ωe of Equation 4 is expressed through combined HNC-type and PY-type approximations as
| (11) |
| (12) |
| (13) |
| (14) |
where β = 1/kT. The first lines of Equations 12 and 13 refer to the PY-type approximations, and the second lines to the HNC-type. Equations 12 and 13 are the combined HNC- and PY-type approximations expressed with ωe and , respectively, and are mixed with the weighting function α defined in Equation 14. Typically, ωe(ε) is well sampled in the favorable portion of the energy coordinate ε, and is well sampled in the unfavorable portion. The weighting function was chosen to respect this numerical observation.
As noted in the “Alanine dipeptide” subsection within the Methodology section, the solute is inserted into pure solvent as a test particle to obtain and through Equations 7 and 8. The overlapping configurations of the inserted solute with solvent molecules then contribute to and at large energies and account for the excluded-volume effect in the solvation free energy. In numerical practice, the large-energy portion was logarithmically meshed through the procedure described in the Appendix of Ref.28. In the present work, 200 bins were prepared between 20 and 1011 kcal/mol, and the solute-solvent energy larger than 1011 kcal/mol was counted in the largest-energy bin. With this scheme, each bin was well sampled since the inserted solute always overlaps with solvent; it should be noted that ε in Equation 3 is the pair energy between solute and solvent, and whenever the solute overlaps with solvent, the sample count for the overlapping ε increases. appears to be small simply because it is given by the averaged count divided by the bin width, which is wide in turn in the large-energy portion. The effect of mesh size was further examined by summing the sample counts in consecutive bins and using the coarsely discretized and thus obtained. It was then observed that the resulting solvation free energy did not change by more than 0.1 kcal/mol, even when “coarse-graining” by 5 times. The value for the largest-energy bin was also varied through the procedure presented in the Appendix of Ref.28, and no effect was seen within the margin of error. In fact, the large-energy portion is the “easy” part of applying Equations 7 and 8 since the inserted solute always overlaps with solvent and the solute-solvent overlap is “used” in obtaining the histogram through Equation 3. The numbers of test-particle insertions were described in the main text and were actually determined to achieve good statistics in the low-energy (attractive) tail of the solute-solvent pair energy, which is not necessarily sampled efficiently in test-particle insertions.
References
- 1.Simonson T. In: Computational biochemistry and biophysics. Becker OM, MacKerrell AD Jr, Roux B, Watanabe M, editors. chap. 10. New York: Marcel Dekker, Inc.; 2001. pp. 169–198. [Google Scholar]
- 2.Chipot C, Pohorille A. Free energy calculations: Theory and applications in chemistry and biology, Springer series in chemical physics. New York: Springer; 2007. [Google Scholar]
- 3.Hansen N, van Gunsteren WF. J. Chem. Theory Comput. 2014;10:2632. doi: 10.1021/ct500161f. [DOI] [PubMed] [Google Scholar]
- 4.Deng N, Zhang BW, Levy RM. J. Chem. Theory Comput. 2015;11:2868. doi: 10.1021/acs.jctc.5b00264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hansmann UHE. Chem. Phys. Lett. 1997;281:140. [Google Scholar]
- 6.Sugita Y, Okamoto Y. Chem. Phys. Lett. 1999;314:141. [Google Scholar]
- 7.Laio A, Parrinello M. Proc. Natl. Acad. Sci. USA. 2002;99:12562. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hamelberg D, Mongan J, McCammon JA. J. Chem. Phys. 2004;120:11919. doi: 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
- 9.Bartels C, Karplus M. J. Comput. Chem. 1997;18:1450. [Google Scholar]
- 10.Dellago C, Bolhuis PG, Csajka FS, Chandler D. J. Chem. Phys. 1998;108:1964. [Google Scholar]
- 11.Faradjian AK, Elber R. J. Chem. Phys. 2004;120:10880. doi: 10.1063/1.1738640. [DOI] [PubMed] [Google Scholar]
- 12.Andrec M, Felts AK, Gallicchio E, Levy RM. Proc. Natl. Acad. Sci. USA. 2005;102:6801. doi: 10.1073/pnas.0408970102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bowman GR, Beauchamp KA, Boxer G, Pande VS. J. Chem. Phys. 2009;131:124101. doi: 10.1063/1.3216567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Noé F, Schütte C, Vanden-Eijnden E, Reich L, Weikl TR. Proc. Natl. Acad. Sci. USA. 2009;106:19011. doi: 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Deng N-j, Dai W, Levy RM. J. Phys. Chem. B. 2013;117:12787. doi: 10.1021/jp401962k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Roux B, Simonson T. Biophys. Chem. 1999;78:1. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 17.Feig M, Brooks CL., III Curr. Opin. Struc. Biol. 2004;14:217. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 18.Tan C, Yang L, Luo R. J. Phys. Chem. B. 2006;110:18680. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 19.Chen J, Brooks CL, III, Khandogin J. Curr. Opin. Struc. Biol. 2008;18:140. doi: 10.1016/j.sbi.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Aguilar B, Shadrach R, Onufriev AV. J. Chem. Theory Comput. 2010;6:3613. [Google Scholar]
- 21.Gallicchio E, Lapelosa M, Levy RM. J. Chem. Theory Comput. 2010;6:2961. doi: 10.1021/ct1002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Young T, Abel R, Kim B, Berne BJ, Friesner RA. Proc. Natl. Acad. Sci. USA. 2007;104:808. doi: 10.1073/pnas.0610202104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Abel R, Young T, Farid R, Berne BJ, Friesner RA. J. Am. Chem. Soc. 2008;130:2817. doi: 10.1021/ja0771033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nguyen CN, Young TK, Gilson MK. J. Chem. Phys. 2012;137:044101. doi: 10.1063/1.4733951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nguyen CN, Cruz A, Gilson MK, Kurtzman T. J. Chem. Theory Comput. 2014;10:2769. doi: 10.1021/ct401110x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Harris RC, Pettitt BM. J. Chem. Theory Comput. 2015;11:4593. doi: 10.1021/acs.jctc.5b00684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Matubayasi N, Nakahara M. J. Chem. Phys. 2000;113:6070. [Google Scholar]
- 28.Matubayasi N, Nakahara M. J. Chem. Phys. 2002;117:3605. erratum, (2003), J Chem Phys 118: 2446. [Google Scholar]
- 29.Matubayasi N, Nakahara M. J. Chem. Phys. 2003;119:9686. [Google Scholar]
- 30.Matubayasi N, Shinoda W, Nakahara M. J. Chem. Phys. 2008;128:195107. doi: 10.1063/1.2919117. [DOI] [PubMed] [Google Scholar]
- 31.Sakuraba S, Matubayasi N. J. Comput. Chem. 2014;35:1592. doi: 10.1002/jcc.23651. [DOI] [PubMed] [Google Scholar]
- 32.Damodaran KV, Banba S, Brooks CL., III J. Phys. Chem. B. 2001;105:9316. [Google Scholar]
- 33.Chang C-E, Gilson MK. J. Am. Chem. Soc. 2004;126:13156. doi: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- 34.Chen W, Chang C-E, Gilson MK. Biophys. J. 2004;87:3035. doi: 10.1529/biophysj.104.049494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wickstrom L, He P, Gallicchio E, Levy RM. J. Chem. Theory Comput. 2013;9:3136. doi: 10.1021/ct400003r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xia J, Flynn WF, Gallicchio E, Zhang BW, He P, Tan Z, Levy RM. J. Comput. Chem. 2015;36:1772. doi: 10.1002/jcc.23996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gebhardt J, Hansen N. Fluid Phase Equilibria. 2016;422:1. [Google Scholar]
- 38.Wickstrom L, Deng N, He P, Mentes A, Nguyen C, Gilson MK, Kurtzman T, Gallicchio E, Levy RM. J. Mol. Recogn. 2016;29:10. doi: 10.1002/jmr.2489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Levy RM, Belhadj M, Kitchen DB. J. Chem. Phys. 1991;95:3627. [Google Scholar]
- 40.Luzhkov V, Warshel A. J. Comput. Chem. 1992;13:199. [Google Scholar]
- 41.Åqvist J, Medina C, Samuelsson JE. Prot. Eng. 1994;7:385. doi: 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
- 42.Carlson HA, Jorgensen WL. J. Phys. Chem. 1995;99:10667. [Google Scholar]
- 43.Kast SM. Phys. Chem. Chem. Phys. 2001;3:5087. [Google Scholar]
- 44.Vener MV, Leontyev IV, Dyakov YA, Basilevsky MV, Newton MD. J. Phys. Chem. B. 2002;106:13078. [Google Scholar]
- 45.Hirata F. Molecular Theory of Solvation. Dordrecht, Netherlands: Kluwer Academic Publishers; 2003. [Google Scholar]
- 46.Fdez Galván I, Sánchez ML, Martín ME, Olivares del Valle FJ, Aguilar MA. J. Chem. Phys. 2003;118:255. [Google Scholar]
- 47.Freedman H, Truong TN. J. Chem. Phys. 2004;121:2187. doi: 10.1063/1.1760741. [DOI] [PubMed] [Google Scholar]
- 48.Chuev GN, Fedorov MV, Crain J. Chem. Phys. Lett. 2007;448:198. [Google Scholar]
- 49.Yamamoto T. J. Chem. Phys. 2008;129:244104. doi: 10.1063/1.3041381. [DOI] [PubMed] [Google Scholar]
- 50.Frolov AI, Ratkova EL, Palmer DS, Fedorov MV. J. Phys. Chem. B. 2011;115:6011. doi: 10.1021/jp111271c. [DOI] [PubMed] [Google Scholar]
- 51.Karino Y, Fedorov MV, Matubayasi N. Chem. Phys. Lett. 2010;496:351. [Google Scholar]
- 52.Karino Y, Matubayasi N. Phys. Chem. Chem. Phys. 2013;15:4377. doi: 10.1039/c3cp43346c. [DOI] [PubMed] [Google Scholar]
- 53.Frolov AI. J. Chem. Theory Comput. 2015;11:2245. doi: 10.1021/acs.jctc.5b00172. [DOI] [PubMed] [Google Scholar]
- 54.Figueirido F, Buono GSD, Levy RM. J. Chem. Phys. 1995;103:6133. [Google Scholar]
- 55.Hummer G, Pratt LR, García AE. J. Phys. Chem. 1996;100:1206. [Google Scholar]
- 56.Banks JL, Beard HS, Cao Y, Cho AE, Damm W, Farid R, Felts AK, Halgren TA, Mainz JR, Daniel T, Murphy Maple, R, et al. J. Comput. Chem. 2005;26:1752. doi: 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 58.Van Der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE, Berendsen HJC. J. Comput. Chem. 2005;26:1701. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 59.Pronk S, Páll S, Schulz R, Larsson P, Bjelkmar P, Apostolov R, Shirts MR, Smith JC, Kasson PM, van der Spoel D, et al. Bioinformatics. 2013;29:845. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hockney RW, Goel SP, Eastwood JW. J. Comput. Phys. 1974;14:148. [Google Scholar]
- 61.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. J. Comput. Chem. 1997;18:1463. [Google Scholar]
- 62.Berendsen HJC, Postma JPMv, van Gunsteren WF, DiNola A, Haak JR. J. Chem. Phys. 1984;81:3684. [Google Scholar]
- 63.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J. Chem. Phys. 1995;103:8577. [Google Scholar]
- 64.Goga N, Rzepiela AJ, de Vries AH, Marrink SJ, Berendsen HJC. J. Chem. Theory Comput. 2012;8:3637. doi: 10.1021/ct3000876. [DOI] [PubMed] [Google Scholar]
- 65.Tribello GA, Bonomi M, Branduardi D, Camilloni C, Bussi G. Comput. Phys. Commun. 2014;185:604. [Google Scholar]
- 66.Beveridge DL, DiCapua FM. Annu. Rev. Biophys. Biophys. Chem. 1989;18:431. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- 67.Straatsma TP, McCammon JA. Ann. Rev. Phys. Chem. 1992;43:407. [Google Scholar]
- 68.Beutler TC, Mark AE, van Schaik RC, Gerber PR, van Gunsteren WF. Chem. Phys. Lett. 1994;222:529. [Google Scholar]
- 69.Ryckaert J-P, Ciccotti G, Berendsen HJC. J. Comput. Phys. 1977;23:327. [Google Scholar]
- 70.Matubayasi N, Kinoshita M, Nakahara M. Cond. Mat. Phys. 2007;10:471. [Google Scholar]
- 71.Saito H, Matubayasi N, Nishikawa K, Nagao H. Chem. Phys. Lett. 2010;497:218. [Google Scholar]
- 72.Karino Y, Matubayasi N. J. Chem. Phys. 2011;134:041105. doi: 10.1063/1.3535560. [DOI] [PubMed] [Google Scholar]
- 73.Takemura K, Guo H, Sakuraba S, Matubayasi N, Kitao A. J. Chem. Phys. 2012;137:215105. doi: 10.1063/1.4768901. [DOI] [PubMed] [Google Scholar]
- 74.Mizukami T, Saito H, Kawamoto S, Miyakawa T, Iwayama M, Takasu M, Nagao H. Int. J. Quant. Chem. 2012;112:344. [Google Scholar]
- 75.Saito H, Iwayama M, Mizukami T, Kang J, Tateno M, Nagao H. Chem. Phys. Lett. 2013;556:297. [Google Scholar]
- 76.Kamo F, Ishizuka R, Matubayasi N. Protein Sci. 2016;25:56. doi: 10.1002/pro.2754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Yamamori Y, Ishizuka R, Karino Y, Sakuraba S, Matubayasi N. J. Chem. Phys. 2016;144:085102. doi: 10.1063/1.4941945. [DOI] [PubMed] [Google Scholar]