Abstract
Objective
Oxygen transport to parenchymal cells occurs mainly at the microvascular level, and depends on convective red blood cell (RBC) flux, which is proportional in an individual capillary to the product of capillary hematocrit and red blood cell velocity. This study investigates the relative influence of these two factors on tissue oxygen partial pressure (Po2).
Methods
A simple analytical model is used to quantify the respective influences of hematocrit, RBC velocity and flow on tissue oxygenation around capillaries. Predicted tissue Po2 levels are compared with a detailed computational model.
Results
Hematocrit is shown to have a larger influence on tissue Po2 than RBC velocity. The effect of RBC velocity increases with distance from the arterioles. Good agreement between analytical and numerical results is obtained and the discrepancies are explained. Significant dependence of mass transfer coefficients on RBC velocity at low hematocrit is demonstrated.
Conclusions
For a given RBC flux in a capillary, the Po2 in the surrounding tissue increases with increasing hematocrit, as a consequence of decreasing intravascular resistance to diffusive oxygen transport from RBCs to tissue. These results contribute to understanding the effects of blood flow changes on oxygen transport, such as occur in functional hyperemia in the brain.
Keywords: tissue oxygenation, blood flow, mathematical modeling
Introduction
Most of the oxygen supply to parenchymal cells is delivered by the microcirculation. Sufficient tissue oxygenation is required to sustain cell metabolism. Oxygen transport to tissue is a complex phenomenon that involves chemical reactions with hemoglobin, convective transport in red blood cells, diffusion and metabolic consumption. Additionally, since the energy requirements of parenchymal cells may be varying in time, oxygen transport to tissue is a dynamic process that needs to be regulated. For example, neurovascular coupling adapts oxygen supply to the fluctuating energy consumption in the brain. In order to understand such regulation mechanisms, knowledge of physiological variables that determine tissue oxygenation is required. In this work, we investigated the influence of hematocrit and blood flow velocity, which are two of the most important variables pertaining to oxygen transport in the microcirculation.
The theoretical analysis of oxygen transport from capillaries dates back to the seminal work by Krogh [21]. The Krogh-Erlang equation provides a solution to the Po2 distribution in a tissue cylinder around a capillary. For much of the following half century, authors followed this approach and tacitly assumed that the intravascular resistance (IVR) to oxygen transport is negligible compared to the tissue resistance. Then, Hellums [17] demonstrated that the particulate nature of blood causes the IVR to have a magnitude similar to the tissue resistance. This study did not explicitly account for the dependence of IVR on hematocrit, although the employed approach would have made this possible. About twenty years later, Hellums et al. [18] reviewed a number of studies about intraluminal resistance to oxygen transport. Among others, Federspiel et al. [10] as well as Federspiel et al. [9] showed the large dependence of IVR on hematocrit in small vessels. Groebe et al. [16] extended their work by considering moving RBCs and the interaction between capillary and tissue space. Later, Eggleton et al. [8] performed numerical simulations of oxygen transport in a capillary and the surrounding tissue to evaluate mass transfer coefficients (MTCs), which are an inverse resistance to oxygen transport. They fitted the MTC dependence on hematocrit using a parabolic equation, which can be used in simulations where the intra- and extravascular oxygen transport are coupled using MTCs [13].
Recent advances in experimental methods have enabled the direct observation of IVR in the microcirculation. Parpaleix et al. [25] used two-photon laser microscopy and phosphorescence quenching to measure oxygen tensions in the rodent cerebral cortex. They observed erythrocyte-associated transients (EATs), which are Po2 variations in capillaries caused by individual RBCs, and confirmed the theoretical predictions by Hellums [17]. Lücker et al. [24] used their dynamic model for oxygen transport with moving RBCs and obtained a close agreement with the results from Parpaleix et al. [25]. Their computations show that the EAT amplitude decreases with hematocrit, which is consistent with the relationship between hematocrit and IVR to oxygen transport. Sakadzic et al. [27] also used two-photon phosphorescence lifetime microscopy and directly observed radial Po2 gradients in arterioles, which are a reflection of IVR. These new experimental techniques open new avenues for the validation of theoretical models.
However, knowledge of IVR is not by itself sufficient to determine tissue Po2. The unloading of oxygen by RBCs along their paths in the microcirculation also needs to be taken into account. Hence, tube hematocrit and related variables (discharge hematocrit, RBC linear density, cell spacing) are not the only determinants of tissue oxygenation. Blood velocity and RBC flow are also variables of paramount importance. Although much theoretical knowledge is available, there is to best of our knowledge no study that systemically quantifies the relative influence of hematocrit, RBC velocity and RBC flow on tissue oxygenation.
In this work, we use an analytical approach based on Hellums [17] and the numerical model by Lücker et al. [24] to investigate how hematocrit and RBC velocity comparatively affect tissue Po2. Our results show that the distance traveled by RBCs and oxygen consumption significantly affects the importance of the above variables. The discrepancies between analytical and numerical solutions are examined, providing a better understanding of the validity range of the analytical model. A novel finding is that MTCs significantly depend on RBC velocity at low to medium hematocrit. These results provide a basis for assessing assumptions used in oxygen transport models in the microcirculation, and contribute to understanding the impact of blood flow regulation mechanisms on tissue oxygenation.
Materials and Methods
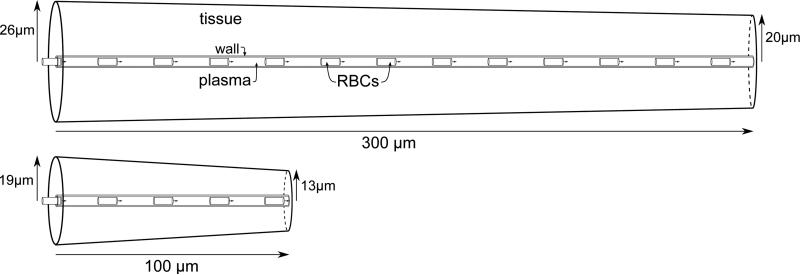
To quantify the influence of blood velocity and hematocrit on tissue oxygenation, we performed computations in axisymmetric cone-shaped domains with a capillary at their center (Figure 1). The computational domain consists of four distinct regions for the RBCs, the plasma, the endothelium and the tissue (indices c, p, w and t, respectively). The tissue has a radius rt,a on the proximal side (where blood flows in) and rt,v on the distal side, and consumes oxygen with a homogeneous rate M0. In the capillary endothelium (rp ≤ r < rw), oxygen consumption is neglected due to its small volume fraction and the high uncertainty in the oxygen consumption by endothelial cells [39]. In the plasma (0 ≤ r < rp), oxygen consumption is also assumed to be zero. In each region, the diffusion and solubility coefficients (D and α, respectively) may take different values. The RBCs are assumed to be cylindrical with length Lrbc and radius rc. The axial coordinate is denoted by x. For simplicity, no interstitial space layer between the endothelium and the tissue was used. Additional computations have shown that the additional of an interstitial space layer as in Eggleton et al. [8] decreases tissue Po2 by ~1 mmHg only.
Figure 1.
Sketches of the computational domains. Top: “cortex geometry” has dimensions that represent the rodent cortex. Bottom: “glomerulus geometry” has dimensions that match the rodent olfactory glomerulus which has a very high capillary density.
A cone-shaped representative tissue domain was employed for two main reasons. First, Sakadzic et al. [27] observed that the radius of the tissue cylinders supplied by capillary segments decreases with the branching order. Second, Lücker et al. [24] observed that the simulated drop in intraluminal oxygen tension along the vessel length agreed much better with the experimental data by Parpaleix et al. [25] when using a tapered cylinder rather than a straight cylinder.
Our results are based on a simple theoretical model developed by Hellums [17] and Roy et al. [26], and on the numerical model by Lücker et al. [24] for the computation of tissue oxygenation. In both models, the two variables of interest are the oxygen partial pressure and hemoglobin saturation, denoted by P and S, respectively. Hematocrit will be expressed in terms of RBC linear density (LD), which is defined by
| (1) |
where Lplasma is the length of the plasma-filled spacing between RBCs. This choice is convenient since LD can be directly observed in capillaries in vivo (e.g., using two-photon laser scanning microscopy [3]) and naturally arises from the theoretical model described below. The tube hematocrit Ht and LD are related by
| (2) |
Analytical model
We use a theoretical model for steady-state oxygen transport from a cylindrical capillary surrounded by a cone-shaped tissue domain. The main assumptions of this model are the absence of axial diffusion of oxygen, cylindrical RBC shapes and homogeneous oxygen release from hemoglobin, which makes it possible to find an analytical solution by elementary means. This approach is based on that of Roy et al. [26] with some modifications.
First, we determine the hemoglobin saturation drop along the capillary. The rate of total oxygen convective transport is given by
| (3) |
where qp is the blood flow rate, HD is the discharge hematocrit, C0 is the oxygen binding capacity of hemoglobin in RBCs and αeff the effective solubility of oxygen in the blood. Oxygen concentration is measured as volume of oxygen per volume of blood, and C0 equals NHb VmolO2, that is, the product of the concentration of heme groups in RBCs and the molar volume of oxygen. To simplify the model, we neglect the Fahraeus effect by assuming that discharge hematocrit and tube hematocrit are equal, so that . Since dissolved oxygen makes up < 8% of the total oxygen blood content (for HD ≥ 0.1 and S ≥ 0.2), we neglect the term αeffP.
Based on these assumptions and the absence of axial diffusion, mass conservation implies that
| (4) |
where QmaxO2 is the convective oxygen capacity of blood in capillaries and is given by
| (5) |
where vrbc is the RBC velocity. The integration of this equation in a cone-shaped domain with left and right radii rt,a and rt,v yields
| (6) |
where Sa is the hemoglobin saturation in equilibrium with the arterial RBC oxygen tension, denoted by Prbc,a. The average oxygen partial pressure in the RBC is related to the hemoglobin saturation by the Hill equation
| (7) |
where P50 is the oxygen partial pressure at hemoglobin half-saturation and n is the Hill exponent. The average Po2 in RBCs at x is obtained by inverting the Hill equation:
| (8) |
To determine the radial variation of Po2, equations for oxygen diffusion in the plasma, the endothelium and the tissue are solved. The steady-state equation for oxygen transport in the tissue is given by
| (9) |
where M0 is the metabolic rate of oxygen consumption (mlO2 cm−3 s−1). In the plasma and the endothelium, oxygen consumption is neglected and the equation reduces to
| (10) |
Within the RBC, the oxygen partial pressure is governed by
| (11) |
where the rate of oxygen unloading from hemoglobin is assumed to be independent of r (unlike in the numerical model below). Eq. (11) yields
| (12) |
where P0 is the Po2 on the center-line. The mean Po2 in the RBC is
| (13) |
It follows from the continuity of fluxes and Eqs. (10) and (11) that
| (14) |
The IVR to oxygen diffusion, K, is defined by Kq = P̄c – P(rw), where q is the oxygen flux per unit length through the capillary wall. Mass conservation implies that , so that
| (15) |
This formulation includes the resistance of the capillary wall. According to this model, the IVR is inversely proportional to the RBC linear density.
Using this model, the oxygen partial pressure at any point in the tissue can be determined as follows. First, the hemoglobin saturation at the corresponding location in the capillary is determined using Eq. (6). Second, the corresponding average oxygen partial pressure P̄ is obtained using the inverted Hill equation (Eq. (8)). Third, the oxygen partial pressure at the outer part of the endothelium is computed using P(rw) = P̄c – Kq. Finally, Po2 at the desired radial position is obtained using the Krogh cylinder model as
| (16) |
Since we aim at quantifying the effects of LD and RBC velocity, it is useful to reformulate tissue Po2 as a function of these variables. For r ≥ rw,
| (17) |
where the last three terms represent the Po2 drops due to convection in the capillary, IVR and consumption in the tissue, respectively, and are defined in Appendix A. The influence of LD and RBC velocity can be assessed by differentiating Eq. (17) with respect to both variables. To this end, we define the non-dimensional variable
| (18) |
For example, the value Z = 2 means that an infinitesimal relative increase in μLD causes a Po2 increase which is twice as large as that caused by the same relative increase in vRBC.
Computational model
We use the model by Lücker et al. [24], in which the unsteady advection-reaction-diffusion equations for oxygen and hemoglobin are solved numerically. The kinetics of oxygen and hemoglobin binding are solved in individual moving RBCs. Following Clark et al. [4], the reaction rates are given by
| (19) |
where k_ is the dissociation rate. As in the analytical model, the oxygen consumption is modeled using zero-order kinetics as
| (20) |
This consumption model can cause negative values of tissue Po2 when vRBC or μLD are low. The Po2 level was set to zero in the grid cells where this occurred.
The governing equations for oxygen and hemoglobin are
| (21) |
and
| (22) |
where v is the blood velocity, which is assumed to be equal to the RBC velocity in the whole capillary lumen. This simplification of plasma convection was shown by Vadapalli et al. [38] to decrease tissue Po2 only by 1.1 mmHg. The diffusion and solubility coefficients (D and α, respectively) may take different values in the RBCs, the plasma, the endothelium and the tissue. The boundary conditions are given by ∂P/∂n = 0 at the domain boundary and ∂S/∂n = 0 at the RBC boundaries. As an initial condition, the analytical solution described above was used and results were extracted after the simulation had become stationary. Eqs. (21) and (22) were numerically solved in a two-dimensional grid using the finite-volume method and coupled using the overlapping grid method presented in Lücker et al. [24]. The discretization of the advection term in Eq. (21) was modified for improved numerical stability, as explained in Appendix B. The other steps of the numerical algorithm are exactly as described in Lücker et al. [24].
Model parameters
We performed computations in two different cone-shaped domains as in Lücker et al. [24] (Figure 1) which will be referred to as cortex domain and glomerulus domain. The results in these two domains will illustrate the influence of metabolic oxygen consumption rate. The larger domain's dimensions correspond to the rodent cerebral cortex. Its length was set to L = 300 μm according to Sakadzic et al. [27] who found an average capillary path length of ~343 μm. The tissue radii were set to rt,a = 26 μm and rt,v = 20 μm, so that the average tissue radius closely matches the measurements by Tsai et al. [35] and Sakadzic et al. [27]. The oxygen consumption was set to 0.001 cm3 O2 cm−3 s−1, which corresponds to the value of 2.63 μmol g−1 min−1 measured by Zhu et al. [41] in the mouse cerebral cortex. The smaller domain has radii rt,a = 19 μm and rt,v = 13 μm that fit the high capillary density in the rodent olfactory glomerulus [22]. Its length was set to L = 100 μm and the taper was fitted to the longitudinal intravascular Po2 variations measured by Parpaleix et al. [25]. Due to the low tissue radius, we increased the oxygen consumption in this domain to 0.003 cm3 O2 cm−3 s−1 to obtain tissue Po2 values in the physiological range for most values of μLD and vRBC. The Po2 value in RBCs at the arterial inlet was set to 90 mmHg, which is the highest RBC Po2 value measured by Parpaleix et al. [25] in rodent brain capillaries. The remaining model parameters are summarized in Table 1. In the numerical model, the grid spacing was set to Δx = 3 μm in the capillary and the time step was chosen so that Δt = Δx/vRBC, which ensures that the absolute numerical error in tissue Po2 at 10 μm or more from the capillary is less than 0.5 mmHg [24]. In the computation of MTCs and Nusselt numbers, the grid cell size was set to Δx = 1μm for increased accuracy. The tolerance in the coupling between the oxygen and hemoglobin equations was set to 10−5.
Table 1.
Model parameters
| Parameter | Description | Value | Units | Reference |
|---|---|---|---|---|
| α rbc | O2 solubility in RBCs | 3.38 ×10−5 | cm3O2 mmHg−1 cm−3 | [8] |
| α p | O2 solubility in plasma | 2.82 ×10−5 | cm3O2 mmHg−1 cm−3 | [8] |
| α w | O2 solubility in endothelium | 3.89 ×10−5 | cm3O2 mmHg−1 cm−3 | [8] |
| α t | O2 solubility in tissue | 3.89 ×10−5 | cm3O2 mmHg−1 cm−3 | [8] |
| Drbc | O2 diffusivity in RBCs | 9.5 ×10−6 | cm2/s | [8] |
| Dp | O2 diffusivity in plasma | 2.18 ×10−5 | cm2/s | [8] |
| Dw | O2 diffusivity in endothelium | 8.73 ×10−6 | cm2/s | [8] |
| Dt | O2 diffusivity in tissue | 2.41 ×10−5 | cm2/s | [8] |
| DHb | Hemoglobin diffusivity in RBCs | 1.44 ×10−7 | cm2/s | [8] |
| k_ | Dissociation rate constant | 44 | s−1 | [8] |
| Lrbc | RBC length | 8.35 | μm | Calculated |
| n | Hill exponent | 2.64 | -- | Fitted from [40] |
| NHb | Molar density of heme groups | 2.03 ×10−5 | mol/cm3 | [8] |
| P 50 | Po2 at hemoglobin half-saturation | 47.9 | mmHg | Fitted from [40] |
| Pcrit | Critical Po2 in tissue | 1.0 | mmHg | [12] |
| Prbc,a | RBC Po2 at capillary entrance | 90 | mmHg | Based on [25] |
| rc | RBC radius | 1.5 | μm | [29] |
| rp | Plasma radius | 2.0 | μm | [35] |
| rw – rp | Capillary wall thickness | 0.6 | μm | [2] |
| V mol,O2 | Molar volume of oxygen | 2.54 ×104 | cm3O2/mol | Ideal gas law at 36.9°C |
| Vrbc | RBC vol ume | 59 | μm3 | [32] |
Results
We computed tissue Po2 for a range of values of RBC linear density and velocity, using both the analytical and the numerical model presented above. This allows us to assess the relative influence of LD, RBC velocity and RBC flow on tissue oxygenation. The analytical and numerical model results are compared, which sheds light on the validity range of the analytical model. Additionally, the dependence of MTCs and the related Nusselt number on LD and RBC velocity is computed.
In both computational domains (Figure 1), the Po2 was computed for values of LD between 0.1 and 0.6, with an increment of 0.02 for LDs between 0.1 and 0.3, and an increment of 0.05 for LDs between 0.3 and 0.6. In the cortex geometry, vRBC was varied between 0.2 and 2.4 mm/s. In the glomerulus domain, values of vRBC between 0.2 and 1.6 mm/s were used. In both cases, an increment of 0.1 mm/s was employed. Therefore, in the cortex and glomerulus geometries, we ran 17 × 23 = 391 and 17 × 15 = 255 simulations, respectively. In the analytical model, the IVR coefficient K was fitted to the results of the numerical model using least squares, instead of using the value given in Eq. (15). We express the results using the coefficient K0.5, which is the IVR coefficient for μLD = 0.5. According to Eq. (15), values of K for arbitrary LD are given by K = 0.5K0.5/μLD.
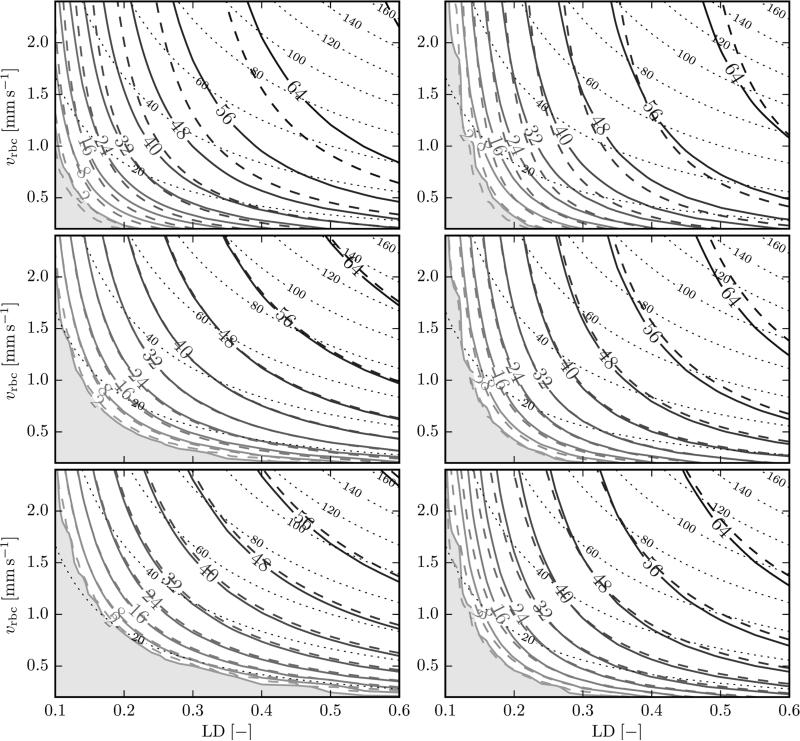
Figure 2 shows tissue Po2 as a function of LD and RBC velocity, at 15 μm from the endothelium (R = 17.6 μm) in the cortex geometry and at 10 μm from the endothelium (R = 12.6 μm) in the glomerulus geometry. The fitted IVR coefficient K0.5 was 4.98 mmHg μm s/μm3O2 in the cortex geometry and 5.43 mmHg μm s/μm3O2 in the glomerulus geometry. These values are significantly lower (by 23% and 16%) than the analytical value K0.5 = 6.43 mmHg μm s/μm3O2 given by Eq. (15). The analytical model results approximately match the numerical calculations with these fitted IVR coefficients. However, the Po2 isolines from both models do not coincide. The deviations are largest at proximal locations. The causes of these discrepancies are discussed below.
Figure 2.
Tissue Po2 as a function of LD and RBC velocity. Solid isolines: numerical results; dashed isolines: analytical model with fitted IVR coefficient. Left: cortex geometry, at 15 μm from the capillary wall (top: x = 40 μm, middle: x = 150 μm, bottom: x = 260 μm). Right: glomerulus geometry, at 10 μm from the capillary wall (top: x = 20 μm, middle: x = 50 μm, bottom: x = 80 μm). The shaded area shows the region where Po2 < 2 mmHg. The dotted lines show isolines of RBC flux (s−1).
In both geometries, tissue Po2 is an increasing function of LD and RBC velocity, as expected. Along any given isoline of RBC flux (qRBC = μLDvRBC/LRBC), Po2 increases with increasing LD, i.e., LD is a stronger determinant of tissue Po2 than RBC velocity. The strength of this variation is indicated by the angle between the Po2 and RBC flow isolines, which is larger at more proximal locations and larger in the glomerulus domain than in the cortex domain.
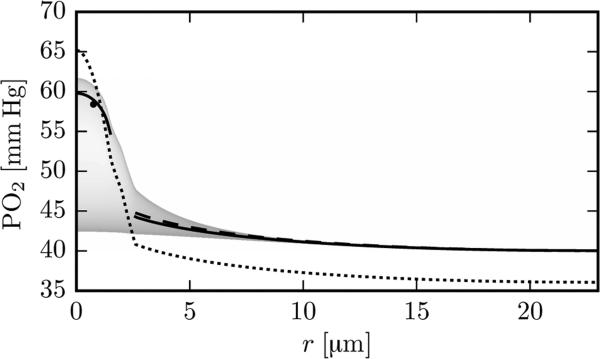
The analytical model considers radial diffusion only of free oxygen within RBCs. In fact, radial oxygen transport in RBCs is facilitated by diffusion of oxyhemoglobin [18], which leads to a smaller Po2 drop for a given rate of delivery. With μLD = 0.3 and vRBC = 1.2 mm/s, the intra-RBC Po2 drop P̄c – P(rc) at x = 150 μm is 6.8 mmHg with the analytical model. The numerical model yields = 3.0 mmHg, where is the oxygen partial pressure averaged over the RBC membrane at r = rc (Figure 3). Without diffusion of hemoglobin in the numerical model, the intra-RBC Po2 drop increases to 4.9 mmHg. This large difference is explained by the fact that most oxygen is released in a thin chemical boundary layer near the RBC membrane [4,18], which almost disappears in the absence of hemoglobin diffusion. The neglect of facilitated diffusion in the analytical model thus accounts for half of the discrepancy between the analytical and fitted IVR coefficients.
Figure 3.
Radial Po2 profile with μLD = 0.3 and vRBC = 1.2 mm/s at x = 150 μm in the cortex geometry. Solid line (in the RBC): Po2 from the numerical model, averaged over the RBC length when the RBC is centered at x = 150 μm; solid line (in the tissue): numerical time-averaged tissue Po2; dashed line: analytical tissue Po2 with fitted IVR coefficient; dotted line: analytical values based on Eqs. (12) to (16), without using an IVR coefficient. The shading indicates the frequency of the Po2 values from the numerical model. The black dot shows the averaged RBC PO2 value obtained from the analytical model.
Axial diffusion of oxygen is neglected by the analytical model. The consequences were examined by running the numerical model without axial diffusion. In this case, the best fit for K0.5 was 5.50 mmHg μm s/μm3O2 in the cortex geometry and 5.93 mmHg μm s/μm3O2 in the glomerulus geometry. These values are ~10% higher than those obtained with axial diffusion, yet still 14% and 8% lower than the analytical IVR coefficients, respectively. This can be explained by numerical axial diffusion introduced by the numerical scheme within the capillary, which has the effect of reducing the predicted IVR coefficient. Comparison with the analytical model in the absence of axial diffusion indicates that the reduction is less than 15%.
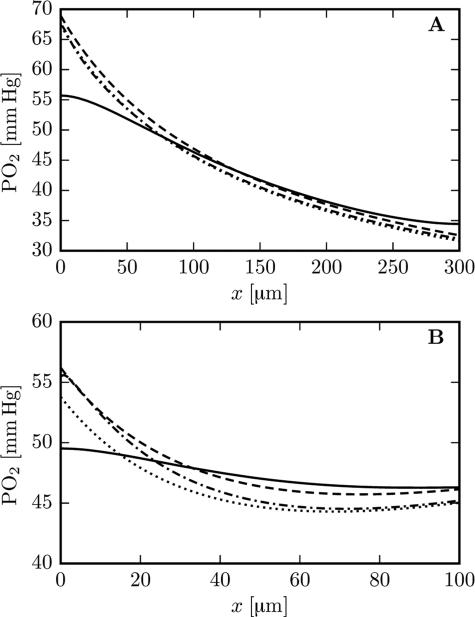
Although the neglect of axial diffusion has only a limited influence on the fitted value of the IVR coefficient, it significantly affects predicted longitudinal profiles of tissue Po2. Figure 4 shows simulated Po2 profiles with and without axial diffusion, together with the respective fits from the analytical model (IVR coefficients set as above). The analytical model fits the simulation results without axial diffusion extremely well. The results with and without axial diffusion differ most near the ends of the capillary. In simulations with axial diffusion, the no-flux boundary condition for Po2 at the domain boundary forces longitudinal Po2 profiles to be flat at x = 0 and x = L. Axial diffusion also smooths the longitudinal Po2 profiles, an effect which is most evident in the shorter glomerulus domain.
Figure 4.
Longitudinal tissue Po2 profiles with and without axial diffusion (μLD = 0.35, vRBC = 1.0 mm/s). Top: cortex geometry with Po2 at 15 μm from the capillary endothelium. Bottom: glomerulus geometry with Po2 at 10 μm from the capillary endothelium. Solid line: numerical model with axial diffusion. Dashed line: analytical fit to the simulation with axial diffusion. Dash-dotted line: numerical results without axial diffusion. Dotted lines: analytical fit to the simulation without axial diffusion. The analytical fits use the IVR coefficients defined in the text.
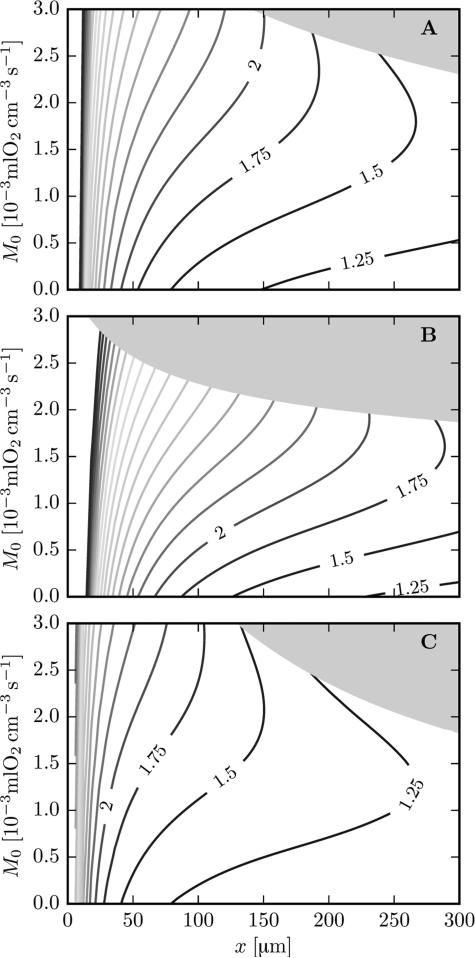
The results in the cortex and the glomerulus geometry display some qualitative differences, such as the higher angle between Po2 and flow isolines at proximal locations and in the glomerulus geometry (Figure 2). We now give a theoretical explanation of this fact. The function Z defined in Eq. (18) is the normalized ratio of the Po2 derivatives with respect to LD and RBC velocity. High values of Z imply that a relative change in LD has a stronger effect on tissue Po2 than the same relative change in RBC velocity. Figure 5 shows values of Z as a function of the axial position x and the metabolic rate of oxygen consumption M0, for several values of LD and RBC velocity. The contours of Z are masked for values of Po2 below 2 mmHg. In all cases, Z is a decreasing function of x. Therefore, the effect of LD changes is highest on the proximal side and Z tends to infinity when x → 0 since the convective Po2 drop vanishes in this case. However, the function Z always stays greater than one, even at distal positions (see Appendix A), implying that a relative change in LD always has a larger effect on tissue Po2 than the same relative change in RBC velocity. The dependency of Z on the oxygen consumption rate is more complex. In most cases, Z is an increasing function of M0. However, at distal locations and low tissue PO2 values (close to hypoxia), values of Z decrease as M0 increases. Figure 5 presents three cases: normal conditions; low LD with high RBC velocity; high LD with low RBC velocity (see the figure legend). The function Z attains its highest values when LD is low (Figure 5B) since tissue Po2 is limited by low hematocrit in this case. Conversely, when RBC velocity is low and LD is high (Figure 5C), Z takes lower values since the low RBC velocity is the limiting factor for oxygen supply in that case.
Figure 5.
Values of the function Z defined in Eq. (18) as a function of the axial position x and the rate of oxygen consumption M0. The computations were done in the cortex geometry. The shaded area shows hypoxic cases (Po2 < 2 mmHg). The highest contour value is 6.0. Top: μLD = 0.35, vRBC = 1.2 mm/s. Middle: μLD = 0.2, vRBC = 2.0 mm/s. Bottom: μLD = 0.5, vRBC = 0.6 mm/s.
We finally examine the dependence of the MTC and the related Nusselt number on LD and RBC velocity. This is also a direct way to compare the results from the numerical model by [24] with previous works. The MTC is defined as , where j̄ is the averaged oxygen flux through the capillary inner wall and is the average oxygen tension at the capillary inner wall around a RBC. The Nusselt number is a nondimensional MTC that here represents the ratio of the total oxygen flux to the diffusive oxygen flux based on the intravascular pressure gradient, and is defined following Hellums et al. (15) by
| (23) |
where P* is the oxygen tension in equilibrium with the average RBC hemoglobin saturation. The Nusselt number is approximately proportional to the MTC when and are close, which holds for medium to high LDs. To compute these quantities, the oxygen flux and wall Po2 were averaged around a RBC centered at xc = L/2. The averaged oxygen flux was given by
| (24) |
and a similar formula was used for Po2 at the capillary inner wall. A tissue cylinder with constant radius rt = 23μm and shorter length L = 83.5μm (= 10Lrbc) was used to avoid zero Po2 values in the tissue. Here, the use of a straight cylinder instead of a tapered domain facilitates result comparison with previous works, such as that by Eggleton et al. [8]. Additional computations showed that the cylinder shape changes MTCs and Nusselt numbers by <1%. RBC Po2 at the capillary entrance was chosen using the analytical model to obtain P̄c(xc) = 40 mmHg. The oxygen consumption rate was set to 0.001 cm3 O2 cm−3 s−1 as in the cortex geometry. At low LDs and erythrocyte velocities, additional changes were needed to avoid anoxic regions in the tissue. At LD = 0.1, the tissue radius was reduced to 16 μm and the domain length was increased L = 125μm (= 15Lrbc) to prevent the integration bounds in Eqs. (24) from overlapping with the domain boundary. Additionally, the RBC Po2 at the inlet was further increased to keep positive tissue Po2 values in the tissue. At vrbc = 0.2 mm/s, the oxygen consumption rate for LD ≤ 0.2 was lowered to prevent anoxic tissue regions from appearing.
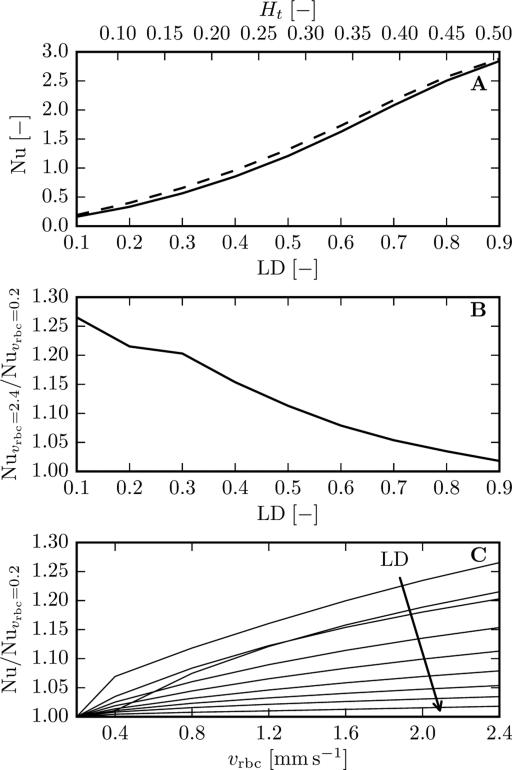
Figure 6 shows the calculated Nusselt numbers as a function of LD and RBC velocity. The obtained MTCs exhibit the same behaviour (Supplementary Figure 1). As found in previous studies (see Hellums et al. [18]), Nu strongly depends on hematocrit and exhibits a weaker dependency on blood velocity. Eggleton et al. [8] studied the MTC dependence on erythrocyte velocity and obtained a MTC increase of 2.7% when vrbc increases from 0.47 to 2.33 mm/s. However, when vRBC was raised from 0.2 to 2.4 mm/s, we found that the Nusselt number increased by >25% for μLD = 0.1 and <2% for μLD = 0.9 (Figure 6B). The Nusselt number is an increasing function of vrbc in the parameter range that was considered (Figure 6C). Additional computations showed that the cone taper has no significant influence on Nu and MTCs (< 1%). Likewise, capillary length and spacing do not have a major influence (< 4% difference between MTCs in the cortex and glomerulus geometries). In addition, the LD-dependent influence of RBC velocity on Nu is affected neither by the grid resolution nor by the time step size. Therefore, the MTC and the Nusselt number exhibit a significant dependence on RBC velocity that decreases with increasing LD.
Figure 6.
Nusselt number as a function of LD and RBC velocity obtained in a straight cylinder with L = 83.5μm and rt = 23μm for RBCs centered at xc = L/2. The tube hematocrit Ht was obtained using Eq. (2). Top: solid line: vrbc = 0.2 mm/s; dashed line: vrbc = 2.4 mm/s. Middle: velocity dependence of the Nusselt number as a function of LD. Bottom: velocity dependence of the Nusselt number; the arrow indicates increasing values of LD.
Discussion
Oxygen partial pressure was computed in two different axisymmetric cone-shaped tissue domains around a capillary. We used a simple analytical model and a numerical model based on the full transport equations for oxygen and hemoglobin. The influences of RBC linear density (or equivalently, tube hematocrit) and RBC velocity were quantified. Results from the analytical and numerical models were compared and the origin of the discrepancies was identified. A theoretical analysis was done to explain the influence of the longitudinal position and the metabolic rate of oxygen consumption on our findings. Finally, the dependence of MTCs on LD and RBC velocity was investigated.
This study points out that RBC linear density (LD) is a very important determinant of tissue Po2. The RBC flux qRBC, which is proportional to both LD and RBC velocity, is a variable of primary importance for tissue Po2. However, the RBC flux alone is not an accurate predictor of tissue Po2, as shown by the angle between Po2 and RBC flow contours in Figure 2. As shown in Eq. (17), tissue Po2 is affected by two terms that depend on LD and vRBC: first, the convective Po2 drop ΔPconv, which is a function of the RBC flux qRBC; second, the intravascular resistance Po2 drop ΔPIVR, which is only a function of LD. This second term causes the deviation between Po2 and RBC flux contours. Therefore, LD is a more important determinant of tissue Po2 than vRBC in the following sense: a relative change in LD causes a higher variation of tissue Po2 than the same relative change in vRBC, i.e. μLD∂P/∂μLD > vRBC∂P/∂vRBC, as proved in Appendix A.
Both the analytical and the numerical models show the circumstances under which the influence of LD is higher. As illustrated by the angles between Po2 and RBC flow contours in the panels in Figure 2, LD is most important for high values of oxygen consumption (glomerulus geometry) and on proximal side. Conversely, for lower values of oxygen consumption (cortex geometry) and on the distal side, Po2 and RBC flow contours are more similar, which shows that the influence of LD is diminished under these conditions. These numerical results are supported by the analytical model. Indeed, the function Z defined in Eq. (18) decreases with the longitudinal position x and increases with the oxygen consumption (except for Po2 levels near hypoxia for the latter). This means that the importance of LD for tissue Po2 decreases with x and generally increases with M0.
The good agreement between results from the theoretical and numerical models shows that the inverse dependence of the IVR coefficient on LD (Eq. (15)) holds for a large range of hematocrit and RBC velocity values. This agrees well with the findings of Eggleton et al. [8] and Vadapalli et al. [38], and highlights the necessity of using hematocrit-dependent MTCs for simulation methods that rely on these coefficients to couple intravascular and extravascular oxygen transport. The inverse dependence mentioned above means that a reduction of hematocrit by a factor of two causes the IVR to double. Therefore, in the presence of hematocrit heterogeneity, the assumption of hematocrit-independent IVR coefficient may yield large errors in the evaluation of oxygen fluxes through the vessel wall. We now review several oxygen modeling works by the standpoint of IVR coefficients or, equivalently, MTCs. Goldman et al. [13] studied the effect of capillary anastomoses and tortuosity on oxygen transport and used the MTCs computed by Eggleton et al. [8]. Similarly, Tsoukias et al. [36] simulated oxygen transport from a three-dimensional vascular network in the presence of hemoglobin-based oxygen carriers using MTCs computed by Vadapalli et al. [38]. Another body of works used the Green's function method developed by Hsu et al. [19] to predict the Po2 distribution in realistic microvascular networks. Some subsequent works (Secomb et al. [29], Secomb et al. [30], Secomb et al. [31]) assumed constant hematocrit values and used the constant IVR coefficients computed in Secomb et al. [29]. However, hematocrit-dependent IVR coefficients can be very easily added to this class of models. Recently, a dual-mesh approach was developed by Linninger et al. [23] and enables fast Po2 calculations in complex vascular networks. The coupling between intravascular and tissue Po2 is based on the wall thickness and a hematocrit-independent oxygen permeability of epithelial tissue. Since this approach does not use Po2 values at the vessel walls, the IVR coefficients computed here or in other works cannot be readily used in that model, but could be adapted based on the positions of the grid nodes.
The influence of LD on oxygen supply to tissue also has important physiological consequences. While blood velocity can be altered by arteriolar dilation in the cerebral cortex [33] or increased heart rate, mechanisms that influence hematocrit play a critical role. For example, during altitude adaptation, systemic hematocrit is increased over 24-48 h by plasma volume reduction and increased erythropoiesis [1]. This increases the oxygen carrying capacity of the blood and decreases the IVR to oxygen transport, hence reduces the risk of hypoxia. However, there may be RBC redistribution mechanisms that act on a faster scale in the microcirculation. Using a discrete RBC tracking model, Schmid et al. [28] hypothesized that pericyte-mediated capillary dilations are an efficient mechanism that can locally alter the distribution of RBCs in microvascular networks. Such a mechanism could reduce the IVR of the capillaries that contain an increased number of RBCs and therefore locally increase the oxygen availability. This could be important at distal locations since Devor et al. [6] suggested that functional hyperemia acts to maintain baseline tissue Po2 at such locations. A local increase in LD could help to compensate for metabolism increases and ensure a safe margin of oxygen supply at the most critical locations.
While the analytical and numerical models used in this study clearly show the higher importance of LD compared to RBC velocity, they exhibit some discrepancies. First, the analytical IVR coefficients given by Eq. (15) overestimate by up to 23% the coefficients obtained by fitting the numerical results. The assumption of homogeneous release of oxygen from hemoglobin and the neglect of hemoglobin-facilitated radial diffusion were identified as the main causes for this, while the absence of axial diffusion in the analytical model only slightly affects the fitted IVR coefficients. However, the analytical model with fitted IVR coefficients agreed closely with the numerical model (Figure 2) away from the proximal and distal domain boundaries. Therefore, numerical models for oxygen transport in microvascular networks that use appropriate IVR coefficients are expected to yield very good approximations of steady-state tissue Po2 away from domain boundaries and at >5μm from capillaries (Figure 3). In particular, the oxygen transport models by Goldman et al. [13] and Hsu et al. [19] can directly use hematocrit-dependent IVR coefficients. Therefore, they are very likely to yield similar tissue Po2 values to those obtained from models with fewer assumptions, such as the one introduced by Lücker et al. [24]. However, accurate simulations of the intravascular Po2 field in capillaries require models with individual RBCs such as that by Eggleton et al. [8] or Lücker et al. [24].
The neglect of axial diffusion in the analytical model has a noticeable effect on longitudinal Po2 profiles (Figure 4). This assumption has been scrutinized in the context of the classical Krogh model [11,12,20]. Here, the largest deviations caused by this simplifying hypothesis were found in the glomerulus geometry, where the oxygen consumption per unit length in the capillary is highest. In such cases, alternative analytical methods that include axial diffusion could prove beneficial. For example, the approach based on spherical diffusion kernels suggested by Grimes et al. [15] could be extended to include the longitudinal oxygen gradient along the vessel. However, the boundary conditions for Po2 at the domain boundary, or the domain geometry itself, would need to be adapted.
Our results can be compared to previous works by means of MTCs and the related Nusselt number (Eq. (23)). As in previous works reviewed by Hellums et al. [18], we obtained a strong dependence of Nu on hematocrit. However, the effect of erythrocyte velocity that we observed differs from previous studies. We found that the increase in Nusselt number with increasing vRBC was significantly greater than that obtained by Eggleton et al. [8] except at high LDs. To explain this discrepancy, we adapted our numerical method to simulate oxygen transport in the moving RBC frame with a relative backwards motion of the tissue, as in Eggleton et al. [8]. Computations with the same geometric and physiological parameters (with the exception of an interstitial fluid layer around the capillary and the presence of myoglobin) were performed. For the same RBC velocity increase, we found an increase in MTC of 7.5% at Ht = 0.43, which is higher than the 2.7% increase reported in [8]. Additional computations with fixed and moving RBCs produced no major difference in the computed MTCs. Two different boundary conditions at the proximal and distal tissue boundary (Krogh-type as in [8] and no-flux) were compared and did not show any significant influence. Therefore, this discrepancy might be explained by the numerical method since we observed that MTCs are slightly sensitive to the grid resolution. However, the absence of details on the numerical method used in [8] made further investigation difficult. The robustness of our results with respect to multiple parameters (capillary length and spacing, cone taper, RBC frame of reference, grid resolution, time step size) provides strong evidence for a significant influence of RBC velocity on MTCs that decreases with increasing LD. This dependence may significantly affect the results of MTC-based oxygen transport simulations in realistic capillary networks as in [30] since the erythrocyte velocity can be very heterogeneous. For example, in the mouse cortex, mean RBC velocities in the range of 2.03 ± 1.42 mm/s have been measured [37].
The major aim of this study was to assess the effect of LD and RBC velocity separately, while keeping other variables constant. However, this process has some limitations. Among others, the oxygen partial pressure Prbc,a in RBCs at the capillary entrance was kept constant. However, during blood flow increases, Po2 in proximal capillaries is also expected to rise due to decreased transit time and/or IVR in arterioles, since they also participate in oxygen supply to tissue [7,27]. The effects of precapillary oxygen supply could be taken into account by parameterizing Prbc,a as a function of LD and vRBC. Similarly, the no-flux boundary condition for Po2 means that our results only pertain to cases where no diffusive interaction between the capillary and a nearby arteriole occurs. The model for metabolic oxygen consumption may have an important influence on the reported tissue Po2 values. Since an oxygen-independent consumption rate yields an analytical solution, we used Eq. (20) in both the analytical and the numerical model. However, the nonlinear Michaelis-Menten model given by M(P) = M0P/(Pcrit + P) has been often used in modeling [12] and there is evidence that the constant Pcrit may be >1 mmHg [14]. Therefore, the low tissue Po2 values are subject to this model uncertainty. Nevertheless, the key findings of this study are not expected to be influenced by the assumed oxygen consumption kinetics. Similarly, changes in pH, carbon dioxide tension or temperature can affect the oxygen dissociation curve, as modeled in [5]. However, our main conclusions are insensitive to the Hill equation parameters (Eq. (7)), as can be seen using the analytical function defined by Eq. (19). Finally, high-frequency fluctuations in LD and RBC velocity are known to occur [3] but their effect was not investigated here.
In conclusion, we have quantified the relative influence of hematocrit and RBC velocity on tissue oxygenation around capillaries using an analytical and a numerical model. These results provide a basis for analyzing the mechanisms by which blood flow and tissue oxygenation are regulated in response to changing functional needs.
Perspective
Using theoretical modeling, hematocrit is shown to have a larger influence on tissue oxygenation around capillaries than red blood cell velocity, with strongest importance near the arterioles and at high oxygen consumption rates. This challenges the common view that, among blood flow variables, solely the oxygen flux into the capillaries determines the tissue oxygen partial pressure. A sound understanding of the determinants of tissue oxygenation is essential to accurately describe how blood flow regulation mechanisms affect oxygen supply.
Supplementary Material
Acknowledgements
The authors are grateful for the valuable discussions with Franca Schmid.
This research was funded by the Swiss National Science Foundation under the grant No. 140660 and NIH grant HL070657.
List of Abbreviations
- EAT
erythrocyte-associated transients
- IVR
intravascular resistance
- LD
linear density
- MTC
mass transfer coefficient
- Po2
oxygen partial pressure
- RBC
red blood cell
Appendix A
We now give analytical expressions for the terms on the right-hand side of Eq. (17). The convective Po2 drop from the capillary inlet to the axial position x is
| (25) |
where S(x) is given by Eq. (6). The intravascular drop P̄c – P(rw) is given by
| (26) |
where is the oxygen flux per unit length and the IVR coefficient K′ = KμLD is independent of μLD. From Eq. (16), the extravascular drop ΔPEV(r) = P(rw) – P(r) depends on neither μLD nor vrbc. From Eq. (5), ΔPconv depends on μLD and vrbc only through their product, and it follows that
| (27) |
The derivative of the IVR term with respect to μLD is given by
| (28) |
The right-hand side of Eq. (28) is positive, and this together with Eqs. (17) and (27) implies that
| (29) |
Therefore, the function Z defined in Eq. (18) is always larger than one.
Appendix B
Here we describe an improved discretization scheme for the advection term in Eq. (21). As in Lücker et al. [24], the pure advection equation
| (29) |
is solved before dealing with the diffusion, reaction and consumption terms. Since the solubility coefficient α takes different values in the RBC and in the plasma, a discretization scheme that is monotone for C = αP may introduce spurious oscillations in P in the capillary, since P is then obtained by dividing C by the variable coefficient α. With the parameters used in Lücker et al. [24], these oscillations were immediately damped by the diffusion term. However, in this study, at high RBC linear densities or velocities, these spurious oscillations did not disappear after the diffusion-reaction step when Eq. (29) was discretized with a conventional method such as the upwind scheme. This led us to improve the numerical scheme for Eq. (29). The new scheme is particularly useful in the simulations without axial diffusion, where spurious oscillations in axial direction would not be damped by diffusion.
The improved method takes advantage from the fact that the exact position of the RBC interface is known at each time step. For simplicity, we describe it in a one-dimensional equidistant grid with a single RBC domain Ωrbc. The oxygen concentration in a grid cell ΩI with width Δx at time step k + 1 is given by
| (30) |
where is the grid cell ΩI shifted backwards by vrbcΔt (Supplementary Figure 2). The oxygen concentration Ck at the previous time step is reconstructed based on the position of the RBC interface and the values of Pk in the grid cells intersected by . Under the assumption that the RBC moves in positive direction and vrbcΔt ≤ Δx, Eq. (30) becomes
| (31) |
with and , as illustrated in Supplementary Figure 2. Finally, the oxygen partial pressure at the new time step is given by .
The conservation property of this scheme is ensured by Eq. (30) which shows that the total oxygen concentration in the domain can only be changed by the boundary conditions. Finally, the observation that implies that the scheme for P can be expressed as for some λ ∈ [0,1]. In particular, the nonnegativity of the coefficients λ and 1 – λ shows that the method is monotone for P, hence cannot introduce spurious oscillations [34, Chapter 13].
References
- 1.Bartsch P, Saltin B. General introduction to altitude adaptation and mountain sickness. Scandinavian journal of medicine & science in sports. 2008;18(Suppl 1):1–10. doi: 10.1111/j.1600-0838.2008.00827.x. [DOI] [PubMed] [Google Scholar]
- 2.Bertossi M, Virgintino D, Maiorano E, Occhiogrosso M, Roncali L. Ultrastructural and morphometric investigation of human brain capillaries in normal and peritumoral tissues. Ultrastruct Pathol. 1997;21:41–49. doi: 10.3109/01913129709023246. [DOI] [PubMed] [Google Scholar]
- 3.Chaigneau E, Oheim M, Audinat E, Charpak S. Two-photon imaging of capillary blood flow in olfactory bulb glomeruli. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:13081–13086. doi: 10.1073/pnas.2133652100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Clark A, Jr., Federspiel WJ, Clark PA, Cokelet GR. Oxygen delivery from red cells. Biophysical journal. 1985;47:171–181. doi: 10.1016/s0006-3495(85)83890-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dash RK, Bassingthwaighte JB. Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3-DPG and temperature levels. Annals of biomedical engineering. 2004;32:1676–1693. doi: 10.1007/s10439-004-7821-6. [DOI] [PubMed] [Google Scholar]
- 6.Devor A, Sakadzic S, Saisan PA, Yaseen MA, Roussakis E, Srinivasan VJ, Vinogradov SA, Rosen BR, Buxton RB, Dale AM, Boas DA. “Overshoot” of O(2) is required to maintain baseline tissue oxygenation at locations distal to blood vessels. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2011;31:13676–13681. doi: 10.1523/JNEUROSCI.1968-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Duling BR, Berne RM. Longitudinal gradients in periarteriolar oxygen tension. A possible mechanism for the participation of oxygen in local regulation of blood flow. Circulation research. 1970;27:669–678. doi: 10.1161/01.res.27.5.669. [DOI] [PubMed] [Google Scholar]
- 8.Eggleton CD, Vadapalli A, Roy TK, Popel AS. Calculations of intracapillary oxygen tension distributions in muscle. Mathematical biosciences. 2000;167:123–143. doi: 10.1016/s0025-5564(00)00038-9. [DOI] [PubMed] [Google Scholar]
- 9.Federspiel WJ, Popel AS. A theoretical analysis of the effect of the particulate nature of blood on oxygen release in capillaries. Microvascular research. 1986;32:164–189. doi: 10.1016/0026-2862(86)90052-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Federspiel WJ, Sarelius IH. An examination of the contribution of red cell spacing to the uniformity of oxygen flux at the capillary wall. Microvascular research. 1984;27:273–285. doi: 10.1016/0026-2862(84)90059-1. [DOI] [PubMed] [Google Scholar]
- 11.Fletcher JE, Schubert RW. Axial diffusion and wall permeability effects in perfused capillary-tissue structures. Biosystems. 1987;20:153–174. doi: 10.1016/0303-2647(87)90042-6. [DOI] [PubMed] [Google Scholar]
- 12.Goldman D. Theoretical models of microvascular oxygen transport to tissue. Microcirculation. 2008;15:795–811. doi: 10.1080/10739680801938289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goldman D, Popel AS. A computational study of the effect of capillary network anastomoses and tortuosity on oxygen transport. Journal of theoretical biology. 2000;206:181–194. doi: 10.1006/jtbi.2000.2113. [DOI] [PubMed] [Google Scholar]
- 14.Golub AS, Pittman RN. Oxygen dependence of respiration in rat spinotrapezius muscle in situ. American journal of physiology Heart and circulatory physiology. 2012;303:H47–56. doi: 10.1152/ajpheart.00131.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grimes DR, Kannan P, Warren DR, Markelc B, Bates R, Muschel R, Partridge M. Estimating oxygen distribution from vasculature in three-dimensional tumour tissue. J R Soc Interface. 2016;13 doi: 10.1098/rsif.2016.0070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Groebe K, Thews G. Effects of red cell spacing and red cell movement upon oxygen release under conditions of maximally working skeletal muscle. Advances in experimental medicine and biology. 1989;248:175–185. doi: 10.1007/978-1-4684-5643-1_22. [DOI] [PubMed] [Google Scholar]
- 17.Hellums JD. The resistance to oxygen transport in the capillaries relative to that in the surrounding tissue. Microvascular research. 1977;13:131–136. doi: 10.1016/0026-2862(77)90122-4. [DOI] [PubMed] [Google Scholar]
- 18.Hellums JD, Nair PK, Huang NS, Ohshima N. Simulation of intraluminal gas transport processes in the microcirculation. Annals of biomedical engineering. 1996;24:1–24. doi: 10.1007/BF02770991. [DOI] [PubMed] [Google Scholar]
- 19.Hsu R, Secomb TW. A Green's function method for analysis of oxygen delivery to tissue by microvascular networks. Mathematical biosciences. 1989;96:61–78. doi: 10.1016/0025-5564(89)90083-7. [DOI] [PubMed] [Google Scholar]
- 20.Kreuzer F. Oxygen supply to tissues: the Krogh model and its assumptions. Experientia. 1982;38:1415–1426. doi: 10.1007/BF01955753. [DOI] [PubMed] [Google Scholar]
- 21.Krogh A. The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. The Journal of physiology. 1919;52:409–415. doi: 10.1113/jphysiol.1919.sp001839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lecoq J, Tiret P, Najac M, Shepherd GM, Greer CA, Charpak S. Odor-evoked oxygen consumption by action potential and synaptic transmission in the olfactory bulb. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2009;29:1424–1433. doi: 10.1523/JNEUROSCI.4817-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Linninger AA, Gould IG, Marinnan T, Hsu CY, Chojecki M, Alaraj A. Cerebral microcirculation and oxygen tension in the human secondary cortex. Annals of biomedical engineering. 2013;41:2264–2284. doi: 10.1007/s10439-013-0828-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lücker A, Weber B, Jenny P. A dynamic model of oxygen transport from capillaries to tissue with moving red blood cells. American journal of physiology Heart and circulatory physiology. 2015;308:H206–216. doi: 10.1152/ajpheart.00447.2014. [DOI] [PubMed] [Google Scholar]
- 25.Parpaleix A, Goulam Houssen Y, Charpak S. Imaging local neuronal activity by monitoring PO(2) transients in capillaries. Nature medicine. 2013;19:241–246. doi: 10.1038/nm.3059. [DOI] [PubMed] [Google Scholar]
- 26.Roy TK, Secomb TW. Theoretical analysis of the determinants of lung oxygen diffusing capacity. Journal of theoretical biology. 2014;351:1–8. doi: 10.1016/j.jtbi.2014.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sakadzic S, Mandeville ET, Gagnon L, Musacchia JJ, Yaseen MA, Yucel MA, Lefebvre J, Lesage F, Dale AM, Eikermann-Haerter K, Ayata C, Srinivasan VJ, Lo EH, Devor A, Boas DA. Large arteriolar component of oxygen delivery implies a safe margin of oxygen supply to cerebral tissue. Nature communications. 2014;5:5734. doi: 10.1038/ncomms6734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schmid F, Reichold J, Weber B, Jenny P. The impact of capillary dilation on the distribution of red blood cells in artificial networks. American journal of physiology Heart and circulatory physiology. 2015;308:H733–742. doi: 10.1152/ajpheart.00335.2014. [DOI] [PubMed] [Google Scholar]
- 29.Secomb TW, Hsu R. Simulation of O2 transport in skeletal muscle: diffusive exchange between arterioles and capillaries. The American journal of physiology. 1994;267:H1214–1221. doi: 10.1152/ajpheart.1994.267.3.H1214. [DOI] [PubMed] [Google Scholar]
- 30.Secomb TW, Hsu R, Beamer NB, Coull BM. Theoretical simulation of oxygen transport to brain by networks of microvessels: effects of oxygen supply and demand on tissue hypoxia. Microcirculation. 2000;7:237–247. [PubMed] [Google Scholar]
- 31.Secomb TW, Hsu R, Park EY, Dewhirst MW. Green's function methods for analysis of oxygen delivery to tissue by microvascular networks. Annals of biomedical engineering. 2004;32:1519.–1529. doi: 10.1114/b:abme.0000049036.08817.44. [DOI] [PubMed] [Google Scholar]
- 32.Shirasawa T, Izumizaki M, Suzuki Y, Ishihara A, Shimizu T, Tamaki M, Huang F, Koizumi K, Iwase M, Sakai H, Tsuchida E, Ueshima K, Inoue H, Koseki H, Senda T, Kuriyama T, Homma I. Oxygen affinity of hemoglobin regulates O2 consumption, metabolism, and physical activity. The Journal of biological chemistry. 2003;278:5035–5043. doi: 10.1074/jbc.M211110200. [DOI] [PubMed] [Google Scholar]
- 33.Tian P, Teng IC, May LD, Kurz R, Lu K, Scadeng M, Hillman EM, De Crespigny AJ, D'Arceuil HE, Mandeville JB, Marota JJ, Rosen BR, Liu TT, Boas DA, Buxton RB, Dale AM, Devor A. Cortical depth-specific microvascular dilation underlies laminar differences in blood oxygenation level-dependent functional MRI signal. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:15246–15251. doi: 10.1073/pnas.1006735107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Toro EF, SpringerLink (Online service) Riemann Solvers and Numerical Methods for Fluid Dynamics A Practical Introduction. Springer-Verlag Berlin Heidelberg; Berlin, Heidelberg: 2009. [Google Scholar]
- 35.Tsai PS, Kaufhold JP, Blinder P, Friedman B, Drew PJ, Karten HJ, Lyden PD, Kleinfeld D. Correlations of neuronal and microvascular densities in murine cortex revealed by direct counting and colocalization of nuclei and vessels. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2009;29:14553–14570. doi: 10.1523/JNEUROSCI.3287-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tsoukias NM, Goldman D, Vadapalli A, Pittman RN, Popel AS. A computational model of oxygen delivery by hemoglobin-based oxygen carriers in three-dimensional microvascular networks. Journal of theoretical biology. 2007;248:657–674. doi: 10.1016/j.jtbi.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Unekawa M, Tomita M, Tomita Y, Toriumi H, Miyaki K, Suzuki N. RBC velocities in single capillaries of mouse and rat brains are the same, despite 10-fold difference in body size. Brain research. 2010;1320:69–73. doi: 10.1016/j.brainres.2010.01.032. [DOI] [PubMed] [Google Scholar]
- 38.Vadapalli A, Goldman D, Popel AS. Calculations of oxygen transport by red blood cells and hemoglobin solutions in capillaries. Artificial cells, blood substitutes, and immobilization biotechnology. 2002;30:157–188. doi: 10.1081/bio-120004338. [DOI] [PubMed] [Google Scholar]
- 39.Vadapalli A, Pittman RN, Popel AS. Estimating oxygen transport resistance of the microvascular wall. American journal of physiology Heart and circulatory physiology. 2000;279:H657–671. doi: 10.1152/ajpheart.2000.279.2.H657. [DOI] [PubMed] [Google Scholar]
- 40.Watanabe T, Takeda T, Omiya S, Hikoso S, Yamaguchi O, Nakano Y, Higuchi Y, Nakai A, Abe Y, Aki-Jin Y, Taniike M, Mizote I, Matsumura Y, Shimizu T, Nishida K, Imai K, Hori M, Shirasawa T, Otsu K. Reduction in hemoglobin-oxygen affinity results in the improvement of exercise capacity in mice with chronic heart failure. J Am Coll Cardiol. 2008;52:779–786. doi: 10.1016/j.jacc.2008.06.003. [DOI] [PubMed] [Google Scholar]
- 41.Zhu XH, Chen JM, Tu TW, Chen W, Song SK. Simultaneous and noninvasive imaging of cerebral oxygen metabolic rate, blood flow and oxygen extraction fraction in stroke mice. NeuroImage. 2013;64:437–447. doi: 10.1016/j.neuroimage.2012.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.