Abstract
Purpose
To develop a new method capable of directly measuring specific absorption rate (SAR) deposited in tissue using the thermoacoustic signal induced by short RF pulse excitation.
Theory
A detailed model based on the thermoacoustic wave generation and propagation is presented.
Methods
We propose a new concept for direct measurement of SAR, to be used as a safety assessment / monitoring tool for MRI. The concept involves the use of short bursts of RF energy and the measurement of the resulting thermoacoustic excitation pattern by an array of ultrasound transducers, followed by image reconstruction to yield the 3D SAR distribution. We developed a simulation framework to model this thermoacoustic SAR mapping concept and verified the concept in vitro.
Results
Simulations show good agreement between reconstructed and original SAR distributions with an error of 4.2%, 7.2%, and 8.4% of the mean SAR values in axial, sagittal, and coronal planes and support the feasibility of direct experimental mapping of SAR distributions in vivo. The in vitro experiments show good agreement with theory (r2 = 0.52).
Conclusions
A novel thermoacoustic method for in vivo mapping of local SAR patterns in MRI has been proposed and verified in simulation and in a phantom experiment.
Keywords: safety, specific absorption rate, thermoacoustics
Introduction
A significant safety concern for MRI in clinical and research practice is the deposition of radiofrequency (RF) power in the body, quantified by the specific absorption ratio (SAR). This is because there is a risk of patient injury through the deposition of high RF power levels within small regions for extended times, leading to local heating with potential tissue damage. The average value of SAR as well as its non-uniformity are concerning at all magnetic field strengths, but become more limiting as field strengths rise into the ultra-high-field (UHF) range. SAR measures the power delivered per mass of tissue, and is therefore cited in units of W/kg. Current technology is not equipped to measure SAR locally; the only quantity that can be easily determined in vivo is the overall average, or global, SAR, which is a measure of the average power absorbed per unit mass of tissue that is delivered to the entire mass of the body part under investigation (e.g. head or torso).
In UHF MRI, higher static field strengths result in higher global specific absorption rate (SAR) values. Additionally, the wave phenomena that emerge in MRI introduce an inherent spatial variation of the electric fields, resulting in spatially-varying SAR patterns. These are commonly referred to as “local SAR” distributions and may show higher variations than observed at lower field strengths (although it is known that SAR is also non-uniform at lower field strengths) [1],[2]. Local SAR variation is hard to predict due to anatomical, tissue compositional and positional variations between patients, as well as variations determined by the transmit RF coil. This difficulty may in fact be the dominant limitation of MRI in general and UHF MRI in particular.
Parallel transmit (pTx) technology, in which multiple transmit RF channels can be controlled independently [1]-[4], has become popular for mitigating the B1+ field non-uniformity problems that occur at higher field strengths. However, an unconstrained combination of the power output of multiple channels can, in a worst-case scenario, cause very strong local heating effects due to constructive interference of the electric field components from each channel, leading to strong local SAR maxima, possibly even stronger than those produced by conventional excitation. This concern has led to the development of SAR-aware pTx methods, which employ knowledge of E-fields in addition to the extra degrees of freedom provided by the multi-transmit coil, to reduce local SAR maxima while simultaneously constraining B1+ inhomogeneity [5]-[10].
To date there is still no good method available to directly and non-invasively measure local SAR in vivo. Current heuristic approaches are based on electromagnetic modeling or B1 mapping [11]-[15]. Some of these use a simple but somewhat conservative estimate of the ratio of the peak local SAR to the global or average SAR in order to account for modeling inaccuracies; typically in the range between 3:1 and 20:1 [16]. The peak local SAR can then be estimated from the measured global SAR by multiplication with this ratio – this method can severely limit the performance achievable by UHF MRI. More advanced SAR-aware pTx methods are based on the concept of virtual observation points but are still based on pre-simulated SAR distributions and not on direct mapping methods [17]-[24]. MR-based electrical properties mapping has shown promise for SAR prediction [23]-[25], but these methods are still approximate. Methods for SAR prediction have also been advanced by researchers concerned about safety in the presence of metallic implants [26]-[29]. Given the strong incentive to develop UHF MRI into a clinical tool, it is paramount to find a viable and accurate method for monitoring the spatially varying SAR pattern, and therefore the actual ratio of peak local SAR to global SAR, as the key parameter in MRI safety.
There have been a number of research efforts to tackle this challenging problem in recent years, but to date a direct in vivo SAR mapping methodology has not been demonstrated. Temperature may be a relevant surrogate measure (and in fact temperature, rather than SAR, is thought to be the primary mechanism for tissue damage); however, state-of-the-art MR thermometry has a relatively coarse temperature resolution of approximately 0.5-1°C [30], which is about an order of magnitude worse than what would be required for precise monitoring of local temperature maxima that may not exceed 1°C by regulatory guidelines [16]. For these reasons and others, SAR has continued as the most widely accepted and implemented RF safety metric in human MRI systems devices.
To address the above unmet needs, this paper describes the development of a new safety assessment/monitoring tool for MRI based on the thermoacoustic effect. Here, we take advantage of the phenomenon that the amplitude of thermoacoustic waves [31]-[36] is directly proportional to the specific absorption rate (SAR) of the RF energy deposited in the tissue. We therefore propose a new concept to measure spatially varying local SAR patterns by measuring thermoacoustic waves and reconstructing their origin from time-domain measurements. The RF coil irradiates a human body with RF energy and therefore creates a SAR distribution throughout the body. By means of altering the RF transmitter to generate RF energy in very short pulses, thermoacoustic waves will be induced within tissue and thus detectable with an appropriate ultrasonic measurement apparatus. This should ultimately lead to a direct measurement technique for local SAR in MRI. The technique should be particularly useful for mapping SAR throughout the human body during UHF MRI. We expect that this work will lead to a new form of local SAR assessment that could make UHF MRI much more clinically applicable by allowing for accurate, patient-specific safety monitoring. In addition to applications in UHF MRI, this tool should also be useful for mapping local SAR at lower fields, and may even permit real-time SAR mapping.
Theory
The thermoacoustic effect was first described in 1880 by Alexander Graham Bell [37], who observed sound emanating from a sheet of rubber that was being illuminated by an intermittent beam of sunlight. In modern days, thermoacoustic imaging is used to combine high RF or microwave contrast with fine ultrasonic spatial resolution [32],[33].
Thermoacoustic signals are ultrasound waves generated through the absorption of pulsed or otherwise modulated RF/microwave energy. Soft biological tissue contains ions, polar molecules, proteins, and other biomolecules that absorb electromagnetic energy. A short-pulsed RF or microwave source is used to irradiate the tissue, and the absorbed energy then causes thermoelastic expansion and radiates thermoacoustic waves from within the irradiated tissue. The RF heating must be rapid enough to produce thermoacoustic waves of sufficient bandwidth to localize the energy deposition. A wideband ultrasonic transducer is then employed to detect the thermoacoustic waves, which carry information about the spatial distribution of absorbed energy. An image reconstruction algorithm is then used to form an image [33],[38],[39].
The theory associated with RF-induced thermoacoustics can be summarized as follows: to excite the thermoacoustic process, a pulse-modulated RF source is used to transmit RF energy into the body. The underlying or carrier frequency of the RF pulse is responsible for depositing energy deep into the tissue – this is the same physical mechanism that leads to the SAR problem of high field MRI. However, it is the modulating envelope of the RF pulse that determines the bandwidth of the thermoacoustic signal. We propose an RF pulse width in the range of several microseconds with rise time on the order of 1μs. This would lead to thermoacoustically-generated signals with frequencies in the range of a few hundred kilohertz, which would propagate with little attenuation through brain tissue and skull, yet have wavelengths small enough to resolve centimeter-scale variations in SAR. Because the RF pulses used to generate a thermoacoustic SAR map would be much shorter than typical pulses used in MR imaging, the energy deposited by these interrogation pulses would be a small fraction of that deposited by a normal MRI scan.
RF absorption
The amount of RF energy deposited in the tissue is quantified by the SAR [W/kg], which is defined as
| (1) |
where E(r,t) is the electric field vector (V/m) at a location r, ρ(r) is the mass density (kg/m3) and σe(r) is the conductivity (S/m).
Under thermal confinement conditions, i.e. the RF pulse length being short (on the order of microseconds) compared to the thermal relaxation time (on the order of seconds, based on a thermal diffusivity of water of 0.143 mm2/s), the amount of electromagnetic energy deposited in the tissue as heat per unit volume per unit time may be written as the product of a space-dependent term for the electromagnetic energy per unit volume H(r) and a unitless time-dependent term I(t), which is the normalized envelope of the RF pulse:
| (2) |
This deposited electromagnetic energy per unit volume per unit time converts to SAR as follows:
| (3) |
H̃(r) and represent the spatial-only variations of H(r, t) and SAR(r, t) under thermal confinement conditions.
Acoustic Wave Propagation
From fluid dynamics, the coupled differential equations for temperature and pressure are given as follows:
| (4) |
| (5) |
Where γ is the specific heat ratio, α is the pressure expansion coefficient, K is the thermal conductivity, cp is the heat capacity, ρ is the density, vs is the speed of sound, t is time, and H is the energy per unit volume and time deposited by the RF source [33].
If the duration of the RF pulse is much shorter than the thermal diffusion time (microseconds vs seconds – this is the thermal confinement condition), thermal diffusion during the pulse can be neglected [33], and the thermal diffusivity term can be set to zero. In soft tissue this criterion is easily satisfied [40],[41]. The two equations can then be decoupled and hence greatly simplified. The time derivative of (4) can then be substituted into (5) to give a wave equation for the thermoacoustic problem:
| (6) |
where the thermodynamic relation α= ρβvs2/γ has been used, with β being the isobaric thermal volume expansion coefficient.
Using (3), the wave propagation equation using SAR as the excitation term becomes:
| (7) |
The thermoacoustic pressure p is thus the solution to the inhomogeneous wave equation. The rapid temperature oscillation due to absorbed power converts every point in space to a pulsating sphere, which becomes the excitation [38]. One key feature of this concept is the linearity of the excited instantaneous pressure with respect to the SAR at each specific location. Note that the time derivative of the RF pulse drives the instantaneous pressure wave, and it is therefore important to achieve a high RF pulse slew rate in order to increase the amplitude of the resulting pressure, and hence the sensitivity of the thermoacoustic SAR mapping process. There may be several factors that limit the RF pulse rise time, such as coil Q, other RF front end band-limiting components, and RF sampling rate; however, having analyzed these factors, we believe that a minimum rise time below 1μs is achievable. A rise time of 1μs would yield a thermoacoustic signal-to-noise ratio of at least 20 dB (see more detailed sensitivity calculation below) which is sufficient to yield good quality thermoacoustic SAR maps.
Methods
Feasibility study in simulation
We studied the feasibility of the proposed technique via simulation, using a human head model with acoustically uniform tissue properties, and an RF pulse of carrier frequency 298 MHz (i.e. 7T). The concept was studied using a combination of two simulation packages; the RF analysis was carried out using a finite difference time domain electromagnetic simulation package (SEMCAD, ZMT GmbH, Zürich, Switzerland), while a finite element multi-physics simulation package (COMSOL, COMSOL Inc., Burlington, MA, USA) was used for the thermoacoustic analysis. The three-dimensional SAR distribution throughout the human head was computed in SEMCAD, using a standard head-sized birdcage coil model and a member of the Virtual Family (Ella, IT'IS, Zürich, Switzerland). This 3D SAR pattern was subsequently registered to an IEC/CENELEC SAM head model, which is available for use in COMSOL. This SAR pattern then served as the spatial excitation distribution for the thermoacoustic simulation according to Eq. (7). The head was modeled as a uniform material of constant speed of sound (1500 m/s), volume expansion coefficient (30 ppm/K) and heat capacity (3700 J/(kg·K)). Given that the full 3D analysis problem becomes computationally very large, calculations were limited to three orthogonal 2-dimensional planes (central axial, sagittal, and coronal planes). An extension to full 3D should be straightforward but was not practical for this initial proof-of-concept work. The time-domain acoustic pressure signals were recorded, mimicking a set of ultrasonic transducers by simulation, in the three central axial, sagittal, and coronal planes, respectively. In each of these three planes, 32 recording locations were distributed at equal angular increment around the head boundary. Spatial maps of the SAR distribution were then reconstructed from these 32 time-domain signals using a delay-and-sum (DAS) algorithm [33],[38] implemented in Matlab (The MathWorks, Natick, MA). In this basic reconstruction algorithm, the signal acquired at each detection point is delayed by the appropriate time of flight with regard to the voxel to be reconstructed. Subsequently, all signals were summed to generate the reconstructed SAR value at the respective voxel.
Experimental proof of concept
An in vitro experimental proof of concept was carried out using a prototype thermoacoustic imaging system (Fig. 1a). This system operates at an RF frequency of 434 MHz and was therefore suitable for mimicking the field variations that we would observe in a human UHF MR scanner, as 434 MHz corresponds to the proton Larmor frequency at a field strength of approximately 10T. The system consisted of two RF channels with a peak power of 5 kW each, exciting a standing wave electromagnetic field pattern by means of two horn antennas located on opposite sides of a polycarbonate water tank. The inside dimensions of the tank were 4 in × 5 in × 8 in (W×L×H) with a wall thickness of 0.5 in. A pulse train with 70 ns pulse rise time, 180 ns pulse width, and pulse repetition rate of 2 kHz was used. Thermoacoustic signals were then acquired using a 128-element ultrasound transducer array (using a 3-dB bandwidth of 2 MHz, centered at 3 MHz), situated at the right-hand side of the tank, as shown in Fig. 3. Reconstruction was performed using a backprojection algorithm. Time information between the RF pulse and the ultrasonic detection is not used, and the RF pulse is assumed to illuminate the whole region of interest at the same instant. The backprojection process differs from CT in important ways. Unlike in x-ray CT, acoustic transit time defines the radius of a curved ray-sum sample of data, and the locations of the transducers define unique views [42]. In principle, the time series of data from the plurality of detector locations constitute sufficient data for image reconstruction from a single RF pulse. In practice, multiple pulses and multiple detector locations are used to improve sampling and signal-to-noise ratio.
Fig. 1.

(a) Experimental thermoacoustic system available for proof of concept, (b) phantom construction: saline concentrations in phantom I: 2.25% in all tubes; in phantom II: from center to outer edge: 5%, 3%, 2.25%, 1.25%.
Fig. 3.
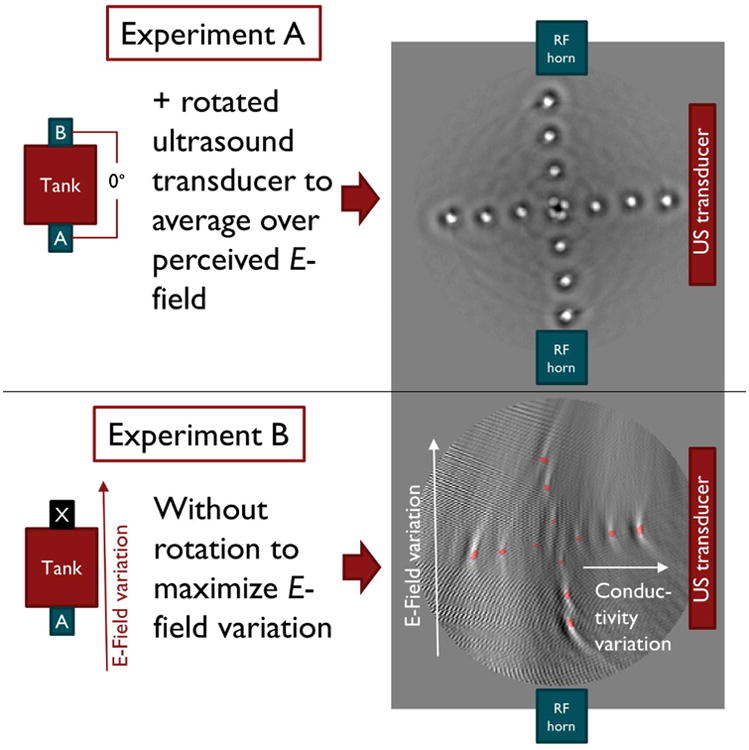
Experimental setup and thermoacoustic images for (A) constant and (B) spatially varying conductivity and E-field. In experiment A the E-field and conductivity variations are kept constant by using two RF horn antennas producing a standing wave pattern and by introducing a rotation of the phantom through the field of view. In experiment B we introduce E-field and conductivity variations on purpose to mimic SAR variations by eliminating one horn antenna and the rotation through the field of view. The different appearance of experiments A and B is attributed to the missing rotation of the phantom in experiment B. Red dots in experiment B denote the saline tube positions.
In order to prove experimental feasibility of in vivo SAR mapping, two experiments were carried out (Fig. 3) using spatially constant (experiment A) and spatially varying (experiment B) SAR distributions. These two conditions were achieved using spatially constant conductivity and E-field (experiment A) and spatially varying conductivity and E-field (experiment B). To this end we constructed two phantoms that each consisted of a single-row grid of saline tubes, equally spaced at a distance of 5 mm in a 3D-printed holder (see Fig. 1b): phantom I had inclusions of constant conductivity (using four saline tubes of equal 5% saline concentration), and phantom II had inclusions of varying conductivity (saline concentrations of 5%, 3%, 2.25%, 1.25%, from edge to center). Constant (experiment A) vs spatially varying (experiment B) E-fields were achieved by exciting both or only one of the two horn antennas, respectively. The “constant” E-field in experiment A is not strictly spatially constant as it is a standing wave pattern created by the RF fields of the two horn antennas. We estimated an SAR variation of 2.4 dB between the central and the outermost saline tube based on the resonant field fall-off for a wavelength of 8 cm in water. Thus, to further improve the constant E-field pattern for experiment A, the phantom was rotated around the center of the field of view (FOV) to spatially average its E-field exposure. Phantom images were acquired with the row of tubes pointing in each of the four principal directions to cover a wide range of field variations; resulting images were summed and yielded a crosshair pattern of tubes. (Fig. 3, top) The average image value for each tube was then determined. All image values were adjusted for constant background image noise and then normalized to the SAR value of the central tube to give values for the experimental SAR variations in all tubes. These values were then compared to the theoretical SAR. In order to produce this value for local SAR according to equation (1), the E-field was measured for both experiment A and B. The E-field amplitudes were measured using a coaxial field probe connected to an oscilloscope, consisting of a voltage probe connected to a 50 Ω attenuator. The requirement for this probe was to evaluate the field variation within the tank and did not yield absolute numbers for the E-field strength. The voltages observed were consistent with the values expected from theory for the forward power used in the horns.
Results
Simulation study
Fig. 2 shows a comparison of the original and reconstructed thermoacoustic SAR patterns and good agreement is obtained in all three planes. The agreement is excellent: the standard deviation of the SAR errors is 0.03 W/kg in the axial plane (a 4.2% deviation from the average axial SAR), 0.18 W/kg in the sagittal plane (7.2% of the mean sagittal SAR), and 0.14 W/kg in the coronal plane (8.4% of the mean coronal SAR). Peak local SAR values for simulation and experiment were 1.89 W/kg vs. 1.86 W/kg in the axial plane, 9.32 W/kg vs. 9.00 W/kg in the sagittal plane, and 3.29 W/kg vs 4.05 W/kg in the coronal plane.
Fig. 2.
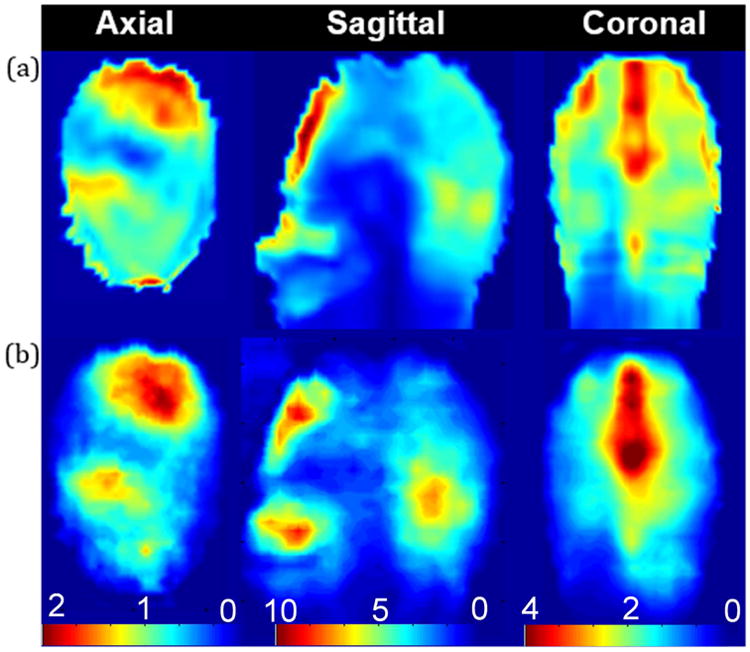
(a) Original 2D SAR pattern in W/kg, (b) 2D SAR pattern after reconstruction from thermoacoustic data. Qualitative agreement is reached in this first proof of concept based on a highly similar SAR distribution in all three planes. The standard deviation is 0.02 W/kg in the axial plane, 0.19 W/kg in the sagittal plane, and 0.12 W/kg in the sagittal plane. Quantitative agreement is clear from the matched overall absolute SAR. Peak local SAR values for simulation and experiment are 1.89 W/kg vs. 1.86 W/kg in the axial plane, 9.32 W/kg vs. 9.00 W/kg in the sagittal plane, and 3.29 W/kg vs 4.05 W/kg in the coronal plane.
Sensitivity analysis
In order to estimate the sensitivity of the experiment, the acoustic sound pressure levels at the ultrasound transducers were calculated for a SAR value of 0.25 W/kg. The instantaneous pressure rise at a location within tissue according to (7) is given by
| (8) |
The amplitude of ∂I(t)/∂t can be estimated from the available bandwidth of the RF pulse. The 3-dB bandwidth of the utilized RF transmitter is given by
| (9) |
which yields a bandwidth of 300 kHz for an RF coil with a Q-factor of 10, corresponding to a maximum rise time of 1 us.
Assuming a rise time of 1μs (which we have determined to be achievable without limitation by coil Q, other front-end components, RF sampling considerations), the instantaneous pressure level at the absorber boundaries can then be calculated, using values for β = 3*10−4 K−1 as the thermal expansion coefficient for soft tissue, cp = 4180 J/(kg·K) as the specific heat capacity of tissue, a tissue density of ρ = 1000 kg/m3 and a SAR deposition of 0.25 W/kg. The calculation yields an instantaneous pressure of 20 Pa. This then forms our estimate for minimum pressure expected in our experiment.
We now estimate the minimum SNR for our thermoacoustic SAR mapping experiment. From [43], the thermal noise (i.e., mean square noise pressure) is given by
Given a body temperature T = 310 K and a speed of sound in tissue c = 1540 ms−1, the expected mean square noise pressure is 1.4 × 10−9 Pa2 Hz−1. In the application we describe here, we anticipate a detection bandwidth of ca. 200 kHz, centered around 200 kHz, yielding an expected root mean square noise pressure of 0.0167 Pa. Thus, the expected thermal noise floor is approximately 62 dB below the predicted peak signal pressure of 20 Pa. This potential signal to noise ratio is an upper bound, and will not be realized in a practical system due to the relatively small total solid angle presented by the ultrasonic transducers (ca. -20 dB), attenuation in the intervening tissues (ca. -15 dB), transduction efficiency of the transducers and noise figure of the receiver electronics (ca. -5 dB), an estimated net SNR of approximately 22 dB.
Experimental proof of concept
The thermoacoustic images resulting from the two in vitro experiments are shown in Fig. 3. Table I shows the corresponding image values for experiment A in comparison to the theoretical relative SAR, with % errors shown. The central area, in which the phantom is placed, measures approximately 30 mm in diameter, and the measured field variations (expressed as standard deviations) are 20.3% in the x-direction and 6.9% in the y-direction. It is seen that in experiment A, SAR errors are low, confirming the uniformity of direct thermoacoustic SAR mapping over the field of view. Remaining errors are attributed to variations in the E-field due to field amplitude variations within the standing wave pattern. Experiment B represents a more realistic scenario; results in Fig. 4 shows good correlation between theoretical and experimental SAR values (r2 = 0.52 for SAR in horizontal row and r2 = 0.85 for SAR in vertical row).
Table I. SAR Values for Experiment A.
| pos. (mm) | SAR in Horizontal Row (theory) | SAR in Horizontal Row (exp) | % err | SAR in Vertical Row (theory) | SAR in Vertical Row (exp) | % err |
|---|---|---|---|---|---|---|
| −15 | 1.00 | 1.01 | 1 | 1.00 | 0.87 | 13 |
| −10 | 1.00 | 0.99 | 1 | 1.00 | 0.85 | 15 |
| −5 | 1.00 | 0.95 | 5 | 1.00 | 0.85 | 15 |
| 0 | 1.00 | 1.00 | 0 | 1.00 | 1.00 | 0 |
| 5 | 1.00 | 0.98 | 2 | 1.00 | 0.87 | 13 |
| 10 | 1.00 | 1.11 | 11 | 1.00 | 1.09 | 9 |
| 15 | 1.00 | 1.09 | 9 | 1.00 | 1.13 | 13 |
Fig. 4.
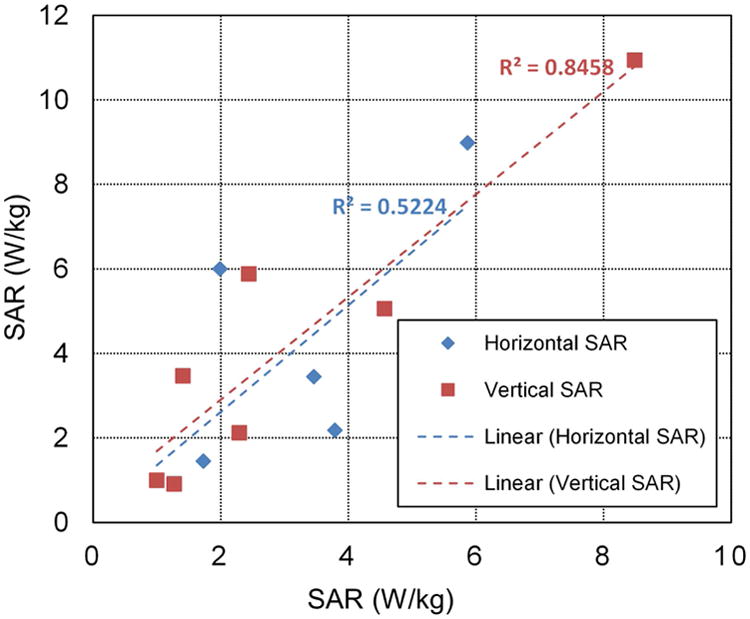
Theoretical vs. experimental SAR values for experiment B.
The different appearance of images in experiment A and B can be explained as follows. To further improve the constant E-field pattern for experiment A, the phantom was rotated around the center of the field of view to spatially average its E-field exposure. This rotation did not occur for experiment B where we desired a strongly varying E-field pattern in order to emulate a highly varying local SAR pattern.
In experiment B, i.e. without rotation, the placement of the 128-element transducer array on one side of the tank resulted in a higher resolution in radial direction as opposed to azimuthal direction as seen from the transducer, since some parts of the phantom were more distant from the transducer than others. This in turn led to blurring of the reconstructed image. In experiment A, i.e. with a rotation of the phantom and a corresponding adaptation of the reconstruction algorithm, this “blurring” effect was mitigated as each azimuthal position reached close proximity to the transducer once throughout the rotation.
This experimental proof of concept comprising experiments A and B was carried out using an existing thermoacoustic imaging platform and we were able to make use of its inherent capabilities by adapting the platform to mimic a varying SAR pattern and its reconstruction. In an actual prototype that is integrated within an MRI system, the ultrasound transducers would be arranged and spaced uniformly around the head and the blurring effects seen in Fig. 3 would be minimized.
Discussion
The presented simulation study suggests the feasibility of thermoacoustic SAR mapping. The two quantities relevant for ultrasonic detection sensitivity are the pulse energy needed for heating tissue (or in other words for generating the SAR(r) excitation term) and the pulse rise time (the ∂I(t)/∂t excitation term), which determines the initial instantaneous pressure rise at each point. The former is mostly limited by the peak power of the RF system due to the short pulse thermal confinement requirement. The RF transmitter on most 7T scanners can deliver a peak power of 8 kW, which in a non-attenuated thermoacoustic experiment would yield an ultrasound pressure of approximately 20 Pa and an SNR of approximately 62 dB. The required pulse modulation in an MRI scanner can be carried out using a separate auxiliary digital synthesizer and/or pulse generator module. This preliminary study used acoustically homogeneous tissue parameters and tissue expansion coefficients. Advanced post-processing techniques readily available from thermo/photoacoustic imaging can be applied to overcome heterogeneity and other non-idealities not described by the proposed model. The human skull would be a significant challenge for diagnostic thermoacoustic imaging, where mm-scale resolution is desired, in which case a much higher ultrasound frequency would be required (e.g. >1 MHz). In our proposed lower resolution SAR mapping scenario, we expect that the skull will not pose a significant problem, given the use of ultrasound frequencies in the range of 200 kHz [44]. This relatively low frequency can be selected to overcome ultrasound waveform aberration and absorption by the human skull, yet should still permit spatial resolution in the range of 1.5 cm in the resulting SAR maps. The spatial resolution of the resulting thermoacoustic image is also defined by the stress confinement criterion, which is proportional to the speed of sound and the excitation period [41]. In the example of our study, we achieved resolutions on the order of one centimeter, which is detailed enough for the creation of a 1g-averaged local SAR map and more than adequate for a 10g-averaged local SAR map. In order to obtain the SAR pattern that would be delivered to the patient during an MR exam, the same coil that is used for the imaging experiment must be selected. Typical MR coils at 7T have loaded Q-factors on the order of 30-40, and therefore will not prevent us from achieving thermoacoustic pulse risetimes of 1μs.
Our aim was to demonstrate the applicability of the proposed thermoacoustic technique to in vivo MRI; we therefore used simulations incorporating realistic human brain models with accurate tissue representation. Since implementing the proposed technology into an MRI system would be challenging, we carried out a simpler proof-of-concept experimental using an existing thermoacoustic imaging system to validate the findings from the simulations. This strategy allowed us to experimentally validate our direct SAR mapping concept before tackling secondary system engineering problems. Future work will report on the successful integration of this technology into an MRI system.
Reception of the thermoacoustic signals and image reconstruction is straightforward in most regions of the body. In the head, the skull bone attenuates the ultrasound signal and its shape causes wavefront aberrations that, if not accommodated, will degrade image quality. Acoustic windows in the skull that are well known from transcranial Doppler can be used in the case of head imaging. For example, the windows present in each temporal bone allow easy placement of two ultrasound transducers to afford a view of most of the interior of the skull. Focused transducers could be physically scanned to probe the interior of the head, one ray at a time; alternatively, multiple-element transducers (with ca. 16 to 1024 elements) and phased-array image reconstruction techniques could be used to reconstruct an image of an entire slice or volume at once, in a manner similar to conventional ultrasound imaging. The ultrasound transducers required for an MRI-compatible system need to be non-magnetic and electrostatically shielded; such transducers exist and have been found to be sufficient to permit operation within the high magnetic field environment.
The use of multiple-element acoustic transducers permits data acquisition and image reconstruction without the need for physical scanning and repeated RF pulses. In principle, with multiple receiver elements, only a single one-microsecond RF pulse is required to produce all the data required to compute an image. However, with the RF power available, practical systems will likely require averaging of multiple pulses. The RF pulses employed for thermoacoustic imaging are typically one microsecond or less in duration, far shorter than a typical imaging pulse. It is expected that the average power and total RF energy deposited in the course of a thermoacoustic imaging SAR scan will remain far less than the power levels commonly used for MR imaging.
Note also that thermoacoustic signal generation in water or tissue has a temperature dependence in addition to a SAR dependence, i.e. the measured ultrasound pressure increases with temperature. Though not directly relevant to the technique proposed here, this is potentially an effect that could be exploited for thermal dose monitoring.
The proposed method represents a radically different approach to current heuristic methods, in which local SAR is estimated from a combination of electromagnetic modeling with measured B1+-fields, and offers a direct and experimental approach to mapping local SAR without the need for modeling.
Conclusion
A novel thermoacoustic method for in vivo mapping of local SAR patterns in MRI has been proposed and verified in simulation and experimental proof of concept has been completed. Estimation of key parameters that would be used in a system scaled-up for used within a human MRI system predicts feasibility of in vivo thermoacoustic SAR mapping.
Acknowledgments
The authors would like to acknowledge research support from NSERC Canada, GE Healthcare, NIH P41 EB015891.
Grant sponsor: NIH P41 EB015891.
Grant sponsor: NSERC. Grant sponsor: GE Healthcare.
References
- 1.Collins CM, Smith MB. Calculations of B(1) distribution, SNR, and SAR for a surface coil adjacent to an anatomically-accurate human body model. Magn Reson Med. 2001;45(4):692–9. doi: 10.1002/mrm.1092. [DOI] [PubMed] [Google Scholar]
- 2.Hoult DI, Phil D. Sensitivity and power deposition in a high-field imaging experiment. J Magn Reson Imaging. 2000;12(1):46–67. doi: 10.1002/1522-2586(200007)12:1<46::aid-jmri6>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 3.Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med. 2004;51(4):775–84. doi: 10.1002/mrm.20011. [DOI] [PubMed] [Google Scholar]
- 4.Katscher U, Börnert P, Leussler C, van den Brink JS. Transmit SENSE. Magn Reson Med. 2003;49(1):144–50. doi: 10.1002/mrm.10353. [DOI] [PubMed] [Google Scholar]
- 5.Martin A, Schiavi E, Eryaman Y, Herraiz JL, Gagoski B, Adalsteinsson E, Wald LL, Guerin B. Parallel transmission pulse design with explicit control for the specific absorption rate in the presence of radiofrequency errors. Magn Reson Med. 2016;75(6):2493–504. doi: 10.1002/mrm.25820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Graesslin I, Vernickel P, Börnert P, Nehrke K, Mens G, Harvey P, Katscher U. Comprehensive RF safety concept for parallel transmission MR. Magn Reson Med. 2015;74(2):589–98. doi: 10.1002/mrm.25425. [DOI] [PubMed] [Google Scholar]
- 7.Guérin B, Setsompop K, Ye H, Poser BA, Stenger AV, Wald LL. Design of parallel transmission pulses for simultaneous multislice with explicit control for peak power and local specific absorption rate. Magn Reson Med. 2015;73(5):1946–53. doi: 10.1002/mrm.25325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Guérin B, Gebhardt M, Cauley S, Adalsteinsson E, Wald LL. Local specific absorption rate (SAR), global SAR, transmitter power, and excitation accuracy trade-offs in low flip-angle parallel transmit pulse design. Magn Reson Med. 2014;71(4):1446–57. doi: 10.1002/mrm.24800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pendse M, Rutt BK. IMPULSE: A Generalized and Scalable Algorithm for Joint Design of Minimum SAR Parallel Transmit RF Pulses. Proc Int Soc Magn Res. 2015;23:0543. doi: 10.1002/mrm.27589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Seifert F, Wübbeler G, Junge S, Ittermann B, Rinneberg H. Patient safety concept for multichannel transmit coils. J Magn Reson Imaging. 2007;26(5):1315–21. doi: 10.1002/jmri.21149. [DOI] [PubMed] [Google Scholar]
- 11.Vaughan JT, Snyder CJ, DelaBarre LJ, Bolan PJ, Tian J, Bolinger L, Adriany G, Andersen P, Strupp J, Ugurbil K. Whole-body imaging at 7T: preliminary results. Magn Reson Med. 2009;(1):244–8. doi: 10.1002/mrm.21751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hand JW, Lau RW, Lagendijk JJ, Ling J, Burl M, Young IR. Electromagnetic and thermal modeling of SAR and temperature fields in tissue due to an RF decoupling coil. Magn Reson Med. 1999;42(1):183–92. doi: 10.1002/(sici)1522-2594(199907)42:1<183::aid-mrm24>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- 13.Gandhi OP, Chen XB. Specific absorption rates and induced current densities for an anatomy-based model of the human for exposure to time-varying magnetic fields of MRI. Magn Reson Med. 1999;41(4):816–23. doi: 10.1002/(sici)1522-2594(199904)41:4<816::aid-mrm22>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 14.Simunić D, Wach P, Renhart W, Stollberger R. Spatial distribution of high-frequency electromagnetic energy in human head during MRI: numerical results and measurements. IEEE Trans Biomed Eng. 1996;43(1):88–94. doi: 10.1109/10.477704. [DOI] [PubMed] [Google Scholar]
- 15.Neufeld E, Fuetterer M, Murbach M, Kuster N. Rapid method for thermal dose-based safety supervision during MR scans. Bioelectromagnetics. 2015;36(5):398–407. doi: 10.1002/bem.21919. [DOI] [PubMed] [Google Scholar]
- 16.IEC 60601-2-33
- 17.Eichfelder G, Gebhardt M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn Reson Med. 2011;66(5):1468–76. doi: 10.1002/mrm.22927. [DOI] [PubMed] [Google Scholar]
- 18.Martin A, Schiavi E, Eryaman Y, Herraiz JL, Gagoski B, Adalsteinsson E, Wald LL, Guerin B. Parallel transmission pulse design with explicit control for the specific absorption rate in the presence of radiofrequency errors. Magn Reson Med. 2016;75(6):2493–504. doi: 10.1002/mrm.25820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wu X, Schmitter S, Auerbach EJ, Ugurbil K, Van de Moortele PF. A generalized slab-wise framework for parallel transmit multiband RF pulse design. Magn Reson Med. 2016;75(4):1444–56. doi: 10.1002/mrm.25689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Boulant M, Wu X, Adriany G, Schmitter S, Ugurbil K, Van de Moortele PF. Direct control of the temperature rise in parallel transmission by means of temperature virtual observation points: Simulations at 10.5 Tesla. Magn Reson Med. 2016;75(1):249–56. doi: 10.1002/mrm.25637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Guerin B, Setsompop K, Ye H, Poser BA, Stenger AV, Wald LL. Design of parallel transmission pulses for simultaneous multislice with explicit control for peak power and local specific absorption rate. Magn Reson Med. 2015;73(5):1946–53. doi: 10.1002/mrm.25325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Oh S, Ryu YC, Carluggio G, Sica CT, Collins CM. Measurement of SAR-induced temperature increase in a phantom and in vivo with comparison to numerical simulation. Magn Reson Med. 2014;71(5):1923–31. doi: 10.1002/mrm.24820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Katscher U, Voigt T, Findeklee C, Vernickel P, Nehrke P, Dössel O. Determination of electrical conductivity and local SAR via B1 mapping. IEEE Trans Med Imaging. 2009;28(9):1365–74. doi: 10.1109/TMI.2009.2015757. [DOI] [PubMed] [Google Scholar]
- 24.Zhang X, Schmitter S, Van de Moortele PF, Lui J, He B. From complex B(1) mapping to local SAR estimation for human brain MR imaging using multi-channel transceiver coil at 7T. IEEE Trans Med Imaging. 2013;32(6):1058–67. doi: 10.1109/TMI.2013.2251653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sbrizzi A, Hoogduin H, Lagendijk JJ, Luijten P, Sleijpen GL, van den Berg CA. Fast design of local N-gram-specific absorption rate-optimized radiofrequency pulses for parallel transmit systems. Magn Reson Med. 2012;67(3):824–34. doi: 10.1002/mrm.23049. [DOI] [PubMed] [Google Scholar]
- 26.Etezadi-Amoli M, Stang P, Kerr A, Pauly J, Scott G. Controlling radiofrequency-induced currents in guidewires using parallel transmit. Magn Reson Med. 2015;74(6):1790–802. doi: 10.1002/mrm.25543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Etezadi-Amoli M, Stang P, Kerr A, Pauly J, Scott G. Interventional device visualization with toroidal transceiver and optically coupled current sensor for radiofrequency safety monitoring. Magn Reson Med. 2015;73(3):1315–27. doi: 10.1002/mrm.25187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ellenor CW, Stang PP, Etezadi-Amoli M, Pauly JM, Scott GC. Offline impedance measurements for detection and mitigation of dangerous implant interactions: an RF safety prescreen. Magn Reson Med. 2015;73(3):1328–29. doi: 10.1002/mrm.25202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Overall WR, Pauly JM, Stang PP, Scott GC. Ensuring safety of implanted devices under MRI using reversed RF polarization. Magn Reson Med. 2010;64(3):823–33. doi: 10.1002/mrm.22468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ghanouni P, Pauly KB, Elias WJ, Henderson J, Sheehan J, Monteith S, Wintermark M. Transcranial MRI-Guided Focused Ultrasound: A Review of the Technologic and Neurologic Applications. AJR Am J Roentgenol. 2015;205(1):150–9. doi: 10.2214/AJR.14.13632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Foster KR, Finch ED. Microwave Hearing: Evidence for Thermoacoustic Auditory Stimulation by Pulsed Microwaves. Science. 1974;185(4147):256–8. doi: 10.1126/science.185.4147.256. [DOI] [PubMed] [Google Scholar]
- 32.Kruger RA, Kopecky KK, Aisen AM, Reinecke DR, Kruger GA, Kiser WL., Jr Thermoacoustic CT with radio waves: a medical imaging paradigm. Radiology. 1999;211(1):275–8. doi: 10.1148/radiology.211.1.r99ap05275. [DOI] [PubMed] [Google Scholar]
- 33.Guo B, et al. Photoacoustic Imaing and Spectroscopy. Vol. 165. CRC Press; 2009. [Google Scholar]
- 34.Winkler SA, Picot PA, Thornton MM, Rutt BK. Direct SAR Mapping by Thermoacoustic Imaging: A Feasibility Study. Proc Int Soc Magn Res. 2014;21:4898. doi: 10.1002/mrm.26517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Winkler SA, Picot PA, Thornton MM, Rutt BK. Direct SAR Mapping by Thermoacoustic Imaging: Experimental Proof-of-Concept. Proc Int Soc Magn Res. 2014;22:3234. [Google Scholar]
- 36.Winkler SA, Picot PA, Thornton MM, Rutt BK, inventors. United States patent US 14/704369, pending. Method and System for Estimating the Specific Absorption Rate of a Tissue Region Prior to a Magnetic Resonance Imaging Scan. 2015 May 05;
- 37.Bell AG. On the Production and Reproduction of Sound by Light. Am J Sci. 1880;20:305–24. [Google Scholar]
- 38.Zhu G, Popovic M, Fang Q. Microwave-Induced Thermoacoustics: Assisting Microwave Tomography. IEEE Trans Magn. 2009;45(3):1645–7. [Google Scholar]
- 39.Kirshin E, Oreshkin B, Zhu GK, Popovic M, Coates M. Microwave Radar and Microwave-Induced Thermoacoustics: Dual-Modality Approach for Breast Cancer Detection. IEEE Trans Biomed Eng. 2013;60(2):354–60. doi: 10.1109/TBME.2012.2220768. [DOI] [PubMed] [Google Scholar]
- 40.Krumholz A, Vanvickle-Chavez SJ, Yao J, Leming TP, Gillanders WE, Wang LVJ. Photoacoustic microscopy of tyrosinase reporter gene in vivo. Biomed Opt. 2011;16(8):080503. doi: 10.1117/1.3606568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Xia J, Yao J, Wanh LV. Photoacoustic tomography: principles and advances. Progress In Electromagnetics Research. 2014;147:1–22. doi: 10.2528/pier14032303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang Y, Xing D, Zeng Y, Chen Q. Photoacoustic imaging with deconvolution algorithm. Phys Med Biol. 2004;49(14):3117–24. doi: 10.1088/0031-9155/49/14/006. [DOI] [PubMed] [Google Scholar]
- 43.Mellen RH. The thermal-noise limit in detection of underwater acoustic signals. J Acoust Soc Am. 1952;24(5):478–80. [Google Scholar]
- 44.De Souza-Daw T, Lewis P, Junor P, Stewart R, Maller J, Manasseh R. Ultrasound detection of the skull-brain interface: A phantom study. 2012 International Conference on Control, Automation and Information Sciences (ICCAIS) 2012;2012:181–6. [Google Scholar]


