Abstract
As a subtype of idiopathic generalized epilepsies, absence epilepsy is believed to be caused by pathological interactions within the corticothalamic (CT) system. Using a biophysical mean-field model of the CT system, we demonstrate here that the feed-forward inhibition (FFI) in thalamus, i.e., the pathway from the cerebral cortex (Ctx) to the thalamic reticular nucleus (TRN) and then to the specific relay nuclei (SRN) of thalamus that are also directly driven by the Ctx, may participate in controlling absence seizures. In particular, we show that increasing the excitatory Ctx-TRN coupling strength can significantly suppress typical electrical activities during absence seizures. Further, investigation demonstrates that the GABAA- and GABAB-mediated inhibitions in the TRN-SRN pathway perform combination roles in the regulation of absence seizures. Overall, these results may provide an insightful mechanistic understanding of how the thalamic FFI serves as an intrinsic regulator contributing to the control of absence seizures.
Keywords: absence seizures, spike and wave discharges, corticothalamic network, feed-forward inhibition, mean-field model
Introduction
Absence epilepsy is a common subtype of idiopathic generalized epilepsies and mainly occurs in the childhood years (Durón et al., 2005; Tolaymat et al., 2015). This chronic neurological brain disorder is characterized by recurrent absence seizures, often leading to sudden periods of impaired consciousness (Crunelli and Leresche, 2002). During its ictal period, the bilaterally synchronous 2–4 Hz spike and wave discharges (SWDs) can be observed on the electroencephalogram (EEG) of patients, which are regarded as the electrophysiological hallmark of absence seizures (Crunelli and Leresche, 2002). Despite that onset mechanisms of absence seizures still remain debated, accumulating evidence indicates that the emergence of 2–4 Hz SWDs during absence seizures critically depends on cerebral cortex (Ctx) and thalamus (Blumenfeld, 2005; Bazhenov et al., 2008; Lytton, 2008; Avoli, 2012; Holt and Netoff, 2013; Depaulis et al., 2016). It has been postulated that properly disrupting abnormal interactions within corticothalamic (CT) system can cause SWD suppression, thus preventing absence seizures.
Previous studies have shown that direct neuronal modulations within the CT system may destabilize the pathological oscillations during absence seizures (Suffczynski et al., 2004; Lüttjohann and van Luijtelaar, 2013; Paz et al., 2013; Taylor et al., 2014, 2015; Fan et al., 2015; Liu et al., 2016). The most frequently reported direct stimulation site is the thalamus. Past experimental evidence has suggested that both closed-loop optogenetic control of thalamus and high frequency thalamic stimulation can dramatically inhibit the occurrence of epileptic seizures (Lüttjohann and van Luijtelaar, 2013; Paz et al., 2013). In addition to these direct interventions, indirect neuronal modulations from several external brain regions have also been identified to be effective in controlling absence seizures (Deransart et al., 1998; Paz et al., 2007; Chen et al., 2014, 2015; Kros et al., 2015a,b). As an intermediate bridge between the Ctx and thalamus, the basal ganglia (BG) are widely considered as an ideal modulation site to prevent absence seizures (Depaulis et al., 1994; Deransart et al., 1998; Paz et al., 2007; Luo et al., 2012). This hypothesis is supported by both experimental and computational evidence, showing that the BG might multiply control absence seizures through the GABAergic nigro-thalamic and pallido-cortical pathways (Deransart et al., 1998; Paz et al., 2005, 2007; Luo et al., 2012; Chen et al., 2014, 2015; Hu et al., 2015; Hu and Wang, 2015). Besides the BG, another ideal candidate to modulate abnormal CT oscillations is the cerebellar nuclei (CN; Kros et al., 2015a,b). Using a mouse model of absence epilepsy, a recent study has found that increasing the frequency and regularity of CN neuronal firing can significantly reduce the occurrence of SWDs and terminate absence seizures (Kros et al., 2015b).
Moreover, recent intensive statistical investigations on neuronal connectivity have revealed that the brain contains some recurring nontrivial patterns of interconnected neurons, termed as “microcircuit motifs” (Sporns and Kötter, 2004; Womelsdorf et al., 2014; Paz and Huguenard, 2015). Interestingly, these microcircuit motifs are found to be linked to each other in a way that does not spoil the independent function of each microcircuit motif, thus postulating to work as basic building blocks of nervous systems and perform critical functional roles in regulating neurodynamics at the circuit level (Sporns and Kötter, 2004; Li, 2008; Guo and Li, 2009; Potjans and Diesmann, 2014; Womelsdorf et al., 2014; Paz and Huguenard, 2015; Yuste, 2015). As one of the most significant microcircuit motifs, the feed-forward inhibition (FFI) has been observed in multiple brain regions, including the neocortex, thalamus, hippocampal, and basal ganglia (Sloviter, 1991; Sun et al., 2005; Assisi et al., 2007; Tepper et al., 2008; Kee et al., 2015; Paz and Huguenard, 2015; Khubieh et al., 2016; Lindahl and Hellgren Kotaleski, 2016). Emerging evidence has suggested that significant loss of FFI in the brain can cause an imbalance between excitation and inhibition of neurons toward excessive excitation (Paz and Huguenard, 2015). Such imbalanced excitation-inhibition might lead to hypersynchronous neural firing activities that are commonly involved in various types of epileptic seizures.
Neurons in the thalamic reticular nucleus (TRN) receive excitatory signals from the Ctx, and send both GABAA- and GABAB-mediated inhibitory signals to the specific relay nuclei (SRN) of thalamus, which are also driven by the excitatory signals from the Ctx. Anatomically, these neural projections together form the so-called thalamic FFI microcircuit motif (Pinault, 2004; Paz and Huguenard, 2015). Although past experimental studies have suggested that restoring cortical excitation in TRN neurons may prevent absence seizures (Paz et al., 2011; Paz and Huguenard, 2015), so far the detailed biophysical mechanisms of SWD suppression induced by this thalamic FFI is still poorly understood. In the present study, we utilize a mean-field CT network model to address this question. We find that both the excitatory Ctx-TRN coupling strength and the relative strength between the GABAB- and GABAA-mediated inhibitions in the TRN-SRN pathway play critical roles in preventing pathological 2–4 Hz SWDs generated by the CT system. These findings highlight the functional importance of thalamic FFI in controlling absence seizures, and might provide insights into the treatment of absence epilepsy.
Methods and analysis
Computational model of the CT network
Previous studies have suggested that the generation of 2–4 Hz SWDs during absence seizures may be caused by abnormal interactions between the Ctx and thalamus (Crunelli and Leresche, 2002; Robinson et al., 2002; Suffczynski et al., 2004; Blumenfeld, 2005; Breakspear et al., 2006; Lytton, 2008; Marten et al., 2009a). To investigate possible roles of the thalamic FFI in controlling absence seizures, we establish a macroscopic-level computational model that describes the population dynamics of the CT network. As shown in Figure 1, our CT network comprises four neural populations, which are indicated as follows: e = excitatory pyramidal neurons, i = inhibitory interneurons, r = TRN and s = SRN. Inspired by anatomical data, three types of neural projections are considered in our CT model (Figure 1). The blue solid and dashed lines with round heads are used to represent the inhibitory projections mediated by GABAA and GABAB synapses, respectively. The red lines with arrow heads are employed to denote the glutamate-mediated excitatory projections. Similar to previous modeling studies, a non-specific external input ϕn is also injected to the SRN to mimic the sensory input (Robinson et al., 2002; Breakspear et al., 2006; Marten et al., 2009a; Chen et al., 2014, 2015). Obviously, our CT network contains the thalamic FFI that lies at the Ctx-TRN-SRN pathway (see the gray shaded pathways in Figure 1).
Figure 1.
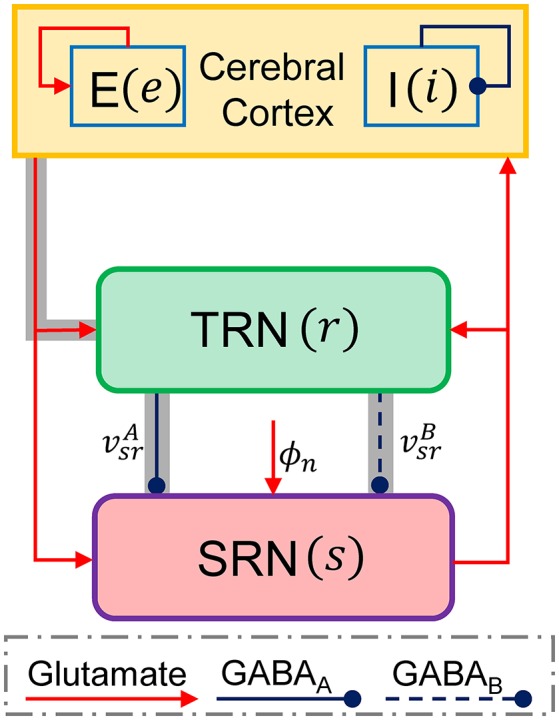
The schematic framework of the corticothalamic network. There are four neural populations that the excitatory pyramidal neural population (e), the inhibitory interneuron population (i), the TRN (r), and SRN (s) in the corticothalamic network. A non-specific external input to the SRN is denoted as ϕn. The connections within the network are mainly mediated by excitatory glutamate described by red lines with arrow heads and inhibitory GABA denoted by blue lines with round heads. The solid and dashed lines from the TRN to SRN are used to distinguish the projections mediated by GABAA () and GABAB () synapses, respectively. The gray shaded pathways show the thalamic feed-forward inhibition (FFI).
In the present study, each neural population in the CT network is simulated using the mean-field model proposed by Robinson and his colleagues (Robinson et al., 2002; Breakspear et al., 2006). For a given neural population a, the population dynamics can be characterized by three state variables: the mean membrane potential Va, the mean firing rate Qa, and the presynaptic activity ϕa. The transformation from the mean membrane potential Va to the mean firing rate Qa obeys a sigmoid function (Robinson et al., 2002; Breakspear et al., 2006; Marten et al., 2009a; Freyer et al., 2011; Yang et al., 2016):
| (1) |
where subscripts a ∈ A = {e, i, r, s} indicate the neural populations considered in the CT network. r represents the spatial position in the brain, θa is the threshold of the mean firing, and σ denotes the standard deviation of the firing rate. Due to the boundedness of the sigmoid function, the maximum firing rate in the Equation (1) ensures the mean firing rate Qa within the physiological range as changing the mean membrane potential Va.
Theoretically, the filtered incoming postsynaptic potentials from presynaptic neural populations in the dendrites lead to fluctuations of the mean membrane potential Va at the position r. This dynamical process can be modeled as (Robinson et al., 2002; Breakspear et al., 2006; Marten et al., 2009a; Freyer et al., 2011):
| (2) |
| (3) |
Here, the Dαβ is a differential operator describing the synaptic and dendritic filtering of incoming signals. The inverses of α and β denote the decay and rise time constants of membrane potential caused by incoming signals, respectively. vab describes the coupling strength from the neural population b to a, and ϕb(r, t) represents the presynaptic activity of the neural population b. Similar to previous modeling studies (Chen et al., 2014, 2015), the transmission delays among most neural populations are ignored in our model. Note that, however, we introduce a delay parameter τ to the GABAB-related incoming pulse rate [i.e., ϕr(r, t − τ)] to mimic the slow kinetics of GABAB receptor-mediated inhibition.
In the Ctx, the propagation effects of excitatory firing rates Qe along the cortical surface satisfy the damped wave equation (Robinson et al., 2002; Breakspear et al., 2006; Marten et al., 2009a; van Albada and Robinson, 2009; van Albada et al., 2009; Freyer et al., 2011; Chen et al., 2014, 2015):
| (4) |
where ∇2 represents the Laplacian operator (the second spatial derivative) and ϕe denotes the electrical field arising from the cortical excitatory neurons firing propagating along axons. The temporal damping rate of pulses is determined by the γe = ve/re, where ve is the conduction velocity and re denotes the characteristic range of axons of excitatory neurons in the Ctx. For other neural populations, their axons are too short to support wave propagation on the relevant scales. This indicates ϕc = F(Vc) (c = i, r, s). On the other hand, because absence seizures are believed to occur simultaneously throughout the brain, it is reasonable to assume that the spatial activities during absence seizures are uniform in our CT model. We therefore ignore the spatial derivative in Equation (4), and the propagation effect of cortical excitatory axonal field can be rewritten as (Breakspear et al., 2006; Marten et al., 2009a; Freyer et al., 2011):
| (5) |
We can further simplify our model by assuming that the mean membrane potential Vi and mean firing rate Qi of the inhibitory interneuron population satisfy Vi = Ve and Qi = Qe. Note that this assumption is reasonable, because the intracortical connections are suggested to be proportional to the number of synapses involved (Robinson et al., 2002, 2004; Breakspear et al., 2006; Marten et al., 2009a; van Albada and Robinson, 2009; van Albada et al., 2009; Freyer et al., 2011; Chen et al., 2014, 2015; Hu et al., 2015). Consequently, we can rewrite our mean-field CT model in the first-order form, as given in the Appendix. It should be noted that the model parameters in the established CT network are adapted from previous studies (Robinson et al., 2002, 2004; Breakspear et al., 2006; Marten et al., 2009a; van Albada and Robinson, 2009; van Albada et al., 2009; Freyer et al., 2011; Chen et al., 2014, 2015; Hu et al., 2015), which are systematically summarized in Table 1. These default parameters are estimated from real physiological data. Unless stated otherwise, we use these default parameter values in the following studies.
Table 1.
Model default parameters.
| Symbol | Value | Unit | Description |
|---|---|---|---|
| 250 | Hz | Cortical maximum firing rate | |
| 250 | Hz | SRN maximum firing rate | |
| 250 | Hz | TRN maximum firing rate | |
| θe, θi | 15 | mV | Mean firing threshold of cortical populations |
| θs | 15 | mV | Mean firing threshold of SRN |
| θr | 15 | mV | Mean firing threshold of TRN |
| vee | 1 | mV s | Coupling strength from PY to PY |
| −vei | 1.8 | mV s | Coupling strength from IIN to PY |
| vre | 0.05 | mV s | Coupling strength from PY to TRN |
| vrs | 0.5 | mV s | Coupling strength from SRN to TRN |
| 0.8 | mV s | Coupling strength from TRN to SRN | |
| ves | 1.8 | mV s | Coupling strength from SRN to PY |
| vse | 2.4 | mV s | Coupling strength from PY to SRN |
| γe | 100 | Hz | Cortical damping rate |
| τ | 50 | ms | Time delay due to slow synaptic kinetics of GABAB |
| α | 50 | s−1 | Synaptodendritic decay time constant |
| β | 200 | s−1 | Synaptodendritic rise time constant |
| σ | 6 | mV | Threshold variability of firing rate |
| vsnϕn | 2 | mV | Non-specific subthalamic input onto SRN |
Model parameters employed in the present study are adapted from previous studies (Chen et al., 2014, 2015) and references cited therein. Unless otherwise noted, we use these default parameter values for simulations. Note that PY and IIN denote excitatory pyramidal neurons and inhibitory interneurons in the cerebral cortex, respectively.
In simulations, our computational model is implemented with custom codes written in Matlab (MathWorks). We use the standard fourth-order Runge-Kutta method for numerically integrating normal differential equations, and employ an algorithm adapted from Matlab dde23 for calculating the delay differential equations (Shampine and Thompson, 2001). The temporal resolution of integration is fixed at 0.05 ms. Additional simulations confirm that this time step is sufficiently small to ensure an accurate simulation of our established CT model. All simulations are carried out for sufficiently long time to collect stable data for further analysis. The computer codes implementing our CT model will be available upon request via email.
Data analysis
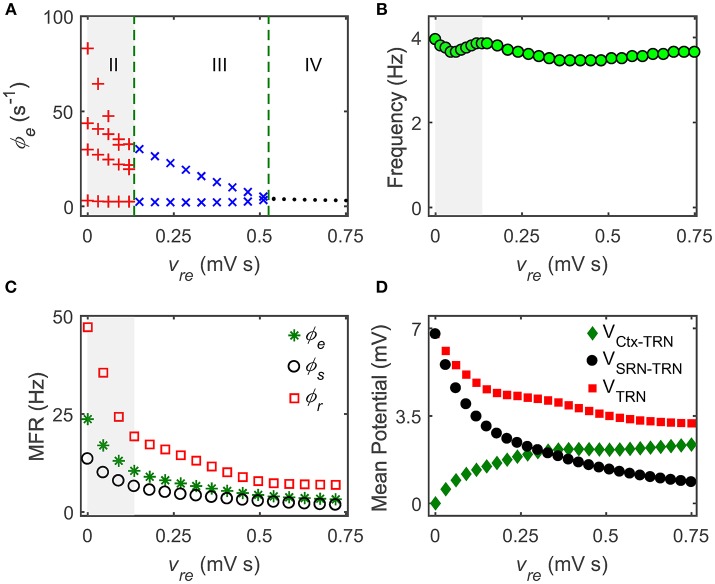
In the present study, we analyze the simulated data generated by our model from various aspects. Note that these data analysis techniques have been described in our previous studies (Chen et al., 2014, 2015). To classify the dynamical states of cortical oscillations, we determine the stable local maximum and minimum values of cortical excitatory axonal fields occurring in one cortical oscillatory period for each experimental setting. For a specific parameter, the state analysis of cortical oscillations is plotted as a function of this critical parameter (for example, see Figure 3). By employing this state analysis technique, we can identify the regions of different dynamical states in the two-dimensional parameter space (for example, see Figure 2). To evaluate the oscillation frequency of cortical oscillations, we compute the power spectral density of the time series ϕe using the Fast Fourier transform. For an experimental setting, the maximum peak frequency emerging in the power spectral density is defined as the dominant frequency of cortical oscillations. By combining both the state and frequency analysis techniques, the boundaries of the typical 2–4 Hz SWDs regions can be further outlined in the two-dimensional parameter space (see the asterisk regions in Figure 2). To understand the biophysical mechanisms underlying the control of absence seizures by the thalamic FFI, we calculate the long-term mean firing rates (MFRs) of three populations that the Ctx, the TRN, and SRN. To quantify impacts of Ctx and SRN on TRN, we further compute the mean potential that from Ctx and SRN to TRN, denoted as VCtx-TRN and VSRN-TRN in Figure 3D. In this work, VCtx-TRN is defined as the product of the vre and the MFRs of Ctx, whereas VSRN-TRN represents the product of the vrs and the MFRs of SRN. The summation of VCtx-TRN and VSRN-TRN is thus defined as the overall effect of Ctx and SRN on TRN (VTRN).
Figure 3.
The Ctx-TRN pathway contributes to controlling absence seizures. (A) State analysis of ϕe as a function of the coupling strength of the Ctx-TRN pathway vre. Enhancing the coupling strength vre could push the firing pattern from the SWD oscillation (II) to the simple oscillation (III) and to the low firing (IV). (B) The dominant frequency of the cortical oscillations ϕe changes with the enhancement of vre. (C) The mean firing rates (MFRs) of three neural populations that the Ctx (“*”), the SRN (“ ◦ ”), and TRN (“ □ ”) as a function of vre. The gray regions in (A–C) describe the regions of the typical 2–4 Hz SWDs, and the dashed green lines are used to show the demarcations of different dynamical states in the control process of absence seizures. (D) Changes of mean potential as a function of vre. VCtx-TRN denotes the mean potential from the Ctx to TRN, VSRN-TRN represents the mean potential from the SRN to TRN, VTRN shows the mean potential of TRN.
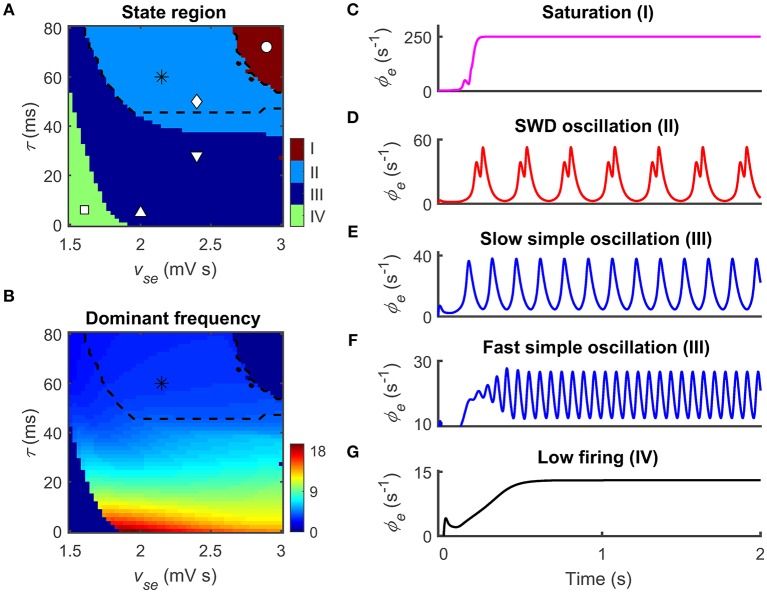
Figure 2.
Two epileptogenic factors inducing absence seizures in the corticothalamic network. The coupling strength vse that from the cerebral cortex to the SRN and the time delay τ caused by the slow kinetics of GABAB receptors are two epileptogenic factors for inducing absence seizures. (A,B) Distributions of dynamical states (A) and dominant frequency (B) in the two-parameter space (vse, τ). Four dynamical states could be observed: the saturation (I), the SWD oscillation (II), the simple oscillation (III) that includes slow and fast simple oscillations, and the low firing (IV). The regions of the typical 2–4 Hz SWDs indicated with asterisk (“*”) are surrounded by black dashed lines both in (A) and (B). (C–G) Five time series of ϕe are used to show the different firing patterns and the corresponding values are given by I (“ ◦ ”), II (“ ◊ ”), III (“ ∇ ” and “ Δ ”), and IV (“ □ ”) in (A).
Results
Our CT model can generate typical 2–4 Hz SWDs by introducing pathological mechanisms
Accumulating experimental data reveal that the generation of absence seizures is tightly associated with abnormal interactions within the CT network (Snead, 1995; Danober et al., 1998). Specifically, both the strong excitatory projections from the Ctx to the SRN and the slow kinetics of GABAB synapses along the TRN-SRN pathway are believed to be critical pathological factors in absence seizures (Destexhe, 1998; Robinson et al., 2002; Breakspear et al., 2006; Marten et al., 2009a,b; Han et al., 2012). Theoretically, the strong coupling strength of the cortico-thalamic pathway tends to induce the high amplitude oscillations, and the slow kinetics of GABAB synapses act as a delayed low-pass filter and can be linked to the production of slow waves. Thus, simultaneous modulation of these two parameters may destroy the normal oscillatory pattern generated in the CT system, triggering the onset of absence seizures.
To examine whether these pathological factors are also available in our CT model, we employ two related parameters: the excitatory coupling strength vse and the GABAB delay τ. Figures 2A,B show the state and frequency analysis in the combined parameter space (vse, τ), respectively. Consistent with previous findings (Chen et al., 2014, 2015), the model exhibits four types of dynamical states with different frequency characteristics. The first dynamical state is the saturation firing that occurs for sufficiently long τ and strong vse (region I in Figure 2A). Under this condition, inhibitions from the TRN to SRN cannot successfully suppress the excessive excitation caused by strong cortico-thalamic interactions. Such excessive excitation drives the firing of cortical neurons to increase from the low firing to the maximum firing in a short time (Figure 2C). For a long GABAB delay τ, the SWD oscillation state appears provided that the excitatory coupling strength vse is appropriately strong. In this case, the TRN-SRN inhibitions mediated by GABAA and GABAB receptors effectively shape SRN firing at different instants. This dual suppression creates double firing peaks for SRN neurons, further leading to the generation of cortical SWDs (region II in Figure 2A). Importantly, most of SWD oscillation region is contained in the typical 2–4 Hz frequency range (asterisk regions in Figures 2A,B), which can be comparable with EEG signals of real patients during absence seizures. On the other hand, the decrease in delay τ mixes the GABAA- and GABAB-induced inhibitions, weakening their double peak shaping effect. For a fixed vse, we therefore observe that the network dynamics can transit from the SWD oscillation state to the simple oscillation state by lowing the GABAB delay (region III in Figure 2A). Theoretically, the boundary between dual time scales and mixed time scale highly depends on the decay and rise time constants of membrane potential in our model (Chen et al., 2014). For each GABAA-induced inhibition caused by TRN neurons, the SRN neurons require a certain level of recovery time to restore their neuronal firing to the rising state. If this recovery time is shorter than the GABAB delay, another firing peak can be created to SRN neurons due to the latter GABAB-induced inhibition. Further, frequency analysis reveals that the dominant frequency of simple oscillation state relies on the GABAB delay. The shorter the delay parameter τ, the faster the simple oscillations generated by our model (Figures 2E,F). However, if the excitatory coupling strength vse is too weak, neural oscillations within the CT network cannot be maintained. In this case, the network dynamics is kicked into the low firing state (region IV in Figures 2A,G).
These findings demonstrate that our model can replicate different dynamical states of human brain. Remarkably, the model successfully generates the typical 2–4 Hz SWDs by introducing previous pathological mechanisms. In the following studies, we set vse = 2.4 mV s and τ = 50 ms as default, and explore the effects of the thalamic FFI on controlling absence seizures.
Roles of the Ctx-TRN pathway in controlling absence seizures
In the brain, the FFI microcircuits are believed to serve as fundamental regulators in balancing neural excitation and inhibition. It is widely accepted that dysfunction of FFI microcircuits might lead to excessive and/or hypersynchronous neural activities and evoke epileptic seizures (Paz and Huguenard, 2015). Importantly, a recent experimental study also showed a specific reduction in Ctx-TRN strength in the GluA4-deficient (Gria4−/−) mice model of absence epilepsy (Paz et al., 2011). We thus hypothesize that the classical thalamic FFI microcircuit, i.e., the Ctx-TRN-SRN pathway (Figure 1, gray lines), may participate in the modulation of absence seizures.
To theoretically validate whether this hypothesis is correct, we concentrate on the TRN and modulate its activation level by changing the coupling strength of the excitatory Ctx-TRN pathway. Figure 3A shows the one-dimensional state analysis as a function of the Ctx-TRN strength vre. Indeed, we find that the Ctx-TRN strength performs an active role in terminating absence seizures. A slight enhancement of the Ctx-TRN strength from its default value can suppress the SWD oscillations and push the model dynamics into the simple oscillation state (Figure 3A). For sufficiently strong strength vre, the model dynamics is even kicked into the low firing state (Figure 3A), implying a strong suppression effect due to the strengthened Ctx-TRN pathway. To characterize the frequency feature of model dynamics, the dominant frequency of neural oscillations is estimated by using the spectral analysis technique. For equivalent GABAA- and GABAB-mediated inhibitions in the TRN-SRN pathway, we observe that the dominant frequency of neural oscillations is stable and insensitive to the excitatory Ctx-TRN strength (Figure 3B).
To understand in detail how the Ctx-TRN pathway inducing SWD suppression arises, we further plot the MFR vs. the excitatory Ctx-TRN pathway strength vre for key neural populations in Figure 3C. As expected, the enhancement of excitatory coupling strength vre tends to excite TRN neurons (Figure 3D, green, indicted by diamonds). However, increasing the TRN activation suppresses the firing of SRN, which subsequently inhibits cortical neurons. Conversely, however, inactivation of SRN neurons will introduce a collision to TRN neurons and reduce their firing in a significant way (Figure 3D, black and red, indicated by circles and squares, respectively). By strengthening the Ctx-TRN pathway, this collision destabilizes the pathological balance and causes an overall inhibition effect in the CT system (Figure 3C). Such inhibition effect on TRN weakens the double peak shaping effect due to the slow kinetics of GABAB receptors. For a relatively strong excitatory Ctx-TRN strength, this GABAB weakening effect is considerable and therefore the generation of SWDs is terminated in our model.
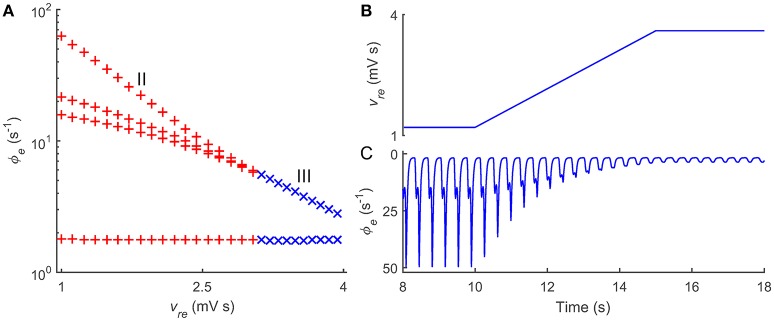
Past studies have demonstrated that several other pathological factors may also lead to typical 2–4 Hz SWD oscillations in the CT system (Robinson et al., 2002; Breakspear et al., 2006). Thus, a natural question is whether such control feature caused by the thalamic FFI is a generalized regulatory mechanism for absence seizures. We try to answer this question by introducing another SWD generation mechanism into our model. In literature, it has been widely reported that long transmission delay between the Ctx and thalamus can drive the CT system to produce the 2–4 Hz SWDs. To apply this pathological factor in our model, we block the GABAB pathway from TRN to SRN, and consider a bidirectional transmission delay τ0/2 between the Ctx and thalamus. Note that several coupling strengths are also adapted to ensure the CT system to generate the SWD oscillation. Our results presented in Figure 4 confirm that the increase in the excitatory coupling strength vre can successfully suppress the typical 2–4 Hz SWDs due to abnormal transmission delay between the Ctx and thalamus, further emphasizing the generality and functional importance of the thalamic FFI in regulating absence seizures.
Figure 4.
Roles of thalamic FFI in controlling absence seizures induced by transmission delays within corticothalamic loop. (A) State analysis of ϕe as a function of the coupling strength vre. The enhancement of the coupling strength vre could push the firing pattern from the SWD oscillation (II) to the simple oscillation (III). (B) Linearly enhancing the Ctx-TRN pathway (vre) to observe the dynamical control process of absence seizures. (C) The changes of cortical oscillations ϕe with linearly increasing vre. Note that in these simulations, the modified parameters are τ0/2 = 40 ms, ves = 3.2 mV s, vse = 3.4 mV s, vre = 1.2 ~ 3.6 mV s, and vsnϕn = 8.0 mV.
Taken together, we show that the thalamic FFI indeed participates in the modulation of absence seizures. Our theoretical observations indicate that normal CT oscillations require a certain level of Ctx-TRN strength, and loss of the Ctx-TRN strength might lead to over-excitation in the CT system and thus cause absence seizures. Importantly, this control manner by the thalamic FFI is found to be a possibly generalized regulatory mechanism for absence seizures and may be extendable to other pathological factors.
Combination roles of GABAA- and GABAB-mediated inhibitions in the TRN-SRN pathway in controlling absence seizures
The TRN-SRN pathway is another component of the thalamic FFI and might therefore also play essential roles in controlling absence seizures. Because neural projections from the TRN to the SRN are mediated by both GABAA and GABAB receptors, we next investigate effects of these two types of inhibitions on the modulation of absence seizures.
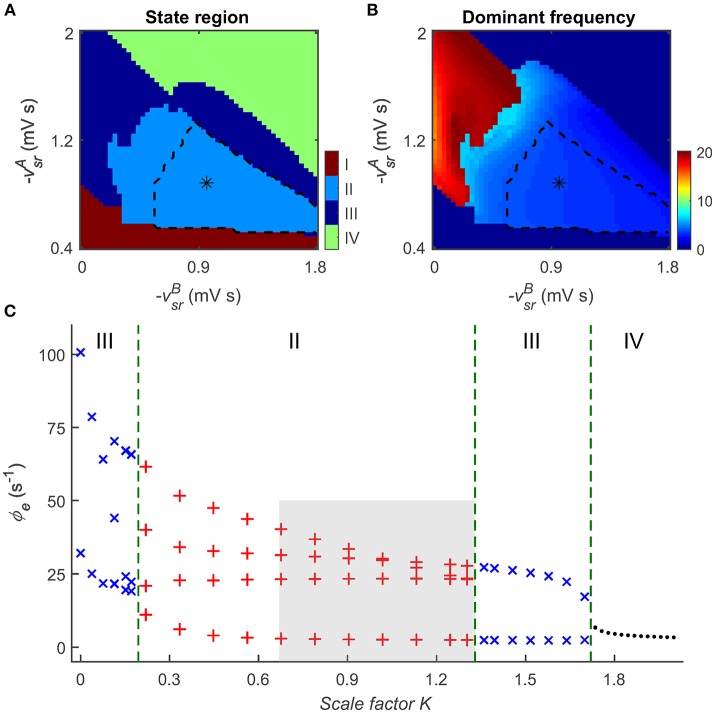
Figure 5A depicts the two-dimensional state analysis in the () panel. Similarly, we identify that four types of dynamical states are distributed in these two-parameter space (Figure 5A), revealing that the dynamics of the CT system depends on both GABAA and GABAB inhibitions. At a low level of GABAA inhibition, the CT system exhibits the saturation firing state (Figure 5A, region I). For a relatively larger GABAB delay that we considered in this work (Destexhe, 1998; Marten et al., 2009a,b), this occurs even when the GABAB inhibition is at a sufficiently high level, indicating that strong disinhibition of GABAA receptors in the TRN-SRN pathway may cause explosion of high-rate activities (Chen et al., 2014). Note that, however, such effect caused by GABAA inhibition might be also dependent on the delay time in the GABAB inhibition. If both GABAA and GABAB inhibitions are too strong, the firing of SRN neurons is extremely inhibited. In this case, the network dynamics is pushed into the low firing state (Figure 5A, region IV). As a consequence, neural oscillations of the CT system can be observed for intermediate GABAA and GABAB inhibitions (Figure 5A, regions II and III). Moreover, we find that the emergence of SWDs is highly associated with a scale factor K, defined as the relative strength of GABAB and GABAA inhibitions in the TRN-SRN pathway. For a fixed GABAA strength , an intermediate K might cause SWDs in the CT system (Figure 5C), thus might serve as a possible pathological factor of absence seizures.
Figure 5.
Combination roles of GABAA- and GABAB-mediated inhibitions in the TRN-SRN pathway in controlling absence seizures. The distributions of dynamical states (A) and dominant frequency (B) in the two-parameter space (). Similar to the results in Figure 2A, there are four dynamical states in this two-parameter space, the regions of the typical 2–4 Hz SWDs indicated with asterisk (“*”) are surrounded by black dashed lines. (C) State analysis of ϕe as a function of the scale factor K, defined as the relative strength of GABAB and GABAA inhibitions in the TRN-SRN pathway. The gray region describes the region of typical 2–4 Hz SWDs, and the dashed green lines are used to show the demarcations of different dynamical states in the control process of absence seizures.
To examine the dependence of neural oscillations on GABAA and GABAB inhibitions, we further perform dominant frequency analysis in the () panel (see Figure 5B). In comparison with the GABAA inhibition, our results suggest that GABAB-mediated inhibition plays a dominant role in determining the frequency of neural oscillations generated by the CT system. At a given GABAA inhibition level, increasing the GABAB strength in the TRN-SRN pathway enhances and prolongs the firing depression of SRN neurons. Such strengthened suppression effect leads to a significant reduction in the frequency of neural oscillations. Accordingly, we observe the fast and slow simple neural oscillations at the low and high levels of GABAB inhibition, and the SWDs with frequency varying from 2 to 6.5 Hz at the intermediate level of GABAB inhibition (Figures 5A,B). Consistent with a previous modeling study (Destexhe, 1999), our frequency analysis suggests that the different oscillatory frequencies in the CT system may be mainly attributable to differences in the kinetics of GABAB-mediated inhibition in the TRN-SRN pathway.
These results indicate that GABAA- and GABAB-mediated inhibitions in the TRN-SRN pathway might play combination roles in controlling absence seizures. An intermediate relative strength of GABAB and GABAA inhibitions might trigger the onset of absence seizures in the CT system, and the dominant frequency of SWDs highly depends on the level of GABAB inhibition.
Discussions
Using a mean-field CT network model, we systematically investigated the roles of thalamic FFI in controlling absence seizures in this study. By computational modeling, we demonstrated that the enhancement of the excitatory Ctx-TRN strength can significantly inhibit typical 2–4 Hz SWDs during absence seizures. Theoretically, this SWD suppression is found to be due to the GABAB weakening effect caused by the collision in TRN neurons. More importantly, we showed that such control manner by the thalamic FFI might be a generalized regulatory mechanism for absence seizures and could be extendable to other pathological factors. Our findings highlight the functional importance of thalamic FFI, which might contribute to the treatment of absence epilepsy.
It has been experimentally reported that loss of the FFI both in thalamus and neocortex might lead to over-excitation of neurons and induce epileptic seizures (Paz and Huguenard, 2015). For example, a recent study has identified a pathophysiological mechanism for the generation of absence seizures in the Gria4−/− mice model of absence epilepsy, for which the TRN receive reduced excitatory inputs from the direct Ctx-TRN neural projections (Paz et al., 2011; Paz and Huguenard, 2015). To a certain extent, this finding is in agreement with our computational observations, but our results established more insightful mechanistic understandings. Similarly, conditionally ablating Cav2.1 channel function in cortical parvalbumin (PV)+ interneurons was found to cause a loss of the FFI in neocortex and result in the generalized absence seizures (Rossignol et al., 2013). In addition, a previous experimental study also showed that selective loss of the FFI in rat somatosensory barrel circuits induce epileptic seizures when thalamocortical afferents are activated (Sun et al., 2005). These experimental findings provide clear evidence that the FFI in thalamus and neocortex is of great importance to maintain the balance of excitation and inhibition, which might provide some inspirations to make anti-epileptic drugs (Paz and Huguenard, 2015).
From the anatomical perspective, the GABAergic inhibitions from the TRN to SRN are mediated by both GABAA and GABAB synapses. Several previous experimental studies have suggested that GABAergic transmission within thalamus might play critical roles in shaping abnormal CT oscillations during absence seizures (Liu et al., 1991, 1992; Snead, 1992), but so far the relevant biophysical mechanisms are still not completely established. Our computational findings presented here indicated that GABAA and GABAB-mediated inhibitions in the TRN-SRN pathway might play combination roles in regulating absence seizures. For an intermediate relative strength of GABAB and GABAA inhibitions, the double suppression caused by these two types of GABA receptors occurring at different time instants are effective and may provide an effective mechanism to create multiple firing patterns for different neural populations. Mechanistically, such double suppression effect is responsible for the onset of absence seizures in the CT system. Remarkably, our model further makes prediction that the dominant frequency of SWDs in the CT system is more sensitive to GABAB-mediated inhibition, and a high level of GABAB inhibition corresponds to a relatively slower oscillation frequency. This observation emphasizes that GABAergic transmission in the thalamic FFI serves as an important intrinsic regulator to modulate the oscillation frequency of SWDs.
The results presented in this work support the idea that significant loss of thalamic FFI might trigger absence seizures (Paz et al., 2011). However, it is worth to notice that the functional roles of the FFI in brain circuits might be diverse and brain region-dependent. In comparison with our current study that enhancing the thalamic FFI could terminate absence seizures, a recent computational study using a basal ganglia-thalamo-cortical network suggested that abnormally strong striatal FFI facilitates to maintain, but not interrupt, synchronous oscillations during absence seizures (Arakaki et al., 2016). Instead, the reduction in the striatal FFI activates medium spiny neurons in the striatum, which might provide potential roles to desynchronize abnormal oscillations and control absence seizures (Arakaki et al., 2016). Moreover, the FFI in neural circuits is not always acting as an opposite depressing the output excitation. Indeed, the FFI might enhance output excitation in some circumstances. For example, as a subset of GABAergic cortical interneurons, the chandelier cells that receive excitatory projections from pyramidal cells. However, it has been observed that these types of interneurons can provide excitatory inputs to their subsequent pyramidal cells (Molnár et al., 2008). Therefore, the functional roles of FFI might highly depend on the involvement of neural circuits and brain regions. Although here we focus on the functional role of thalamic FFI in suppressing absence seizures, it should be noted that the feedback from SRN to TRN might also impact our model dynamics. In additional simulations, we have shown that decreasing the coupling strength of SRN-TRN pathway could push the cortical firing pattern from the SWD oscillation state to the saturation firing state, which is a non-physiological brain state (see Supplementary Figure 1). Further, investigation is needed to uncover the importance of SRN-TRN pathway in controlling absence seizures.
Although our model is designed to capture basic modulations of absence seizures by thalamic FFI, it can be extended to investigate other related issues. For example, deep brain stimulation (DBS) has been demonstrated to be a powerful neurosurgical procedure to treat epileptic seizures (Lega et al., 2010; Fisher and Velasco, 2014; Pantoja-Jiménez et al., 2014). Recent experimental studies have shown that applying high-frequency DBS with suitable current intensity to both SRN and TRN can significantly reduce the occurrence of absence seizures (Lüttjohann and van Luijtelaar, 2013; Pantoja-Jiménez et al., 2014). Nevertheless, so far the most effective thalamic DBS target for treating absence seizures is still debated. In future studies, it is of importance and deserves to use our developed model to determine the most effective thalamic DBS target as well as its corresponding optimal stimulation parameters. On the other hand, several other mental illness, such as the generalized tonic-clonic epilepsy, Parkinson's disease, neurogenic pain and depression, are also reported to be highly associated with the CT dysrhythmia (Llinás et al., 1999). Theoretically, the CT model established in this work might provide a modeling framework for further exploring underlying functional roles of thalamic FFI in these mental illnesses. In addition, considering that suppression of absence seizures in the CT model is a dynamical control process, we will further try to investigate how to control this system from the view of dynamical control in our following work.
To summarize, we have performed mechanistic studies to examine underlying effects of thalamic FFI on the control and modulation of absence seizures. Our results showed that the FFI in thalamus not only contributes to suppressing absence seizures, but also serves as an intrinsic regulator to modulate the oscillation frequency of SWDs generated in the CT system. These observations established an insightful mechanistic understanding on how the thalamic FFI regulates typical 2–4 Hz SWDs during absence seizures, and might provide insightful physiological implications into the treatment of absence seizures.
Author contributions
MC, DG, YX, and DY conceived and designed the experiments. MC performed the experiments and data analysis. MC and DG wrote the paper.
Funding
This work was supported by National Natural Science Foundation of China (No. 81571770, No. 81330032, No. 61527815, No. 81371636).
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix: model equations
The model equations are:
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
| (A7) |
| (A8) |
Supplementary material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fncom.2017.00031/full#supplementary-material
References
- Arakaki T., Mahon S., Charpier S., Leblois A., Hansel D. (2016). The role of striatal feedforward inhibition in the maintenance of absence seizures. J. Neurosci. 36, 9618–9632. 10.1523/JNEUROSCI.0208-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assisi C., Stopfer M., Laurent G., Bazhenov M. (2007). Adaptive regulation of sparseness by feedforward inhibition. Nat. Neurosci. 10, 1176–1184. 10.1038/nn1947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avoli M. (2012). A brief history on the oscillating roles of thalamus and cortex in absence seizures. Epilepsia 53, 779–789. 10.1111/j.1528-1167.2012.03421.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazhenov M., Timofeev I., Fröhlich F., Sejnowski T. J. (2008). Cellular and network mechanisms of electrographic seizures. Drug Discov. Today Dis. Models 5, 45–57. 10.1016/j.ddmod.2008.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blumenfeld H. (2005). Cellular and network mechanisms of spike-wave seizures. Epilepsia 46, 21–33. 10.1111/j.1528-1167.2005.00311.x [DOI] [PubMed] [Google Scholar]
- Breakspear M., Roberts J. A., Terry J. R., Rodrigues S., Mahant N., Robinson P. A. (2006). A unifying explanation of primary generalized seizures through nonlinear brain modeling and bifurcation analysis. Cereb. Cortex 16, 1296–1313. 10.1093/cercor/bhj072 [DOI] [PubMed] [Google Scholar]
- Chen M., Guo D., Li M., Ma T., Wu S., Ma J., et al. (2015). Critical roles of the direct GABAergic pallido-cortical pathway in controlling absence seizures. PLoS Comput. Biol. 11:e1004539. 10.1371/journal.pcbi.1004539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M., Guo D., Wang T., Jing W., Xia Y., Xu P., et al. (2014). Bidirectional control of absence seizures by the basal ganglia: a computational evidence. PLoS Comput. Biol. 10:e1003495. 10.1371/journal.pcbi.1003495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crunelli V., Leresche N. (2002). Childhood absence epilepsy: genes, channels, neurons and networks. Nat. Rev. Neurosci. 3, 371–382. 10.1038/nrn811 [DOI] [PubMed] [Google Scholar]
- Danober L., Deransart C., Depaulis A., Vergnes M., Marescaux C. (1998). Pathophysiological mechanisms of genetic absence epilepsy in the rat. Prog. Neurobiol. 55, 27–57. 10.1016/S0301-0082(97)00091-9 [DOI] [PubMed] [Google Scholar]
- Depaulis A., David O., Charpier S. (2016). The genetic absence epilepsy rat from Strasbourg as a model to decipher the neuronal and network mechanisms of generalized idiopathic epilepsies. J. Neurosci. Methods 260, 159–174. 10.1016/j.jneumeth.2015.05.022 [DOI] [PubMed] [Google Scholar]
- Depaulis A., Vergnes M., Marescaux C. (1994). Endogenous control of epilepsy: the nigral inhibitory system. Prog. Neurobiol. 42, 33–52. 10.1016/0301-0082(94)90020-5 [DOI] [PubMed] [Google Scholar]
- Deransart C., Vercueil L., Marescaux C., Depaulis A. (1998). The role of basal ganglia in the control of generalized absence seizures. Epilepsy Res. 32, 213–223. 10.1016/S0920-1211(98)00053-9 [DOI] [PubMed] [Google Scholar]
- Destexhe A. (1998). Spike-and-wave oscillations based on the properties of GABAB receptors. J. Neurosci. 18, 9099–9111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A. (1999). Can GABAA conductances explain the fast oscillation frequency of absence seizures in rodents? Eur. J. Neurosci. 11, 2175–2181. 10.1046/j.1460-9568.1999.00660.x [DOI] [PubMed] [Google Scholar]
- Durón R. M., Medina M. T., Martínez-Juárez I. E., Bailey J. N., Perez-Gosiengfiao K. T., Ramos-Ramírez R., et al. (2005). Seizures of idiopathic generalized epilepsies. Epilepsia 46, 34–47. 10.1111/j.1528-1167.2005.00312.x [DOI] [PubMed] [Google Scholar]
- Fan D., Wang Q., Perc M. (2015). Disinhibition-induced transitions between absence and tonic-clonic epileptic seizures. Sci. Rep. 5:12618. 10.1038/srep12618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher R. S., Velasco A. L. (2014). Electrical brain stimulation for epilepsy. Nat. Rev. Neurol. 10, 261–270. 10.1038/nrneurol.2014.59 [DOI] [PubMed] [Google Scholar]
- Freyer F., Roberts J. A., Becker R., Robinson P. A., Ritter P., Breakspear M. (2011). Biophysical mechanisms of multistability in resting-state cortical rhythms. J. Neurosci. 31, 6353–6361. 10.1523/JNEUROSCI.6693-10.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo D., Li C. (2009). Stochastic and coherence resonance in feed-forward-loop neuronal network motifs. Phys. Rev. E 79:051921. 10.1103/physreve.79.051921 [DOI] [PubMed] [Google Scholar]
- Han H. A., Cortez M. A., Snead O. C. (2012). GABAB receptor and absence epilepsy, in Jasper's Basic Mechanisms of the Epilepsies, 4th Edn., eds Noebels J., Avoli M., Rogawski M., Olsen R., Delgado-Escueta A. (Bethesda: Oxford University Press; ), 242–256. 10.1093/med/9780199746545.003.0019 [DOI] [Google Scholar]
- Holt A. B., Netoff T. I. (2013). Computational modeling of epilepsy for an experimental neurologist. Exp. Neurol. 244, 75–86. 10.1016/j.expneurol.2012.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu B., Wang Q. (2015). Controlling absence seizures by deep brain stimulus applied on substantia nigra pars reticulata and cortex. Chaos Solitons Fractals 80, 13–23. 10.1016/j.chaos.2015.02.014 [DOI] [Google Scholar]
- Hu B., Guo D., Wang Q. (2015). Control of absence seizures induced by the pathways connected to SRN in corticothalamic system. Cogn. Neurodyn. 9, 279–289. 10.1007/s11571-014-9321-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kee T., Sanda P., Gupta N., Stopfer M., Bazhenov M. (2015). Feed-forward versus feedback inhibition in a basic olfactory circuit. PLoS Comput. Biol. 11:e1004531. 10.1371/journal.pcbi.1004531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khubieh A., Ratté S., Lankarany M., Prescott S. A. (2016). Regulation of cortical dynamic range by background synaptic noise and feedforward inhibition. Cereb. Cortex 26, 3357–3369. 10.1093/cercor/bhv157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kros L., Eelkman Rooda O. H. J., De Zeeuw C. I., Hoebeek F. E. (2015a). Controlling cerebellar output to treat refractory epilepsy. Trends Neurosci. 38, 787–799. 10.1016/j.tins.2015.10.002 [DOI] [PubMed] [Google Scholar]
- Kros L., Eelkman Rooda O. H. J., Spanke J. K., Alva P., Van Dongen M. N., Karapatis A., et al. (2015b). Cerebellar output controls generalized spike-and-wave discharge occurrence. Ann. Neurol. 77, 1027–1049. 10.1002/ana.24399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lega B. C., Halpern C. H., Jaggi J. L., Baltuch G. H. (2010). Deep brain stimulation in the treatment of refractory epilepsy: update on current data and future directions. Neurobiol. Dis. 38, 354–360. 10.1016/j.nbd.2009.07.007 [DOI] [PubMed] [Google Scholar]
- Li C. (2008). Functions of neuronal network motifs. Phys. Rev. E 78:037101. 10.1103/physreve.78.037101 [DOI] [PubMed] [Google Scholar]
- Lindahl M., Hellgren Kotaleski J. (2016). Untangling basal ganglia network dynamics and function: role of dopamine depletion and inhibition investigated in a spiking network model. eneuro 3:ENEURO.0156-16.2016. 10.1523/ENEURO.0156-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S., Wang Q., Fan D. (2016). Disinhibition-induced delayed onset of epileptic spike-wave discharges in a five variable model of cortex and thalamus. Front. Comput. Neurosci. 10:28. 10.3389/fncom.2016.00028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z., Vergnes M., Depaulis A., Marescaux C. (1991). Evidence for a critical role of GABAergic transmission within the thalamus in the genesis and control of absence seizures in the rat. Brain Res. 545, 1–7. 10.1016/0006-8993(91)91262-Y [DOI] [PubMed] [Google Scholar]
- Liu Z., Vergnes M., Depaulis A., Marescaux C. (1992). Involvement of intrathalamic GABAB neurotransmission in the control of absence seizures in the rat. Neuroscience 48, 87–93. 10.1016/0306-4522(92)90340-8 [DOI] [PubMed] [Google Scholar]
- Llinás R. R., Ribary U., Jeanmonod D., Kronberg E., Mitra P. P. (1999). Thalamocortical dysrhythmia: a neurological and neuropsychiatric syndrome characterized by magnetoencephalography. Proc. Natl. Acad. Sci. U.S.A. 96, 15222–15227. 10.1073/pnas.96.26.15222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C., Li Q., Xia Y., Lei X., Xue K., Yao Z., et al. (2012). Resting state basal ganglia network in idiopathic generalized epilepsy. Hum. Brain Mapp. 33, 1279–1294. 10.1002/hbm.21286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lüttjohann A., van Luijtelaar G. (2013). Thalamic stimulation in absence epilepsy. Epilepsy Res. 106, 136–145. 10.1016/j.eplepsyres.2013.03.009 [DOI] [PubMed] [Google Scholar]
- Lytton W. W. (2008). Computer modelling of epilepsy. Nat. Rev. Neurosci. 9, 626–637. 10.1038/nrn2416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marten F., Rodrigues S., Benjamin O., Richardson M. P., Terry J. R. (2009a). Onset of polyspike complexes in a mean-field model of human electroencephalography and its application to absence epilepsy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 367, 1145–1161. 10.1098/rsta.2008.0255 [DOI] [PubMed] [Google Scholar]
- Marten F., Rodrigues S., Suffczynski P., Richardson M. P., Terry J. R. (2009b). Derivation and analysis of an ordinary differential equation mean-field model for studying clinically recorded epilepsy dynamics. Phys. Rev. E 79:021911. 10.1103/PhysRevE.79.021911 [DOI] [PubMed] [Google Scholar]
- Molnár G., Oláh S., Komlósi G., Füle M., Szabadics J., Varga C., et al. (2008). Complex events initiated by individual spikes in the human cerebral cortex. PLoS Biol. 6:e222. 10.1371/journal.pbio.0060222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantoja-Jiménez C. R., Magdaleno-Madrigal V. M., Almazán-Alvarado S., Fernández-Mas R. (2014). Anti-epileptogenic effect of high-frequency stimulation in the thalamic reticular nucleus on PTZ-induced seizures. Brain Stimul. 7, 587–594. 10.1016/j.brs.2014.03.012 [DOI] [PubMed] [Google Scholar]
- Paz J. T., Huguenard J. R. (2015). Microcircuits and their interactions in epilepsy: is the focus out of focus? Nat. Neurosci. 18, 351–359. 10.1038/nn.3950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz J. T., Bryant A. S., Peng K., Fenno L., Yizhar O., Frankel W. N., et al. (2011). A new mode of corticothalamic transmission revealed in the Gria4−/− model of absence epilepsy. Nat. Neurosci. 14, 1167–1173. 10.1038/nn.2896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz J. T., Chavez M., Saillet S., Deniau J. M., Charpier S. (2007). Activity of ventral medial thalamic neurons during absence seizures and modulation of cortical paroxysms by the nigrothalamic pathway. J. Neurosci. 27, 929–941. 10.1523/JNEUROSCI.4677-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz J. T., Davidson T. J., Frechette E. S., Delord B., Parada I., Peng K., et al. (2013). Closed-loop optogenetic control of thalamus as a tool for interrupting seizures after cortical injury. Nat. Neurosci. 16, 64–70. 10.1038/nn.3269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz J. T., Deniau J. M., Charpier S. (2005). Rhythmic bursting in the cortico-subthalamo-pallidal network during spontaneous genetically determined spike and wave discharges. J. Neurosci. 25, 2092–2101. 10.1523/JNEUROSCI.4689-04.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinault D. (2004). The thalamic reticular nucleus: structure, function and concept. Brain Res. Rev. 46, 1–31. 10.1016/j.brainresrev.2004.04.008 [DOI] [PubMed] [Google Scholar]
- Potjans T. C., Diesmann M. (2014). The cell-type specific cortical microcircuit: relating structure and activity in a full-scale spiking network model. Cereb. Cortex 24, 785–806. 10.1093/cercor/bhs358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson P. A., Rennie C. J., Rowe D. L. (2002). Dynamics of large-scale brain activity in normal arousal states and epileptic seizures. Phys. Rev. E 65:041924. 10.1103/PhysRevE.65.041924 [DOI] [PubMed] [Google Scholar]
- Robinson P. A., Rennie C. J., Rowe D. L., O'connor S. C. (2004). Estimation of multiscale neurophysiologic parameters by electroencephalographic means. Hum. Brain Mapp. 23, 53–72. 10.1002/hbm.20032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossignol E., Kruglikov I., Van Den Maagdenberg A. M. J. M., Rudy B., Fishell G. (2013). CaV2.1 ablation in cortical interneurons selectively impairs fast-spiking basket cells and causes generalized seizures. Ann. Neurol. 74, 209–222. 10.1002/ana.23913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shampine L. F., Thompson S. (2001). Solving DDEs in Matlab. Appl. Num. Math. 37, 441–458. 10.1016/S0168-9274(00)00055-6 [DOI] [Google Scholar]
- Sloviter R. S. (1991). Feedforward and feedback inhibition of hippocampal principal cell activity evoked by perforant path stimulation: GABA-mediated mechanisms that regulate excitability in vivo. Hippocampus 1, 31–40. 10.1002/hipo.450010105 [DOI] [PubMed] [Google Scholar]
- Snead O. C., III. (1992). Evidence for GABAB-mediated mechanisms in experimental generalized absence seizures. Eur. J. Pharmacol. 213, 343–349. 10.1016/0014-2999(92)90623-C [DOI] [PubMed] [Google Scholar]
- Snead O. C. (1995). Basic mechanisms of generalized absence seizures. Ann. Neurol. 37, 146–157. 10.1002/ana.410370204 [DOI] [PubMed] [Google Scholar]
- Sporns O., Kötter R. (2004). Motifs in brain networks. PLoS Biol. 2:e369. 10.1371/journal.pbio.0020369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suffczynski P., Kalitzin S., Lopes Da Silva F. H. (2004). Dynamics of non-convulsive epileptic phenomena modeled by a bistable neuronal network. Neuroscience 126, 467–484. 10.1016/j.neuroscience.2004.03.014 [DOI] [PubMed] [Google Scholar]
- Sun Q.-Q., Huguenard J. R., Prince D. A. (2005). Reorganization of barrel circuits leads to thalamically-evoked cortical epileptiform activity. Thalamus Relat. Syst. 3, 261–273. 10.1017/S1472928807000283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor P. N., Thomas J., Sinha N., Dauwels J., Kaiser M., Thesen T., et al. (2015). Optimal control based seizure abatement using patient derived connectivity. Front. Neurosci. 9:202. 10.3389/fnins.2015.00202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor P. N., Wang Y., Goodfellow M., Dauwels J., Moeller F., Stephani U., et al. (2014). A computational study of stimulus driven epileptic seizure abatement. PLoS ONE 9:e114316. 10.1371/journal.pone.0114316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tepper J. M., Wilson C. J., Koós T. (2008). Feedforward and feedback inhibition in neostriatal GABAergic spiny neurons. Brain Res. Rev. 58, 272–281. 10.1016/j.brainresrev.2007.10.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolaymat A., Nayak A., Geyer J. D., Geyer S. K., Carney P. R. (2015). Diagnosis and management of childhood epilepsy. Curr. Probl. Pediatr. Adolesc. Health Care 45, 3–17. 10.1016/j.cppeds.2014.12.002 [DOI] [PubMed] [Google Scholar]
- van Albada S. J., Robinson P. A. (2009). Mean-field modeling of the basal ganglia-thalamocortical system. I: firing rates in healthy and parkinsonian states. J. Theor. Biol. 257, 642–663. 10.1016/j.jtbi.2008.12.018 [DOI] [PubMed] [Google Scholar]
- van Albada S. J., Gray R. T., Drysdale P. M., Robinson P. A. (2009). Mean-field modeling of the basal ganglia-thalamocortical system. II: dynamics of parkinsonian oscillations. J. Theor. Biol. 257, 664–688. 10.1016/j.jtbi.2008.12.013 [DOI] [PubMed] [Google Scholar]
- Womelsdorf T., Valiante T. A., Sahin N. T., Miller K. J., Tiesinga P. (2014). Dynamic circuit motifs underlying rhythmic gain control, gating and integration. Nat. Neurosci. 17, 1031–1039. 10.1038/nn.3764 [DOI] [PubMed] [Google Scholar]
- Yang D.-P., Mckenzie-Sell L., Karanjai A., Robinson P. A. (2016). Wake-sleep transition as a noisy bifurcation. Phys. Rev. E 94:022412. 10.1103/PhysRevE.94.022412 [DOI] [PubMed] [Google Scholar]
- Yuste R. (2015). From the neuron doctrine to neural networks. Nat. Rev. Neurosci. 16, 487–497. 10.1038/nrn3962 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.