Abstract
The Carr–Purcell–Meiboom–Gill (CPMG) experiment is one of the most classical and well-known relaxation dispersion experiments in NMR spectroscopy, and it has been successfully applied to characterize biologically relevant conformational dynamics in many cases. Although the data analysis of the CPMG experiment for the 2-site exchange model can be facilitated by analytical solutions, the data analysis in a more complex exchange model generally requires computationally-intensive numerical analysis. Recently, a powerful computational strategy, geometric approximation, has been proposed to provide approximate numerical solutions for the adiabatic relaxation dispersion experiments where analytical solutions are neither available nor feasible. Here, we demonstrate the general potential of geometric approximation by providing a data analysis solution of the CPMG experiment for both the traditional 2-site model and a linear 3-site exchange model. The approximate numerical solution deviates less than 0.5% from the numerical solution on average, and the new approach is computationally 60,000-fold more efficient than the numerical approach. Moreover, we find that accurate dynamic parameters can be determined in most cases, and, for a range of experimental conditions, the relaxation can be assumed to follow mono-exponential decay. The method is general and applicable to any CPMG RD experiment (e.g. N, C′, Cα, Hα, etc.) The approach forms a foundation of building solution surfaces to analyze the CPMG experiment for different models of 3-site exchange. Thus, the geometric approximation is a general strategy to analyze relaxation dispersion data in any system (biological or chemical) if the appropriate library can be built in a physically meaningful domain.
Keywords: Carr–Purcell–Meiboom–Gill (CPMG), geometric approximation, relaxation dispersion experiments, three-site exchange
Graphical Abstract
1. Introduction
The CPMG experiment has been proven a very powerful tool in NMR spectroscopy to quantitatively characterize the (microsecond to millisecond) conformational dynamics in biological macromolecules1–5. The experiment has been used to understand interconversion rates of functional states in enzymes1,3,4 and to reveal structural information of the low-populated “invisible” conformations of macromolecules2,5. However, many of the successful cases have been limited to the simple 2-site exchange model. As the biological systems studied become more complex, it is reasonable to assume that more sophisticated exchange models will be required1,6–9; however, presently, it is cumbersome to accurately analyze the data of the CPMG experiment in a more complex exchange model.
The mathematical analysis for the analytic solutions of the CPMG experiment under different assumptions and different exchange models has been presented and discussed in the literature over the past half-century6,7,10–16. The important ground work was first established by Allerhand et al.10–12, who showed that mono-exponential decay dominates the CPMG experiment for most cases in the 2-site exchange model, as well as for all fast-exchange cases. Later, the most general analytic solution of the CPMG experiment was derived for the 2-site exchange model by Carver and Richards16, which has been further improved recently13. Moreover, the approximate analytic solution for the N-site model was proposed in the fast exchange regime12, which has been applied to analyze experimental data7. In spite of lengthy efforts from many spin physicists6,7,12,14, the general analytic solution for a more complex model (i.e. a linear 3-site exchange) has not yet been characterized, and it was even shown that a simple algebraic expression is not possible for a multi-site exchange model (n>2)14.
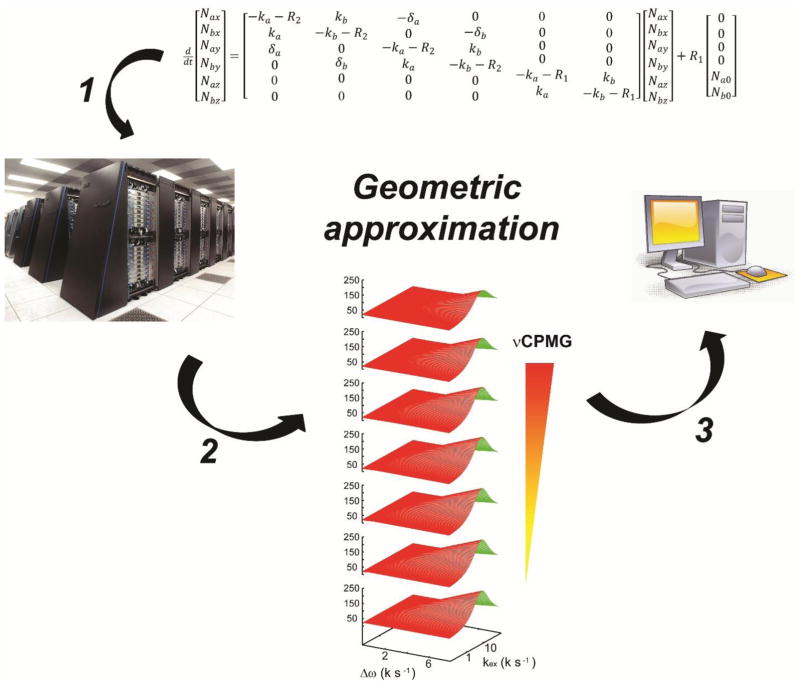
Recently, a new computational strategy, geometric approximation17, was developed to analyze the sophisticated data from adiabatic relaxation dispersion experiments18. The strategy is composed of several steps (Fig. 1): 1) to formulate a computable mathematical problem based on a well-established physical theory, 2) to analyze the geometric features of the solution surface, under the assumption of continuity, using a high-performance computing system, and to save the geometric features in a library, and 3) to approximate the solution surface, based on the library, during data analysis in personal computers. This new strategy allows accurate data analysis in any system, within a given domain, with minimal computational power17. The generality of the new computational approach implies the potential broader application of this technique to other problems in data analysis. For the case at hand, analysis of data for the CPMG experiment in a multi-site exchange by geometric approximation, two main hurdles need to be resolved; (1) to build an appropriate library for the high dimensional solution surface, which could potentially become very large for a complex exchange model, and (2) to consider the potential multi-exponential decay of the experiment.
Figure 1.
The general strategy of geometric approximation in accelerating data analysis. 1) To formulate a computable mathematical problem based on a well-established physical theory. 2) To analyze the geometric features of the solution surface by a supercomputing system under the assumption of continuity and to save the geometric features in the library. 3) To approximate the solution surface based on the library during data analysis in personal computers.
The concepts of the geometric approximation methodology have been proposed and validated previously for the analysis of adiabatic relaxation dispersion experiments 17. Herein, we explore the geometric features of the solution surfaces for the CPMG experiment acting on both the simple 2-site exchange model and a linear 3-site exchange model. It is essential to build an algorithm to match experimental data onto the solution surfaces using geometric approximation, which is shown to have equal or better accuracy than the well-known analytic solutions for 2-site exchange. It became readily clear that initial attempts to extend the approach of building libraries from 2-site exchange to a given linear 3-site exchange model could not be utilized. This approach will result in computing a prohibitively large library. Hence, a new strategy for building a high dimensional solution surface is developed to significantly reduce the size of the library for 3-site exchange. The resulting, effective library is three orders of magnitude smaller than what would be produced by the approach of directly computing the uniform grid on all independent variables. Finally, extensive numerical analysis, of relaxation in the CPMG experiment for the linear 3-site exchange model, reveals that relaxation is dominated by mono-exponential decay in most cases when there exists a dominant state (p>80%). Accurate dynamic parameters can be extracted from the simulated data for the common experimental conditions using geometric approximation. The new approach of building the library can be used to provide a solution not only for the linear 3-site model but also for other 3-site exchange models. The above examples demonstrate the generality and the potential of geometric approximation in accelerating accurate data analysis in general.
2. Methods (geometric approximation)
Any solution surface in Euclidean space can be arbitrarily approximated by a finite number of polynomial functions under the assumptions of continuity and compactness. Here, this principle is applied to the CPMG experiment, where we first consider the case of the 2-site exchange model. For simplicity, we assume that the contribution of the different intrinsic R2 rates of two different states in the relaxation dispersion can be neglected, and the experiment is dominated by mono-exponential decay (which has been proven to be true in most cases10,11). Then, the effective R2 rate observed in the CPMG-RD experiment can be expressed by the following expressions:
| [1] |
| [2] |
In Eq [2], R2,eff is the effective R2 rate, R2,int is the intrinsic R2 rate in the absence of exchange, and g(…) is the Rex rate, where Δω is the chemical shift difference between the two states, kex is the chemical exchange rate, pa is the population of state A, and νCPMG is the frequency of the π pulses (1/2τcp, where τcp = 2 times the interval between two π pulses). After analyzing simulated relaxation dispersion profiles with respect to different parameters as described before17, it becomes clear that the four-dimensional surfaces can be interpreted using geometric approximation based on the libraries generated by directly computing over a uniform grid. A multidimensional solution library was computed as follows (ks−1 = 103 s−1): the grid spacing in the Δω dimension was chosen as 0.1 ks−1, the grid spacing in the kex dimension (on the logarithmic scale) was chosen as x100.05, the grid spacing in the pa dimension was chosen as 4%, and the grid spacing in the νCPMG dimension (on the logarithmic scale) was chosen as x100.05. The solution libraries consist of 80 points in the Δω dimension (spanning the domain of 0 to 8 ks−1), 61 points in the kex dimension (spanning the domain of 0.1 to 100 ks−1), 12 points in the pa dimension (spanning the domain of 50 to 100%), and 43 points in the νCPMG dimension (spanning the domain of 20 to 2500Hz). Two libraries (the decay of A and the decay of A+B) were computed based on the above grid spacing, each of which took approximately 1 day using a 128-core Linux cluster computer system. Each library consists of approximately 2.5 million points and is approximately 61 MB in size. Use of these libraries to analyze CPMG data will be presented below.
Next, we consider the case of CPMG in the presence of a linear 3-site exchange model, Eq [3]. The complexity of the problem for multisite (≥3) exchange requires some general assumptions in order to simplify the problem. Here, we assume that only the decay of the state A is measured, the state A is the dominant spectral feature (>80%), and the contribution of the different intrinsic R2 rates for different states in the relaxation dispersion can be neglected. Again, the experiment is assumed to be dominated by mono-exponential decay (vide infra). The direct extension approach of building libraries for this model is daunting at first glance, wherein extension of the fine grid spacing used to build the solution surface for the 2-site exchange model would expand the library for the total Rex rate to a 7-dimensional library (Eq [4]) containing 29 billion points and take about 18 thousand days to compute using a 128-core Linux cluster computer system. The expected library would be approximately 710 GB in size, and it could not be efficiently utilized to map for experimental solutions in a personal computer. Furthermore, since all of the dynamic parameters are correlated with each other in contributing to the relaxation dispersion, there is no direct way to linearly decompose the high dimensional Rex surface (Eq [4]) into several smaller dimensional ones. However, to address this problem, the total Rex rate can be decomposed into several components (Eq [5]), where the high-dimensional component is treated with a relaxed grid spacing while retaining enough accuracy for data analysis. Application of this strategy reduces both the computational time and the size of the total library by thousands-fold compared to the simple extension of the direct approach. This new approach can be taken to build the solution surface and search algorithm for the three-site exchange model in general.
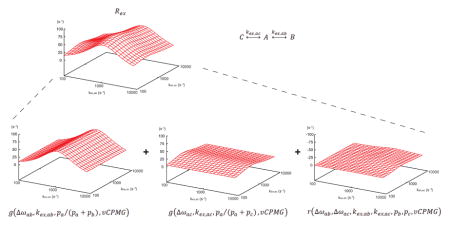
For the case of a linear 3-site exchange model (Eq [3]), the effective R2 rate can be expressed and decomposed into the following equations (Eqs [4], [5]):
| [3] |
| [4] |
| [5] |
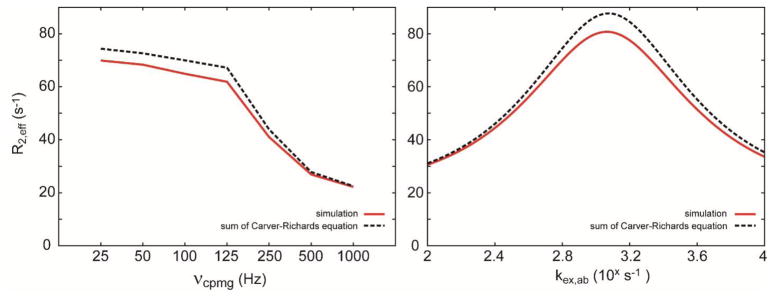
In Eq [4], R2,eff is the effective R2 rate of the state A, R2,int is the intrinsic R2 rate of the state A, and f(…) is the total Rex rate. In Eq [5], g(…) is the Rex rate for the 2-site exchange, r(…) is the residue function, the difference between the total Rex rate and the sum of the two Rex rates for two 2-site exchange events, Δωij is the chemical shift difference, kex is the chemical exchange rate, px is the population of the state x, and νCPMG is the frequency of the π pulses. Since the solution surface g(…) is already determined for the two-site case (vide supra), only the residue function r(…) needs to be determined using a separate application of geometric approximation. Because the two functions represented by g(…) are the major contributions in the total Rex rate f(…), the grid spacing for the residue function r(…) can be significantly relaxed (Fig. 2).
Figure 2.
The difference between the total Rex rates for a linear 3-site exchange model and the summation of two Rex rates for the 2-site exchange model. Chemical shifts are 0.1 kHz for state A, 0.3 kHz for state B, and 0.2 kHz for state C with respect to the π pulses. The chemical exchange rate between state A and state C is fixed at 5 kHz. The state A is 85%, and the state B is 10%. The longitudinal relaxation is 1 s−1 and the transverse relaxation is 20 s−1. The constant time period is set as 40 ms. In the left panel, the chemical exchange rate between state A and state B is fixed at 0.1 kHz while varying the νCPMG frequency (νCPMG = 25, 50, 100, 125, 250, 500, 1000 Hz). In the right panel, the νCPMG frequency is fixed at 25 Hz while varying the chemical exchange rate. The total Rex rates for a linear 3-site exchange model were simulated, and the Rex rates for the two 2-site exchange events in a linear 3-site exchange model were approximated by the Carver-Richards equation.
After analyzing the residue function r(…) with respect to different parameters, the grid spacing can be relaxed while retaining enough accuracy for data analysis. The solution library was computed using the grid spacing in the Δω dimension of 0.5 ks−1, the grid spacing in the kex dimension (on the logarithmic scale) of x100.3, the grid spacing in the px dimension of 4%, and the grid spacing in the νCPMG dimension (on the logarithmic scale) of x100.1. The solution libraries consist of 16 points in the Δωab dimension (spanning the domain of 0 to 7.5 ks−1), 31 points in the Δωac dimension (spanning the domain of −7.5 to 7.5 ks−1), 8 points for each of kex,ab and kex,ac dimensions (spanning the domain of 0.1 to 10 ks−1), 6 points for each of pb and pc dimensions (assuming pa > 80%), and 22 points in the νCPMG dimension (spanning the domain of 20 to 2500Hz). Computation of the library took 16 days using a 128-core Linux cluster computer system and consists of approximately 25 million points (approximately 400 MB in size).
All the numerical simulations were performed with modified Bloch-McConnell equation (6X6 for the 2-site exchange and 9X9 for the 3-site exchange) using Euler’s method including the second order correction term. Starting from the initial population, the operators in the transverse plane experience chemical shift evolution, chemical exchange, and intrinsic relaxation following the formulation of Bloch-McConnell equation. The ideal π pulses are applied to invert the signs of the operators at the time according to the νCPMG frequency. The effective relaxation rate for state A (or for state A and state B) is determined at the end of the relaxation period. The Rex rate will be calculated as the difference between the effective relaxation rate and the intrinsic relaxation rate. No errors were introduced for the following data analysis.
All of the following data analyses employed the statistical Monte Carlo sampling method described previously17 and adapted to the 2-site and 3-site exchange models for the CPMG experiment. Input CPMG RD data were simulated using the appropriate Bloch McConnell equations, separately for 2-site and 3-site exchange, and analyses are performed using the combination of geometric approximation and Monte Carlo sampling. The algorithm aims to minimize the distance function between the observed (simulated) relaxation rates and values calculated as geometric approximations from the nearest grid points in the surface library by varying the dynamic parameters. Once the minimum is reached, a set of the dynamic parameters giving relaxation rates closest to the observed ones will be reported. In order to achieve the global minimum, 100 different runs of Monte Carlo sampling from randomized initial dynamic parameters are performed for a given input data set. Each run is composed of 10,000 steps of the random grid search and then 5,000 steps of random-walk during simulated annealing. Among 100 results from 100 different runs of Monte Carlo sampling, the 10 results with the best scores are used for statistical analysis.
3. Results
The application of geometric approximation to the CPMG experiment (geoCPMG) in the 2-site exchange model is straightforward and successful, due to the lower dimensionality of the solution surface and the fine grid spacing. We evaluated the accuracy of the geoCPMG approach by examining the deviation between the direct numerical solution for R2,eff, based on input parameters, and the approximate solution derived either from the standard analytic solution using the Carver-Richards equation13 or the geoCPMG approach. Table 1 illustrates that the geoCPMG approach provides more accurate solutions.
Table 1.
Deviation of the approximate solution surfaces and the approximate analytic solution from the numerical solutions. To compare the approximate solutions with the numerical ones, 10000 random points were chosen. The simulated experimental conditions were also randomly chosen within the νCPMG range of 20~2500 Hz and the constant time range of 30~50 ms. Errors are expressed as percentages of the deviations from the numerical solutions.
| Carver-Richards equation | Geometric approximation | |||
|---|---|---|---|---|
| 2-site exchange | Linear 3-site exchange | |||
| A | A+B | A | ||
| Average deviation | 2.1% | 0.25% | 0.075% | 0.34% |
| Standard deviation | 2.7% | 0.39% | 0.12% | 1% |
| Largest deviation | 31% | 9.2% | 1.9% | 24% |
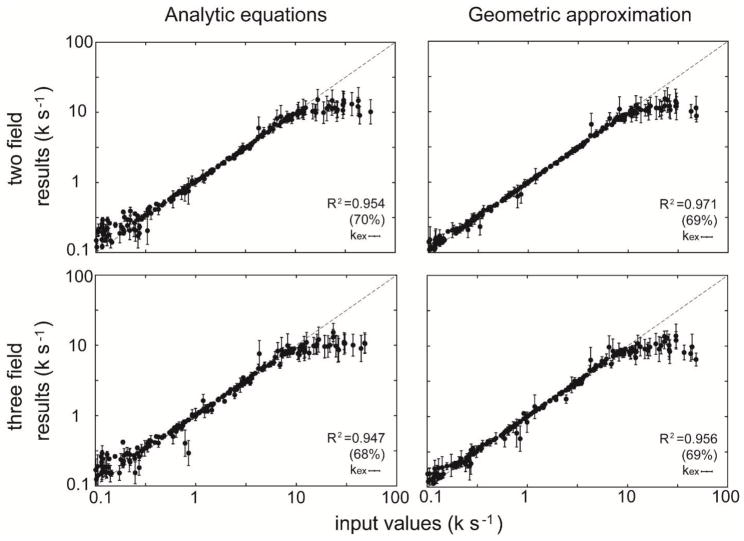
The extraction of dynamic parameters from CPMG RD data was tested using 300 separate data sets simulated for different CPMG frequencies (νCPMG = 25, 50, 100, 125, 250, 500, 1000 Hz). Simulations were performed using either two or three magnetic field strengths. The extracted values of kex are compared to the input values in Fig. 3 and Supp. Fig. 1. Moreover, in terms of the extraction of dynamic parameters from the simulated data, geoCPMG can significantly improve the accuracy in the moderately slow exchange regime (< 300 s−1) (Fig. 3). Overall, the geoCPMG approach provides a very efficient analysis of CPMG RD data and provides slightly better accuracy.
Figure 3.
Fitting the simulated relaxation data of constant-time CPMG experiments (40 ms) in the 2-site exchange model at two (14.1T, and 18.8T) or three (14.1T, 16.5T, and 18.8T) magnetic fields using approximate analytic solutions15,16 or geoCPMG. The 300 data sets of different CPMG frequencies (νCPMG = 25, 50, 100, 125, 250, 500, 1000 Hz) were simulated. The fit results are plotted against the input values, and those with large standard deviations (S.D. of kex > 100.2) during Monte Carlo sampling are not shown. The coefficient of determination (R2) is calculated for each case. The numbers in the parentheses are the percentages of the data remained after filtering out the results with large standard deviations.
Next, we consider the 3-site exchange model presented above, and first investigate the accuracy of the approximate solution surface. The solution surface for the CPMG experiment in the linear 3-site exchange model has an average deviation less than 0.5% from the numerical solution (Tab. 1), but it is 60,000-fold more efficient than that of the numerical one in terms of computation. We found that its accuracy is still better than the conventional analytic solution for the simple 2-site exchange model (Tab. 1) even when the size of the library is significantly reduced. Moreover, in the comparison of the approximate solution and the numerical solution, the constant time period during the numerical simulation is a floating parameter. Therefore, the small average deviation and the small standard deviation imply that (i) the total Rex value is insensitive to the various constant time periods (ranging from 30 ms to 50 ms), and (ii) Rex can be approximated by our solution surface. Statistically, the CPMG experiment in the linear 3-site exchange is dominated by mono-exponential decay in most cases when there exists a dominant state (>80%).
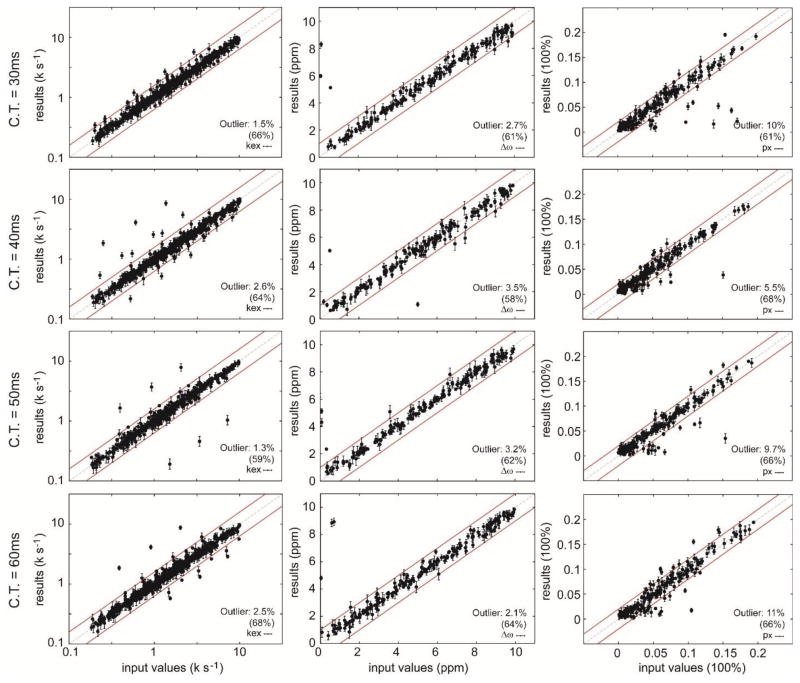
Finally, validation is required to insure that the approximate solution surface can be used to extract accurate dynamic parameters under various experimental conditions. We randomly simulated 300 data sets of the CPMG experiments for each constant time period, and each data set represented two different fields (14.1 T, and 18.8 T) and three different temperatures (280 K, 290 K, and 300 K), where it was assumed that the reaction rates and temperatures follow the Arrhenius equation. Our single solution surface for the linear 3-site exchange model was used to analyze those different data sets. Consistently, we found that our solution surface can generally provide accurate dynamics parameters in the various experimental conditions with only a few outliers (Fig. 4). Interestingly, when the same 300 data sets were analyzed using the solution surface for the simple 2-site exchange model, we found that the average fitting error is below 3% of the simulated values (Supp. Fig. 2), which implies that the relaxation dispersion data generally contain insufficient information to specify an exchange model under common experimental conditions.
Figure 4.
Fitting the simulated relaxation data of constant-time CPMG experiments in a linear 3-site exchange model at different constant time periods for three temperatures (280 K, 290 K, and 300 K) and two magnetic fields (14.1 T, and 18.8 T) using geometric approximation. The νCPMG frequencies for each constant time (C.T.) were given between 25 and 1000 Hz, and the 300 data sets were simulated with random dynamic parameters. The fit results are plotted against the input values, and those with large standard deviations (SD of kex > 100.1, SD of Δω >0.5 ppm, SD of px > 1%) during Monte Carlo sampling are not shown. The kex values include kex,ab and kex.ac at three different temperatures. The Δω values include Δωab and Δωac. The px values include pa, pb, and pc. The percentage of the outliers (outside of the input values by two SD) is calculated for each case. The numbers in the parentheses are the percentages of the data remained after filtering out the results with large standard deviations.
4. Discussion
Originally, the geometric approximation methodology was designed to efficiently provide accurate solutions for the adiabatic relaxation dispersion experiments17. It implied that the approach is very general, and here we have proven that the method also works in a different experimental setting. The generality of this methodology is due to two main factors: (i) the mathematical theorem is aimed at any continuous real function with a compact domain in Euclidean space, and (ii) many sophisticated mathematical problems can be decomposed into a series of simple computable operations. Taking advantage of computational clusters and supercomputing systems, the geometric features of a solution surface can be characterized and saved in a library for future data analysis using standard desktop computers. However, because only limited information can be computed and saved in a file, it is very critical to build a library for the high dimensional solution surface in an efficient way. In the previous study, we accomplished this efficiency by reducing the dimensionality of the solution surfaces. Here, we decomposed the solution surface into the low-dimensional one with more geometric features and the high-dimensional one with less geometric features, which enabled relaxing the grid spacing of the libraries. In a given area, the higher order polynomial functions can approximate more complex geometric features, which allows the approximation of more drastic changes in the curvature of the surface. However, the absolute values and the total fluctuations of the surface are not generally considered as limiting factors in building a high-dimensional surface. Therefore, it is possible to relax the grid spacing by increasing the maximal order of polynomial approximation, but the acceleration in computation will be significantly reduced due to the fact that the number of coefficients to be calculated will grow exponentially. Therefore, in order to successfully apply this new methodology to a problem, it is critical both to compress the size of the library and to efficiently extract the information from the library.
In tests of these new solutions for the CPMG experiment for 2-site and 3-site exchange models, two important facts were found. First, the accuracy of the fit kex and the fit Δω is better than that of the fit population, which may be due to using only one population in our simulated conditions. Second, the CPMG data sets simulated by a linear 3-site exchange model can still be fit well by the solution for the 2-site exchange model in many cases. Even with 6 data sets from multiple temperatures (280 K, 290 K, and 300 K) and magnetic fields (14.1 T, and 18.8 T), the average fitting error is below 3% of the simulated values. Our finding implied that, statistically, it is experimentally difficult to distinguish the 3-site exchange from the 2-site exchange by fitting the data without prior knowledge, such as known chemical shift differences, population differences in the 2-site exchange, or known additional states from crystal structures. On the other hand, even if a given data set can be fit well by the 2-site exchange model, no guarantee can be given for the correctness of the answer without any independent information on the exchange model. Moreover, due to many possible exchange geometries and higher dimensional solution surfaces, our results imply that it is increasingly difficult to clearly identify a specific exchange model in the multi-site exchange case (n>2) using only the relaxation dispersion data. It is worth mentioning that several successful cases have shown it is possible to differentiate multi-site exchange models from the 2-site exchange model through global analysis of multiple nuclei1,8–9. This approach assumes that the relaxation dispersion of multiple nuclei come from the same type of motions, which may not always be the case. The experimental errors may not be completely random and, often, the number of replicate experimental datasets is generally small; hence, it is possible to over-interpret the data based on χ2 values (The true experimental errors may be larger than the measurement errors, and the true experimental values may not be equal to the means of measurement values). Further work is required to determine how to consider global analyses to improve the geometric approximation approach and the possible discrimination between exchange models.
Here, we successfully applied this computational technique to provide the first general solution for the CPMG experiment in a given linear 3-site exchange model. We also show that the CPMG experiment for the linear 3-site exchange model (with a dominant state >80%) is dominated by mono-exponential decay, within the defined domain of our solution surface. The algorithm can provide accurate dynamic parameters for the common experimental conditions with few outliers. In fact, the solution surface can reveal dynamic parameters with the νCPMG frequencies (20~2500 Hz) and constant time periods (30~60 ms) commonly used in the experimental setting. It is also worth noting that, based on our extensive simulations and that of others19, the CPMG experiment will be extremely insensitive for a very long constant time and the data analysis will be complicated and exhibit a greater error for a very short constant time. Finally, this approach serves as an example for building solution surfaces for other models of 3-site exchange, such as a circular 3-site exchange model or a linear 3-site exchange model with the dominant state A at one end.
5. Conclusion
Geometric approximation is a general strategy to provide fast and accurate solutions for data analysis. The solution for the CPMG experiment under either a 2-site or a given linear 3-site exchange model is provided, and the search algorithm based on the solution can determine accurate dynamic parameters in most cases. The analysis method can be applied to any CPMG RD experiment (N, C′, Cα, and Hα), thus providing a general approach for accurate analyses. These results further support the generality of analyzing complex physical processes via the geometric approximation methods. Further work is required to explore the impact of experimental noise and the potential benefits of global and/or multi-nuclei data fitting to provide more robust analyses of 3-site exchange models.
Supplementary Material
Highlights.
New strategy significantly reduces computational time and size of the solution library.
geoCPMG applicable to all relaxation dispersion experiments, e.g. N, C′, Cα, and Hα
Linear 3-site exchange model with a dominant state (>80%) characterized by mono-exponential decay under CPMG.
General solution for a linear 3-site exchange model can determine accurate dynamic parameters.
Acknowledgments
This work was supported by the Intramural Research Program of the National Cancer Institute.
The solution libraries and search algorithm software is available from the authors upon request.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Sugase K, Dyson HJ, Wright PE. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature. 2007;447:1021–1025. doi: 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
- 2.Korzhnev DM, Religa TL, Banachewicz W, Fersht AR, Kay LE. A transient and low-populated protein-folding intermediate at atomic resolution. Science. 2010;329:1312–1316. doi: 10.1126/science.1191723. [DOI] [PubMed] [Google Scholar]
- 3.Henzler-Wildman KA, et al. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 4.Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- 5.Mulder FA, Mittermaier A, Hon B, Dahlquist FW, Kay LE. Studying excited states of proteins by NMR spectroscopy. Nat Struct Biol. 2001;8:932–935. doi: 10.1038/nsb1101-932. [DOI] [PubMed] [Google Scholar]
- 6.Tollinger M, Skrynnikov NR, Mulder FA, Forman-Kay JD, Kay LE. Slow dynamics in folded and unfolded states of an SH3 domain. J Am Chem Soc. 2001;123:11341–11352. doi: 10.1021/ja011300z. [DOI] [PubMed] [Google Scholar]
- 7.Grey MJ, Wang C, Palmer AG., 3rd Disulfide bond isomerization in basic pancreatic trypsin inhibitor: multisite chemical exchange quantified by CPMG relaxation dispersion and chemical shift modeling. J Am Chem Soc. 2003;125:14324–14335. doi: 10.1021/ja0367389. [DOI] [PubMed] [Google Scholar]
- 8.Schneider R, et al. Visualizing the molecular recognition trajectory of an intrinsically disordered protein using multinuclear relaxation dispersion NMR. J Am Chem Soc. 2015;137:1220–1229. doi: 10.1021/ja511066q. [DOI] [PubMed] [Google Scholar]
- 9.Libich DS, Tugarinov V, Clore GM. Intrinsic unfoldase/foldase activity of the chaperonin GroEL directly demonstrated using multinuclear relaxation-based NMR. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:8817–8823. doi: 10.1073/pnas.1510083112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Allerhand A, Gutowsky HS. Spin—Echo NMR Studies of Chemical Exchange. I. Some General Aspects. The Journal of Chemical Physics. 1964;41:2115–2126. doi: 10.1063/1.1696165. [DOI] [PubMed] [Google Scholar]
- 11.Allerhand A, Gutowsky HS. Spin-Echo Studies of Chemical Exchange. II. Closed Formulas for Two Sites. The Journal of Chemical Physics. 1965;42:1587–1599. doi: 10.1063/1.1696165. [DOI] [PubMed] [Google Scholar]
- 12.Allerhand A, Thiele E. Analysis of Carr—Purcell Spin-Echo NMR Experiments on Multiple-Spin Systems. II. The Effect of Chemical Exchange. The Journal of Chemical Physics. 1966;45:902–916. [Google Scholar]
- 13.Baldwin AJ. An exact solution for R2,eff in CPMG experiments in the case of two site chemical exchange. J Magn Reson. 2014;244:114–124. doi: 10.1016/j.jmr.2014.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jen J. Chemical Exchange and Nmr T2 Relaxation - Multisite Case. J Magn Reson. 1978;30:111–128. [Google Scholar]
- 15.Luz Z, Meiboom S. Nuclear Magnetic Resonance Study of Protolysis of Trimethylammonium Ion in Aqueous Solution - Order of Reaction with Respect to Solvent. J Chem Phys. 1963;39:366–370. [Google Scholar]
- 16.Carver JP, Richards RE. General 2-Site Solution for Chemical Exchange Produced Dependence of T2 Upon Carr-Purcell Pulse Separation. J Magn Reson. 1972;6:89–105. [Google Scholar]
- 17.Chao FA, Byrd RA. Geometric Approximation: A New Computational Approach To Characterize Protein Dynamics from NMR Adiabatic Relaxation Dispersion Experiments. J Am Chem Soc. 2016;138:7337–7345. doi: 10.1021/jacs.6b02786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mangia S, Traaseth NJ, Veglia G, Garwood M, Michaeli S. Probing slow protein dynamics by adiabatic R(1rho) and R(2rho) NMR experiments. J Am Chem Soc. 2010;132:9979–9981. doi: 10.1021/ja1038787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yuwen T, Sekhar A, Kay LE. Evaluating the influence of initial magnetization conditions on extracted exchange parameters in NMR relaxation experiments: applications to CPMG and CEST. J Biomol Nmr. 2016;65:143–156. doi: 10.1007/s10858-016-0045-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.