The growth of carbon chains in IRC +10216 mapped with ALMA

Abstract

Linear carbon chains are common in various types of astronomical molecular sources. Possible formation mechanisms involve both bottom-up and top-down routes. We have carried out a combined observational and modeling study of the formation of carbon chains in the C-star envelope IRC +10216, where the polymerization of acetylene and hydrogen cyanide induced by ultraviolet photons can drive the formation of linear carbon chains of increasing length. We have used ALMA to map the emission of λ 3 mm rotational lines of the hydrocarbon radicals C₂H, C₄H, and C₆H, and the CN-containing species CN, C₃N, HC₃N, and HC₅N with an angular resolution of ~1″. The spatial distribution of all these species is a hollow, 5-10″ wide, spherical shell located at a radius of 10-20″ from the star, with no appreciable emission close to the star. Our observations resolve the broad shell of carbon chains into thinner sub-shells which are 1-2″ wide and not fully concentric, indicating that the mass loss process has been discontinuous and not fully isotropic. The radial distributions of the species mapped reveal subtle differences: while the hydrocarbon radicals have very similar radial distributions, the CN-containing species show more diverse distributions, with HC₃N appearing earlier in the expansion and the radical CN extending later than the rest of the species. The observed morphology can be rationalized by a chemical model in which the growth of polyynes is mainly produced by rapid gas-phase chemical reactions of C₂H and C₄H radicals with unsaturated hydrocarbons, while cyanopolyynes are mainly formed from polyynes in gas-phase reactions with CN and C₃N radicals.

1. Introduction

Linear acetylenic carbon chains, with a polyyne (−C≡C)_n−H or cyanopolyyne (−C≡C)_n−C≡N backbone, have long been observed in a wide range of astronomical environments, such as cold molecular clouds, star-forming regions, photon-dominated regions, and the ejecta of evolved stars (Morris et al. 1976; Winnewisser & Walmsley 1978; Guélin et al. 1978; Broten et al. 1978; Bujarrabal et al. 1981; Cernicharo & Guélin 1996; Pardo et al. 2005; Gupta et al. 2009; see Loomis et al. 2016 for a recent disproof of HC₁₁N detection). The chemical synthesis of carbon chains in these environments has been a matter of debate over the years, with hypotheses based on top-down mechanisms involving very small carbonaceous grains or aromatic polycyclic hydrocarbons as precursors (Kroto et al. 1987; Pety et al. 2005), and bottom-up chemical schemes driven by cosmic rays or ultraviolet photons (Herbst & Leung 1989; Fukuzawa et al. 1998; Cernicharo 2004).

Carbon chains are particularly conspicuous in circumstellar envelopes around carbon-rich Asymptotic Giant Branch (AGB) stars, which are also the main factories of carbonaceous dust grains in the Galaxy. Circumstellar envelopes provide an ideal laboratory in which to study the formation of carbon chains because of their relative simplicity in geometry, velocity field, and composition of the precursor material. Because chemical processes take place as matter is ejected from the star through a nearly isotropic outflow, the sequential formation of molecules can be tracked as a function of the radial position in the envelope. The central AGB star is not expected to emit at ultraviolet wavelengths and thus the main source of ultraviolet photons is the ambient radiation field from nearby stars. Chemical models point to a bottom-up scenario in which the formation of carbon chains of increasing length occurs because of ultraviolet-driven polymerization of C₂H₂ and HCN. These small precursors are injected into the expanding wind from the inner circumstellar regions and are photodissociated in the outer circumstellar layers, where the external ambient ultraviolet field is no longer blocked by the circumstellar dust and gas. In these outer regions, the production of the radicals C₂H and CN drives the growth of acetylenic carbon chains (Glassgold et al. 1986; Nejad & Millar 1987; Cherchneff et al. 1993; Cherchneff & Glassgold 1993; Millar & Herbst 1994; Millar et al. 2000; Agúndez 2009; Cordiner & Millar 2009; Li et al. 2014).

Owing to its close proximity and brightness, most observational studies of circumstellar envelopes have focused on the prototypical carbon star envelope IRC +10216. In this source, brightness distributions of rotational lines of the radicals C₂H and CN, and polyyne and cyanopolyyne chains such as C₄H, C₃N, HC₃N, and HC₅N have been mapped using single dish radiotelescopes such as IRAM 30m (Audinos et al. 1994) and radio interferometers such as BIMA (Bieging & Tafalla 1993; Dayal & Bieging 1995), IRAM Plateau de Bure (Guélin et al. 1993, 1997, 1999; Lucas et al. 1995), VLA (Dinh-V-Trung & Lim 2008), and SMA (Patel et al. 2011; Cooksy et al. 2015). Despite their moderate sensitivity and angular resolution (ranging from 2″ to 11″), these observations were able to constrain the presence of C₂H, CN, and the aforementioned carbon chains to an outer hollow shell of a few arcseconds of width located at a distance between 10″ and 20″ from the star. This finding implies that whatever the mechanism of formation of carbon chains in IRC +10216, it is only activated in a very specific region of the outer envelope. However, there are still many open questions such as whether all carbon chains occur precisely in the same circumstellar region or whether there is some degree of radial stratification depending on the carbon chain length. A deeper look into the exact chemical mechanisms behind the formation of carbon chains requires observations with a significantly higher sensitivity and angular resolution.

In this article, we present sensitive ALMA observations of IRC +10216 in several rotational lines of carbon chains across the λ 3 mm band. The observations have an angular resolution of ~1″, which allows us to resolve the detailed structure and to precisely locate the circumstellar regions where the emission of each carbon chain arises. A chemical model has been developed to interpret the observations and to explain the carbon chain chemistry that is taking place in the outer envelope of this archetypal carbon star.

2. Observations

A λ 3 mm spectral survey of IRC +10216 covering the frequency range 84.0-115.5 GHz was carried out with ALMA band 3 during Cycle 2. Observations were obtained with compact and extended array configurations. The field of view (primary beam) of the 12m ALMA antennas ranges from ~69″ at 84 GHz to ~50″ at 115.5 GHz. Additional observations were performed with the IRAM 30m telescope to recover the flux filtered out by the interferometer. Observations were centered on the position of the star, with coordinates $\text{J}2000.0\text{R}.\text{A}.\mathrm{=}{09}^{\text{h}}{47}^{\text{m}}{57}_{.}^{\text{s}}446\text{and}\text{Dec}.\mathrm{=13}\text{°}16^{\prime }{43}_{.}^{″}86,$ according to the position of the λ 1 mm continuum emission peak (Cernicharo et al. 2013). A thorough description of the spectral survey will be presented elsewhere (Cernicharo et al., in preparation). Here, we focus on the large-scale emission of carbon chains. For the emission lines studied here, data from the ALMA compact and extended configurations were merged, after continuum subtraction, with the short-spacings data obtained with IRAM 30m, providing an angular resolution of ~1″.

There are several emission lines from carbon chains in the λ 3 mm ALMA spectrum of IRC +10216. In this article we focus on linear carbon chains of the families of polyynes and cyanopolyynes. With respect to polyynes, we concentrate on the radicals of increasing length C₂H, C₄H, and C₆H, which belong to a chemical series resulting from the addition of C₂ subunits. These radicals are chemical descendants of acetylene and the symmetric polyynes C₄H₂ and C₆H₂, molecules that lack a permanent electric dipole moment and thus cannot be observed at these wavelengths. For cyanopolyynes, we study the emission of the radical CN, the cyanopolyynes HC₃N and HC₅N, and the related radical C₃N. We concentrated on these seven species because they display intense emission lines in the λ 3 mm spectrum of IRC +10216 and share a close chemical relationship as precursors or members of the family of acetylenic carbon chains.

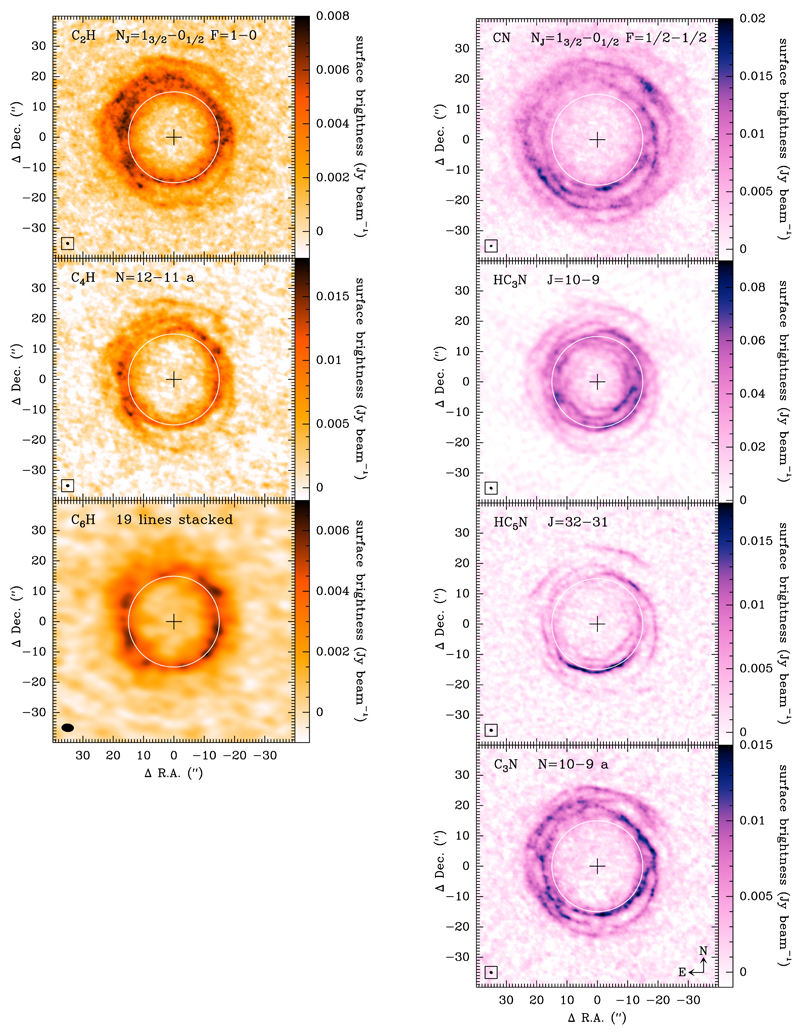
An overview of the spatial distribution of C₂H, C₄H, and C₆H (left side) and CN, HC₃N, HC₅N, and C₃N (right side) is shown in Fig. 1, where we plot the brightness distribution of a representative line of each species, averaged over a velocity range of 3 km s⁻¹ centered at V_LSR = V_sys (where V_sys = −26.5 km s⁻¹ for IRC +10216; Cernicharo et al. 2000). The choice of this velocity range is very convenient for spherically expanding envelopes such as IRC +10216 because the maps show the brightness distribution in a plane perpendicular to the line of sight intersecting the star, allowing us to identify the radial dependence of the emission.

Fig. 1.

Brightness distributions of λ 3 mm rotational transitions of the polyyne-like radicals C₂H, C₄H, and C₆H, and the cyanopolyyne-like species CN, HC₃N, HC₅N, and C₃N, averaged over a velocity range of width 3 km s⁻¹ centered at V_LSR = V_sys. Details on the maps can be found in Section 2. The maps are centered on the star, indicated by a cross, and the synthesized beam (~1″ in all maps but that of C₆H, where it is ~3″) is shown in the bottom left corner of each panel. A white circle of radius 15″ centered on the star is drawn to facilitate comparison among maps.

C₂H and CN. For the small radicals C₂H and CN, only the N = 1 − 0 rotational transition of each falls within the frequency range of the survey. This transition in turn consists of two spin-rotation fine structure components, which in turn are further split into several hyperfine components due to the nuclear spin of the hydrogen (C₂H) or nitrogen (CN) nucleus. Some of the hyperfine components which are blended in the spectrum of IRC +10216 are closer in frequency than half the linewidth, which is given by the terminal expansion velocity of the envelope (14.5 km s⁻¹; Cernicharo et al. 2000), implying that the emission at V_LSR = V_sys for one component is contaminated by blue- or red-shifted emission from the overlapping component. These components are therefore not adequate to trace the spatial distribution of C₂H or CN in the plane of the sky. In the top left panel of Fig. 1 we show the spatial distribution of C₂H through a map of the J = 3/2 − 1/2 F = 1 − 0 component, lying at 87328.625 MHz, which is the most intense free of blending component. In this map the synthesized beam is $1_{.}^{″}07\times 0_{.}^{″}92$ and the rms per 3 km s⁻¹ channel is 0.4 mJy beam⁻¹. In the case of CN, there are various intense non-overlapping components that show similar brightness distributions. The spatial distribution of CN is illustrated in the top right panel of Fig. 1 through the brightness distribution of the J = 3/2 − 1/2 F = 1/2 − 1/2 component, whose rest frequency is 113499.644 MHz. For this map, the synthesized beam is $0_{.}^{″}85\times 0_{.}^{″}74$ and the rms per 3 km s⁻¹ channel is 1.0 mJy beam⁻¹.

C₄H and C₃N. The radicals C₄H and C₃N have four and three, respectively, rotational transitions (each consisting of a spin-rotation doublet) within the frequency range 84.0-115.5 GHz. The brightness distributions of the individual lines of the two species are discussed in Appendix A. In Fig. 1 we show the emission map of a selected line of each of these radicals to illustrate their spatial distributions in IRC +10216. The maps of C₄H and C₃N in Fig. 1 have a similar angular resolution, $1_{.}^{″}\mathrm{14\times }{0}_{.}^{″}98\text{and}{1}_{.}^{″}10\times 0_{.}^{″}92,$ respectively, and sensitivity, with rms levels per 3 km s⁻¹ channel of 1.3 and 0.7 mJy beam⁻¹, respectively.

HC₃N and HC₅N. The cyanopolyynes HC₃N and HC₅N have several rotational transitions within the frequency range covered, three in the case of HC₃N and up to 12 for HC₅N. A detailed discussion on the brightness distributions of the individual lines of the two molecules is also presented in Appendix A. In Fig. 1, the spatial distributions of HC₃N is traced by the emission of the J = 10−9 line in a map with an angular resolution of $1_{.}^{″}\mathrm{08\times }{0}_{.}^{″}81$ and a rms per 3 km s⁻¹ channel of 0.9 mJy beam^-1, while the distribution of HC₅N is illustrated by the emission of the J = 32 − 31 line, with an angular resolution of $1_{.}^{″}11\times 0_{.}^{″}99$ and a rms per 3 km s⁻¹ channel of 0.6 mJy beam⁻¹.

C₆H. The radical hexatriynyl, C₆H, has a plethora of rotational transitions in the λ 3 mm spectrum of IRC +10216, consisting of two series of doublets arising from the ²Π_1/2 and ²Π_3/2 spin-orbit fine structure states, the former lying 21.6 K above the latter. Due to the lower sensitivity of the interferometric data of each individual line, we only considered ALMA data obtained with the compact configuration and stacked the maps of a selected list of 19 lines, all free of blending and observed with a sufficient quality, to obtain a more sensitive map of the spatial distribution of C₆H (see Fig. 1). Because we have omitted the ALMA data obtained with the extended configuration, the angular resolution of the C₆H map is of the order of ~3″, i.e., significantly poorer than in the rest of maps shown in Fig. 1. The set of C₆H lines stacked cover a wide range of upper level energies, 64-86 K for lines from the ²Π_3/2 state and 86-113 K for ²Π_1/2 lines, and thus it is possible that their different excitation requirements result in different brightness distributions. However, we note that on the basis of the behaviour of other molecules such as HC₅N (see Appendix A), such differences are unlikely to be larger than the current angular resolution of ~3″.

3. Observed spatial distributions of carbon chains

A cursory view of the maps shown in Fig. 1 reveals a clear and well-defined ring structure in the seven species studied: the three hydrocarbon radicals C₂H, C₄H, and C₆H, and the four cyanides CN, HC₃N, HC₅N, and C₃N. The maps correspond to the emission at the line center, i.e., at V_LSR = V_sys, and thus indicate how the emission is distributed along a plane perpendicular to the line of sight intersecting the star. The two-dimensional ring structure, together with the emission maps at red- and blue-shifted velocities (not shown in Fig. 1), indicate that the three-dimensional structure of the seven species consists of a hollow spherical shell with a width of 5-10″ located at a distance between 10″ and 20″ from the star. This distribution was already known for most species studied here from previous interferometric maps, albeit at lower angular resolution (see Guélin et al. 1997 and references therein).

The higher angular resolution of the ALMA observations presented here reveals that in fact the broad, 5-10″ wide, hollow shell consists of several clumpy thinner shells of width 1-2″, which are not fully concentric, as indicated by the arcs which cross each other and by a spiral-like structure seen in the ~1″ resolution maps of Fig. 1. This type of substructure was seen earlier in IRC +10216 at larger scales in light scattered by dust grains (Mauron & Huggins 1999; Leão et al. 2006) and in emission from CO (Cernicharo et al. 2015), and has been interpreted in terms of episodic or discontinuous mass loss owing to the presence of a binary companion (Cernicharo et al. 2015). Observations carried out with the VLA at an angular resolution of ~2-3″ also showed that the cm-wavelength emission of HC₃N and HC₅N consists of clumpy shells consistent with a non-isotropic and episodic mass loss process (Dinh-V-Trung & Lim 2008). More recently, high angular resolution ALMA observations of the emission in different molecular lines have also provided hints of departures from the spherical symmetry and spiral-like structures in the inner regions of the envelope (Decin et al. 2015; Velilla Prieto et al. 2015; Agúndez et al. 2015; Quintana-Lacaci et al. 2016). The ~1″ angular resolution maps (see Fig. 1 using white circles as a reference) show that the molecular shell is not exactly centered on the position of the star but shifted by a few arcseconds in the NE direction. It seems as though the shell of carbon chains is compressed from the SW direction, a result that is also observed at larger scales in CO (Cernicharo et al. 2015). It is currently unclear whether this feature is the result of an enhanced ultraviolet illumination from the direction of the Galactic plane (SW) or it is linked to the non isotropic character of the mass loss process. It is noteworthy that, unlike some of the previous observations at lower angular resolution (see, for example, the case of C₂H in Guélin et al. 1997), the maps in Fig. 1 show no evidence of axial symmetry.

The structure of thin shells and inter-crossing arcs is common to the emission distribution of the different species studied (at least for those mapped with ~1″ angular resolution; see Fig 1). These similarities indicate that the maxima of brightness correspond to locations where there is an enhancement in the total volume density of matter, and not in the fractional abundance of a particular species. Such a finding is consistent with some mechanism that has shaped the envelope by driving the mass loss process out of the strictly uniform isotropic character.

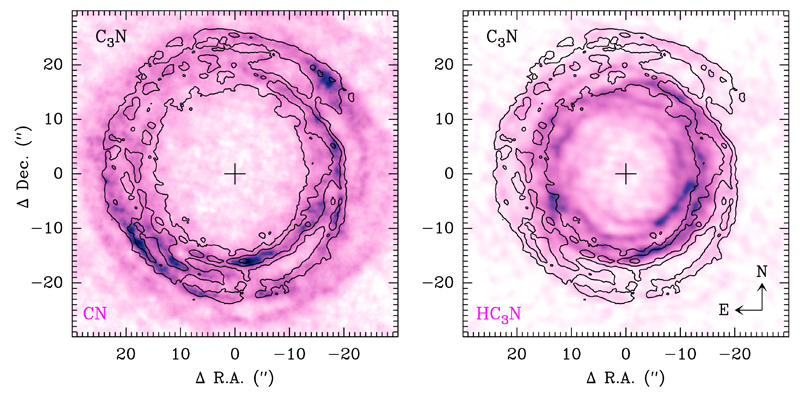
The brightness distributions of different species reveal subtle differences. Even if there is a good match between the arcs and shells seen for different species, when one moves radially from the star some arcs or thin shells that are observed in some species are not seen in others, which provides information about the chemical particularities of each species. This point is illustrated in Fig. 2, where we superimpose the emission distribution of the radical C₃N, shown as contours, on the brightness distribution of the small radical CN and of the cyanopolyyne HC₃N. Referring first to the left panel of Fig. 2, the shells and arcs in C₃N are well matched by CN, although it is also true that CN shows shells beyond ~20″ which are not seen in C₃N. That is, the CN radical extends farther from the star than the radical C₃N. Referring now to the right panel in Fig. 2, we note again that the shells and arcs in C₃N are well matched by similar structures in HC₃N. Also note that the well-defined outer arcs indicated by the lowest contour in the NW and SW directions in C₃N are well matched by tenuous, although appreciable, features in HC₃N. In this case, HC₃N shows shells inward of ~14″ that are not seen in its radical C₃N, which leads us to conclude that, in the framework of an expanding envelope, the cyanopolyyne HC₃N appears in regions where the radical C₃N has not yet been formed.

Fig. 2.

Emission distribution of C₃N N = 10 − 9 (black contours) superimposed on the brightness distribution of CN N = 1 − 0 (color map in the left panel) and of HC₃N J = 10 − 9 (color map in the right panel).

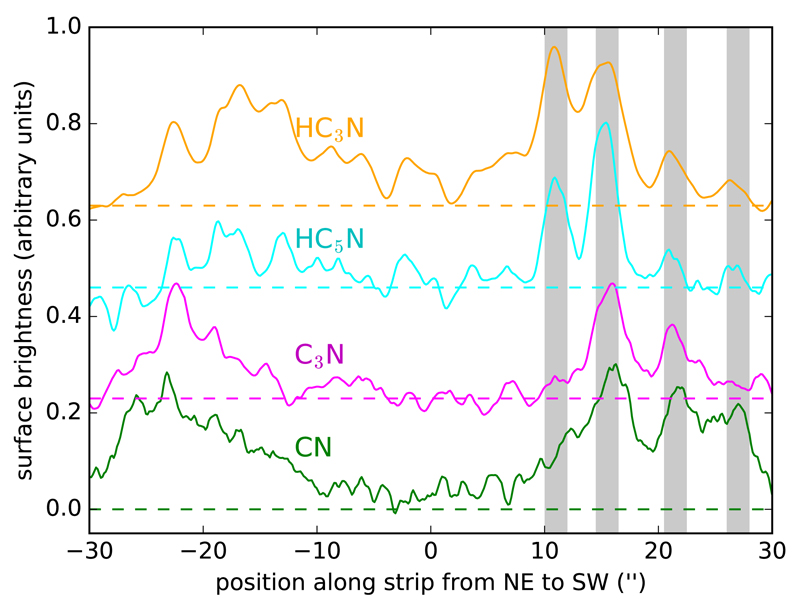
Fig. 3 shows in a different way how emission distributions of different species match each other. In this plot we have extracted the surface brightness along a strip intersecting the star at PA = 45° from the maps of the cyanides CN, C₃N, HC₃N, and HC₅N shown in Fig. 1. There are several aspects that are worthy of comment. First, the brightness distributions along the strip selected are not symmetrical with respect to the position of the star, indicating that the circumstellar shells are not strictly concentric, but instead consist of intersecting arcs and a spiral-like structure. Second, if we focus on the SW direction (positive values along x-axis), there are several shells of width ~2″ at approximately $+{11}^{″},+{15}_{.}^{″}5,+{21}_{.}^{″}5,\text{and}\text{+}27″$ from the star. These shells are however not traced by the four species. The shells at $+{15}_{.}^{″}5\text{and}\text{+}{21}_{.}^{″}5$ are seen in the four species. The shell at +11″ is traced by the cyanopolyynes HC₃N and HC₅N, but not by the radicals C₃N and CN, and the farthest one at +27″ is mostly seen in CN and to a lesser extent in the cyanopolyynes. Therefore, among the four cyanides, the cyanopolyynes appear at shorter radii than their radicals, while the radical CN is the one that extends farther in the envelope.

Fig. 3.

Brightness distributions of the cyanides HC₃N, HC₅N, C₃N, and CN along a strip intersecting the star at PA = 45^°. Curves correspond to the maps shown in Fig. 1 and have been arbitrarily scaled and shifted in the y-axis for display. Horizontal dashed lines indicate the zero of intensity. Grey vertical shadows indicate the positions of brightness maxima in the SW direction from the star, at ${11}^{″},{15}_{.}^{″}5,{21}_{.}^{″}5,\text{and}\mathrm{27″.}$

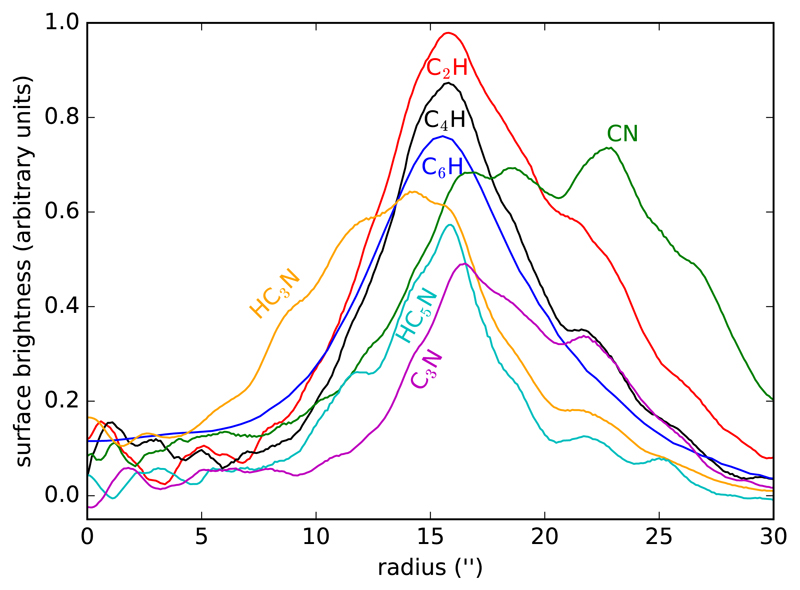
Information on the radial distribution of the species can be obtained by azimuthal average of the brightness distribution (see Fig. 4). The lack of strictly concentric shells, with arcs that cross each other within a spiral-like arrangement, produces a smoothing effect when azimuthally averaging. That is, the spatial resolution is degraded by averaging shells that are not strictly at the same radial position. Still, the information provided by this plot is of great utility in analyzing whether species share the same radial regions or whether there is some degree of stratification as a function of radius. The hydrocarbon radicals C₂H, C₄H, and C₆H reach their maximum brightness at the same radial position, between ${15}_{.}^{″}5\text{and}\mathrm{16″},$ although the smallest one, C₂H, extends somewhat farther than the heavier ones. The cyanides, however, show much more disparate radial distributions. The distribution of HC₃N is the one which is most shifted to inner regions, as it emerges at radii as short as 7″ while the rest emerge at radial distances greater than 10″. The radial distribution of CN is also markedly different from the rest of the species as it extends out to radial distances beyond 30″. As for HC₅N, it appears at the same radial distance than CN and disappears with HC₃N, while the radical C₃N appears somewhat farther than the cyanopolyynes HC₃N and HC₅N. All this information is of great value in understanding the formation mechanism of each of these species in IRC +10216 and will be the subject of further discussion in Section 4.

Fig. 4.

Radial brightness distributions of the hydrocarbon radicals C₂H, C₄H, and C₆H, and of the cyanides CN, HC₃N, HC₅N, and C₃N, calculated by azimuthal average of the brightness distributions shown in Fig. 1. Curves have been arbitrarily scaled in the y-axis for display.

4. Model

The ALMA emission maps of carbon chains obtained toward IRC +10216 provides an excellent opportunity to determine the main chemical processes responsible for their formation along the circumstellar outflow. To this end we have constructed a simple model of IRC +10216 that consists of a spherical envelope of gas and dust which expands around an AGB star with a constant velocity. The parameters of the star and envelope have been taken from Agúndez et al. (2012), i.e., the adopted mass loss rate is 2 × 10⁻⁵ M_⊙ yr⁻¹. For the distance, we use the recent value of 123 pc determined by Groenewegen et al. (2012). First we constructed a chemical model to describe the chemical composition of the gas as it expands, and then we carried out radiative transfer calculation to convert the abundance radial distributions into brightness radial distributions which can be compared with the ALMA observations.

4.1. Chemical model: formation of carbon chains

In the chemical model, the gas is assumed to expand isotropically from an initial radius of 2 × 10¹⁴ cm. We consider as parent molecules at the initial radius H₂, CO, C₂H₂, CH₄, C₂H₄, H₂O, N₂, HCN, NH₃, CS, H₂S, SiS, SiO, SiH₄, PH₃, and HCP, with abundances from Agúndez et al. (2012) and a value of 4 × 10⁻⁵ relative to H₂ for N₂, based on chemical equilibrium calculations and a solar elemental abundance for nitrogen. Of special interest for the formation of carbon chains in the outer envelope are the parent molecules C₂H₂ and HCN, for which the adopted abundances relative to H₂ are 8 × 10⁻⁵ and 4 × 10⁻⁵, respectively (Fonfría et al. 2008). We assume that the envelope is externally illuminated by the local ultraviolet radiation field of Draine (1978). Under the assumption of a smooth envelope and adopting the N_H / A_V ratio of 1.87×10²¹ cm⁻² mag⁻¹ determined for the local interstellar medium by Bohlin et al. (1978), chemical models of IRC +10216 predict that photochemistry occurs at shorter radii than indicated by interferometric observations (see, e.g., discussion in Appendix B of Agúndez & Cernicharo 2006 and Figures 1 and 4 in Cordiner & Millar 2009). For the purpose of reproducing the observed radial location of carbon chains, we have adopted a N_H / A_V ratio 1.5 times lower than the canonical interstellar value of Bohlin et al. (1978), regardless of the implicit assumption on the dust opacity. The adopted cosmic-ray ionization rate of H₂ is 1.2 × 10⁻¹⁷ s⁻¹, a value typical of the local interstellar medium that is well suited for IRC +10216, according to observations of HCO⁺ (Agúndez & Cernicharo 2006; Pulliam et al. 2011). We use a large network of gas-phase chemical reactions, whose rate constants have been taken from the literature on gas-phase chemical kinetics and from the UMIST and KIDA databases (McElroy et al. 2013; Wakelam et al. 2015). More details on the reactions important for the chemistry of carbon chains in IRC +10216 and on the rate constants are given below.

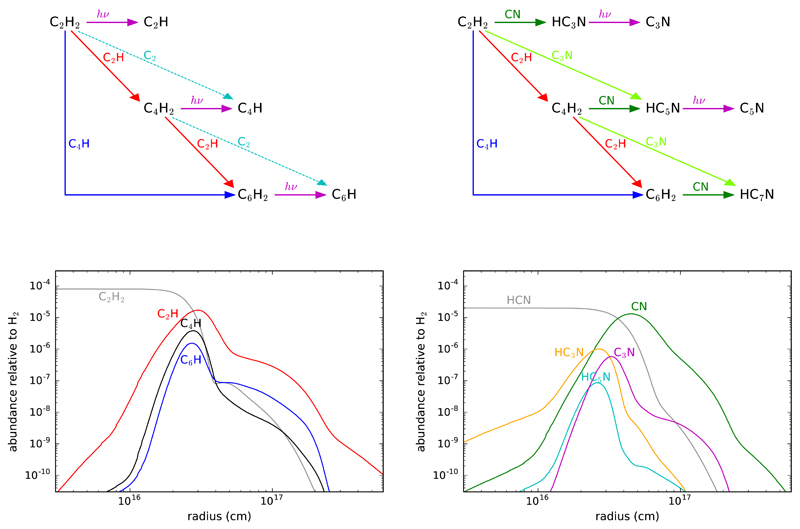
Fig. 5 summarizes some salient features of the chemical model in relation to the growth of carbon chains in IRC +10216. According to the model, the formation of carbon chains begins when the parent molecules C₂H₂ and HCN are photodissociated, in the region of the outer envelope where A_V~1 mag, producing the radicals C₂H and CN. A series of rapid neutral-neutral reactions involving these radicals then drives the growth of carbon chains. The schemes shown on top of Fig. 5, inspired by Millar & Herbst (1994), illustrate the main processes involved in the synthesis of polyynes and cyanopolyynes. The schemes include only those processes which, according to the chemical model, are the main contributors to the formation of each species. Nevertheless, a discussion of the reliability of these schemes and whether other types of reactions may play a role follows.

Fig. 5.

Chemical schemes of growth of polyyne and cyanopolyyne carbon chains in IRC +10216 and calculated fractional abundances as a function of radius.

The formation of carbon chains begins with the photodissociation of C₂H₂ and HCN, whose cross sections are well known from laboratory experiments. We computed photodissociation rates for the local ultraviolet radiation field of Draine (1978) and dust shielding factors (see Table 1) using the Meudon PDR code (Le Petit et al. 2006). For C₂H₂ we adopted the photoabsorption cross section measured by Cooper et al. (1995) and subtracted the photoionization cross section from the compilation by Hudson (1971) to obtain the cross section of photodissociation, which is assumed to yield the C₂H radical with a 100 % efficiency. For HCN, photodissociation is assumed to yield only CN radicals with the cross section measured by Nuth & Glicker (1982). Acetylene photodissociates faster than hydrogen cyanide, which translates into a shorter photodissociation radius for C₂H₂ (see bottom panels in Fig. 5). The photodissociation rates computed here for C₂H₂ and HCN are similar to those given in the compilation of Heays et al. (2017). These authors, however, compute a photodissociation rate of acetylene which is about twice smaller than our value, which would shift the photodissociation radius of C₂H₂ to somewhat outer radii with respect to our predictions.

Table 1.

Important processes for the chemistry of carbon chains in IRC +10216

Process	α	β	γ	ΔT (K)	Notes and references
Bimolecular gas-phase chemical reactionsa
C2H + C2nH2 → C2n+2H2 + H	9.19 × 10−11	−0.29	0	15-295	Based on C2H + C2H2 (Chastaing et al. 1998)
C4H + C2nH2 → C2n+4H2 + H	1.82 × 10−10	−1.06	66	39-300	Based on C4H + C2H2 (Berteloite et al. 2010)
C2 + C2nH2    → C2n+2H + H	3.04 × 10−10	−0.14	0	24-300	Based on C2 + C2H2 (Páramo et al. 2008)
CN + C2nH2   → HC2n+1N + H	2.82 × 10−10	−0.54	22	25-295	Based on CN + C2H2 (Sims et al. 1993)
C3N + C2nH2 → HC2n+3N + H	3.21 × 10−10	−0.12	0	24-294	Based on C3N + C2H2 (Fournier 2014)
Photodissociation processesb
C2H2 + hν  → C2H + H	4.40 × 10−9		2.46		Cooper et al. (1995)
C4H2 + hν  → C4H + H	1.09 × 10−8		2.19		Ferradaz et al. (2009); 100 % C4H + H (Silva et al. 2008)
C6H2 + hν  → C6H + H	1.78 × 10−8		1.83		Kloster-Jensen et al. (1974); Shindo et al. (2003)
HCN + hν   → CN + H	1.93 × 10−9		2.82		Nuth & Glicker (1982)
HC3N + hν → C3N + H	4.55 × 10−9		2.45		Ferradaz et al. (2009)
→ C2H + CN	3.43 × 10−9		2.47		wavelength-dependent branching ratios (Silva et al. 2009)
HC5N + hν → C5N + H	8.84 × 10−9		1.94		Fray et al. (2010)
→ C4H + CN	6.66 × 10−9		1.94		branching ratios of H and CN channels based on HC3N

^aRate constants have units of cm³ s⁻¹ and are given by the expression k(T) = α(T/300)^β exp(−γ/T). ΔT is the valid temperature range of the rate constant expression. The subindex n has values 1, 2, 3, 4, ….

^bPhotodissociation rates have units of s⁻¹ and are given by the expression K = α exp(−γA_v).

4.1.1. Polyynes

The main pathway for forming polyynes of increasing chain length with an even number of carbon atoms involves successive reactions with the radical C₂H,

$${\text{C}}_2\text{H}+{\text{C}}_{2n}{\text{H}}_2\to {\text{C}}_{2n+2}{\text{H}}_2+\text{H},$$ (1)

where diacetylene (C₄H₂) is synthesized when n = 1, triacetylene (C₆H₂) is formed when n = 2, and so on. The reaction between C₂H and C₂H₂ is fast at low temperatures. The measured rate constant in the temperature range 15-295 K shows a slight negative temperature dependence, with values in the range (1.1 – 2.3) × 10⁻¹⁰ cm³ s⁻¹ (Chastaing et al. 1998). There are no measurements of the rate constant at low temperatures for n > 1. The reaction between C₂H and C₄H₂ has been studied theoretically and experimentally using the crossed beams technique (Landera et al. 2008; Gu et al. 2009). These studies indicate that the kinetics of the reaction at low temperatures should be similar to that of the reaction C₂H + C₂H₂, with a rate constant of the same order of magnitude and the H loss channel strongly favored. Reactions of C₂H with polyynes larger than C₄H₂ can be reasonably expected to proceed in a similar way, although there are no experimental or theoretical studies on the kinetics of reaction (1) with n > 2.

Triacetylene (C₆H₂) and larger polyynes are also formed by another route involving the C₄H radical,

$${\text{C}}_4\text{H}+{\text{C}}_{2n}{\text{H}}_2\to {\text{C}}_{2n+4}{\text{H}}_2+\text{H},$$ (2)

where the reaction of C₄H and C₂H₂ has been experimentally found to be rapid at low temperatures, with a rate constant of (1.5 – 2.6) × 10⁻¹⁰ cm³ s⁻¹ in the temperature range 39-300 K (Berteloite et al. 2010). For polyynes larger than C₆H₂, routes similar to reactions (1) and (2) but involving radicals larger than C₄H, such as C₆H and C₈H, are likely to show a similar kinetic behavior (see, e.g., Sun et al. 2015) and thus to contribute significantly to the formation of large polyynes in environments such as IRC +10216.

Once the polyynes have been formed, the corresponding radicals, such as C₄H and C₆H, form directly by photodissociation, although reactions involving C₂ are also important but to a lesser extent. Diacetylene and triacetylene are easily photodissociated owing to their large absorption cross sections in the ultraviolet. The photodissociation rate of C₄H₂ has been computed from the photoabsorption cross section measured by Ferradaz et al. (2009), after subtraction of the photoionization cross section measured by Schwell et al. (2012). The main channel in the photodissociation of C₄H₂ is the production of C₄H radicals (Silva et al. 2008). For C₆H₂, the photoionization cross section has not been measured and therefore the photodissociation rate has been directly computed from the photoabsorption cross section measured by Kloster-Jensen et al. (1974) and Shindo et al. (2003), assuming that the main channel is C₆H + H.

The reactions involving C₂ of interest here are

$${\text{C}}_2+{\text{C}}_{2n}{\text{H}}_2\to {\text{C}}_{2n+2}\text{H}+\text{H},$$ (3)

where the radicals C₄H and C₆H form by addition of C₂ subunits to C₂H₂ and C₄H₂, respectively. The reaction between C₂ and C₂H₂ is rapid at low temperatures, with a rate constant of (2.4 – 4.8) × 10⁻¹⁰ cm³ s⁻¹ in the temperature range 24-300 K (Canosa et al. 2007; Daugey et al. 2008; Páramo et al. 2008). The low-temperature kinetics of reactions of C₂ with C₄H₂ and larger polyynes has not been studied experimentally, and thus in the model we assume that they proceed with the same rate constant as the C₂ + C₂H₂ reaction.

According to the model, reactions (1) and (2) account for the bulk of formation of polyynes in IRC +10216, while the radicals are mainly formed by photodissociation of the corresponding polyynes and by reaction (3). Other types of reactions, which are rapid and might be important synthetic routes in other environments, contribute little in IRC +10216 because they involve reactants which are not abundant enough in this source. For example, neutral carbon atoms and CH radicals have been experimentally found to react rapidly at low temperatures with C₂H₂ (Chastaing et al. 2001; Clary et al. 2002; Canosa et al. 1997; Loison & Bergeat 2009) and they probably react rapidly with C₄H₂ and larger polyynes as well. These reactions tend to produce unsaturated carbon chains with an odd number of carbon atoms and in fact, in the chemical model, are major formation routes to species such as C₃H, C₃H₂, and C₅H, which are abundant in IRC +10216. However, here we focus on the chemistry of carbon chains C_nH and C_nH₂ with n even, species for which reactions involving C atoms and CH radicals are not important.

Molecular anions have been found to play a non-negligible role in the formation of neutral carbon chains in dark clouds (Walsh et al. 2009), and thus it is worth discussing whether they play a similar role in IRC +10216. According to the chemical model, reactions of the type

$${\text{C}}_{2n}{\text{H}}^{-}+\text{H}\to {\text{C}}_{2n}{\text{H}}_2+{\text{e}}^{-},$$ (4)

which are rapid (Eichelberger et al. 2007), appear high in the list of reactions that contribute most to the formation of polyynes, especially at radii beyond ~15″ from the star. However, since the precursor anion C_2nH⁻ is mostly formed from its neutral counterpart C_2nH, which is in turn formed by photodissociation of the respective polyyne C_2nH₂, the net contribution of reaction (4) to the formation of polyynes and growth of carbon chains is essentially zero.

4.1.2. Cyanopolyynes

Cyanopolyynes in IRC +10216 are formed in a bottom-up scenario analogous with polyynes (see scheme on the top-right of Fig.5). We first concentrate on the potentially important synthetic route given by the reaction

$${\text{C}}_{2n}\text{H}+\text{H}{\text{C}}_{2m-1}N\to \text{H}{\text{C}}_{2n+2m-1}N+\text{H},$$ (5)

where the simplest case is with n = 1 and m = 1, which corresponds to the reaction between C₂H and HCN to form HC₃N. The rate constant of this reaction has not been measured at low temperatures but measurements in the temperature range 297-360 K (Hoobler & Leone 1997) and theoretical studies (Fukuzawa & Osamura 1997) point to the presence of an activation barrier of ~800 K that would make the reaction too slow at low temperatures. For this reason, we assume that reaction (5) shows the same kinetic behavior for values of n and/or m higher than one, i.e., for reactions of C₂H, C₄H, or larger radicals with HCN, HC₃N, or larger cyanopolyynes. As a consequence, reaction (5) is not efficient in IRC +10216, and is the reason it does not appear in the scheme on the top-right of Fig. 5. The UMIST and KIDA databases make different assumptions on the kinetic behavior of reaction (5) for n and/or m >1. For example, the UMIST database does not consider these reactions while in the KIDA database some of these, e.g., the reaction C₂H + HC₃N, are assumed to be rapid at low temperatures. It would be of great interest to study the low-temperature chemical kinetics of reactions such as C₂H + HC₃N and C₄H + HCN to clarify whether there are some values of n and m for which reaction (5) is rapid at low temperatures, and thus contributes to the growth of cyanopolyynes in IRC +10216 and in cold interstellar clouds.

If reaction (5) is indeed completely closed at low temperatures, then the growth of cyanopolyynes does not occur at the expense of cyanopolyynes of lower size but at the expense of polyynes in reactions involving the CN radical

$$\text{C}\text{N}+{\text{C}}_{2n}{\text{H}}_2\to \text{H}{\text{C}}_{2n+1}N+\text{H}\mathrm{,}$$ (6)

where C₂H₂ serves as the precursor of HC₃N, the polyyne C₄H₂ for HC₅N, and so on. Reaction (6) with n = 1, i.e., CN + C₂H₂, has been experimentally found to be fast at low temperatures, with a rate constant of (2.6 – 4.7) × 10⁻¹⁰ cm³ s⁻¹ in the temperature range 25-298 K (Sims et al. 1993). Other studies confirm that the reaction proceeds without an activation barrier yielding HC₃N as the main product (Fukuzawa & Osamura 1997; Huang et al. 2000; Choi et al. 2004). Reaction (6) with n = 2, i.e., CN + C₄H₂, is also rapid at room temperature, with a measured rate constant of 4.2 × 10⁻¹⁰ cm³ s⁻¹ (Seki et al. 1996a), although it has not been experimentally studied at low temperatures. Theoretical calculations and crossed beams experiments, however, indicate that the reaction of CN with C₄H₂ as well as those of CN with larger polyynes are rapid at low temperatures and provide an efficient route to large cyanopolyynes (Fukuzawa et al. 1998; Zhang et al. 2009). According to our chemical model, reaction (6) serves as the main formation route to cyanopolyynes in IRC +10216.

For cyanopolyynes larger than HC₃N, there is another important formation route involving the radical C₃N

$${\text{C}}_{\text{3}}\text{N}+{\text{C}}_{2n}{\text{H}}_2\to \text{H}{\text{C}}_{2n+3}N+\text{H}\mathrm{.}$$ (7)

Indeed it has been recently found that the radical C₃N reacts as fast as the radical CN with C₂H₂, with a rate constant of (2.5 – 4.7)×10⁻¹⁰ cm³ s⁻¹ in the temperature range 24-294 K (Fournier 2014). Assuming that the same kinetic behavior holds for C₃N reacting with C₄H₂ and longer polyynes, reaction (7) becomes an important formation route of cyanopolyynes. In fact, in our chemical model reactions (6) and (7) contribute similarly to the formation of HC₅N. Moreover, routes similar to reactions (6) and (7) but involving radicals larger than C₃N, such as C₅N, are likely significant contributors to the formation of cyanopolyynes larger than HC₅N in IRC +10216.

The radicals C₃N and C₅N are mainly formed by direct photodissociation of the corresponding cyanopolyynes, HC₃N and HC₅N, respectively. As with polyynes, cyanopolyynes have large absorption cross sections at ultraviolet wavelengths and are thus easily photodissociated. The photodissociation rate of HC₃N has been computed from the photoabsorption cross section measured by Ferradaz et al. (2009), after subtraction of the photoionization cross section measured by Leach et al. (2014). We have adopted the wavelength-dependent branching ratios computed by Silva et al. (2009) for the two open channels, C₃N + H and C₂H + CN, which are in agreement with experiments (Halpern et al. 1988; Clarke & Ferris 1995; Seki et al. 1996b). In the case of HC₅N, the ionization potential and photoionization cross section are not known, and therefore the photodissociation rate has been computed from the photoabsorption cross section measured by Fray et al. (2010), where we have assumed that the H and CN channels occur with similar branching ratios as for HC₃N.

4.2. Radiative transfer models: emission of carbon chains

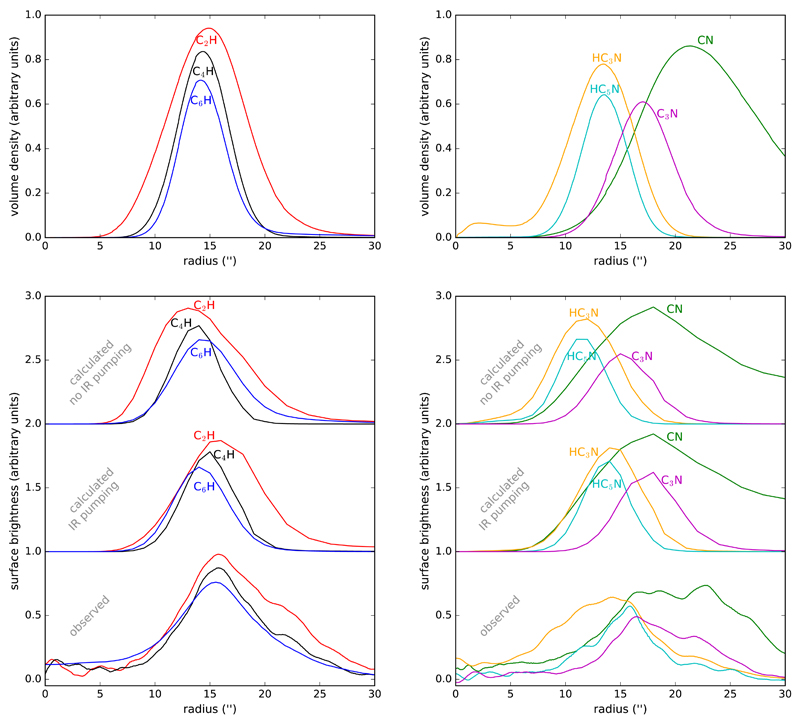
In the top panels of Fig. 6, the abundance radial profiles calculated for C₂H, C₄H, and C₆H (left), and for CN, HC₃N, HC₅N, and C₃N (right) are shown, in which abundances are expressed in absolute rather than relative terms, i.e., as number of particles per unit volume. These abundance distributions provide a good indication of how the rotational emission of each species is distributed as a function of radius in the plane of the sky. Nevertheless, significant differences can arise depending on the transition owing to excitation effects, because of the way the rotational levels are populated through collisions and radiative processes such as infrared pumping at different radii. To take into account these effects we have carried out excitation and radiative transfer calculations to convert the abundance radial distributions into radial brightness distributions of λ 3 mm transitions, which can in turn be compared with the ALMA observations.

Fig. 6.

Top panels.– Calculated radial distributions of abundances expressed as number of particles per unit volume. Curves have been arbitrarily scaled in the y-axis for display. Bottom panels.– Comparison between calculated (neglecting and including infrared pumping) and observed radial distributions of the emission at velocities around V_LSR = V_sys for the lines of C₂H, C₄H, and C₆H (left), and CN, C₃N, HC₃N, and HC₅N (right) plotted in Fig. 1. The observed brightness distributions are those previously shown in Fig. 4. Curves have been arbitrarily scaled and shifted along the y-axis for display.

The radiative transfer calculations have been performed with the multi-shell LVG code and physical model of IRC +10216 used by Agúndez et al. (2012), with the radial abundance distributions calculated with the chemical model. The calculations require spectroscopic and collision excitation data, which have different degrees of accuracy depending on the species and type of data. Rotational constants of the ground vibrational state, and for some species, vibrationally excited states as well, are well known from microwave laboratory experiments: C₂H (Müller et al. 2000; Killian et al. 2007), CN (Klisch et al. 1995), C₄H and C₃N (Gottlieb et al. 1983), C₆H (Linnartz et al. 1999), HC₃N (Thorwirth et al. 2000), and HC₅N (Bizzocchi et al. 2004). Dipole moments have been measured for the radical CN (Thompson & Dalby 1968) and the closed electronic-shell species HC₃N (DeLeon & Muenter 1985) and HC₅N (Alexander et al. 1976), and ab initio theoretical values, with significantly higher uncertainties, have been calculated for the radicals C₂H, C₄H, C₆H (Woon 1995), and C₃N (McCarthy et al. 1995).

In addition to thermal excitation via collisions with H₂ and He, absorption of infrared photons and pumping to excited vibrational states, followed by radiative decay to rotational levels in the ground vibrational state, is an important excitation mechanism of molecules in IRC +10216 (Deguchi & Uyemura 1984; Agúndez & Cernicharo 2006; González-Alfonso et al. 2007; Agúndez et al. 2008, 2015; Cordiner & Millar 2009; Daniel et al. 2012; De Beck et al. 2012). Here, we have included excitation through infrared pumping for all studied species, mostly through bands lying in the mid infrared, where the flux in IRC +10216 is large (Cernicharo et al. 1999). In the case of the radicals, to facilitate the excitation and radiative transfer calculations, we have collapsed the fine rotational structure and simply treated these species as linear molecules with a ¹Σ electronic state. For C₂H, we have included the first four vibrationally excited states of the bending mode (ν₂ = 1, 2, 3, 4), and the first vibrationally excited states of the stretching modes (ν₁ = 1 and ν₃ = 1). The vibrationally excited state that plays the most important role, via infrared pumping, in the excitation of C₂H in IRC +10216 is ν₂ = 1, which lies 371 cm⁻¹ above the ground vibrational state. The wavelengths and strengths of the vibrational bands have been taken from Tarroni & Carter (2004). For the radical CN, we have included the v = 0 → 1 band, lying at 2042 cm⁻¹ (Hübner et al. 2005; Brooke et al. 2014), which however plays a minor role on the excitation of the λ 3 mm lines in IRC +10216. For HC₃N, we have included the first excited states of the vibrational bending modes ν₅ and ν₆, which have strong fundamental bands at 663 and 498 cm⁻¹. The wavelengths and strengths of the vibrational bands are from the compilation by J. Crovisier¹, which are based on extensive laboratory work (e.g., Uyemura et al. 1982; Jolly et al. 2007). For cyanodiacetylene, we have included the first excited states of the vibrational bending modes ν₇ and ν₈, whose calculated fundamental bands, lying at 566 and 685 cm⁻¹, have been found to be important for the rotational excitation of HC₅N in IRC +10216 (Deguchi & Uyemura 1984). For the radicals C₄H, C₆H, and C₃N there is little information on the wavelengths and strengths of vibrational bands. For these species we have instead included a generic vibrationally excited state lying at 15 µm above the ground vibrational state, with an Einstein coefficient of spontaneous emission of 5 s⁻¹ for the P(1) transition of the vibrational band. A similar treatment, with slightly different parameters, was adopted for C₄H and C₆H by Cordiner & Millar (2009).

Rate coefficients for rotational excitation induced by collisions with H₂ and He are scarce in the literature for the species studied here. We have adopted the rate coefficients calculated by Dumouchel et al. (2010) for HCN in collisions with He, properly corrected by the square root of the ratio of reduced masses with He and H₂, for the excitation of the radicals C₂H and CN. Green & Chapman (1978) calculated rate coefficients for the excitation of HC₃N in collisions with He, and those values, corrected for H₂ and extrapolated to higher J levels through the IOS approximation when needed, have been used for HC₃N as well as for the radicals C₃N and C₄H. For the longer carbon chains HC₅N and C₆H, we have adopted collision rate coefficients from the approximate generic expression given by Deguchi & Uyemura (1984).

The calculated radial distributions of brightness in the plane of the sky are shown in the bottom panels of Fig. 6, in comparison with the observed ones. We leave the discussion of the comparison between calculated and observed emission distributions for Section 5 and focus here on the comparison between radial distributions of abundance and emission (top panels and upper and middle curves in bottom panels of Fig. 6). When infrared pumping is neglected and rotational excitation occurs exclusively through collisions with H₂ and He (upper curves in bottom panels of Fig. 6), calculations show that the radius where the λ 3 mm emission is maximum does not exactly coincide with where the number of particles per unit volume is maximum. In general, the emission tends to peak a few arcseconds inward from where the abundance is maximum. This is evident in C₂H, CN, C₃N, and the cyanopolyynes HC₃N and HC₅N. The origin of this effect is that the circumstellar envelope has strong radial gradients of density and temperature. More internal regions are characterized by denser and warmer gas, and the excitation of rotational levels by collisions is more favorable. Thus, the radius of maximum brightness represents a compromise between a high absolute abundance and a high excitation rate through collisions. The shift to shorter radii of the maximum of brightness becomes more pronounced for high-J transitions, whose upper levels are high in energy and are more difficult to excite through collisions in the lower density environments.

The situation may change significantly when infrared pumping to excited vibrational states is included in the calculations (middle curves in bottom panels of Fig. 6). If a species has strong vibrational bands at wavelengths at which the flux of infrared photons in the envelope is high, then infrared pumping may dominate over collisions in exciting the rotational levels of the ground vibrational state. Our calculations indicate that for most of the species studied here, infrared pumping plays an important role in the excitation of the λ 3 mm lines, and in some cases has important consequences for the emerging line intensities and radial distributions of the brightness. Infrared pumping tends to increase the excitation temperatures of the rotational transitions of the ground vibrational state and the intensities of the rotational lines, and extends the emission region to outer locations in the envelope. The importance of this effect, however, varies depending on the species and transition. Among the species studied here, infrared pumping has a marked effect on the brightness radial distribution of the λ 3 mm lines of C₂H (through absorption of 27 µm photons and pumping to the ν₂ = 1 state), HC₃N (by excitation of the ν₅ = 1 and ν₆ = 1 states with 15 µm and 20 µm photons), and HC₅N (exciting the ν₇ = 1 and ν₈ = 1 states with 14.6 and 17.7 µm photons). In contrast, there is little effect of infrared pumping on the emission distribution of the N = 1 – 0 line of CN, which can only be pumped by 4.9 µm photons through the fundamental band of the stretching mode of the C–N bond. In the case of the radicals C₄H, C₆H, and C₃N, the hypothesized vibrational band at 15 µm has different effects on the λ 3 mm emission distribution of each species, the effects being more marked for C₃N, somewhat less important for C₄H, and of little importance for C₆H. We however would like to stress that the lack of knowledge of the wavelengths and strengths of vibrational bands for these three radicals create significant uncertainties in the predicted brightness radial distributions. Moreover, the presence of density enhancements in the form of arcs, which are not included in the current model, will increase the importance of collisions with respect to infrared pumping, modifying the relative roles of both processes in the excitation of the λ 3 mm lines.

In summary, although the abundance radial distribution provides a good, first-order estimate of how the λ 3 mm emission is distributed radially, there can be shifts of up to several arcseconds depending on the peculiarities of the excitation of each species.

5. Discussion

A comparison between the observed and calculated λ 3 mm emission distributions of carbon chains allows us to draw conclusions about the formation mechanism of carbon chains in IRC +10216. For this discussion we focus on Fig. 6, specifically on the bottom panels, where calculated and observed brightness radial distributions are compared. We concentrate on the emission distributions calculated when infrared pumping is taken into account (middle curves in bottom panels of fig. 6), which are more realistic than those obtained when excitation by collisions is only considered (upper curves in bottom panels of fig. 6), even if just an approximate treatment of the pumping scheme is adopted, as occurs for the radicals C₄H, C₆H, and C₃N. Before drawing firm conclusions, we must keep in mind that the observed brightness radial distributions are the result of an azimuthal average of the brightness distributions shown in Fig. 1. These maps show the existence of an azimuthal structure, with shells that are not strictly concentric, as indicated by the presence of inter-crossing arcs, probably the consequence of a mass loss process that is not strictly continuous and isotropic. Because the envelope in our model is the result of an isotropic uniform mass loss process, and the angular resolution has been degraded in the observational data owing to the azimuthal average, the comparison between the calculated and observed emission distributions can only be done to first order, and not at the sub-arcsecond level.

Observations locate the emission of the three hydrocarbon radicals C₂H, C₄H, and C₆H at the same radial position in the envelope, with maxima between ${15}_{.}^{″}5$ and 16″ from the star. It is remarkable that the chemical model also predicts a similar behavior of the abundance radial profiles, with a slight radial stratification in which the radial position decreases as the size of the radical increases (see top-left panel in Fig. 6). This radial stratification is slightly more marked when abundances are converted into brightness distributions (middle curves in bottom-right panel of Fig. 6), although the predictions for C₄H and C₆H have to be viewed with caution due to the approximate treatment of infrared pumping. Taking into account that the formation of these radicals in the chemical model occurs sequentially with respect to increasing size (see scheme on the top-right of Fig. 5), one might intuitively expect that the time delay needed to produce an increase in the size of the carbon chain (e.g., to go from C₂H to C₄H via the reaction C₂H + C₂H₂ followed by the photodissociation of C₄H₂) should result in a radial shift, in which the larger carbon chains should appear later in the expansion, and thus farther from the star. Such behaviour is neither predicted by the chemical model nor observed in the maps, which is a consequence of the rapidity at which photochemistry takes place compared with the expansion of the envelope in IRC +10216. This finding is important, since it limits the use of the brightness radial distributions of C₂H, C₄H, and C₆H as a chemical clock. The chemical model predicts that a significant radial stratification with hydrocarbon radicals C_2nH of increasing size would take place only if the chemical reactions were significantly slower or the expanding wind were significantly faster. We stress that this conclusion is reached using numerical simulations to model the circumstellar chemistry, and that simple timescale arguments may lead to erroneous conclusions.

The CN-bearing species show more diverse brightness radial distributions than the hydrocarbon radicals as a result of a slightly different chemistry. We first note that the emission of the radical CN shows a rather broad radial distribution, extending to radii greater than 30″. This observational fact is correctly predicted by the chemical and excitation model. The slower photodissociation rate of HCN, compared to that of C₂H₂, is at the origin of the much more extended radial distribution of CN emission with respect to that of C₂H. A second interesting aspect is that the observed emission of HC₃N appears at rather short radial distances (i.e., inner to 10″), a fact that is fairly well reproduced by the model. Such an early appearance is related to the fact that HC₃N is mainly formed in the reaction between C₂H₂, a parent molecule which is injected from the innermost circumstellar regions and is destroyed by photodissociation in the outer envelope, and CN, a daughter species that is formed by photodissociation of HCN. Therefore, HC₃N must be formed when the abundances of both reactants, having nearly complementary distributions, are high enough. This situation occurs in a transition region of the envelope where the abundance of acetylene decreases as the gas expands while that of CN increases. Thus, species whose direct precursor is a parent species may be considered as first-generation daughter species as opposed to second-generation daughter species, which are instead formed from precursors that are themselves daughter species. First-generation daughter species, such as HC₃N, thus tend to appear earlier in the expansion than second-generation daughter species, such as the radicals C₄H, C₆H, and C₃N. The observed emission of the longer cyanopolyyne HC₅N rises at larger radii than that of HC₃N, an observational fact that is not reproduced by the model, which instead predicts similar radial distributions for both cyanopolyynes in terms of both the abundance and the λ 3 mm emission. The early appearance of HC₅N in the model can be traced to the important contribution of the formation route involving the C₃N + C₂H₂ reaction, which involves as reactant the parent species C₂H₂ and thus occurs in inner regions than the other important HC₅N-forming reaction CN + C₄H₂. Stated differently, the model predicts for HC₅N a more marked character of first-generation daughter species than suggested by observations. The discrepancy for HC₅N is more likely due to the chemical model rather than to the excitation and radiative transfer calculations.

An interesting piece of information is provided by the availability of observational data for the electronic closed-shell molecule HC₃N and its photodissociation descendant C₃N. The observations show that the brightness distribution of C₃N is shifted to outer radii with respect to that of HC₃N (see bottom-right panel in Fig. 6), a result that is well reproduced by the current model. This result suggests that analogous pairs of species, whose spatial distribution may be more difficult to map, may behave similarly as, for example, occurs for the pair HC₅N/C₅N, in which the rotational lines of the radical are too weak to map, or the pairs C₄H₂/C₄H and C₆H₂/C₆H, where the polyynes lack a permanent dipole moment.

A last aspect that is worth discussing concerns the fact that the model assumes a density radial distribution that decreases smoothly with increasing radius, while observations show that a good fraction of the circumstellar matter is locked into clumpy arcs. The non-uniform density structure can affect the abundance and emission radial distributions of the molecules in different ways. First, external ultraviolet photons can penetrate more easily through the regions between clumps where the density of gas and dust is depressed, allowing photochemical processes to take place inside the envelope (Decin et al. 2010; Agúndez et al. 2010). This effect can explain the formation in inner circumstellar regions of some key molecules such as the hydrides H₂O and NH_3, for which conventional chemical models are not able to account for their formation. In contrast, our ALMA observations show that carbon chains, which are efficiently produced by photochemistry, are confined to the outer envelope, with no or little presence in inner regions. The action of photochemistry in the inner envelope must therefore affect only a few selected regions or be selective with respect to the formation of different types of molecules owing to, for example, temperature effects (warm photochemistry in inner regions vs. cold photochemistry in the outer envelope). Second, the existence of shells and arcs where the density is enhanced over the surrounding medium may provide shelters to carbon chains, because the enhanced densities boost the rates of carbon chain-forming reactions and provide a more efficient shielding against photodestruction. Higher densities also increase the rates of rotational excitation by collisions with H₂ and He. Density-enhanced shells may therefore provide environments where both the fractional abundance and the emission in rotational lines of carbon chains are enhanced over the surrounding medium. These effects have been studied by Brown & Millar (2003) and more recently by Cordiner & Millar (2009) in a spherical model of the envelope with shells located at specific radii where densities are enhanced over the surrounding circumstellar medium. The model predicts that the radial distribution of carbon chains narrows and the rotational emission is mainly confined to the shells of enhanced density. Some features observed with the IRAM and VLA interferometers (Guélin et al. 1997, 1999; Dinh-V-Trung & Lim 2008) are reproduced by this model, but there are important discrepancies for species such as C₄H. In view of the rich azimuthal structure revealed by the ALMA maps, next generation chemical models of IRC +10216 will probably need to relax the spherical assumption and to either study the chemistry radially at different PA in the plane of the sky or move to a three-dimensional model of the envelope that takes into account the entire structure of shells and arcs which make up the circumstellar envelope.

6. Concluding remarks

We have carried out a combined observational and modeling study to understand the growth of carbon chains in the C-star envelope IRC +10216. We have used ALMA to map at high sensitivity and high angular resolution the emission of λ 3 mm rotational lines of the hydrocarbon radicals C₂H, C₄H, and C₆H, and the CN-containing species CN, C₃N, HC₃N, and HC₅N. All of these species are distributed in a hollow spherical shell of width 5-10″ located at a distance of 10-20″ from the star, and none show appreciable compact emission around the star. The broad 5-10″ wide hollow shell seen at an angular resolution of ~1″ shows various thin shells of width 1-2″, which are not strictly concentric, pointing to a discontinuous and non-isotropic mass loss process that could be driven by the presence of a companion star. The hydrocarbon radicals C₂H, C₄H, and C₆H show very similar radial distributions, while the CN-containing species show a radial stratification, with HC₃N appearing at shorter radii and the CN radical extending out to larger radii. This behavior is reasonably well reproduced by our chemical model, which validates a scenario of carbon chain growth initiated by photodissociation of acetylene and hydrogen cyanide, rapid gas-phase chemical reactions of C₂H and C₄H radicals with unsaturated hydrocarbons as the main mechanism responsible for the growth of polyynes, and reactions of CN and C₃N radicals with unsaturated hydrocarbons as the dominant formation routes to cyanopolyynes.