Arctic greening from warming promotes declines in caribou populations

A greener Arctic does not benefit caribou; the shift in tundra vegetation due to warming is associated with declining caribou herds.

Abstract

The migratory tundra caribou herds in North America follow decadal population cycles, and browsing from abundant caribou could be expected to counteract the current climate-driven expansion of shrubs in the circumpolar tundra biome. We demonstrate that the sea ice cover in the Arctic Ocean has provided a strong signal for climate-induced changes on the adjacent caribou summer ranges, outperforming other climate indices in explaining the caribou-plant dynamics. We found no evidence of a negative effect of caribou abundance on vegetation biomass. On the contrary, we found a strong bottom-up effect in which a warmer climate related to diminishing sea ice has increased the plant biomass on the summer pastures, along with a paradoxical decline in caribou populations. This result suggests that this climate-induced greening has been accompanied by a deterioration of pasture quality. The shrub expansion in Arctic North America involves plant species with strong antibrowsing defenses. Our results might therefore be an early signal of a climate-driven shift in the caribou-plant interaction from a system with low plant biomass modulated by cyclic caribou populations to a system dominated by nonedible shrubs and diminishing herds of migratory caribou.

INTRODUCTION

The populations of migratory tundra caribou (Rangifer tarandus Linn.) in North America show synchronized, cyclic, or quasi-cyclic fluctuations with a periodicity in the range of 40 to 90 years (1–3). The mechanisms behind the fluctuations are largely unknown but could be related to climatic oscillations (4, 5), density-dependent interactions with forage plants (6, 7), or interactions with predators (8). The recent warming of the Arctic has been accompanied by increasing vegetation biomass (9–11) mainly attributed to the expansion of tall, deciduous shrubs into the tundra ecosystems (12–15). This “shrubification” is expected to alter important attributes of the ecosystem such as carbon sequestration, snow cover, productivity, fire regimes, and hydrology (13). However, experimental enclosure studies (7, 16–18) as well as large-scale observational studies (19–21) suggest that grazing, browsing, and trampling by caribou and other herbivores could counteract the current changes in Arctic vegetation [see the review by Christie et al. (22)]. From these observations, one could expect that tundra vegetation biomass would be inversely related to the cyclic abundance of migratory caribou and, furthermore, that lagged density-dependent interactions with forage plants might play a role in sustaining the cyclicity of the populations. Here, we analyze population data from 11 migratory tundra caribou herds across North America from Alaska to Labrador (Fig. 1A). We ask how the population dynamics for the last 35 years have been related to climate, measured by summer temperatures, snow cover and sea ice cover close to the summer ranges, and to vegetation biomass measured by the normalized difference vegetation index (NDVI).

Fig. 1. Population dynamics of migratory tundra caribou herds in Arctic North America.

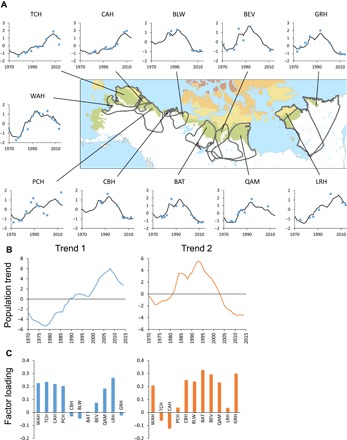
(A) Graphs are standardized (log-transformed and z-scored) caribou population data (blue filled circles) and population trends (black lines) fitted by a DFA model, including two common trends. The map shows the tundra biome (colored areas) and herd ranges (gray lines). (B) Population trends derived from the DFA model and (C) the corresponding factor loading for each caribou herd. Herd identity is indicated by a three-letter code (from west to east).

RESULTS

Caribou population trends

Dynamic factor analysis (DFA) (23) revealed two major population trends across the 11 caribou herds (Fig. 1). Both trends showed a minimum during the mid-1970s and an increase during the 1980s and early 1990s. Trend 2 reached a maximum in 1994 and has been decreasing since then, whereas trend 1 continued to increase until 2008. Thus, the major difference between the two trends was that trend 1 reached a maximum about 14 years later than trend 2 (Fig. 1B). Except for the Porcupine herd (PCH), which has followed a different pattern, combinations of the two trends produced a relatively close fit to the census data (Fig. 1A). Herds with a maximum around 2008 (that is, trend 1) included two herds in Alaska [the Teshekpuk Lake caribou herd (TCH) and the Central Arctic caribou herd (CAH)] and the George River herd (GRH) in Québec and Newfoundland and Labrador. Herds with a maximum around 1994 included five herds in Central Canada [the Cape Bathurst herd (CBH), the Bluenose-West herd (BLW), the Bathurst herd (BAT), the Beverly herd (BEV), and the Qamanirjuaq herd (QAM)], the Western Arctic Herd (WAH) in Alaska, and the Leaf River herd (LRH) in Québec. Thus, there was no strong systematic west-to-east gradient in the loadings of the two trends (Fig. 1C), suggesting that the population maximum was reached in different years depending on regional or local factors. In short, the herds have therefore followed similar population trends across the continent, but the timing of the population maximum differed between herds on a local or regional scale.

Structural equation models of caribou population dynamics, climate, and NDVI

Except for the May temperature, the climate variables showed a dominating warming trend during the study period (1979–2015) in all summer pastures (Fig. 2 and table S1). The most pronounced indication of warming was the shrinkage of the annual sea ice (Pearson’s r = −0.67), followed by an earlier date of snow melt (Pearson’s r = −0.38). NDVI during May showed no particular trend, whereas NDVI from June to August showed a strong increasing trend in all summer ranges (Fig. 2 and table S1).

Fig. 2. Time series of climate indicators and NDVI.

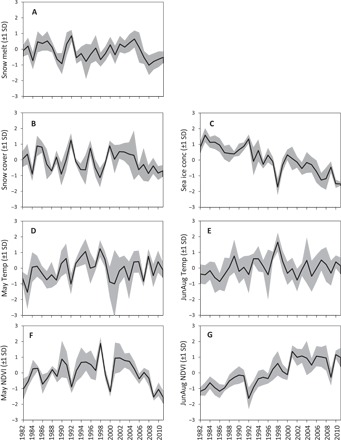
Bold lines represent the average, and gray areas represent the variance (SD) among the 11 caribou summer pastures. All data were z-scored with respect to caribou herd. (A) Date of snow melt. (B) Annual snow cover. (C) Annual sea ice concentration. (D) May temperature. (E) June-to-August temperature. (F) May NDVI. (G) June-to-August NDVI.

The causal diagram outlining the hypothesized relationships between climate, plant biomass on the spring and summer pastures, and caribou population dynamics is shown in Fig. 3. The diagram served as a basis for the formulation of the structural equation (SE) models where we tested the relationships between herd size, climate variables, May NDVI, June-to-August NDVI, and caribou population growth. The influences of the different climate variables were examined in separate models. Moreover, to explore the impact of time lags between the environmental variables and the resulting population dynamics, we constructed models with time lags between the NDVI and climate data and the caribou data (see Materials and Methods). The five different climate variables were modeled with four different time lags, resulting in 20 separate SE models (Table 1). For each model, we initially included all possible links according to the causal diagram and then successively removed nonsignificant (α = 0.05) terms guided by the Akaike information criterion (AIC) (see Materials and Methods). Model fit and parameter estimates are reported in Table 1.

Fig. 3. Causal diagram of the relationship between climate, plant biomass, and caribou.

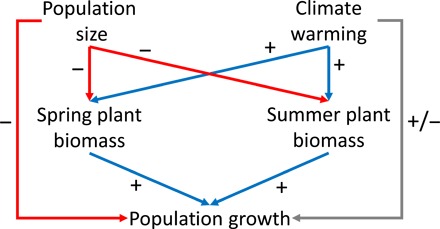
The diagram represents the hypothesized paths in the causal network linking population size, climate, plant biomass on spring and summer pastures, and population growth. The network was used as a basis for the formulation of the SE models. A warmer climate was expected to increase the plant biomass on the spring and summer pastures with favorable consequences for caribou population growth. However, climate could also affect population growth through other pathways such as forage availability or insect harassment. We expected increased herd size to reduce population growth either through reduced plant biomass due to increased grazing or through other negative density-dependent mechanisms.

Table 1. SE models with different climate variables and time lags.

Initial models were formulated according to the causal diagram in Fig. 3. For each model, nonsignificant (P ≥ 0.05) terms were removed successively using the AIC. Asterisks (*) indicate removed terms. Bold numbers indicate parameter estimates significantly (P < 0.05) different from zero. RMSEA, root mean square of approximation; CFI, confirmatory fit index; NS, not significant.

Model specification		Model fit						Standardized parameter estimates
Climate variable included in the model	Time lag (years)	χ2 (df, P value)	CFI	RMSEA	R2 endogenous variables			May NDVI		JunAugNDVI		Population growth
					May NDVI	JunAug NDVI	Population growth	Climate variable	Population size	Climate variable	Population size	Climate variable	Population size	May NDVI	JunAug NDVI
Annual sea ice concentration	0	0.43 (1, 0.51)	1	0	0.143	0.588	0.286	0.23	0.32	−0.77	*	0.25	−0.14	*	−0.29
	1	0.63 (3, 0.89)	1	0	0.148	0.530	0.230	0.25	0.30	−0.73	*	*	*	*	−0.48
	2	0.53 (3, 0.91)	1	0	0.117	0.477	0.210	0.21	0.26	−0.69	*	*	*	*	−0.46
	3	0.39 (2, 0.82)	1	0	*	0.572	0.149	*	*	−0.73	−0.15	*	*	*	−0.39
Date of snowmelt	0	0.28 (1, 0.59)	1	0	0.154	0.140	0.285	0.24	0.34	−0.37	*	−0.18	−0.15	*	−0.55
	1	1.02 (3, 0.80)	1	0	0.079	0.139	0.264	*	0.28	−0.37	*	−0.21	*	*	−0.55
	2	1.28 (4, 0.87)	1	0	0.065	0.040	0.210	*	0.26	−0.20	*	*	*	*	−0.46
	3	0.42 (2, 0.81)	1	0	*	0.083	0.149	*	*	−0.20	−0.22	*	*	*	−0.39
Annual snow cover	0	0.57 (1, 0.45)	1	0	0.146	0.068	0.288	0.22	0.33	−0.26	*	−0.19	−0.14	*	−0.53
	1	2.84 (3, 0.42)	1	0	0.071	0.083	0.308	*	0.27	−0.29	*	−0.26	*	0.16	−0.57
	2	2.34 (4, 0.67)	1	0	0.068	0.013	0.211	*	0.26	*	*	*	*	*	−0.46
	3	0.37 (1, 0.54)	1	0	*	0.043	0.149	*	*	*	−0.21	*	*	*	−0.39
May temperature	0	3.07 (3, 0.38)	0.998	0.017	0.191	0.025	0.246	0.29	0.31	0.19	*	*	*	*	−0.50
	1	2.85 (3, 0.42)	1	0	0.156	*	0.259	0.29	0.24	*	*	*	*	0.13	−0.49
	2	3.39 (3, 0.34)	0.988	0.042	0.232	*	0.224	0.42	0.19	*	*	*	*	*	−0.47
	3	3.99 (4, 0.41)	1	0	0.144	0.083	0.149	0.35	*	*	−0.23	*	*	*	−0.39
June-to-August temperature	0	3.28 (4, 0.51)	1	0	0.107	0.045	0.246	*	0.33	0.21	*	*	*	*	−0.50
	1	1.43 (3, 0.70)	1	0	0.070	0.100	0.287	*	0.27	0.32	*	−0.21	NS	0.13	−0.43
	2	1.16 (3, 0.76)	1	0	0.066	0.031	0.248	*	0.26	0.18	*	−0.20	*	*	−0.42
	3	1.51 (2, 0.47)	1	0	*	0.075	0.149	*	*	0.18	−0.23	*	*	*	−0.39

The annual sea ice concentration had a strong negative impact on the June-to-August NDVI, outperforming the other climate variables both in terms of standardized effect sizes and variance explained (Table 1). Caribou population size had negligible impacts on the June-to-August NDVI, and contrary to our expectations, we found a weak positive relationship between population size and May NDVI for time lags less than 3 years. Although we found a weak positive effect of May temperature, the models explained, in general, a relatively small proportions of the variation in the May NDVI (maximum R² = 0.23). Contrary to our expectations, population growth was mainly explained by a strong negative relationship with the June-to-August NDVI. The climate variables, population size, and May NDVI had only minor impacts on population growth. However, because of the strong negative relationship between sea ice and the June-to-August NDVI, some of the variance in population growth was also explained by the sea ice concentration in the model where the path from sea ice to population growth was included. Increasing the time lag between the environmental variables and the caribou data did not change the overall pattern but tended to reduce the variance explained by the models. In summary, the models suggested a strong negative effect of sea ice concentration on the summer plant biomass and a negative impact of summer plant biomass on the population growth of caribou. The relationships are shown in Fig. 4. On the basis of the models in Table 1, we selected a final model with no time lag and annual sea ice concentration as the major climate variable. In addition, we also included May temperature, which showed a positive relationship with the May NDVI in the initial models. The model is outlined in Fig. 5.

Fig. 4. Relationships between sea ice, summer NDVI, and caribou population growth.

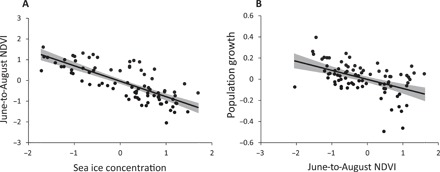
The plots show the relationships between the variables of the two dominating paths singled out by the SE models. (A) Sea ice concentration and NDVI during June to August. (B) June-to-August NDVI and caribou population growth. Lines and shaded areas are univariate linear regressions with 95% confidence interval.

Fig. 5. SE model of climate, plant biomass, and caribou.

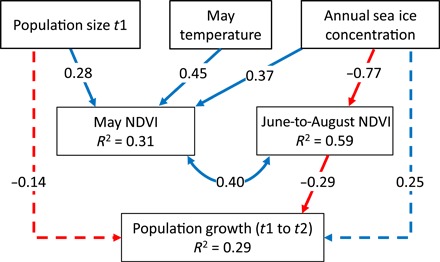
Final SE model with no time lag and annual sea ice concentration and May temperature as the selected indices of climate. Model fit: χ² = 2.05, df = 3, P = 0.562, CFI = 1.00, RMSEA = 0.00. Initial model was formulated according to the causal diagram in Fig. 3. Nonsignificant (P ≥ 0.05) terms were removed from the model using the AIC. Straight lines with arrowheads are the remaining paths with hatched lines indicating nonsignificant effects (P ≥ 0.05). Numbers on the arrows are the standardized parameter estimates. The covariance between May NDVI and June-to-August NDVI is shown as a curve with arrowheads on both ends. Sample size for the model was 81, and the correlation matrix for the data is given in table S3.

DISCUSSION

The DFAs of the tundra caribou populations in Arctic North America revealed that similar population dynamics occurred across the continent but with regional and local differences in the timing of the population maximum (Fig. 1). The large-scale synchrony might suggest that a Moran effect, possibly related to climate forcing, has been working as an exogenous driver on the herds (24). Sea ice cover in the Arctic Ocean is an important driver of Arctic climate and might greatly affect the terrestrial tundra ecosystems (25–27). Here, the annual sea ice concentration provided a strong signal for climate-induced changes on the adjacent caribou summer ranges, outperforming other climate indices in explaining summer NDVI and consequently the caribou population dynamics. Sea ice loss is expected to promote local warming over adjacent land areas and hence trigger an increase in terrestrial primary production through an extended growing season and thawing of permafrost (25). The present study adds to several studies reporting a climate-driven greening of the Arctic (9–11). Using SE modeling, we showed that most of the climate effect on the caribou populations was mediated through the increase in summer NDVI and that the climate-induced greening had a negative impact on caribou population growth. Including other indices of climate in the models, such as snow cover, date of snowmelt, spring temperature, or summer temperature, did not alter this conclusion. Moreover, including time lags in the population response to the environmental variables also did not have any substantial impact on the results.

In the SE model, we hypothesized that large herds of caribou could reduce the plant biomass by browsing. However, contrary to previous studies (7, 16, 19, 20), we found no evidence of a “top-down” effect of caribou on the vegetation biomass. Our results indicated a weak positive effect of herd size on the May NDVI. One explanation for this counterintuitive result might be that the critical calving period, and thereby the counts of animals on the calving grounds, was affected by an early spring green-up (28), being biased toward higher counts in years with a high May NDVI.

Our results support a climate-driven “bottom-up” hypothesis in which a warmer climate has increased the plant biomass on the summer pastures, resulting in declining caribou populations. This result suggests that the climate-induced greening was accompanied by a deterioration of pasture quality, possibly through a change in the composition and availability of forage plants (29–31). It is well established that the greening of the Arctic is mainly attributed to the expansion of tall erect deciduous shrubs in the Arctic tundra biome (12–15). In North America, expanding shrubs such as birch and alder (that is, Betula nana exilis, Betula glandulosa, and Alnus viridus) contain antibrowsing toxins (resins) that deter browsing from mammals (22, 29). These shrubs respond readily to climate warming, and because the antibrowsing defense gives them a competitive advantage over the more edible Salix (willow) species (22), they dominate the shrub expansion in several areas, replacing moss-, grass-, and herb-dominated vegetation [see the review by Myers-Smith et al. (13)]. Moreover, the expansion of shrubs reduces the lichen cover (15), which is an important winter forage for caribou. In summary, the current shift to a shrub-dominated tundra might therefore reduce the availability of high-quality caribou forage. Antibrowsing defense among the expanding species makes it less likely that herbivores such as caribou could halt the shift. On the contrary, the preferred browsing of less-defended plants might, in fact, facilitate the expansion of alder and resin birch (22). Several studies have documented strong impacts of herbivory on important forage plant species (7, 16–18), suggesting that the presented results are likely to reflect changes in the cover of dwarf and tall shrubs (resin birch species). In conclusion, the results presented here might therefore be an early signal of a climate-driven shift in the caribou-plant interaction from a sparsely vegetated system with a wide range of forage plants, heavily browsed by abundant and fluctuating caribou populations, to a system characterized by a dense cover of resin shrubs (22, 29), with diminishing herds of migratory caribou.

MATERIALS AND METHODS

Caribou data

The migratory tundra caribou in North America belong to three different subspecies: R. tarandus groendlandicus (between Hudson Bay and Mackenzie River), R. tarandus granti (west of Mackenzie River), and R. tarandus caribou (south and east of Hudson Bay) (2). On the basis of more or less distinct calving grounds, the migratory tundra caribou is further divided into more than 20 different herds or populations (2). A herd typically counts many thousand individuals and uses huge areas extending from 10,000 to 100,000 km². The seasonal migration covers the coastal Arctic tundra, where calving takes place in late spring, and the northern boreal forests, where parts of the herd spend the winter.

We collected population census data of caribou from management and census reports (table S2). The population censuses were conducted during early summer when the herds are congregated in specific calving grounds on the tundra. Data on individual caribou tagged with satellite transmitters aided in delineating the calving grounds. The herds were counted with respect to the number of breeding females; this was carried out from airplanes flying along transects systematically laid out over calving grounds (see references in table S2). On the basis of the survey data and assumptions about herd composition, estimates of herd size (number of adults and 1-year-olds) with confidence intervals were calculated. Because of limited data and uncertain estimates during the early years, we only included data from 1970 to present. Furthermore, we limited the sample to herds with ranges overlapping both the tundra biome defined by Walker et al. (32) and the northern boreal forests (see Fig. 1). Finally, we excluded herds with less than seven population censuses, thus excluding the Bluenose-East, Ahiak, and Lorillard herds. Because of difficult logistics and high costs, population surveys were conducted infrequently and with varying intervals. The median number of years between successive surveys was 3 years (minimum, 1 year; maximum, 17 years). The final data set included 11 herds with 7 to 16 population censuses between 1970 and 2014. In total, the data set comprised 114 population censuses. Herd ranges (Fig. 1) were extracted from maps in management reports showing the range of habitat utilization by individual caribou tagged with satellite transmitters (see references in table S2). The habitat used by the herds varies annually according to factors such as herd size, climatic fluctuations, and pasture conditions. An exact delineation of a herd’s range was therefore not feasible. Because we were interested in broad-scale relationships with vegetation and climate, we used the maximum known habitat extent. The herd’s “summer range” was confined to the intersection between the tundra area defined by Walker et al. (32) and the total herd range, and this pasture area was used as the basis when extracting climate and NDVI data.

Climate data

The number of climate stations with continuous observations in the Arctic is low, and few stations have continuous time series covering long time spans. We therefore used the monthly mean temperature data from the National Centers for Environmental Prediction Reanalysis database (33) with a global resolution of 2.5° latitude and 2.5° longitude (www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.derived.html). For each herd range (Fig. 1), we extracted temperature data from the tundra biome defined by Walker et al. (32) from 1970 to 2014. We used two measures for spring and summer temperatures: MayTemp and JunAugTemp (average temperature from June through August), respectively. MayTemp was expected to be important for the spring thaw-up, whereas JunAugTemp represents the average temperature during the growth season. Data were missing for some herds and years (38 cases for both MayTemp and JunAugTemp). Missing values were imputed as the average value from the neighboring herd ranges.

The sea ice cover of the Arctic Ocean has a broad impact on the Arctic climate (34). The aggregated annual sea ice concentration reflects the length of the open-water period and could be a relatively robust measure of the summer climate in the adjacent coastal tundra area (27). We used the monthly 25 × 25–km² Bootstrap sea ice concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS, Version 2 (35) downloaded from http://nsidc.org/data/docs/daac/nsidc0079_bootstrap_seaice.gd.html. Sea ice concentration within 1000 km from each herd’s tundra range was aggregated on an annual basis from 1979 to 2014. The distance was chosen to maximize the ocean area sampled while, at the same time, being representative for each herd’s summer range and avoid overlap between adjacent herds.

Data on the weekly presence of snow cover are available on a 25 × 25–km² grid from 1966 to 2014 (36) from the National Snow and Ice Data Center (ftp://sidads.colorado.edu/pub/DATASETS/nsidc0046_weekly_snow_seaice/). Pixels for each herd’s tundra range were extracted, and two variables were calculated from the resulting data set: (i) annual snow cover, defined as the total proportion of pixels with snow cover during a year, and (ii) timing of snowmelt, defined as the first week during a 4-week period with no snow-covered pixels. To cancel out any systematic differences in the climate variables among herds, the climate variables were standardized to mean = 0 and SD = 1 (z-scored) for each herd range.

Vegetation data

To capture vegetation seasonal and interannual signatures over tundra caribou habitat ranges, we used the Global Inventory Modeling and Mapping Studies (GIMMS) NDVI data set obtained from the Advanced Very High Resolution Radiometer sensors onboard the National Oceanic and Atmospheric Administration satellite series (7–18). NDVI is a global vegetation indicator combining the red and near-infrared reflectances, and it has been broadly applied as a proxy of vegetation leaf area, biomass, and physiological functioning (37). The latest version of GIMMS NDVI3g provides the longest, continuous, and consistent global vegetation records that span from 1981 to 2011 with a native resolution of 1/12° at bimonthly temporal resolution (38). Recently resolved high-latitude discontinuity issue and improved snowmelt and cloud detection granted a better observation for high-latitude vegetation dynamic research. With the use of a given quality flag (for example, snow and cloud), the Savitzky-Golay filter was used to smooth the NDVI3g time series because it maintains distinctive seasonal vegetation trajectories and minimizes various atmospheric effects (39, 40).

For each herd range (Fig. 1), we extracted NDVI data from the tundra biome defined by Walker et al. (32) from 1982 to 2011, aggregated on a monthly basis from May to August. Inspection of the data revealed correlation among adjacent months; however, the correlation decreased for increasing time lag such that the correlation between standardized NDVI in May and August was slightly negative (r = −0.208). We decided to use two measures from the resulting data set: MayNDVI and JunAugNDVI. MayNDVI was the aggregated NDVI during May, approximately representing the spring greening period with a high MayNDVI indicating an early green-up. JunAugNDVI was the aggregated NDVI index in the growth season from June through August, thus being a proxy for the total plant biomass available in the tundra habitat during summer.

Dynamic factor analysis

Unlike time series techniques such as spectral analysis and autoregressive integrated moving average models, DFA can handle short, nonstationary time series containing missing values (41). Specifically, DFA is a technique for analyzing common trends in multiple time series (23, 41). Thus, DFA is a dimension-reduction technique designed for time series, similar to the more traditional multivariate factor analysis. We used the MARSS package (42) in R version 3.2.0 (43) to analyze the time series of caribou.

In general, a DFA model is described by

$$\mathit{n} \text{time series} = \text{linear combination of} \mathit{m} \text{common trends} + \text{level parameter} + \text{covariates} + \text{error term}$$ (1)

Within the MARSS package (44), the DFA model with covariates is given by

$$\begin{array}{c}{\mathit{x}}_{\mathit{t}}={\mathit{x}}_{\mathit{t}+1}+{\mathit{w}}_{\mathit{t}} \text{where} {\mathit{w}}_{\mathit{t}}:\mathit{M}\mathit{V}\mathit{N}(0,\mathit{Q})\\ {\mathit{y}}_{\mathit{t}}=\mathit{Z}{\mathit{x}}_{\mathit{t}}+\mathit{a}+\mathit{D}{\mathit{d}}_{\mathit{t}}+{\mathit{v}}_{\mathit{t}} \text{where} {\mathit{v}}_{\mathit{t}}:\mathit{M}\mathit{V}\mathit{N}(0,\mathit{R})\\ {\mathit{x}}_0:\mathit{M}\mathit{V}\mathit{N}(\mathrm{\mu },\mathrm{\Lambda })\end{array}$$ (2)

The x equation is the state process, and the y equation is the observation process. The observations (y) were modeled as a linear combination of m hidden trends (x) and factor loadings (Z) plus some offset (a) and covariates (d). x_t is the m × 1 vector of states at time t, and w_t is the m × 1 vector of process errors. y_t is the n × 1 vector of observations, and v_t is the n × 1 vector of nonprocess errors. Z_t is an n × m matrix containing the factor loadings. The q × 1 vector d_t is a q × 1 vector containing the q covariates at time t, and the n × q matrix D contains the effects of the covariates on the observations. The MARSS package fits the models via maximum likelihood using a constrained expectation-maximization algorithm (42).

Without constraining the parameters in the model, the DFA model is unidentifiable (44). In particular, because of variable time series length and a large number of missing values, the complexity of the models that we could analyze was limited. As a consequence, the models would not converge when assuming covariance and different observation variance among the time series, and therefore, all models were modeled with a constant observation error and no covariance, that is, R was of the form “diagonal and equal” (44). Furthermore, no offset was included (a = 0), and the time series were z-scored before entering the analyses.

The time series of caribou were analyzed from 1970 to 2014 (number of time steps, 44; number of time series, 11; number of censuses, 114) without covariates (that is, excluding the d-term from Eq. 2). Models with more than two trends (m) did not converge. The model including two trends showed a better fit in terms of AICc (AICc = 210.7) than a model with only one trend (AICc = 295.2), and the two-trend model was selected accordingly (Fig. 1, B and C).

SE modeling

SE modeling is a method for studying the relationships in causal networks and is increasingly used for investigating complex natural systems (45, 46). In the present climate-pasture-caribou system, we investigated the relationships between climate, pastures, grazing pressure, and caribou population dynamics. This network includes several possible mediating pathways, suggesting that SE modeling would be a suitable approach (45, 47). As a starting point, we generated a conceptual model (causal diagram), representing a family of possible models (Fig. 3). We hypothesized that a warmer climate would increase the plant biomass on the spring and summer pastures (9–11), which could be beneficial for caribou population growth (28, 48). However, climate could also influence the population growth through other pathways; for example, less snow cover during spring could enhance the availability of forage before and during calving (28, 49), and/or a warmer climate during summer could increase insect harassment and be detrimental for population growth (50, 51). Increased herd size could reduce the plant biomass through grazing (7, 16, 19, 20) and thus induce negative density dependence (49). Other density-dependent mechanisms are also possible, for example, through competition for limited forage resources not reflected by plant biomass or through increased infections of parasites such as oestrid flies (Oestridae) (52). In the proposed causal diagram (Fig. 3), caribou herd size and climate represent exogenous variables, plant biomass on spring and summer pastures would be a mediating factor, and caribou population growth would be an endogenous variable. On the basis of the conceptual model, we formulated SE models using the available variables of caribou, climate, and NDVI.

To represent the population growth, we calculated the intrinsic population growth rate (r_t1) in the interval between two successive population censuses (year t1 and year t2)

$${\mathit{r}}_{\mathit{t}1}=\frac{\text{ln}{\mathit{N}}_{\mathit{t}2}-\text{ln}{\mathit{N}}_{\mathit{t}1}}{\mathit{t}2-\mathit{t}1}$$ (3)

Note that the time interval between successive population censuses (t2 − t1) varied between 1 and 17 years with a median of 3 years (see “Caribou data” above). To represent the climate and plant biomass influencing the population growth during this period, we averaged the climate and NDVI data in the period from the first census to the year before the last census, [t1, t2 − 1], assuming a direct effect of climate and plant biomass on caribou survival and reproduction. To represent herd size, we used population size at time = t1. Thus, we assumed that the caribou population at census t1 was representative for the grazing pressure and other density-dependent mechanisms in the following year(s) until the next census. To make population size comparable among herds, the values of herd size were first log-transformed and then z-scored for each individual herd. To investigate possible lagged effects of climate and plant biomass on the population growth, we analyzed separate models with climate and NDVI data averaged on the interval [t1 − T, t2 − 1 − T], where T is the time lag. We investigated models with T ranging from 0 to 3 years.

We used the lavaan package (53) in R to analyze the SE models. We assumed linear Gaussian relationships, and maximum likelihood was used for estimation. The model fit was evaluated by the χ² test, RMSEA, and CFI. The data set included five indices of climate: temperature in May, temperature in June to August, annual sea ice concentration, annual snow cover, and date of snow melt. Initially, the climate variables were combined into one composite climate variable in the SE model (54). However, possibly because of complex relationships among the climate variables combined with a restricted sample size, this model had a poor fit (χ² = 39.9, df = 8, P < 0.001, CFI = 0.81, RMSEA = 0.22). Therefore, we adopted to investigate the influence of each climate variable in separate models. In addition, we investigated models with different time lags (T) between the environmental variables and the caribou data. For each model, we first included all possible links suggested by the causal diagram (Fig. 3). Next, nonsignificant (P > 0.05) paths were successively removed, depending on whether the simplified model had an acceptable fit and the AIC of the simplified model was less or equal to the original model.

The correlation matrices for the lagged and nonlagged data are reported in table S3. The length of the period available for analyses was restricted by the time series of NDVI (from 1982 to 2011), and the sample size for the nonlagged data was 81. Sample sizes for the lagged data were 78 for T = 1 year, 74 for T = 2 years, and 72 for T = 3 years.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/4/e1601365/DC1

table S1. Linear time trends in climate (1979–2014) and NDVI variables (1982–2011).

table S2. Data set of migratory tundra caribou in North America.

table S3. Correlation matrices of variables used in SE models of caribou, climate, and NDVI.