Abstract
The global signal is widely used as a regressor or normalization factor for removing the effects of global variations in the analysis of functional magnetic resonance imaging (fMRI) studies. However, there is considerable controversy over its use because of the potential bias that can be introduced when it is applied to the analysis of both task-related and resting-state fMRI studies. In this paper we take a closer look at the global signal, examining in detail the various sources that can contribute to the signal. For the most part, the global signal has been treated as a nuisance term, but there is growing evidence that it may also contain valuable information. We also examine the various ways that the global signal has been used in the analysis of fMRI data, including global signal regression, global signal subtraction, and global signal normalization. Furthermore, we describe new ways for understanding the effects of global signal regression and its relation to the other approaches.
Keywords: fMRI, global signal, physiological noise, vigilance, motion, general linear model
1. Introduction
The development of methods to mitigate the effects of noise has played a key role in the development of functional magnetic resonance imaging (fMRI). One approach that has gained widespread adoption is the removal of a global signal component, either as a preprocessing step or through its inclusion as a nuisance regressor in general linear model analyses. This approach is commonly referred to as global signal regression (GSR). However, the use of GSR has sparked a great deal of controversy, especially in the analysis of resting-state fMRI studies where some investigators routinely remove the effects of the global signal while others argue strongly against its use (Murphy et al., 2009; Fox et al., 2009; Saad et al., 2012; Burgess et al., 2016; Murphy and Fox, 2016).
At first glance, it is rather surprising that such a simple signal should spark so much debate. After all the computation of the global signal is straightforward – it is simply the mean of the voxel time-series within the brain. What could be controversial about projecting out the effects of this global signal? We believe that there are several factors that have led to the continuing controversy. First, because the global signal is a “catch-all” signal that reflects the contributions of a variety of noise components, it is not always clear what exactly GSR is removing. Second, while GSR is a fairly straightforward mathematical operation, it still involves the regression of a mean time course (with hundreds of time points or more) from each voxel time series in the brain (ranging from tens to hundreds of thousands of voxels), where the exact numbers of time points and voxels depends on the duration and the temporal and spatial resolutions of the acquisition. Due to the large size of the signal space, it can be difficult to understand the effects of GSR not only on the signals themselves but also on the relation (e.g. correlation) between signals from different regions. Furthermore, it has not been clear how well the arguments made with relatively low-dimensional simulations apply to the high-dimensional datasets obtained in experiments. Finally, with the growing evidence supporting a link between neural activity and the global signal, there has been some concern that GSR may also be removing information that is of interest.
Our goal in this paper is to provide a deeper understanding of the characteristics of the global signal and its role in the analysis of fMRI studies. We will begin by examining the components of the global signal, focusing primarily on the contributions due to low-frequency drifts, motion, physiological activity, and neural fluctuations. We will then review the use of the global signal in the analysis of both task-related and resting-state fMRI studies. Although our focus will be on GSR, we will also examine related methods such as global signal subtraction and global signal normalization. We will conclude with a look at emerging methods for understanding both the global signal and GSR.
2. What is the global signal?
In this section, we review the basic properties of the global signal. Although the basic definition of the global signal is rather straightforward, we will see that there is considerable variability in the implementation of this definition. We will also build up an intuitive picture of the global signal as a time-varying measure of spatial homogeneity.
2.1. Computation of the global signal
The concept of the global signal was first introduced into the fMRI literature by Zarahn et al. (1997), who defined the global signal as the mean time course computed over all voxels within the brain. While the global signal can be calculated from the raw image time series, it is usually computed after some degree of preprocessing. However, the extent of the pre-processing can vary greatly across studies. In some studies, the global signal is computed after the application of a minimal set of preprocessing operations, typically consisting of some combination of image registration, slice-timing correction, and spatial smoothing (Power et al., 2014; Satterthwaite et al., 2013; Fox et al., 2005). For these studies, the global signal has been found to be most strongly correlated with signals from gray matter regions, with lower and more variable correlations observed for signals from white matter and ventricular regions (Power et al., 2014, 2016). In other studies, the global signal is calculated after minimal preprocessing and the removal of additional nuisance regressors, such as low-frequency trends, motion-related regressors, and white matter and cerebrospinal fluid signals (Erdogan et al., 2016; He and Liu, 2012; Zarahn et al., 1997). When external measures of cardiac and respiratory activity are available, additional physiological noise regressors can be removed from the data prior to the computation of the global signal (Wong et al., 2012, 2013).
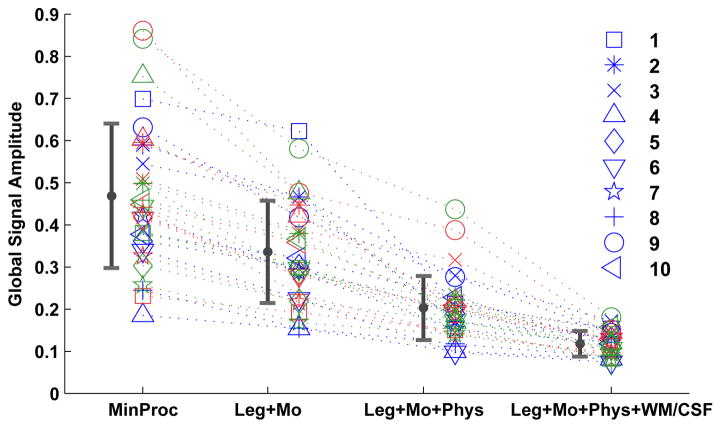
Examples of the global signal from a representative scan previously analyzed in (Wong et al., 2013) are shown in Figure 1. Four different variations of the global signal are presented, corresponding to different sets of nuisance regressors, ranging from an empty set for the minimal preprocessing case (shown in blue) to a full complement of regressors, consisting of low-frequency, motion-related, physiological, and white matter and cerebrospinal fluid nuisance terms (shown in cyan). As the set of regressors is expanded, there is a clear decrease in the overall amplitude of the signal. This trend can also be seen in Figure 2, where we have plotted the global signal amplitudes from 30 scans using each of the four preprocessing variations applied to data from (Wong et al., 2013). Note that for the purpose of this paper and consistent with the terminology used in (Wong et al., 2013), the term GS amplitude will refer to the standard deviation of the GS computed across all time frames within a scan. There is a wide range of amplitudes in the minimally processed data, and this range decreases as the set of nuisance regressors is expanded. By normalizing the amplitudes in each set by their respective values in the minimally processed case (i.e. the GS amplitude obtained with each pre-processing approach was divided by the amplitude obtained with minimal pre-processing), we can gain a sense of the average percent variance explained by each set of regressors. On average, the low-frequency and motion regressors explain 48% of the variance of the global signal. The addition of physiological noise regressors explains an additional 31% of the variance. Further addition of white matter and cerebrospinal fluid regressors explains another 14% of the variance. On average, only 7% of the variance of the minimally processed global signals remains after the contributions of the complete set of nuisance regressors have been removed.
Figure 1.
Examples of global signal time series computed after (1) minimal preprocessing (MinProc, blue), (2) MinProc plus removal of low-frequency (Leg: Legendre polynomial) and motion-related (Mo) nuisance terms (Leg+Mo; green), (3) MinProc plus removal of low-frequency, motion-related, and physiological (Phys) nuisance terms (Leg+Mo+Phys; red), and (3) MinProc plus removal of low-frequency, motion-related, physiological, and white matter and cerebral spinal fluid (WM/CSF) nuisance terms (Leg+Mo+Phys+WM/CSF; cyan). WM and CSF regions were defined using partial volume thresholds of 0.99 for each tissue type and morphological erosion of two voxels in each direction to minimize partial voluming with gray matter. Additional details about the processing are provided in (Wong et al., 2013).
Figure 2.
Global signal amplitude (in units of percent change) as a function of preprocessing approach for 30 scans. Bars indicate mean plus or minus one standard deviation. With respect to the MinProc set, the means of the normalized variances of the global signals are 0.52, 0.21 and 0.07 for the Leg+Mo, Leg+Mo+Phys, and Leg+Mo+Phy+WM/CSF sets, respectively. As an example, this means that the variances of the global signal in the Leg+Mo set are on average 52% of the respective variances of the global signals in the MinProc set. These data are from the eyes-closed scans in the pre-dose control, post-dose control, and pre-dose caffeine sessions described in (Wong et al., 2013)
What determines which form of the global signal should be used? When the primary goal is to remove global effects from the data, then the minimally processed version is typically used and the global signal is included as an additional nuisance regressor term in a general linear model (GLM) analysis of the data (Power et al., 2014). In this case there is no need to remove the other nuisance regressors from the global signal, since the GLM analysis projects out the signal component that lies in the signal subspace spanned by all of the nuisance regressors (including the global signal). On the other hand, when the primary goal is to further our understanding of the neural components of the global signal, then it is desirable to project out nuisance components that are thought to be unrelated to neural activity (Wong et al., 2013). However, as we shall discuss in more detail below, the determination of whether or not a nuisance component is unrelated to neural activity is not necessarily straightforward.
2.2. Normalization Options
Another source of variabilty in the computation of the global signal arises from different choices in the normalization of the blood oxygenation level dependent (BOLD) fMRI signal. As the raw fMRI signal from the scanner is acquired in arbitrary units, it is necessary to perform some type of normalization to assess the relative change in the signal (Goebel, 2015). A common choice is to compute the percent BOLD signal change from some baseline value, as the percent signal change has a meaningful connection with brain physiology (Buxton et al., 2004). For task-related studies, the baseline value is typically computed as the average signal during a control condition, whereas for resting-state studies, the baseline value is usually computed as the mean signal over the entire scan. In some studies, the normalization is performed on a per-voxel basis, so that a unique baseline value from each voxel is used to compute the local percent change BOLD signal time series (Goebel, 2015). These normalized time series are then averaged to compute the global signal as described in (Wong et al., 2013; Murphy et al., 2009). In other studies (Fox et al., 2009; Power et al., 2014), the data (from all voxels and time points within a scan) are normalized so that the mean or mode of all the signals value is equal to a pre-specified scalar (typically either 100 or 1000). (Note that when the scalar is equal to 100, then subtracting 100 from the grand-mean scaled value yields a percent change value). This later approach is sometimes referred to as grand-mean scaling and is equivalent to the per-voxel normalization method when baseline values are constant across voxels. In general, baseline values are not constant across across voxels, reflecting spatial inhomogeneities associated with the acquisition and underlying brain anatomy. As a result, the global signals computed after per-voxel normalization and grand-mean scaling will not be exactly the same. However, in most cases the differences are relatively small because the variation in baseline values tends to be moderate and the effects of baseline values that are greater than the grand-mean will tend to cancel out the effects of lower baseline values. For example, let us consider three voxels each with a change of 10 arbitrary units from their respective baseline values of 900, 1000, and 1100, with a grand-mean value of 1000. With grand-mean scaling, the average percent change across voxels is simply ((910 + 1010 + 1110)/(3 · 1000)) − 1 = 1%. With per-voxel normalization, the average percent change across voxels is (10/900 + 10/1000 + 10/1100)/3 = 1.01%. Nevertheless, care does need to be taken when using per-voxel normalization to avoid voxels with abnormally small baseline values (e.g. due to susceptibility-related signal dropouts) that can exhibit abnormally high percent signal changes (e.g. a 20% BOLD signal change would typically be considered abnormal and beyond what is expected from the underlying physiology). This can be achieved through the application of a lower threshold on the baseline values and an upper threshold on percent change values.
Another normalization approach that is less commonly used is the z-normalization approach (Carbonell et al., 2011) in which the mean from each voxel time series is normalized to have zero mean and unit variance. This approach is useful when looking at the spatial correlation structure of the data as the correlation coefficient between the z-normalized time series is simply given by the respective inner product (He and Liu, 2012). However, this normalization approach eliminates the physiological meaning of the amplitude of the global signal and therefore is not recommended for studies in which the amplitude is compared across subjects or conditions.
2.3. The Global Signal as a Measure of Spatial Homogeneity
Because it is defined as the mean time course over the brain, the value of the global signal at each time point reflects the spatial homogeneity at that time. When the spatial homogeneity is high (i.e. most voxels are either positive or negative), then the voxel values sum constructively and the global signal will tend to take on either positive or negative values. On the other hand, when the spatial homogeneity is low (i.e. there are roughly equal proportions of positive and negative voxel values), the voxel values tend to cancel out and the global signal value will tend to zero. These basic properties of the global signal are demonstrated in Figure 8(a), where the BOLD fMRI images from a representative subject and slice are shown over 17 time points in the top row of panel (a), along with colored bars above the images indicating the value of the global signal at each time point. At time point 82 the image is relatively homogeneous with negative values, leading to a large negative value for the global signal. At time point 94 the image is mostly positive with a large positive global signal value. In contrast, the images from time points 85 to 90 are all relatively heterogeneous with a roughly equal mix of negative and positive values. As a consequence the global signal value is relatively small at these time points. We will examine this property of the global signal more closely in Section 5.5.
Figure 8.
Approximating the effects of GSR with temporal downweighting and censoring. (a) Examples of brain images from a representative subject and slice prior to (uncorrected) and after the application of GSR (2nd and 3rd rows, respectively) are shown. Global signal values for the uncorrected images are indicated by the colored bars in the first row. The GSR ratios are indicated by the colored bars in the 4th row, and reflect the average downweighting due to GSR at each time point. Multiplication of the uncorrected images by the GSR ratio yields the downweighted images in the 5th row. In the 6th row, images at time points for which the expected GSR ratio is less than 0.5 are censored (i.e. multiplied by zero) while the uncorrected images are retained for the remaining time points. (b) The GSR ratio decreases as an approximately linear function of the global signal magnitude. Each dot represents the GSR ratio from a single time point from one of 68 scans (a total of 12580 time points). The dashed red-line indicates a censoring function that multiplies images by zero when the expected GSR ratio (i.e. linear approximation) is less than 0.5. (c) PCC seed correlation maps obtained before GSR, after GSR, and after application of GSR ratio weighting, and GS censoring. Maps are shown for 10 representative scans. For GS censoring, time points with an expected GSR ratio of less than 0.5 were censored, and the percentage of time points censored is indicated at the bottom. (d) The average GSR ratio for each scan (computed as the mean of GS ratios across all time points within a scan) is plotted versus the global 50 signal amplitude for that scan (computed as the standard deviation of the global signal across the scan).
While any source of signal or noise in the fMRI time series can contribute to the global signal, the simple arguments presented above suggest that those sources that give rise to spatially widespread effects will lead to the largest increases or decreases in the global signal. As a result, in discussing potential contributions to the global signal, we will focus on sources that tend to have a spatially widespread effect on the fMRI time series.
3. Nuisance Components in the Global Signal
In this section we describe the unwanted nuisance components that can contribute to the global signal. These are termed “nuisance” components because they are generally thought to reflect fluctuations unrelated to the underlying neural activity that is of interest. However, as we will discuss below in Subsection 4.6, the line between nuisance and information can sometimes be difficult to delineate. Tables 1 and 2 provide a summary of the primary signal sources that are discussed both in this section and in Section 4, which will consider components of the global signal that may contain information of interest.
Table 1.
Summary of Potential Contributors to the Global Signal (GS). Additional references are provided in the text. A detailed review of sources and mechanisms can be found in (Liu, 2016).
| Source | Description | References |
|---|---|---|
| MRI System | Drifts and instabilities in radiofrequency, gradient, and shim subsystems and components can create artifactual signals. Contributions should be minimal for a well maintained system. | Foerster et al. (2005); Power et al. (2016) |
| Physiological Drift | Slowly varying physiological processes (e.g. fatigue). Contribution is not well characterized. | Evans et al. (2015); Yan et al. (2009) |
| Motion | Time-varying displacement of tissue components causes signal changes and spin history effects. | Hajnal et al. (1994); Power et al. (2015, 2016) |
| Cardiac | Fluctuations in cardiac rate drive changes in blood flow and oxygenation. | Shmueli et al. (2007); Chang et al. (2009) |
| Respiration | Modulates magnetic field, carbon dioxide levels, cerebral blood flow, cardiac rate, and pulse pressure. | Windischberger et al. (2002); Birn et al. (2006); Wise et al. (2004); Berntson et al. (1993) |
| Vigilance | GS amplitude decreases as mean vigilance levels rise. Temporal fluctuations in GS are negatively correlated with vigilance fluctuations. | Wong et al. (2013, 2015); Chang et al. (2016); Falahpour et al. (2016) |
Table 2.
Variability in global signal amplitude and fluctuations. The first four rows list the percent variance in global signal amplitude variability (across scans) that is explained by the source. The fifth row indicates the percent variance of the differences in global signal amplitude values between conditions (e.g. pre and post caffeine) that are explained by differences in mean vigilance. The sixth row indicates the percent variance of global signal fluctuations that is explained by vigilance fluctuations. For the results from (Power et al., 2016), the values indicate the percent variance both before and after the application of denoising; and when using either all subjects or only those subjects for which the mean framewise displacment was less then 0.2 mm. For the vigilance results in (Wong et al., 2013, 2015; Falahpour et al., 2016), the values were obtained across all subjects after censoring of timepoints for which the electroencephalographic (EEG) measures were corrupted by motion.
| Source | Before Denoising | After Denoising | References | ||
|---|---|---|---|---|---|
|
| |||||
| Low-motion | All | Low-motion | All | ||
| Motion | 16% | 50% | 21% | 32% | Power et al. (2016) |
| Cardiac | 13% | 30% | 8% | 16% | |
| Respiratory | 34% | 20% | 30% | 27% | |
|
| |||||
| Mean Vigilance | across scans | 25% | Wong et al. (2013, 2015) | ||
| difference between conditions | 64%–81% | ||||
|
| |||||
| Vigilance Fluctuations | across time within a scan | 10%–20% | Chang et al. (2016); Falahpour et al. (2016) | ||
3.1. Low Frequency Drift and System-Related Artifacts
Low-frequency drift refers to slow time-varying components in the fMRI time series with periods on the order of 60 seconds or more. A portion of the drift term can arise from system instabilities, such as a slow drift in the shim system leading to slow time-varying distortions and shifts of the acquired images (Foerster et al., 2005). However, for a well maintained system these effects should be fairly minimal (Glover et al., 2012; Liu et al., 2015). Low-frequency drifts can also reflect slowly varying changes in brain physiology due to factors such as fatigue (Evans et al., 2015; Yan et al., 2009). Both the system-related and physiological sources can give rise to low-frequency signal drifts with widespread spatial extent, thus contributing to the overall global signal. Low-frequency drifts are typically treated as nuisance components and removed with either high pass filtering or the inclusion of low-frequency drift terms as regressors in the analysis process. Common choices for the regressor terms are the low-order Legendre polynomials (e.g linear and quadratic terms) and low-frequency sine and cosine terms (Friston et al., 1995a; Cox, 1996).
In addition to low-frequency drifts, there are a host of system-related artifacts that can contribute to the global signal (Liu, 2016; Power et al., 2016). These include instabilities in the radiofrequency and gradient subsystems. Power et al. (2016) reported that maps of the spatial distribution of the global signal can be effective for identifying scans with system artifacts. For example, they found that instabilities in the radiofrequency subsystem resulted in pronounced asymmetries in the spatial distribution maps. As with the low frequency drifts, these types of instabilities should be minimized in a well operating system.
3.2. Motion
Motion has long been recognized as a significant source of artifactual signal changes in both task-related and resting-state fMRI studies (Hajnal et al., 1994; Power et al., 2015; Liu, 2016). As noted by Power et al. (2015) motion typically causes nearby voxels to act in the same manner (i.e. correlated signal changes), while for distant voxels the signal changes can be correlated or anti-correlated. Motion that gives rise to widespread and similar changes over the entire brain will lead to changes in the global signal. In addition, for resting-state fMRI, this type of motion will cause an increase in the magnitude of correlation estimates between distant voxels (Satterthwaite et al., 2013; Power et al., 2015). Power et al. (2016) reported the motion could account for up to 49% of the variance (across different scans) in the global signal amplitude (i.e. standard deviation of the global signal across a scan). When high-motion timepoints were excluded from the analysis, the percent variance explained decreased to 16%.
When examining framewise displacement signals (an index of the motion differences over time), Power et al. (2014) found that time periods with pronounced increases in framewise displacment were often, but not always, associated with both global signal increases and decreases. The global signal response to motion was found to be complex and multi-phasic with a great deal of variability between incidents. Decreases were observed more than increases, and sometimes lasted for tens of seconds after an increase in displacement. Similarly, Satterthwaite et al. (2013) found that displacement increases led to global signal decreases, with the size of the decrease scaling with the magnitude of the displacement, but found that the duration of the decreases was less than 6 seconds. Power et al. (2014) attributed the discrepancy to the fact that Satterthwaite et al. (2013) looked at the average effects of displacement, whereas their study looked at individual examples of the global signal response to motion, which were highly variable in their signal characteristics, reflecting differences in the timing and duration of the motion, the trajectory of the motion, and the relative signal intensities of the affected voxels (Power et al., 2015).
It should be noted that Hallquist et al. (2013) found that a mismatch between the frequency contents of the data and the regressors used in preprocessing could also give rise to motion-related global signal changes, but this mismatch has been largely addressed by changes to the preprocessing approaches used in the more recent studies discussed here (Power et al., 2015).
3.3. Cardiac and Respiratory Components
The primary source of cardiac-induced signal change is thought to be cardiac pulsations, which can lead to dynamic changes in the relative distribution of brain tissue, blood, and cerebrospinal fluid (Dagli et al., 1999; Hu et al., 1995; Bhattacharyya and Lowe, 2004). As these pulsation-related artifacts are fairly localized to regions around the large arteries (Dagli et al., 1999; Glover et al., 2000; Restom et al., 2006) their contribution to the global signal can be limited. On the other hand, fluctuations in the cardiac rate have been shown to exhibit spatially widespread correlations with the resting-state fMRI signal (Shmueli et al., 2007). It has been proposed that the observed effects reflect low-frequency changes in cerebral blood flow and metabolism driven by the heart rate variations (Chang et al., 2009). The variations in heart rate are in turn tightly linked to fluctuations in respiratory activity (Power et al., 2016). Furthermore, variations in pulse pressure are also coupled with respiratory activity and a recent study found that they may also contribute to global signal fluctuations (Power et al., 2016). The same study reported that 30% of the variance (across different scans) in the global signal amplitude (i.e. standard deviation of the global signal across a scan) could be explained by the standard deviation (across a scan) in the heart rate time course. When high-motion timepoints were excluded from the analysis, the percent variance explained decreased to 13%.
A number of potential mechanisms have been proposed to account for the effect of respiratory activity on the fMRI signal (Liu, 2016). The mechanisms that are most likely to produce spatially widespread signal changes include magnetic susceptibility-related effects due to expansions and contractions of the chest cavity and walls, and bulk motion of the head related to the action of breathing (Brosch et al., 2002; Raj et al., 2001; Hu et al., 1995; Windischberger et al., 2002; Glover et al., 2000). In addition, the respiratory modulation of carbon dioxide levels (a potent vasodilator) can lead to dynamic variations in cerebral blood flow levels. These in turn give rise to widespread fluctuations in the BOLD fMRI signal that can contribute to the global signal (Birn et al., 2006; Wise et al., 2004). For example, Birn et al. (2006) found that the global signal was significantly correlated (r = −0.5; at a latency of 8.8s) with changes in respiratory volume per time (RVT). Power et al. (2016) recently reported that 20% of the variance (across different scans) in the global signal amplitude (i.e. standard deviation of the global signal across a scan) could be explained by the standard deviation (across a scan) in the RVT time course. When high-motion timepoints were excluded from the analysis, the percent variance explained increased to 34%.
3.4. Vascular Components
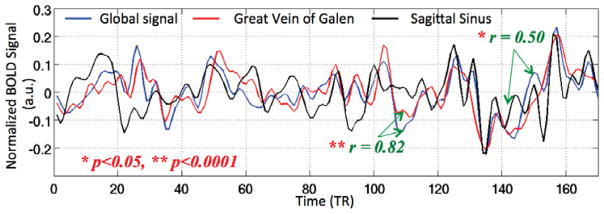
He et al. (2010) observed that the BOLD signal in the large draining veins was highly correlated with the global signal, reflecting the fact that the signal in the draining veins reflects fluctuations in the average deoxyghemoglobin content from the upstream venules. An example of this phenomenon is shown in Figure 3 where the global signal (computed after exclusion of the draining vein regions) is highly correlated with the signals from both the great vein of Galen and the sagittal sinus. He et al. (2010) noted that differences between the global and draining vein signals might be partly attributed to spatial variations in the hemodynamic delays between the venules and the draining veins. It was later shown that the hemodynamic delays computed between the BOLD time series from each voxel and either the global signal or the sagittal sinus signal were similar to the delays assessed using contrast-based perfusion MRI (Amemiya et al., 2014; Christen et al., 2015; Lv et al., 2013; Tong et al., 2016). This effect has been used to map hemodynamic delays in patients with Moyamoya disease and acute strokes (Amemiya et al., 2014; Christen et al., 2015; Lv et al., 2013). Although the global signal is typically assessed using BOLD fMRI, it has also been shown that a significant global signal exists in arterial spin labeling MRI measures of cerebral blood flow (Dai et al., 2016), with an average amplitude of 7.6% relative to the baseline level of blood flow.
Figure 3.
The global signal is highly correlated with the signals from the great vein of Galen (red) and the sagittal sinus (black).
Recently, Erdogan et al. (2016) have shown that the global signal in the brain is significantly correlated (mean r = 0.51 assuming optimal lags) with functional near-infrared spectroscopy (fNIRS) measures of low frequency oscillations (LFO) in oxygenation levels in the fingertip, suggesting a systemic hemodynamic contribution to the global signal. In prior related work, the same research group had shown widespread correlations of peripheral fNIRS measures (both from the fingers and the toes) with resting-state fMRI signals in the brain (Tong et al., 2012). Due to the high temporal sampling rate of the fNIRS measures, the authors were able to filter out the primary effects of cardiac and respiratory fluctuations from their fNIRS measures and focus on low-frequency signals (0.01 Hz to either 0.10 Hz in (Erdogan et al., 2016) or 0.15 Hz in (Tong et al., 2012)). However, it is important to note that low pass filtering does not eliminate the potential low-frequency contributions due to cardiac and respiratory variability. The origins of the LFOs are not completely understood, but it has been proposed that they reflect fluctuations in systemic circulation signals, due in part to the complex dynamics associated with the regulation of blood pressure and flow (Erdogan et al., 2016). As cardiac and respiratory functions are regulated by the autonomic nervous system, part of the correlation between the global signal and the peripheral LFO signal may reflect the direct effects of autonomic activity on fMRI signals in the brain.
3.5. Region-based Nuisance Components
When direct measures of physiological sources are not available, estimates obtained from large vessels, white matter, the ventricles, and soft tissues of the face have been used as proxy measures (Anderson et al., 2011; Behzadi et al., 2007; Lund et al., 2006; Curtis and Menon, 2014; Bianciardi et al., 2009; Jo et al., 2010). Two main approaches have been proposed: (1) use of the mean signal from a nuisance region as a regressor and (2) use of the top principal components from the nuisance regions. In comparing these approaches, Muschelli et al. (2014) found that the component-based approach performed better than the mean signal approach, partly reflecting the fact that component-based approaches can preserve information that may otherwise be averaged out when using the mean signal. A specific example of the second approach is the aCompCor method (Behzadi et al., 2007), in which an anatomical mask is used to define regions that consist almost entirely of either white matter or cerebrospinal fluid, a principal components analysis is performed on the time series in each region, and the top components are then selected as noise regressors. This method has been shown to be effective for identifying and removing signal components due to cardiac fluctuations, respiratory activity, and subject motion. Yeo et al. (2015) reported that aCompCor regressors explained an average of 62% of the variance of the global signal variance in their study. Furthermore, Chai et al. (2012) found that aCompCor could reveal anti-correlations in resting-state fMRI data without the need for GSR. A potential limitation of the region-based approaches is that they often rely on effective segmentation of different tissue types (e.g. differentiating gray matter from white matter). Any errors in the segmentation process can lead to partial voluming effects, in which signals of interest (e.g. from gray matter) can leak into estimates of the nuisance components Jo et al. (2010); Power et al. (2016). In addition, emerging work regarding the potential detection of functional signals in white matter suggests that some level of caution may be needed when using white matter signals as proxies for noise (Gawryluk et al., 2014).
4. Information in the global signal
In the section above we reviewed a number of the “nuisance-like” components that can contribute to the global signal. Because these components comprise such a large fraction of the variance of the global signal, approaches that use the global signal as a “catch-all” regressor are highly effective for minimizing the contributions of these nuisance components. However, there is also growing evidence for the existence of a significant neural component in the global signal, suggesting that there may be valuable information that may be lost when the global signal is removed.
4.1. Global correlation between neuroelectrical and fMRI signals
In a study using simultaneous measures of local field potentials (LFP) and BOLD signals in a non-human primate model, Schölvinck et al. (2010) found widespread correlations between the LFP power fluctuations from single cortical electrodes and the resting-state BOLD signals measured across the entire cerebral cortex. Consistent patterns of global correlation were found for both upper gamma-range frequencies (40 to 80 Hz) and lower frequencies (2 to 15 Hz), with a stronger degree of coupling when the animals’ eyes were closed. Because of the widespread nature of the correlations, the authors concluded that there was a tight coupling between underlying neural activity and the global component of resting-state fMRI activity.
Wen and Liu (2016a) used a novel algorithm (Wen and Liu, 2016b) to separate broadband and oscillatory components in the power spectra of electrophysiological signals, and applied this approach to the analysis of simultaneous resting-state EEG-fMRI data acquired in humans. They found that the broadband fluctuations in EEG power (across a frequency range of 1 to 100 Hz and averaged across channels) showed a spatially widespread and positive correlation with the fMRI data, with a time lag of approximately 5 seconds between the EEG power and fMRI signal. They also found a spatially widespread but negative correlation between the EEG power and the fMRI data with a time lag of about 12.5 seconds, but the reason for the appearance of both positive and negative correlations was deemed to be “entirely mysterious”. A potential limitation of the study is that only low frequency drift signals were removed prior to the computation of the correlation estimates. As a result, the observed correlations may have been affected by motion-related and physiological confounds.
4.2. Global Signal Amplitude and EEG vigilance
In simultaneous EEG-fMRI studies of human subjects, Wong et al. (2013) found that the amplitude of the global signal was inversely correlated with EEG measures of vigilance across subjects and experimental runs, with higher vigilance states characterized by lower global signal amplitudes (defined as the standard deviation of the global signal). In addition, they found that increases in EEG vigilance measures associated with the ingestion of caffeine were significantly correlated with decreases in the global signal amplitude. EEG vigilance was defined as the root mean squared (rms) amplitude in the alpha band divided by the rms amplitude in the delta and theta bands (Horovitz et al., 2008; Olbrich et al., 2009), which is equivalent to the alpha slow-wave index (ASI) used in prior studies (Jobert et al., 1994; Larson-Prior et al., 2009; Muller et al., 2006). Prior to the computation of the global signal, the authors removed motion-related and physiological nuisance terms so as to minimize the impact of these potential confounds on their analysis.
In a follow-up study, Wong et al. (2015) compared measures of global signal amplitude and EEG vigilance in the eyes-open and eyes-closed states and found that changes (eyes-open minus eyes-closed) in the global signal amplitude were negatively correlated with the associated changes in EEG vigilance. Interestingly, the slope of this relation was found to be similar to that of the previously observed association between caffeine-related changes in the global signal amplitude and EEG vigilance, thus providing evidence for a fundamental relation between global signal amplitude and EEG vigilance. The existence of this inverse relation between global signal amplitude and EEG vigilance is also consistent with prior findings that have shown that both the amplitude of the BOLD signal (as measured in specific regions) and the amplitude of the global signal (measured across the whole brain) increases as subjects enter into light sleep stages and exhibit lower levels of vigilance (Fukunaga et al., 2006; Horovitz et al., 2008; Larson-Prior et al., 2009; Olbrich et al., 2009). Similarly, the global signal amplitude has been found to be significantly higher in subjects in a sleep deprived state as compared to a well-rested state (Yeo et al., 2015). In addition, the level of anti-correlation between the default mode network (DMN) and task positive network (TPN) has been shown to decrease (consistent with an increase in global signal) during the transition to light sleep (Larson-Prior et al., 2011; Sämann et al., 2011).
Wen and Liu (2016a) used the analysis approach discussed in the previous subsection to study broadband fluctuations in macaque electrocorticographic (ECoG) and human magnetoencephalographic signals. The strength of the correlations in the ECoG data was found to vary with arousal state, with the magnitude of the correlation decreasing as subjects moved from sleep to an eyes-closed awake state and then on to an eyes-open awake state. To first order, the ECoG findings are consistent with the fMRI findings of decreases in global signal amplitude (i.e. standard deviation) as vigilance increases.
4.3. Dynamic fluctuations in arousal and the global signal
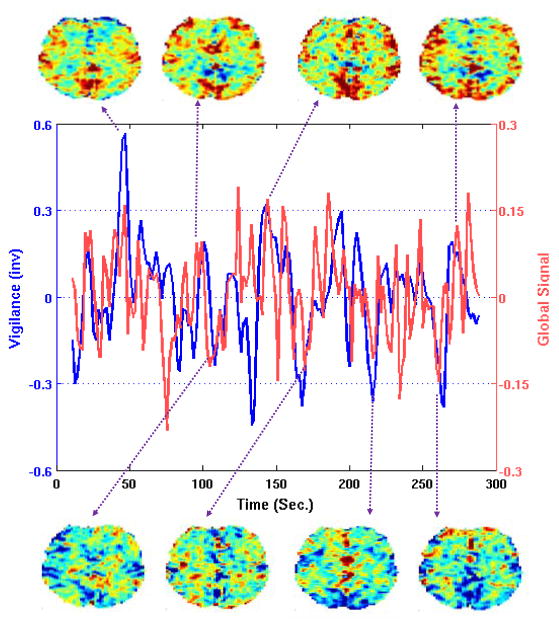
In a recent study that included a reanalysis of data from (Schölvinck et al., 2010), Chang et al. (2016) found evidence for a significant negative correlation between the global signal time course and LFP measures of arousal, where LFP arousal was defined by taking the ratio of the spectral amplitudes in the beta and theta bands. These LFP measures of arousal were tightly linked with time-varying behavior arousal measures (assessed as the degree of eye opening as the animals opened and closed their eyes spontaneously in nearly complete darkness). Using simultaneous EEG-fMRI data acquired in humans, Falahpour et al. (2016) demonstrated in a preliminary study the existence of a negative correlation between the global signal and EEG vigilance time courses over the course of a scan. An example of this relation is shown in Figure 4 where the correlation between the global signal (green) and EEG vigilance time course (after convolution with a hemodynamic response function; blue) is r = −0.28. Note that for display purposes the mean of the EEG vigilance time course has been removed and the resulting time course has been inverted (i.e. multiplied by −1). The global signal tends to exhibit positive peaks when vigilance is low and has negative peaks when vigilance levels are high. Examples of images near these peaks are also shown in the figure, revealing a trend towards images biased towards positive voxel values when vigilance is low and biased towards negative voxel values when vigilance is high. Although the two studies used different definitions of vigilance (i.e. different ratios of EEG bands), these findings are consistent with those of (Chang et al., 2016). The link between global activity and dynamic changes in arousal finds further potential support in the observations of Pisauro et al. (2016), who used pupilometry to measure arousal states in mice. They found that increases in arousal were associated with decreases in an optical measure of global hemodynamic activity.
Figure 4.
Global signal (green) is negatively correlated with EEG vigilance time course (blue; inverted for display) over the course of a scan. Examples of images that occur near vigilance peaks (and valleys in the global signal) are shown below the plot, while images that occur near vigilance valleys (and peaks in the global signal) are shown above the plot.
While the neurobiological mechanisms linking vigilance to global fluctuations are not well understood, it is thought that the global nature of the fluctuations may reflect widespread projections of various arousal systems onto the cortex (Jones, 2005; Picchioni et al., 2013). Using large-scale simulations, Deco et al. (2014) found that globally coordinated activity in a model network increased as cholinergic neuro-modulation of arousal decreased. Although further work is needed, the existing evidence suggests that images with high GS magnitudes (i.e. uniformly positive or negative) may be associated with temporal peaks and valleys in the state of vigilance or arousal.
4.4. Quasi-periodic Patterns
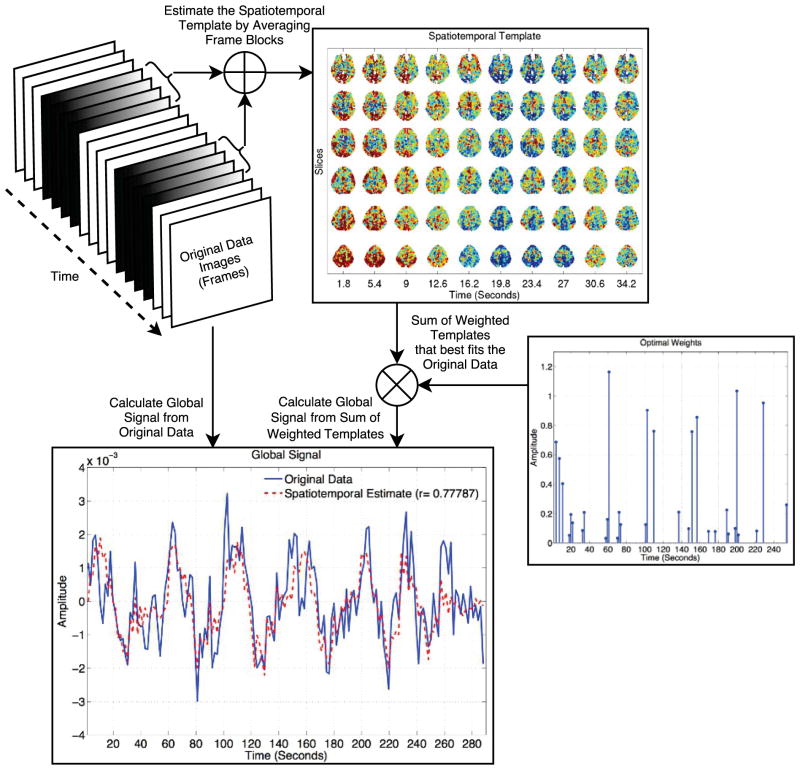
In the dynamic analysis of resting-state fMRI, quasi-periodic spatiotemporal patterns have been observed in both animal and human studies (Majeed et al., 2011, 2009; Thompson et al., 2014). These are spatiotemporal motifs (i.e. a pattern defined across time and space) with a duration of tens of seconds that repeat in a somewhat periodic manner across the course of a scan. The motifs appear as quasi-periodic “waves” of activity that move across the brain. Although the origin of these spatiotemporal patterns is not well understood, they have been shown to be related to electrophysiological measures of resting-state activity in rats (Thompson et al., 2014). In addition, Matsui et al. (2016) recently used calcium-based imaging to identify globally propagating waves of activity in the neocortex of mice. Noting that the spatiotemporal patterns involved coordinated activity over the whole brain, Nalci et al. (2016b) examined the relation between the patterns and the global signal. Using the approach of (Majeed et al., 2011), they identified spatiotemporal patterns in resting-state fMRI data and then used a sparse estimation approach to estimate the weighted sum of spatiotemporal patterns that provided the best fit to the original data. An example of this approach is shown in Figure 5 in which the global signal is highly correlated with the average of the weighted sum of templates. This preliminary finding suggests that the activity represented by quasi-periodic spatiotemporal patterns may account for a significant fraction of the global signal. However, further work is needed to understand both the origins of the quasi-periodic patterns and their potential link with the global signal.
Figure 5.
Spatiotemporal templates (upper right) are estimated using the approach of (Majeed et al., 2011). A sparse estimation approach is then used to estimate the optimal weighted sum of templates that best fits the original data, with the estimated weights shown in lower right of the figure. The global signal of the original data (blue) is highly correlated (r = 0.78) with the global signal of the weighted sum.
4.5. Potential Diagnostic Information in the Global Signal
There is also some evidence that the global signal may carry diagnostic information. For example, Yang et al. (2014) reported that the variance of the global signal was significantly higher in patients with schizophrenia as compared to normal controls. Using biologically informed computational modeling, the authors argued that the increase in variance reflected an increase in neural coupling at both local and long-range scales. However, the authors also acknowledged that the potential confound of vigilance differences between groups would need to be carefully considered in follow-up work. Furthermore, Hahamy et al. (2014) reported a contradictory finding of reduced global connectivity (consistent with reduced global signal variance) in subjects with schizophrenia. In a study comparing adolescents with autism spectrum disorder to typically developing controls, Gotts et al. (2012) correlated the global signal with each voxel time series in the brain to study the spatial distribution of the global signal, and found that the correlation was significantly reduced in several brain regions for the autistic subjects. These clinical research studies used standard denoising approaches to reduce the effects of nuisance terms (e.g. motion, cardiac and respiratory activity). In light of the limitations of these methods, the contribution of residual nuisance effects cannot be ruled out as a source of the global signal differences (Power et al., 2016).
4.6. When Nuisance becomes Information
In the sections above we have made the implicit assumption that motion-related and physiological signal components should be viewed as nuisance terms, unrelated to the neural activity that is of interest. However, this assumption overlooks the reality that the brain, which is the object of study, is the generator of both the signals of interest and the so-called “nuisance” components (Liu, 2016). For example, signal fluctuations due to subject motion, respiration, and cardiac activity all have their origins in the brain networks that control these functions (Iacovella and Hasson, 2011; Yuan et al., 2013). In addition, it has been found that the likelihood that a subject’s data exhibits “nuisance” components (such as motion-related artifacts) may reflect an underlying neurobiological trait (Zeng et al., 2014). Thus, as our understanding of the neural mechanisms that give rise to “nuisance”-related activity increases, it is likely that our understanding of the information that is contained in the global signal will also expand.
5. The Role of the Global Signal in fMRI Analysis
We now turn our attention to the role of the global signal in the analysis of fMRI studies. We take a largely historical approach and begin in Subsection 5.1 with a review of the initial application of the global signal in the context of task-related fMRI experiments. Although the global signal continues to receive some attention in this context, it has found much broader usage in the analysis of resting-state fMRI studies, most notably in the form of a widely used pre-processing approach known as global signal regression that is discussed in Subsection 5.2. However, there has also been quite a bit of controversy regarding the use of global signal regression, as described in Subsection 5.3. New insights into the relation between global signal regression and alternate approaches for addressing the effects of the global signal are provided in Subsection 5.4. In Subsection 5.5, we consider a recently introduced framework for understanding the effects of global signal regression. This is followed by a brief discussion in Subsection 5.6 of the role of the global signal in the emerging area of dynamic functional connectivity analysis.
5.1. The Global Signal in Task-Related fMRI Analysis
The first extensive treatment of the global signal in the analysis of fMRI studies was presented by Zarahn et al. (1997), who noted the prior use of global covariates in PET and fMRI studies by (Friston et al., 1995b, 1990). Zarahn et al. (1997) hypothesized that its use as a covariate could be useful for reducing the effects of spatially coherent noise, thereby improving the ability to detect functional activations in task-related fMRI studies. They demonstrated that the global signal reflected a large degree of spatial coherence between voxel time series, with a larger coherence observed for lower frequencies. In addition, the magnitude of the coherence was much greater than could be explained by spatial smoothing of the data. In correlating the global signal with individual voxel time series, they found that the correlations were largely positive, spatially widespread, and not limited to any signal tissue type or brain region. Furthermore, the spatial patterns of the correlations differed from those typically associated with motion-related artifacts, indicating that the correlations were not solely due to motion. When analyzing null data sets, they found that the inclusion of the global signal as a covariate in a general linear model (GLM) centered the observed test statistic distribution and reduced the variance of false positive rates across noise datasets.
In a companion paper (Aguirre et al., 1997) the authors went on to examine the effect of the global signal on the analysis of fMRI scans containing behavioral tasks. Across the sample that was studied, they found a significant correlation between the global signal and the behavioral paradigm. The presence of this correlation was expected to decrease sensitivity, since the global signal can explain some of the signal variance that would otherwise be explained by the behavioral paradigm. However, the authors found a trend towards increased sensitivity, suggesting that the inclusion of the global signal also removed some of the signal variance that would have otherwise been unexplained. They furthermore found that inclusion of the global signal led to an increase in the number of voxels that were found to be negatively correlated with the task.
This issue was further examined in (Aguirre et al., 1998) who stressed the following distinction between confounds and nuisance variables – the inclusion of a confound can change the relationship between the data and the independent variable of interest whereas the inclusion of a nuisance variable will only affect the estimated error variance. This difference in effects is due to the correlation between the confound and the independent variables of interest. In the case of the intermittent button pressing task, the inclusion of the global signal as a covariate decreased the magnitude and spatial extent of positive task-related activity and also led to the appearance of regions that showed negative task-related activations, thus suggesting that the global signal should be treated as a confound. Based on these observations, Aguirre concluded that when the global signal is used, areas of positive activity should be viewed as having a “suprathreshold” relationship with the experimental design that is above and beyond the correlation with the global signal. In addition, he noted that caution should be used when interpreting negative activations, since they can arise whenever the signal is less correlated with the task than with the global signal.
The reason for caution can be understood by considering a simple example in which the global signal g is the sum g = gT + gU of a task-related component gT and an uncorrelated component gU. Next we consider a voxel time series x = bgU that is a scaled version of the uncorrelated component of the global signal, where b is an arbitrary scalar. Expressed in this manner, the signal has zero loading onto the task and the corresponding voxel would have zero activation. To assess what happens when the global signal is included as a covariate, we rewrite the signal as x = bg − bgT, which has a positive loading onto the global signal but a negative loading onto the task. Thus a voxel that was considered to have no task-related activation prior to the inclusion of the global signal as a covariate can appear to have a negative task-related activation after inclusion of the global signal.
As we shall see below, the issues in interpreting negative task-related activations would find a parallel in later concerns about the interpreting negative correlations in resting-state fMRI. It is also interesting to note that the negative activations observed in (Aguirre et al., 1998) were located in regions that were later found to be part of the default mode network (DMN), a brain network that shows a decrease in metabolic activity during the execution of goal-directed behaviors and is one of the main networks studied in resting-state fMRI (Raichle et al., 2001). Although the use of the global signal as a covariate is supported in some software programs, such as SPM, its use in task-related fMRI has been rather limited, due in part to the concerns raised above. As an example of a recent use case, Mayhew et al. (2016) used the global signal as a covariate to explain inter-trial variability in a task-related BOLD experiment. In contrast, the global signal would find wide adoption as a covariate in the analysis of resting-state fMRI studies.
5.2. Global Signal Regression
The process of GSR (in the form that is widely used at present) was first explicitly described in (Macey et al., 2004) for a task-related experiment designed to differentiate the global effects of hypercapnia from its local effects. In contrast to the prior work where both task and global signal covariates were employed, Macey et al. (2004) did not use a task covariate and simply regressed the global signal out of each voxel time series. They then computed the average fMRI signal after GSR in the dorsal medulla and were able to show that the resulting signal peaked during the early phase of hypercapnia and was thus distinct from the longer lasting global effects of hypercapnia.
Erdogan et al. (2016) recently proposed a variation of GSR in which a voxel-wise delay is applied to the global signal prior to regression in order to take into account the vascular latencies described in Section 3.4. While the proposed method can increase the amount of global signal-related variance that is removed, there may be potential issues (i.e. handling of multiple comparisons) associated with the need to search over multiple delays to find the optimal delay on a per-voxel basis. Further work will be needed to determine if these issues can be adequately addressed. On a related note, it may also be useful to examine the effects of vascular latencies on the computation of the global signal and determine whether there are better approaches for computing the signal.
Because it does not require a task covariate, GSR is ideally suited for resting-state fMRI studies in which there is no explicit task. Researchers can simply apply GSR to reduce the effects of spatially correlated confounds in their time series prior to the computation of correlations between different brain regions. The application of GSR has been found to greatly improve the functional specificity of resting-state correlation maps (Fox et al., 2009; He and Liu, 2012). In addition, GSR has also been shown to reduce the effects of motion on functional connectivity estimates (Power et al., 2015; Yan et al., 2013a; Satterthwaite et al., 2013). Power et al. (2014) demonstrated that GSR largely eliminated the spatially homogenous signal responses associated with motion, including long-lasting (e.g. tens of seconds) responses. These long-lasting responses were not attenuated by other types of correction methods, such as regression using signals from white matter and cerebral spinal fluid regions. In addition, current model-based methods do not appear to be as effective as GSR for removing global artifacts due to motion, cardiac activity, and respiratory activity (Power et al., 2016).
GSR has also been found to perform better than other state-of-the-art correction approaches, such as those based on independent component analysis, for removing globally distributed motion-related artifacts (Burgess et al., 2016; Power et al., 2016). Furthermore, Satterthwaite et al. (2013) found that GSR greatly reduced motion-related correlations between distant voxels. Finally, Yan et al. (2013b) reported that GSR outperformed partial correlation approaches in suppressing the effects of motion on estimates of network parameters.
GSR was also a key preprocessing step in the first studies reporting a negative correlation between resting-state times series in the default mode (DMN) and the task positive networks (TPN) (Fox et al., 2005; Fransson, 2005). These findings suggested an intriguing picture in which the brain alternates in time between a more introspective state where the BOLD signal is high in the DMN and low in the TPN and an externally directed state in which the signal is high in the TPN and low in the DMN. Because of this negative correlation, the DMN and TPN have been referred to as anti-correlated networks.
As shown in Appendix A, it is theoretically possible for GSR to inject artifactual components into resting-state voxel time series that did not originally contain these components. However, further study will be needed to characterize the extent to which this phenomenon actually occurs in practice.
5.3. Controversy over global signal regression
In a seminal paper that first raised concerns about the use of GSR, Murphy et al. (2009) put forth the claim that the observed anti-correlation might be artifactual rather than reflecting the true relationship between the DMN and TPN. They showed that the mathematics of GSR imposed a constraint on the sum of the correlation values between the signal from a seed region and the signals from all other voxels (not including the seed voxels), such that the sum after GSR must be negative. As a result, even if there are no negative correlations prior to GSR, the GSR operation must necessarily lead to the existence of some negative correlations.
Fox et al. (2009) acknowledged the validity of the mathematical arguments, but argued that the characteristics of the correlation maps obtained with GSR were not solely determined by the mathematical constraint but instead reflected underlying neurobiological properties. For example, they showed that negative correlations between the DMN and TPN could be observed even without the application of GSR. This finding would be supported by later studies that also demonstrated the existence of anti-correlations without GSR (Chai et al., 2012; Chang and Glover, 2009; Liang et al., 2012; Wong et al., 2012). For example, Wong et al. (2012) found that the administration of caffeine led to the presence of anti-correlations that were similar to those obtained with GSR.
Fox et al. (2009) also argued that the mathematical constraint pointed out by Murphy et al. (2009) could not account for the spatial distribution of the observed negative correlations, which are well confined to regions known to be modulated by tasks in the opposite direction to the response in the DMN. Furthermore, they argued that the constraint could not account for the consistency of the observed spatial patterns across subjects.
The discussion started by Murphy et al. (2009) and Fox et al. (2009) spawned a number of subsequent studies that further examined the effects of GSR. The concern about the spurious nature of the anti-correlations induced by GSR was echoed by several studies (Anderson et al., 2011; Weissenbacher et al., 2009; Saad et al., 2012) that used mathematical arguments and small-scale simulations similar to those of (Murphy et al., 2009). In addition Gotts et al. (2013) and Hahamy et al. (2014) argued that GSR could distort estimates of group differences in resting-state functional connectivity.
On the other hand, Carbonell et al. (2014) introduced a metric for assessing whether negative correlations were likely to be induced by GSR and used this metric to conclude that the anticorrelations between DMN and TPN were not simply a mathematical artifact. Similarly, Chen et al. (2012) proposed a method for determining when to use GSR. In analyzing functional connectivity networks, Hayasaka (2013) found that estimates obtained without GSR were positively biased and contained anomalous network characteristics (such as hub nodes along the superior edge of the interhemispheric fissure), providing further support for the use of GSR. Power et al. (2015) expressed concern that the bias attributed to GSR was largely based on results from low-dimensional simulations (e.g. two or three regions were used in (Murphy et al., 2009; Saad et al., 2012)) and stated that further work was needed to see how well the mathematical arguments applied to the higher dimensional datasets that are typically acquired in actual studies (e.g. hundreds of regions, tens of thousands of voxels). Finally, Keller et al. (2013) found that GSR improved the correlation between the BOLD signal and measures of neural power fluctuations.
The concerns about GSR have led to the development of a number of alternate approaches for dealing with global signal confounds in resting-state fMRI. He and Liu (2012) noted the existence of a linear relation between the amplitude of the global signal (calculated as its standard deviation) and the mean amplitude of the voxel-wise resting-state BOLD time series and argued that this relation was consistent with a view of the global signal as an “additive” confound. (An additional consequence of this relation is that a reduction in global signal amplitude will lead to a reduction in the mean BOLD signal amplitude and related measures, such as the amplitude of low-frequency fluctuations (ALFF; Yang et al. (2007))). He and Liu (2012) further noted that the presence of this confound decreased the median angle between the voxel-time series and the global signal and used this insight to propose a median-angle shift approach for reducing the confound. Carbonell et al. (2011) proposed the use of the first principal component as a regressor in place of the global signal. However, because of the high degree of similarity between the first principal component and the global signal (Carbonell et al., 2011; He and Liu, 2012), regression using the first principal component necessarily produces results that are highly similar to those obtained with the global signal. Marx et al. (2013) introduced a method for removing both additive and multiplicative global components from fMRI time series and used simulations to show that their method had the potential to introduce less bias into the correlation estimates as compared to GSR. For group level analyses, Saad et al. (2013) proposed the use of the average brain-wide correlation as a covariate. Since the average brain-wide correlation is equivalent to the squared amplitude of the global signal (when all voxel time series have been normalized to unit norm), this approach essentially uses the squared amplitude as a covariate.
Despite the controversy regarding GSR, it is still a widely used approach (Power et al., 2015; Li et al., 2015). Indeed, Power et al. (2016) have argued that any potential drawbacks due to GSR must be weighed against the significant concerns about the global artifacts that are present in most fMRI scans. Due in part to the effectiveness of GSR in removing these artifacts, none of the alternatives that we have discussed so far has been broadly adopted. However, there is a related method that is quite commonly used in resting-state fMRI analyses. This is the global signal subtraction approach that is a standard pre-processing step in a number of software implementations of independent components analysis (ICA), a popular approach for the analysis of resting-state fMRI data (Remes et al., 2011). In the next section, we explore in detail the connection between GSR and global signal subtraction and also consider an additional related method known as global signal normalization.
5.4. Relation between Global Signal Regression, and Global Signal Subtraction, and Global Signal Normalization
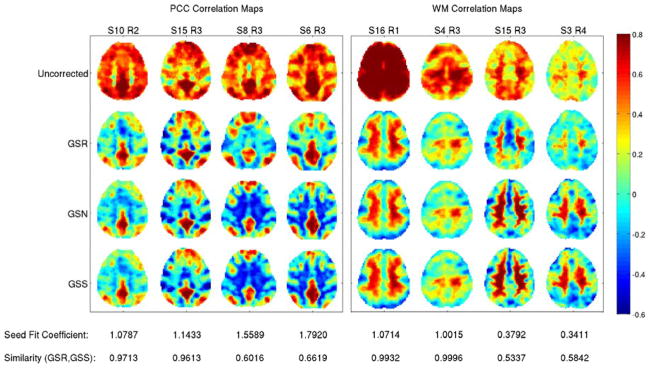
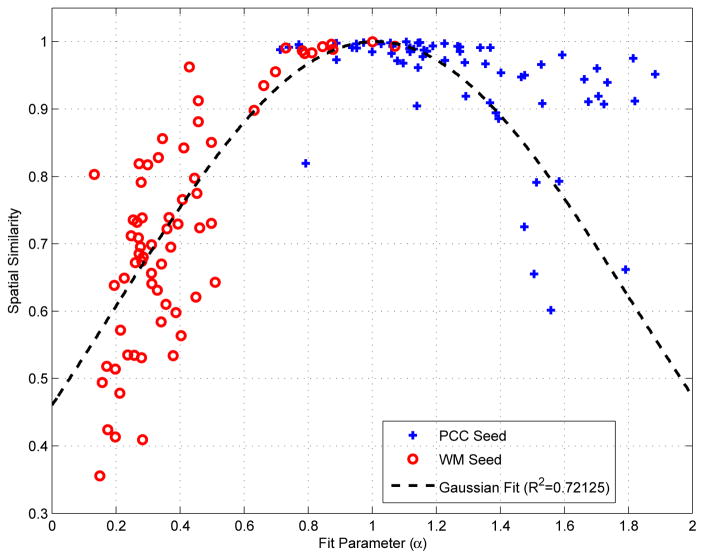
In comparing GSR to global signal subtraction (GSS), the key difference is that GSR finds the optimal fit (through regression) between each voxel time series and the global signal prior to removal of an appropriately scaled version of the global signal, whereas GSS simply subtracts the global signal from each voxel time series, without any voxel-specific scaling. The two processes are identical when the GSR fit coefficient equal to 1.0. As shown in Appendix B, the mean value (across voxels) of the GSR fit coefficient is equal to 1.0. However, the fit coefficient for any given voxel can be quite different from 1.0. In Figure 6, we show representative correlation maps formed using a seed voxel time series from either the posterior cingulate cortex (PCC) or a white matter (WM) region of interest after application of GSR, GSS, and global signal normalization (discussed below). The GSR fit coefficients (for the seed voxel time series) and the spatial correlations between the maps obtained with GSR and GSS are indicated below the plots. The cosine similarity values between PCC seed maps for GSR and GSS range from 0.60 to 0.97, while for WM seed maps the similarity values range from 0.53 to 1.0. Figure 7 shows the PCC and WM seed fit coefficients versus the cosine similarities between the corresponding connectivity maps obtained after GSR and GSS across 68 different scans. The degree of similarity between the GSR and GSS maps depends on the closeness of the fit coefficient to 1.0, with a high degree of similarity between GSR and GSS maps when the coefficient is close to 1.0. As the fit coefficient deviates from the ideal value of 1.0, the spatial correlations decrease sharply for the WM seed maps and more gradually for the PCC seed maps.
Figure 6.
Posterior-cingulate cortex (PCC) and white-matter (WM) seed correlation maps obtained prior to GSR and after the application of GSR, global signal normalization (GSN), and global signal subtraction (GSS). Consistent with the approximation shown in Appendix C, GSN and GSS yield nearly identical maps for all scans. The cosine similarities between the GSR and GSS maps are indicated by the values listed at the bottom along with the corresponding GSR fit coefficients for the seed time courses. As the fit coefficient values approach 1.0, the GSR and GSS maps become more similar.
Figure 7.
Cosine similarity between the connectivity maps obtained after GSR and GSS for PCC (blue) and WM (red) seed time courses versus the corresponding GSR fit coefficients. Similarity values are very high (r > .90) when the fit coefficients are close to 1.0 (at which point GSR and GSS are equivalent operations with respect to the seed time course). As the fit coefficient deviates from 1.0, the similarity values decrease for both seeds, rather sharply for the WM seed and relatively slowly for the PCC seed. A Gaussian fit R2 = 0.74 is shown by the black-dashed line.
While more investigation is needed to understand the similarities between GSR and GSS, these preliminary findings indicate that the concerns that have been raised about studies that use GSR are also likely to apply to studies that use GSS. For example, as discussed above, some ICA implementations use the GSS approach as a pre-processing step and Remes et al. (2011) have reported differences in ICA results obtained with and without global signal subtraction, with slightly better performance observed with subtraction. On the other hand, some ICA implementations do not use GSS and the effect of the global signal on these implementations is not entirely clear (Remes et al., 2011). Two recent studies (Power et al., 2016; Burgess et al., 2016) reported that the use of an ICA-based denoising algorithm (that did not use GSS) had limited effectiveness in removing global signal components, specifically those related to motion and respiration. Overall, further work is needed to provide a better understanding of the effect of the global signal on ICA-based analyses.
Global signal normalization (also referred to as frame-to-frame intensity stabilization) is an alternate method for accounting for the effects of global signal confounds (Fox et al., 2009; Desjardins et al., 2001; Gavrilescu et al., 2002; Dai et al., 2016). In the global signal normalization approach, all computations, including calculation of the global signal, are performed prior to the removal of the temporal means of the voxel time courses. At each time point, the image data are divided by the global signal and then a constant term (typically equal to 1.0) is subtracted from the normalized images prior to the computation of inter-voxel correlations. A key difference is that the global signal used in the normalization approach has a large positive mean while the global signal used in both GSR and global signal subtraction typically has zero mean. (Note that even when the mean is not explicitly removed from the global signal, it is effectively removed through the inclusion of a constant term in analyses that use multiple linear regression to remove nuisance terms.) Taking into account this difference, it can be shown that the global signal normalization process can be well approximated by subtracting out the zero mean global signal from each demeaned voxel time series (see Appendix C). Thus, global signal normalization and global signal subtraction are essentially equivalent approaches. An example of this equivalence is provided in Figure 6. Furthermore, it can be shown that global signal normalization is similar to GSR when GSR is applied to the data before the temporal means have been subtracted (see Appendix D). However, as discussed above, it is important to note that GSR is typically applied after subtraction of the temporal means.
5.5. GSR as a Temporal Downweighting Process
As discussed above, in the prior studies and debates concerning the use of GSR, a combination of mathematical arguments, empirical findings, and simulations have been used to examine the strengths and limitations of the approach (Fox et al., 2009; Murphy et al., 2009; Saad et al., 2012; He and Liu, 2012). However, the process of GSR has remained somewhat mysterious as it is not easy to visualize the process of regression with a global mean signal in a high-dimensional signal space.
We have recently proposed a new way of looking at GSR in which the main effects of GSR are approximated as a temporal downweighting process such that data from time points with relatively large global signal magnitudes are greatly attenuated while data from time points with relatively small global signal magnitudes are largely unaffected (Nalci et al., 2016a). (Note that here we use the term magnitude to refer to the absolute value of the global signal at each time point in a scan, which is distinct from our use of the term amplitude to refer to the standard deviation of the global signal over the course of the scan) An example of these effects is shown in rows 1 through 3 of panel (a) in Figure 8. Large global signal magnitudes (i.e. both large positive and negative values) occur at those time points where the uncorrected (i.e. prior to GSR) brain images in row 2 exhibit greater spatial homogeneity, while small global signal magnitudes correspond to images where there are similar proportions of negative and positive voxel values. After GSR (row 3), the voxel values in images at time points with large global signal magnitude are greatly attenuated, whereas the images with small global signal values are minimally affected. For each time point, we compute the average downweighting factor as the average across voxels of the ratio between the voxel value after GSR to the corresponding voxel value of the uncorrected image. We denote this metric as the GSR ratio and have plotted it in row 4 of panel (a). As shown in panel (b), the GSR ratio decreases in an approximately linear fashion with the magnitude of the global signal. In other words, the average degree of downweighting increases with global signal magnitude. Note that when the global signal magnitude is equal to zero the GSR ratio is equal to 1.0, since voxel time series are unaffected by GSR at these time points (i.e. subtracting zero has no effect).
In row 5 of panel (a) we have multiplied the uncorrected images from row 2 by the GSR ratio to obtain downweighted images. As a limiting case of the downweighting process, we can also simply censor images from those time points where the degree of downweighting is large. Row 6 in panel (a) shows the effect of censoring (i.e multiplying by zero) images at time points where the expected GSR ratio is less than 0.5 (see (Nalci et al., 2016a) for details), while retaining the original uncorrected images for the remaining time points.
Resting-state correlation maps obtained with the seed signal from the posterior cingulate cortex (PCC) and after applying GSR and the downweighting and censoring approaches are shown in panel (c) of Figure 8 for a representative slice from each of 10 different scans. Maps obtained with the uncorrected data (i.e. after preprocessing but before GSR) are shown in the top row. From a qualitative viewpoint, the correlation maps obtained after GSR are very similar to those obtained after either downweighting by the GSR ratio or censoring. This suggests that the main effects of GSR on resting-state correlation maps are well approximated by both the downweighting and censoring approaches. More detailed comparisons are provided in (Nalci et al., 2016a).
By averaging the GSR ratio across the duration of a scan, we can obtain a measure of the overall degree of downweighting due to GSR for each scan. In Figure 8(d), we find that GSR ratio shows an inverse dependence on global signal amplitude (computed as the standard deviation over time of the global signal within the scan). Thus, for scans in which there are large global signal fluctuations, the average downweighting due to GSR will also be larger.
The temporal downweighting framework represents a simple and intuitive way of understanding the effects of GSR. Instead of having to visualize how regression affects each individual voxel time series, we can simply consider how the data from each time point is downweighted prior to the computation of functional correlations. For example, the downweighting framework may help to explain the effectiveness of GSR in attenuating motion-related artifacts, such as those shown in the signal intensity plots in Figure 7 of (Power et al., 2014). In the limit of global signal censoring, the data from each time point is either included in (weighting of 1.0) or excluded (weighting of 0.0) from the computation. Within the subset of retained images, there is no mathematical constraint that forces the existence of negative correlations, as these images are not modified by the censoring operation. Thus anticorrelations between the DMN and TPN that are seen in both the GSR and global signal censored PCC maps in Figure 8(c) are unlikely to be simply an artifact induced by GSR. Instead, the negative correlations are inherent in the data for the retained time points where the global signal magnitude is low. Indeed, the spatial patterns observed in the retained time points are similar to those that have been observed in studies showing that key features of resting-state functional connectivity maps can be obtained using a fraction of the original time points (Tagliazucchi et al., 2016; Liu and Duyn, 2013).
5.6. The Global Signal and Dynamical Functional Connectivity
In resting-state fMRI studies of dynamic functional connectivity, temporal variations in the correlation between signals from different brain regions or networks are examined, typically using a sliding-window type analysis (Hutchison et al., 2013). Although analysis methods in this relatively new research area are still evolving, many studies use some type of correction for global signal effects (e.g. either GSR or global signal subtraction for ICA-based approches) (Laumann et al., 2016; Shine et al., 2016; Wang et al., 2016), although there are exceptions (Gonzalez-Castillo et al., 2015; Demirtaş et al., 2016). In a study that did not use GSR, Demirtaş et al. (2016) found that the relative magnitude of the global signal (e.g. high or low) was associated with the level of dynamic phase coupling between different brain regions. Even in studies that use GSR, the global signal may still have an effect on the analysis. As noted above, GSR can be approximated as a temporal downweighting process, in which the degree of the downweighting varies in time with the magnitude of the global signal. In a sliding window type analysis performed after GSR, the analysis window will move across temporal segments with varying levels of effective downweighting. For scans where there is a large degree of downweighting, the temporal variations in the downweighting are likely to have a significant effect on the time-varying correlation estimates. Further work to understand the impact of the global signal on dynamic functional connectivity measures is clearly needed.
6. Conclusion
The global signal currently plays an integral part in the analysis of fMRI studies. This is especially true for resting-state fMRI studies in which the efficacy of GSR has led to its widespread adoption for both standard resting-state analyses and emerging approaches, such as methods for characterizing dynamic functional connectivity. Yet despite its widespread use there is still a great deal of confusion and controversy regarding the use of the global signal in fMRI analyses. In some cases, this has led researchers to report two versions of their results, one version with GSR and another without GSR (Yeo et al., 2015; Yang et al., 2014). Part of the confusion stems from the difficulty in understanding the effects of GSR in the large-dimensional signal space that researchers typically encounter in fMRI studies. The size of this signal space is rapidly increasing with improvements in fMRI acquisition methods. The temporal downweighting framework offers a simpler way to understand the effects of GSR and we expect that it will lead to further developments that will enable researchers to better address global signal effects in their studies.
At the same time, it will be critical to continue to develop our understanding of the sources that contribute to the global signal, as this will enable a better appreciation of the effects of GSR and other approaches. For example, the current evidence suggests that the global signal takes on large values (either positive or negative) when there are large deviations in vigilance levels. When considered in conjunction with the temporal downweighting framework, this observation suggests that a primary effect of GSR is to attenuate the effects of vigilance variations over the course of a resting-state fMRI time series, since GSR will largely downweight the data from those time points with large vigilance deviations.
Future investigations into the origins of the global signal will benefit not only from studies focused on the global signal but also from studies that aim to understand the basic mechanisms underlying resting-state fMRI. In this regard, a better understanding of the complex relations between the arousal system, the autonomic nervous system, and the resting-state fMRI signal will be very useful (Iacovella and Hasson, 2011; Yuan et al., 2013). At the same time, it is important to note that the investigation of a signal that has largely been considered a nuisance term has led to a better appreciation of the effects of vigilance and arousal on resting-state fMRI measures. We anticipate that future studies will reveal more aspects of the information that lies in this global “nuisance” signal.
Acknowledgments
We would like to thank Dr. Hongjian He for preparing the initial version of Figure 3. This work was partially supported by NIH grant R21MH112155 and a UC San Diego Frontiers of Innovation Scholars Program (FISP) Project Fellowship.
Appendix A. Injection of Artifactual Components by GSR
Here we address the possibility of the injection of artifactual components by GSR that was raised by one of the reviewers of this article. Let the global signal g = gN + gM be the sum of a desired neuronal component gN and an undesired artifactual component gM (e.g. due to motion). We assume that gN and gM are zero-mean and uncorrelated, such that . We next consider a voxel time series x = bgN that is a scaled version of the neuronal component with no contribution from the artifactual component. Applying GSR to this time series results in the following:
| (A.1) |
| (A.2) |
| (A.3) |
Thus, it is possible for GSR to inject an artifactual component into a voxel time-series.
Appendix B. Global Signal Subtraction and GSR
In the global signal subtraction (GSS) approach, the global signal is simply subtracted from each voxel to yield xGSS = x − g where xGSS, x, and g are column vectors representing the voxel time series after global signal subtraction, the original voxel time series, and the global signal, respectively. Note that without loss of generality, we assume that all signals are zero-mean percent normalized time series (i.e. they represent percent BOLD signal changes).
The process of GSR is described as xGSR = x − αg where the fit coefficient α = (gTg)−1 gT x. GSR and GSS are equivalent when α = 1.0. For a given scan, we find that the mean value of the fit coefficient (computed over voxels) is equal to 1.0. The proof is as follows:
| (B.1) |
| (B.2) |
| (B.3) |
| (B.4) |
| (B.5) |
where αi and xi denote the fit coefficient and time series, respectively, for the ith voxel and N is the number of voxels.
Appendix C. Global Signal Normalization and Global Signal Subtraction
In the global signal normalization approach, computations are performed prior to the removal of the voxel-wise temporal means or percent normalization. Thus, we can define the un-normalized global signal gU as the sum gU = ḡ1M + g̃ of a mean term ḡ and a zero-mean fluctuation term g̃, where 1M indicates a M × 1 column vector of ones. An un-normalized voxel time series is similarly defined as xU = x̄1M + x̃. The process of intensity stabilization (or GS normalization) is formally defined as
| (C.1) |
where diag (gU) denotes the matrix with gU along the diagonal (Fox et al., 2009).
To proceed, let g̃[i] and x̃ [i] denote the values of g̃ and x̃ at the ith time point. Then the normalized values are
| (C.2) |
| (C.3) |
| (C.4) |
| (C.5) |
| (C.6) |
where we have made use of the fact that the magnitude of the fluctuations in fMRI GS time series are typically only a few percent at most of the overall mean, so that ḡ ≫ g̃ [i]. In addition we assumed that x̄ = ḡ, where this last relation holds because we can always scale the data such that the means of all the voxels are the same. Thus, to first order the process of GS normalization is equivalent to simply taking the difference between the percent change voxel time series x̃ [i]/x̄ and the percent change global signal g̃[i]/ḡ. Using vector notation, the approximation to GS normalization is expressed as the difference x − g of the percent normalized voxel time series and global signals. Thus, GS normalization and GS subtraction are nearly identical methods. Note that an initial version of this proof was presented in (Nalci et al., 2016a).
Appendix D. Comparing Global Signal Normalization with GSR
It turns out that global normalization and GSR give similar results when we leave the mean in prior to GSR. Borrowing the notation from the previous section, the proof is as follows:
| (D.1) |
where we have made use of the relations from the previous section ḡ ≫ g̃ [i] and x̄ = ḡ, as well as the related relation ḡ ≫ x̃[i]. In addition, we have made use of the facts that by definition g̃T 1M = 0, x̃T 1M = 0, and . Aside from the lack of normalization by the scalar ḡ this is identical to the result obtained for global normalization.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aguirre GK, Zarahn E, D’esposito M. Empirical analyses of BOLD fMRI statistics. II. Spatially smoothed data collected under null-hypothesis and experimental conditions. NeuroImage. 1997 Apr;5(3):199–212. doi: 10.1006/nimg.1997.0264. [DOI] [PubMed] [Google Scholar]
- Aguirre GK, Zarahn E, D’esposito M. The inferential impact of global signal covariates in functional neuroimaging analyses. NeuroImage. 1998 Oct;8(3):302–306. doi: 10.1006/nimg.1998.0367. [DOI] [PubMed] [Google Scholar]
- Amemiya S, Kunimatsu A, Saito N, Ohtomo K. Cerebral hemodynamic impairment: assessment with resting-state functional MR imaging. Radiology. 2014 Feb;270(2):548–555. doi: 10.1148/radiol.13130982. [DOI] [PubMed] [Google Scholar]
- Anderson JS, Druzgal TJ, Lopez-Larson M, Jeong EK, Desai K, Yurgelun-Todd D. Network anticorrelations, global regression, and phase-shifted soft tissue correction. Human Brain Mapping. 2011 Jun;32(6):919–934. doi: 10.1002/hbm.21079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behzadi Y, Restom K, Liau J, Liu TT. A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. Neuroimage. 2007 Aug;37(1):90–101. doi: 10.1016/j.neuroimage.2007.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berntson GG, Cacioppo JT, Quigley KS. Respiratory sinus arrhythmia: autonomic origins, physiological mechanisms, and psychophysiological implications. Psychophysiology. 1993 Mar;30(2):183–196. doi: 10.1111/j.1469-8986.1993.tb01731.x. [DOI] [PubMed] [Google Scholar]
- Bhattacharyya PK, Lowe MJ. Cardiac-induced physiologic noise in tissue is a direct observation of cardiac-induced fluctuations. Magnetic Resonance Imaging. 2004 Jan;22(1):9–13. doi: 10.1016/j.mri.2003.08.003. [DOI] [PubMed] [Google Scholar]
- Bianciardi M, Van Gelderen P, Duyn JH, Fukunaga M, De Zwart JA. Making the most of fMRI at 7 T by suppressing spontaneous signal fluctuations. NeuroImage. 2009 Jan;44(2):448–454. doi: 10.1016/j.neuroimage.2008.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. NeuroImage. 2006 Jul;31(4):1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- Brosch JR, Talavage TM, Ulmer JL, Nyenhuis JA. Simulation of human respiration in fMRI with a mechanical model. IEEE transactions on bio-medical engineering. 2002 Jul;49(7):700–707. doi: 10.1109/TBME.2002.1010854. [DOI] [PubMed] [Google Scholar]
- Burgess GC, Kandala S, Nolan D, Laumann TO, Power J, Adeyemo B, Harms MP, Petersen SE, Barch DM. Evaluation of Denoising Strategies To Address Motion-Correlated Artifact in Resting State fMRI Data from the Human Connectome Project. Brain connectivity. 2016 Aug; doi: 10.1089/brain.2016.0435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB, Uludağ K, Dubowitz DJ, Liu TT. Modeling the hemodynamic response to brain activation. NeuroImage. 2004;23(Suppl 1):S220–33. doi: 10.1016/j.neuroimage.2004.07.013. [DOI] [PubMed] [Google Scholar]
- Carbonell F, Bellec P, Shmuel A. Global and system-specific resting-state fMRI fluctuations are uncorrelated: principal component analysis reveals anti-correlated networks. Brain connectivity. 2011;1(6):496–510. doi: 10.1089/brain.2011.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carbonell F, Bellec P, Shmuel A. Quantification of the impact of a confounding variable on functional connectivity confirms anti-correlated networks in the resting-state. NeuroImage. 2014 Feb;86:343–353. doi: 10.1016/j.neuroimage.2013.10.013. [DOI] [PubMed] [Google Scholar]
- Chai XJ, Castañón AN, Ongür D, Whitfield-Gabrieli S. Anticorrelations in resting state networks without global signal regression. NeuroImage. 2012 Jan;59(2):1420–1428. doi: 10.1016/j.neuroimage.2011.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Cunningham JP, Glover GH. Influence of heart rate on the BOLD signal: the cardiac response function. NeuroImage. 2009 Feb;44(3):857–869. doi: 10.1016/j.neuroimage.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover GH. Effects of model-based physiological noise correction on default mode network anti-correlations and correlations. NeuroImage. 2009 Oct;47(4):1448–1459. doi: 10.1016/j.neuroimage.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Leopold DA, Schölvinck ML, Mandelkow H, Picchioni D, Liu X, Ye FQ, Turchi JN, Duyn JH. Tracking brain arousal fluctuations with fMRI. Proceedings of the National Academy of Sciences of the United States of America. 2016 Apr;113(16):4518–4523. doi: 10.1073/pnas.1520613113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Chen G, Xie C, Ward BD, Li W, Antuono P, Li SJ. A method to determine the necessity for global signal regression in resting-state fMRI studies. Magnetic Resonance in Medicine. 2012 Dec;68(6):1828–1835. doi: 10.1002/mrm.24201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christen T, Jahanian H, Ni WW, Qiu D, Moseley ME, Zaharchuk G. Noncontrast mapping of arterial delay and functional connectivity using resting-state functional MRI: a study in Moyamoya patients. Journal of magnetic resonance imaging : JMRI. 2015 Feb;41(2):424–430. doi: 10.1002/jmri.24558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Computers and biomedical research, an international journal. 1996 Jun;29(3):162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Curtis AT, Menon RS. Highcor: a novel data-driven regressor identification method for BOLD fMRI. NeuroImage. 2014 Sep;98:184–194. doi: 10.1016/j.neuroimage.2014.05.013. [DOI] [PubMed] [Google Scholar]
- Dagli MS, Ingeholm JE, Haxby JV. Localization of cardiac-induced signal change in fMRI. NeuroImage. 1999 Apr;9(4):407–415. doi: 10.1006/nimg.1998.0424. [DOI] [PubMed] [Google Scholar]
- Dai W, Varma G, Scheidegger R, Alsop DC. Quantifying fluctuations of resting state networks using arterial spin labeling perfusion MRI. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism. 2016 Mar;36(3):463–473. doi: 10.1177/0271678X15615339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G, Hagmann P, Hudetz AG, Tononi G. Modeling Resting-State Functional Net-works When the Cortex Falls Sleep: Local and Global Changes. Cerebral Cortex. 2014 Dec;24(12):3180–94. doi: 10.1093/cercor/bht176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demirtaş M, Tornador C, Falcón C, López-Solà M, Hernández-Ribas R, Pujol J, Menchón JM, Ritter P, Cardoner N, Soriano-Mas C, Deco G. Dynamic functional connectivity reveals altered variability in functional connectivity among patients with major depressive disorder. Human Brain Mapping. 2016 Aug;37(8):2918–2930. doi: 10.1002/hbm.23215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desjardins AE, Kiehl KA, Liddle PF. Removal of confounding effects of global signal in functional MRI analyses. NeuroImage. 2001 Apr;13(4):751–758. doi: 10.1006/nimg.2000.0719. [DOI] [PubMed] [Google Scholar]
- Erdogan SB, Tong Y, Hocke LM, Lindsey KP, Frederick Bd. Correcting for Blood Arrival Time in Global Mean Regression Enhances Functional Connectivity Analysis of Resting State fMRI-BOLD Signals. Frontiers in human neuroscience. 2016;10(311):1–22. doi: 10.3389/fnhum.2016.00311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans JW, Kundu P, Horovitz SG, Bandettini PA. Separating slow BOLD from non-BOLD baseline drifts using multi-echo fMRI. NeuroImage. 2015 Jan;105:189–197. doi: 10.1016/j.neuroimage.2014.10.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falahpour M, Wong CW, Liu TT. The resting state fMRI global signal is negatively correlated with time-varying EEG vigilance. Proceedings of the 24th Annual Meeting of the ISMRM; 2016. p. 641. [Google Scholar]
- Foerster BU, Tomasi D, Caparelli EC. Magnetic field shift due to mechanical vibration in functional magnetic resonance imaging. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2005 Nov;54(5):1261–1267. doi: 10.1002/mrm.20695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME. The global signal and observed anticor-related resting state brain networks. Journal of Neurophysiology. 2009 Jun;101(6):3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransson P. Spontaneous low-frequency bold signal fluctuations: An fmri investigation of the resting-state default mode of brain function hypothesis. Human brain mapping. 2005;26(1):15–29. doi: 10.1002/hbm.20113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Frackowiak RS, Turner R. Characterizing dynamic brain responses with fMRI: a multivariate approach. NeuroImage. 1995a Jun;2(2):166–172. doi: 10.1006/nimg.1995.1019. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Liddle PF, Dolan RJ, Lammertsma AA, Frackowiak RS. The relationship between global and local changes in PET scans. Journal of Cerebral Blood Flow & Metabolism. 1990 Jul;10(4):458–466. doi: 10.1038/jcbfm.1990.88. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Turner R, Frackowiak RS. Characterizing evoked hemodynamics with fMRI. NeuroImage. 1995b Jun;2(2):157–165. doi: 10.1006/nimg.1995.1018. [DOI] [PubMed] [Google Scholar]
- Fukunaga M, Horovitz SG, Van Gelderen P, De Zwart JA, Jansma JM, Ikonomidou VN, Chu R, Deckers RHR, Leopold DA, Duyn JH. Large-amplitude, spatially correlated fluctuations in BOLD fMRI signals during extended rest and early sleep stages. Magnetic Resonance Imaging. 2006 Oct;24(8):979–992. doi: 10.1016/j.mri.2006.04.018. [DOI] [PubMed] [Google Scholar]
- Gavrilescu M, Shaw ME, Stuart GW, Eckersley P, Svalbe ID, Egan GF. Simulation of the effects of global normalization procedures in functional MRI. NeuroImage. 2002 Oct;17(2):532–542. [PubMed] [Google Scholar]
- Gawryluk JR, Mazerolle EL, D’Arcy RCN. Does functional MRI detect activation in white matter? A review of emerging evidence, issues, and future directions. Frontiers in neuroscience. 2014;8:239. doi: 10.3389/fnins.2014.00239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Li TQ, Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magnetic Resonance in Medicine. 2000 Jul;44(1):162–167. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Glover GH, Mueller BA, Turner JA, van Erp TGM, Liu TT, Greve DN, Voyvodic JT, Rasmussen J, Brown GG, Keator DB, Calhoun VD, Lee HJ, Ford JM, Mathalon DH, Diaz M, O’Leary DS, Gadde S, Preda A, Lim KO, Wible CG, Stern HS, Belger A, McCarthy G, Ozyurt B, Potkin SG. Function biomedical informatics research network recommendations for prospective multicenter functional MRI studies. Journal of magnetic resonance imaging : JMRI. 2012 Jul;36(1):39–54. doi: 10.1002/jmri.23572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goebel R. Analysis of Functional MRI Data. In: Ugurbil K, Berliner L, Uludag K, editors. fMRI: From Nuclear Spins to Brain Function. Ch. 12. Springer; 2015. pp. 311–364. [Google Scholar]
- Gonzalez-Castillo J, Hoy CW, Handwerker DA, Robinson ME, Buchanan LC, Saad ZS, Bandettini PA. Tracking ongoing cognition in individuals using brief, whole-brain functional connectivity patterns. Proceedings of the National Academy of Sciences of the United States of America. 2015 Jul;112(28):8762–8767. doi: 10.1073/pnas.1501242112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gotts SJ, Saad ZS, Jo HJ, Wallace GL, Cox RW, Martin A. The perils of global signal regression for group comparisons: a case study of Autism Spectrum Disorders. Frontiers in human neuroscience. 2013;7:356. doi: 10.3389/fnhum.2013.00356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gotts SJ, Simmons WK, Milbury LA, Wallace GL, Cox RW, Martin A. Fractionation of social brain circuits in autism spectrum disorders. Brain : a journal of neurology. 2012 Sep;135(Pt 9):2711–2725. doi: 10.1093/brain/aws160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahamy A, Calhoun V, Pearlson G, Harel M, Stern N, Attar F, Malach R, Salomon R. Save the global: global signal connectivity as a tool for studying clinical populations with functional magnetic resonance imaging. Brain connectivity. 2014 Aug;4(6):395–403. doi: 10.1089/brain.2014.0244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajnal JV, Myers R, Oatridge A, Schwieso JE, Young IR, Bydder GM. Artifacts due to stimulus correlated motion in functional imaging of the brain. Magnetic Resonance in Medicine. 1994 Mar;31(3):283–291. doi: 10.1002/mrm.1910310307. [DOI] [PubMed] [Google Scholar]
- Hallquist MN, Hwang K, Luna B. The nuisance of nuisance regression: spectral misspecification in a common approach to resting-state fMRI preprocessing reintroduces noise and obscures functional connectivity. NeuroImage. 2013 Nov;82:208–225. doi: 10.1016/j.neuroimage.2013.05.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayasaka S. Functional connectivity networks with and without global signal correction. Frontiers in human neuroscience. 2013;7:880. doi: 10.3389/fnhum.2013.00880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He H, Liu TT. A geometric view of global signal confounds in resting-state functional MRI. NeuroImage. 2012 Feb;59(3):2339–48. doi: 10.1016/j.neuroimage.2011.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He H, Shin DD, Liu TT. Resting state BOLD fluctuations in large draining veins are highly correlated with the global mean signal. Proceedings of the 18th Annual Meeting of the ISMRM; 2010. p. 3488. [Google Scholar]
- Horovitz SG, Fukunaga M, De Zwart JA, Van Gelderen P, Fulton SC, Balkin TJ, Duyn JH. Low frequency BOLD fluctuations during resting wakefulness and light sleep: a simultaneous EEG-fMRI study. Human Brain Mapping. 2008 Jun;29(6):671–682. doi: 10.1002/hbm.20428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu X, Le TH, Parrish T, Erhard P. Retrospective estimation and correction of physiological fluctuation in functional MRI. Magnetic Resonance in Medicine. 1995 Aug;34(2):201–212. doi: 10.1002/mrm.1910340211. [DOI] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Della Penna S, Duyn JH, Glover GH, Gonzalez-Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C. Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage. 2013 Oct;80:360–378. doi: 10.1016/j.neuroimage.2013.05.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacovella V, Hasson U. The relationship between BOLD signal and autonomic nervous system functions: implications for processing of ”physiological noise”. Magnetic Resonance Imaging. 2011 Dec;29(10):1338–1345. doi: 10.1016/j.mri.2011.03.006. [DOI] [PubMed] [Google Scholar]
- Jo HJ, Saad ZS, Simmons WK, Milbury LA, Cox RW. Mapping sources of correlation in resting state fMRI, with artifact detection and removal. NeuroImage. 2010 Aug;52(2):571–582. doi: 10.1016/j.neuroimage.2010.04.246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones BE. From waking to sleeping: neuronal and chemical substrates. Trends in pharmacological sciences. 2005 Nov;26(11):578–586. doi: 10.1016/j.tips.2005.09.009. [DOI] [PubMed] [Google Scholar]
- Keller CJ, Bickel S, Honey CJ, Groppe DM, Entz L, Craddock RC, Lado FA, Kelly C, Milham M, Mehta AD. Neurophysiological investigation of spontaneous correlated and anticorrelated fluctuations of the BOLD signal. Journal of Neuroscience. 2013 Apr;33(15):6333–6342. doi: 10.1523/JNEUROSCI.4837-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson-Prior LJ, Power JD, Vincent JL, Nolan TS, Coalson RS, Zempel J, Snyder AZ, Schlaggar BL, Raichle ME, Petersen SE. Modulation of the brain’s functional network architecture in the transition from wake to sleep. Progress in Brain Research. 2011;193:277–294. doi: 10.1016/B978-0-444-53839-0.00018-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson-Prior LJ, Zempel JM, Nolan TS, Prior FW, Snyder AZ, Raichle ME. Cortical network functional connectivity in the descent to sleep. Proceedings of the National Academy of Sciences of the United States of America. 2009 Mar;106(11):4489–4494. doi: 10.1073/pnas.0900924106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laumann TO, Snyder AZ, Mitra A, Gordon EM, Gratton C, Adeyemo B, Gilmore AW, Nelson SM, Berg JJ, Greene DJ, McCarthy JE, Tagliazucchi E, Laufs H, Schlaggar BL, Dosenbach NUF, Petersen SE. On the Stability of BOLD fMRI Correlations. Cerebral Cortex. 2016 Sep; doi: 10.1093/cercor/bhw265. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li JM, Bentley WJ, Snyder AZ, Raichle ME, Snyder LH. Functional connectivity arises from a slow rhythmic mechanism. Proceedings of the National Academy of Sciences of the United States of America. 2015 May;112(19):E2527–35. doi: 10.1073/pnas.1419837112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang Z, King J, Zhang N. Anticorrelated resting-state functional connectivity in awake rat brain. NeuroImage. 2012 Jan;59(2):1190–1199. doi: 10.1016/j.neuroimage.2011.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu TT. Noise contributions to the fMRI signal: An overview. NeuroImage. 2016 Sep;143:141–151. doi: 10.1016/j.neuroimage.2016.09.008. [DOI] [PubMed] [Google Scholar]
- Liu TT, Glover GH, Mueller BA, Greve DN, Rasmussen J, Voyvodic JT, Turner JA, van Erp TGM, Mathalon DH, Andersen K, Kun L, Brown GG, Keator DB, Calhoun VD, Lee HJ, Ford JM, Diaz M, O’Leary DS, Gadde S, Preda A, Lim KO, Wible CG, Stern HS, Belger A, McCarthy G, Ozyurt B, Potkin SG. Quality Assurance in Functional MRI. In: Ugurbil K, Berliner L, Uludag K, editors. fMRI: From Nuclear Spins to Brain Function. Ch. 10. Springer; 2015. pp. 245–270. [Google Scholar]
- Liu X, Duyn JH. Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proceedings of the National Academy of Sciences of the United States of America. 2013 Mar;110(11):4392–4397. doi: 10.1073/pnas.1216856110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lund TE, Madsen KH, Sidaros K, Luo WL, Nichols TE. Non-white noise in fMRI: does modelling have an impact? NeuroImage. 2006;29(1):54–66. doi: 10.1016/j.neuroimage.2005.07.005. [DOI] [PubMed] [Google Scholar]
- Lv Y, Margulies DS, Cameron Craddock R, Long X, Winter B, Gierhake D, Endres M, Villringer K, Fiebach J, Villringer A. Identifying the perfusion deficit in acute stroke with resting-state functional magnetic resonance imaging. Annals of neurology. 2013 Jan;73(1):136–140. doi: 10.1002/ana.23763. [DOI] [PubMed] [Google Scholar]
- Macey PM, Macey KE, Kumar R, Harper RM. A method for removal of global effects from fMRI time series. NeuroImage. 2004 May;22(1):360–366. doi: 10.1016/j.neuroimage.2003.12.042. [DOI] [PubMed] [Google Scholar]
- Majeed W, Magnuson M, Hasenkamp W, Schwarb H, Schumacher EH, Barsalou L, Keilholz SD. Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans. NeuroImage. 2011 Jan;54(2):1140–1150. doi: 10.1016/j.neuroimage.2010.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majeed W, Magnuson M, Keilholz SD. Spatiotemporal dynamics of low frequency fluctuations in BOLD fMRI of the rat. Journal of magnetic resonance imaging : JMRI. 2009 Aug;30(2):384–393. doi: 10.1002/jmri.21848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marx M, Pauly KB, Chang C. A novel approach for global noise reduction in resting-state fMRI: APPLECOR. NeuroImage. 2013 Jan;64:19–31. doi: 10.1016/j.neuroimage.2012.09.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsui T, Murakami T, Ohki K. Transient neuronal coactivations embedded in globally propagating waves underlie resting-state functional connectivity. Proceedings of the National Academy of Sciences of the United States of America. 2016 Jun;113(23):6556–6561. doi: 10.1073/pnas.1521299113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayhew SD, Mullinger KJ, Ostwald D, Porcaro C, Bowtell R, Bagshaw AP, Francis ST. Global signal modulation of single-trial fMRI response variability: Effect on positive vs negative BOLD response relationship. NeuroImage. 2016 Mar;133:62–74. doi: 10.1016/j.neuroimage.2016.02.077. [DOI] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? NeuroImage. 2009 Feb;44(3):893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Fox MD. Towards a consensus regarding global signal regression for resting state functional connectivity MRI. NeuroImage. 2016 Nov; doi: 10.1016/j.neuroimage.2016.11.052. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muschelli J, Nebel MB, Caffo BS, Barber AD, Pekar JJ, Mostofsky SH. Reduction of motion-related artifacts in resting state fMRI using aCompCor. NeuroImage. 2014 Aug;96:22–35. doi: 10.1016/j.neuroimage.2014.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nalci A, Rao B, Liu TT. Global Signal Regression Acts as a Temporal Downweighting Process in Resting-State fMRI. NeuroImage. 2016a doi: 10.1016/j.neuroimage.2017.01.015. In Press. [DOI] [PubMed] [Google Scholar]
- Nalci A, Rao B, Liu TT. Sparse Estimation of Quasi-periodic Spatiotemporal Components in Resting-State fMRI. Proceedings of the 24th Annual Meeting of the ISMRM; 2016b. p. 3824. [Google Scholar]
- Olbrich S, Mulert C, Karch S, Trenner M, Leicht G, Pogarell O, Hegerl U. EEG-vigilance and BOLD effect during simultaneous EEG/fMRI measurement. NeuroImage. 2009 Apr;45(2):319–332. doi: 10.1016/j.neuroimage.2008.11.014. [DOI] [PubMed] [Google Scholar]
- Picchioni D, Duyn JH, Horovitz SG. Sleep and the functional connectome. NeuroImage. 2013 Oct;80:387–396. doi: 10.1016/j.neuroimage.2013.05.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisauro MA, Benucci A, Carandini M. Local and global contributions to hemodynamic activity in mouse cortex. Journal of Neurophysiology. 2016 Jun;115(6):2931–2936. doi: 10.1152/jn.00125.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, Petersen SE. Methods to detect, characterize, and remove motion artifact in resting state fMRI. NeuroImage. 2014 Jan;84:320–341. doi: 10.1016/j.neuroimage.2013.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Plitt M, Laumann TO, Martin A. Sources and implications of whole-brain fMRI signals in humans. NeuroImage. 2016 doi: 10.1016/j.neuroimage.2016.09.038. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL, Petersen SE. Recent progress and outstanding issues in motion correction in resting state fMRI. NeuroImage. 2015 Jan;105:536–551. doi: 10.1016/j.neuroimage.2014.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proceedings of the National Academy of Sciences. 2001;98(2):676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj D, Anderson AW, Gore JC. Respiratory effects in human functional magnetic resonance imaging due to bulk susceptibility changes. Physics in medicine and biology. 2001 Dec;46(12):3331–3340. doi: 10.1088/0031-9155/46/12/318. [DOI] [PubMed] [Google Scholar]
- Remes JJ, Starck T, Nikkinen J, Ollila E, Beckmann CF, Tervonen O, Kiviniemi V, Silven O. Effects of repeatability measures on results of fMRI sICA: a study on simulated and real resting-state effects. NeuroImage. 2011 May;56(2):554–569. doi: 10.1016/j.neuroimage.2010.04.268. [DOI] [PubMed] [Google Scholar]
- Restom K, Behzadi Y, Liu TT. Physiological noise reduction for arterial spin labeling functional MRI. NeuroImage. 2006 Jul;31(3):1104–1115. doi: 10.1016/j.neuroimage.2006.01.026. [DOI] [PubMed] [Google Scholar]
- Saad ZS, Gotts SJ, Murphy K, Chen G, Jo HJ, Martin A, Cox RW. Trouble at rest: how correlation patterns and group differences become distorted after global signal regression. Brain connectivity. 2012;2(1):25–32. doi: 10.1089/brain.2012.0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS, Reynolds RC, Jo HJ, Gotts SJ, Chen G, Martin A, Cox RW. Correcting brain-wide correlation differences in resting-state FMRI. Brain connectivity. 2013;3(4):339–352. doi: 10.1089/brain.2013.0156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sämann PG, Wehrle R, Hoehn D, Spoormaker VI, Peters H, Tully C, Holsboer F, Czisch M. Development of the brain’s default mode network from wakefulness to slow wave sleep. Cerebral Cortex. 2011 Sep;21(9):2082–2093. doi: 10.1093/cercor/bhq295. [DOI] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Gerraty RT, Ruparel K, Loughead J, Calkins ME, Eickhoff SB, Hakonarson H, Gur RC, Gur RE, Wolf DH. An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. NeuroImage. 2013 Jan;64:240–256. doi: 10.1016/j.neuroimage.2012.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schölvinck ML, Maier A, Ye FQ, Duyn JH, Leopold DA. Neural basis of global resting-state fMRI activity. Proceedings of the National Academy of Sciences of the United States of America. 2010 Jun;107(22):10238–10243. doi: 10.1073/pnas.0913110107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shine JM, Koyejo O, Poldrack RA. Temporal metastates are associated with differential patterns of time-resolved connectivity, network topology, and attention. Proceedings of the National Academy of Sciences of the United States of America. 2016 Aug;113(35):9888–9891. doi: 10.1073/pnas.1604898113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmueli K, Van Gelderen P, De Zwart JA, Horovitz SG, Fukunaga M, Jansma JM, Duyn JH. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. NeuroImage. 2007 Nov;38(2):306–320. doi: 10.1016/j.neuroimage.2007.07.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Siniatchkin M, Laufs H, Chialvo DR. The Voxel-Wise Functional Connectome Can Be Efficiently Derived from Co-activations in a Sparse Spatio-Temporal Point-Process. Frontiers in neuroscience. 2016;10:381. doi: 10.3389/fnins.2016.00381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson GJ, Pan WJ, Magnuson ME, Jaeger D, Keilholz SD. Quasi-periodic patterns (QPP): Large-scale dynamics in resting state fMRI that correlate with local infraslow electrical activity. NeuroImage. 2014 Jan;84(C):1018–1031. doi: 10.1016/j.neuroimage.2013.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Y, Hocke LM, Licata SC, Frederick Bd. Low-frequency oscillations measured in the periphery with near-infrared spectroscopy are strongly correlated with blood oxygen level-dependent functional magnetic resonance imaging signals. Journal of biomedical optics. 2012 Oct;17(10):106004. doi: 10.1117/1.JBO.17.10.106004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Y, Lindsey KP, Hocke LM, Vitaliano G, Mintzopoulos D, Frederick Bd. Perfusion information extracted from resting state functional magnetic resonance imaging. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism. 2016 Feb; doi: 10.1177/0271678X16631755. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Ong JL, Patanaik A, Zhou J, Chee MWL. Spontaneous eyelid closures link vigilance fluctuation with fMRI dynamic connectivity states. Proceedings of the National Academy of Sciences of the United States of America. 2016 Aug;113(34):9653–9658. doi: 10.1073/pnas.1523980113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissenbacher A, Kasess C, Gerstl F, Lanzenberger R, Moser E, Windischberger C. Correlations and anticorrelations in resting-state functional connectivity MRI: a quantitative comparison of preprocessing strategies. NeuroImage. 2009 Oct;47(4):1408–1416. doi: 10.1016/j.neuroimage.2009.05.005. [DOI] [PubMed] [Google Scholar]
- Wen H, Liu Z. Broadband Electrophysiological Dynamics Contribute to Global Resting-State fMRI Signal. Journal of Neuroscience. 2016a Jun;36(22):6030–6040. doi: 10.1523/JNEUROSCI.0187-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen H, Liu Z. Separating Fractal and Oscillatory Components in the Power Spectrum of Neurophysiological Signal. Brain Topography. 2016b Jan;29(1):13–26. doi: 10.1007/s10548-015-0448-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Windischberger C, Langenberger H, Sycha T, Tschernko EM, Fuchsjäger-Mayerl G, Schmetterer L, Moser E. On the origin of respiratory artifacts in BOLD-EPI of the human brain. Magnetic Resonance Imaging. 2002 Oct;20(8):575–582. doi: 10.1016/s0730-725x(02)00563-5. [DOI] [PubMed] [Google Scholar]
- Wise RG, Ide K, Poulin MJ, Tracey I. Resting fluctuations in arterial carbon dioxide induce significant low frequency variations in BOLD signal. NeuroImage. 2004 Apr;21(4):1652–1664. doi: 10.1016/j.neuroimage.2003.11.025. [DOI] [PubMed] [Google Scholar]
- Wong CW, DeYoung PN, Liu TT. Differences in the resting-state fMRI global signal amplitude between the eyes open and eyes closed states are related to changes in EEG vigilance. NeuroImage. 2015 Aug;124(Pt A):24–31. doi: 10.1016/j.neuroimage.2015.08.053. [DOI] [PubMed] [Google Scholar]
- Wong CW, Olafsson V, Tal O, Liu TT. Anti-correlated networks, global signal regression, and the effects of caffeine in resting-state functional MRI. NeuroImage. 2012 Oct;63(1):356–364. doi: 10.1016/j.neuroimage.2012.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong CW, Olafsson V, Tal O, Liu TT. The amplitude of the resting-state fMRI global signal is related to EEG vigilance measures. NeuroImage. 2013 Dec;83:983–990. doi: 10.1016/j.neuroimage.2013.07.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Cheung B, Kelly C, Colcombe S, Craddock RC, Di Martino A, Li Q, Zuo XN, Castellanos FX, Milham MP. A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics. NeuroImage. 2013a Aug;76:183–201. doi: 10.1016/j.neuroimage.2013.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Craddock RC, He Y, Milham MP. Addressing head motion dependencies for small-world topologies in functional connectomics. Frontiers in human neuroscience. 2013b;7:910. doi: 10.3389/fnhum.2013.00910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan L, Zhuo Y, Ye Y, Xie SX, An J, Aguirre GK, Wang J. Physiological origin of low-frequency drift in blood oxygen level dependent (BOLD) functional magnetic resonance imaging (fMRI) Magnetic Resonance in Medicine. 2009 Apr;61(4):819–827. doi: 10.1002/mrm.21902. [DOI] [PubMed] [Google Scholar]
- Yang GJ, Murray JD, Repovs G, Cole MW, Savic A, Glasser MF, Pittenger C, Krystal JH, Wang XJ, Pearlson GD, Glahn DC, Anticevic A. Altered global brain signal in schizophrenia. Proceedings of the National Academy of Sciences of the United States of America. 2014 May;111(20):7438–7443. doi: 10.1073/pnas.1405289111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H, Long XY, Yang Y, Yan H, Zhu CZ, Zhou XP, Zang YF, Gong QY. Amplitude of low frequency fluctuation within visual areas revealed by resting-state functional MRI. NeuroImage. 2007 May;36(1):144–152. doi: 10.1016/j.neuroimage.2007.01.054. [DOI] [PubMed] [Google Scholar]
- Yeo BTT, Tandi J, Chee MWL. Functional connectivity during rested wakefulness predicts vulnerability to sleep deprivation. NeuroImage. 2015 May;111:147–158. doi: 10.1016/j.neuroimage.2015.02.018. [DOI] [PubMed] [Google Scholar]
- Yuan H, Zotev V, Phillips R, Bodurka J. Correlated slow fluctuations in respiration, EEG, and BOLD fMRI. NeuroImage. 2013 Oct;79:81–93. doi: 10.1016/j.neuroimage.2013.04.068. [DOI] [PubMed] [Google Scholar]
- Zarahn E, Aguirre GK, D’esposito M. Empirical analyses of BOLD fMRI statistics. I. Spatially unsmoothed data collected under null-hypothesis conditions. NeuroImage. 1997 Apr;5(3):179–197. doi: 10.1006/nimg.1997.0263. [DOI] [PubMed] [Google Scholar]
- Zeng LL, Wang D, Fox MD, Sabuncu M, Hu D, Ge M, Buckner RL, Liu H. Neurobiological basis of head motion in brain imaging. Proceedings of the National Academy of Sciences of the United States of America. 2014 Apr;111(16):6058–6062. doi: 10.1073/pnas.1317424111. [DOI] [PMC free article] [PubMed] [Google Scholar]