Resurgence as Choice

Abstract

Resurgence is typically defined as an increase in a previously extinguished target behavior when a more recently reinforced alternative behavior is later extinguished. Some treatments of the phenomenon have suggested that it might also extend to circumstances where either the historic or more recently reinforced behavior is reduced by other non-extinction related means (e.g., punishment, decreases in reinforcement rate, satiation, etc.). Here we present a theory of resurgence suggesting that the phenomenon results from the same basic processes governing choice. In its most general form, the theory suggests that resurgence results from changes in the allocation of target behavior driven by changes in the values of the target and alternative options across time. Specifically, resurgence occurs when there is an increase in the relative value of an historically effective target option as a result of a subsequent devaluation of a more recently effective alternative option. We develop a more specific quantitative model of how extinction of the target and alternative responses in a typical resurgence paradigm might produce such changes in relative value across time using a temporal weighting rule. The example model does a good job in accounting for the effects of reinforcement rate and related manipulations on resurgence in simple schedules where Behavioral Momentum Theory has failed. We also discuss how the general theory might be extended to other parameters of reinforcement (e.g., magnitude, quality), other means to suppress target or alternative behavior (e.g., satiation, punishment, differential reinforcement of other behavior), and other factors (e.g., non-contingent versus contingent alternative reinforcement, serial alternative reinforcement, and multiple schedules).

1. Introduction

Resurgence is typically defined as an increase in a previously extinguished behavior when a more recently reinforced behavior is also placed on extinction (e.g., Cleland et al., 2001; Epstein, 1985; Lattal and Wacker, 2015). The phenomenon is potentially clinically important because it is likely a source of relapse of problem behavior following widely used treatments involving differential reinforcement of alternative behavior (i.e., DRA; see Volkert et al., 2009, for discussion). In such treatments, a problem behavior is placed on extinction and a more appropriate alternative behavior is reinforced (e.g., a functional communication response). Resurgence is said to occur when the problem behavior increases as a result of omission of reinforcement for the alternative behavior during treatment lapses or when treatment ends. In addition to such undesirable outcomes, resurgence might also contribute to the generation of more positive behavioral effects. For example, the phenomenon might be involved when historically effective behavior recurs under changing circumstances to allow for appropriate adaptation, problem solving, and creativity (e.g., Epstein, 1985; Shahan and Chase, 2002). Thus, a more thorough understanding of resurgence could have far reaching implications for understanding how temporally distant past experiences provide a source of potential behavior (be it good or bad) under current conditions.

Despite the definition of resurgence above, both early (e.g., Epstein, 1985) and more recent (e.g., Lattal and Wacker, 2015) treatments of the phenomenon have suggested that it might extend to circumstances where either the historic or more recently reinforced behavior is reduced by other non-extinction related means (e.g., punishment, satiation, decreases in reinforcement rate). This broader view of resurgence is appealing because the recurrence of previous behavior under such conditions may indeed reflect the same general processes, and it also more easily accommodates potentially related clinical phenomena. The theory of resurgence developed here is consistent with this broader view of the phenomenon.

The purpose of this paper is to present a theory of resurgence in which the phenomenon is considered to result from the same processes generally thought to govern choice. In short, the general theory proposed here suggests that resurgence arises from changes in the relative values of two (or more) options across time: one that was historically more valuable and one that has been more recently valuable. The merits of pursuing a choice-based theory of resurgence are manifold. First, as we will more fully development below, it is relatively straightforward to characterize behavior in resurgence preparations as resulting from an ongoing choice between a target and an alternative behavior. Second, a choice-based theory provides an account of resurgence that allows it to be incorporated into an overarching choice-based account of operant behavior–an account that has served as a cornerstone for the field. Third, the long tradition of well-developed quantitative theories of choice provides numerous insights into how the determinants of resurgence might be formalized quantitatively.

Although the theory we will present is grounded in the more general conception of resurgence discussed above (e.g., Epstein, 1985; Lattal and Wacker, 2015), most empirical data and the two dominant accounts of resurgence have focused on extinction-induced resurgence in the more restrictive sense. Thus, we will begin by reviewing these two accounts, specifically Behavioral Momentum Theory (Shahan and Sweeney, 2011) and Context Theory (see Trask et al., 2015, for a recent statement)–focusing primarily on their shortcomings. Next, we will provide a general description of a choice-based account and then provide an example of how that account might be formalized to provide a more specific quantitative model of extinction-induced resurgence. Finally, we will explore how a choice-based theory might be applied to other resurgence-inducing operations. Along the way, we will consider existing areas in need of additional research and novel predictions of the choice-based theory.

2. Behavioral Momentum Theory of Resurgence

Behavioral Momentum Theory (e.g., Nevin and Grace, 2000) provides a quantitative account of the persistence of operant behavior under conditions of disruption. The theory suggests response rates and response strength (i.e., resistance to change) are two separate aspects of behavior controlled by different processes. Response rates are governed by the contingent response-reinforcer relation, but resistance to change is governed by the Pavlovian discriminative stimulus-reinforcer relation. As a result, all sources of reinforcement within a discriminative-stimulus context, be they contingent on the target behavior, non-contingent, or even contingent on a different behavior, are predicted to contribute to the persistence of the target behavior under conditions of disruption. This prediction has been widely confirmed under a variety of circumstance (e.g., Nevin et al., 1990; Shahan and Burke, 2004; see Nevin and Shahan, 2011, for review).

The extension of Behavioral Momentum Theory to resurgence (Shahan and Sweeney, 2011) is based specifically on the augmented momentum model of extinction (Nevin and Grace, 2000). This model suggests that decreases in behavior during extinction result from increasingly disruptive effects across time of: a) terminating the contingency between a response and a reinforcer and, b) generalization decrement from removal of reinforcers from the context. The model suggests that experience with higher rates of reinforcement within a discriminative-stimulus context prior to extinction renders an operant response more resistant to the disruptive effects of extinction. Quantitatively that is,

$$log(\frac{B_t}{B_0})=\frac{-t(c+dr)}{r^b}$$ (1)

where B_t is the response rate at time t in extinction, B₀ is the base-line response rate, and r is the rate of reinforcement within the context in baseline. The model has three free parameters, where c is the suppressive effect of breaking the response-reinforcer contingency, d scales disruption associated with elimination of reinforcers from the situation (i.e., generalization decrement), and b is sensitivity to baseline reinforcement rate. As time in extinction increases, disruption increases (in the numerator of the right side of the equation), but is counteracted by previous experience with higher reinforcement rates in the context (in the denominator). Reinforcement in the context (i.e., r) includes all sources of reinforcement, regardless of whether they are contingent on the target response or not. From the perspective of this model, resistance to extinction is governed by the strength of the behavior, which is a power function (i.e., r^b) of the overall rate of reinforcement in the context of the pre-extinction baseline.

Shahan and Sweeney (2011) extended Eq. (1) to resurgence by suggesting that alternative reinforcement during extinction of a target behavior has two effects. First, alternative reinforcement serves as an additional source of disruption of the target behavior. Second, alternative reinforcement further strengthens the target behavior by serving as an additional source of reinforcement in the context. Thus,

$$log(\frac{B_t}{B_0})=\frac{-t(\mathit{kRa}+c+dr)}{{(r+R_a)}^b}$$ (2)

where all terms are as in Eq. (1). The added variable R_a is the rate of alternative reinforcement during extinction and the added free parameter k scales the disruptive impact of the alternative reinforcement during extinction. Thus, the model has four free parameters. The inclusion of kR_a increases the disruptive impact in the numerator, with higher rates of alternative reinforcement producing more suppression of the target behavior. When alternative reinforcement is removed during resurgence, kR_a is zero and the target behavior increases as a result of the release from suppression. In addition, because R_a is included in the denominator, alternative reinforcement experienced during extinction also contributes to the future strength of the target behavior, and thus to resurgence.

Although this quantitative model incorporated resurgence into a larger theoretical context and provided a reasonably good account of the data existing at the time, the theory has encountered difficulties with some of its core predictions (see Craig and Shahan, 2016; for a more thorough discussion). For example, both Sweeney and Shahan (2013b) and Craig and Shahan (2016) have found that target responding during extinction is in some cases more persistent when alternative reinforcement is available than when it is not (i.e., extinction alone). Such increases in the persistence of a target response during extinction plus an alternative source of reinforcement should not happen according to Eq. (2) because any source of alternative reinforcement should increase the numerator, and thus disruption. As a result, these findings raise serious questions about the adequacy of the conceptual foundations of Eq. (2) in terms of the processes linking alternative reinforcement to increases in disruption within the framework of the augmented model of extinction (i.e., Eq. (1)). Although the data from such experiments during tests for resurgence were generally consistent with the basic model prediction that higher rates of alternative reinforcement should generate greater increases in responding when they are removed, the conceptual foundation of the model with respect to what is responsible for these effects (release from greater disruption with higher R_a) appears to be incorrect.

In addition, from its inception Eq. (2) has had problems with respect to how to incorporate the proposed added response-strengthening effects of alternative reinforcement (i.e., R_a in the denominator). This difficulty is rooted in its forbearer, Eq. (1). Specifically, in Eq. (1), the pre-extinction rate of reinforcement experienced in baseline is carried over unchanged into extinction because r remains unchanged. As a result, decreases in responding during extinction are driven only by the growth of the disruption term across extinction. In extending the model to resurgence with Eq. (2), Shahan and Sweeney (2011) followed this same logic and assumed that the alternative rate of reinforcement (i.e., R_a) added to the contextual reinforcement conditions (i.e., r + R_a) and remained there with the transition to the resurgence test. However, two problems arise from this assumption.

First, it remains unclear how one should incorporate additional changes in the rate of alternative reinforcement that might occur across the course of extinction. For example both, Sweeney and Shahan (2013b) and Winterbauer and Bouton (2012) examined the effects of alternative-reinforcement thinning on resurgence. In such thinning procedures, the rate of alternative reinforcement is reduced across sessions of extinction of the target behavior. Applying the same logic as above when R_a was added to the denominator, one might consider adding each subsequent alternative-reinforcement rate. But, doing so would lead to the absurd prediction that such decreases in alternative-reinforcement rate would produce greater response strength (and greater resurgence) than a situation where the original higher rate of alternative reinforcement is maintained throughout.

Second, the assumption of the additivity of baseline reinforcement rates and alternative-reinforcement rates is somewhat odd in the first place. If response strength is driven by the Pavlovian stimulus-reinforcer relation between a discriminative stimulus context and reinforcers obtained in that context, it is strange to assume the replacement of reinforcement of a target response with reinforcement for an alternative response should increase response strength. For example, if the target behavior is reinforced on a VI 15-s schedule (i.e., 240 reinforcers/h) during baseline and then an alternative behavior is reinforced on a VI 15-s schedule during extinction of the target, why should the Pavlovian stimulus reinforcer relation be assumed to be associated with 240 + 240 = 480 reinforcers/h? The overall rate of reinforcement in the context has not changed, and certainly it has not doubled. This issue arises from broader questions that have never been answered about how the original augmented model (Eq. (1)) should be applied across conditions with changes in reinforcement rate (see Craig et al., 2015; Shahan and Sweeney, 2011; for discussion). At present, an alternative way of incorporating changes in alternative-reinforcement rate across extinction that does not fundamentally alter the basic logic of the augmented model has not suggested itself. As a result, attempting to fix the momentum-based model of resurgence would appear to first require fixing the basic augmented model of extinction. Although it could be possible to generate a version of the augmented model that better characterizes changes in reinforcement rates across conditions, such a modified model would not address the problem with the other core assumption of the resurgence model that alternative reinforcement should always serve as an additional source of disruption (e.g., Sweeney and Shahan, 2013b; Craig and Shahan, 2016).

In short, in addition to the conceptual difficulties arising from the empirical failures of the model with respect to how alternative reinforcement is treated as a disruptor in the numerator of Eq. (2), there are additional conceptual difficulties about how alternative reinforcers are treated as a source of additional response strength in the denominator. As a result, both of the core assumptions made to extend behavioral momentum to resurgence appear to be difficult to sustain without a fundamental reworking of the theory, including the progenitor augmented model of extinction (i.e., Eq. (1); see Craig and Shahan, 2016; for full discussion).

The above issues notwithstanding, Eq. (2) also fails to provide any account of another outcome sometimes observed in experiments on resurgence. Eq. (2) predicts that as soon as alternative reinforcement is removed during a resurgence test, target responding increases and then decreases across further sessions of testing in extinction. This outcome does often occur in the literature (e.g., Sweeney and Shahan, 2013b; see Shahan and Sweeney, 2011, for review). However, target responding during resurgence tests often also occurs at a lower rate in early sessions of extinction of the alternative behavior, before increasing and again decreasing with additional sessions (see Podlesnik and Kelley, 2015; for review). In its present form, Eq. (2) has no means to account for such bitonic functions across sessions of resurgence testing.

Thus, although the Behavioral Momentum-Based theory of resurgence has been useful for generating research and for providing a broader theoretical context in which to frame resurgence, the problems with the core theoretical assumptions of the model, its empirical failings, and more general empirical problems for Behavioral Momentum Theory in general (see Craig et al., 2014 for review) suggest that an alternative approach may be more useful in generating a viable quantitative theory of resurgence. This conclusion is bolstered by the fact that the theory as developed thus far is only applicable to extinction-induced resurgence, and thus fails to provide insights into resurgence in the broader sense described in the Introduction section above.

3. Context Theory

The contextual account of resurgence is based upon a more general approach to relapse phenomena (e.g., renewal, spontaneous recovery, reinstatement) that characterizes post-extinction increases in operant or Pavlovian responding as resulting from retrieval from memory of previously learned associations under ambiguous circumstances (e.g., Bouton, 2002, 2004). Specifically, when an association is formed between either a conditional stimulus (CS) and an unconditional stimulus (US) or between a response and an outcome and is then followed by extinction, the meaning of the CS or the response becomes ambiguous as a result of these conflicting associations. Contextual stimuli serve as occasion setters for disambiguating these conflicting memories such that contexts that are more similar to the initial training context promote retrieval of the original learning, but conditions more similar to the extinction context promote retrieval of extinction learning. Further, the approach suggests that new inhibitory learning occurs during extinction, in the case of operant behavior (on which we will focus here), learning to withhold responding. This new inhibitory learning in extinction is suggested to be highly contextually dependent, such that changes in the contextual stimulus conditions produce failures of this new learning to generalize–thus resulting in increases in responding. It is important to note that the theory does not specify how the original excitatory conditioning or the inhibitory conditioning during extinction occurs (see McConnell and Miller, 2014). Instead, it defers to and depends upon other traditional associative theories with a number of theoretical complexities and uncertainties of their own (e.g., see Gallistel and Gibbon, 2002, for discussion).

Regardless, the core phenomenon in the contextual approach in general and as applied to resurgence is renewal. In a typical renewal procedure responding is established within one context (i.e., Context A; e.g., combinations of distinct flooring, scents, and chamber markings with rats) and then extinguished in a different context (i.e., Context B). Renewal is said to occur when either a return to Context A (i.e., ABA renewal) or testing in a novel Context C (i.e., ABC renewal) produces an increase in responding relative to the final level of responding in Context B. The short version of the contextual account of resurgence is that it is simply a form of renewal.

Originally, Bouton and Swartzentruber (1991) suggested that resurgence is a form of ABA renewal, but more recently Bouton and colleagues have suggested that it might be more appropriate to consider it a form of ABC renewal (e.g., Bouton et al., 2012; Trask et al., 2015; Winterbauer and Bouton, 2010). The idea is that resurgence is driven by changing contextual stimuli generated by reinforcer deliveries across conditions. Specifically, during baseline training of the target response, reinforcers are provided for the target response (Context A). With the transition to extinction of the target response and reinforcement of the alternative behavior, reinforcers now become available for the alternative, and these reinforcers serve as the context for learning to inhibit the target response (i.e., Context B). When the alternative behavior is also placed on extinction, this constitutes a novel context (i.e., Context C) characterized by the absence of reinforcement for either behavior. Thus, the hypothesized learning to withhold the target behavior that occurred in Context B fails to generalize to Context C, and target responding increases as a result of retrieval of the original association. Using this framework, Bouton and colleagues have argued that all data within the resurgence literature can be explained (see Trask et al., 2015) by specifying how various experimental manipulations in the literature might be characterized as changes in context.

Although the contextual account provides a general framework within which to place resurgence and may appear to provide a comprehensive explanation of resurgence data, the nature of the account raises serious concerns for us. In essence, the account suggests that any time resurgence occurs, the increase in behavior can simply be attributed to context change. As a result, it is difficult to see the account as an explanation, as opposed to simply a post-hoc description of experimental outcomes. A wide variety of changes in the external or internal environment of the organism (e.g., overt stimuli, emotions, mood, deprivation state, expectation of events, time, reinforcers and their absence, drug states) have been characterized as changes in context (cf. Bouton, 2002; McConnell and Miller, 2014). In practice, such changes in context must be inferred from the increases in behavior they seek to explain, even if they are explicitly arranged with distinctive stimuli, but especially if they are not. As one example, there has been considerable research on the rate and distribution of alternative reinforcers across sessions of extinction on resurgence (e.g., Craig and Shahan, 2016; Schepers and Bouton, 2015; Sweeney and Shahan, 2013b; Winterbauer and Bouton, 2010, 2012). The context approach interprets the effects of such manipulations in terms of the contextual changes produced by the changing reinforcer rates–with larger reinforcement rate changes constituting greater context changes (Bouton and Trask, 2016). The difficulty is not that reinforcer rate might be a discriminable feature of the environment, but that any increase in target behavior is said to result from such changes in context and any failure to see expected increases is attributed to failures of those changes to be discriminable enough to constitute a context change for the organism. Conversely, manipulations that are predicted to reduce context change but nevertheless generate similar amounts of resurgence are attributed to unanticipated context changes associated with those manipulations (see especially Winterbauer and Bouton, 2012). When applied in this fashion and without any formal specification of the factors that would allow one to say definitively what should constitute a context change, the context account does not always allow even clear directional predictions. Thus, whatever the virtues of the contextual account with respect to generality it is difficult to consider it a viable theory of resurgence given the lack of specificity/precision and falsifiability (see also McConnell and Miller, 2014; Podlesnik and Kelley, 2015; for related critiques).

However, it is worth noting that Bai et al. (2016) have attempted to begin to quantify some aspects of the context approach with respect to resurgence under limited conditions. Full development of a more general quantitative version of Context Theory might lead to a more viable version of the account. Until then, the notion of context might be viewed as serving as an all-purpose conceptual free parameter with nearly no constraints.

Even with its current level of flexibility, it is notable that Context Theory has also failed to address the bitonic target response-rate functions sometimes obtained in resurgence experiments. It is not immediately apparent why a contextual change engendered by removal of alternative reinforcement would sometimes be weaker (generating less resurgence) in earlier sessions of testing for resurgence, only to then be followed by increases in context change, and then again by decreases in context change. Regardless, as far as we know, Context Theory has never been used to propose any functional form of the response-rate function across sessions of resurgence testing. In addition, the vast majority of experiments inspired by and reported within the framework of Context Theory have conducted only a single session of resurgence testing (e.g., Bouton and Schepers, 2014; Schepers and Bouton, 2015; Winterbauer and Bouton, 2010; Winterbauer et al., 2013). Thus, it is impossible to evaluate both what the obtained response-rate functions might have been and how Context Theory might be applied to such data.

Finally, as with the Behavioral Momentum-Based Theory, Context Theory is built upon the assumption that resurgence is an extinction-related phenomenon. The application of the general contextual approach is based on the assertion that the new learning that occurs during extinction of a target response is highly contextually dependent, and thus susceptible to failures to generalize. The broader treatment of resurgence discussed above in the Introduction section and developed more fully in the next section suggests that extinction-induced resurgence is a specific instance of a broader phenomenon. Given the flexibility and lack of specificity of the contextual approach, it is not difficult to imagine how context change might be imposed upon and used as an explanatory construct for these more general conditions. However, in our opinion, doing so would likely further weaken the apparent value of the approach by making it more obvious that by explaining everything, it might actually explain very little.

Nevertheless, as will become apparent below, the Resurgence as Choice model (RaC) developed here does share some similarities with Context Theory. Most importantly, RaC involves the comparison of changing relative values of reinforcement sources across time. For such relative valuation comparisons to be made, the properties of the outcomes determining value must be discriminated and they must be remembered across time. However, instead of these valuations serving to disambiguate uncertainties about which of multiple conflicting associations are relevant, RaC suggests that the relative valuations are directly responsible for how an organism allocates its behavior to the available options (i.e., choice).

4. The Resurgence as Choice (RaC) model

The general approach to resurgence proposed here is that the probability of some target behavior is a function of the value of the outcomes historically obtained from that option relative to the value of the outcomes obtained more recently from an alternative option. Thus,

$$pT=\frac{V_T}{V_T+V_{\mathit{Alt}}}$$ (3)

where pT is the conditional probability of the target behavior given that a response occurs and V_T and V_Alt represent the current values of the target and alternative options. As is likely obvious, this expression is a restatement of the concatenated matching law (Baum and Rachlin, 1969). The concatenated matching law is an extension of Herrnstein’s (1961) matching law which suggested that the relative rates of responding to two mutually exclusive response options (B₁ and B₂) is equal to the obtained relative rates of reinforcement obtained at those two options (R₁ and R₂), and thus,

$$\frac{B_1}{B_1+B_2}=\frac{R_1}{R_1+R_2}.$$ (4)

Baum and Rachlin (1969) extended this formulation by suggesting that other parameters of the outcomes (e.g., magnitude, immediacy, quality, punishment, etc.) could be incorporated into the matching law by subsuming them into the construct of value (i.e., V) such that,

$$\frac{B_1}{B_1+B_2}=\frac{V_1}{V_1+V_2}$$ (5)

Thus, from this perspective the relative allocation of behavior to two options is governed by relative value of the two options, with value determined by the concatenated effects of the parameters of reinforcement for those options. The expression B₁/(B₁ + B₂) is really just the conditional probability of B₁, and can be written as pB₁, as we have done in Eq. (3) above.¹

A voluminous experimental and theoretical literature has been generated by matching theory since it was first proposed nearly 60 years ago (see Commons et al., 1982; Davison and McCarthy, 1988; Herrnstein et al., 1997; for book-length treatments). This literature is a rich source of suggestions about how the determinants of choice can be formulated quantitatively, what processes might be responsible for matching, and how matching theory might be extended to a vast array of choice-related situations. Many of these developments could prove useful in understanding resurgence and for generating quantitative models addressing the details of specific experimental arrangements. Indeed, in further exploring RaC below, we will make use of some of these previous developments, but many more are available for potential future refinement and extensions to additional circumstances.

RaC as presented at the general level in Eq. (3) is really just a conceptual framework within which to view resurgence. Because allocation to an historically productive target option (i.e., pT) is governed by the value of the outcomes produced by that option (V_T) relative to the those produced by an alternative option (V_Alt), any decrease in V_Alt (all else being equal) would be expected to produce an increase in pT. The assertion of RaC is that resurgence is the result of just such an increase. To understand resurgence within this framework, consider an example. Imagine a rat responding on one lever on a variable-interval (VI) 15-s schedule of reinforcement. Next imagine that an additional lever is introduced that also produces reinforcement on a VI 15 s while the initial lever continues to produce reinforcement on a VI 15 s. Given what we know about choice and the matching law (Eq. (5)), no one would be surprised to see responding decrease on the initial lever, nor to see that if the second lever is then placed on extinction that responding on the initial lever would increase. What has seemed special about resurgence in the past is that the initial target behavior is placed on extinction with the introduction of the second lever. Nevertheless, if the initial target option maintains some residual value (V_T) across extinction, resurgence can be viewed as being similar to the example in which reinforcement remained for the target. Further, any other manipulation applied to first decrease the value of the target option (V_T) and then the value of the alternative option (V_Alt) might be expected to produce similar effects in both examples. From this conceptual framework, the way to formalize resurgence is to determine how various outcomes are related to value and how changes in those outcomes affect the values of the options across time.

In the absence of formalization of how various parameters of the outcomes obtained at the options determine value across time, RaC is at the same level of specificity and flexibility as Context Theory. Indeed, in its most general form, the concatenated matching law upon which RaC is based is arguably tautological and unfalsifiable (Rachlin, 1971)–like Context Theory. Similar to the dependence of Context Theory on post-hoc inferences of context change based on changes in responding, RaC at this level can infer post-hoc changes in the relative values of V_T and V_Alt across time based on changes in pT. In short, without more specificity, RaC is only a framework for generating more specific, quantitative hypotheses about the processes at work. By generating and testing such quantitative statements about the processes at work, this approach could lead to recognition of failures in our understanding, and thus, to future refinements. As a demonstration of this approach, we will next provide a sketch of one way in which resurgence in the typical extinction-induced sense might be formalized.

4.1. The Temporal Weighting Rule (TWR)

In a typical experiment to examine extinction-induced resurgence, three phases are used. In the Phase 1, a target behavior (e.g., left lever press) is reinforced according to some schedule of reinforcement (e.g., a VI 15-s schedule). In Phase 2, the target behavior is placed on extinction and simultaneously a different, alternative behavior (e.g., right lever press) is made available and reinforced on some schedule (e.g., a VI 15 s). In Phase 3, the alternative behavior is also placed on extinction and resurgence is said to occur when the initial target behavior increases in frequency compared to Phase 2. All else being equal, these changing rates of the outcomes for the two options (i.e., reinforcement rates) would be a likely determinant of the values of the two options from the standpoint of RaC.

In attempting to extend matching theory to extinction-induced resurgence, Cleland et al. (2001) noted a difficulty associated with incorporating reinforcement rates associated with the two options(R₁ and R₂). Specifically, during Phase 2, the reinforcement rate associated with the target behavior is zero, as is the reinforcement rate for both the target and alternative behaviors in Phase 3. Thus, a straightforward application of the matching law (e.g., Eq. (4)) would fail to make any predictions about the allocation of behavior because both sides of the equation would equal zero in Phases 2 and 3. What is required to make such a framework feasible is a means to incorporate how the experience of past reinforcement is carried forward in time and combined with present circumstances (in this case, extinction) to determine value. Although there are many approaches to this issue (e.g., Davis et al., 1993; Davison and Hunter, 1979; Killeen, 1981), we have chosen to use the Temporal Weight Rule (TWR; see Devenport and Devenport, 1994; Mazur, 1996; for reviews) for both empirical and theoretical reasons that will be discussed more fully below.

The TWR provides a means to calculate how organisms weight varying past experiences as a function of the relative recency of those experiences. Specifically, the rule suggests:

$$w_x=\frac{1/t_x}{{\displaystyle \sum _{i=1}^n}1/t_i}$$ (6)

where w_x is the weight to be applied to a particular past experience. The numerator of this expression represents the recency of that particular past experience with t_x being the time between the past experience and the present (t_x is calculated as T−τ_x + 1, where T is the present time and τ_x is the time point for which t_x is being calculated–t_i is calculated similarly). Thus, more recent experiences (i.e., smaller t_x) receive greater weighting (i.e., w_x). The denominator is simply the sum of all the recencies of past experiences, some number n of which are under consideration. Thus, the rule provides a weighting for each of a series of experiences across time (i.e., w₁, w₂,... w_n), and because each recency is divided by the sum of all the recencies in the series, these weightings always sum to 1. Each w_x represents, therefore, a relative recency.²

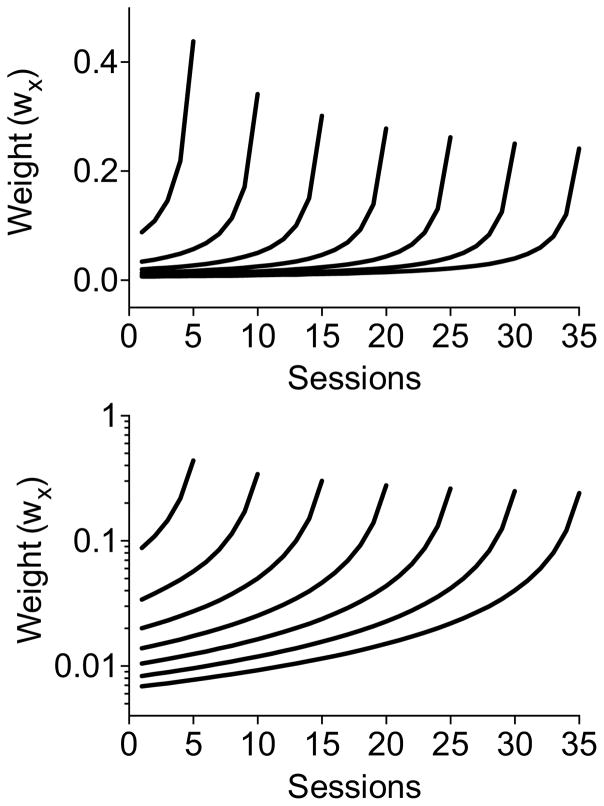
The top panel of Fig. 1 shows weightings for examples of series of experiences at different time points across 35 sessions. Specifically, in this example, t_x is measured in number of sessions (i.e., one every day), with the most recent session having t_x = 1 (the far right end of each series), the second most recent having t_x = 2, and so on. For visual clarity, example weightings are provided only for series after every 5 sessions but, of course, a weighting function would be associated with every session increment. These functions characterizing how w_x decays from the present session to sessions in the past are hyperbolic.³ As such, the weights associated with the most recent sessions initially decline quickly as they recede into the past (moving to the left on the x-axis), but the functions decelerate such that weightings for sessions from the more distant past decline more slowly. As a result, recent experience can have a relatively large impact, but the effects of the more distant history tend to linger for a long time. To make this feature of the weighting functions more clear, the bottom panel of Fig. 1 shows the same functions as the top, but with a logarithmic y-axis.

Fig. 1.

The top panel shows sample weighting functions generated by Eq. (6) (i.e., the Temporal Weighting Rule). Functions are presented after every five sessions. The bottom panel shows the same functions with a logarithmic y-axis.

To determine the value (i.e., V) of an option, the outcome experienced for that option at each time point in the past (i.e., O_x) is simply multiplied by the weighting for that time point (i.e., w_x), and then all of the weighted outcomes are summed (e.g., Devenport and Devenport, 1994; Devenport et al., 1997; Mazur, 1996) such that:

$$V=\sum _x{w}_x{O}_x$$ (7)

If more than one option is available, Eqs. (6) and (7) are applied to the series of outcomes experienced at each of the options and a value is calculated for each option (i.e., V₁ & V₂). Probability of choosing an option is then determined by calculating the relative values of the options [i.e., p₁ = V₁/(V₁ + V₂) as in Eqs. (3) and (5) above].

Devenport and colleagues have shown that, thus applied, the TWR accounts well for the foraging behavior of a variety of organisms in situations with variable patch outcomes across time (e.g., Devenport and Devenport, 1993, 1994; Devenport et al., 1997). Devenport et al. (1997) have also shown that the TWR can account for spontaneous recovery (i.e., an increase in extinguished responding with the simple passage of time).⁴ Further, Mazur (1996) has demonstrated that the rule can be extended to account for the spontaneous recovery of previous response allocations in choice situations with transitory changes in relative reinforcement rates (see also Gallistel et al., 2001). These findings are important for two reasons. First, as both Devenport and colleagues and Mazur discuss, the TWR has provided an account of such findings where other approaches fail (e.g., an exponentially weighted moving average, Killeen, 1982). Second, the application of the TWR to spontaneous recovery demonstrates that the approach can provide an account of one of the core relapse phenomena. Thus, it seems that the TWR could be promising as a means to account for resurgence.

4.2. The TWR and extinction-iduced resurgence

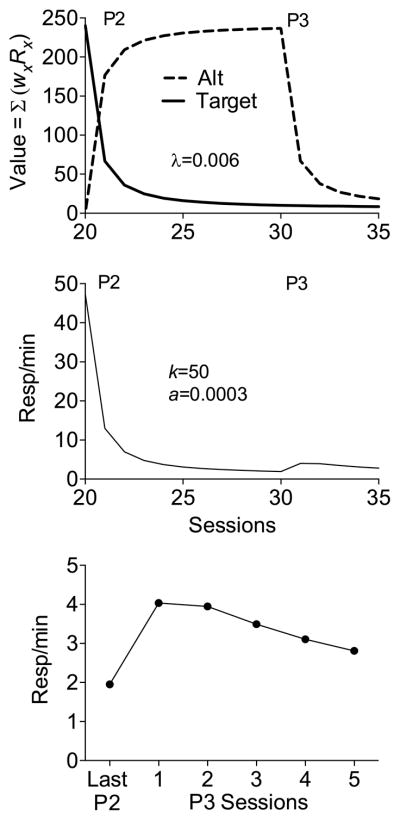
To understand how the TWR might be applied to extinction-induced resurgence, consider Fig. 2. The top panel displays an example of changing reinforcement rates across the typical three phases in a resurgence experiment. The target behavior is reinforced on a VI 15-s schedule in Phase 1 for 20 sessions. Next, in Phase 2, the target behavior is placed on extinction for 10 sessions and the alternative behavior is reinforced on VI 15 s. In Phase 3, both the target and alternative behaviors are extinguished for 5 sessions. The resulting reinforcement rates (i.e., reinforcers/h) depicted in the figure are the input to the TWR across time. The middle panel of Fig. 2 shows sample weighting functions generated by Eq. (6). Again, functions are presented for only every 5 sessions for visual clarity, but each session increment would have a corresponding new weighting function. To obtain values for the target (V_T) and alternative (V_Alt) options across sessions, the weighting for each session (w_x from Eq. (6)) defined by the current session’s weighting function is applied to the past reinforcement rates for the target (R_xT) and alternative (R_xAlt) and then summed across all sessions for that weighting function:

$$V_T=\sum _x{w}_x{R}_{xT}{V}_{\mathit{Alt}}=\sum _x{w}_x{R}_{\mathit{xAlt}}$$ (8)

Fig. 2.

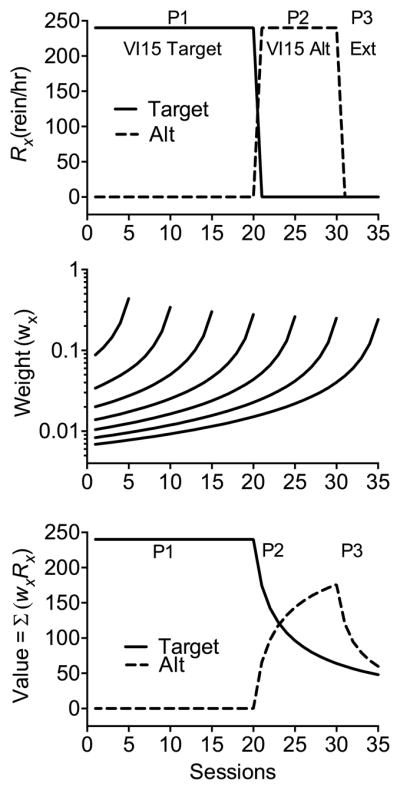
The top panel shows arranged reinforcement rates for the target and alternative options in a sample resurgence experiment. The middle panel shows sample weighting functions as in Fig. 1. The bottom panel shows the value functions for the target and alternative options across sessions resulting from the application of Eq. (8). P1 = Phase 1, P2 = Phase 2, and P3 = Phase 3.

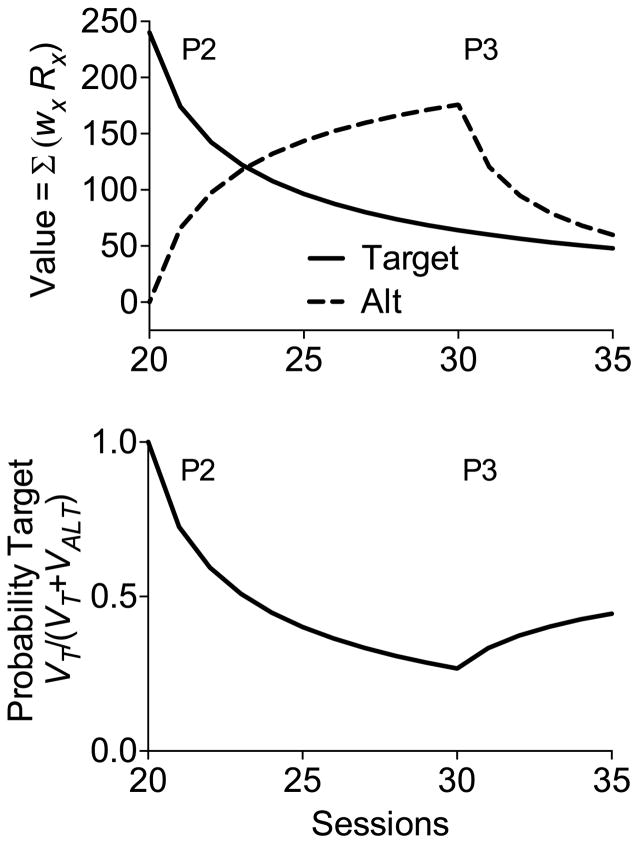
The resulting values for V_T and V_Alt across sessions are plotted in the bottom panel of Fig. 2. Note that at the beginning of Phase 2 when the target is placed on extinction, V_T drops quickly at first and then more slowly as time progresses. In addition, V_Alt increases with the introduction of reinforcement for the alternative behavior. Finally, like V_T in Phase 2, V_Alt decreases quickly at first in Phase 3 when the alternative is placed on extinction, and then more slowly as sessions continue. Because these changes in value in Phases 2 and 3 are of primary interest, the top panel Fig. 3 shows V_T and V_Alt across these sessions. Most importantly, the bottom panel of Fig. 3 shows how the values of V_T and V_Alt are translated into the probability of the target behavior (i.e., pT) according to Eq. (3) above. Note that pT decreases across sessions of Phase 2, but when the alternative behavior is also placed on extinction in Phase 3, pT increases across sessions as a result of increases in the relative value of V_T. From the perspective of RaC, this increase in pT is resurgence. The reason that relative values change in this way is the hyperbolic form of the weighting function across sessions and the slower decline of value it generates across increasing sessions of extinction. Thus, the history of reinforcement for the target option in Phase 1 is carried forward as V_T into Phases 2 and 3 where its lingering impact can be revealed when there is a decrease in V_Alt.⁵ These changes in value across time and the increase in pT (i.e., resurgence) are a natural outcome of the TWR.

Fig. 3.

The top panel shows value functions for the target and alternative options across Phases 2 & 3 as presented in Fig. 2. The bottom panel shows changes in the probability of the target response across sessions generated by using these daily values in Eq. (3).

4.3. Scaled Temporal Weighting rule (sTWR)

Although application of the TWR to changes in the reinforcement conditions across a typical resurgence paradigm might provide a basic framework for understanding how the probability of a target response varies across phases, one aspect of Fig. 3 suggests that this framework might be incomplete. Specifically, the decreases in pT across Phase 2 appear to be too gradual, and pT remains rather high at the end of Phase 2. Real data from resurgence experiments often show rather precipitous declines to near-zero levels of the target behavior across Phase 2. In Fig. 3, the decreases in pT across Phase 2 are strictly dictated by the TWR as formalized in Eq. (6). Eq. (6) asserts that the weighting applied to any past experience (i.e., w_x) is determined only by the relative recency of that experience. The equation includes no means to account for potential variations in how immediacy might differentially impact an organism’s weighting of the past as a result of either individual differences or past and present experimental parameters. However, a simple modification of the TWR can supply the approach with additional flexibility to incorporate such potential differences in how recency might impact the weighting of past experiences. Specifically, we propose a scaled temporal weighting rule (sTWR) in which recencies are scaled such that:

$$w_x=\frac{1/t_x^c}{{\displaystyle \sum _{i=1}^n}1/t_i^c}$$ (9)

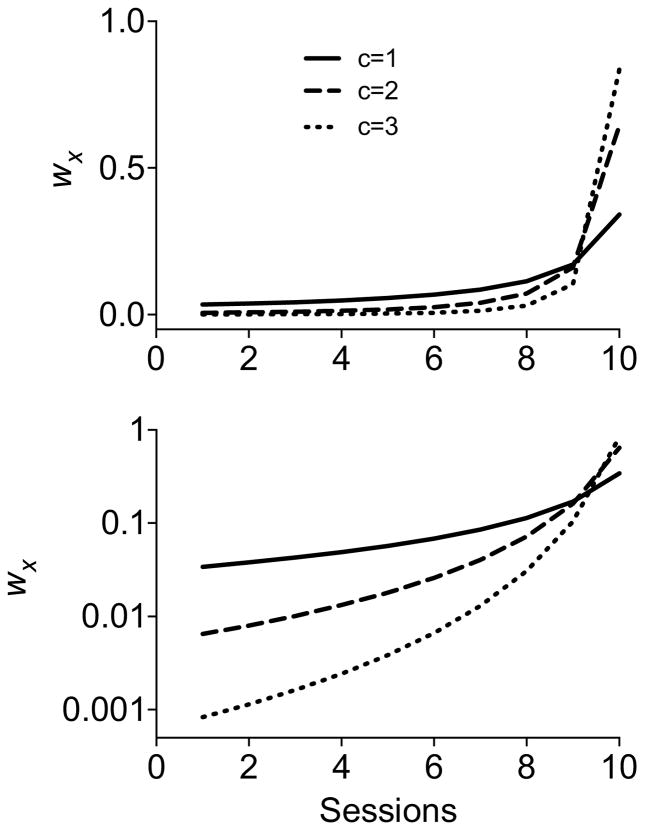
where all terms are as in Eq. (6), and the added term c is scaling exponent on the time from a previous experience to the present. The top panel of Fig. 4 shows how variations in c, what we will call the currency term, impact w_x across ten sessions. When c = 1, Eq. (9) is simply the unscaled TWR from Eq. (6). As c increases, additional weight is given to more recent experiences and less weight is given to experiences from the more distant past. Because all recencies are scaled in Eq. (9), the weightings across all the experiences under consideration continue to sum to 1, as was true for Eq. (6)–only the distribution of these weightings across the past are impacted by increases in c. Importantly, the weighting functions generated by Eq. (9) across sessions, maintain the basic hyperbolic decreases generated by the TWR.⁶ The bottom panel of Fig. 4 shows the same functions as the top, but with a logarithmic y-axis.

Fig. 4.

The top panel shows weighting functions generated by Eq. (9) (i.e., the scaled temporal weighting rule; sTWR). Functions are presented for three different values of the currency term (i.e., c). The bottom panel shows the same functions with a logarithmic y-axis.

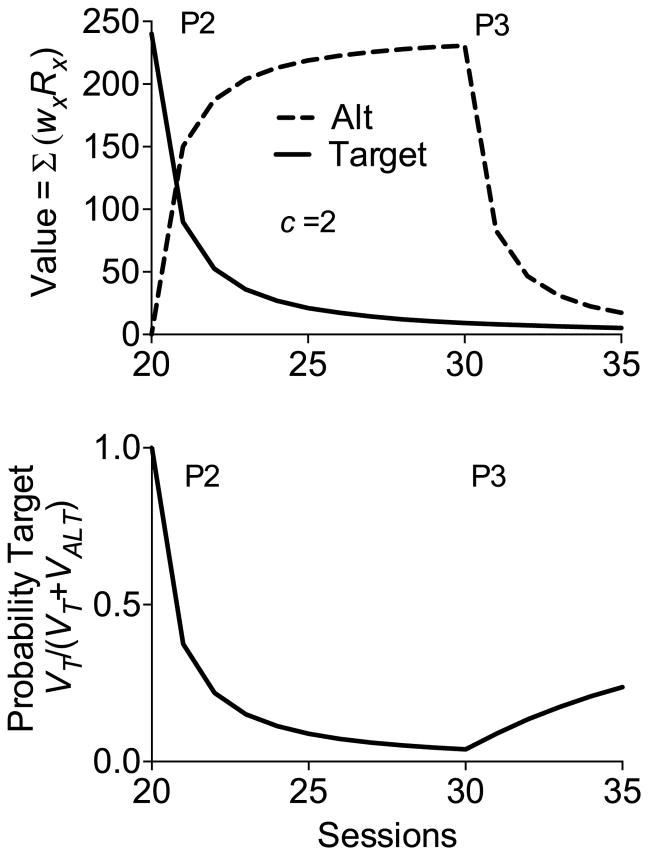
Fig. 5 shows value functions and pT derived from application of the sTWR (i.e., Eq. (9)) to the same reinforcement conditions as in Fig. 3, but with a currency parameter set at c = 2. Note that both the value of V_T in Phase 2 and the value of V_Alt in Phase 3 decrease more steeply and to lower levels than with the unscaled TWR (i.e., c = 1) as depicted in Fig. 3. In addition, the sTWR in Fig. 5 still produces the increase in pT across sessions of Phase 3 (i.e., resurgence). Thus, with c > 1, the sTWR appears to produce changes in pT across sessions that are more likely to accurately reflect the reality of resurgence experiments.

Fig. 5.

The top panel shows value functions from Eq. (8) for the target and alternative options across Phases 2 & 3 generated by application of Eq. (9) (sTWR with c = 2) to the reinforcement rates across conditions depicted in the top panel of Fig. 2. The bottom panel shows changes in the probability of the target response across sessions generated by using these daily values in Eq. (3).

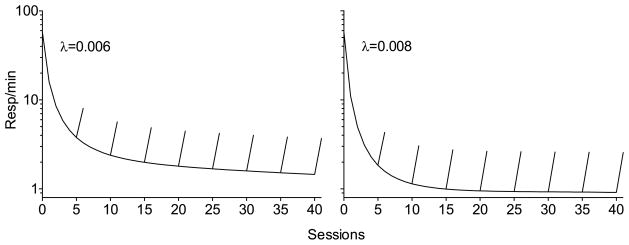
Any number of variables could impact the value of c, and thus how organisms weight the past. In the absence of rules specifying how it is related to experimental parameters, c would be just a free parameter in the model (as would likely be the case with potential individual or species differences). However, one variable that has been of particular interest in resurgence experiments is the rate of reinforcement (see Craig and Shahan, 2016; for review), and there are good reasons to suspect that c could be related to this variable. To that end, consider the fact that the value function for V_T generated by the sTWR across sessions of extinction in Phase 2 reflects only the history of reinforcement associated with the target option (i.e., the history for the alternative does not enter into the calculation of V_T –and vice versa). Thus, across Phase 2, V_T describes how extinction reduces the value of the target, regardless of whether or not alternative reinforcement is available. As a result, increases in c and the steeper decreases in V_T they produce should reflect variables related to resistance to extinction. Although many variables are known to impact resistance to extinction and could affect c, most important for present purposes is the fact that with simple schedules of reinforcement, more frequent reinforcement generates less resistance to extinction.⁷ In the extreme, where continuous reinforcement generates less resistance to extinction than intermittent reinforcement, this is the well-known partial-reinforcement-extinction-effect (i.e., PREE; see Gallistel, 2012; Mackintosh, 1974; for reviews). However, the effect also extends to less extreme conditions in which higher rates of intermittent reinforcement in single schedules generate less resistance to extinction than do lower rates of intermittent reinforcement (e.g., Baum, 2012; Cohen, 1998; Cohen et al., 1993; Craig and Shahan, 2016; Shull and Grimes, 2006). Based on the sTWR, however, if a single value of c is applied to conditions arranging different reinforcement rates (including with c = 1–the unscaled TWR), all reinforcement rates will generate value functions that decrease from baseline levels at the same rate across sessions of extinction, suggesting no differential resistance to extinction. As a result, the approach would fail to capture PREE-like effects with different reinforcement rates. Given that any experiment on resurgence would necessarily arrange some reinforcement rate, this is an important issue to address.

Therefore, following Killeen (1981) we agree that animals should “pay more attention to recent events” when the frequency of reinforcement is high, and to be “guided by events that have happened over some relatively long period of time” when reinforcement rate is low. Thus, c should be expected to increase with increases in the frequency of reinforcement. Although any number of functions could be used to characterize how c should vary with reinforcement rates (e.g., Killeen uses an additional exponentially weighted moving average), we have found that a linear function based on running reinforcement rate for an option is adequate for present purposes.⁸ Thus,

$$c=\lambda r+1$$ (10)

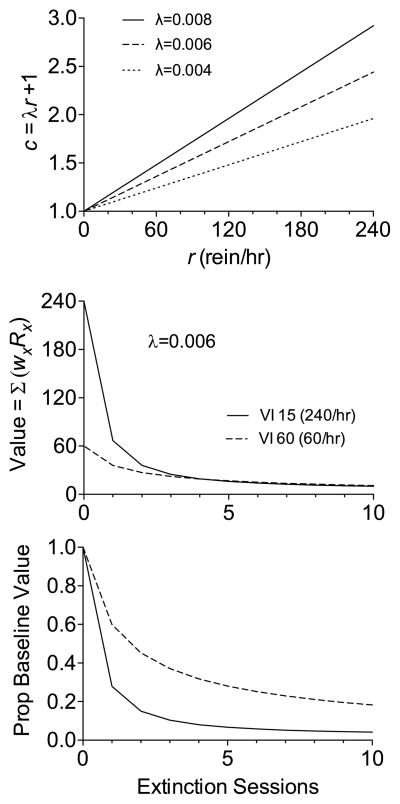
where λ is a parameter modulating how quickly the currency term increases with reinforcement rate (i.e., r). Importantly, r reflects the overall average running reinforcement rate (in reinforcers/h) for an option across all of the sessions it has been available. A value of the c parameter is generated for and applied to each of the options separately (i.e., the target and alternative options) based on the running average reinforcement rate for each of those options. In effect, this approach suggests that the overall running average frequency of events experienced for an option determines the degree to which more recent events impact weightings for outcomes from that option. An option that has historically produced reinforcers at a high frequency generates heavier weighting of recent events at that option, but an option that has historically produced reinforcers at a lower rate generates less weighting of recent events at that option and a broader weighting of the past. If a static value of r were used in the determination of c (e.g., the last reinforcer rate experienced in baseline), then c would fail to adapt to the rate at which events are encountered at an option across time. As a result of using the running average reinforcer rate for an option, as r approaches zero, c approaches 1 (i.e., the unscaled TWR) and the organism takes a broader view of the past.

The top panel of Fig. 6 shows how c varies with reinforcement rates with different values of λ according to Eq. (10). The middle panel of Fig. 6 shows value functions across sessions of extinction generated by the sTWR with λ = 0.006 following reinforcement on VI 15-s versus VI 60-s reinforcement. Although value generated by the VI 15-s schedule is higher at the end of baseline (i.e., zero on the x-axis) than for the VI 60 s, value for the VI 15 s decreases more quickly with the introduction of extinction. To highlight this effect, the bottom panel of Fig. 6 shows the same functions as the middle panel, but presented as a proportion of the initial baseline value. Thus, when equipped with a currency term determined by reinforcement rate via Eq. (10), the sTWR generates value functions across extinction sessions that are consistent with PREE-like effects in single schedules. Before moving forward with the application of the sTWR to resurgence under different reinforcement-rate conditions, it would be desirable to first have a model to generate absolute rates of responding, as opposed to just changes in pT across phases, as has so far been the case. Thus, we first turn our attention to this issue.

Fig. 6.

The top panel shows the relation between average running reinforcement rate for an option (i.e., r) and the value of the currency term (i.e., c) as determined by Eq. (10). Functions are presented for three different λ parameters. The middle panel shows value functions during 10 sessions of extinction following reinforcement on a VI15-s or VI60-s schedule with λ = 0.006. The bottom panel shows the same value functions presented as a proportion of the value at the end pre-extinction training (i.e., x = 0 in the middle panel).

4.4. Response output

There are many ways one might build a model to convert changes in pT to changes in response rates. Here we provide an example of one such model,

$$B_T=\frac{{kV}_T}{V_T+V_{\mathit{Alt}}+1/A}$$ (11)

where B_T is target-response rate (resp/min) and V_T and V_Alt are as above. The parameter k is asymptotic baseline response rates, and A reflects the level of arousal. Obviously, the model is inspired by Herrnstein’s (1970) absolute response-rate version of the Matching Law. Notably, rather than using Herrnstein’s R_e parameter (i.e., extraneous sources of reinforcement) in the denominator, we assume that overall output is modulated by invigorating effects of reinforcement (i.e., arousal) in a manner inspired by Killeen (1994). Because 1/A appears in the denominator, higher values of A tend to generate higher response rates (i.e., rates approach k more quickly with increases in V_T). This approach is superior to the use of R_e for present purposes because it is likely that the overall level of arousal (and response rate) will vary across the phases of a resurgence experiment in a way that would be difficult to capture with a fixed R_e. For example, although pT from Eq. (3) (bottom panel Fig. 5) continuously increases across the sessions of resurgence testing in Phase 3, no reinforcer deliveries are occurring across those sessions and response rates are likely to decrease, generated here by decreases in arousal (i.e, A). The question that remains is how the value of A should be calculated across sessions.

Again, there are many possible ways one could formalize the relationship between reinforcement rates and arousal. Killeen (e.g., 1994) has suggested that arousal is a linear function of reinforcement rate. Further, Gibbon (1995) and Gallistel et al. (2001) have suggested that arousal in choice situations is a linear function of overall reinforcement rates across the alternatives (i.e., R₁ + R₂). However, because there is no reinforcement arranged in Phase 3, the current reinforcement rates obviously will not do. Of course, this is the problem for which the TWR was recruited to solve above. Thus, we suggest that the overall level of arousal (i.e., A) is a linear function of the summed values of the options (V_T and V_Alt) such that:

$$A=a(V_T+V_{\mathit{Alt}})$$ (12)

where the parameter a is the slope of the relation between arousal and value.⁹ In short, this approach assumes that the overall level of arousal is governed by the overall current value of the prospects for the two options. As a result, the decreases in value for both options across the sessions of Phase-3 extinction would produce consistent decreases in A across those sessions. In short, as the effects of all reinforcement recede into the past, arousal will decrease. Importantly, although the overall level of behavioral output would be expected to decrease across Phase 3, the increases in pT across that phase suggest that an increasing proportion of the responses that do occur will be to the target option.

The top panel of Fig. 7 shows value functions for Phases 2 and 3 generated by Eqs. (9) and (10) with λ = 0.006 and reinforcement conditions as described in the earlier examples (i.e., target = VI 15 s; alternative = VI 15 s). The middle panel shows response rates generated from these value functions by Eqs. (11) and (12) with k = 50 and a = 0.0003. Note that removal of alternative reinforcement in Phase 3 results in an increase in target-response rates (i.e., resurgence). As is typically the case in resurgence experiments, the increase in target responding in Phase 3 is relatively small compared to baseline levels of responding. The bottom panel of Fig. 7 zooms in on the resurgence effect in Phase 3 in a manner more typical of how resurgence is presented in the literature. Note that target responding increases with the removal of alternative reinforcement in the first session of Phase 3 and then declines thereafter. Thus, when supplied with assumptions about how the relative values of target and alternative options change across time and how those relative values might be converted into response rates, the general framework suggested by RaC appears capable of generating a potentially viable quantitative account of resurgence.

Fig. 7.

The top panel shows value functions generated by the sTWR (Eq. (9)) using a currency term (i.e., c) determined by reinforcement rates according to Eq. (10) with λ = 0.006. Phase 1 target = VI15, Phase 2 alternative = VI15. The middle panel shows absolute response rates based on this value functions generated by Eq. (11). The bottom panel provides a zoomed view of the last day of Phase 2 and five Phase 3 resurgence sessions.

4.4.1. Response rates, arousal, and resurgence

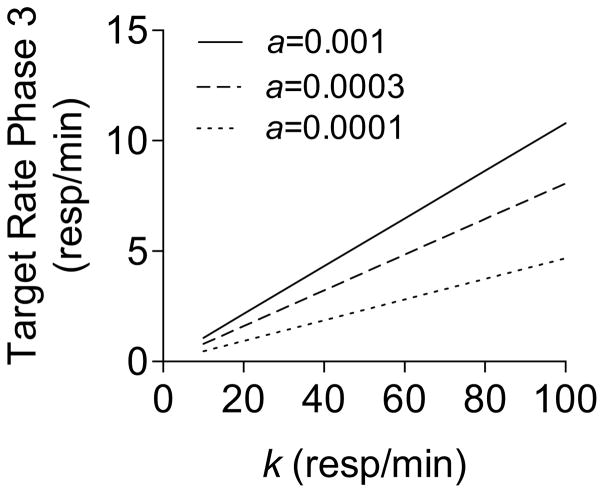
As reviewed by Trask et al. (2015), a reliable finding in the study of resurgence is that higher rates of Phase-1 responding are associated with higher rates of responding during resurgence testing in Phase 3 (e.g., de Silva et al., 2008; Winterbauer et al., 2013). From the current perspective, this result is a natural outcome of Eq. (11). The k parameter scales the relative valuations of the target and alternative options into the units of the target response in responses/min and represents asymptotic baseline rate of the target. Thus, higher values of k are associated with higher rates of the target response. Specifically, Eq. (11) suggests that response rates during Phase 3 are a linear function of asymptotic baseline response rates (i.e., k). This prediction is consistent with data presented by Sweeney and Shahan (2013b, see their Fig. 8 showing that Phase 3 response rates were indeed a linear function of Phase-1 response rates). Further, given that response output is modulated by 1/A in Eq. (11), higher levels of arousal also generate higher response rates in Phase 3 via higher values of the a parameter. Fig. 8 shows the relation between asymptotic baseline response rate (i.e., k) and response rates on the first day of Phase-3 resurgence testing generated with VI 15-s reinforcement for both the target and alternative options and λ = 0.006 as above in Fig. 7. Fig. 8 also shows that the slope of this function is steeper, and thus response rates during resurgence testing are higher at the same k value, as the value of a increases.

Fig. 8.

The relation between target response rates in the first session of Phase 3 (resurgence) and asymptotic baseline response rates (i.e., k in Eq. (11)). Functions are shown for three different a parameter values relating arousal to overall value of the options in Eq. (12).

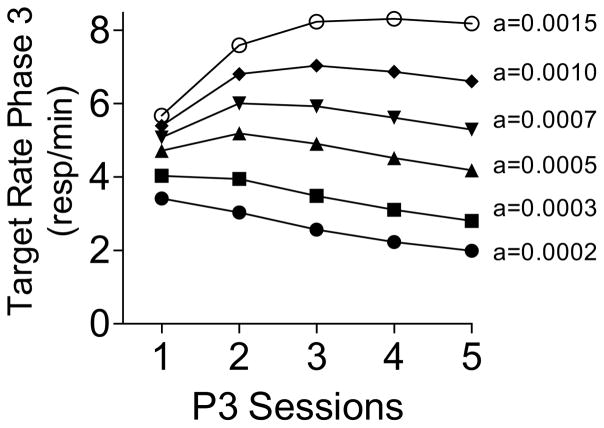
In addition to affecting the rate of the target response on the first day of resurgence testing in Phase 3 as shown in Fig. 8, it is important to note that changes in the a parameter also affect the shape of the target response-rate function across additional sessions of Phase 3. Fig. 9 shows target-response rates across 5 days of Phase-3 resurgence testing with a range of a values.¹⁰ Other parameters are as in the figures above (i.e., k = 60, λ = 0.006, Target = VI 15 s, Alternative = VI 15 s). As in Fig. 8, lower levels of the a parameter (i.e., the scalar for converting value into arousal, A), are associated with roughly linear decreases in target-response rates across Phase 3. However, as the a parameter increases, response rates begin to take on a bitonic form, initially increasing before beginning to decrease. At the highest values of a, the response rate functions begin to show less of a decrease at later sessions. Thus, RaC suggests that response-rate functions during the course of resurgence testing are sometimes bitonic (see Podlesnik and Kelley, 2015) and sometimes not because of potential differences in arousal during resurgence testing. As noted above, neither Behavioral Momentum Theory nor Context Theory provides an account of such response-rate functions across resurgence test sessions. It is important to remember that the source of this function in terms of RaC is the increasing probability of the target response (i.e., pT in Eq. (3)) associated with changes in the relative values of the target (V_T) and alternative options (V_Alt) across Phase 3. However, those increases in pT across resurgence testing sessions are counteracted by decreases in arousal due to the absence of recent reinforcement. In the end, the shape of the response-rate function depends upon the value of the a parameter which governs the extent to which overall reductions in the value of both options are converted into arousal. This interpretation suggests that research directly manipulating variables potentially related to arousal (e.g., deprivation, etc.) might allow direct experimental control of the shape of the response-rate function across sessions of resurgence testing.

Fig. 9.

Target response rates across 5 sessions of Phase-3 (resurgence) test sessions generated with different a parameter values in Eq. (12).

4.4.2. Bias

Although most experiments examining resurgence use target and alternative responses that are topographically similar (e.g., two lever presses or response keys), some experiments use responses that are topographically different (e.g., Craig and Shahan, 2016; Lieving and Lattal, 2003; Podlesnik et al., 2006; Sweeney and Shahan, 2013b). In circumstances where the responses are topographically different, there is the possibility that differences in the responses (e.g., difficulty, distance from food hopper, etc.) could lead to bias for one response over the other. Starting with Baum’s (1974) generalized matching law, bias has been treated formally in matching theory as a source of preference for one alternative that is independent of the conditions of reinforcement arranged by the options. McDowell (2005) has shown how such bias can be incorporated into Herrnstein’s (1970) absolute response-rate version of the matching law. Thus following McDowell we suggested that bias can be incorporated into RaC such that,

$$B_T=\frac{{kV}_T}{V_T+V_{\mathit{Alt}}/b+1/A}$$ (13)

where all terms are as in Eq. (11) and the added parameter b represents bias. Values of b > 1 represent bias for the target option and b < 1 represent bias for the alternative option. Thus equipped, RaC could accommodate bias associated with the use of topographically different responses for the target and alternative options. In cases where topographically similar responses are used, b would be expected to be approximately 1 and could be omitted.

4.5. Model summary

RaC as developed above has three core components summarized in Fig. 10. First, in the most general sense, RaC suggests that probability of a target response (pT) is a function of the relative values of the target (V_T) and alternative (V_Alt) options according to Eq. (3). Second, the values of the two options across time are determined by the relative recencies of past experiences of reinforcement at those options according to Eqs. (8) and (9). The extent to which relative immediacy impacts value may depend on any number of factors (captured by the currency term c), but one factor that is likely to have such effects is the rate of reinforcement. The effects of reinforcement rate on c are determined by Eq. (10), where the λ parameter represents the degree to which c increases with increases in overall running average reinforcement rate for each option. Third, absolute response rates, as opposed to pT, are generated by the response-output function (i.e., Eq. (13)). Eq. (13) suggests that response output is a function of asymptotic baseline response rates (k), potential response bias (b), and arousal (A). Arousal is determined by Eq. (12), where the parameter a represents the extent to which overall value of the options is converted into arousal. Thus, as applied here, the model has four free parameters (i.e., λ, k, a, and b). However, the bias parameter (b) would be expected to be near 1 in typical experiments where topographically similar responses are used, and thus could be omitted, leaving the model with three free parameters.

Fig. 10.

Summary of the major components of the RaC model.

It is important to note at this point that the specific model of resurgence summarized in Fig. 10 is meant only to illustrate how the general framework provided by RaC might be formally developed to account for resurgence. We have made a number of assumptions about how specific processes might be involved and how they may combine to generate resurgence. Any number of these assumptions could be wrong or in need of modification. Nevertheless, as we will show below, despite any weaknesses in the assumptions of this example model, the general framework provided by RaC appears to provide a reasonably good account of many data from the resurgence literature that were problematic for Behavioral Momentum Theory.

5. Application of RaC to extinction-induced resurgence

5.1. Effects of Phase-1 and Phase-2 reinforcement rate

As noted above, the effects of reinforcement rate on resurgence have posed a serious difficulty for Behavioral Momentum Theory. Thus, we begin with a treatment of the most extensive dataset from a single experiment examining the effects of reinforcement rates on resurgence in single schedules by Craig and Shahan (2016). The experiment examined the effects of variations in Phase-1 and Phase-2 reinforcement rates in six groups of rats. In Phase 1, three groups earned food pellets for lever pressing on a VI 15-s schedule and three other groups on a VI 60-s for 30 sessions. In Phase 2, lever pressing was extinguished for all groups for 20 sessions, and subgroups received no alternative reinforcement or alternative reinforcement (i.e., the same food pellet at Phase 1) for nose-pokes on the opposite wall of the chamber on a VI 15-s or VI-60-s, thus resulting in six groups: VI 15 VI 15, VI 15 VI 60, VI 15 Ext, VI 60 VI 15, VI 60 VI 60, & VI 60 Ext. In Phase 3, nose poking was extinguished for 5 sessions for the groups that had received alternative reinforcement in Phase 2.

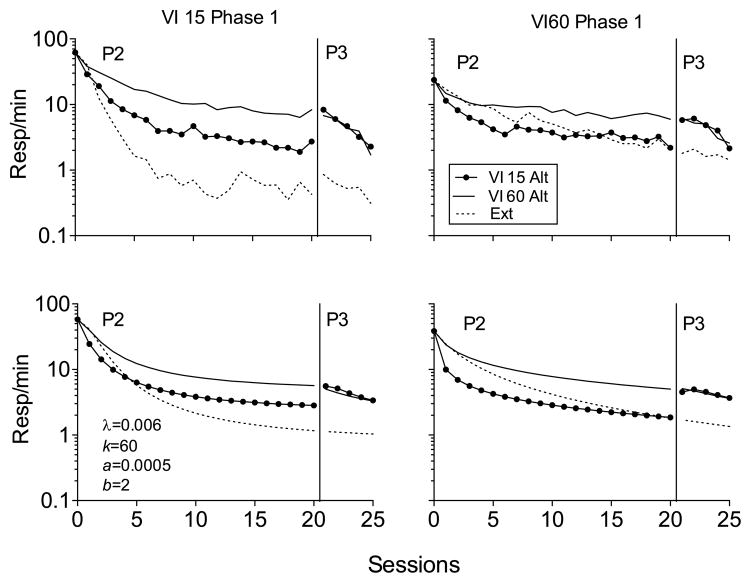
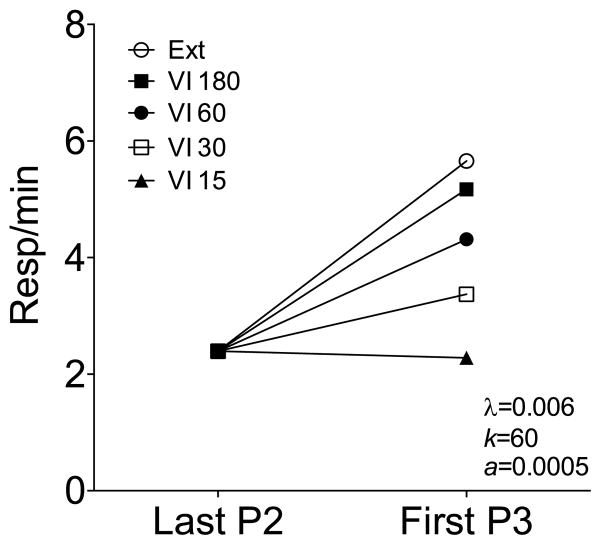
The top panels of Fig. 11 show the data from the Craig and Shahan (2016) experiment. The only notable difference for the groups that had received Phase-1 reinforcement on a VI 15-s schedule (i.e., top left panel) versus VI 60-s schedule (top right panel) was that responding for the VI15 Ext group decreased more quickly than for the VI60 Ext group (i.e., a PREE-like effect). The rate of baseline reinforcement had no meaningful impact on Phase-2 or Phase-3 responding for the other groups. However, higher-rate alternative reinforcement during Phase 2 (groups VI 15 VI 15 and VI 60 VI 15) generated lower target response rates than did lower-rate alternative reinforcement (i.e., VI 15 VI 60 and VI 60 VI 60). Nevertheless, lower-rate alternative reinforcement generated higher rates of responding during Phase 2 than was observed for the groups that had received no alternative reinforcement. As discussed above, this outcome is a major contradiction to the predictions of Behavioral Momentum Theory. A similar result with low-rate alternative reinforcement was also previously obtained by Sweeney and Shahan (2013b, discussed below), but the Craig and Shahan experiment was the first to obtain greater responding in Phase 2 with high-rate alternative reinforcement than with no alternative reinforcement. With respect to Phase 3, removal of high-rate alternative reinforcement produced resurgence for the VI 15 VI 15 and VI 60 VI 15 groups, whereas removal of lower rate alternative reinforcement for the VI 15 VI 60 and VI 60 VI 60 groups did not. Importantly, response rates for the high-rate and low-rate alternative-reinforcement groups did not differ during Phase 3. The reason the high-rate alternative-reinforcement groups showed resurgence and the low-rate groups did not was that response rates were lower in Phase 2 for the high-rate alternative-reinforcement groups. The bottom panels of Fig. 11 show that RaC provides a reasonably good simulation of this complex pattern of data with λ = 0.006, k = 60, a = 0.0005, and b = 2. The inclusion of the bias parameter is consistent with a bias for the target lever press over the alternative nose poke on the back wall of the chamber. In this case, bias for the target lever might have been present because the lever was closer to the food aperture (which was located on the front wall of the chamber).

Fig. 11.

The top panels show data replotted data from Craig and Shahan (2016). The bottom panels show simulations generated by RaC. Details in text.

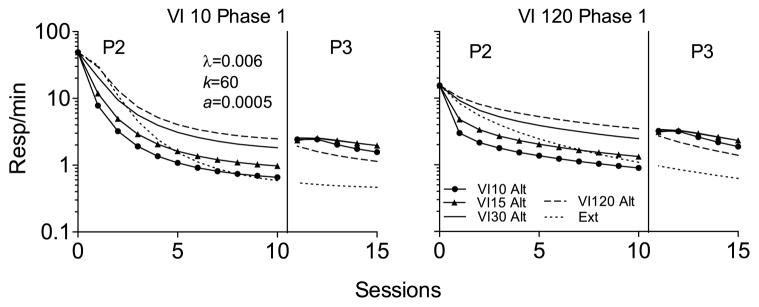
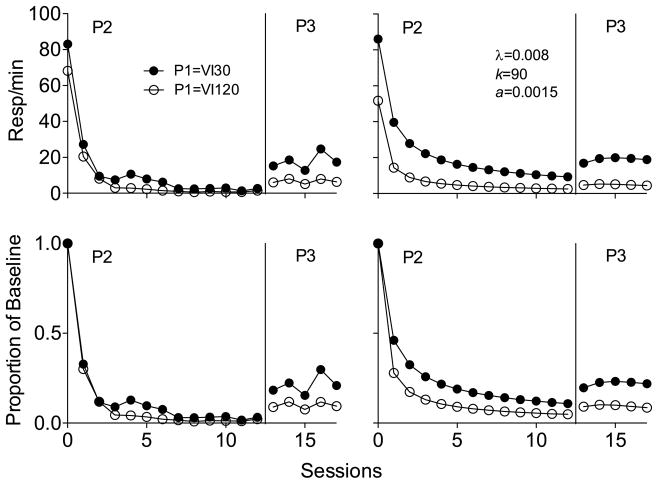
A couple of features of the Craig and Shahan (2016) experiment are somewhat atypical for many resurgence experiments. First, Phases 1 (i.e., 30 sessions) and 2 (i.e., 20 sessions) were quite lengthy. Second, the alternative response was topographically different from the target response, thus necessitating the inclusion of the bias parameter. Thus, it is of some interest to examine the effects of different reinforcement rates on the output of RaC under more typical conditions. In addition, examination of a wider range of a reinforcement rates would be useful. Fig. 12 shows simulations generated by RaC following 20 sessions of Phase-1 reinforcement on either a VI 10-s schedule or a VI 120-s schedule. In addition, Phase-2 alternative-reinforcement schedules ranging from VI 10 s to VI 120 s (i.e., 360-30 rein/h) are shown. Parameter values are as presented in Fig. 11, except that the bias parameter has been omitted. Across the wider range of values shown, the same basic pattern emerges as was true in Fig. 11. First, even with a 12-fold difference in Phase-1 rates of reinforcement (i.e., VI 10 versus VI 120) the model generates the same basic pattern of results. Second, lower rates of alternative reinforcement generate more target responding during Phase 2 than do higher rates of reinforcement. Third, lower rates of alternative reinforcement tend to generate more target responding during Phase 2 than does extinction alone. Fourth, high rates of alternative reinforcement (i.e., VI 10 and VI 15 Alt) generate responding that tends to be reduced below the levels of extinction alone earlier in Phase 2. In the later sessions of Phase 2, higher rates of alternative reinforcement (i.e., VI 15) can generate slightly elevated response rates as compared to extinction alone. The degree to which this later effect is observed would depend upon the length of Phase 2, and on any potential bias for the target over the alternative response (as was apparent in Fig. 11). Fourth, the increase in responding generated by the removal of alternative reinforcement with the transition between Phases 2 and 3 depends upon the rate of alternative reinforcement. The removal of higher rates of alternative reinforcement generates larger increases with the transition to Phase 3 (i.e., resurgence) because response rates tend to be lower in Phase 2 with those higher reinforcement rates. The lowest rate of alternative reinforcement (i.e., VI 120) generates the highest rates of responding during Phase 2, but fails to generate any increase in responding in Phase 3. Fifth, response rates in Phase 3 do not differ meaningfully as a result of different rates of alternative reinforcement, except for the lowest rate of alternative reinforcement (i.e., VI 120), which generates somewhat lower response rates.

Fig. 12.

Simulations of RaC across a range of alternative reinforcement rates following either VI10-s or VI120-s reinforcement of the target in Phase 1.

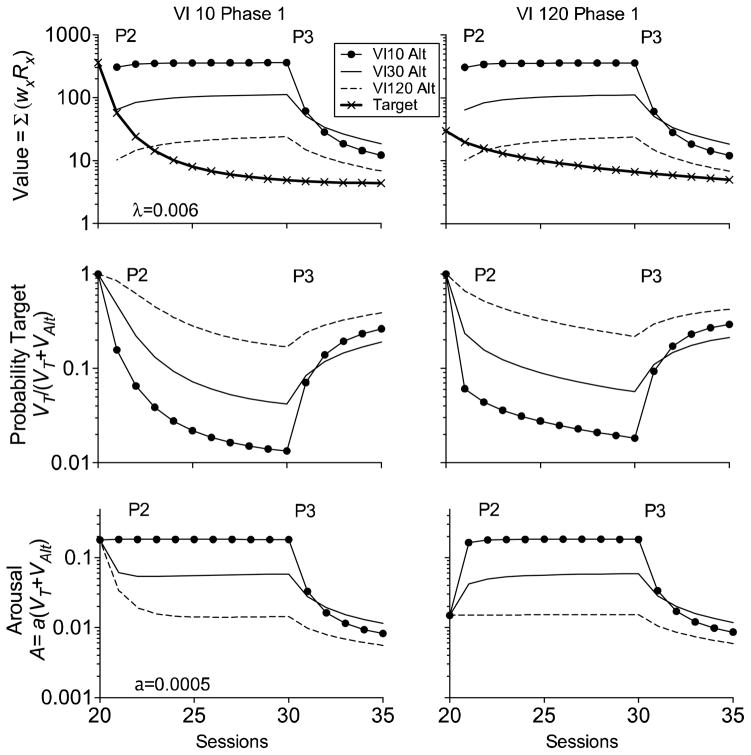
To aid understanding of the simulations of RaC in Fig. 12, the top panels of Fig. 13 show the value functions generated by Eq. (9) that serve as the basis for those simulations. Note that because the value functions calculated for V_T and V_Alt are independent of one another, the functions for V_Alt at different rates of alternative reinforcement (i.e., VI 10 Alt, VI 30 Alt, VI 120 Alt) are exactly the same following Phase-1 reinforcement on the VI 10-s (top left) and VI 120-s schedules (top right). However, as would be expected, in Phase 1 (data points on the y-axes) the higher rate of target reinforcement in Phase 1 (VI 10) generates a higher V_T than does the lower rate of Phase-1 reinforcement (VI 120). Nevertheless, after an initially steeper decrease in V_T with the VI 10-s schedule in the first couple of sessions of Phase 2, the two V_T functions are very similar across the rest of Phase 2. This similarity in the value functions for the different Phase-1 reinforcement rates across all but the early sessions of extinction is a direct result of the hyperbolic form of the weightings generated by the sTWR across sessions and the dependence of the currency term (i.e., c) on running rate of reinforcement for each option (Eq. (10)).

Fig. 13.

Value functions (top panels), probability of the target (middle panels), and arousal (bottom panels) associated with the simulations shown in Fig. 12.

The middle panels of Fig. 13 show the impact of these value functions on the probability of the target response [i.e., pT = V_T /(V_T + V_Alt)]. Note that changes in pT across Phases 2 and 3 are similar following Phase-1 target reinforcement on VI 10 s or VI 120 s. These similar functions are the main reason that Phase-1 rate of target reinforcement has little impact on responding in Phases 2 and 3, as demonstrated above in Figs. 11 and 12. These value functions also demonstrate the reason that higher rates of alternative reinforcement generate lower target-response rates than do lower rates of alternative reinforcement. With higher rates of alternative reinforcement, V_Alt is higher, and thus pT is lower. In short, less behavior is allocated to the target because the value of the alternative is higher. With the change to Phase 3 and the removal of alternative reinforcement, pT increases dramatically when high-rate alternative reinforcement (e.g., VI 10 Alt) is removed because of the precipitous decline in V_Alt. In other words, the removal of the high rate of alternative reinforcement produces a shift in the allocation of behavior to the target (i.e., resurgence). A similar but less dramatic shift occurs following the somewhat lower rate of alternative reinforcement (VI 30 Alt), but importantly, the two value functions arrive at nearly the same place with the change to Phase 3, resulting in similar pT functions during this phase. When a very low rate of alternative reinforcement is arranged (VI 120 Alt), however, the value function of the alternative (V_Alt) is much closer to the value function for the target, and thus more behavior is allocated to the target across Phase 2 (i.e., pT is higher). Removal of the low rate of alternative reinforcement also produces a less precipitous decline in the value of the alternative, and thus relatively small increases in pT.

The bottom panels of Fig. 13 show how arousal [i.e., A = a(V_T + V_Alt)] changes across sessions. Because arousal is driven by the sum of the value functions and V_T is contributing only small values across all but the first couple of sessions of Phase 2, the arousal functions largely track the form of V_Alt across Phases 2 and 3. Although arousal may be higher for the higher rates of alternative reinforcement, the low probability of the target response under these conditions means that little target behavior is generated. With the transition to Phase 3, arousal declines following removal of all Phase-2 reinforcement rates, thus generating specific response-rate functions across Phase-3 sessions that depend on a in Eq. (12).

Given the simulations and data above, RaC suggests that the rate of reinforcement for the target response in Phase 1 would be expected to have little impact on resurgence in single schedules. However, the rate of alternative reinforcement in Phase 2 would be expected to have an impact. Higher rates of alternative reinforcement generate larger increases in responding from the levels obtained at the end of Phase 2, and all but the lowest rates of alternative reinforcement would be expected to generate roughly similar overall rates of responding in Phase 3. Overall, these suggestions of RaC are consistent with the body of results generated when rates of Phase-1 or Phase-2 reinforcement are varied in resurgence experiments using single schedules of reinforcement (e.g., Bouton and Trask, 2016; Craig et al., 2016; Craig and Shahan, 2016; Leitenberg et al., 1975; Sweeney and Shahan, 2013b; Winterbauer and Bouton, 2010). The effects of differential reinforcement rates in multiple schedules are a different story, and will be addressed in a section below.

In summary, the broad conceptual framework of RaC and the specific example model presented in Fig. 10 appear to provide a reasonable account of the effects of reinforcement rate on extinction-induced resurgence in simple schedules. In short, responding in Phases 2 and 3 is governed by the relative value of the target and alternative options. The example model in Fig. 10 shows one way in which changes in value across sessions could be formalized and then used to generate expected rates of responding.

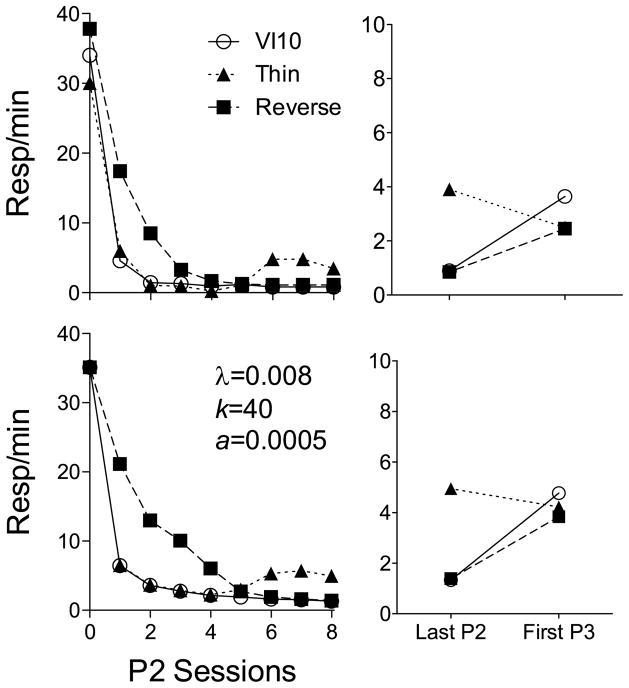
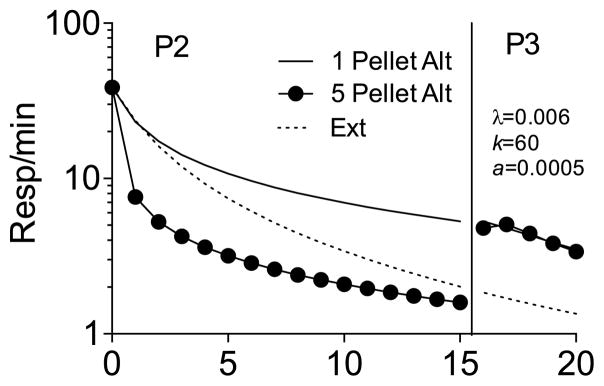
5.2. Changes in alternative-reinforcement rate across Phase 2

As noted above, an additional difficulty for Behavioral Momentum Theory was the effects of changes in the rate of alternative reinforcement during Phase 2. For example, Sweeney and Shahan (2013b) examined the effects of high, low, thinning, and no alternative reinforcement on resurgence in single schedules with rats. In Phase 1, lever pressing was reinforced for all rats on a VI 45-s schedule for 10 sessions. In Phase 2, nose poking on the back wall of the chamber was reinforced at different rates for four groups across 10 sessions. A high-rate group earned alternative reinforcement on a VI 10-s schedule, a low-rate group on a VI 100-s schedule, and an extinction-control group earned no reinforcement for nose pokes. The thinning group initially earned alternative reinforcement for nose pokes at the same rate as the high-rate group (VI 10 s), but the schedule increased daily by 10 s, ultimately delivering the same rate of alternative reinforcement as the low-rate group (i.e., VI 100 s) in the session prior to resurgence testing. In Phase 3, nose poking of all groups was placed on extinction. The top-left panel of Fig. 14 shows that during Phase 2, the high-rate (VI 10-s) group showed lower response rates than both the low-rate (VI 100-s) and extinction groups. However, as in the Craig and Shahan (2016) experiment and the simulations in Fig. 12 above, the low-rate group showed higher Phase-2 response rates than the extinction group. Response rates for the thinning group were similar to the high-rate group early in Phase 2 when the reinforcement rates for the groups were similar, but response rates were similar to the low-rate group at the end of Phase 2 when their alternative-reinforcement rates then were similar to that group. The top-right panel of Fig. 14 shows that with the removal of alternative reinforcement in the transition from Phase 2 to Phase 3, responding increased for the high-rate group from its lower Phase-2 level, but not for any of the other groups–for which Phase-2 response rates were higher. Despite the increase in responding for only the high-rate group from Phase 2 to 3, response rates did not differ significantly between the three alternative-reinforcement groups in Phase 3. This general pattern of results is consistent with the simulations of RaC above. The bottom panels of Fig. 14 show that a simulation based on the specific details of this experiment with λ = 0.008, k = 20, a = 0.0005, and b = 1.5 provides a good approximation of the pattern of results. Although the simulation of response rates for the high-rate group in Phase 3 appears to be somewhat lower than the data, individual-subject data presented in Sweeney and Shahan suggest that the mean for this group was inflated by one rat with especially high response rates. Calculation of the mean excluding this rat results in the data from the high-rate group being nearly the same as for the thinning group–and again, even including this rat there were no statistical differences between the three groups that received alternative reinforcement.

Fig. 14.

The top panels show data from Sweeney and Shahan (2013b) in Phase 2 (left) and Phase 3 (right). The bottom panels show a simulation generated by RaC. Last P2 and First P3 refer to the last session of Phase 2 and the first session of Phase 3, respectively.

Schepers and Bouton (2015) conducted a similar experiment in which they compared the effects of thinning and reverse thinning of alternative-reinforcement rates across Phase 2. Specifically, in Phase 1, all rats received reinforcement for lever presses on a VI 30-s schedule for 12 days. In Phase 2, three groups of rats received alternative reinforcement for pressing a different lever on a VI 10-s schedule, a thinning schedule, or a reverse thinning schedule. Specifically, the thinning group received alternative reinforcement on a VI 10-s schedule for the first 4 sessions, and then VI 19.5, VI 75, VI 300, and VI 1200 s across the next four sessions. The reverse-thinning group received the same VI values across sessions, but in reversed order. In Phase 3, alternative lever pressing was extinguished for all groups. The top-left panel of Fig. 15 shows response rates for the VI 10 group and the thinning group were similar in the early sessions of Phase 2 when these two groups received similar rates of alternative reinforcement. However, responding for the thinning group increased in the later sessions of Phase 2 when alternative reinforcement was reduced. The opposite pattern of responding across Phase 2 was obtained with the reverse thinning group–response rates were higher than for the VI 10 group in early sessions when the reverse thinning group received much lower alternative-reinforcement rates, but response rates were similar to the VI 10 group in later sessions when alternative-reinforcement rates were similar. The top-right panel shows responding in the last session of Phase 2 and in Phase 3 when alternative reinforcement was removed. Responding increased with the transition to Phase 3 for both the VI 10 and reverse-thinning groups (albeit somewhat less for the reverse thinning group), both of which had experienced a high rate of alternative reinforcement at the end of Phase 2 (and had correspondingly low response rates at the end of Phase 2). Responding for the thinning group remained high at the end of Phase 2 (in which this group received alternative reinforcement at a low rate) and further decreased with the removal of alternative reinforcement. The bottom panels of Fig. 15 show that RaC provides a reasonable simulation of these data with the same parameters used above for the Sweeney and Shahan (2013b) experiment, absent the bias parameter (i.e., λ = 0.008, k = 20, a = 0.0005).

Fig. 15.

The top panels show data from Schepers and Bouton (2015, Experiment 2) in Phase 2 (left) and Phase 3 (right). The bottom panels show a simulation generated by RaC. Last P2 and First P3 refer to the last session of Phase 2 and the first session of Phase 3, respectively.

The results of these two experiments on the effects of changes in alternative-reinforcement rate are consistent with the conclusions reached above about the effects of alternative-reinforcement rate on responding in Phases 2 and 3. Higher rates of alternative reinforcement in Phase 2 generate lower target-response rates in Phase 2 than do lower rates of alternative reinforcement. Decreases from a high rate of alternative reinforcement to no alternative reinforcement in Phase 3, or even to the dramatically lower rates of alternative reinforcement during Phase 2 for the thinning groups, generate increases in target responding (i.e., “early” resurgence). However, decreases from a low rate of alternative reinforcement like that arranged for the thinning groups at the end of Phase 2 do not generate increases in target responding. Despite the fact that shifts from high-rate reinforcement generate increases in responding from the low levels in Phase 2, the rates of responding generated in Phase 3 by such shifts do not differ based on the rate of alternative reinforcement experienced in Phase 2.

Although the quantitative details of the application of RaC to the effects of reinforcement rates on resurgence can seem complex, the basic conceptual framework is quite simple. Higher rates of alternative reinforcement drive the allocation of behavior away from the target response more in Phase 2 because of greater decreases in the relative value of the target option. Resurgence occurs with the removal of higher rates of alternative reinforcement in Phase 3 because of precipitous decreases in the value of the alternative option, and thus increases in the relative value of the target option. The data from experiments on changes in rates of alternative reinforcement across Phase 2 are instructive because they highlight the fact that exactly the same process governs responding during Phases 2 and 3–allocation in both phases is driven by the shifting relative values of the options.

5.3. Alternations of alternative reinforcement and extinction during Phase 2

A different way in which alternative-reinforcement rate has been varied in Phase 2 is with alternating exposures to alternative reinforcement and its absence across sessions of extinction of the target response (e.g., Schepers and Bouton, 2015; Sweeney and Shahan, 2013a; cf. Wacker et al., 2011). These studies have consistently found that removal of alternative reinforcement for a session in Phase 2 generates an increase in the rate of the target response (i.e., in essence “early” resurgence during Phase 2). When alternative reinforcement is reintroduced in the following session, target-response rates decrease. Across repeated exposures to these on/off cycles of alternative reinforcement as Phase 2 continues, the magnitude of the increase in target-response rate gets smaller. The effects of exposures to such on/off cycles of alternative reinforcement on resurgence in Phase 3 as compared to a condition in which alternative reinforcement is available in every session, however, have been mixed in the limited data available.

For example, in Schepers and Bouton (2015) rats received reinforcement for lever presses on a VI 30-s schedule for 12 days in Phase 1. In Phase 2, one group of rats received alternative reinforcement for pressing a different lever on a VI 10-s schedule in every session. A second group received daily alternating exposures to VI 10-s alternative reinforcement and extinction (i.e., on/off). A third group received alternative reinforcement in every session at the average rate provided to the on/off group across Phase 3 (i.e., a VI 17.5-s schedule). In Phase 3, alternative reinforcement was removed for all groups in a resurgence test session. The top-left panel of Fig. 16 shows the data from Phase 2 of the experiment. In sessions in which alternative reinforcement was available for all groups (i.e., sessions 1, 3, 5, and 7), response rates were low for all groups–with the average group (VI 17.5) showing marginally higher response rates than for the other groups, both of which received a higher rate of alternative reinforcement (i.e., VI 10) on those days. In sessions in which alternative reinforcement was removed for the on/off group (i.e., sessions 2, 4, and 6), response rates increased relative to the other groups. In addition, the increase in response rates for the on/off group across subsequent removals became smaller. The bottom-left panel of Fig. 16 shows that RaC generates a reasonably good simulation of these effects in Phase 2 with the same parameter values used in Fig. 15.

Fig. 16.

The top panels show data from Schepers and Bouton (2015, Experiment 3) in Phase 2 (left) and Phase 3 (right). The bottom panels show a simulation generated by RaC. Last P2 and First P3 refer to the last session of Phase 2 and the first session of Phase 3, respectively.

The top-right panel of Fig. 16 shows data for the transition from the last session of Phase 2 to Phase 3 in which alternative reinforcement was removed for all groups. Target responding increased for the VI 10 and average groups to similar levels in Phase 3–consistent with the effects and simulations above. Responding for the on/off group was significantly lower than for the other two groups and did not show a significant increase as compared to Phase 2. The bottom-right panel of Fig. 16 shows that RaC does a good job of simulating the data for the VI 10 and average groups. However, the simulation suggests similar response rates for the on/off group and the other two groups, rather than showing lower response rates as suggested by the data. Although this mischaracterization of Phase-3 responding for the on/off group could reflect a failure of the model, it may be premature to accept that conclusion. Specifically, Sweeney and Shahan (2013a) conducted a very similar experiment with pigeons in which alternating periods of alternative reinforcement and extinction in Phase 2 were compared to conditions in which alternative reinforcement was available in all sessions of Phase 2. They found the same pattern of results in Phase 2 as Schepers and Bouton (2015), but individual subject data (their Fig. 7) showed similar increases in target responding in Phase-3 responding for the groups–consistent with the simulations of RaC in Fig. 16. Thus, the discrepant findings in the literature suggest that additional experiments will be required to determine whether or not the preliminary version of RaC developed here will need to be modified to account for the effects of periods of on/off alternative reinforcement on resurgence.

5.4. Duration of Phase-2 exposure to alternative reinforcement

The effects of different durations of exposure to alternative reinforcement in Phase 2 on resurgence in Phase 3 is another factor that could be of special interest in applied settings, especially if longer exposure to DRA treatments can reduce subsequent resurgence. Two studies have directly examined the effects of Phase-2 duration on subsequent resurgence in the laboratory and they have generated mixed results. Leitenberg et al. (1975) reported that resurgence was similar for groups of rats exposed to three or nine sessions of Phase-2 alternative reinforcement, but no significant increase in responding was observed for a group that experienced 27 sessions of Phase 2 (although mean response rates do suggest a small increase). Unfortunately, many details of the Leitenberg et al. experiment are not reported, including the schedule of reinforcement in Phase 2. Nevertheless, based on this experiment, it appears that lengthy exposure to alternative reinforcement in Phase 2 might reduce subsequent resurgence. In contrast, Winterbauer et al. (2013) reported that 4, 12, and 36 sessions of exposure to Phase-2 alternative reinforcement produced statistically equivalent levels of resurgence, although mean response rates were somewhat higher for the 4-session group than for the other groups. Based on this study, it would appear that vastly different durations of exposure to Phase 2 have no statistically significant impact on resurgence. However, Winterbauer et al. reinforced the alternative behavior in Phase 2 on a fixed-ratio (FR) 10 schedule of reinforcement. Unfortunately, the different durations of exposure to Phase 2 generated different response rates (and correspondingly different reinforcement rates) in the groups, thus confounding variations in Phase-2 reinforcement rate and duration of exposure to alternative reinforcement. As a result, there are no easily interpretable data on the effects of duration of Phase 2 on resurgence.

What does RaC predict about the effects of Phase-2 duration on resurgence? Fig. 17 shows two simulations in which the effects of different Phase-2 durations ranging from 5 to 40 sessions (in 5-session increments) were examined. Note that with the exception of the increases generated by each Phase-3 test every five sessions, the functions for all the different durations of Phase 2 are the same and are not discernable on the figure (the single consistently decreasing function). The left panel shows the simulation with λ = 0.006 and the right panel with λ = 0.008. Other parameters are as in Figs. 11, 12, and 13 above (k = 60, a = 0.005). Thus, increases in responding in Phase 3 following a particular number of Phase-2 sessions appear as increases from that single function at different time points. Although the higher value of λ generates more rapid overall decreases in responding across Phase 2, the functions in the two panels otherwise show a similar pattern. Two features of this simulation are noteworthy. First, across a wide range of Phase-2 durations, response rates during the Phase-3 test are very similar to one another. This is especially true with the functions generated with λ = 0.008, although it is important to note that the logarithmic y-axis emphasizes the rather small differences in response rate across a similarly wide range on the function with λ = 0.006. Second, very short durations of Phase 2 tend to generate somewhat higher Phase-3 response rates than do longer durations, but this difference is due largely to the higher response rates at the end of Phase 2 for the shorter durations. Regardless, with the more steeply declining Phase-2 function generated with λ = 0.008, the difference between the shortest (i.e., 5 sessions) and longest (i.e., 40 sessions) duration of Phase 2 is less than 2 responses per minute using these parameters.

Fig. 17.

Simulations of the effects of different durations of exposure to Phase-2 alternative reinforcement generated by RaC. The two panels use different λ parameters for Eq. (10).

The simulations in Fig. 17 suggest that short durations of exposure to Phase 2 could generate higher responses rates in Phase 3 than intermediate and long durations, but the effects of Phase-2 duration might be difficult to detect statistically given the usual variance in Phase-3 responding across subjects. The degree to which the effects of duration of Phase 2 are detectable would be expected to depend upon the degree to which subjects weight the more recent past. With larger λ values, the currency term c would be greater, meaning that subjects who weight the past less heavily (see Figs. 4 and 10) would be less likely to show discernable differences in resurgence with short versus long Phase-2 durations. Effects of short versus long durations of Phase 2 might be more easily detected with subjects who weight the past more heavily (i.e., smaller λ and thus smaller c values). Regardless, intermediate and long durations of exposure to Phase 2 would be predicted to be unlikely to generate a discernable difference in resurgence. Despite the interpretive difficulties with both the Leitenberg et al. (1975) and Winterbauer et al. (2013) experiments noted above, these predictions appear roughly consistent with the data from those experiments. In Leitenberg et al., shorter durations of Phase 2 (3 and 9 sessions) generated resurgence, whereas a considerably longer duration generated an increase that was not statistically significant. In Winterbauer et al., 4, 12, and 36 sessions of Phase 2 generated statistically equivalent increases in responding, but mean response rates in Phase 3 were somewhat elevated following the shortest duration of Phase 2 (i.e., 4 sessions). Clearly additional data from more extensive and carefully controlled experiments will be required to fully understand the effects of Phase-2 duration on subsequent resurgence and to assess the adequacy of the specific version of RaC developed here.

At this point it is important to note an overlap between the effects of duration of Phase 2 presented in Fig. 17 and the effects of alternating periods of on/off alternative reinforcement described in the previous section. As it turns out, the simulations in Fig. 17 also describe what would be expected if a single group of subjects was exposed to a 40-session long Phase 2, with removals of alternative reinforcement every five sessions. The increases in responding generated by these periodic removals are not discernably different from the increases depicted in Fig. 17. This raises a question: Why did response rates clearly decrease across successive removals of alternative reinforcement across Phase 2 in the experiments described above (see Fig. 16)? The reason is that both Schepers and Bouton (2015) and Sweeney and Shahan (2013a) examined such alternations with only short durations of Phase 2. Schepers and Bouton examined daily alternations across a total of seven Phase-2 sessions and Sweeney and Shahan across only six Phase-2 sessions. Thus, the data from these experiments would correspond to a range around and before the shortest Phase-2 duration in the simulation in Fig. 17, and exactly the pattern of responding observed across Phase 2 in these experiments would be expected.

The correspondence between the simulated effects of duration of Phase 2 and alternating periods of on/off reinforcement also raises another question. As noted above, the simulations in Fig. 17 show that a wide range of longer durations of exposure to Phase 2 should produce roughly equivalent increases in responding with the transition to Phase 3. Thus, the same wide range of longer exposures to on/off alternative reinforcement would also be expected to produce similar levels of resurgence. However, Wacker et al. (2011) observed that repeated occasional removals of alternative reinforcement across several months provided as part of a functional-communication training (FCT) intervention with children with developmental disabilities ultimately produced no resurgence. In contrast, Winterbauer et al. (2013) reported that even a long duration (36 sessions) of exposure to constant Phase-2 alternative reinforcement produced resurgence. But, Schepers and Bouton (2015) reported that just seven sessions of alternating on/off alternative reinforcement might reduce resurgence compared to constant alternative-reinforcement groups (but see Sweeney and Shahan, 2013a for contrasting results). Thus, the limited data available could be interpreted to suggest that, contrary to the simulations in Fig. 17, resurgence might occur robustly after even prolonged periods of constant alternative reinforcement, but be reduced by much shorter exposures to alternating periods of on/off alternative reinforcement. However, the discrepancies between the data of some of these experiments (i.e., Sweeney & Shahan versus Schepers & Bouton), the confounding variables in some (Winterbauer et al.), and the substantial procedural and subject difference with others (Wacker et al.) prevent one from making comparisons across studies with any reasonable amount of confidence. Thus, it remains to be seen if the characterization of these effects generated by RaC will be appropriate or not.

Given these considerations, we suggest that an experiment directly comparing a wide range of Phase-2 durations with constant alternative reinforcement to periodic removals and replacement of alternative reinforcement (i.e., on/off) at similar time points could reveal important information about the processes governing resurgence. RaC in the form developed here suggests that the two procedures should have similar effects across a wide range of durations of Phase 2. If the data suggest otherwise, then some aspect of RaC as developed here would likely be in need of modification. In addition to these theoretical concerns, such an experiment could have a relatively immediate impact on DRA-based interventions (e.g., FCT) by determining if on/off alternative-reinforcement produces less ultimate resurgence (i.e., greater maintenance of treatment effects) than constant alternative reinforcement for similar durations.

5.5. Magnitude of alternative reinforcement in Phase 2

Although there has been a considerable amount of research on the effects of differential rates of alternative reinforcement on subsequent resurgence, in applied settings it is common for differential magnitudes of alternative reinforcement to be used in DRA-based treatments (e.g., Fiske et al., 2014; Higgins et al., 2007; Lerman et al., 1999, 2002; Petry et al., 2012; Silverman et al., 1999; Volkert et al., 2005). Consistent with the effects of higher rates of alternative reinforcement discussed above, larger magnitudes of alternative reinforcement in such treatments typically more effectively reduce problem behavior. However, the effects of differences in reinforcement magnitude on resurgence have never been directly examined in these settings. In addition, to the best of our knowledge, there have been no laboratory experiments examining this issue. Given the widespread use of different reinforcer magnitudes in DRA-based treatments, research in both the laboratory and in the clinic on the effects of this variable on resurgence would seem warranted. It should be relatively straightforward to incorporate the effects of magnitude of alternative reinforcement into RaC to make predictions about what effects manipulation of this variable could have. In addition, exploration of this issue permits a demonstration of the potential utility of the value-based approach employed by RaC.

As noted above, RaC assumes that the value of the options is governed by the combined effects of different parameters of reinforcement in accordance with the concatenated matching law (Baum and Rachlin, 1969). Accordingly, to determine the value of the options, the weighting provided by the sTWR could be applied to a multiplicative combination of reinforcement rate and magnitude such that:

$$V_T=\sum _x{w}_x(R_{xT}{A}_{xT})V_{\mathit{Alt}}=\sum _x{w}_x(R_{\mathit{xAlt}}{A}_{\mathit{xAlt}})$$ (14)

where A_xT and A_xAlt represent the amount of reinforcement provided by the target and alternative options in a given session, respectively. For example, imagine an experiment in which target responding is reinforced with a single pellet in Phase 1 on a VI 60-s schedule and different groups receive either one pellet, five pellets, or no alternative reinforcement (i.e., Ext) for pressing a second lever on a VI 60-s schedule. In Phase 3, all alternative reinforcement is removed. As a result of the multiplicative effects of reinforcer rate and magnitude, the terms within the parentheses in Eq. (14) would be 60 × 1 = 60 for the target and 60 × 5 = 300 for the alternative. In short, the relevant calculations in RaC would be based on the density of reinforcement, rather than just rate. Thus, using a five-pellet alternative reinforcer would be expected to have the same effects as arranging 300 reinforcers/h (i.e., a VI 12 s) for the alternative and predict similar effects to those described in the section above.

Based on this approach, Fig. 18 shows a simulation provided by RaC using the same parameter values as in the simulations of rate of alternative reinforcement in Fig. 12 above. Note that the five-pellet group shows lower response rates than the one-pellet group during Phase 2. In addition, the one-pellet group shows higher response rates than the Ext group across much of Phase 2. In addition, response rates are lower for the five-pellet group than for the Ext group across most of Phase 2. Finally, in Phase 3, the five-pellet group shows an increase in responding (i.e., resurgence) while the one-pellet group does not. Despite the increase for the five-pellet group, response rates do not differ for the five-pellet and one-pellet groups during Phase 3. The lack of resurgence for the one-pellet group after VI 60-s reinforcement in Phases 1 and 2 is consistent with the results of Craig and Shahan (2016) using VI 60-s schedules and one pellet as described above. But, importantly, the inclusion of a larger magnitude reinforcer with these same schedules does produce resurgence in the simulation. Although the one-pellet group did not show resurgence in Craig and Shahan with the same reinforcement rates, an increase to five pellets in Phase 2 would be expected to increase the value of the alternative option (i.e., V_Alt) in a manner similar to increases in reinforcement rate, and thus generate resurgence.

Fig. 18.

Simulations of the effects of different magnitudes of alternative reinforcement during Phase 2 generated by RaC.

5.6. Quality of alternative reinforcement in Phase 2

In applied settings, the reinforcers employed in DRA-based treatments are often qualitatively different from those that previously maintained the target behavior (see Higgins et al., 2004; Volkert et al., 2009; for reviews). Some laboratory studies of resurgence have used alternative reinforcers that are qualitatively different from the reinforcer initially used for the target behavior (e.g., Podlesnik et al., 2006; Quick et al., 2011; Shahan et al., 2015; Winterbauer et al., 2013). Although these experiments have demonstrated that removal of a qualitatively different alternative reinforcer can produce resurgence, relatively little else is known about how qualitative differences in target and alternative reinforcers impact resurgence. For example, it is not known if differences in the quality of alternative reinforcement generate similar effects to differences in rate of alternative reinforcement as discussed above. Nevertheless, one way to incorporate differences in the quality of an alternative reinforcer into RaC is to assume that such qualitative differences serve as a source of bias toward either the target or alternative options. This approach has been used previously to incorporate the effects of qualitatively different reinforcers into the generalized matching law (e.g., Miller, 1976). In terms of RaC, this would involved using the bias term of Eq. (13) such that qualities of alternative reinforcement that are greater than those for the target would assume b < 1 (i.e., bias for the alternative) and those that are lesser than for the target would assume b > 1 (i.e., bias for the target). Given that such an approach would not incorporate qualitative differences directly into the calculation of values of the options, such differences would not have any effect on arousal via Eq. (12). Ignoring such potential effects of quality on arousal would seem to be problematic (e.g., imagine the likely difference in arousal generated by a piece of steak versus a piece of kibble for a dog). Thus, taking this approach it would probably be necessary to also incorporate the bias term into the calculation of arousal in Eq. (12) (e.g., A = a (V_T + V_Alt /b)).

Given the current lack of data on how qualitative differences in reinforcement affect resurgence, it would seem premature to speculate further here about this issue and others (e.g., reinforcer substitutability). Regardless, existing theoretical developments within the literature on Matching Theory suggest that RaC could be extended to similarly account for the effects of qualitative differences in alternative reinforcement on resurgence.

5.7. Contingent versus non-contingent alternative reinforcement in Phase 2

Although the use of alternative reinforcement contingent upon an alternative behavior (i.e., DRA) is a common treatment for problem behavior, another effective treatment involves the use of alternative reinforcers that are presented non-contingently (i.e., non-contingent reinforcement, NCR; see Richman et al., 2015). Direct laboratory comparisons of the effects of DRA and NCR in a resurgence paradigm have generated mixed results. For example, Winterbauer and Bouton (2010) found that with rats, VI reinforcement for alternative behavior and yoked variable-time (i.e., VT) reinforcement produced similar suppression of target behavior during Phase 2, and similar amounts of resurgence in Phase 3. Using a considerably more complicated multiple-schedule procedure with pigeons, Sweeney et al. (2014) also found that removal of both DRA and NCR resulted in resurgence, but Phase-2 response rates were considerably lower with DRA than with NCR. Although the source of the discrepancy between these experiments is not entirely clear, RaC might provide a way to begin to understand it.

One way the (mixed) effects of DRA versus NCR might be incorporated into RaC is to assume that, in the absence of any explicitly defined alternative behavior, some NCR reinforcers might be misattributed to the target option (sometimes conceptualized as adventitious reinforcement). Burgess and Wearden (1986) suggested that the response-rate reducing effects of superimposed non-contingent reinforcers could be incorporated into Herrnstein’s (1970) absolute response-rate version of the matching law through such a misallocation process:

$$B=\frac{k(R_1+{pR}_2)}{R_1+R_2+R_e}$$ (15)

where all terms are as above (with R₂ here referring to non-contingent reinforcers) and the new parameter p representing some proportion of those non-contingent reinforcers that function as reinforcers for the measured behavior B. Thus, with a higher p parameter, non-contingent reinforcers would have less of a response-rate reducing effect, because in effect they are serving as R₁. A similar reinforcer misallocation approach has been proposed in more general Matching-Law based theories to account for two or more explicitly defined choice responses (e.g., Davison and Jenkins, 1985; see Davison and Nevin, 1999, for review), and has been employed by Bai et al. (2016) to account for “local-level resurgence” in a free-operant psychophysical procedure. One approach to begin incorporating such a misallocation process into RaC could be to include a similar p parameter into the calculations of reinforcement rates in Eq. (8) such that:

$$V_T=\sum _x{w}_x(R_{xT}+{pR}_{\mathit{xAlt}})V_{\mathit{Alt}}=\sum _x{w}_x(R_{\mathit{xAlt}}(1-p))$$ (16)

Using this approach, non-contingent alternative reinforcement would be expected to increase the value of the target option during Phase 2 if p > 0. The degree to which the value of the target is increased by NCR would increase as p approaches 1. With DRA, however, it is unlikely (but not impossible) under normal circumstances that a meaningful proportion of alternative reinforcers would be misallocated to the target, as opposed to the explicitly defined alternative behavior (i.e., p would be expected to be close to zero). Thus, differences across experiments in the effects of NCR versus DRA on Phase-2 responding could be the result of differences in how likely it is that non-contingent alternative reinforcers are misallocated to the target behavior.

Although Eq. (16) suggests one possible approach to how the effects of NCR might be incorporated into RaC, further development of the approach will require additional data. Experiments examining the viability of this approach might vary conditions likely to impact the misallocation of alternative reinforcers to the target option (e.g., presence versus absence of a required delay between target responses and non-contingent reinforcers, variations in the discriminability between explicitly defined target and alternative behaviors). Regardless, as was true with considerations of alternative-reinforcement magnitude and quality above, the extensive literature on choice behavior could provide a number of insights into how to most effectively extend RaC to such variables with obvious clinical relevance.

5.8. Serial DRA

An experiment by Lambert et al. (2015) suggests that reinforcement and then extinction of a series of alternative behaviors during the course of extinction of a target behavior can reduce subsequent resurgence of the target behavior. Specifically, using adults with developmental disabilities as participants, Lambert et al. reinforced an arbitrary response in Phase 1 (e.g., toggle light switch). In Phase 2, three different arbitrary alternative responses were introduced for a few sessions each, with each response placed on extinction before the next was introduced and reinforced. Each successive alternative response remained available after it was placed on extinction, and the subsequent response was introduced and then reinforced. The final resurgence test occurred when the third and final alternative response was placed on extinction. This serial-DRA procedure was compared to a control condition in which only a single alternative response was reinforced for the duration of Phase 2, as in a typical resurgence experiment. The data showed that the typical-resurgence control condition generated an increase in target responding in Phase 3. The serial DRA procedure, however, generated nearly no increase in target responding across the three participants in Phase 3. Instead, with the extinction of the last alternative response in Phase 3, previously reinforced alternative responses tended to increase. This outcome could have important clinical implications because, 1) it demonstrates a method by which resurgence of target behavior can be eliminated, and 2) alternative responses in clinical settings are typically desirable responses.

The approach to resurgence provided by RaC provides a fairly straightforward way to understand the outcome of the Lambert et al. experiment. In the most general sense, the probability of the target response across Phases 2 and 3 is determined by the relative value of the target option according to Eq. (3). When each alternative response is introduced and then placed on extinction, RaC suggests that the value of that alternative does not drop to zero, but rather decreases hyperbolically with time as a result of the sTWR. In addition to this lingering value of the previous alternative options, as each new alternative response is introduced the value for that option would also contribute to the relative valuation of the target option. Thus, with three alternative responses Eq. (3) would become,

$$pT=\frac{V_T}{V_T+V_{\mathit{Alt}1}+V_{\mathit{Alt}2}+V_{\mathit{Alt}3}}$$ (17)

where all terms are as above and subscripts denote values for each alternative option in the series. As a result, the added value contributed by the series of alternative responses across time would be expected to keep the relative value of the target option low when the final alternative response is placed on extinction. In short, RaC suggests that serial DRA might prevent resurgence of the target behavior because the history of reinforcement with a series of alternative behaviors serves to keep the relative value of the target low during the resurgence test. Given the potential clinical importance of the effects of serial DRA on resurgence, we suggest that this is an area that could strongly benefit from additional basic and applied research.

6. Resurgence and non-extinction induced changes in relative value

The sections above described one approach for formalizing how changes in the relative value of the target option driven by extinction of the target and alternative options might lead to resurgence. As noted above, the general framework provided by RaC suggests that the same processes might be at work when the values of the alternative or target options are changed by other means. In the next two sections we explore how RaC might be extended to such cases.

6.1. Resurgence after other means of changing the value of the alternative option

The example model presented in Fig. 10 above was used to characterize how extinction of the alternative option decreases its value, and thus, increases the relative value of the target. Application of the same approach can be used to understand how other means of decreasing the value of the alternative might also induce resurgence.

6.1.1. Changes in the rate of alternative reinforcement

In the context of the model, extinction of the alternative represents a decrease in the rate of reinforcement for the alternative to zero, and the resultant change in value across time. Given this approach, less extreme changes in the rate of alternative reinforcement would also be expected to reduce its value and to produce some degree of resurgence. Fig. 19 shows simulations of RaC following Phase-1 reinforcement of the target on a VI 15-s schedule and then Phase-2 reinforcement on a VI 15-s schedule. Simulations are provided for a range of reinforcement rates in Phase 3 arranged by different VI schedules (i.e., VI 15 s – Ext). The model suggests that larger decreases in the rate of alternative reinforcement in Phase 3 should generate larger increases in the target response. Reducing the rate of alternative reinforcement by half (i.e., VI 30) produces little change in the target response, but more extreme reductions generate increases in responding that more closely approximate those generated by a transition to extinction.

Fig. 19.

Simulations generated by RaC of the effects of different sized downshifts in reinforcement rate with the transition from Phase 2 to Phase 3. Reinforcement in both Phases 1 & 2 was on VI15-s schedule. Last P2 and First P3 refer to the last session of Phase 2 and the first session of Phase 3, respectively.

Only one experiment has examined the possibility of resurgence induced by a shift to a non-zero rate of alterative reinforcement (Lieving and Lattal, 2003). Lieving and Lattal showed with pigeons that a shift from VI 30-s alternative reinforcement in Phase 2 to VI 360-s reinforcement in Phase 3 generated considerably less resurgence than did a subsequent shift to extinction. Although the simulation in Fig. 19 is consistent with the direction of this effect, the 12-fold decrease in reinforcement represented by the shift from VI 30 s to VI 360 s appears to have generated less resurgence than might be expected based on a similar-fold shift (i.e., VI 15–VI 180) in the simulation. Obviously, this difference could reflect a failing of RaC. However, it is difficult to reconcile the Lieving and Lattal data with the effects of shifts in alternative reinforcement in Phase 2 obtained by Schepers and Bouton (2015) in their study of reinforcement thinning with rats. In Schepers and Bouton, a shift in alternative reinforcement from a VI 10 s to a VI 75 s in Phase 2 (Session 6 in Fig. 15 above) produced an increase in target responding that was similar to that produced by a shift from VI 10 s to extinction during Phase 3 with a different group (VI 10 in the right panel of Fig. 15 above). These effects were well described by RaC. It is unclear why a larger shift from VI 30 s to VI 360 would produce little resurgence in Lieving and Lattal, but a shift from VI 10 to VI 75 would in Schepers and Bouton (although a species difference is possible). Clearly additional research on the effects of shifts in the rate of alternative reinforcement in Phase 3 are needed to clarify the degree to which such shifts induce resurgence relative to a shift to extinction and to evaluate the characterization of these effects provided by RaC.

In addition, given the characterization of the effects of magnitude and quality of alternative reinforcement by RaC in the above sections, RaC would predict that shifts in the magnitude or quality of an alternative reinforcer could also generate increases in target responding that are dependent on the size of the shift. To our knowledge, no such experiments have been conducted (but for a related experiment see Bouton and Trask, 2016; below).

6.1.2. Response-dependent to response-independent alternative reinforcement

The simulation in Fig. 19 showing no increase in target responding when there is no change in the rate of alternative reinforcement in Phase 3 (i.e., VI 15 in Phase 3 in the figure) has implications for understanding the absence of effects of transitions to response-independent alternative reinforcement in Phase 3. Experiments examining such shifts from response-dependent alternative reinforcement in Phase 2 to the same rate of response-independent reinforcement in Phase 3 have found no resurgence of target responding (Lieving and Lattal, 2003; Winterbauer and Bouton, 2010; Marsteller and St Peter, 2014). This outcome is consistent with the framework provided by RaC. Such changes to response-independent reinforcement involve no decrease in the rate of alternative reinforcement, and therefore no decreases in the value of the alternative (and no change in pT).

A recent experiment by Bouton and Trask (2016, Experiment 2) has combined elements of the two issues discussed just above. Specifically, target lever pressing of rats was reinforced with one type of food pellet (e.g., grain; O1) on a VI 30-s schedule in Phase 1. In Phase 2, target lever pressing was extinguished and presses to a second lever produced a different type of food pellet (e.g., sucrose; O2) on a VI 30-s schedule. In Phase 3, different groups received no pellets, response-independent food pellets that were the same as in Phase 1 (i.e., O1), or response-independent pellets that were the same as in Phase 2 (i.e., O2). Response-independent pellets for both groups were delivered at the same rate as in Phase 2. The group that had received no pellets in Phase 3 showed a typical resurgence effect, as expected. The group that continued to receive the same pellets at the same rate as in Phase 2 (i.e., O2) but response-independently showed no resurgence, consistent with the discussion above. The third group that received response-independent pellets that were the same as those in Phase 1 (i.e., O1), however, appeared to show an increase in responding that was similar to that for the no-pellet group. We shall discuss the result in some detail because Bouton and Trask argue that it provides unique support for the role of discriminative properties of the Phase-2 reinforcer in resurgence.

As a reminder, Context Theory suggests that it is the discriminative properties of the Phase 2 reinforcer that serve as the context (i.e., Context B) for learning to inhibit the target response. Thus, the theory suggests a change in those reinforcers should constitute a change in context (i.e., Context C) and generate resurgence. Accordingly, Bouton and Trask (2016) note that “If the O1 pellet is sufficiently different from the O2 pellet that provided the context of R1’s [the target’s] extinction during Phase 2, the context hypothesis predicts response recovery in this group.” Although the data from the experiment might appear to confirm this prediction, a number of uncertainties with respect to interpretation remain. First, and most importantly, the subsequent experiment (i.e., Experiment 3) failed to replicate the increase in responding obtained for the critical group receiving response-independent O1 reinforcers in Phase 3. The only difference between the experiments was that O2 during Phase 2 was delivered response-independently, a change that the authors noted should have had no effect based on their previous research (Winterbauer and Bouton, 2010). We suspect that this failure to replicate could be due to an artifact generated by an interaction between procedural and data analysis procedures in Experiment 2. Unlike Experiment 3 and previous experiments on resurgence, two daily sessions were conducted in Experiment 2, the second of which began only 1.5 h after the first ended. By itself, this aspect of the procedure might not be of concern, but it was also combined with an atypical data analysis. Specifically, rather than statistically evaluating session-wide response rates during the Phase 3 resurgence test compared to session-wide response rates at the end of Phase 2, the sessions were broken into two 15-min blocks with the evaluation of resurgence based on a comparison of the final 15 min of the last session of Phase 2 and the first 15 min of the Phase 3 test session. As the authors note, the comparison of response rates from only the end of one session and the beginning of the next raises the possibility that spontaneous recovery could have contributed to the increases in responding for the critical groups. Thus, in an attempt to rule out this possibility, responding from the last 15 min of the second-to-last Phase 2 session (i.e., session 11) was compared to responding in the first 15 min of the last Phase 2 session (i.e., session 12), when there had been no manipulation of the alternative reinforcer. Although this analysis showed no significant spontaneous recovery, the two sessions chosen for the analysis appear to have come from the same day, and thus occurred only 1.5 h apart. The corresponding analysis for resurgence with the transition between Phases 2 and 3 was conducted on two sessions (i.e., sessions 12 & 13) that appear to have occurred 24 h apart, rather than 1.5 h. Thus, the analysis does not rule out the possibility that the increase observed for the critical group receiving O1 during Phase 3 was due to spontaneous recovery associated with the longer period between the sessions. Regardless, if changes in context generated by the discriminative properties of the Phase-2 reinforcer are the primary determinant of all resurgence effects, then it should be easy to reliably demonstrate the effects of explicit manipulations of those discriminative properties using methods and analyses (e.g., single daily sessions, and whole-session response rates) employed in standard resurgence experiments. Nevertheless, if the findings of Bouton and Trask (2016, experiment 2) are accepted at face value or it turns out that response-independent deliveries of the Phase 1 reinforcer (i.e., O1) following a different reinforcer is Phase 2 (i.e., O2) reliably generate resurgence, RaC might provide a different interpretation. From the perspective of RaC, a reversion to response-independent deliveries of the Phase-1 target reinforcers could be considered to generate an increase in the value of the target (i.e, V_T), and thus, an increase in the probability of the target (i.e., pT). We shall return to the possibility that revaluations of the target option might generate resurgence in a section below examining changes in the value of the target option.

Finally, it is worth noting that a stronger test of the hypothesis that changes in the discriminative features of the Phase-2 reinforcer generate resurgence would be to switch to the delivery of a novel reinforcer (i.e., O3) in Phase 3, rather than the same reinforcer that was used in Phase 1 (i.e., O1). Interestingly, similar to the discussion of serial DRA above, RaC would seem to suggest that such a shift to a novel reinforcer is Phase 3 should not produce resurgence if that reinforcer is similarly valued to the reinforcer used in Phase 2 (i.e., generates indifference in a separate preference assessment), even if the two reinforcers have clearly different discriminative properties. On the other hand, Context Theory would seem to predict that, regardless of having similar value to the Phase 2 reinforcer, a clearly discriminatively different novel Phase-3 reinforcer should generate resurgence. Such an experiment might help to differentiate the basic conceptual frameworks provided by RaC and Context Theory.

6.1.3. Decreasing the value of the alternative via punishment

Wilson and Hayes (1996) demonstrated with humans that punishment of alternative responding in the form of negative feedback (i.e., “WRONG”) generated resurgence of complex conditional discrimination responding. To our knowledge, no other experiment has examined whether or not punishment of an alternative behavior can lead to resurgence of previously extinguished target responding. Importantly, in the Wilson and Hayes experiment, alternative responding was also placed on extinction. Thus, it remains unknown if punishing an alternative response while it continues to produce alternative reinforcement would generate resurgence. Regardless, RaC suggest that it could. The addition of punishment for the alternative would be expected to decrease the value of the alternative, and thus to generate increases in extinguished target responding. In terms of formalizing such effects, we will simply note that punishment has been incorporated into the matching law most effectively by assuming that punishers subtract from the reinforcers provided by an option (de Villers, 1980; see Critchfield et al., 2003; for review). Following this approach, one could incorporate punishment of the alternative into RaC much like those of reinforcement magnitude in Eq. (14). In this case, however, calculations of value would involve subtracting the rate of punisher deliveries from the rate of ongoing reinforcement. An additional parameter would likely be required to place punisher deliveries into the same scale as reinforcer deliveries. However, given the complete absence of data, we will not pursue this issue further here.

6.1.4. Devaluation of the alternative through satiation or taste aversion

Finally, the general notion that decreases in the value of an alternative option should generate resurgence of target responding suggests a potentially interesting line of research. Devaluations of an alternative reinforcer that is qualitatively different from the target reinforcer in Phase 1 via reinforcer specific satiation (e.g., Balleine and Dickinson, 1998) or conditioned taste aversion (Adams and Dickinson, 1981) might be expected to generate resurgence of target responding. Such experiments might prove useful for further differentiating a value-based approach such as RaC from an approach based solely on the discriminative properties of reinforcers. The reason is that such devaluation operations have been shown to impact the value of reinforcers while potentially leaving their signaling effects intact (Ostlund and Balleine, 2007). Importantly, it would be critical to ensure that such devaluations of the alternative reinforcer do not also impact the value of the target. In many cases, although such devaluation operations decrease responding for the devaluated reinforcer more than for a non-devalued reinforcer, responding maintained by the non-devalued reinforcer often does show some decreases in rate (e.g., Podlesnik and Shahan, 2009b). Even modest decreases in the value of a target reinforcer could counteract the necessary changes in the relative value of the target option, and thus preclude resurgence. Thus, such experiments would need to be conducted with extreme care in order to be informative about the role of devaluation of the alternative in generating resurgence.

6.2. Resurgence after other means of changing the value of the target option

Thus far, we have only examined resurgence of a previously reinforced target behavior that was suppressed by extinction. As noted in the Introduction section, resurgence has typically been defined in terms of the recurrence of such extinguished behavior. Nevertheless, RaC suggests that the same basic processes could be relevant to recurrence of target behavior that is suppressed via other means. RaC would suggest that such suppression of a target behavior results from a decrease in the value of the target option, and that its recurrence results from an increase in the relative value of the target when an alternative response is also devalued subsequently.

A few experiments have examined resurgence of target responding suppressed via punishment, but all of these experiments have simultaneously placed the target on extinction (Kestner et al., 2015; Okouchi, 2015; Rawson and Leitenberg, 1973). These experiments have generated mixed results with some showing resurgence after a combination of extinction plus punishment (Okouchi, 2015; Rawson and Leitenberg, 1973), and some not (Kestner et al., 2015). Regardless, at present, it is unknown if removal of alternative reinforcement produces resurgence of a target behavior that has been suppressed by punishment without extinction of the target behavior. Nevertheless, the approach suggested by RaC would be the same as described for punishment of the alternative behavior in Phase 3 above. RaC might formalize the value-decreasing effects of punishment of the target response by pursuing a subtractive model of punishment as described above. Thus, punisher deliveries would be expected to subtract from the value the target option, but a decrease in the value of the alternative option in Phase 3 would be expected to increase the relative value of the target and generate resurgence. Further development and evaluation of this approach must await additional data.

A number of experiments have demonstrated resurgence after target behavior has been suppressed with a DRO contingency (e.g., Doughty et al., 2007; de Silva et al., 2008; Lieving and Lattal, 2003). In such DRO procedures, alternative reinforcement is delivered contingent upon withholding the target response for some period of time. Resurgence is then examined by removing the DRO reinforcement. A formal application of RaC to DRO-suppressed target would require specifying quantitatively how a DRO contingency reduces the value of the target across time. Although there are many ways one might approach this problem, a promising avenue is the suggestion that DRO has its effects as a result of negative punishment (Rolider and Van Houren, 1990). Specifically, Rolider and Van Houten suggested that DRO contingencies decrease the rate of behavior because continued occurrence of the target behavior results in a reduction in reinforcement rate. Thus, RaC could treat the effects of DRO on the value of the target in a manner similar to that described with other forms of punishment above.

Finally, although more difficult to formalize quantitatively, resurgence might also be expected with changes in the value of the alternative after target responding has been decreased by other devaluation procedures (e.g., decreases in motivation, taste aversion, etc.). Perhaps more interestingly, the approach suggested by RaC suggests that increases in the value of the target option in Phase 3 might also generate resurgence, even in the absence of changes to the alternative reinforcer. For example, target responding of rats might be reinforced with water deliveries in Phase 1, and then extinguished in Phase 2 while an alternative response produces food deliveries. Changes in thirst induced by greater water deprivation or saline injections might be expected to increase the relative value of the target, and thus produce resurgence. Such an outcome would contribute additional evidence that extinction-induced resurgence as typically examined is just one instance of a broader phenomenon producing shifts in the allocation of behavior with changes in relative value across time.

7. Multiple schedules and momentum-like effects

RaC as developed above did a good job simulating the effects of reinforcement rates in Phases 1 and 2 on subsequent resurgence in single schedules of reinforcement. In such schedules, we noted that the rate of target reinforcement in Phase 1 has little effect on resurgence, but that higher rates of alternative reinforcement in Phase 2 tend to generate more resurgence. RaC generates such effects as a result of its assumption that higher rates of reinforcement increase the weight given to more recent experiences via increases in the currency term as described by Eqs. (9) and (10). Such an increase in currency with higher reinforcement rates allows RaC to accommodate PREE-like effects (i.e., more persistent responding in Phase 2 following lower reinforcement rates in Phase 1; see Fig. 6 above). However, higher Phase-1 reinforcement rates generally appear to increase the persistence of Phase-2 target responding and to generate greater resurgence in Phase 3 when arranged within the component stimuli of multiple schedules of reinforcement (e.g Cançado, Abreu-Rodrigues, & Aló, 2015; Kuroda et al., 2016; Podlesnik and Shahan 2009a; Podlesnik and Shahan, 2010). Why should differential Phase-1 reinforcement rates have one effect in Phase 2 in simple schedules and a different effect in multiple schedules? Unfortunately, the exact sources of these differences remain unclear, even within the framework of Behavioral Momentum Theory (see Craig and Shahan, 2016, for full discussion).

Although we will not pretend to have a complete answer to the question above, RaC can potentially provide some insights worthy of further exploration. In the application of RaC to single-schedule experiments above, the currency term c was calculated independently for each response option via Eq. (10), presented again here for convenience:

$$c=\lambda r+1$$

where r is the average running rate of reinforcement obtained at a particular response option and λ is a parameter modulating how quickly c increases with reinforcement rate. The most important consideration for present purposes is that a c value was calculated for each response option based on the running reinforcement rate for that option. In experiments examining the effects of different Phase-1 reinforcement rates on resurgence using multiple schedules, the same response is typically used in both components of the multiple schedule (e.g., the same response key for pigeons, but different colors in the different components). If one follows the logic of the application of RaC to single schedules, then it might be appropriate to use the running average reinforcement rate for the response itself (regardless of multiple-schedule component) to determine c. Indeed, using a common c value across components generates momentum-like effects if calculations of the value of the target in the two multiple-schedule components (via Eq. (8)) are based upon the different target-reinforcement rates (i.e., R_x) in those components. Although, a common c term produces similar proportional decreases in the value of the target (i.e., V_T) across components following different baseline reinforcement rates, differential changes in the magnitude of the denominator [i.e., V_T + V_Alt + 1/A, with A = a (V_T + V_Alt)] relative to the numerator (i.e., kV_T) in the response output functions for the two components can lead to greater proportional decreases in response rates for a component with a lower baseline reinforcement rate.

For example, Podlesnik and Shahan (2010) arranged a VI 30-s (120/h) schedule of food reinforcement for pigeons’ Phase-1 key pecking in one component and a VI 120-s (30/h) schedule in the other. The same key lit different colors was used for the target response in the two components. In Phase 2, pecking a second key in both components was reinforced on a VI 30-s schedule while responding to the initial key was extinguished. In Phase 3, responding to the second key was also extinguished. The top-left panel of Fig. 20 shows the data from the experiment. Target responding in Phase 2 occurred at a somewhat higher rate in the component associated with the higher rate of target reinforcement in Phase 1 (i.e., VI 30 s). In addition, target-response rates in Phase 3 were clearly higher in the component that had arranged the higher rate of reinforcement in Phase 1. Consistent with the original data presentation of Podlesnik and Shahan and such multiple schedule experiments in general, the bottom-left panel shows the same data but presented as a proportions of Phase-1 response rates. The conversion to proportion of baseline has little impact on the interpretation of the data given that there was no major difference in baseline response rates.

Fig. 20.

The left panels show data replotted data from Podlesnik and Shahan (2010). The right panels show a simulation generated by RaC. The top panels are expressed in absolute response rates and the bottom panels in terms of proportion of Phase-1 (baseline) rates.

In applying RaC as described above to the Podlesnik and Shahan (2010) data, the average of the running reinforcement rates [i.e., r = (120 + 30)/2 = 75 rein/h in Phase 1] for pecking the target key would be used for calculating c in both components. Based on this common c value, the sTWR is applied to the reinforcement rates experienced for target-key pecking in the two components (120/h and 30/h) to determine the values of the target and alternative options for use in Eq. (11) applied separately to generate responding in each component. The resulting simulation is presented in the top-right panel of Fig. 20, and expressed as a proportion of Phase-1 response rates in the bottom-right panel. The simulation clearly suggests greater persistence of responding in the VI 30-s Phase-1 component than in the VI 120-s component. In addition, resurgence of target responding in Phase 3 is greater in the VI 30-s component than in the VI 120-s component. The simulation obviously overpredicts the difference in Phase-2 responding compared to the data. In addition, simulated Phase-2 responding appears to be more persistent in both components than suggested by the data. These differences between the data and the simulation in Phase 2 suggest that using the simple average running reinforcement rate to calculate c might not be entirely correct. Nevertheless, the simulation suggests that using a common c value for the common target response in both components of a multiple schedule could hold promise as a means for extending RaC to resurgence in multiple schedules.

Another way momentum-like effects have been demonstrated in resurgence experiments employing multiple schedules is with the use of added non-contingent reinforcement in one of the components in Phase 1 (see Podlesnik and Shahan, 2009a, 2010). The rates of response-dependent reinforcers are generally equal in the two components. The effects of such added non-contingent reinforcers in Phase 1 have been investigated because of the assertion of Behavioral Momentum Theory that persistence in Phase 2 and resurgence in Phase 3 are the result of the effects of the overall Pavlovian stimulus-reinforcer relations arranged by the component stimuli. Added non-contingent reinforcers would be expected to degrade the response-reinforcer relation for the target response in the component in which they are arranged, but at the same time improve the Pavlovian stimulus reinforcer relation (see Nevin et al., 1990). As a result, Phase-1 response rates should be lower in the component with added non-contingent reinforcers, but persistence in Phase 2 (as measured as a proportion of Phase-1 response rates) and resurgence should be greater in that component. Results from such experiments examining resurgence in multiple schedules have been consistent with these predictions of Behavioral Momentum Theory (Podlesnik and Shahan, 2009a; Podlesnik and Shahan, 2010).

To understand how RaC might be applied to such experiments, consider that the added non-contingent reinforcers in Phase 1 serve as an additional undefined option in the component in which they are presented. Thus, the response output function would become,

$$B_T=\frac{{kV}_T}{V_T+V_{NC}+V_{\mathit{Alt}}+1/A}$$ (18)

where all terms are as above, V_NC is the value of the undefined option, and A = a(V_T + V_NC + V_Alt). In Phase 1, V_Alt would be zero as usual, and V_NC would be zero in the component without the added non-contingent reinforcers. In the component with the added non-contingent reinforcers, V_NC would be calculated via the sTWR in the same way as V_T and V_Alt based on the rate of the non-contingent reinforcers (i.e., R_xNC). The c terms for each option would be calculated for each option in the usual fashion based on the running reinforcement rate. As in the multiple-schedule example above, the c term for the common target response in the two components would be based on the average running reinforcement rate for the target response across the components. In this case, however, it would not matter because the two components generally arrange the same rate of contingent reinforcement for the target response in such experiments. Given this approach, the presence of V_NC in only the component with added non-contingent reinforcers would be expected to decrease target response rates (i.e., B_T) as compared to the component without non-contingent reinforcers because V_T is the same in both components. In Phase 2, both V_T and V_NC would decrease as usual according the sTWR, and V_Alt would assume a value determined by the rate of alternative reinforcement. In Phase 3, resurgence in both components would be expected as V_Alt decreases. Using this approach, the left panels of Fig. 21 show a simulation generated by RaC following Phase-1 reinforcement on a VI 120-s schedule in one component and a VI 120-s + VT 30-s schedule in the other and using the same parameters as in Fig. 20. In Phase 2, all target and non-contingent reinforcers are removed and an alternative response is reinforced on a VI 30-s schedule. In Phase 3, the alternative response is placed on extinction. The top-left panel shows absolute response rates, and the bottom-left panel shows responding as a proportion of Phase 1 response rates. The model does, in fact, generate lower absolute response rates in the component with the added non-contingent reinforcers in Phase 1 (data points on the y-axis). In addition, responding in Phases 2 and 3 as a proportion of baseline is greater for the component with the non-contingent reinforcers. Although the model captures the basic pattern of data from such experiments, it predicts a difference in Phase 1 absolute response that a considerably larger than the modest differences usually obtained. Thus, it appears that something else is likely at work.

Fig. 21.

The top panels shows simulations of absolute rates of target responding in Phases 2 and 3 following Phase 1 reinforcement in a multiple schedule with equal rates of contingent reinforcement in both components and added non-contingent reinforcement in one component. The bottom panels are expressed in terms of proportion of Phase-1 (baseline) rates. Parameter values are the same as in Fig. 20 with the addition of the p parameter in the simulations in the right-hand panels. See text for details.

One reason absolute response rate may not be as low as predicted by Eq. (18) for the component with the added non-contingent reinforcers is that there is the possibility that some of the non-contingent reinforcers are misattributed to the explicitly defined response (i.e., adventitious reinforcement). In the discussion of DRA versus NCR alternative reinforcement above, we suggested how such misattribution might be incorporated into RaC in Phase 2 via Eq. (16). Following the same logic, misattribution of non-contingent reinforcers to the target response in a component of a multiple schedule in Phase 1 might be incorporated such that,

$$V_T=\sum _x{w}_x(R_{xT}+{pR}_{\mathit{xNc}})V_{NC}=\sum _x{w}_x(R_{\mathit{xNC}}(1-p))$$ (19)

where V_T is the value of the target option, R_xT are reinforcers contingent upon the target option, and R_xNC are non-contingent reinforcers. Similar to Eq. (16) above, p is a parameter representing the proportion of non-contingent reinforcers attributed to the target option. Thus, increases in p toward 1 would result in a greater proportion of the non-contingent reinforcers being attributed to the target response. The shared value of c for the common target response in the two multiple-schedule components used to obtain w_x via the sTWR is obtained as described above for multiple schedules and includes the proportion of non-contingent reinforcers allocated to the target response as determined by p. The V_T and V_NC values calculated by Eq. (19) would then be used in the response-output function (i.e., Eq. (18)). As a result, increases in V_NC would be expected to impact the rate of the target response in a manner that is dependent on p. When p is closer to 1, V_NC would be lower, and V_T and the target response rate would be higher because most of the non-contingent reinforcers are attributed to the target option. When p is closer to zero, V_NC would be higher, and V_T and the target response rate would be lower because most of the non-contingent reinforcers are attributed to the undefined option. The panels on the right of Fig. 21 show the same simulations as the panels on the left, but using Eq. (19) with p = 0.25. Note that absolute response rates remain lower in the component with the added non-contingent reinforcers, but the difference in response rates is smaller than for the simulation in the left panels without the p parameter. In addition, inclusion of the p parameter results in higher absolute response rates and higher response rates as a proportion of baseline across much of Phase 2 and in Phase 3 for the component with the added non-contingent reinforcers. These outcomes are generally consistent with the results of experiments that have examined such effects (Podlesnik and Shahan, 2010, 2009a). Thus, RaC appears to provide a reasonable simulation of the effects of added non-contingent reinforcers in one component of a multiple schedule during Phase 1 on the persistence of Phase-2 target responding and resurgence.

Thus, this section has demonstrated one approach to how RaC might be used to reconcile the dissimilar effects of differential Phase-1 reinforcement rates on resurgence in experiments employing single versus multiple schedules of reinforcement. The application of RaC above generated greater persistence of target responding in a multiple-schedule component associated with a higher rate of contingent reinforcement or a higher rate of contingent plus added non-contingent reinforcement. This later finding is a hallmark of Behavioral Momentum Theory, and RaC suggests that it might be accounted for without invoking the effects of the Pavlovian stimulus-reinforcer relation on response strength employed by Behavioral Momentum Theory. Instead, RaC suggests that such effects might be due to shifts in the allocation of target responding that are driven by changes in the value of a target option across time (as a result of scaled temporal weighting), potential misattribution of some non-contingent reinforcers to the target option (cf. Burgess and Wearden, 1986), and to the invigorating/arousing effects of the current values of the options in the components (cf. Killeen, 2000; Nevin, 1994, 2003). Given that the basic processes suggested by RaC would apply similarly to single and multiple schedule performances outside of experiments on resurgence, those processes might also provide a foundation upon which to construct a viable choice-based theoretical alternative to Behavioral Momentum Theory in general (cf. Baum, 2002; see Nevin et al., 1990, for discussion of a choice-based approach).

8. Summary and conclusion

The theory of resurgence presented here suggests that resurgence can be understood to result from the same processes generally thought to govern choice. In its most general form, the theory suggests that resurgence results from changes in the allocation of behavior driven by changes in the values of the target and alternative options across time. Specifically, resurgence occurs when there is an increase in the relative value of an historically effective target option as a result of a subsequent devaluation of a more recently effective alternative option. We have shown how this general approach can be used to generate a more specific quantitative model of how extinction of the target and alternative responses might produce such changes in relative value across time. The example model does a good job simulating the effects of differential rates of target and alternative reinforcement in experiments employing single schedules of reinforcement under a variety of conditions. The model provides an account of these and other effects where Behavioral Momentum Theory failed, and it does so with the same number or fewer free parameters. The overall theory provides a framework within which other parameters of reinforcement (e.g., magnitude, quality) might be incorporated into more specific quantitative formulations. Further, the theory suggests how other means to suppress target or alternative behavior (e.g., satiation, punishment, DRO) might be formalized and how the effects of other factors (e.g., NCR versus DRA, serial DRA, multiple schedules) might be usefully approached. Thus, we conclude the theory may hold promise as a general account of resurgence and for incorporating the phenomenon into the broader theoretical framework provided by theories of choice.