Membrane Mechanics of Primary Afferent Neurons in the Dorsal Root Ganglia of Rats

Abstract

Membrane mechanics is an important biological factor regulating many cellular functions including cell motility, intercellular and intracellular signaling, gene expression, and membrane ion channel activity. Primary afferent neurons transduce sensory information about temperature, touch, and pain. These sensory functions may be profoundly affected by the states of primary afferent neuron mechanics. However, membrane mechanics of primary afferent neurons is largely unknown. In this study, we established the optical trapping technique for determining membrane mechanics of cultured primary afferent neurons of the dorsal root ganglia (DRG). We further determined the roles of cytoskeleton and membrane lipids in DRG neuron mechanics. We found that DRG neurons had a plasma membrane tension of ∼54 pN/μm, and the tension was significantly decreased to ∼29 pN/μm by cytochalasin D treatment to disrupt actin cytoskeleton and increased to ∼79 pN/μm by methyl-β-cyclodextrin treatment to sequester membrane cholesterol. DRG neuron membrane stiffness was not significantly affected by the cytoskeleton disruption but was significantly increased after cholesterol sequestration. Our findings elucidate membrane mechanical properties of primary afferent neurons, which provide, to our knowledge, a new perspective on their sensory functions.

Introduction

Plasma membrane tension in eukaryotic cells serves as a master regulator of biological events such as endocytosis, exocytosis, cell motility and spreading, membrane mechanotransduction, and many other cell functions (1, 2, 3). As a principal factor of cell mechanics, plasma membrane tension profoundly impacts cell functions by multiple mechanisms such as affecting membrane ion channel activity, intracellular signaling, and gene expression (1, 2, 3). Dorsal root ganglion (DRG) neurons are sensory cells that give rise to primary afferent fibers that innervate different tissues including the skin, muscle, joints, and internal organs in mammals. Primary afferent fibers sense sensory stimuli such as mechanical forces, temperatures, chemical messengers, and pain; these sensory functions are essential for life. Sensory stimuli are transduced by different receptors and ion channels that are mainly located on the plasma membranes of the primary afferent fibers (4). For example, mechanical stimuli are transduced by mechanically activated channels including Piezo2 (5) and tentonin3 (6) in primary afferent neurons. The activity of ion channels can be impacted or directly gated by plasma membrane tension in primary afferent neurons. However, little is currently known about the plasma membrane tension of primary afferent neurons under physiological or pathological conditions.

Previous studies on cell plasma membrane tension and its functional impacts were mainly performed on nonneuronal cells. Plasma membrane tension displays a broad range of magnitudes among different cell types. For example, epithelial cells and melanoma cells have plasma membrane tensions as low as ∼10 and ∼20 pN/μm, respectively. In contrast, Caenorhabditis elegans sperm cells and keratocytes have plasma membrane tensions as high as ∼150 and ∼280 pN/μm, respectively (1). For neuronal cells, studies have shown that membrane tension is ∼16 pN/μm in cortical neurons (7) and ∼40 pN/μm in Molluscan neurons from Lymnaea stagnalis (8). Importantly, plasma membrane tensions can be significantly changed in the same cells under different conditions. For example, plasma membrane tension was significantly reduced when macrophage cells were activated, which facilitates the phagocytic functions of these cells (7). Plasma membrane tension of a cell is attributed to two main factors—the in-plane membrane tension (T_m) and the membrane-cytoskeleton adhesion (γ) (1, 2, 3). The in-plane membrane tension is the tension of the lipid bilayer, and it is mainly due to hydrostatic pressure; the membrane-cytoskeleton adhesion is mainly due to the linkage of phospholipid-binding protein to cytoskeleton (2). These two factors are dynamically regulated, which largely account for the differences of plasma membrane tension in cells.

Several experimental approaches, including the micropipette aspiration method, atomic force microscopy, and the optical trapping technique have been used to study mechanical properties of cell membranes (1, 2). The optical trapping technique uses laser tweezers to trap a bead and then uses the bead to pull a membrane tether from a cell. By measuring the force of membrane tether, plasma membrane tension and membrane stiffness can be determined. The optical trapping technique has several advantages compared with other methods. Pulling membrane tethers with optically trapped beads is a highly sensitive method to measure membrane tension (2). The optical trapping technique has a high resolution in the femtonewton-to-piconewton range and can continuously monitor the instantaneous tether force, which is particularly important in studying membrane mechanical properties dynamically (9). The optical trapping technique for membrane tension measurements can be applied to morphologically irregular cells and cell membrane compartments such as growth cones (10). In this study, we established the optical trapping technique for determining mechanical properties of DRG neurons grown in culture, and we further investigated contributions of membrane-cytoskeleton adhesion and membrane lipid bilayer properties to the membrane tension of these sensory neurons.

Materials and Methods

Cell preparation

Female Sprague Dawley rats aged 5–9 weeks were used. Animal care and use conformed to National Institutes of Health (NIH, Bethesda, MD) guidelines for care and use of experimental animals. Experimental protocols were approved by the Institutional Animal Care and Use Committee of the University of Alabama at Birmingham.

DRG neuron cultures were prepared as described in Jia et al. (11). In brief, rats were deeply anesthetized with isoflurane (Henry Schein, New York, NY) and sacrificed by decapitation. DRGs from cervical to lumbar sections were rapidly dissected out bilaterally in Leibovitz-15 medium (Mediatech, Manassas, VA) and incubated for 1 h at 37°C in minimum essential medium for suspension culture (S-MEM; Invitrogen, Grand Island, NY) with 0.2% collagenase and 0.5% dispase and then triturated to dissociate neurons. The dissociated DRG neurons were then plated on glass coverslips (Size No. 1 with thickness of 130–170 μm) precoated with poly-D-lysine (12.5 μg/mL in distilled H₂O) and laminin (20 μg/mL in Hank’s Buffered Salt Solution (HBSS); BD Biosciences, San Jose, CA), and maintained in MEM culture medium (Invitrogen, Carlsbad, CA) that also contained 5% heat-inactivated horse serum (JRH Biosciences, Lenexa, KS), uridine/5-fluoro-2′-deoxyuridine (10 μM), 8 mg/mL glucose, and 1% vitamin solution (Invitrogen). The cultures were maintained in an incubator at 37°C with a humidified atmosphere of 95% air and 5% CO₂. Cells were used between 2 and 5 days after plating. To perform optical trapping experiments, a coverslip with cultured DRG neurons was placed in a recording chamber and then mounted on the piezo-controlled stage of the optical trapping system. Cells were perfused at the rate of 1 mL/min with a Krebs solution that contained 145 mM NaCl, 5 mM KCl, 2 mM MgCl₂, 2 mM CaCl₂, 10 mM glucose, 10 mM HEPES, at pH 7.3 and an osmolarity of 320 mOsm. The Krebs solution was filtered through a 0.2 μm filter before being used. The perfusion of the Krebs solution was stopped 5 min before applying laser tweezers for optical trapping experiments. All experiments were performed at the room temperature of 24°C. In some experiments cells were incubated with 10 μM cytochalasin D (CD), 10 μM latrunculin, 3 or 10 mM methyl-β-cyclodextrin (MβCD) for 30 min before optical trapping experiments.

Optical trapping system

We used the OTM211 Optical Trapping System, which consisted of the OTM200 Tweezer System (Thorlabs, Newton, NJ) integrated with a model No. IX83 Inverted Microscope (Olympus, Melville, NY). The trapping source for the optical tweezer is a power- and wavelength-stabilized 1064-nm infrared (IR) laser with the maximal power output of 5 W, which is split into two independently steerable trapping beams with up to 2.5 W optical power per beam. In our experiment, we only used one trapping beam, at 2.5 W, for optical trapping. The optical trapping system also includes a force measurement module capable of making measurements in the femtonewton-to-piconewton range. The force measurement module equips the quadrant photodiode detectors that monitor the relative displacement of the trapped bead from the laser beam axis. The IX83 Inverted Microscope (Olympus) that is integrated into our optical trapping system includes a 1.3 NA trapping objective (100×, oil immersion), a differential interference contrast and IR condenser, a high-resolution computerized XYZ piezo stage, and a high-resolution (1600 × 1200) charge-coupled device camera (Basler, Ahrensburg, Germany) for bright field and IR images. In addition, an epifluorescence imaging system with a highly sensitive charge-coupled device camera was also integrated into our optical trapping system. A graphical user interface (GUI) software was used to run the optical trapping system for calibrations and general trapping experiments. The GUI controls the camera display, laser power, stage position, trap focus, data sampling, and other functionalities. The optical trapping system was placed on an antivibration table (AMETEK, Berwyn, PA) to achieve a mechanical stability, and potential electrical noise was shielded by a Faraday cage.

Preparation of beads and calibration of optical traps

Microparticles (beads) made by silicon dioxide (Cat. No. 44054; Sigma-Aldrich, St. Louis, MO) at the diameter of 5 μm were used. The beads were diluted with Krebs solution and used at a final concentration of 5%. The bead solution was well mixed with a vortex mixer for 20 s. A glass electrode with a tip diameter of 7–10 μm was filled with the bead solution (∼5 μL). The electrode was then attached to an electrode holder on the stage of the optical trapping system. A small positive pressure was applied to the electrode to eject a small amount of beads into the optical trapping focal position at the center of the field until a single bead was trapped optically by the laser tweezers.

Calibration of the optical trap was performed for each bead before using it for pulling a membrane tether. The calibration generates parameters that were used to convert the bead position shift to tether forces. The position of the bead in the trap was tracked using the quadrant detectors that can track bead position shift at a nanometer-scale. The calibration of the optical trap was achieved by viscous drag of the bead through the bath solution in the microscope focal plane. The viscous drag force was generated by oscillatory motion of the bead by the piezo-driven stage at the frequency of 64 Hz, amplitude of 0.15 μm, and duration of 1 s for each test; a total of five tests were performed. Power spectrum for the viscous drag under the above oscillatory motion was then generated and Lorentzian fitting was applied to the power spectrum to yield detector response (β, m/V) and trap stiffness (κ, N/m). The calibrated parameter values of β and κ for each bead were used for calculating the tether force of each experiment.

For both calibration and optical trapping experiments (see below), beads were trapped at the height of 5–8 μm above the coverslip surface; at these heights, consistent calibration parameters were obtained. The height <5 μm displayed a high value of trapping stiffness due to a viscous coupling of the bead to the coverslip surface (10).

Optical trapping experiments

All experiments were performed with beads being trapped at 5–8 μm above the coverslip surface to minimize viscous coupling between the beads and the coverslip surface. To form and pull a membrane tether, a bead was trapped at the center of the optical field. The optical trapping center containing the trapped bead was kept at the same position throughout the experiments. To make the trapped bead contact DRG membranes, we moved the DRG neuron toward the bead. This was achieved by forwardly moving the microscope stage. Once the cell membrane touched a bead, the forward movement was stopped for 5 s, to allow membranes to adhere to the bead. Then the stage was moved backward, to separate the cell from the bead. Both forward and backward movement of the stage were at a constant velocity of 1 μm/s for 10 s (10 μm) using the computerized piezo controller. If a tether was successfully pulled out, the cell was kept at the same position to allow the tether to be held at the stationary phase for 5 s. The positions of the bead in the trap during the tether formation, extension, and stationary phase were monitored by the quadrant photodiode detector and measured using GUI software at a sampling rate of 10 KHz. Shift in bead position was measured as the value of voltage, which was converted to the force of the tether based on the trap calibration parameters of each bead.

Measurement of radius of membrane tether: Fluorescent densitometry

Membrane tether radius was too small to be measured directly under bright field with 100× objective. We measured membrane tether radius by using a fluorescent densitometry method (12) with modification. In brief, DRG neurons were incubated with the fluorescent dye DiI (2.5 μg/mL) for 10 min at 37°C to label cells. After the incubation, DiI-containing solution was washed off by Krebs solution. Optical trapping experiments were performed in the same manner as that for nonlabeled cells described above. A fluorescent image of the membrane tether was taken at the focal plane of the tether. A fluorescent image of an axon was then taken at the axon focal plane, which was usually ∼4 μm lower than the membrane tether’s optical trapping focal plane. A bright field image of the same axon was also acquired. Because the radius of the proximal segment of an axon could be measured directly with high accuracy under bright field with 100× objective, the axonal segment was used as a reference in the fluorescent densitometry method. With background fluorescence subtracted, the fluorescent intensity of the membrane tether and of the axon for a unit length of 100 pixels was integrated using an image processing software (ImageJ; National Institutes of Health, Bethesda, MD).The integrated fluorescent intensity per unit length (Ĩ) of the tubular membranes of tether or axon is Ĩ = 2I(1 + 3β/4) × 2πR × dl (12), where I is the fluorescent illumination, β is a constant, R is the radius of a membrane tether or an axon, and dl is the unit length of the membrane tether or the axon. Dividing the above equation for membrane tether (Ĩ_Tether = 2I(1 + 3β/4) × 2πR_Tether × dl) by the equation for axon (Ĩ_axon = 2I(1 + 3β/4) × 2πR_axon × dl) yields R_Tether = R_axon(Ĩ_Tether/Ĩ_axon).

Scanning electron microscopy

Optical trapping experiments were performed in the same manner as described above. After extracting the tether from the cell, the bead was moved toward the cover glass to allow adhesion for 30 s. Cells in the dish were then fixed in 2.5% glutaraldehyde in 0.1 M cacodylate buffer (pH 7.4) for 90 min at room temperature. Cells were rinsed with 0.1 M cacodylate buffer and postfixed with 0.1% OsO₄ in 0.1 M cacodylate buffer for 60 min at room temperature. Cells were washed with double distilled water three times for 5 min and then dehydrated using an ethanol series (30, 50, 70, 90, and 100%). Ethanol displacement was accomplished with three changes of hexamethyldisilazane and residual hexamethyldisilazane was evaporated in a fume hood before mounting cover glass on specimen stubs for the sputter coating using a Denton Sputter Coater (Denton Vacuum, Moorestown, NJ). The observation of tether was carried out using a Quanta 650 Scanning Electron Microscope (FEI, Hillsboro, OR).

Determination of DRG neuron plasma membrane tensions and membrane bending stiffness

Plasma membrane tension (T) was calculated based on the equation T = F₀/4πR_t (2, 8), and the membrane bending stiffness (B, bending modulus) was calculated based on the equation B = F₀ × R_t/2π (2, 8); here, F₀ is stationary tether force, and R_t is membrane tether radius.

Actin filament staining with phalloidin

Cultured DRG neurons on glass coverslips were fixed in 4% paraformaldehyde in PBS for 20 min. Cells were then washed with PBS three times each for 5 min. Cells were permeabilized with 0.1% Triton X-100 in PBS for 7 min, and then washed with PBS three times each for 5 min. They were incubated with CytoPainter Phalloidin-iFluor 488 (1:1000; Abcam, Cambridge, UK) in 1% BSA-PBS for 60 min. After washing with PBS three times each for 5 min, cells were mounted with fluorescent mounting medium.

Data analysis

The bead position shifts were recorded by GUI software and converted to the force of the tether based on the trap calibration parameters using Microsoft Office Excel (Microsoft, Redmond, WA). Data represent mean ± SE, ^∗p < 0.05; ^∗∗p < 0.01; ^∗∗∗p < 0.001 (Student’s t-test).

Results

Pulling membrane tethers from DRG neurons by the optical trapping technique

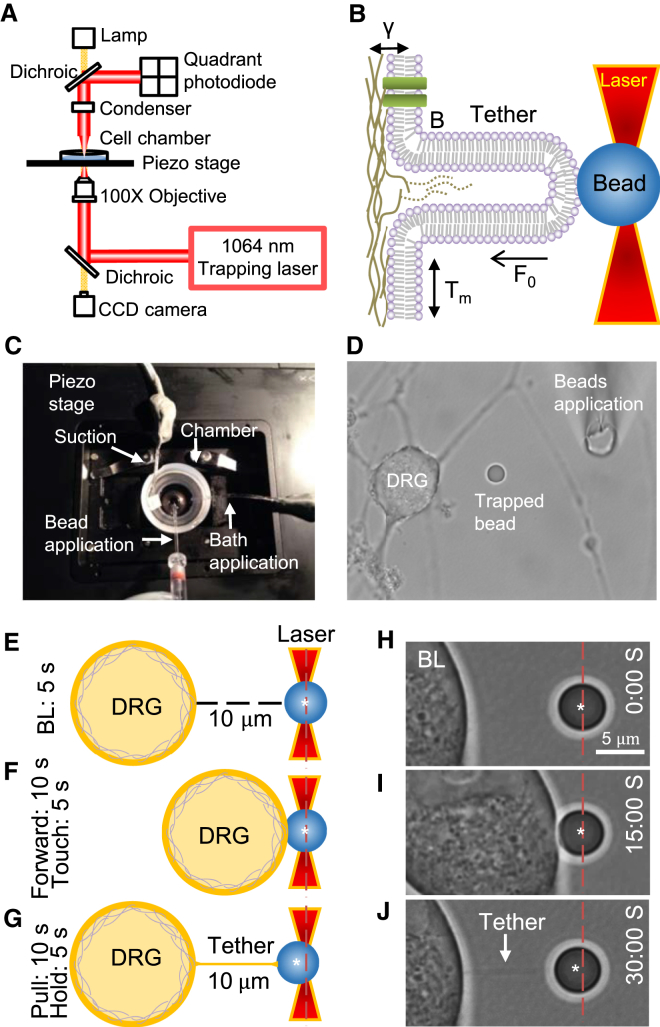
The optical trapping technique uses laser tweezers (Fig. 1 A) to trap a bead in laser beam (Fig. 1 B). The trapped bead is then used as a handle to pull a membrane tether, a nanometer plasma membrane tube (Fig. 1 B). By measuring the forces that are needed to hold the membrane tether at the stationary phase (F₀), the parameters of membrane mechanics including plasma membrane tension (T) and membrane bending stiffness (B) can be determined mathematically. The plasma membrane tension is the sum of in-plane bilayer membrane tension (T_m) and the tension due to membrane and cytoskeleton adhesion (γ). Fig. 1 C shows our experimental arrangement on the piezo-controlled stage for pulling the membrane tether from DRG neurons. In each experiment, a bead was trapped optically by laser tweezers at the center of the field (Fig. 1 D); a DRG neuron was then moved toward the bead and after a brief contact with the bead (Fig. 1, E, F, H, and I), the neuron was then moved backward away from the bead (Fig. 1, G and J). This movement was achieved by the piezo-controlled stage. A membrane tether could be formed and extended during the backward movement of the cell (Fig. 1, G and J). The optical shadow of the tether, which was very thin, could be seen under the 100× objective (Fig. 1 J) and the tether pulled the bead slightly off the center of the optical trap (Fig. 1, G and J).

Figure 1.

Setup and procedures of the optical trapping technique for measuring membrane mechanics of dorsal root ganglion neurons. (A) Main components of optical trapping setup. The optical trapping technique uses infrared laser to trap a bead whose position relative to the center of the laser beam is detected by the position-sensing device quadrant photodiode. (B) The bead in the optical trap is used as a handle to hold cell membranes and to allow pulling a membrane tether. Membrane tether exerts a force to shift bead position in the laser trap. By measuring the position shift, tether force (F₀) can be determined and parameters about membrane mechanics can then be derived mathematically. These parameters include in-plane membrane tension (T_m), tension due to the plasma membrane-cytoskeletons adhesion (γ), and membrane bending stiffness (B). The measured total plasma membrane tension T = T_m + γ = F₀/4πR_t and the membrane bending stiffness B = F₀ × R_t/2π, where R_t is the radius of membrane tether. (C) Stage arrangement for the application of the optical trapping technique to dorsal root ganglion neurons in culture. The stage is controlled be a piezo device that precisely moves cells on the stage in x-y-z directions. (D) Image shows a cultured DRG neuron and an optically trapped bead in a recording chamber viewed under a 100× objective. (E–G) Schematic diagrams illustrate optical trapping procedures for pulling a membrane tether from a DRG neuron by a laser-trapped bead. The cell is positioned 10 μm away from the bead and kept in this position for 5 s (BL, baseline; E). The cell is then moved toward the bead at the speed of 1 μm/s until it touches the bead (10 s), and the cell is kept at this position for 5 s (F). The cell is then pulled away from the bead, returned to original position (10 s), and held in this stationary position for 5 s (G). During these procedures, the bead position in the trap is recorded continuously by the quadrant photodiode. (H–J) An example shows an actual optical trapping experiment on a cultured DRG neuron. O’clock time is shown in each procedure from (H) to (J). A membrane tether was pulled out from the neuron (arrow indicated in J). Each vertical red line in (E)–(J) is the center of the laser trap and each white asterisk indicates the center of the bead.

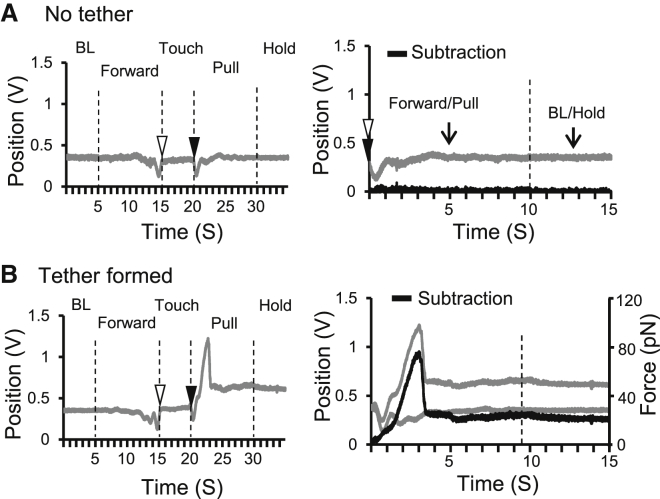
The bead position shift was detected by the optical position sensor quadrant photodiode. However, the movement of a DRG neuron toward or away from an optically trapped bead generated optical artifacts due to the interference of DRG neuron’s optical shadow with the laser beam. These optical artifacts showed two symmetric downward deflections as detected by the quadrant photodiode (Fig. 2 A, left). These artifacts could be removed by a subtraction method (Fig. 2 A, right) to allow precisely determining the actual bead positions in the optical trap. Fig. 2 B (left) shows an experiment in which a membrane tether was successfully pulled out, extended, and held at the stationary phase. The shift of the bead position due to the membrane tether force was corrected by applying the subtraction method (Fig. 2 B, right).

Figure 2.

Determination of bead positions in the optical trap during pulling DRG neuron membrane tethers. (A) Optical artifacts and their cancelation for an optical trapping experiment. Optical artifacts are best demonstrated in the attempt that does not pull out a membrane tether. (Left) A trace shows optical artifacts (downward deflections) caused by DRG cell shadow when the cell is moved forward and backward near the optically trapped bead. The artifacts due to the forward and backward movement are symmetric. (Right) Artifact cancelation is made by subtracting the mirror points of the trace with the alignment at the two points indicated by the open and solid arrowheads. The subtracted values (black trace) yield a straight line at the position of 0 V position. Note that the bead position is registered in the values of voltages by the quadrant photodiode. (B) (Left) A trace shows upward deflection caused by the formation, extension, and holding of a DRG membrane tether. Note that the optical artifacts of the two downward deflections are present before pulling out the membrane tether. (Right) Mirror subtraction of forward trace (gray, upper) from pulling trace (gray, lower) yields the actual bead position (black) during the tether formation, extension, and holding.

Determination of the forces of DRG neuron membrane tethers

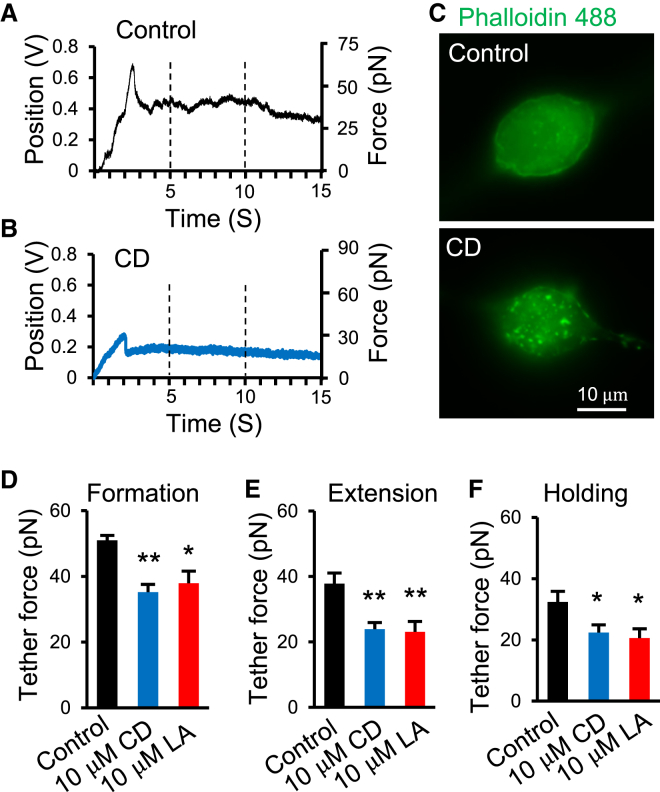
We applied the optical trapping technique to pull membrane tethers from DRG neurons under both control condition and after the treatment with 10 μM CD or 10 μM latrunculin (LA) to disrupt actin filaments. Fig. 3, A and B are the sample traces showing bead positions in the optical trap during pulling membrane tethers from a control DRG neuron (Fig. 3 A) and a CD-treated DRG neuron (Fig. 3 B). The forces of membrane tether corresponding to bead position shifts are also indicated in right axis of Fig. 3, A and B. In both control and CD-treated groups, a larger force was needed for membrane tether formation, which is followed by a rapid reduction of the force during tether extension and holding at the stationary phase. CD treatment resulted in the disruption of actin filaments in DRG neurons, as indicated by the staining of actin filaments with phalloidin; the staining with phalloidin displayed even distribution in control (Fig. 3 C, upper panel) but had a punctate appearance after the treatment of DRG neurons with 10 μM CD for 30 min (Fig. 3 C, lower panel). We calculated trapping forces needed for tether formation (Fig. 3 D), extension (Fig. 3 E), and holding at the stationary phase (Fig. 3 F) in control group, CD-treated, and LA-treated DRG neurons. The tether formation forces were 50.3 ± 1.8 pN (n = 16) in control and reduced to 35.2 ± 2.2 pN (n = 8, p < 0.01) after CD treatment and 37.9 ± 3.7 pN (n = 12, p < 0.05) after LA treatment; the tether extension forces were 37.8 ± 3.2 pN (n = 12) in control and reduced to 23.9 ± 2 pN (n = 12, p < 0.01) after CD treatment and 23.1 ± 3.1 pN (n = 12, p < 0.01) after LA treatment; the tether holding forces at the stationary phase (F₀) were 32.4 ± 3.4 pN (n = 12) in control and reduced to 22.4 ± 2.5 pN (n = 8, p < 0.05) after CD treatment and 20.6 ± 3.0 pA (n = 12, p < 0.05) after LA treatment.

Figure 3.

Forces of tether formation, extension, and holding in control and cells treated with CD and latrunculin to disrupt actin filaments. (A and B) Sample traces show bead positions in the optical trap during membrane tether formation (the peak), extension (after the peak to 10 s), and holding (10 to 15 s) for a control DRG neuron (A) and a DRG neuron after 30 min treatment with 10 μM CD (B). The axis on the right side of (A) or (B) shows the corresponding tether forces converted from the bead position shift. (C) Sample images show actin staining by phalloidin in DRG neurons in control (upper panel) and after 30 min treatment with 10 μM CD (lower panel). (D–F) Summary data of the tether forces during membrane tether formation (D, the values at the peaks), extension (E, the values between 5 to 10 s), and holding (F, the values between 10 to 15 s). In (D)–(F), black bars are the control group, blue bars are cells after the treatment with 10 μM CD, and red bars are cells after the treatment with 10 μM latrunculin. Data represent mean ± SE, ^∗p < 0.05; ^∗∗p < 0.01.

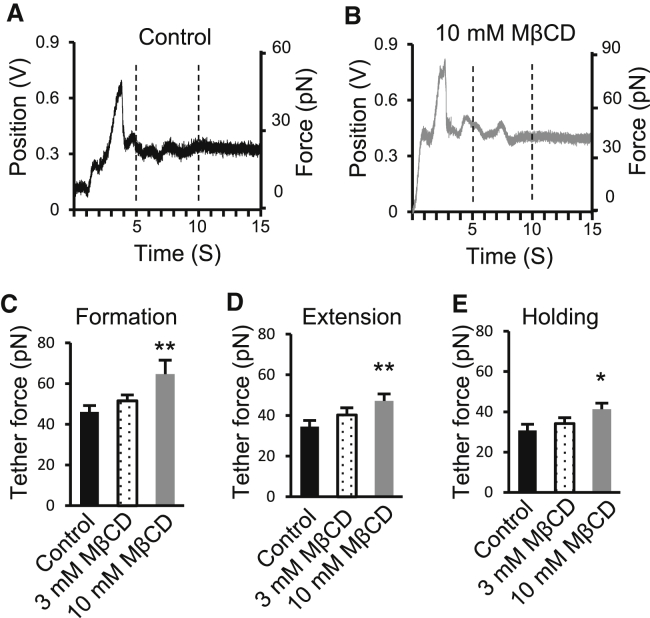
We determined the effects of MβCD, a reagent commonly used to sequester membrane cholesterol, on the forces of membrane tethers. The pulling of membrane tether from DRG neurons treated with 3 mM MβCD showed slight but not significant increases in calculated trapping force (n = 6); significantly larger increases in trapping force were observed in DRG neurons treated with 10 mM MβCD (Fig. 4, A–E). The tether formation forces were 46.1 ± 3 pN (n = 7) in control and increased to 64.7 ± 4.8 pN (n = 7, p < 0.01) after 10 mM MβCD treatment (Fig. 4 C); the tether extension forces were 34.5 ± 3 pN (n = 7) in control and increased to 47.1 ± 3.5 pN (n = 7, p < 0.01) after 10 mM MβCD treatment (Fig. 4 D); the tether holding forces were 30.8 ± 3 pN (n = 7) in control and increased to 41.3 ± 3 pN (n = 7, p < 0.05) after 10 mM MβCD treatment (Fig. 4 E).

Figure 4.

Forces of tether formation, extension, and holding in control and cells treated with methyl-β-cyclodextrin to sequester membrane cholesterol. (A and B) Sample traces show bead positions in the optical trap during membrane tether formation (arrow indicated), extension, and holding for a control DRG neuron (A) and a DRG neuron after 30 min treatment with 10 mM MβCD (B). The axis on the right side of (A) or (B) shows the corresponding tether forces converted from the bead position shift. (C–E) Summary data of the tether forces during membrane tether formation (C), extension (D), and holding (E). In (C)–(E), black bars are the control group, dotted bars are cells after treatment with 3 mM MβCD, and shaded bars are cells after the treatment with 10 mM MβCD. Data represent mean ± SE, ^∗p < 0.05; ^∗∗p < 0.01.

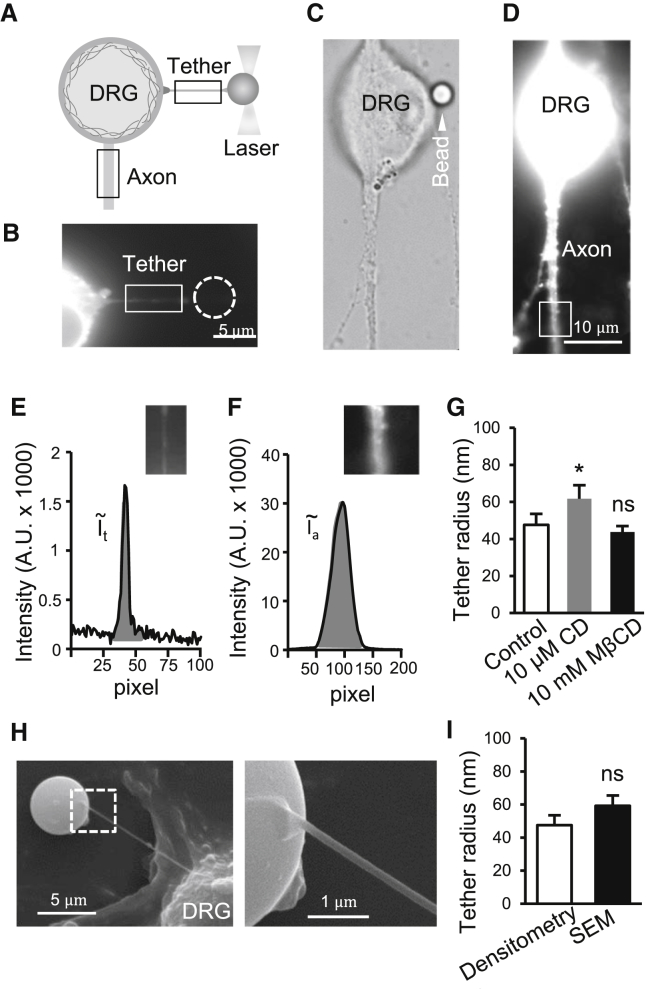
Determination of the radii of membrane tethers pulled from DRG neurons

We determined the radius of the membrane tether because it is an essential parameter for calculating plasma membrane tension. The membrane tethers were too thin to be directly measured with high accuracy under the bright field with a 100× objective. In this study, we used fluorescent densitometry to determine the radii of membrane tethers. DRG neurons were labeled with DiI, a membrane binding fluorescent dye. After pulling out a membrane tether from a DiI-labeled DRG neuron (Fig. 5, A and B), a fluorescent image was taken for the membrane tether (Fig. 5 B) and another fluorescent image was taken for the proximal segment of an axon of the same DRG neuron (Fig. 5, C and D). The axonal segment of the same cell was used as a reference for determining the radius of each membrane tether. We measured integrated fluorescence per unit length along the tether (Fig. 5 E) and the proximal segment of DRG neuron axon (Fig. 5 F). Derived from these measures, the radii of membrane tethers were determined to be 47 ± 5 nm (n = 8) in controls and were significantly increased to 61 ± 7 nm (n = 9, p < 0.05) after CD treatment (Fig. 5 G). We also determined the effects of MβCD on membrane tether radii. Membrane tether radii in DRG neurons treated with MβCD were 43.7 ± 3 nm (n = 7), and were not significantly different from the control group (Fig. 5 G).

Figure 5.

Measurement of the radii of membrane tethers by fluorescent densitometry. (A) Schematic diagram illustrates procedures of measuring the radii of membrane tethers by fluorescent densitometry. DRG neurons are prelabeled with the fluorescent dye DiI. Fluorescent intensities in a segment of tether (boxed region) and a segment of axon (boxed region) of a neuron are measured and used for fluorescent densitometry. (B) Image shows a membrane tether pulled out from a DRG neuron prelabeled with DiI. (C) Bright field image of the DiI-labeled DRG neuron and the proximal segment of its axon. The cell is the same one shown in (B) before the tether was pulled out. The arrowhead indicates the bead used for pulling the membrane tether as in (B) before the tether was pulled out.. (D) Same as (C), except the fluorescent image of the cell was taken. (E) Graph shows DiI fluorescent intensity of the unitary length (100 pixels) across the membrane tether in the boxed region. The area under the curve (shaded) is the integrated fluorescent intensity of the membrane tether segment (ĩ_t). (F) Graph shows DiI fluorescent intensity of the unitary length (100 pixels) across the axon in the boxed region. The area under the curve (shaded) is the integrated fluorescent intensity of the axon segment tether (ĩ_a). (G) Tether radii determined by the fluorescent densitometry for DRG neurons under control condition (open bar), after the treatment of cells with 10 μM CD to disrupt actin filaments (shaded bar), or with 10 mM MβCD to sequester membrane cholesterol (solid bar). (H) SEM images of a membrane tether pulled with a bead from a DRG neuron in normal bath solution. (Left panel) Image at 10,000× showing the membrane tether, the bead, and a small portion of the DRG neuron. (Right panel) Image at 40,000× showing a portion of the bead and the tether. (I) Summary data comparing membrane tether radii measured by the fluorescent densitometry method (open bar) and the SEM method (solid bar). Data represent mean ± SE, ^∗p < 0.05; ns, not significantly different.

We used scanning electron microscopy (SEM) to validate our fluorescent densitometry method used for measuring tether radii in this study. SEM images in Fig. 5 H show a tether pulled from a DRG neuron in normal bath solution. The radii of tethers measured by the SEM method were 59 ± 6 nm (n = 5, Fig. 5 I), not significantly different from those measured in normal bath solution by the fluorescent densitometry method (48 ± 6 nm, n = 6).

Determination of DRG neuron plasma membrane tension and membrane bending stiffness

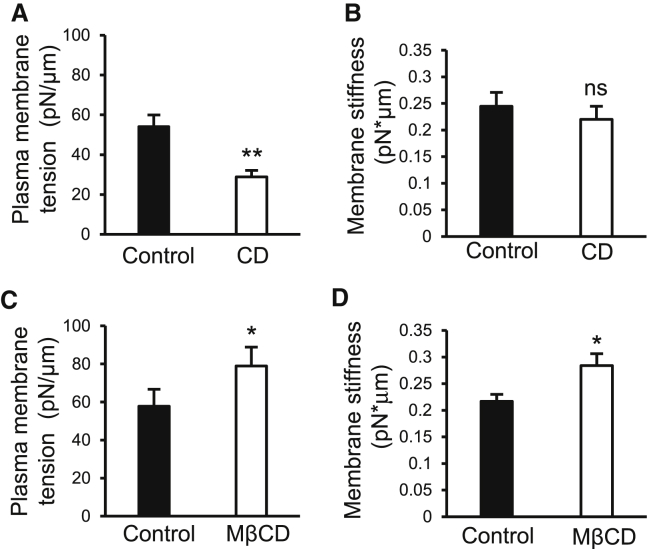
The measurements of the radii and the membrane tether holding forces at the stationary phase (F₀) allowed us to determine membrane mechanics including plasma membrane tension (T) and membrane bending stiffness (B). The plasma membrane tension was 54 ± 5 pN/μm in the control group, and was significantly decreased by nearly half to 29 ± 3 pN/μm after the treatment of DRG neurons with 10 μM CD for 30 min to disrupt DRG neuron cytoskeleton (Fig. 6 A). The membrane bending stiffness was measured to be 0.244 ± 0.02 10 pN^∗μm under the control condition and was not significantly changed after the treatment with CD (Fig. 6 B). The treatment of DRG neurons with 10 mM MβCD for 30 min to sequester DRG membrane cholesterol significantly increased plasma membrane tension to 79 ± 10 pN/μm (n = 8, p < 0.05; Fig. 6 C) in comparison with the control group. The treatment of DRG neurons with MβCD also resulted in a significant increase in membrane bending stiffness to 0.287 ± 0.02 pN^∗μm (n = 8, p < 0.05; Fig. 6 D).

Figure 6.

Plasma membrane tension and stiffness of DRG neurons in the control group and after the disruption of acting filaments with CD or sequestration of membrane cholesterol with MβCD. (A) Plasma membrane tension of DRG neurons under the control condition and after the treatment of cells with 10 μM CD for 30 min. (B) Membrane bending stiffness of DRG neurons under the control condition (solid bar) and after the treatment of cells with 10 μM CD for 30 min (open bar). (C) Plasma membrane tension of DRG neurons under the control condition (solid bar) and after the treatment with 10 mM MβCD for 30 min (open bar). (D) Membrane bending stiffness of DRG neurons under the control condition (solid bar) and after the treatment with 10 mM MβCD (open bar). Data represent mean ± SE, ^∗p < 0.05; ^∗∗p < 0.01; ns, not significantly different.

Discussion

In this study we have established an optical trapping technique to study membrane mechanics of cultured DRG neurons and determined the contributions of membrane-actin adhesion and membrane cholesterol to DRG neuron membrane mechanics. We show that DRG neuron plasma membrane tensions were ∼50 pN/μm. This indicates that DRG neurons have a low plasma membrane tension in comparison with cells such as keratocytes (12), outer hair cells (13), and C. elegans sperm cells (14). However, DRG neuron plasma membrane tensions were relatively higher than very soft cells such as melanoma cells (15) and cultured cortical neurons (7). We show that plasma membrane tension, but not membrane stiffness, in DRG neurons can be significantly reduced after the disruption of actin filaments in DRG neurons by treating these cells with CD. This suggests that membrane-cytoskeleton interaction significantly contributes to DRG neuron plasma membrane tensions. In contrast, the sequestration of cholesterol in DRG neuron membranes after treating the cells with MβCD significantly increases DRG neuron plasma membrane tensions as well as membrane stiffness. To our knowledge, this study is the first to use the optical trapping technique to characterize DRG neuron membrane mechanics.

While membrane mechanics of a cell can be studied by several different methods, tether pulling with optically trapped beads is the most sensitive technique to study membrane mechanics (2). It is generally believed that the thin cylindrical membrane structure of a membrane tether pulled from a cell does not contain any cytoskeleton (16, 17, 18), and the forces for pulling a tether results in the separation between plasma membranes and their underlying linkages to cytoskeleton (16). In this study on DRG neuron mechanics, we have found that the forces needed for tether formation, extension, and tether holding at the stationary phase for DRG neurons are very different. A significantly stronger force is needed for tether formation, which is followed by a rapid reduction of the force for tether extension and tether holding. These differences in the tether forces at different stages are also observed in previous studies of pulling membrane tethers from other cells, which indicates a larger energy barrier for initial tether formation (7, 12, 19). The tether force at the stationary phase (F₀), i.e., the force of holding a tether without further extension, is known to be the sum of the forces to overcome plasma membrane bending and separate plasma membranes from cytoskeleton (2). Measuring the tether force at the stationary phase is essential for determining membrane mechanics including the plasma membrane tension and the membrane bending stiffness.

Determination of plasma membrane tension and membrane bending stiffness by the optical trapping technique requires precisely measuring tether radius. Most previous studies measured tether radius by using SEM, a time-consuming process performed off the stage of an optical trapping system (18, 19). In this study, we used fluorescent densitometry to determine membrane tether radius (12). The measurement can be quickly performed on the stage of optical trapping system. We have validated the fluorescent densitometry method with SEM. The tether radii determined in our study are in the range of tether radii of other cells measured using SEM. Plasma membrane tension of DRG neurons determined by the optical trapping technique in this study is in the same magnitude, but higher than the measured values by using the micropipette aspiration method in our previous study (11). A possible factor contributing to the higher values of the measured plasma membrane tensions of DRG neurons in this study is the much higher sensitivity of the optical trapping technique in comparison with the micropipette aspiration method. In addition, the optical trapping technique has no requirement of cell morphology but the micropipette aspiration method would not be highly accurate if a testing cell is not morphologically in a perfectly round shape, and DRG neurons in cultures are not perfectly round. Therefore, the values of plasma membrane tensions measured should be more accurate in this study.

The relatively low membrane tension of DRG neurons may be partially due to the presence of a large amount of membrane reservoirs formed by caveolae and other membrane invaginations. The presence of these membrane reservoirs was shown to be able to buffer plasma membrane tensions in other cell types (2, 8). The presence of large membrane reservoirs in DRG neurons was suggested by our previous study showing that DRG neuron surface areas could be substantially increased under osmotic swelling (11). The low plasma membrane tensions of a cell could also be due to weak plasma membrane-actin interaction. A previous study has shown that cortical neurons in culture have low plasma membrane tension of ∼16 pN/μm (7), and this low plasma membrane tension indicates very weak plasma membrane-cytoskeleton interaction because the membrane tension in these cells was near the tension of pure lipid bilayer membranes without cytoskeleton (15). In contrast, plasma membrane tensions in our cultured DRG neurons are severalfold higher than the pure lipid bilayer membranes, suggesting that in DRG neurons there are significant interactions between plasma membranes and cytoskeleton. The significant contribution of plasma membrane-cytoskeleton interaction to DRG neuron plasma membrane tension is also evidenced by our finding that plasma membrane tension was significantly reduced when these cells are treated with CD to disrupt actin cytoskeleton. In this study we also show that DRG neuron membrane tension and membrane stiffness are significantly increased after using MβCD to sequester membrane cholesterol. This result is consistent with a previous study demonstrating increased plasma membrane tension and membrane pending stiffness of fibroblast cells after cholesterol depletion by MβCD (19). Alternatively, changes in cholesterol content may affects adhesion between the plasma membrane and the cortical cytoskeleton, which in turn affects plasma membrane tensions. Cholesterol is known to act as a bidirectional regulator of membrane stiffness in a temperature-dependent manner and its presence in plasma membranes maintains membrane fluidity at lower temperatures. Our experiments were performed at a temperature much lower than the physiological condition of 37°C. This may be a factor contributing to the increased membrane bending stiffness and membrane tension in DRG neurons after MβCD treatment.

We have previously shown that plasma membrane tension has a profound impact on Piezo2-mediated mechanical responses (11). It would be interesting to know in the future whether plasma membrane tensions of primary afferents may be altered under pathological conditions to impact their sensory functions such as the sense of touch and pain.

Author Contributions

J.G.G. designed research; and H.K. and J.G.G. performed research, analyzed data, and wrote the article.

Editor: Joseph Falke.