Can a Bayesian Belief Network Be Used to Estimate 1-year Survival in Patients With Bone Sarcomas?

Abstract

Background

Extremity sarcoma has a preponderance to present late with advanced stage at diagnosis. It is important to know why these patients die early from sarcoma and to predict those at high risk. Currently we have mid- to long-term outcome data on which to counsel patients and support treatment decisions, but in contrast to other cancer groups, very little on short-term mortality. Bayesian belief network modeling has been used to develop decision-support tools in various oncologic diagnoses, but to our knowledge, this approach has not been applied to patients with extremity sarcoma.

Questions/purposes

We sought to (1) determine whether a Bayesian belief network could be used to estimate the likelihood of 1-year mortality using receiver operator characteristic analysis; (2) describe the hierarchal relationships between prognostic and outcome variables; and (3) determine whether the model was suitable for clinical use using decision curve analysis.

Methods

We considered all patients treated for primary bone sarcoma between 1970 and 2012, and excluded secondary metastasis, presentation with local recurrence, and benign tumors. The institution’s database yielded 3499 patients, of which six (0.2%) were excluded. Data extracted for analysis focused on patient demographics (age, sex), tumor characteristics at diagnosis (size, metastasis, pathologic fracture), survival, and cause of death. A Bayesian belief network generated conditional probabilities of variables and survival outcome at 1 year. A lift analysis determined the hierarchal relationship of variables. Internal validation of 699 test patients (20% dataset) determined model accuracy. Decision curve analysis was performed comparing net benefit (capped at 85.5%) for all threshold probabilities (survival output from model).

Results

We successfully generated a Bayesian belief network with five first-degree associates and describe their conditional relationship with survival after the diagnosis of primary bone sarcoma. On internal validation, the resultant model showed good predictive accuracy (area under the curve [AUC] = 0.767; 95% CI, 0.72–0.83). The factors that predict the outcome of interest, 1-year mortality, in order of relative importance are synchronous metastasis (6.4), patient’s age (3), tumor size (2.1), histologic grade (1.8), and presentation with a pathologic fracture (1). Patient’s sex, tumor location, and inadvertent excision were second-degree associates and not directly related to the outcome of interest. Decision curve analysis shows that clinicians can accurately base treatment decisions on the 1-year model rather than assuming all patients, or no patients, will survive greater than 1 year. For threshold probabilities less than approximately 0.5, the model is no better or no worse than assuming all patients will survive.

Conclusions

We showed that a Bayesian belief network can be used to predict 1-year mortality in patients presenting with a primary malignancy of bone and quantified the primary factors responsible for an increased risk of death. Synchronous metastasis, patient’s age, and the size of the tumor had the largest prognostic effect. We believe models such as these can be useful as clinical decision-support tools and, when properly externally validated, provide clinicians and patients with information germane to the treatment of bone sarcomas.

Clinical Relevance

Bone sarcomas are difficult to treat requiring multidisciplinary input to strategize management. An evidence-based survival prediction can be a powerful adjunctive to clinicians in this scenario. We believe the short-term predictions can be used to evaluate services, with 1-year mortality already being a quality indicator. Mortality predictors also can be incorporated in clinical trials, for example, to identify patients who are least likely to experience the side effects of experimental toxic chemotherapeutic agents.

Introduction

Primary malignant bone cancers are rare, known to present late with advanced stage at diagnosis, and have a 12% to 47% 1-year mortality risk depending on healthcare resources [9, 30, 32, 43]. One-year mortality is a quality indicator for cancer diagnosis and treatment which correlates to stage at presentation [8, 25, 31]. Strategies to improve public awareness, primary care engagement, screening uptake, and access to diagnostic services aim to diagnose cancers earlier, thus at a lower stage to improve survival outcomes at 1 year in line with other European countries [19, 24]. We also are seeing 1-year mortality estimates for cardiovascular and neurologic conditions, with researchers developing mortality predictors and decision-support tools [4, 6, 27, 44].

Bone sarcomas are a challenge to treat and require complex multidisciplinary discussions to define individualized strategies to suit each patient. Bearing in mind the patient’s demographics, tumor characteristics, and resources, surgeons weigh the merits of chemotherapy, tumor resection margins, and limb reconstruction techniques [42]. When debating treatment a clinician’s survival estimate can be inaccurate, and we require better prognostication [15]. A decision-support tool can facilitate this process using evidence drawn from past patient outcomes [14]. Current staging systems estimate 5-year survival and lose discriminatory power with high-grade tumors, such as osteosarcoma [1, 11]. Five years may be considered a long time to evaluate the efficacy of changes in practice and delivery of service. We believe that short-term mortality is best suited to these tasks and there is no evidence-based statistical tool to predict 1-year mortality in patients with bone sarcomas.

Bayesian belief network modeling has been used to develop decision-support tools in various oncologic diagnoses [12, 14, 35–37]. The preferred statistical method for this is logistic regression [14], based on inferential statistics which tests the probability of the null hypothesis without considering prior knowledge or beliefs. A probability less than 5% (p < 0.05) is commonly used to deem sample data unlikely, in which case the alternative hypothesis is accepted. Bayesian methods use conditional probabilities to generate a ratio of likelihood of a specific hypothesis, a direct test. Bayesian belief networks readily identify relationships of conditional dependence, how and under what circumstances the value assumed by one factor depends on the value(s) of other factors. This is very intuitive and something we do every day as clinicians. Maki et al. [22] suggests that Bayesian belief network may overcome the limitations of current staging systems. Bayesian belief network models are useful in clinical situations because they maintain functionality in the setting of incomplete or outlying input data and have the ability to analyze large datasets. We believe the Bayesian belief network is well suited for analysis of variables inherent to the treatment of sarcomas because it is capable of codifying highly complex relationships into clear graphic representations that are easily understood.

With this in mind, we sought to (1) determine whether a Bayesian belief network could be used to estimate the likelihood of 1-year mortality in patients with primary sarcomas of bone using receiver operator characteristic (ROC) analysis; (2) describe the hierarchal relationships between prognostic and outcome variables; and (3) determine whether the model was suitable for clinical use using decision curve analysis.

Materials and Methods

The research was conducted at a tertiary referral center for orthopaedic oncology serving a population of approximately 18 million for patients with primary bone tumors. All patients with a newly diagnosed bone sarcoma who underwent treatment at the center were identified from the institution’s prospectively maintained database between 1970 and 2012. The study included 3499 patients, of whom 395 died within 1 year of diagnosis. Data extracted for analysis included patient demographics, tumor characteristics at diagnosis, and survival. Patients presenting for treatment of a local recurrence where the primary tumor had been treated previously were excluded from the study; similarly benign tumors (n = 2) or metastatic lesions (n = 1) and those lacking a tissue diagnosis (n = 3) were excluded from the final Bayesian belief network analysis leaving a total of 3493 patients.

Patients underwent staging (plane radiographs, MRI [from 1990 onward], CT of the thorax, and radionuclide scanning) at the time of diagnosis to identify the presence of metastatic disease and were treated according to national guidelines [17]. Staging was defined by the American Joint Committee on Cancer (AJCC) [1] and the classification of Enneking et al. [11]. Patients were routinely followed up in the outpatient clinic for 10 years, which comprised a review every 3 months for the first 2 years, with a chest radiograph performed at each visit [17]. Distant metastasis and local recurrence were treated on an individual basis, offering resection and adjuvant chemotherapy or radiotherapy where appropriate. The date and cause of death retrieved from our database were verified by the West Midlands Cancer Intelligence Unit, which records clinical data for all patients with cancer in England. We are confident that all patients in this study have accurate 1-year mortality data since mortality data were verified with the West Midlands Cancer Intelligence unit, and so no patients were lost to followup with respect to this endpoint.

A summary of the features was performed, comparing the prevalence of each feature in patients who died within 1 year with those of patients who survived. These features recorded either categorical (Table 1) or continuous data (Table 2). Eleven candidate features were chosen based on availability at the time of diagnosis and in most cases scientific evidence associating features with survival in patients with bone sarcoma (Table 3). Some of the candidate features were not suitable for the final model owing to greater than 30% missing data or detection bias (Table 3). The date of diagnosis was defined as the date of confirmed histologic diagnosis. Extremity tumors distal to the shoulder or hip were regarded as distal upper and distal lower, respectively, at the shoulder girdle as proximal upper, and at the pelvic girdle as proximal lower. Thus a lesion of the proximal humerus was categorized as proximal upper and those of the proximal femur as proximal lower. For analysis purposes, tumor size was recorded as the maximum dimension in centimeters in any plane on CT or MRI, at the time of diagnosis. Tumor grade and stage were recorded after radiologic and histologic investigations and patients were managed through a multidisciplinary team.

Table 1.

Categorical variables dichotomized by status at 1 year from diagnosis

Category	Alive	Dead	Significance
Sex
Female	1286	162
Male	1812	233	0.850
Grade
High	2311	326
Intermediate	314	60
Low	470	8	0.001
Location
Head and neck	18	2
Lower extremity	1922	199
Pelvic girdle	515	129
Upper extremity	427	44
Upper trunk	211	20	0.001
Metastasis at diagnosis
No	2750	261
Yes	348	134	0.001
Pathologic fracture
No	2727	308
Yes	371	87	0.001

The sum of patients does not always equate to 3493 owing to missing data; a chi-square analysis was performed for each variable; significance is reported for each univariate analysis.

Table 2.

Distribution of continuous variables in patients alive or dead at 1 year after diagnosis

Variable	Alive (interquartile range)	Dead (interquartile range)
Age of patient* (years)	22 (14–17)	43 (18–67)
Size of tumor* (cm)	9.5 (7–13)	12 (9–17)
Time to metastasis* (days)	472 (271–826)	133.5 (35–213)
Time to local recurrence* (days)	514 (317–917)	177.5 (109–232)

Median values reported; comparison of size is limited by missing data (49%); Mann-Whitney U test was performed on the distribution of each variable; *p < 0.05.

Table 3.

Description of candidate features selected for the final analysis

Candidate feature	Variables	Outcome
Age	Continuous (years)	Included in analysis
Gender	Male or female	Included in analysis
Size	Continuous (cm)	51% missing data; included in analysis with “missing category”
Location	Five categories (pelvic girdle, lower or upper extremity, upper trunk, and head and neck)	Included in analysis
Grade	High, intermediate, low	Included in analysis
Alkaline phosphatase	Continuous	36% missing data; excluded owing to investigation bias
Metastasis at diagnosis	Yes or no	Included in analysis
Pathologic fracture at diagnosis	Yes or no	Included in analysis
Diagnosis	46 histologic diagnoses	Excluded from analysis owing to number of histologic subtypes
Site	85 variants	Subcoded to location category
Status at 1 year after diagnosis	Alive or dead	Included in analysis
Year of diagnosis	Calendar year	7% missing data; excluded from analysis

The proportion of missing data is quantified.

We developed a Bayesian belief network model for bone sarcoma data. Before model development, 20% of the entire dataset was extracted to an independent test set using R^© Version 3.0.2 (R Foundation for Statistical Computing, Vienna, Austria). The proportion of patients surviving longer than 1 year (88%) was kept equal between sets. This process resulted in a bone sarcoma training set containing 2794 records and a test set containing 699 records. The Bayesian belief network model was developed in a manner similar to that previously described using commercially available machine learning software (FasterAnalytics™; DecisionQ, Washington, DC, USA) [12]. Briefly, all 11 variables (features) were considered as candidate features for inclusion in the model. We used equal-area binning based on prior distributions learned from the training set. In an effort to balance goodness-of-fit against robustness, a parsimony metric was used to reduce the risk of overfitting the final model to the training data. Using a stepwise process, unrelated and redundant features were pruned from the preliminary models to produce the final model.

To account for missing data in the training set (Table 3), we used a passive, truncation-based imputation algorithm [3]. We imputed values for features in which missing data represented less than 30% of the total record count and for which there was no adequate substitute feature. The imputation algorithm was applied to eight features in the Bayesian belief network model (patient age, tumor size, tumor grade, metastasis, location, fracture, sex, and inadvertent excision), which was trained to estimate the likelihood of survival 1 year after diagnosis by discriminating two possible outcomes (death within 1 year: yes or no). Because Bayesian belief networks can be used to describe relationships of conditional dependence, for example, how the value of one feature depends on the value(s) of other features, the hierarchal relationships between features can be displayed graphically. For this study, prior distributions (the value or values each feature is likely to assume under various circumstances) were estimated from the training set and thus were not specified a priori. Unrelated and redundant features were pruned to generate the final model. We performed validation using the test set containing the 699 records not used for model development and calculated the area under the ROC (area under the curve [AUC]) to assess accuracy of the model. Validation was considered successful if the AUC was greater than 0.7 and was determined a priori. To determine the relative importance of each first-degree associate in estimating the likelihood of 1-year survival, we first calculated each feature’s contribution to overall AUC by omitting each, in turn, and performing validation using the holdout set, as described previously. To estimate each first-degree associate’s relative importance, we ranked each according to its contribution to the overall AUC and divided by the lowest value.

A decision curve analysis evaluates whether a given model is suitable for clinical use. The analysis tests the consequences of a false positive or false negative result [14, 41]. We constructed decision curves with the intention to treat based on survival at 1 year generated from the Bayesian belief network. The graph plots a range of threshold probabilities against net benefit. The threshold probability is the probability estimate (from model) that would cause a clinician to procrastinate over treatment strategies, for example, in a skeletally immature patient whether to use allograft reconstruction, a growing prosthesis, or a conventional endoprosthesis based on the invasiveness of surgery, rehabilitation, survival estimate, and growth potential. It is the point at which one becomes indecisive regarding whether to offer a particular therapy. Thresholds are clinician-, patient-, and situation-specific and the decision curve analysis evaluates model performance over a range of threshold probabilities [14]. Net benefit is defined as a single patient who duly receives an appropriate treatment based on the model output [41].

Results

The clinical data for 11 candidate features were encoded in a Bayesian belief network to estimate the probability of death within 1 year of diagnosis. Based on the network structure there are five first-degree associates related to survival at 1 year (Fig. 1). Inadvertent excision of the tumor before histologic diagnosis was a second-degree associate, conditional to grade and pathologic fractures. Similarly, patient’s sex and tumor location were second-degree associates which have an indirect relationship with outcome at 1 year. We successfully generated a predictive model that can be used as a clinical decision-support tool. Model accuracy was determined by cross validating the training (n = 2794) and test sets (n = 699) to calculate the area under the ROC (AUC = 0.767; 95% CI, 0.72–0.83). The AUC quantifies the discriminative ability, or accuracy, of the model. The model performs well when classifying the probability that a patient who died within 1 year has a higher predicted probability of death compared with a patient who did not die [7].

Fig. 1.

The Bayesian belief network structure defines five first-degree associates that are directly related to the outcome (line); second-degree associations have an indirect relationship with the outcome (dotted line). Only 4.2% of patients underwent an inadvertent excision and the prevalence of synchronous metastasis or pathologic fracture was 13.98% and 13.57% respectively.

First-degree associates to death at 1 year were: the presence of synchronous metastasis, increasing age of the patient, larger tumor size, higher histologic grade, and presentation with a pathologic fracture (Fig. 1). To estimate each first-degree associate’s relative importance, we ranked each according to its contribution to the overall AUC and divided by the lowest value (pathologic fracture). In doing so, we established the hierarchal relationship of the variables with outcome at 1 year. Metastasis at diagnosis had the largest influence (6.4 times greater than pathologic fracture) followed by increasing age (3), increasing tumor size (2.1), histologic grade (1.8), and last, the presence of a pathologic fracture at diagnosis (1).

To clarify, because we are not testing the null hypothesis in the classic sense, we do not calculate a p value. Models such as the Bayesian belief network presented in this study are evaluated using measures of accuracy and classification ability (ROC analysis), which contains 95% CI estimate as a measure of uncertainty, and by decision curve analysis. Ideally, these metrics would be applied to a unique “holdout set,” as we have done, or an external validation set, which will be the focus of further studies.

With a trained and tested model, we can add evidence, given knowledge of a specific case, to generate a personalized prediction of mortality risk. For example, a 33-year-old patient with a 12-cm tumor of high histologic grade and metastasis has a 79.1% probability of surviving 1 year. Using the model, all potential first-degree associate configurations and survival predictions can be tabulated. This contingency table can be easier to interact with than a web-based decision support tool (Table 4). Overall survival estimates, from 120 combinations of associate features, ranged from 35.6% to 99.7%. It is clear that metastasis at diagnosis and increasing age have the greatest discriminatory power (Table 4).

Table 4.

Inference table based on four first-degree associates

Inferential examples	Age (years)	Grade	Metastasis	Size (cm)	Mortality risk
1	< 14	High	None	< 7	1.5%
2	14–23	High	None	< 7	1.8%
3	24–51	High	None	< 7	2.2%
4	> 51	High	None	< 7	7.7%
5	24–51	Intermediate	None	< 7	2.3%
6	> 51	Intermediate	None	< 7	5.8%
7	24–51	Low	None	< 7	0.3%
8	> 51	Low	None	< 7	0.7%
9	14–23	High	Yes	< 7	6.6%
10	< 14	High	None	7–9.9	3.6%
11	14–23	High	None	7–9.9	4.5%
12	24–51	High	None	7–9.9	5.4%
13	> 51	High	None	7–9.9	17.3%
14	24–51	Low	None	7–9.9	0.8%
15	> 51	Low	None	7–9.9	1.6%
16	< 14	High	Yes	7–9.9	12.4%
17	14–23	High	Yes	7–9.9	15.0%
18	24–51	High	Yes	7–9.9	17.6%
19	> 51	High	Yes	7–9.9	44.0%
20	< 14	High	None	10–15	4.4%
21	14–23	High	None	10–15	5.5%
22	24–51	High	None	10–15	6.6%
23	> 51	High	None	10–15	20.6%
24	> 51	Intermediate	None	10–15	16.0%
25	24–51	Low	None	10–15	1.0%
26	> 51	Low	None	10–15	2.0%
27	< 14	High	Yes	10–15	14.8%
28	14–23	High	Yes	10–15	17.9%
29	24–51	High	Yes	10–15	20.9%
30	> 51	High	Yes	10–15	49.2%
31	< 14	High	None	> 15	8.0%
32	14–23	High	None	> 15	9.8%
33	24–51	High	None	> 15	11.6%
34	> 51	High	None	> 15	32.6%
35	> 51	Intermediate	None	> 15	26.2%
36	24–51	Low	None	> 15	1.9%
37	> 51	Low	None	> 15	3.7%
38	14–23	High	Yes	> 15	29.0%
39	24–51	High	Yes	> 15	33.0%
40	> 51	High	Yes	> 15	64.0%

Estimates of probability ranged from 0.3% to 64.4%; examples with a case probability > 0.5% from the 120 inferential variations are presented, these describe the relationship of each interdependent feature and the likelihood of death within 1 year of diagnosis.

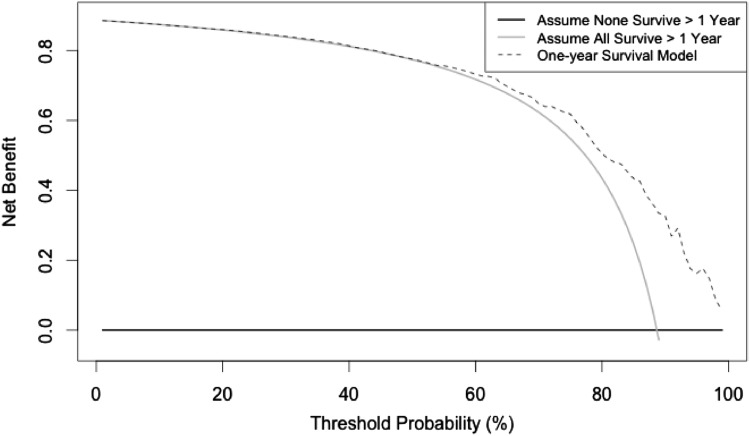
A decision curve analysis helps to weigh the clinical consequences of over- or underestimating mortality based on model output. The x-axis of the decision curve represents a threshold probability, which is the point at which one would be indecisive about offering a particular treatment. For example, clinicians have a low threshold for treating healthy patients, and a higher threshold for treating sick patients. Thresholds are patient-, clinician-, and situation-dependent, therefore it is important that decision curve analysis evaluates model performance over a broad range of clinically relevant threshold probabilities. The decision curve does not estimate the likelihood of 1-year survival (the Bayesian belief network serves this purpose), but it helps determine whether the Bayesian belief network model should or should not be used in certain situations. The current decision curve analysis shows the Bayesian belief network model is either equivalent, or better than, adopting a “treat all” philosophy, when basing treatment decisions. For illustrative purposes we discuss a middle-aged patient with a large high-grade pelvic tumor and metastasis (1-year mortality p = 42.3%). In light of this evidence the clinician and patient may deliberate treatment options, namely the role of chemotherapy, planned positive margins, and limb reconstruction to mobilize early and retain function, or hindquarter amputation to achieve local clearance. False optimism may result in a dying patient undergoing reconstruction of a limb which requires extensive recovery and rehabilitation, and subsequently may experience prosthetic complications that were, in hindsight, avoidable. False pessimism could result in an unnecessary amputation to achieve local clearance in a patient who lives more than a year with reduced mobility and the risk of soft tissue complications. Clinicians can accurately base treatment decisions on the 1-year model rather than assuming all patients, or no patients, will survive greater than 1 year (Fig. 2). For threshold probabilities less than approximately 0.5, the model is no better or no worse than assuming all patients will survive. Thus, as the threshold probability (probability estimate of survival) decreases the model loses benefit. Net benefit, defined as a single patient who duly receives the correct survival estimate based on the model output, was capped at 88.5%, which was the proportion of patients who survived more than 1 year. We can safely recommend the model be used for all threshold probabilities.

Fig. 2.

Net benefit is plotted on this decision curve analysis graph against threshold probabilities and shows the benefit of intervention based on decision to treat from a model output. Threshold probability (p^t), is the probability of survival at which the surgeon would recommend treatment. Net benefit = ([true positive count/n] − [false positive count/n]) × (p^t / 1 − p^t).

Discussion

Bone sarcomas are uncommon, difficult to treat, and result in patients tending to present late with advanced disease [43]. It is important to understand why these patients die early and predict those at risk [29]. The goal of this study is to provide a decision-support tool that will personalize the short-term survival risk of patients with a diagnosis of bone sarcoma to facilitate complex treatment decisions and align patients’ expectations. Bayesian belief networks are suited to this task, combining conditional probabilities and machine learning software to compute large datasets [14]. We showed that a Bayesian belief network can be used to predict 1-year mortality and identified the hierarchal relationship of the factors with increased risk of death. In order of importance these are: synchronous metastasis, patient’s age, tumor size, histologic grade, and presentation with a pathologic fracture. The model’s discriminative accuracy is good with an AUC of 0.76, comparable to other models [4, 21, 37]. Decision curve analysis supported the model for clinical use across all threshold levels; net benefit was higher for the model with threshold probabilities of survival greater than 50%.

The results of this study must be considered in the context of its limitations. The data were gathered from a single institution’s registry. This is a prospectively maintained database with consistent definitions and uniform assessment. Patients were referred for investigation of a suspected bone tumor, and the population studied is from a highly selective tertiary center and may not be representative of other populations. In this scenario overfitting can occur with Bayesian belief networks, which would cause the results of the decision curve analysis to be overly optimistic. As such, despite showing positive net benefit, the model must undergo external validation to show its applicability in other patient populations. Prospective external validation will be the focus of further research. We chose not to include certain variables in the model, and we cannot state whether their inclusion would have improved the predictive power of the final model. Alkaline phosphatase and lactate dehydrogenase were collected in patients with osteosarcoma and had greater than 30% missing data [10, 40]. Tumor necrosis after chemotherapy, the ability to downstage the tumor, and resection margins are key prognostic indicators [2, 3]. However, these are not available at the time of diagnosis and are not among the factors that can be modified to diagnose patients earlier. Future work could investigate treatment variables, to generate a modified prognostic score. The model does not differentiate by histologic subtype to enhance the usability of the final predictive model by end users and because of small subtype sample sizes. The final model output managed to generate five first-degree associates despite grouping all histologic subtypes together. This suggests that age, metastasis at diagnosis, and grade, for example, are more important than the specific tumor subtype. The contingency table provides sample survival estimates for low-grade tumors such as chondrosarcoma, which we know biologically behave differently than osteosarcoma or Ewing’s sarcoma (Table 4). We recognize that other methods of analysis, including proportional hazard regression, decision tree, or artificial neural network analysis, may be used to successfully estimate risk of death. However, the Bayesian belief network used for this analysis is particularly well suited for analysis of complex interactions intrinsic to the treatment of soft tissue tumors [13]. To our knowledge, however, this technique has not been applied to primary malignancies of bone. In addition, Bayesian techniques are particularly useful in the setting of missing input data common to registry data and clinical practice in general.

Bayesian belief networks are being used by clinicians to support diagnostic and treatment decisions [14, 35–37]. For the first time, we have a visual representation of the factors that are related to 1-year survival and their relationship to each other. Not only does this enhance the understanding of the factors that are important, the model can generate objective personalized mortality risks specific to a patient’s circumstances. This prediction can be used to support treatment decisions or counsel patients. In third-world countries, where chemotherapy lacks funding and amputation has negative perceptions, it can be used as a tool to educate patients [32]. In skeletally immature patients prognostic estimates can help guide whether a patient is suitable for a growing prosthesis, an invasive growing prosthesis, allograft reconstruction, or conventional limb salvage with an endoprosthesis [20, 39]. A hypothetical example would be where the clinician decides to neglect the growth potential of a child who has a poor prognosis and opts for an endoprosthesis that will provide short-term function and quality of life. The model could be incorporated in the selection process for targeted chemotherapy, or in the most advanced cases whether amputation or planned positive margins retain quality of life and autonomy [16, 45]. After external validation the model will be available as a web-based tool for clinicians to use [33].

The final Bayesian belief network we used in this study differs from studies reporting the factors related to long-term survival [3, 9, 10, 23, 26, 28]. Tumor location and sex were second-degree associates and histologic grade had less discriminatory power than metastasis, increasing age, and tumor size. Grade was only 1.8 times better than pathologic fracture at discriminating survival. Although we included all histologic subtypes (eg, osteosarcoma, Ewing’s sarcoma, and chondrosarcoma), three-quarters of the patients had high-grade tumors (2624 of 3493). Current evidence would struggle to discriminate between these high-grade malignancies [1, 11], highlighting the strength of this model which prioritizes the predictive value of other features. The final model adds to existing evidence which debates the prognostic value of pathologic fractures [5, 34, 38] .

Tumor stage is an important predictor of 1-year mortality in breast, prostate, colorectal, ovarian, and lung cancer [25]. The staging systems for bone sarcoma are the AJCC system [1] and that of Enneking et al. [11]. These are heavily dependent on histologic grade and metastasis at diagnosis to discriminate malignancies and estimate 5-year survival. The AJCC system stratifies patients in four risk groups with 5-year survival decreasing from 98% in Stage 1 to 30% in Stage 5 [1]. Nomograms also have been developed to try to predict survival [21]. Although generic survival systems after diagnosis of cancer exist, these lack validation in patients with bone sarcoma, limiting their use [4, 6]. The model described in this study will generate a specific mortality estimate that is more valuable to patients and clinicians than estimates of risk by hazard ratios or relative risk. Bayesian belief networks use conditional probabilities and machine learning software to solve complex interactions between variables and the outcome of interest. This statistical technique has been successfully applied to 1-year mortality for patients with primary bone sarcoma, and we showed that synchronous metastasis, increasing patient age, larger tumor size, higher tumor grade, and pathologic fracture are influential, in that order. To improve 1-year mortality, which is a proxy for advanced stage at diagnosis, we should focus on the modifiable variables such as tumor size [18, 19]. Strategies to raise public awareness, engagement with primary care doctors, and availability of diagnostic resources may reduce the stage at presentation and improve 1-year survival. Decision curve analysis supported use of the model as an adjunct to clinical decisions specific to the treatment of bone sarcomas. These may be related to the use of chemotherapy, surgical resection margins, or the most-suitable limb salvage procedure. Modeling tumor markers and treatment factors such as tumor necrosis and resection margins were beyond the scope of this study, but may provide better prognostication in the future. We believe cohesive models such as the Bayesian belief network described herein can be useful as clinical decision-support tools and, when properly externally validated, provide clinicians and patients with information germane to the treatment of bone sarcomas.